Finding Transition Pathways Using the String Method with Swarms of Trajectories

Abstract

An approach to find transition pathways in complex systems is presented. The method, which is related to the string method in collective variables of Maragliano et al. [J.Chem. Phys. 125:024106 (2006)], is conceptually simple and straightforward to implement. It consists in refining a putative transition path in the multi-dimensional space supported by a set of collective variables using the average dynamic drift of those variables. This drift is estimated on-the-fly via swarms of short unbiased trajectories started at different points along the path. Successive iterations of this algorithm, which can be naturally distributed over many computer nodes with negligible inter-processor communication, refine an initial trial path toward the most probable transition path (MPTP) between two stable basins. The method is first tested by determining the pathway for the C_7eq to C_7ax transition in an all-atom model of the alanine dipeptide in vacuum, which has been studied previously with the string method in collective variables. A transition path is found with a committor distribution peaked at 1/2 near the free energy maximum, in accord with previous results. Lastly, the method is applied to the allosteric conformational change in the nitrogen regulatory protein C (NtrC), represented here with a two-state elastic network model. Even though more than 550 collective variables are used to describe the conformational change, the path converges rapidly. Again, the committor distribution is found to be peaked around 1/2 near the free energy maximum between the two stable states, confirming that a genuine transition state has been localized in this complex multi-dimensional system.

I. INTRODUCTION

Conformational changes in large biomolecules are complex and slow processes taking place on timescales that are beyond the reach of brute force molecular dynamics simulations. Assuming that the conformational transitions occur between stable states implies that the long-time behavior of the system can be described in terms of transition rate constants. A central concept in the characterization of slow processes is the potential of mean force along the reaction coordinate describing the mechanism of the transition [1]. In practice, however, identifying a “good” reaction coordinate able to capture the microscopic mechanism that is responsible for the dynamical bottleneck separating the stable states in a complex system is challenging. To help resolve this issue, it is sometimes useful to use methods like umbrella sampling to map out the free energy landscape explicitly for a few promising coordinates. The latter can then be examined to reveal the mechanism and seek out the most plausible pathway between stable states (see [2], for example). Nonetheless, the efficiency of umbrella sampling methods scales poorly with the number of coordinates used, and their applicability becomes prohibitive when the dimensionality of the subspace is greater than 2 or 3. To reduce the computational cost, it is possible, as in metadynamics [3] or the adaptive biasing force (ABF) method [4] to bias the simulations on-the-fly within a given subspace spanned by a few coordinates to avoid spending time sampling irrelevant regions. All of these strategies, however, become inefficient if more than a few coordinates are explored. Ultimately, it is clear that a very large number of coordinates need to be considered in order to capture the mechanism governing conformational changes in proteins accurately. Thus, to determine optimal reaction coordinates for describing conformational transitions, one may need to explore pathways on a free energy surface of high dimensionality.

Many methods have been developed to determine proper transition pathways between stable states [5–15]. One class of techniques explores the reaction without making any a priori assumptions about reaction mechanisms. These techniques include transition path sampling (TPS) [9] and the original string method [10] (see also [16]). Important advances to TPS for diffusive systems have been transition interface sampling [17], and the development of efficient methods to sample double-ended paths [18]. Application of any of these path sampling methods to large, diffusive conformational transitions in proteins, however, remains a daunting task. Moreover, gaining physical insight from analyzing the pathway or ensemble of pathways found, such as determining the transition state ensemble, is often as computationally intensive as finding the paths themselves.

The recently developed string method of Maragliano et al. [12] is based on a different strategy. It aims to discover the minimum free energy path (MFEP) and the free energy along the path in the subspace corresponding to a large but finite set of coordinates, z, referred to as “collective variables”. The MFEP method builds paths onto the free energy surface as a function of the collective variables. This is advantageous because many of the stiff degrees of freedom that are often present in the potential energy surface governing the underlying microscopic dynamics can be integrated out. Since a path is a quasi one-dimensional construct in this high dimensional space, little efficiency is lost by increasing the number of collective variables to describe the transition. In contrast, each additional coordinate used in umbrella sampling requires the mapping of another dimension in the multi-dimensional free energy landscape. Moreover, if the set of collective variables used to describe the mechanism is large enough (i.e., all the relevant reaction coordinates are included), then the MFEP is also an isocommittor path. In that case, the transition pathway found is a well-ordered set of states representing the progress of the reaction from one basin to another.

In the original formulation of the string method in collective variables, the string, or parameterized curve representing the transition pathway, was evolved as a collection of images by estimating the mean force and the metric tensor at each image with constrained dynamics simulations. Here, we propose to evolve the string instead by using a swarm of trajectories initiated from each image to estimate the average drift of each image in collective variable space.

The theoretical framework is elaborated in Section II. The details of the computational models and the simulations are given in Section III. All the results are presented in Section IV, followed by a general discussion in Section V. The paper is concluded in Section VI with an outlook to future work.

II. THEORETICAL BACKGROUND

Consider a molecular system described by the Cartesian coordinates X ∈ ℝ^3N and the potential energy U(X). The equilibrium statistics of the system at a temperature T is given by the Boltzmann distribution,

$$P(\mathbf{X})=\frac{e^{-\beta U(\mathbf{X})}}{\int d\mathbf{X}{e}^{-\beta U(\mathbf{X})}}$$ (1)

where β = 1/k_BT is one over Boltzmann’s constant times the temperature. We are interested in characterizing the slow transitions between two basins corresponding to stable states defined by a set of n collective variables z = {z₁, z₂, …z_n}, such that n ≪ N. To this end, the most probable transition path (MPTP), loosely defined as the most probable sequence of time-ordered configurations visited during a transition between the two states, is a very useful and powerful concept. Defining the potential of equilibrium mean force for the collective variables z as,

$$e^{-\beta \mathcal{W}(\mathbf{z})}=\frac{\int d\mathbf{X}\delta (\mathbf{z}-{\mathbf{z}}^{\prime }[\mathbf{X}])e^{-\beta U(\mathbf{X})}}{\int d\mathbf{X}{e}^{-\beta U(\mathbf{X})}}$$ (2)

we assume that, over some coarse-grained timestep δτ, the collective variables evolve according to non-inertial Brownian dynamics on a free energy surface [19],

$$z_i(\delta \tau )=z_i(0)+\sum _j(\beta D_{ij}[\mathbf{z}(0)]F_j[\mathbf{z}(0)]+{\partial }_{z_j}{D}_{ij}[\mathbf{z}(0)])\delta \tau +R_i(0)$$ (3)

where D_ij is the diffusion tensor, F_i = −∂_i(z) is the mean force, and R_i(0) is a Gaussian thermal noise, with 〈R_i(0)〉 = 0, and 〈R_i(0) R_i(0)〉 = 2D_ijδτ. The timestep, δτ, is, in some sense, similar to the lag time used in Markov models [20, 21]. In principle, the value of an appropriate δτ for a specific system would need to be established.

It should be emphasized that no assumptions are made here about the underlying microscopic dynamics that govern the evolution of the Cartesian coordinates X(t) giving rise to the effective non-inertial dynamics of the collective variables z. In fact, the variables X(t) need not evolve with either Brownian or Langevin dynamics, and may instead evolve with Newtonian dynamics as is often the case in all-atom MD simulations of biomolecular systems with explicit solvent. In the present development, we forgo entirely the question of how the effective dynamics of z might emerge from the microscopic dynamics of X.

Let us now consider a path z(α) connecting two stable states in the system. The path is a list of collective variables parameterized by α, where α = 0 corresponds to the starting state and α = 1 corresponds to the final state. The MPTP has the property that a system initiated anywhere along the path connecting the two stable basins has the highest probability to evolve while remaining along the path. In Eq. 3, this condition on the MPTP is met when the thermal noise R_i is equal to zero (i.e., R_i is a Gaussian variable with zero mean so zero is its most probable value). Equivalently, this is realized when the system evolves according to,

$$z_i(\alpha )=z_i({\alpha }^{\prime })+\sum _j(\beta D_{ij}[\mathbf{z}(0)]F_j[\mathbf{z}(0)]+{\partial }_{z_j}{D}_{ij}[\mathbf{z}(0)])\delta \tau$$ (4)

If the diffusion tensor were independent of z, then the MPTP has the property that (DF)^⊥ = 0 everywhere along the path. We note that this path differs from one constructed such that F^⊥ = 0, which is not invariant upon a change of scale of the collective variables. Therefore, the diffusion tensor establishes the “metric” in the subspace of the collective variables.

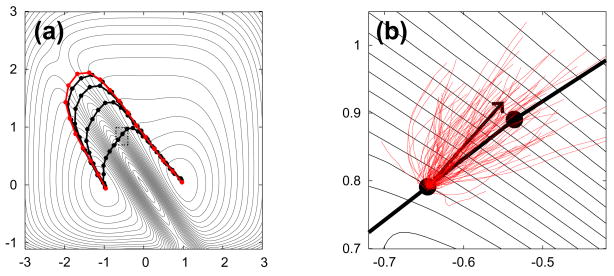
In practice, a path is represented by an ordered sequence of M discrete “images”, {z⁽¹⁾, z⁽²⁾, …, z^(M)}. An algorithm for converging an arbitrary initial path of M images toward the MPTP would evolve each image until the propagation only moved each image along the path. In other words, at convergence, there should be no movement of the images perpendicular to the path. One may note, however, that repeated propagation according to Eq. 4 will also move the images downhill toward the regions of low free energy, which is undesirable. A solution to resolve this issue is to impose a constraint on the distances between path images after each iteration [10]. For example, an equal Euclidean distance could be maintained between each image. Such a constraint prevents images from pooling together into the stable basins, allowing the reaction path to remain well-resolved, especially in high energy transition regions. This idea is an important insight of the string method [10, 12, 22, 23], and is called re-parameterization. A depiction of an algorithm to find the MPTP by evolving the images with re-parameterization is shown in Fig. 1.

Fig. 1.

The contours represent schematically a free energy surface in two dimensions and the lines with circles are paths and their discretized images on this surface. (a) This series of paths illustrate the iteration of an initial path until it converges to a most probable transition path (shown in red) as discussed in the text. (b) A detail of a portion of the path, which is outlined by the dashed rectangle in (a) showing a depiction of estimating the drift of an image with a swarm of trajectories. The images on this path have yet to converge because there is an overall drift of the short trajectories whose displacement is not solely along the current path. The thin red lines depict a swarm of trajectories initiated in the vicinity of one of the images. The thick black arrow deviating from the image indicates the direction of the average drift and points to where the image evolves before re-parameterization.

To evolve an initial path toward the MPTP, an approximation to the propagation corresponding to Eq. 4 is needed. A natural way to accomplish this is to use the average drift evaluated from an ensemble of unbiased trajectories of length δτ initiated from each image [24],

$$\begin{array}{l}\overline{\mathrm{\Delta }{z}_i(\delta \tau )}=\overline{z_i(\delta \tau )-z_i(0)}\\ \equiv \sum _j(\beta D_{ij}[\mathbf{z}(0)]F_j[\mathbf{z}(0)]+{\partial }_{z_j}{D}_{ij}[\mathbf{z}(0)])\delta \tau \end{array}$$ (5)

where it has been assumed that the thermal noise R_i in Eq. 3 cancels out by construction (averages over an ensemble of trajectories with constrained initial conditions are indicated as overline bars). The swarm-of-trajectories estimation method is depicted schematically in Fig. 1(b) for a segment of a path shown in Fig. 1(a). For each image, the system X is first thermalized with a bias potential restraint to keep the collective variables near z^(m), and then those restraints are released to generate the unbiased trajectory. In this way, a formal estimate of the average drift is achieved without any assumptions about the dynamical character of X(t). After evolution, the path is then modified to satisfy the re-parameterization conditions as in the original string method in collective variables [10, 12, 22, 23]. This process can be repeated any number of times to generate a collection of unbiased trajectories, each starting near one of the M images of the path.

In practice, one cycle of the swarm-of-trajectories string method for determining the MPTP consists of 5 steps:

1. Prepare a configuration with X coordinates for each of the M images of the path whose corresponding collective variables z are close to the value z^(m), for m = 1, M.

2. Generate an equilibrium (thermalized) trajectory for the each of the M images with z restrained around the value z^(m), for m = 1, M.

3. Using configurations from the trajectories generated in (ii) as initial configurations, run large numbers of short unbiased trajectories for each of the M images.

4. Use the resulting average displacement, $\overline{\mathrm{\Delta }{\mathbf{z}}^{(m)}}$, to determine the position in collective variable space of each of the M images.

   Re-parameterize the path to ensure that the images are equidistant in collective variable space.

This cycle should be repeated until convergence is reached. Details for how each of these steps are accomplished in specific applications will be addressed below.

The swarm-of-trajectories string method for evolving the images along the path is based upon the following observation. Because the collective variables obey the BD dynamics via Eq. 3, the converged MPTP has the property that ${\overline{\mathrm{\Delta }\mathbf{z}}}^{\perp }=0$. In effect, once the path described by this condition has been determined, it traces the trajectory that the overdamped dynamics of the variable z follow after starting at the saddle point without the random kicks caused by the thermal noise. From this point of view, the MPTP corresponds to the zero-temperature path on the free energy surface (z), though the evolution of the degrees of freedom, X, of the all-atom system is nonetheless taking place at a finite (non-zero) temperature. This may affect the convergence. However, since the algorithm is working in the subspace of the collective variables where the free energy landscape is expected to be significantly smoother than the potential energy, U(X), getting trapped in local minima may not be a critical issue.

III. COMPUTATIONAL DETAILS

1. Alanine dipeptide in vacuum

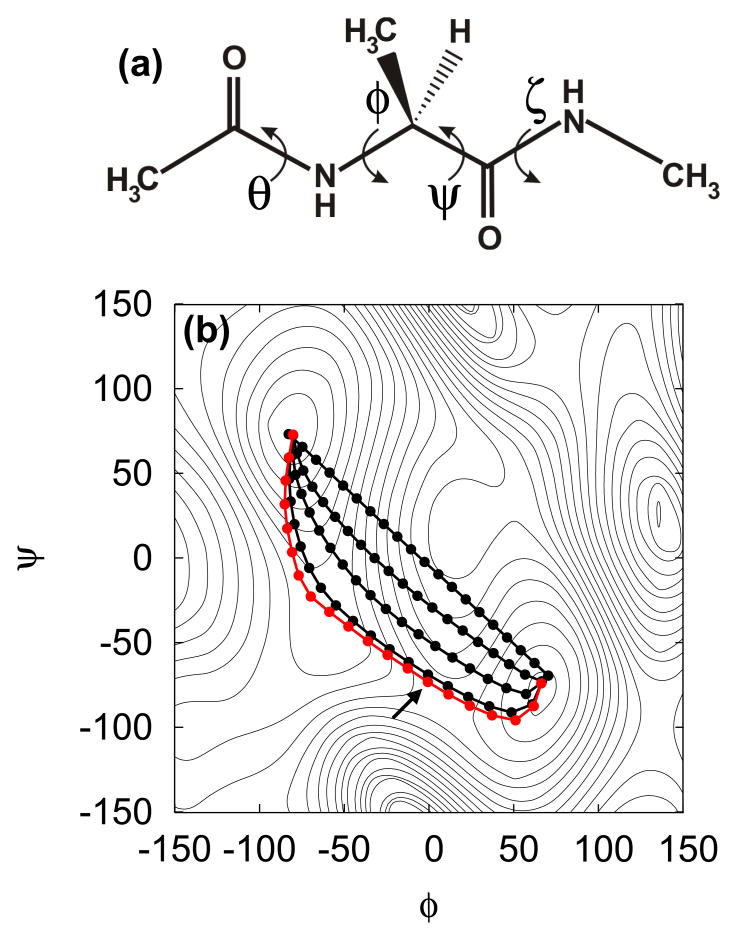
The structure of alanine dipeptide is shown in Fig. 2(a). For this system, all calculations were performed using the CHARMM simulation program [25] and the CHARMM22 force field without the CMAP correction [26]. Langevin dynamics trajectories were generated with a uniform friction coefficient of 10.0 ps⁻¹ on all atoms at 300 K. The simulations were run in vacuum and a dielectric constant of 1 was used. When needed, harmonic dihedral restraints with a force constant of 1000 kcal/mol/rad² were applied using the MMFP module. A timestep of 2.0 and 0.5 fs were used during the free and restrained simulations, respectively. The four dihedral angles φ, ψ, θ, and ζ, indicated in Fig. 2(a), were used as collective variables to describe the path, following [12].

Fig. 2.

(a) Structure of the alanine dipeptide molecule and the dihedral angles used in describing the path. (b) The projection onto the φ − ψ plane of the pathway described by the 4 collective variables (φ, ψ, θ, and ζ in panel (a)) for the C_7eq-C_7ax transition of the alanine dipeptide. The red curve shows the position of the converged pathway and the arrow indicates the position of the transition state/free energy maximum along this path (see Fig. 3). The contour lines are an adiabatic map in φ − ψ space.

An initial path in dihedral space was created by linearly interpolating 20 images between the two stable states defined by (φ, ψ, θ, ζ) = (−82.7, 73.5, 1.6, −4.3) for C_7eq and (φ, ψ, θ, ζ) = (70.5, −69.5, −0.8, 5.7) for C_7ax. Though the stable states were defined as in [12], their precise definition is not expected to be critical since the end-points were allowed to move during the relaxation of the path. Due to the simplicity of the system, the configurations (in Cartesian coordinate space) of alanine dipeptide corresponding to the collective variables along the initial path were built using the internal coordinates (IC) module in CHARMM with dihedral angles fixed at the interpolated values along the path. This straightforward procedure is convenient here because the simulated system is a small molecule in vacuum, though a restrained simulation would normally be required to prepare the atomic coordinates, X, of a system near the target collective variable values. Each of the prepared configurations was then minimized with dihedral restraints and thermalized with Langevin dynamics.

Each iteration of the path involved the following simulation protocol: (i) construct the dipeptide from internal coordinates such that the dihedral angles are close to the target collective variables of the current path and perform 1000 steps of restrained minimization followed by 10000 steps of a restrained Langevin simulation to thermalize the system; (ii) run 50000 steps of restrained dynamics; (iii) generate 250 short 20 step unbiased trajectories with no restraints initialized from configurations taken from the restrained equilibrium run in the previous step; (iv) update the position of the images using the average drift of the swarm of trajectories; and (v) re-parameterize the path. Step (v) involved a linear re-parameterization of the path (see Eq. 49 and Eq. 50 in [12]). The path was relaxed for 100 iterations following this procedure.

The committor distributions [27, 28] along the transition path of alanine dipeptide were calculated as follows. The committor, p_A, was defined as the probability that a given configuration, with initial velocities averaged over a Gaussian distribution, commits to basin A defined as having a dihedral angle φ< 0. A set of independent initial configurations was first obtained by running a restrained MD simulation at values of ((φ, ψ, θ, ζ) corresponding to a target position along the path. One thousand initial configurations were extracted from this restrained trajectory every 1000 steps. A hundred trajectories of 500 steps were run from each configuration. Values of the committor, p_A, were then calculated and binned into a histogram.

2. Two-state elastic network model of NtrC^r

A two-state elastic network model to represent the allosteric protein domain NtrC^r was constructed as follows. Each residue of the protein was represented by a single particle (e.g., the carbon α position of the residue). For a protein of N residues, a configuration would therefore be described by the Cartesian coordinates X = (x₁, x₂, …, x_N). The energetics of the model were governed by:

$$U(\mathbf{X})=-\frac{1}{{\beta }_m}ln(exp(-{\beta }_m{U}^{\text{A}}(\mathbf{X}))+exp(-{\beta }_m{U}^{\text{B}}(\mathbf{X})))+U^{\text{R}}(\mathbf{X})$$ (6)

Here, U^A(X) and U^B(X) are the (Tirion) [29, 30] elastic network model energies of each stable state:

$$U^{\text{A},\text{B}}(\mathbf{X})=\frac{1}{2}{k}^{\text{A},\text{B}}\sum _{ij}^N{D}_{ij}^{\text{A},\text{B}}{(\mathrm{\Delta }{\mathbf{x}}_{ij}-\mathrm{\Delta }{\mathbf{x}}_{ij}^{\text{A},\text{B}})}^2$$ (7)

where Δx_ij = |x_i − x_j|, k^A and k^B are the elastic network model force constants for each state and $D_{ij}^{\text{A}}$ and $D_{ij}^{\text{B}}$ are the contact matrices given by:

$$D_{ij}^{\text{A},\text{B}}=\{\begin{array}{cc}1,& \mathrm{\Delta }{\mathbf{x}}_{ij}^{\text{A},\text{B}}<d^{\text{A},\text{B}}\\ 0,& \text{otherwise}\end{array}$$ (8)

The contact matrices indicate that only pairs of residues within a certain radius, d^A for state A and d^B for state B, should be held harmonically around the target distances, $\mathrm{\Delta }{\mathbf{x}}_{ij}^{\text{A}}$ and $\mathrm{\Delta }{\mathbf{x}}_{ij}^{\text{B}}$. For our model, we took the target distances to be those of the alpha carbon positions of the experimentally determined structures (Fig. 4). The first term in equation 6 therefore exponentially mixes two harmonic basins to create a two-state system with a Boltzmann weighting in the manner of [31]. The parameter, β_m, modulates the height of the barrier between the two states, and is not to be confused with the actual temperature of the system. Following [32], we modified the elastic force constants constants, k^A,B, to reduce the unphysical strain imposed by the elastic network model framework on large amplitude conformational changes (see below).

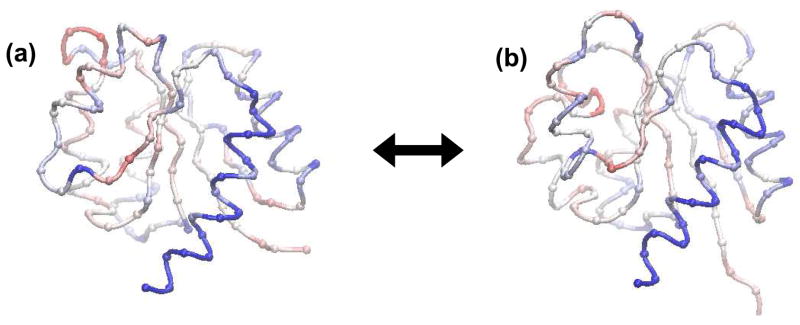
Fig. 4.

The inactive (a) and active (b) conformations of the nitrogen regulatory protein C receiver domain (NtrC^r). The beads represent the positions of the alpha carbons along the backbone and correspond to the coarse-grained locations of the residues in the two-state elastic network model. The coloring represents the average elastic strain energy per residue (see text) on a blue-white-red scale where blue represents residues with a low strain energy and red represents residues with a high strain energy. The bulk of the conformational transition takes places in the upper left region of the protein.

The final term in Eq. 6 is the repulsive potential

$$U^{\text{R}}(\mathbf{X})=\epsilon \sum _{ij}^N{\left(\frac{\sigma }{\mathrm{\Delta }{\mathbf{x}}_{ij}}\right)}^{12}$$ (9)

where ε modulates the strength of the repulsion and σ controls its length scale. This term represents the hard core repulsion between different residues.

The dynamics of the two-state elastic network model was propagated with Langevin dynamics at a temperature of 300 Kelvin with a uniform mass and friction of 100 AMU and 30 ps⁻¹, respectively, per coarse-grained particle. The elastic network force constants, k^A and k^B, were set equal and defined, according to [32], as site-dependent force constants, k_ij, such that $k_{ij}=min\{{\epsilon }_k/{(\mathrm{\Delta }{\mathbf{x}}_{ij}^{\text{A}}-\mathrm{\Delta }{\mathbf{x}}_{ij}^{\text{B}})}^2,0.2\text{kcal}{\text{mol}}^{-1}{Å}^{-2}\}$ where ε_k was taken to be 0.5 kcal/mol. The carbon alphas of the averaged NMR structures, Protein Data Bank ID’s 1DC7 and 1DC8, were used as reference states for the contact matrices, $D_{ij}^{\text{A}}$ and $D_{ij}^{\text{B}}$, respectively, and d^A = d^B = 11.5 Å. The parameters, ε and σ, for the hard core repulsion term, U^R, were chosen to be 1 kcal/mol and 2.5 Å, respectively. The timestep was taken to be 2.5 fs when the system was restrained and 50 fs when the system was free. Finally, the exponential mixing coefficient, β_m, was taken to be 0.005.

An initial path in collective variable space was created by linearly interpolating 50 images between the two stable states defined by a set of 553 inter-residue distances. Due to the complexity of the conformational change involved in this system, initial structures along the path cannot be constructed in the same way as done with alanine dipeptide. Instead, the initial path for the conformational change in NtrC^r was prepared using a targeted simulation technique. The crystal structure (1DC7) was gradually pulled from one image to another along the initial pathway defined in collective variable space. For each image, 10000 steps of restrained dynamics with 100 kcal/mol harmonic restraints on each of the 553 inter-residue distances was run using as an initial configuration the last configuration from the restrained dynamics run of the previous image.

The iteration of the path method followed a protocol similar to that of alanine dipeptide described above. (i) Thermalize an initial configuration (here, the initial configuration corresponded to the final configuration of the image from the last iteration) for 10000 steps with Langevin dynamics for each image; (ii) Run an additional 50000 steps of a restrained dynamics simulation at each of the images saving a configuration every 500 steps in preparation for the next step; (iii) Initiate 100 short (10 step) trajectories from the configurations saved in the previous step; (iv) update the position of the images using the average drift of the swarm of trajectories; and; (v) re-parameterize the path. The path was relaxed for 100 iterations following this procedure.

The committor distributions were also calculated in the same way as for alanine dipeptide. We ran 100 trajectories of 2000 steps from a configuration of interest each time with velocities drawn randomly from a Gaussian distribution. The initial configurations used were obtained from restrained dynamics run at various points along the path. A configuration was considered committed to basin A if its RMSD was less than 2 Å from the inactive NtrC^r conformation.

For comparison, the transition was also characterized in terms of the order parameter Δη, the difference in the fraction of the number of native contacts between the two stable states, Δη = η^A − η^B [33]. The free energy profile as a function of Δη was computed using 140 umbrella sampling windows with the harmonic bias potential $U_{\text{N}C}^i=\frac{1}{2}{k}_{\text{N}C}{(\mathrm{\Delta }\eta -\mathrm{\Delta }{\eta }^i)}^2$. Native contacts were defined with a cutoff of 6.5 Å using the experimental NMR structures. For the purpose of performing restrained simulations with Δη we define the fraction of native contacts as:

$${\eta }^{\text{A},\text{B}}=\frac{1}{{\eta }_{\text{tot}}^{\text{A},\text{B}}}\sum _{ij\in \text{NC}}{\eta }_{ij}^{\text{A},\text{B}}$$ (10)

where ${\eta }_{\text{tot}}^{\text{A},\text{B}}$ is the total number of contacts in each conformation, the sum is over all native contact pairs, and ${\eta }_{ij}^{\text{A},\text{B}}$ is the sigmoidal function:

$${\eta }_{ij}^{\text{A},\text{B}}=\frac{1}{1+exp((\mathrm{\Delta }{\mathbf{x}}_{ij}-\gamma \mathrm{\Delta }{\mathbf{x}}_{ij}^{\text{A},\text{B}})/w)},$$ (11)

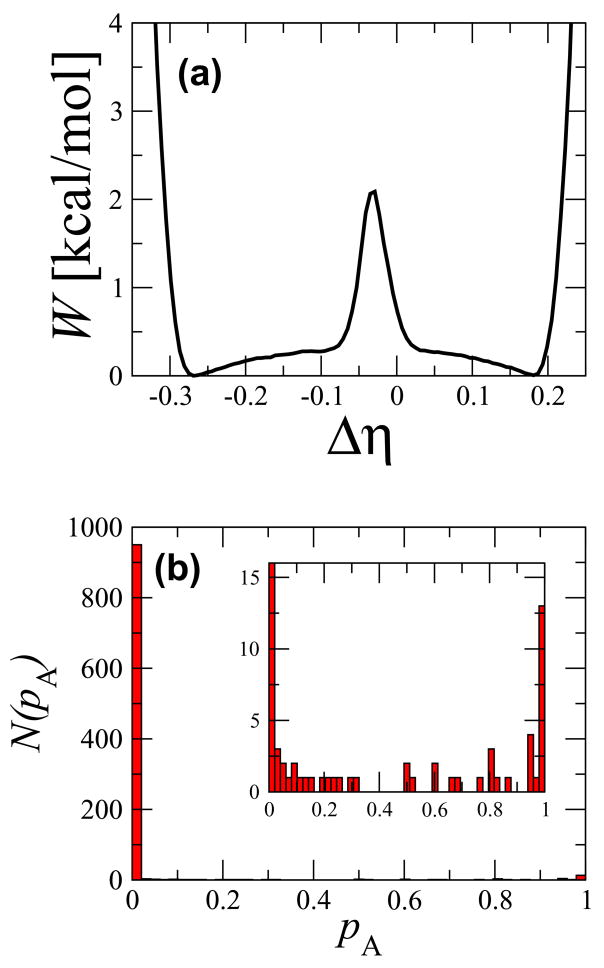
where γ = 1.2 and w = 0.1 Å. The windows ranged from values of Δηⁱ = −0.35 to 0.35 with k_NC = 50 kcal/mol. Different windows were combined with the weighted histogram analysis method (WHAM) [34]. The committor was calculated by running 100 short trajectories of 2000 steps initiated from 1000 independent configurations restrained to be at a value of Δη = −0.03 corresponding to the top of the free energy barrier in Fig. 6(a).

Fig. 6.

(a) Free energy as a function of the difference of the fraction of native contacts, Δη, between the active and inactive states. (b) The committor distribution for configurations restrained to be at the value of Δη corresponding to the maximum of the free energy barrier in (a). The inset shows the same distribution on a magnified y-axis scale.

IV. RESULTS

A. Application of the swarm-of-trajectories string method to the alanine dipeptide

First, the swarm-of-trajectories string method is illustrated for the C_7eq to C_7ax transition in the alanine dipeptide. The conformational transitions in the alanine dipeptide molecule, shown in Fig. 2(a), have been the subject of several previous studies [12, 35–37]. This is due, in part, to its biological relevance, but also to its simplicity. Of particular interest is the transition between the the C_7eq and C_7ax conformation, corresponding to two stable basins in the potential energy surface shown as a function of the φ and ψ torsion angles in Fig. 2(b).

Previous studies found that the φ and ψ angles are not, in fact, “good” reaction coordinates for describing the C_7eq-C_7ax transition. In other words, a dynamic description based on these two angles φ and ψ alone is actually insufficient to correctly track down the dynamical progress of the system [35, 36]. The implication is that other degrees of freedom, which cannot be ignored, must be strongly coupled to the transition. In their study, Maragliano et al [12] found that the four dihedral angles φ, ψ, θ, and ζ, shown in Fig. 2(a), could describe the transition pathway dynamically. To make the comparison with their studies more transparent, we use the same choice of collective variables.

The swarm-of-trajectories string method was initiated from a linearly interpolated path and then iterated for 100 cycles to determine the MPTP between the C_7eq and C_7ax conformations. The resulting four dimensional transition pathway projected onto two dimensions is shown in Fig. 2(b). The free energy along the final converged path is shown in the top panel of Fig. 3. The estimate of the free energy along this path was obtained by integrating the total derivative of the free energy along the path [12]:

$$\begin{array}{l}\mathcal{W}(\mathbf{z}(\alpha ))-\mathcal{W}(\mathbf{z}(0))={\int }_0^{\alpha }\frac{d\mathcal{W}}{d{\alpha }^{\prime }}d{\alpha }^{\prime }\\ ={\int }_0^{\alpha }\sum _{i=1}^n\frac{d{\mathbf{z}}_i({\alpha }^{\prime })}{d{\alpha }^{\prime }}\frac{\partial \mathcal{W}(\mathbf{z}({\alpha }^{\prime }))}{\partial {\mathbf{z}}_i}d{\alpha }^{\prime }.\end{array}$$ (12)

Fig. 3.

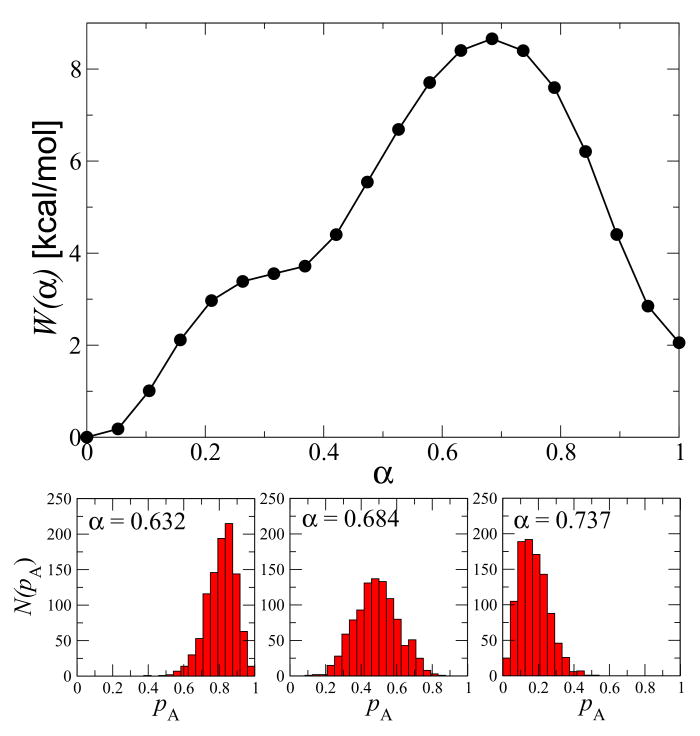
(Top panel) The free energy along the converged path for the C_7eq-C_7ax transition of the alanine dipeptide. (Bottom panels) Distributions of the committor, p_A, at three α positions near the free energy maximum.

In other words, the path free energy can be found as a sum over the product of the mean force at each image multiplied by the curvature of the path at that point. With no additional computational effort, the mean force can be estimated for each image during the restrained equilibration step using the displacement of the collective variables from their target positions along the path. This free energy estimation method is discussed in detail in [12]. We found that the path converged after 80 iterations because the fluctuations of the free energy along the path during the last 20 iteration cycles were small (i.e., within the size of the circles in Fig. 3).

To demonstrate that the final path is dynamically relevant, we calculated the committor distributions near the free energy barrier [27]. If the path is indeed an isocommittor path, then the distribution of the committor, p_A, along the path should move monotonically from 1 to 0 and the distribution of the committor for the image at the free energy maximum should characterize the transition state ensemble. This is shown in the bottom panel of Fig. 3. We note that a previous study found that only 2 dihedrals are necessary to describe this conformational change in alanine dipeptide (either φ and θ or ψ and θ [35]). As mentioned earlier, we chose 4 dihedrals as a proof of principle that this method can describe pathways with many collective variables. This demonstrates that a dynamically relevant path can be found even with the introduction of dynamically irrelevant collective variables.

B. Application of the swarms-of-trajectories string method to NtrC^r

To illustrate the swarms-of-trajectories string method in the case of a non-trivial multidimensional system, we determined the MPTP for a model of the nitrogen regulatory protein C receiver domain (NtrC^r), a two-state allosteric protein involved in bacterial signal transduction [38, 39]. Phosphorylation of an aspartate residue modulates the population equilibrium between the active and inactive conformations and atomic structures of both these conformations have been solved by NMR [39].

For the sake of simplicity, we use a coarse-grained two-state elastic network model of the protein such that each residue is represented by a single particle (the carbon α). The present model is constructed to incorporate the topological constraints arising from the connectivity of the polypeptide chain as well as the residue-residue core repulsion. The details of the model, described above, builds on previous work describing similar models [31, 32, 40–42]. Although such coarse-grained models are highly simplified caricatures of a protein, they provide a useful framework for understanding conformational changes. By construction, our model possesses some of the fundamental ingredients that are at the origin of the complexity of the atomic motions during the conformational change. This should be adequate for the purpose of illustrating the method with a non-trivial multi-dimensional system.

The two states of the NtrC^r elastic network model are shown in Fig. 4. The coloring scheme corresponds to the average strain energy per residue. The strain energy is a measure of the extent of inter-residue distance change during the conformational transition and is here defined as $s_{ij}={(\mathrm{\Delta }{\mathbf{x}}_{ij}^{\text{A}}-\mathrm{\Delta }{\mathbf{x}}_{ij}^{\text{B}})}^2$. This is also the quantity used to modulate the value the elastic force constants (see methods). The average strain energy of the ith residue is defined as Σ_js_ij/N_i where N_i is the number of residues having elastic interactions with residue i. The figure illustrates that the conformational change mainly occurs on the left side of the protein, the switching region.

A priori, string-based transition path methods remain effective even if a very large number of collective variables is used to describe the path in NtrC^r. Thus, we chose an exhaustive list of over 550 inter-residue distances to characterize the transition. The list of distances was taken to be the target distances in the two stable states, which differed by more than a cutoff value of ΔΔx in absolute value. That is, the intermolecular distance between residue i and j was included if $\mid \mathrm{\Delta }{\mathbf{x}}_{ij}^{\text{A}}-\mathrm{\Delta }{\mathbf{x}}_{ij}^{\text{B}}\mid >\mathrm{\Delta }{\mathbf{x}}_{min}$. Here, we took Δx_min = 5 Å, resulting in 553 distances.

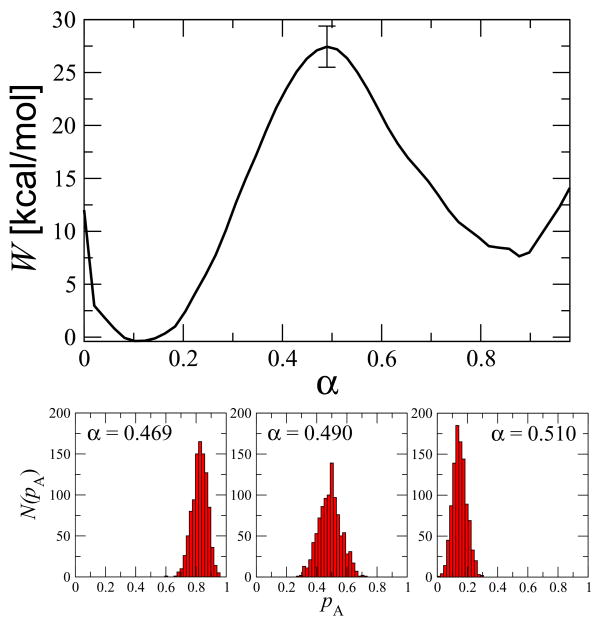
The free energy along the NtrC^r pathway is shown in the top panel of Fig. 5. The free energy barrier converged to ~ 30 kcal/mol from an initial value of ~ 400 kcal/mol resulting from the targeted simulation technique after 50 iterations. As a test of the dynamical relevance of the path obtained and the suitability of using a large set of inter-residue distances as appropriate reaction coordinates for describing the conformational change, we calculated the committor distribution, N(p_A), at several images along the converged string. The lower panel of Fig. 5 shows N(p_A) at three points along the path indicating that we have indeed found an isocommittor path. A large collection of inter-residue distances is therefore a good reaction coordinate for protein conformational changes, at least for the coarse-grained model studied here. Moreover, our modification of the original string method in collective variables still retains the ability to find isocommittor pathways in a complex system.

Fig. 5.

(Top panel) The free energy along the string averaged over the last 50 iterations. A representative error bar, corresponding to the standard deviation over these 50 samples, is shown at the free energy maximum. (Bottom panels) Distributions of the committor, p_A, at three α positions near the free energy maximum.

To illustrate the difficulty in finding a subset of dynamically meaningful collective variables in a multi-dimensional system, we tested the ability of the fraction of native contacts, η, a reaction coordinate that is commonly used in protein folding [28, 33], to describe the conformational change. Since we are studying the transition between two conformations of a protein, the collective variable we used was the difference in the fraction of native contacts between the two states, Δη. We began by computing the free energy, or potential of mean force, 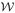(Δη), shown in Fig. 6(a). The free energy has a well-pronounced barrier separating two stable basins, though the maximum is much smaller than in Fig. 5. If Δη were indeed a good reaction coordinate for describing the conformational transition, then an ensemble of configurations restrained to be at the free energy maximum should have a committor distribution peaked around 0.5, indicating that they all belong to the dynamical bottleneck in the conformational transition. Instead, we find that the committor is mostly peaked at 0, with a few examples of values greater than 0 that are randomly distributed (Fig. 6(b)). This indicates that the difference in the fraction of native contacts is not a suitable reaction coordinate for describing this conformational change [28].

V. DISCUSSION

The string method with swarms of trajectories presented here is conceptually simple and straightforward to implement. Using the information from the average systematic drift of the collective variables from short trajectories, the algorithm progressively refines an initial trial path toward the most probable transition path (MPTP) between two stable basins. The method was illustrated with applications to conformational transitions in alanine dipeptide and to a two-state elastic network model of the allosteric nitrogen regulatory protein C receiver domain (NtrC^r). Calculated committor distributions confirm that genuine transition states were localized. In the applications, the CHARMM program was used to simulate alanine dipeptide and an in-house program was used to simulate the two-state network model. The main iteration cycle was driven via scripts external to the simulation programs, so that a number of MD package could be used to propagate the system. Furthermore, the method lends itself naturally to a distributed computing strategy, since it is based on a large number of independent asynchronous calculations that require very infrequent communications. From this point of view, the computational effort for relaxing a path is spent very effectively.

The swarms-of-trajectories string method exploits the natural BD time-evolution of z(t), which is constructed on-the-fly from the complete and unbiased dynamics of X(t). This provides a route to estimate both the average drift and the magnitude of the fluctuations:

$$\overline{\mathrm{\Delta }\mathbf{z}(\delta \tau ):\mathrm{\Delta }\mathbf{z}(\delta \tau )}=2\mathbf{D}\delta \tau$$ (13)

Thus, the swarm-of-trajectories can be used to estimate the first two moments of a local Gaussian approximation to the short-time propagator, P [z(τ), z^′(τ + δτ)], valid only in the neighborhood of z,

$$P_{\delta \tau }[\mathbf{z},{\mathbf{z}}^{\prime }]\propto exp\left[(\mathbf{z}-{\mathbf{z}}^{\prime }-\overline{\mathrm{\Delta }\mathbf{z}})·{(\overline{\mathrm{\Delta }\mathbf{z}:\mathrm{\Delta }\mathbf{z}})}^{-1}·(\mathbf{z}-{\mathbf{z}}^{\prime }-\overline{\mathrm{\Delta }\mathbf{z}})\right]$$ (14)

Clearly, a proper estimate of the propagator in the neighborhood of z will depend on the choice of δτ. As discussed in [24], δτ should be longer than the molecular relaxation time governing the fast initial relaxation processes of the system, but should not be so long that the curvature of the underlying free energy surface begins to be resolved. Evidence of the latter could be determined from monitoring the time evolution of the averages and standard deviations of different trajectories within a swarm. More systematic methods for choosing a proper δτ will be explored in future work.

One could imagine using a chain of such short-time propagators to evaluate the probability of different path realizations. Considering a given path of length τ = Mδτ, supported by M images at {z⁽¹⁾, z⁽²⁾, …z^(M)}, the probability of this path realization is proportional to

$${\mathcal{P}}_{\text{path}}[{\mathbf{z}}^{(1)},{\mathbf{z}}^{(2)},\dots {\mathbf{z}}^{(M)};\tau ]\propto P_{\delta \tau }[{\mathbf{z}}^{(1)},{\mathbf{z}}^{(2)}]\times P_{\delta \tau }[{\mathbf{z}}^{(2)},{\mathbf{z}}^{(3)}]\times \dots P_{\delta \tau }[{\mathbf{z}}^{(M-1)},{\mathbf{z}}^{(M)}]$$ (15)

By definition, the MPTP corresponds to the particular realization that maximizes [z⁽¹⁾, z⁽²⁾, …z^(M); τ], while asymptotically taking the time τ to infinity. It is in this sense that the MPTP corresponds to a noiseless path (effectively, at a temperature of “zero”). These considerations could be helpful to handle the contributions from paths deviating away from the MPTP, which are obtained by allowing finite temperature fluctuations of the string.

Lastly, it is worthwhile noting that there are similarities and differences between the present approach and the string method in collective variables introduced by Maragliano et al. [12], which largely inspired out efforts. From the applications presented in this work, particularly in the alanine dipeptide example, it appears that the MPTP found with the swarm-of-trajectories string method is similar to the MFEP, which would be found by the string method in collective variables. The underlying perspective of the two methods, however, is somewhat different. In particular, we are making the assumption that the collective variables effectively evolve according to overdamped non-inertial BD over some coarse-grained timestep δτ. This leads to Eq. 4 to evolve an initial path toward the MPTP. Such an assumption is not invoked in ref. [12], where a variational argument was used to derive the evolution equation for relaxing an initial path toward the MFEP (see section III in [12]). This led to Eq. 18 of ref. [12] to evolve an initial path toward the MFEP. The M tensor in the latter, which is evaluated as a local average, is not identical to the effective diffusion tensor D in Eq. 4, which is estimated from unbiased trajectories of length δτ. Therefore, it appears that the propagation of the images to relax the path in the two approaches is not exactly the same. More work will be needed to clarify this point further.

VI. CONCLUSION

An approach based on the string method in collective variables of Maragliano et al. [12] to determine transition pathways in complex systems was presented. This method progressively refines an initial trial path toward the most probable transition path (MPTP) between two stable basins by using the average drift of the collective variables, estimated on-the-fly via a swarm of short unbiased trajectories. The method was implemented and illustrated with applications to two non-trivial systems. In both cases, a genuine transition state region was localized, as demonstrated by committor distributions. This implies that, in principle, one may be able to initiate reactive trajectories from the transition state and perform TPS simulations [9]. Similarly, the converged, parametrized path along α could serve as a framework for other methods, such as the λ-interfaces in transition interface sampling [17], for calculating dynamical quantities

The string method with swarm-of-trajectories to determine the MPTP is conceptually simple and computationally efficient. During an iteration, the computations required for each image on the string can be distributed to separate compute nodes. From a practical point of view, the required iterative procedure can be implemented at a script level for any MD program, as long as the desired biasing restraints are available. The approach is flexible and a number of additional concepts and idea could readily be implemented. For example, in the spirit of the finite temperature string method [22], random kicks could be included to evolve the images during each iteration. This would allow the possibility of avoiding local minima, as well as sampling multiple transition pathways.

Our hope is that the present method will be useful in the study of conformational changes in large protein systems. More work will obviously be needed to refine practical and formal aspects of the method in real biomolecular applications. In particular, computational strategies to exploit the MPTP in the calculations of transition rates would be useful. Technical issues such as re-parameterization, finite-temperature evolution, exploring the dependence on the coarse-grained timestep, δτ, and parallel tempering, will also require additional efforts. Lastly, additional clarification of the physical significance of the path of maximum probability should help deepen our understanding of string-based methods.