Patterns of Muscular Strain in the Embryonic Heart Wall

Abstract

The hypothesis that inner layers of contracting muscular tubes undergo greater strain than concentric outer layers was tested by numerical modeling and by confocal microscopy of strain within the wall of the early chick heart. We modeled the looped heart as a thin muscular shell surrounding an inner layer of sponge-like trabeculae by two methods: calculation within a two-dimensional three-variable lumped model and simulated expansion of a three-dimensional, four-layer mesh of finite elements. Analysis of both models, and correlative microscopy of chamber dimensions, sarcomere spacing, and membrane leaks, indicate a gradient of strain decreasing across the wall from highest strain along inner layers. Prediction of wall thickening during expansion was confirmed by ultrasonography of beating hearts. Degree of stretch determined by radial position may thus contribute to observed patterns of regional myocardial conditioning and slowed proliferation, as well as to the morphogenesis of ventricular trabeculae and conduction fascicles.

Introduction

Spatial variation in cell proliferation is a fundamental mechanism in the morphogenesis of the embryonic vertebrate heart (Jeter and Cameron, 1971; Taber, 1998b). Location within the geometry of the developing heart may be a signal for slowed or arrested proliferation; cells along the inner surface slow or stop proliferation compared with cells on the outer surface (reviewed by Thompson et al., 2003), a pattern found also in mice (Sedmera et al., 2003). Furthermore, observed plasticity of initial withdrawal from the cell cycle suggests that preexisting genetic state or molecular environment of these cells may not be the only mediators of this spatial pattern of withdrawal, that differences in physical parameters across the wall may directly affect cell proliferation (deAlmeida et al., 2007). Physical parameters that vary significantly with position across the condensed wall of a contracting and expanding tube include stress, strain, and energy consumption (Omens, 1998; Denslow et al., 1999); particularly pertinent here are biological sensors transducing strain (Morgan and Baker, 1991; Palmieri et al., 2002; Hoshijima, 2006).

Early embryonic vertebrates hearts do not have a condensed homogenous myocardium. The initial departure from a thin-walled tube during development is the formation of a highly porous trabeculated layer (Sedmera et al., 2000). Because of the added variable of such lacunae within condensed tissue, it is not clear that the transmural pattern of strain dictated by a solid wall is also the pattern that exists in a trabeculated structure. While some mathematical modeling has analyzed such a porous wall (Yang et al., 1994), specifics of transmural strain variation have not been addressed. To investigate this question, we analyzed a simple two-dimensional (2D) mathematical model that suggests the limits of behavior for this type of structure. In a separate approach, we calculated the behavior of finite elements of an expandable 3D mesh approximating the tubular chick heart during contraction cycle. We present here the results of those analyses and correlation with regional strain assessed in fixed hearts by confocal microscopy of chamber dimensions and sarcomere spacing. Wall thickness changes in beating hearts were assessed by ultrasonography. Finally, regional variation in stretch was imaged by the distribution of cellular membrane leaks in variably stretched or contracted hearts.

Results

Orientation of Modeling and Experimentation

A 3D mesh diagram of a Hamburger and Hamilton stage (HH) stage 21 chick heart is shown in Figure 1a. The 2D transmural section chosen for analysis is shaded in Figure 1a and diagramed in 2D contracted state (Fig. 1b) and in two distinct expanded states, with solid wall (Fig. 1c), or with trabecular spaces (*, Fig. 1d). Cross-sectional wall area is held constant. With no allowance for trabeculae (case Fig. 1c), an increase of 7% along outer perimeter results in 18% increase along inner layer (red) and a decrease of some 12% in wall thickness at the ventricular apex. Introduction of trabecular lacunae that open during expansion (*, Fig. 1d) can reduce deformation along inner layers, in this case to 9%, and wall thickness, including lacunae, actually increases by 5–6%.

Fig. 1.

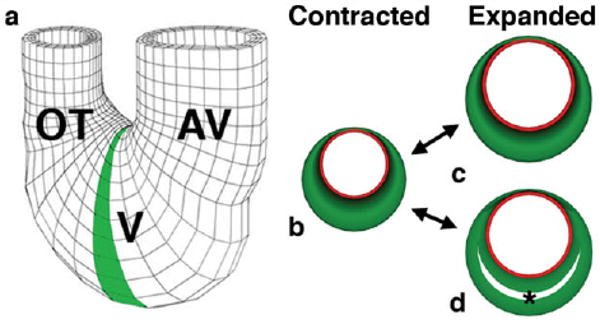
Orientation to models and problem. a: A three-dimensional (3D) mesh diagram of tubular chick heart exterior, showing atrioventricular canal (AV), ventricular loop (V) and outflow tract (OT). a,b: The 2D cross-sectional plane selected for further analysis is shaded (a), and diagramed in contracted state (b), with the subendocardial layer in red and the muscle cross-sectional area (green) held constant. c,d: Two plausible expanded states are shown: solid wall (c) or with trabecular spaces (d) (*).

Analysis of 3D Finite Element Model

A four-layer mesh model (Fig. 2) was constructed by connecting inner and outer contours of radial sectors of the looped U-shaped heart from confocal images from orthogonal sections of the stage 21 heart in systole. Computer simulation of expansion of this mathematical construct clearly show greater strain (red-shifted areas) along inner elements in both 2D sagittal cross-section (Fig. 2a) and in 3D representation of the posterior half-heart (Fig. 2b), with minimal strains in outer layers and intermediate strains in midwall layers. Strains were normalized at each point in the contraction/expansion cycle to equivalent total strain among all elements in the global model, so that color shift toward red represents increasing linear deformation (strain) of individual finite elements. It should be noted that no assumptions concerning passive or active material properties of such elements are required; they are simply connected lengths.

Fig. 2.

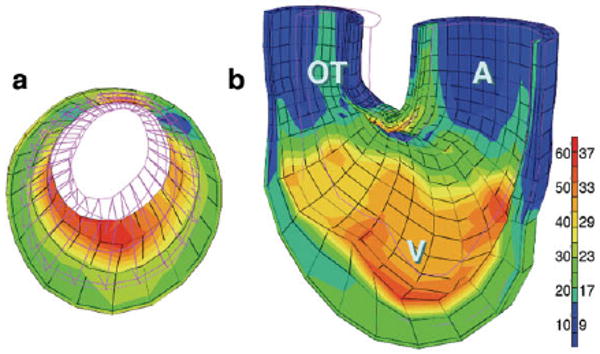
Finite element modeling of stage 21 chick heart with a four-layer mesh shows greater strain (red) along inner layers at maximum expansion. a: A two-dimensional (2D) section across ventricular loop (shaded in Fig. 1a). b: A 3D global mesh oriented as in Figure 1a, with anterior half removed to show interior surfaces. Scale shows percentage elongation of initially unloaded elements along left, with corresponding fractional shortening (as percentage) shown to right.

Analysis of 2D Lumped Model

Figure 3a,b diagrams expanded and contracted states respectively, for the three components of our 2D lumped model: concentric circular endocardial and epicardial perimenters (of radius R, r) and an intervening trabecular layer containing circular spaces of radius ρ. For a straight tube of incompressible muscle, the cross-sectional area occupied by muscle remains constant and variation of these three parameters during contraction must follow the equations developed in the Experimental Procedures section. The interdependency of fractional shortening of these three components, together with calculated change in wall thickness, can be plotted as shown in Figure 3c. Analysis of this fractional shortening (FS) map shows: (1) the strains of these four model components depend upon each other in a continuous, nonlinear manner; (2) subendocardial FS remains greater than subepicardial FS unless trabecular FS increases beyond an unrealistic level of 140% of either (blue zone); (3) for a given subendocardial FS (black curves), decreases in subendocardial FS correspond with increases in trabecular FS; (4) wall thickness actually increases with expansion across most of this map (red curves), until trabecular FS drops to approximately 50% of subendocardial FS, below which the wall would actually thicken during contraction. Comparison of these calculations from 2D modeling with chamber dimensions and sarcomere spacing in expanded and contracted chick hearts are presented below.

Fig. 3.

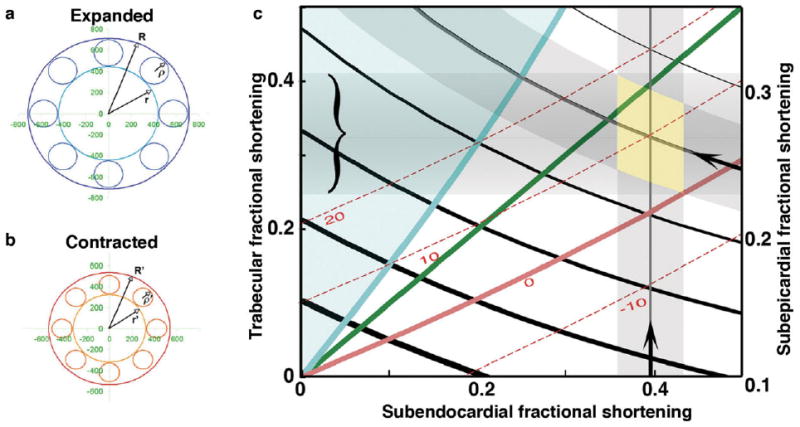
a,b: The circular approximation lumped model of a cross-section of a trabeculated myocardial tube consists of three elements represented in expanded state (a) and contracted state (b) as follows: the outer (subepicardial) radius R, R', inner (subendocardial) radius r, r', and trabecular radius ρ, ρ '. c: As developed in the Experimental Procedures section, parameters of this model can be plotted, to analyze interdependency of strains within each of these elements. Shortening fraction along subendocardial and subepicardial layers, taken from chamber measures presented in Table 1, are shown along lower and right axes (arrows, with shaded SEM); predicted trabecular shortening falls within range bracketed along left axis. Calculated curves for wall thickness changes (red) suggest thickening during expansion by approximately 10% for observed fractional shortening values. The green diagonal depicts equality of subendocardial and trabecular strains. Blue curve represents that unlikely but mathematically possible case in which subendocardial and epicardial strains are equal, beyond which both are exceeded by trabecular strain (blue region).

Microscopy of Chamber Dimensions and Sarcomere Spacing in Fixed Hearts

Sagittal sections of hearts fixed in expanded and contracted states were examined in clear acrylamide slab sections to see how predictions of our mathematical modeling matched the behavior of myocardial layers. We chose HH stage 23 chick hearts, in which abundant aligned sarcomeres could be found in all layers of interest by whole-mount fluorescence immunostaining for alpha-actinin and confocal microscopy. Chamber dimensions and sarcomere spacing within the sagittal ventricular cross-section analyzed above are illustrated in Figure 4 and tabulated in Table 1 and Figure 5. Maximal and minimal base-to-apex dimensions of inner and outer contours and their circumferences were measured as shown in Figure 4a,b. Sarcomeres were imaged and their spacing measured within five rectangular regions oriented along the circumference at the lesser and greater curvature of the ventricular loop (bracketed regions in Fig. 4a); images along inner and outer layers of the greater curvature are shown enlarged in Figure 4c,d. Sarcomere series, reflecting myofibril arrays, were highly aligned with chamber circumference in inner layers of the greater curvatures and both surfaces of the inner curvature, three of the five layers studied (Fig. 4a, brackets). Myofibrils among midwall trabeculae, however, ranged in orientation from circumferential to radial, with no preferred orientation obvious in expansion or contraction (see below).

Fig. 4.

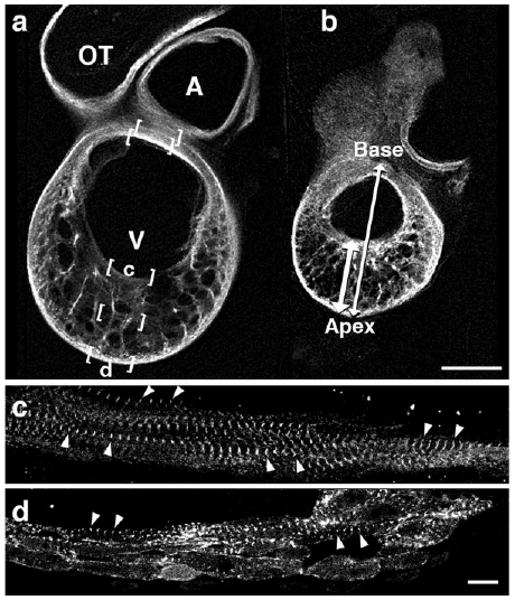
a,b: Confocal images of sagittal acrylamide sections at HH stage 23 in expanded (a) or contracted (b) states, stained for alpha-actinin. Base-to-apex and apical wall thickness measures were taken as shown in b (double arrows). c,d: Sarcomere lengths were measured at five bracketed locations (a), two of which are shown here at higher magnification (c,d). Scale bar = 400 microns in a,b, 10 microns in c,d.

Table 1. Chamber Dimensions and Sarcomer Spacing (microns).

	EXPANDED	CONTRACTED	FRACTIONAL SHORTENING
CHAMBER MEASURES
Base-apex diameter (Lesser to greater curvature)	1427.00 (42.6, 10)	1071.38 (24.5, 8)	0.25 +/− 0.028
Apical Wall thickness (including trabeculae)	543.15 (20.8, 10)	427.46 (26.6, 6)	0.21 +/− 0.057
Outer circumference	4291.40 (102.4, 10)	3248.05 (35.7, 10)	0.24 +/− 0.020
Inner circumference	2495.13 (82.5, 10)	1506.61 (79.7, 8)	0.40 +/− 0.038
SARCOMERE SPACING
GREATER CURVATURE
Outer layer	2.27 (0.07, 12)	1.80 (0.07, 9)	0.21 +/− 0.039
Trabeculae	2.36 (0.06, 10)	1.69 (0.04, 8)	0.28 +/− 0.024
Inner layer	2.71 (0.09, 12)	1.76 (0.09, 9)	0.35 +/− 0.041
LESSER CURVATURE
Inner layer	2.43 (0.11, 12)	1.88 (0.04, 9)	0.23 +/− 0.038
Outer layer	2.45 (0.09, 12)	1.83 (0.04, 9)	0.25 +/− 0.033

Fig. 5.

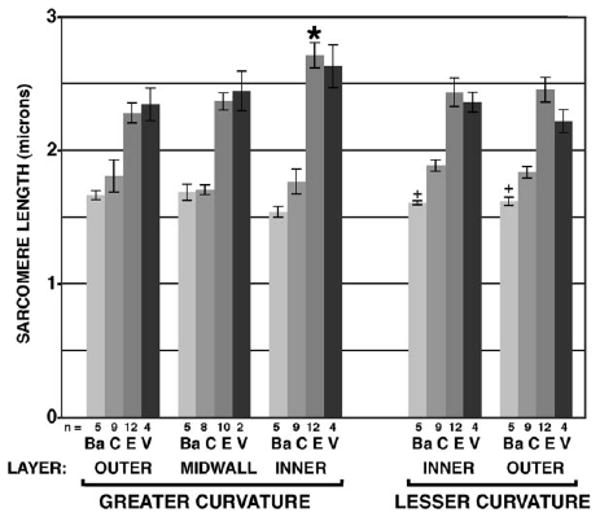
Bar graph of sarcomere spacing at five locations across ventricular wall (bracketed in Fig. 4a), from outer layer of greater curvature (left) to outer layer of lesser curvature (right). At each location, sarcomeres were imaged in n hearts fixed in four states: contracted (Ba, C) or expanded (E, V), as explained in the text. n = number of hearts, error bars show standard error of each mean.

Measures from sagittal sections tabulated in Table 1 show that all individual measures differed significantly between contracted and expanded states (P < 0.01), as expected. “Base-to-apex” dimension, greatest diameter across the tubular heart in this sagittal plane, decreased by 24.9% between expanded and contracted states. Apical wall thickness actually decreased by 21.3% during contraction, contrary to the compact wall model diagramed in Figure 1c. Measures of chamber circumference indicated shortening of the outer layer by 24.3%; shortening along the innermost layer appeared significantly higher (39.6%), values highlighted by arrows in Figure 3c. These corresponded to significant differences in sarcomeric shortening, 20.8% along subepicardial layer and 34.9% along subendocardial layer. Along the lesser curvature, fractional shortening of sarcomere spacing in inner and outer layers appeared intermediate, at 22.5% and 25.2%, respectively, and did not appear to differ in this sample. Among midwall trabeculae, sarcomere spacing decreased by 28.4% between expanded and contracted states, intermediate to excursions observed in adjacent inner and outer layers. In comparison, finite elements within the Xie global mesh model (Fig. 2) undergo fractional shortening along inner and outer layers of the greater curvature of 35.2% and 12.5%, respectively.

Measures of sarcomere spacing in stage 23 hearts are presented as a bar graph in Figure 5. These were taken from mid-sagittal sections at five locations (Fig. 4, brackets) and four states of expansion/contraction. For each location, measures are given for contracted (C) and expanded (E) states, tabulated as corresponding fractional shortening in Table 1. Smaller cohorts of hearts were hypercontracted in barium (Ba) or hyperexpanded in relaxation buffer (V). Sarcomere spacing at all five locations tested showed significant lengthening when fixed in expanded or hyperexpanded state compared with either contracted state (P < 0.05). Among hearts fixed in either expanded state, salient differences were seen in increased spacing of sarcomeres along inner layer muscle fibers of the greater curvature when compared with any other location (P < 0.05, *, Fig. 5). Among hearts fixed in contraction, slight but significant further shortening in the presence of barium was found along both layers of inner curvature (+), but not elsewhere. Differences reported here among wall regions or contraction states were not significantly altered by small imaging corrections detailed in the Experimental Procedures section.

Echocardiography of Beating Hearts

Changes in wall thickness during the cardiac cycle were assessed in beating hearts by 2D echocardiography as shown in Figure 6. Measures of apical wall thickness at systole and diastole demonstrated significant increases during diastole of 8–13.9% at HH stages 20–24. Care was taken in imaging in the mid-sagittal plane free of encroachment by lateral walls; such artifact would only tend to diminish differences measured by this method, as such encroachment was more apparent in contraction than expansion.

Fig. 6.

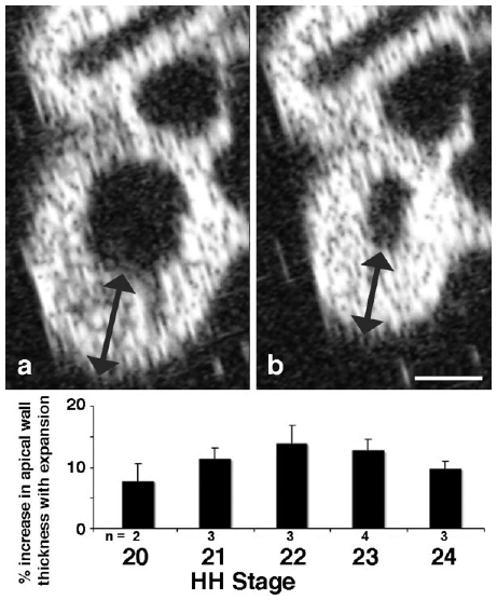
Echocardiagraphic assessment of ventricular wall thickness during contraction cycle. Live embryos were imaged from front for presentation in left sagittal plane across looped ventricle, as in Figure 4. Ventricular wall thickness near apex (arrows) was measured at embryonic stages 20–24. Note consistent thickening of apical wall during expansion throughout this embryonic period. Scale bar = 400 microns.

Distribution of Sarcomere Spacing With Orientation

To assess dependence of strain measures upon orientation, as well as further to test assumptions inherent in our modeling, sarcomeric spacing was compared with fibril orientation along the three major orthogonal axes of the ventricular loop at HH stage 23 (Fig. 7). Normalization of sarcomeric spacing within each small sample volume allows display in polar coordinates of some 4–500 data points in each hemicircle, representing local variation in sarcomere length with orientation irrespective of regional or specimen variation. When imaged from cardiac apex, subendocardial fibers along trabecular crests (Fig. 7a) appeared highly aligned along superior–inferior axis, as expected, whereas subepicardial fibers showed uniform sarcomere spacing at apparently random orientations (Fig. 7b). Within mid-trabecular layers, imaged from frontal (Fig. 7c) or sagittal (Fig. 7d) planes, essentially uniform distributions of sarcomeric spacing with fiber angle were observed. When these data were further divided into major quadrants, statistical comparison of lengths or angles showed no significant differences, except for the highly anisotropic alignment of fibers in subendocardial trabecular ridges along the superior–inferior axis (Fig. 7a); shifts with expansion or contraction were not apparent.

Fig. 7.

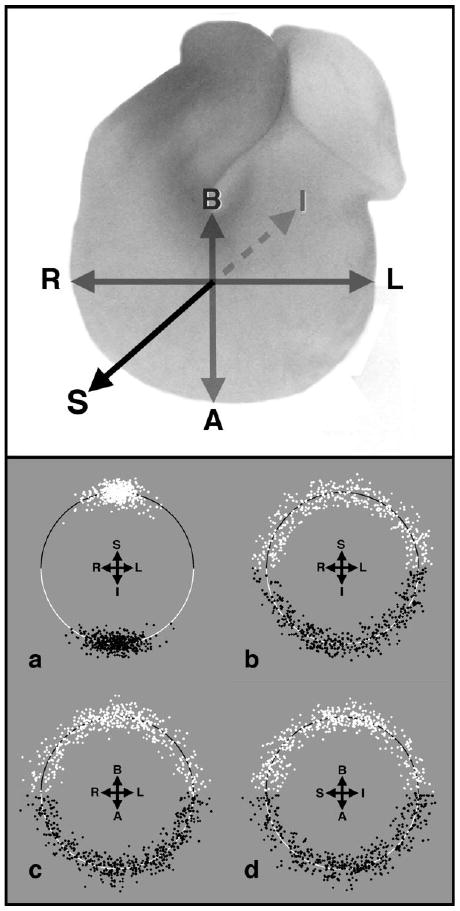
Assessment of directional variation of sarcomeric spacing. Upper panel diagrams the three orthogonal axes across the looped ventricle against which fiber angles and sarcomere spacing were measured: right–left (R,L), basal–apical (B,A), and superior–inferior (S,I). Lower panel shows arrays of fiber angles (± 90°) in selected regions of hearts fixed in expansion (white) or contraction (black), with sarcomere spacing normalized within each subsample to plot against hemicircles of unit radius. a,b: Subendocardial (a) and subepicardial (b) fibers were viewed from cardiac apex. c,d: Midwall trabeculae were imaged from cardiac frontal plane (c) or in left sagittal view (d).

Assessment of Membrane Permeability Under Stretch

Further indication of greater strain along inner wall myocytes came from dye leakage experiments in inflated hearts contrasted with relaxed control hearts, as illustrated in Figure 8. Propidium iodide and 3000 molecular weight (MW) fluorescent dextran were perfused through the hepatic sinus of dissected hearts at HH stage 22–29, either inflated in Tyrode's solution or gently perfused in relaxation buffer (see the Experimental Procedures section). Upon inflation perfusion, both dyes became localized within myocytes along apical subendocardial trabeculae, but parietal myocardial layers remained devoid of labeled cells (Fig. 8a,b), indicative of lesser stretch. Control hearts gently perfused in relaxed state showed little membrane damage anywhere in the heart, except near sites of control pinholes (Fig. 8c,d) or dissection damage (Fig. 8c, arrowhead, *). At HH stage 29 (Fig. 8e,f), both cytosolic and nuclear dyes were taken up along innermost trabeculae and within the interventricular septum (Fig. 8e, arrowhead).

Fig. 8.

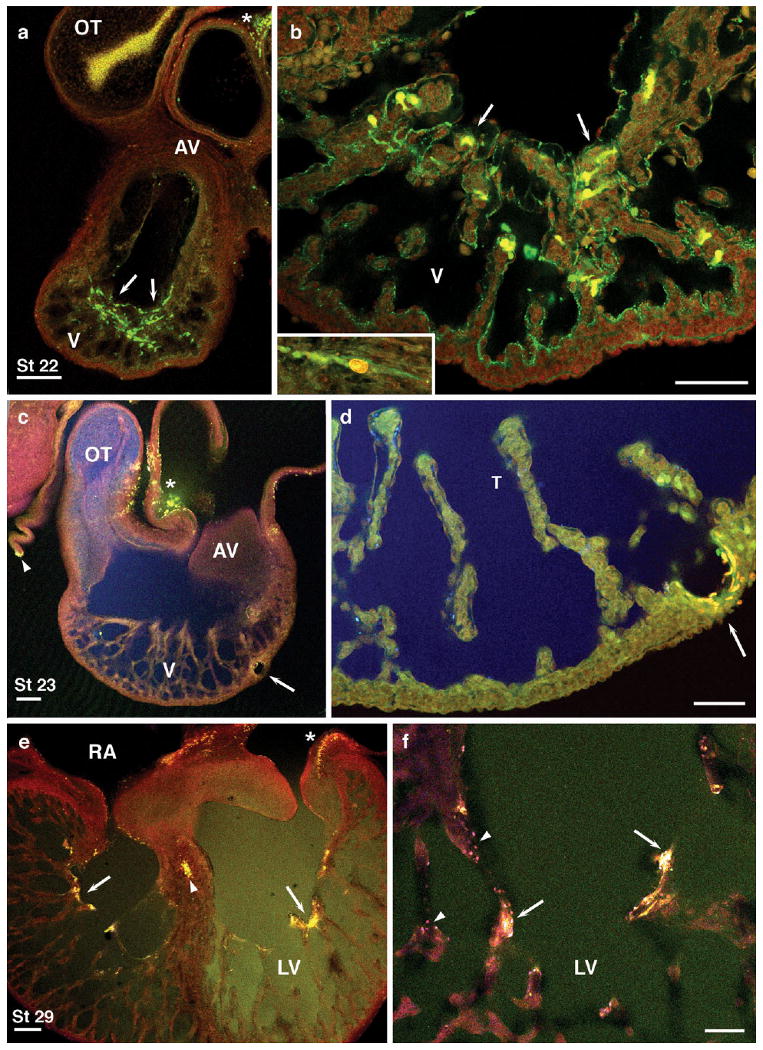
a,b: Cell membrane leaks to propidium iodide (red) and 3000 molecular weight (MW) dextran (green) were found along apical subendocardial layers and adjacent trabeculae (brown) in inflated Hamburger and Hamilton (HH) stage 22 hearts (arrows) and along inner wall of atrioventricular (AV) canal (inset, b). c,d: Control hearts perfused in relaxed state showed little such damage, except near sites of control pin holes (arrows) or dissection damage (c, arrowhead, *). Larger dextrans (MW 10,000 also diffused freely throughout the heart; blue, c,d). e,f: At HH stage 29, cytosolic and nuclear dyes were taken up along innermost trabeculae and within the interventricular septum and atria (e, arrowhead, *). Scale bars = 200 microns in a,c,e, 100 microns in b,d,f.

Discussion

Uneven wall strain in a pulsing muscular tube, with greater strain along inner layers, is demonstrated here in the early embryonic chick heart and in two complementary numerical models. Both models illustrate that the constraints of ventricular geometry subject subendocardial layers to a greater differential of stretch than that experienced by outer layers. Such a strain gradient is graphically apparent in the expanding 3D mesh model of calculated finite elements (Fig. 2). While the porous layer of tissue in the developing ventricles provides a potential degree of freedom that does not exist in the condensed myocardium of fully developed hearts, the 2D lumped sum model (Fig. 3) suggests that peak strain at the endocardial surface might be avoided only by even higher strains within trabecular layers. Imaging of sarcomere spacing in stage 23 hearts immunostained for alpha-actinin measured greatest sarcomeric lengthening at expansion along innermost trabecular strands or shelves along the crest of the developing interventricular septum; midwall trabecular sarcomeres exhibited excursions intermediate to measures along inner and outer wall (Figs. 4, 5). The pattern of spacings of Z-disks observed in sarcomeres at sites across the wall in the stage 23 heart agrees with the predictions of both mathematical models. Variation in Z-disk spacing between contracted and expanded states was greater for subendocardial sarcomeres than for subepicardial or midwall sarcomeres. The changes in wall thickness measured in fixed hearts (Table 1) and by echocardiography (Fig. 6) accord well with predictions of the 2D lumped model. Sarcomere lengths in both contraction states did not vary measurably with orientation (Fig. 7), indicating rapid redistribution of local stresses in midwall and parietal planes during dissection and fixation. Among midwall trabeculae in all three dimensions (Fig. 7c,d) and subepicardial fibrils within the apical plane (Fig. 7b), myocardial strain appeared essentially isotropic, indicating high compliance of myofibrillar arrays and uniform local strain in the static fixation states examined. Within these regions, assumptions of equivalent local strain invoked in both finite element (3D) and planar lumped sum (2D) models appear to be satisfied. The two models differ in that the finite element model as constructed assumes a smooth and locally isotropic interior myocardial surface. The planar 2D lumped sum model accommodates the trabecular shelves and highly anisotropic circumferential alignment of fibers observed in sagittal plane along subendocardial layers of the ventricular apex (Figs. 4c, 7a). The freedom of those inner, largely circumferential fibers from lateral stress inherent in the finite element model may contribute to the apical wall thickening with expansion as predicted (Fig. 3c) and observed in beating hearts (Fig. 6). Finally, the distribution of large-molecular leaks along trabecular strands in experimentally inflated hearts (Fig. 8), also demonstrates heightened stretch of interior fibers relative to parietal heart wall. Thus, in the looped tubular chick heart as first trabecular ridges form, our models and in situ observations are in fundamental accord. Both approaches highlight the greatest stretch experienced by developing myocytes along subendocardial layers.

Limitations of our modeling and measuring approach are several. We have used measures from fixed hearts as strain gauges with which to measure deformation in chosen layers and directions at two static extremes: contraction and expansion. Although both models are based upon a theoretical continuum of global intermediate states, regional divergence from models and measures may certainly occur within the rapidly beating heart. Similarly, an approach based upon strains alone may not adequately reflect stress; this report brings no new information concerning myofibril density, size, or energy consumption, which vary greatly across the immature heart wall and are much more difficult to measure. In addition, although not invalidating models or conclusions, variation in strain calculated from sarcomere spacing and from chamber dimensions may reflect geometries beyond those inherent in the models as constructed. For example, differences in shortening fractions calculated from chamber dimensions and from sarcomere spacing might reflect deformation of a fiber mesh rather than the highly circumferential alignment modeled in the 2D lumped model and seen along subendocardial layers in sagittal section. A hinged mesh can stretch more than its individual elements. Reservations also remain concerning myocardial compliance and its regional variation. The locally isotropic strains measured in orthogonal axes in mid- and outer layers (Fig. 7) suggest high compliance at both extreme static states, that the geometry of trabecular mesh and polygonal subendocardial layer may thus actually contribute to ephemeral pliancy rather than stiffness. It is interesting in this regard to note the slight tightening of sarcomere spacing in the presence of barium, significant only among highly circumferential myofibrils within the nontrabeculated wall of the inner curvature (Fig. 5); stiffness in this region is greater than that found elsewhere in the tubular heart (Zamir et al., 2003). Finally, slight differences in strain measures at the two contracted states, as well as at the two expanded states, might be attributable to contractile reserve near both systole and diastole, respectively; the extremes studied here may seldom be reached in the beating heart. Despite these limitations, both models are robust in that conclusions remain unaltered by variation of inputs well beyond the range of our measures.

The modeling presented here differs in several respects from previous approaches, notably in its simplicity. Earlier modeling of laminar shells along muscular tubes modeled higher stress along inner layers (Taber, 1991), as posited here, and extended such modeling to assess wall stiffness and residual strain (Taber et al., 1993, 1995), including predicted behavior during looping. Porosity or trabeculation was thought to contribute to increasing wall stiffness, as well as to intramural blood flow (Taber, 1991; Yang et al., 1994), before establishment of coronary vasculature (Sedmera et al., 2000). The adult left ventricle, in which strain increases with depth, has long been the subject of measures and modeling, reviewed by Yin (1981) and by Waldman et al. (1985), who invoked such gradients in the progressive imbrication of inner layers away from the concentric patterns found in embryonic hearts. Arts et al. (1994) modeled a sector of left ventricular wall, showing that divergence from aligned concentric arrays toward imbricated, helical pathways could form without feedback through differential strain, although progressive imbrication of myofiber layers in the left ventricle of the chick embryo heart does respond to altered function (Tobita et al., 2005). Such helical layering may serve to redistribute load during normal or pathological cardiac function (Young et al., 1994; Denslow, 2000) and, together with diagonal fascicles diverging from concentric laminar arrangement, may contribute to the wall thickening observed during contraction in the adult heart (Lunkenheimer et al., 2006; Anderson et al., 2006, 2008), contrary to the thickening during expansion observed here in the trabeculated immature wall.

Despite the simplicity of our modeling, the analytical approach and structural findings presented here clearly demonstrate that the constraints of basic geometry provide a potentially strong epigenetic factor in the development of trabeculated myocardial structure. While recent years have been marked by significant increases in understanding of genetic regulation of cardiac development, epigenetic regulation has been the subject of less study. However, there has been increasing interest in factors such as myocardial stress/strain, blood fluid dynamics, and geometric constraints in both adult and developing hearts (Hogers et al., 1995; Taber, 1998a,b; Omens, 1998; Denslow et al., 1999; Gourdie et al., 1999, 2003; Hove et al., 2003; Sedmera et al., 2005). It has been suggested that, from the standpoint of physics, it is more likely for a cellular sensor to detect strain rather than stress (Arts et al., 1994; Omens, 1998). Strain sensors in the sarcomeric apparatus have been partially characterized (Knoll et al., 2002; Hoshijima, 2006) and titin appears with earliest sarcomeric organization in the chick heart (Tokuyasu and Maher, 1987). This suggests one immediate molecular consequence of the added stretch we predict and observe along subendocardial layers. Increased force transduction by titin isoforms at higher sarcomere lengths (Linke, 2008) suggests that stress gradients may be steeper than strain gradients, as we model them assuming linear stress/strain relations. Stretch sensitivity has been implicated in several molecular concomitants of hypertrophy in mammals (Liang and Gardner, 1998; Ergul et al., 2000; Palmieri et al., 2002; Pikkarainen et al., 2003, 2006; Ennis et al., 2005; Lemmens et al., 2006; Stones et al., 2007). A perhaps distinct molecular consequence of strain gradients may be the redistribution and action of growth factors such as FGF-2, released by physical stretch, depleted in the inner layers of chick ventricle (Joseph-Silverstein et al., 1989), and active in local control of myocyte proliferation (Mima et al., 1995). These considerations of differential strain pertain following experimental removal of epicardium, in which the normal transmural pattern of myocyte proliferation is maintained (Pennisi et al., 2003).

The initial emergence of trabeculae from the ventricular wall may also be driven by strain, through geometry as demonstrated here, through early withdrawal from proliferation, or both. Advanced muscular conditioning contributes to terminal differentiation and it is along such early trabeculae that the first nondividing myocytes are found (Thompson et al., 2003). Early avian trabeculae emerge as anterior–posterior shelves (Sedmera and Thomas, 1996), well illustrated in scanning electron microscope (SEM) studies (Sedmera et al., 2000; Taber and Zahalak, 2001). Such ridges persist into adult life in lower vertebrates (Van Mierop and Kutsche, 1984), where they may aid in routing laminar blood flow. Spacing between ridges has been modeled across a 2D sheet of contractile elements within a cohesive matrix (Taber and Zahalak, 2001), and formation of such ridges in vivo appears to depend upon cadherin-mediated myocyte–myocyte contacts (Ong et al., 1998). Thus, the extreme measures of sarcomeric spacing observed here along subendocardial layers suggest a role of differential strain during expansion, and subsequent vigorous contraction, in the formation of early trabeculae; they appear to be pulled inward from the parietal myocardium.

Strain gradients may contribute both to coordinated contraction and to organization of ventricular conduction arborizations. In the chick, maturation of conduction appears responsive to altered loading (Reckova et al., 2003), mediated in part through endothelin activation (Hall et al., 2004; Sedmera et al., 2008), as initially peristaltoid contraction along the tubular myocardium gives way to mature apical-to-basal activation along interior trabecular arborizations (de Jong et al., 1992; Chuck et al., 1997). Before that transition, radial depolarization across the anterior surface of the heart can be visualized with voltage-sensitive dyes in both chick and mouse (Thompson et al., 2003; Sedmera et al., 2004, 2005). Stretch sensitivity of membrane depolarization was demonstrated in the early chick heart by Rajala et al. (1977) and uneven strain described here may serve a mechanistic role, through anisotropic distribution of trabecular prestress, in coordinating cardiac contraction. We thus suggest that the fan-like radiation of early trabecular ridges across the ventricle of the looped, tubular chick heart, and the higher strain along such ridges demonstrated in the present study, are conducive to organization and function of early conduction pathways, that expansion of the heart during diastolic loading sets the stage for subsequent depolarization along the highly stretched fascicles of the anterior septal branch, as well as multiple fascicles along the posterior inner surface which coalesce to form the definitive conduction axis.

Additional evidence for extreme stretch among early trabeculae comes from dye permeability demonstrations (Fig. 8). Such macromolecular leaks, much larger than stretch-sensitive ion channels, can occur under normal and extreme physiological conditions and do not always lead to cell death (reviewed Miyake and McNeil, 2003). In light of the location of such leaks near sites of subsequent apoptosis in inner trabeculae in the developing chick (Cheng et al., 2002) and mouse (Barbosky et al., 2006), and strain-induced apoptosis demonstrated with cardiac myocytes in vitro (Cheng et al., 1995), we speculate here that strain-induced cell death may play a mechanistic role in the normal pruning of trabecular and conduction arborizations as the early heart matures.

Experimental Procedures

Development of Finite Element Model

White Leghorn chick embryos were incubated in ovo at 38.5°C and dissected into Tyrode's solution. HH stage 21 hearts were fixed in unloaded state and embedded in clear acrylamide (Germroth et al., 1995) for Vibratome slab sectioning at 150 microns for x,y,z imaging by confocal microscopy in orthogonal planes. Image stacks were assembled into a 3D workspace for tracing of outer and interior contours smoothed to innermost trabeculae. This 3D orthogonal construct was then redivided into 26 radial sectors as shown in Figure 1a for affixing finite elements connected along and between inner and outer layers, with two intermediate layers interpolated from those points. Expanded and contracted states of this global construct were calibrated to experimental pressure–volume data from external silhouettes of video recordings of beating hearts (Keller et al., 1991). The resulting 3D mesh was then expanded from contracted to expanded state by computer simulation through 22 finite element analyses performed on an eight-CPU SGI PowerChallenge server. Individual result files representing strain of individual elements normalized to global equivalent strain at each state were assembled for post-processing with MSC Mentat and graphic presentation as shown in Figure 2. Further detail can be found in Xie and Perucchio (2001) and Xie (2002, Chapter 8 and Appendix A).

Development of 2D, Three-Compartment Lumped Model

The model selected for analysis was a cross-section of a thick walled, cylindrical tube as used by Yang et al. (1994). The wall of the tube is composed of three layers of myocardium (Fig. 1): (1) an elastic outer layer, (2) a porous mid-layer composed of a network of incompressible strands and sheets of trabecular tissue enclosing lacunae, and (3) a thin inner band that encircles the lumen. The geometry a such a 2D cross-section of the ventricle of the postlooping embryonic heart can be analyzed as a three-node, lumped model in terms of subepicardial, trabecular, and subendocardial elements, each with distinct strain. The term lumped refers to the fact that individual trabeculae or circumferential areas of tissue are not modeled separately, but are instead grouped so as to be described under single parameters within the mathematical model. While the actual embryonic chick heart has much greater complexity than that of the model, the structure must still, in the mean, behave within the boundaries established by the fundamental physics of this model. More specifically, while fiber patterns, layering, and particular cytoskeletal structure within the wall may affect the quantitative level of physical effects, the overall pattern of strain across the thickness of the wall will be determined by the constraints of geometry.

The contraction of a three-layered cylindrical tube can be described in terms of three parameters. These are the full radius of the tube, R, the radius of the lumen, r, and the average radius of the trabecular spaces, ρ (Fig. 3). The basic equation for the total cross-sectional area occupied by muscle is:

$$\text{A}=\pi {\text{R}}^2-\pi {\text{r}}^2-\text{n}\pi {\rho }^2$$ (1)

Rearranging this equation for the lumen radius gives:

$${\text{r}}^2={\text{R}}^2-\text{n}{\rho }^2-\text{A}/\pi$$ (2)

A second equation is generated by differentiation of this equation and rearrangement to give an expression for the differential in the trabecular radii:

$$d\rho =\text{R}d\text{R}/(\text{n}\rho )-\text{r}d\text{r}/(\text{n}\rho )$$ (3)

The measure of strain that we will use is dx/x, equivalent in the instantaneous case to fractional shortening. A third equation is generated by defining alpha as the ratio between the strain along the inner surface: dr/r, and the strain along the outer surface, dR/R. We have substituted the radii for the circumferences in these quantities because the ratio of diameter to circumference is constant, making radial strain equal to circumferential strain.

$$\text{d}\text{r}/\text{r}=\alpha \text{d}\text{R}/\text{R}$$ (4)

This relation can be substituted into Equation [3] to give:

$$\text{R}\text{dR}-\left[{\text{R}}^2-\text{n}{\rho }^2-\text{A}/\pi \right]\alpha \text{dR}/\text{R}-\text{n}\rho d\rho =0$$ (5)

Rearrangement leads to a final equation relating trabecular and subepicardial strain:

$$\text{d}\rho /\rho =[(1-\alpha ){\text{R}}^2/(\text{n}{\rho }^2)+\alpha (1+\text{A}/(\text{n}\pi {\rho }^2))]d\text{R}/\text{R}$$ (6)

The quantity alpha incorporates the relative subendocardial strain into this equation. Using Equations [1], [4], and [6] and the measured wall density at expansion of 32.4% muscle, interdependency of strains throughout the model can be mapped within a fractional shortening space as presented in Figure 3.

Measurements of Chambers and Sarcomeres in Fixed Chick Hearts

For imaging sarcomeres, HH stage 23 hearts were rinsed free of blood by gentle perfusion through the hepatic sinus and fixed for 1 hr with 4% buffered paraformaldehyde in four states:

(1) contracted (immersed in fixative), (2) hypercontracted in 2.5 mM BaCl₂ (Chen et al., 2005), before immersion fixation, (3) expanded by high flow, low pressure perfusion by mouth micropipette through the hepatic sinus with chest wall intact (Pexieder, 1981), or (4) hyperexpanded with chest wall removed for perfusion with relaxation buffer (phosphate buffered saline containing 30 mM KCl, 10 μM Verapamil, 10 μM ethylenediaminetetraacetic acid, Schroder et al., 2002). Whole-mount immunostaining was carried out for 48 hr with primary mouse monoclonal antibody against alpha-actinin (Sigma A-7811), then Cy-2–labeled goat anti-mouse IgG (Jackson Immunoresearch Labs) each diluted 1:200 in buffer containing 10 mM sodium phosphate, 100 mM KCl, 1 mM MgCl₂, 0.1% Triton X-100, 0.02% sodium azide, pH 7.4, with 48-hr rinses.

Confocal Imaging

Immunostained hearts were embedded in 15% acrylamide blocks (Germroth et al., 1995) oriented for sectioning and examination initially in left sagittal plane. Acrylamide sections 150 microns thick were mounted in 50% glycerol in saline and examined with a Leica TCS SP2 AOBS confocal microscope system. Chamber contours were imaged at ×5 (2.92 microns/pixel). For measuring relative areas of trabecular muscle and lacunar spaces, confocal image stacks were taken across the mid-sagittal cross-section of the ventricle at ×10 (1.46 microns/pixel) with slices 20 microns apart. Areas occupied by trabecular muscle or lacunae were estimated by the point-counting method of Cavalieri, yielding a value of 32.4 ± 2.2% muscle in nine hearts measured at expansion. Sarcomeric spacing was imaged with a ×63 water immersion lens (N.A. 1.2) at a zoom of 1.16 giving an in-plane pixel dimension of 0.200 microns; stacks of 20 images (1,024 × 256 pixels) were collected at 0.5-micron intervals. Such stacks were taken at five locations, along inner and outer layers of lesser and greater ventricular curvature and within the central third of the apical trabecular wall, shown in brackets in Figure 4a.

Measurement of Sarcomere Spacing in Sagittal Plane

Sarcomere spacing was measured in digital confocal images using ImageJ software in series of sarcomeres coursing sufficiently close to the imaging plane to show three or more consecutive Z-bands. At least 5 and up to 20 separate sarcomere chains were measured at each site in each specimen. Errors in measuring sarcomere spacing due to divergence of fibrils from the x,y viewing plane were estimated in 3D reconstructions as follows. At each of the 5 sampling regions within the sagittal plane (Fig. 4a), subsets of 20 fibrils showing at least 3 adjacent z-bands in a single x,y confocal plane were chosen by intersection with a random grid overlay. Confocal x,y,z series near that fibril were then rotated about the z-axis to align that fibril along the local x-axis, then rotated about the y-axis for re-measure of apparent spacing in 3D projections spanning ± 20°. Such errors proved small (0.35 to 1.21%), as confirmed by 3D processing within Amira software, much more laborious. Sarcomere lengths measured in single planes in ImageJ were tabulated without further correction. Statistical significance of observed differences was tested by two-way analysis of variance and individual t-tests, with P values < 0.05 taken as significant.

Measurement of Sarcomere Spacing and Fibril Orientation in Orthogonal Planes

Additional series of acrylamide-embedded specimens were oriented for sectioning and confocal examination, as above, along the three orthogonal axes diagramed in Figure 7. To accentuate local variation in sarcomere lengths with orientation and avoid observed variation between muscle layers or specimens, sarcomere spacing and orientation were recorded within local 40 × 40 micron regions and sarcomere lengths were then normalized within each subsample. Such data were plotted in polar coordinates, with orientation ± 90° about respective axes, and lengths proportional to that normal unit circle, as shown in Figure 7. Note that lack of polarity of muscle fibers allows display of both contracted and expanded data sets within the same full circle. Inner and outer layers at the greater curvature were imaged from the cardiac apex, with three such regions analyzed to a depth of twenty microns in each of six hearts in contraction and six in expansion. Among midwall trabeculae, subregions (40 × 40 × 40 microns) across regions of fiber divergence were imaged in frontal and sagittal planes; six subregions from each of three hearts in either orientation in each of the two states, expanded and contracted.

Ultrasound Imaging

Embryos from HH stage 19–24 were dissected free of membranes, flushed free of blood with Tyrode's solution to improve echo contrast, and pinned supine on Sylgard supports, oriented so as to image mid-ventricular cross-section in sagittal plane from superior surface of heart. Perfusion through dorsal aorta supplied continuously variable pressure from 0–50 mm H₂O; temperature was maintained at 37.5 ± 0.5°C. Ultrasound imaging was performed as recently described (McQuinn et al., 2007) with a Vevo660 ultrasound biomicroscopy system (VisualSonics, Toronto, Canada) using a RM708 scanhead with center frequency of 55 MHz. For each heart, five to seven regular cardiac cycles were recorded at 30 Hz for subsequent edge enhancement and measure of apical wall thickness at systole and diastole.

Assessment of Membrane Leakiness

For assessing membrane permeability, hearts were inflated as above in Tyrode's solution containing 1 mg/ml fluoresceinated dextran (MW 3000, Molecular Probes) and 1 mg/ml propidium iodide four times over 4 min and rinsed for 3 min before perfusion fixation as above. Control hearts were carefully pinned so as to minimize abrasion, then relaxed as above and perfused gently over 4 min with dyes in relaxation buffer, rinsed for 3 min and fixed. Availability of dye molecules throughout the tissue was confirmed by localization of dye in cells near damage from 200 micron pins placed in apical myocardium and by distribution of 10,000 MW Alexa 647 dextran (Molecular Probes, 0.5 mg/ml) imaged in a separate channel.