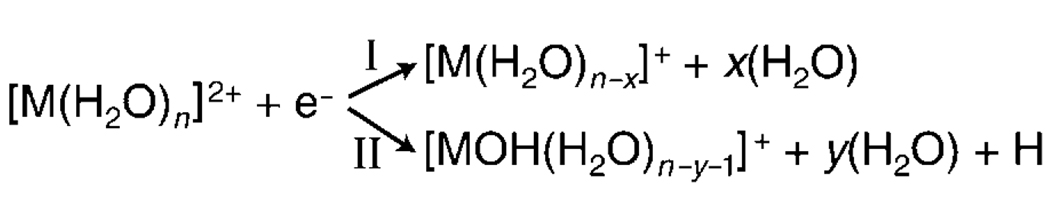Directly Relating Gas-Phase Cluster Measurements to Solution-Phase Hydrolysis, the Absolute Standard Hydrogen Electrode Potential, and the Absolute Proton Solvation Energy

Abstract

Solution-phase, half-cell potentials are measured relative to other half-cell potentials, resulting in a thermochemical ladder that is anchored to the standard hydrogen electrode (SHE), which is assigned an arbitrary value of 0 V. A new method for measuring the absolute SHE potential is demonstrated in which gaseous nanodrops containing divalent alkaline-earth or transition-metal ions are reduced by thermally generated electrons. Energies for the reactions 1) M-(H₂O)₂₄²⁺(g)+e⁻(g)→M(H₂O)₂₄⁺(g) and 2) M(H₂O)₂₄²⁺(g)+e⁻(g)→MOH(H₂O)₂₃⁺(g)+H(g) and the hydrogen atom affinities of MOH(H₂O)₂₃⁺(g) are obtained from the number of water molecules lost through each pathway. From these measurements on clusters containing nine different metal ions and known thermochemical values that include solution hydrolysis energies, an average absolute SHE potential of +4.29 V vs. e⁻(g) (standard deviation of 0.02 V) and a real proton solvation free energy of −265 kcal mol⁻¹ are obtained. With this method, the absolute SHE potential can be obtained from a one-electron reduction of nanodrops containing divalent ions that are not observed to undergo one-electron reduction in aqueous solution.

Introduction

In solution, oxidation and reduction potentials of half-cell reactions cannot be measured in isolation, but are measured relative to other half-cell potentials that are referenced to a common electrode, thus establishing a ladder of relative thermochemical values. The universally accepted “anchor” to this electrochemical series is the standard hydrogen electrode (SHE), e⁻+H⁺→(1/2)H₂(g), which is assigned an arbitrary half-cell potential of exactly 0 V. Establishing an absolute electrochemical scale would enable direct comparisons of half-cell potentials to other absolute thermodynamic values, such as those readily obtained in the gas or solid phases. For example, absolute half-cell potentials are important for developing semiconductor and electrolyte junctions,[1] in which the Fermi level of the electrolytic solution and the work function of the solid semiconductor determine the potential of the solid/electrolyte cell.

The subject of determining the absolute electrode potential has been of considerable interest and has stimulated many different approaches to obtain a value.[2–15] However, because of the difficulty of directly measuring an absolute potential and because of the relatively wide range of values that have been reported from the different methods, this topic has remained controversial;[2–15] it has even led one of the leaders in this field to conclude that “despite the numerous discussions, nobody seems seriously convinced of the arguments of the others.”[2]

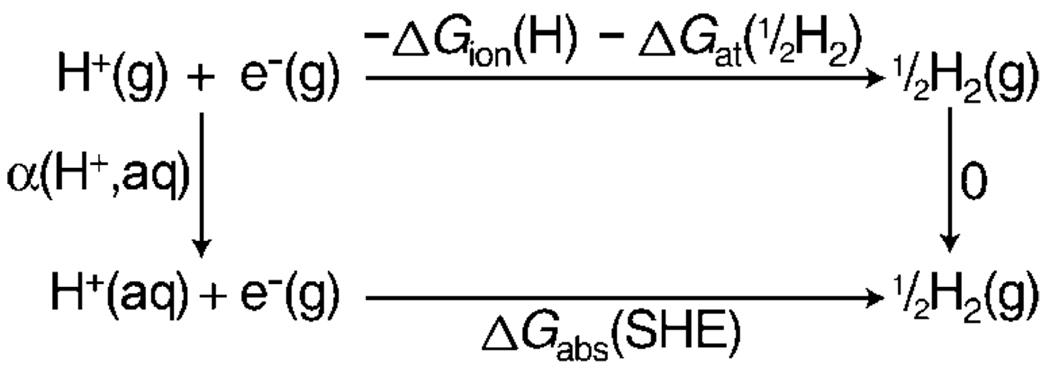
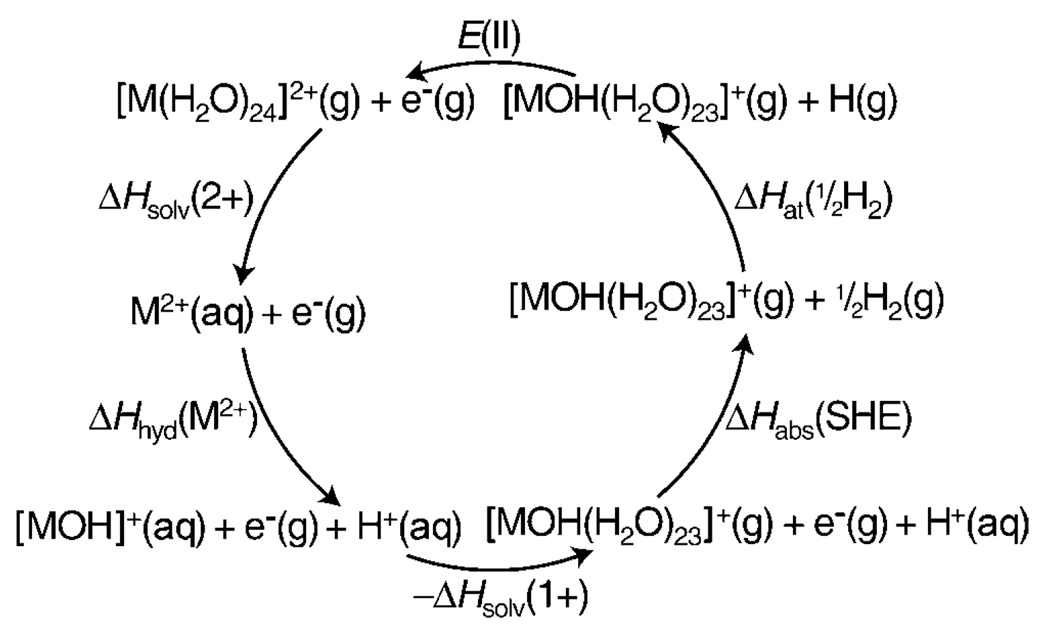
The International Union of Pure and Applied Chemists (IUPAC) recommended definition for the absolute SHE potential is the SHE potential referenced to a gas-phase electron at infinite distance, that is, H⁺(aq)+e⁻(g)→½H₂(g).[3] Estimates of the absolute potential of the SHE versus a free electron[3–12] have been obtained from a variety of methods. One such method uses the thermodynamic cycle shown in Scheme 1,[3, 4] in which α(H⁺,aq) is the real solvation Gibbs free energy of H⁺(g), ΔG_ion(H) is the ionization Gibbs free energy of H(g), ΔG_at(½H₂) is the atomization Gibbs free energy of ½H₂(g), and ΔG_abs(SHE) is the absolute free energy of the SHE versus a free electron. This thermodynamic Born–Haber type cycle results in Equation (1) and is used to obtain the absolute potential of the SHE from the Faraday relation, ΔG = −nFE, in which n is the number of transferred electrons, F is the Faraday constant, and E is the reaction potential.

$$\mathrm{\Delta }{G}_{\text{abs}}(\text{SHE})=-\mathrm{\Delta }{G}_{\text{at}}(\raisebox{1ex}{$1$}\!\left/ \!\raisebox{-1ex}{$2$}\right.{\mathrm{H}}_2)-\mathrm{\Delta }{G}_{\text{ion}}(\mathrm{H})-\alpha ({\mathrm{H}}^{+},\text{aq})$$ (1)

Scheme 1.

Because ΔG_ion(H) and ΔG_at(½H₂) are well known, then the value of ΔG_abs(SHE) is readily obtained if the value of α(H⁺,aq) is known, and vice versa. The real solvation Gibbs free energy of the proton is given by Equation (2) in which μ(H⁺,aq) is the chemical potential of the hydrated proton, e is the elementary charge, and χ(aq) is the surface potential of the vacuum/water interface due to the orientation of water molecules at the interface.

$$\alpha ({\mathrm{H}}^{+},\text{aq})=\mu ({\mathrm{H}}^{+},\text{aq})+e\chi (\text{aq})$$ (2)

The IUPAC reported value for the absolute SHE potential (+4.44 V)[3] is obtained by using a value for α(H⁺,aq) of −260.0 kcal mol⁻¹, which was reported by Farrell and McTigue.[16] This value was obtained by measuring the potential across a high-resistance voltaic cell (Δϕ) given by Equation (3), in which Hg(N₂) is a mercury jet electrode that is separated from a flowing HCl solution by an atmosphere of N₂ gas, “≡” represents the high-resistance N₂ gap, and the HCl solution is in contact with a hydrogen half-cell (Pt, H₂), as a function of HCl molality (m).

$$\text{Hg}({\mathrm{N}}_2)|\equiv |\text{HCl}(\text{aq},m)|\text{Pt},{\mathrm{H}}_2$$ (3)

It was shown that Δϕ is proportional to the surface potential of the HCl solution/air interface. The Δϕ value was measured as a function of HCl concentration from 20 mm to 1 mm, and extrapolated to infinite dilution by using the dependence of the surface potential on ionic strength derived from a theoretical model.[17] A simplifying assumption is that the difference between the surface potential of the HCl solution, χ(HCl,m), and that of pure water, χ(aq), will vary linearly and monotonically as a function of −χ(aq)I^1/2/[(Bλ)⁻¹+I^1/2], in which I is the ionic strength of the HCl solution, B is the appropriate Debye–Hückel constant, and λ is the persistence length defined in the theoretical model, from a concentration of 20 mm to infinite dilution. Fitting the measured data from 20 to 1 mm, results in a linear dependence. By assuming that Bλ = 2, the slope and intercept of this line are +25 and −55.9 mV, respectively; these values correspond to χ(aq) and Δϕ in the limit of infinite dilution, Δϕ(aq). The real solvation energy of the proton (−260.0 kcal mol⁻¹) is obtained from the value of Δϕ(aq) by using a thermodynamic cycle that includes the work function of Hg, and the atomization and ionization energies of molecular and atomic hydrogen, respectively. Because this value is obtained by using a theoretical model of the air/water interface[17] to calculate the dependence of the surface potential of the HCl solution as a function of HCl concentration, it is interesting to compare the surface potential obtained in these experiments to more recently calculated values of χ(aq). A value for χ(aq) of −18 mV was recently reported from quantum-mechanical molecular dynamics simulations.[18] Other calculations that used empirical interaction potentials for water resulted in even more negative χ(aq) values ranging from −110 to −890 mV.[19, 20] The positive value obtained by Farrell and McTigue is inconsistent with these calculated values, but does fall within the range of many other previously reported values (−1.1 V to +0.5 V).[21] If the surface potential of water is negative or much different than +25 mV, the assumptions in extrapolating data from 1 mm to infinite dilution must be questioned, as this would imply that the Δϕ values measured by Farrell and McTigue[16] should not depend linearly and monotonically as a function of −χ(aq)I^1/2/[(Bλ)⁻¹+I^1/2], which could result in a much different intercept and different values for Δϕ(aq) and α(H⁺,aq). For example, the theoretical model[17] used in the Farrell and McTigue extrapolation was originally used to obtain a value of −0.05 V for χ(aq) from a different set of experimental data.[5, 17]

Other approaches towards obtaining the absolute SHE potential have been investigated.[5–10] For example, the potential differences between emersed versus immersed electrodes of electrolytic solutions have been measured, and a value of +4.7 V for the absolute SHE potential was obtained from two separate measurements.[5, 6] However, reorientation of adsorbed molecules upon the electrode when emersed versus immersed may explain the differences between these and other lower estimates for the absolute SHE potential.[22] Another method is to determine μ(H⁺,aq) and combine this value with the surface potential of water, from Equations (1) and (2), to obtain the value of the absolute SHE potential. Computational methods have been used to obtain values for the solvation free energy of the proton that range from −254.4 to −266.7 kcal mol⁻¹.[23–25] A novel cluster-pair correlation scheme that incorporates both gas- and solution-phase experimental solvation data for many different ions has also been used obtain a value of −265.9 kcal mol⁻¹ for the solvation free energy of the proton.[7, 8, 26–28] Relating these reported values for the solvation free energy of the proton to the SHE potential has been questioned, because of the apparent controversy as to whether or not some of these calculated values are μ(H⁺,aq) or α(H⁺,aq), that is, whether these values include χ(aq).[8, 9, 23, 24] By using the most recent value of χ(aq) from quantum-mechanical molecular dynamics calculation for χ(aq), −18 mV, absolute SHE potential values between +4.2 and +4.7 V are obtained from the range of calculated values for the proton solvation free energy.

Because of the wide range of SHE values obtained from previous indirect measurements and computational approaches, it is interesting to investigate more direct experimental methods to measure reduction potentials. We recently introduced a new gas-phase ion nanocalorimetry technique,[29–36] based on the ion thermometer method of Cooks and co-workers,[37] in which electrochemistry on large “aqueous” nanodrops is performed in vacuo to obtain absolute half-cell potentials in bulk solution.[29, 30] Water nanodrops containing individual redox active Cu²⁺ and [M(NH₃)₆]³⁺, for M = Ru, Co, Os, Cr, and Ir, can capture thermally generated electrons and results in loss of water molecules from the droplet.[29] The adiabatic ion–electron recombination energy (RE) is equal to the energy removed by the lost water molecules. The REs can be related to absolute reduction potentials in bulk solution. By comparing these absolute reduction potentials to experimental relative potentials in solution,[29] a value for the absolute SHE potential of +4.2±0.4 V was obtained. This method has the advantages that solvent reorganization energy resulting from the change in ion charge state is reflected in the measured RE, but this method does require that the corresponding relative one-electron reduction potential in solution to be either known or measurable.

In addition to the water molecule loss observed for larger clusters, electron capture (EC) by smaller hydrated metal ions can result in the loss of a hydrogen atom and water molecules. These two dissociation pathways are shown in Scheme 2.

Scheme 2.

EC by Ca(H₂O)_n²⁺ results in dissociation only by pathway II for n≤22, whereas only pathway I occurs for n≥30.[31] At n = 24, the abundance of each pathway is comparable and both pathways result in the loss of about ten water molecules from the reduced precursor.

Here, reduction of hydrated M(H₂O)₂₄²⁺, M = Mg, Ca, Sr, Mn, Fe, Co, Ni, Cu, and Zn, which results in the loss of an H atom and water molecules, is investigated and a value for the absolute SHE potential is obtained through a route that is largely independent of our previous method. The energy for the pathway for loss of atomic hydrogen and water molecules is shown to be directly related to hydrolysis in solution. From these and other known thermochemical data, the absolute SHE potential and α(H⁺,aq) can be obtained from a single cluster measurement. Unlike our previous method, this new method does not use relative solution-phase redox potentials to obtain the absolute SHE potential. Thus, a value for the SHE potential can be obtained from one-electron reduction of moderate-size gaseous nanodrops containing metal ions that do not undergo a one-electron reduction in solution.

Results and Discussion

Nanodrop fragmentation pathways upon electron capture

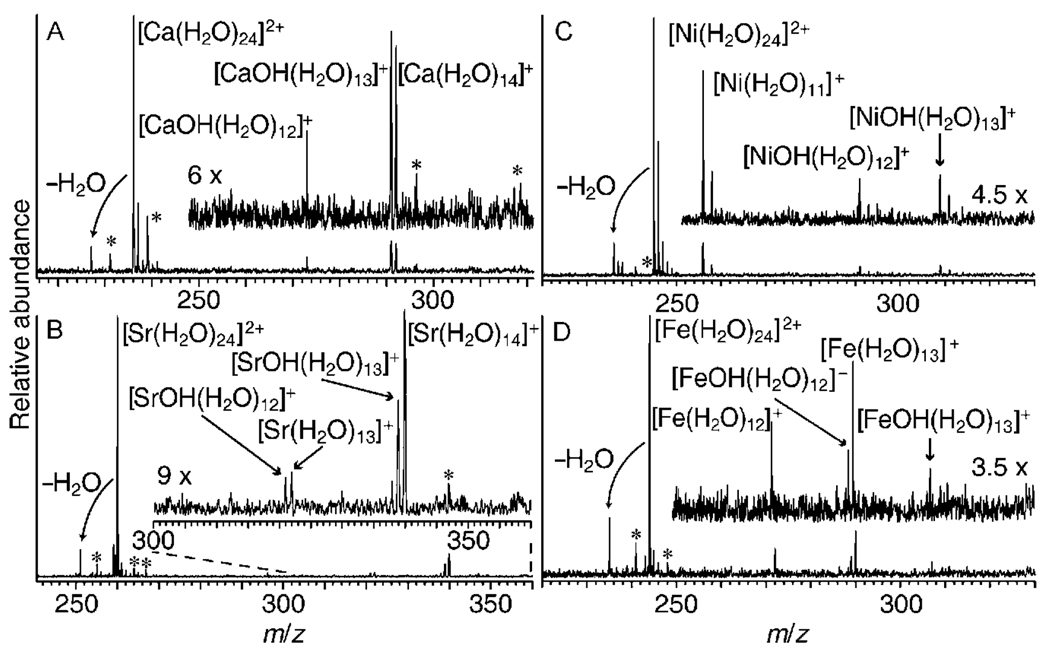
EC by [M(H₂O)₂₄]²⁺ results the exclusive loss of a hydrogen atom and water molecules (pathway II) for M = Mg, but only water molecule loss (pathway I) occurs for M = Ba. For M = Ca; the ratio of ions formed through the two pathways (II/I) is about 2:1, whereas this ratio is about 1:2 for M = Sr (Figure 1A and B). These results indicate that H atom loss is more favorable with increasing charge density of the metal ion. The difference between the numbers of water molecules lost through each pathway is essentially the same for M = Ca and Sr, which suggests that the barrier to loss of an H atom from the reduced cluster is small.

Figure 1.

Mass spectra resulting from EC by [M(H₂O)₂₄]²⁺ for M = Ca (A), Sr (B), Ni (C), and Fe (D). Noise peaks are indicated by asterisks. Peaks corresponding to [SrOH(H₂O)₁₂]⁺ and [SrOH(H₂O)₁₃]⁺ have a 7% contribution from [⁸⁷Sr(H₂O)₁₃]⁺ and [⁸⁷Sr(H₂O)₁₄]⁺, respectively.

EC of [M(H₂O)₂₄]²⁺, M = Mn, Fe, Co, Ni, Cu and Zn, results in dissociation by both pathways (representative data shown in Figure 1C and D). In contrast to the alkaline-earth-metal ions, the average number of water molecules lost through each pathway can differ dramatically (Table 1). For example, EC by [Cu(H₂O)₂₄]²⁺ results in the loss of an average of 16.3 and 10.6 water molecules through pathways I and II, respectively. The average number of water molecules lost through pathway II ranges from about 10.2 to 10.6 for the different metal ions, whereas an average of 10.0 to 16.3 water molecules are lost by pathway I (Table 1). For all clusters, the product ion distributions are remarkably narrow, indicating that the range of internal energy deposition is also very narrow.

Table 1.

Nanodrop hydrogen atom affinities, absolute standard hydrogen electrode potentials, and related values.

	〈x〉[a,f]	〈y〉[b,f]	E(I)[c,f] [kcal mol−1]	E(II)[d,f] [kcal mol−1]	HA[e,f] [kcal mol−1]	ΔHhyd(M2+)[g] [kcal mol−1]	ΔHabs(SHE)[h] [eV]	ΔGabs(SHE)[i] [eV]
Mn	12.0(1)	10.2(1)	138.6(3)	116.0(2)	22.5(3)	13.8(6)	−4.00	−4.25
Fe	11.2(1)	10.4(1)	128.0(3)	118.5(7)	9.6(7)	12.6(6)	−4.04	−4.30
Co	12.2(1)	10.4(1)	42.0(2)	118.3(5)	23.6(6)	12.9(6)	−4.05	−4.31
Ni	13.1(1)	10.3(1)	154.0(2)	117.3(3)	36.6(4)	13.4(6)	−4.03	−4.29
Cu	16.3(1)	10.6(1)	206(1)	121.1(3)	85(1)	10.6(6)	−4.07	−4.33
Zn	11.6(1)	10.4(1)	134.6(2)	118.9(6)	15.7(6)	11.9(6)	−4.04	−4.29
Mg[j]	–	10.2(1)	–	115.8(5)	>8.6	14.3(6)	−4.01	−4.27
Ca	10[k]	10.2(1)	>113	116.0(3)	>8.6	14.7(6)	−4.03	−4.29
Sr	10.1(1)	10.2(1)	>114.3	115.8(3)	>8.6	15.2(6)	−4.04	−4.30

^[a]The average number of water molecules lost through pathway I, 〈x〉, upon EC by [M(H₂O)₂₄]²⁺.

^[b]The average number of water molecules lost through pathway II, 〈y〉, upon EC by [M(H₂O)₂₄]²⁺.

^[c]Enthalpies of Equation (4), E(I), obtained for each [M(H₂O)₂₄]²⁺.

^[d]Enthalpies of Equation (5), E(II), obtained for each M(H₂O)₂₄²⁺.

^[e]Hydrogen atom affinities (HA) of [MOH(H₂O)₂₃]⁺.

^[f]Error range is propagated from the signal-to-noise ratio in each corresponding mass spectrum.

^[g]M²⁺ solution hydrolysis enthalpies, ΔH_hyd(M²⁺), from reference [59].

^[h]Enthalpy (ΔH_abs) of the absolute SHE obtained for each M²⁺ ion.

^[i]Free energy (ΔG_abs) of the absolute SHE obtained for each M²⁺ ion.

^[j]Products resulting from pathway I were not observed for M = Mg.

^[k]Only the x = 10 product was observed for the pathway I reaction for M = Ca.

Nanodrop hydrogen atom affinities

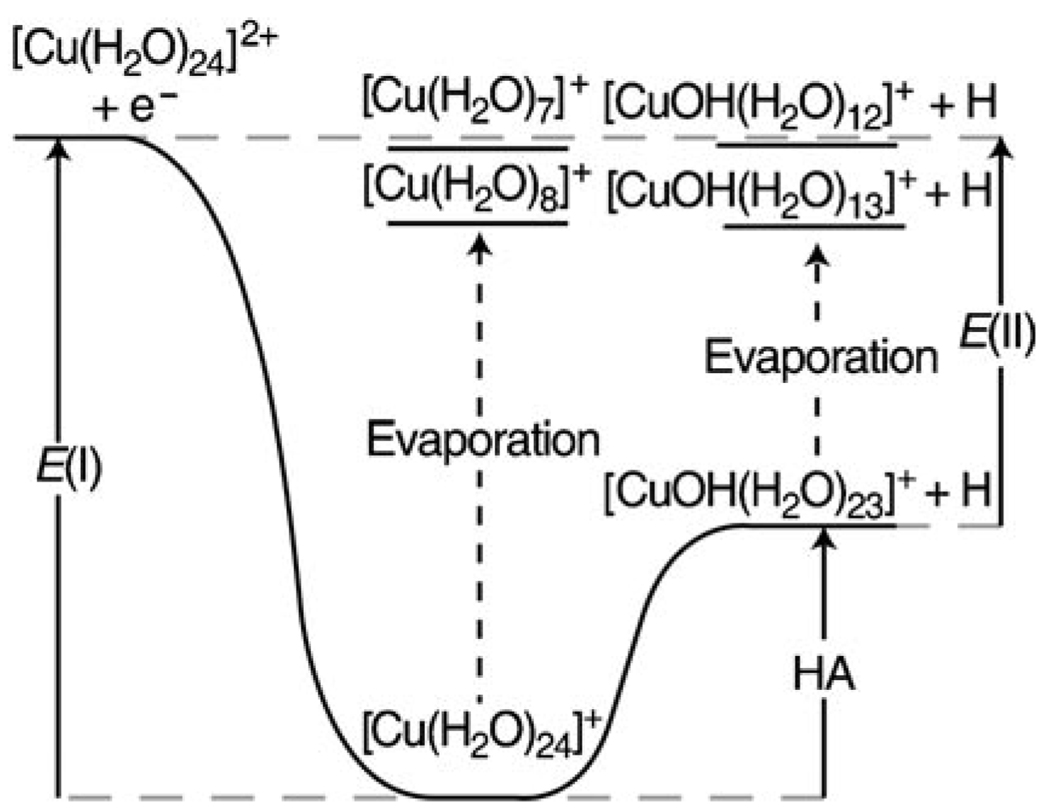
These results can be rationalized in context of the energy diagram in Figure 2, in which E(I) is the recombination energy corresponding to the reaction given in Equation (4) and is determined from the number of water molecules lost through pathway I.

$${[\mathrm{M}{({\mathrm{H}}_2\mathrm{O})}_{24}]}^{2+}(\mathrm{g})+{\mathrm{e}}^{-}(\mathrm{g})\to {[\mathrm{M}{({\mathrm{H}}_2\mathrm{O})}_{24}]}^{+}(\mathrm{g})$$ (4)

Figure 2.

The recombination energy, E(I), and the energy corresponding to the formation of [CuOH(H₂O)₂₃]⁺ +H, E(II), is obtained from the average number of water molecules that evaporate for each pathway. The hydrogen atom affinity, HA, of the [CuOH(H₂O)₂₃]⁺ cluster is the difference between E(I) and E(II). The top grey dashed line indicates the energy of the products and reactants; the bottom grey dashed line indicates the energy of the reduced precursor at the same temperature of the precursor. The black dashed lines indicate the evaporation of water molecules from the reduced clusters.

E(II) is the energy corresponding to the reaction given in Equation (5) and is obtained from the number of water molecules lost through pathway II.

$${[\mathrm{M}{({\mathrm{H}}_2\mathrm{O})}_{24}]}^{2+}(\mathrm{g})+{\mathrm{e}}^{-}(\mathrm{g})\to {[\text{MOH}{({\mathrm{H}}_2\mathrm{O})}_{23}]}^{+}(\mathrm{g})+\mathrm{H}(\mathrm{g})$$ (5)

Under the conditions of these experiments, heat exchange between the ions that capture an electron and the surroundings by means of collisional or radiative energy transfer is negligible owing to the low pressure (≤10⁻⁸ Torr) and rapid energy loss through water evaporation from the cluster. Thus, both reaction pathways correspond to adiabatic processes in which the energy of the products is equal to the energy of the reactants (Figure 2). The energies obtained from the numbers of water molecules lost from the reduced clusters correspond to the isothermal reaction,[29] like values obtained from standard calorimetry techniques. The difference between E(II) and E(I), corresponding to the reaction given in Equation (6), is the negative of the hydrogen atom affinity (HA) of MOH(H₂O)₂₃⁺(g).

$${[\text{MOH}{({\mathrm{H}}_2\mathrm{O})}_{23}]}^{+}(\mathrm{g})+\mathrm{H}(\mathrm{g})\to {[\mathrm{M}{({\mathrm{H}}_2\mathrm{O})}_{24}]}^{+}(\mathrm{g})$$ (6)

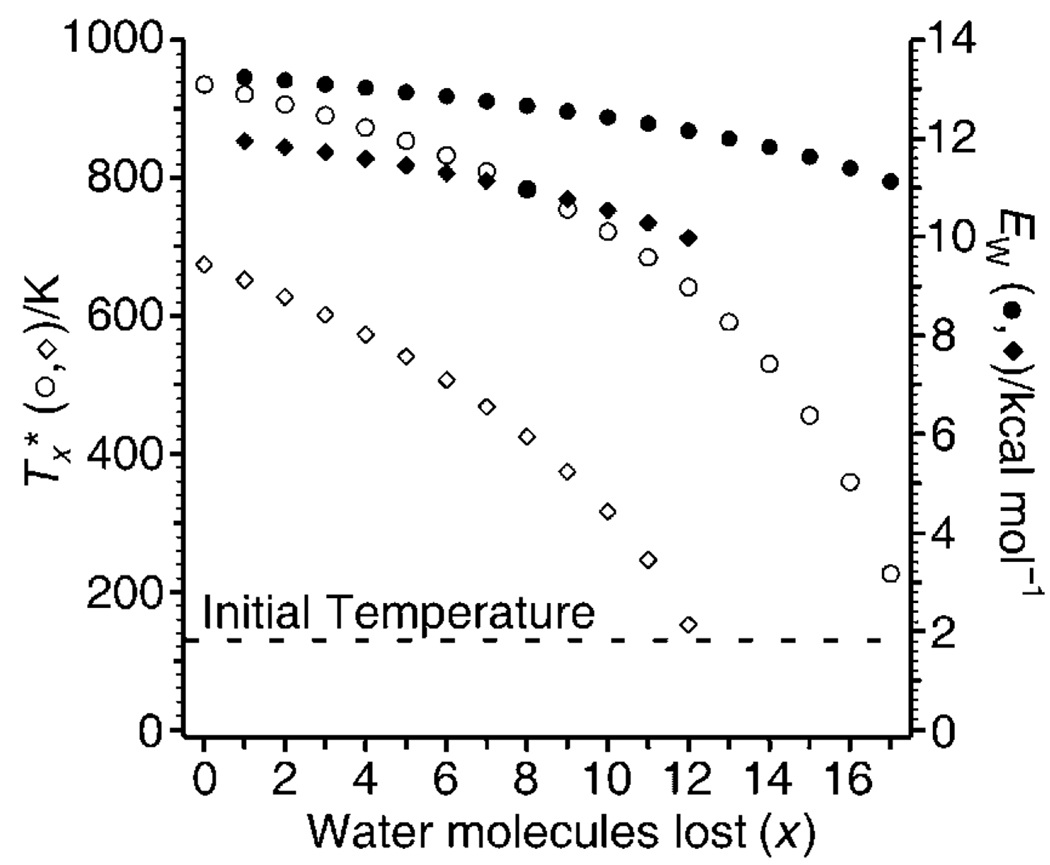
To obtain a quantitative measure of E(I) and E(II) from the average number of water molecules lost, the threshold dissociation energies and the energy partitioned into translational, rotational, and vibrational modes of these water molecules must be known.[29] Because water binding energies for the size clusters investigated here have not been measured, threshold dissociation energies were calculated by using the Thomson liquid-drop model.[38, 39] Sequential hydration energies calculated by using a discrete implementation of this model compare very well to experimental data for both mono- and divalent metal ions,[38] and should be increasingly accurate with increasing cluster size. Although the metal-ion identity is not included in this implementation of the model, water binding energies rapidly approach the bulk heat of vaporization with increasing cluster size and become largely independent of ion identity, even for divalent metal ions that have as few as a dozen or so water molecules attached.[38] Thus, this model should provide reasonably accurate water-molecule binding energies for the much larger, singly charged, reduced clusters investigated here. Little vibrational energy should partition into the evaporated water molecules, because these modes should not be significantly populated under these conditions. The translational and rotational energy partitioned into the products is modeled by iteratively solving for the effective temperature (T*) and the internal energy of the clusters upon reduction and sequential evaporation, which results in the observed water molecule loss due to EC,[29] to obtain the average energy partitioned into the ionic and neutral products, (5/2)kT*,[40–43] in which k is the Boltzmann constant. As examples, the effective temperatures of the reduced clusters, [Cu(H₂O)_24−x]⁺ and [Fe(H₂O)_24−x]⁺, as a function of water molecules lost (x) and the energy removed by each of these water molecules are shown in Figure 3. In these experiments, all M(H₂O)_n²⁺ investigated are thermalized to a temperature of ~130 K prior to EC. Upon EC, the effective temperature of [Cu(H₂O)₂₄]⁺ increases from the initial precursor temperature of ≈130 to ≈940 K, whereas that for M = Fe increases to ≈670 K. The clusters have the same number of degrees of freedom; the higher effective temperature of the former cluster is due to the higher RE. Loss of each water molecule reduces the cluster temperature, so that less energy partitions into translational and rotational modes for each sequential water molecule that is lost. For M = Cu, the calculated energy removed by each sequential water molecule, which is the sum of the water molecule binding energy from the Thomson liquid-drop model and the energy partitioned into translations and rotations upon water molecule loss as a function of reduced cluster temperature, ranges from 13.2 to 11.1 kcal mol⁻¹, for the first and last respective water molecules lost; for M = Fe, these energies range from 12.0 to 10.0 kcal mol⁻¹, respectively. The higher energy removed upon sequential water evaporation (E_W) for M = Cu is due to the larger recombination energy and hence the higher temperatures of the reduced clusters.

Figure 3.

Calculated cluster effective temperatures (T_x*, open symbols) and energy removed upon sequential water evaporation (E_W, closed symbols) as a function of water molecules lost, x, for [Cu(H₂O)_24−x]⁺ (circles) and [Fe(H₂O)_24−x]⁺ (diamonds). The dashed-line indicates the initial precursor temperature (≈130 K).

The RE value obtained from the average number of water molecules lost from the cluster corresponds to a lower limit of the actual value, because additional energy up to the energy removed by a single water molecule may be deposited into the cluster without observing the loss of an additional water molecule. To correct for this effect, which should result in more accurate RE values, the observed average water molecule loss is increased by half a water molecule to obtain RE values. Adjusting our previously reported value (+4.2 V)[29] to include this correction results in a value of +4.45 V for the absolute SHE potential. The RE values reported here include this correction.

Values of E(I), E(II), and the HAs are given in Table 1. These are the first experimentally determined HAs to hydrated metal-ion clusters. For clusters containing a transition-metal ion, the HAs range from ≈10 to 85 kcal mol⁻¹ for M = Fe and Cu, respectively, and all these values are greater than the binding energy of a water molecule (≈8.6 kcal mol⁻¹). These results are consistent with previous studies in which [M(H₂O)_n]⁺, M = Mn, Fe, Co, Ni, Cu and Zn,[44–46] for n up to ≈50, are only observed to fragment through water molecule loss with blackbody infrared radiative dissociation (BIRD), a method that favors the lowest energy dissociation pathways. The order in which the H atom is eliminated from the cluster ions after EC can potentially affect the value obtained for E(II), but this effect should be small. Because the HAs of the transition-metal-ion clusters are much greater than the binding energy of a water molecule, hydrogen-atom loss from the reduced cluster should occur before substantial evaporative cooling of the cluster ion.

The number of water molecules lost through each pathway for Ca- and Sr-containing clusters is nearly the same, indicating that loss of a hydrogen atom has only a small barrier. [Ca(H₂O)_n]⁺ ions formed in a cluster ion source are stable for n>≈13, but [CaOH(H₂O)_n]⁺ is observed for 4<n≤13.[47] This suggests that the HA of [CaOH(H₂O)_n]⁺ is greater than the water binding energy (8.6 kcal mol⁻¹) for n>13, but less than the binding energy of water for 4<n≤13. In the EC experiments for M = Ca and Sr, the smaller [M(H₂O)_n]⁺ clusters that initially react by pathway I may subsequently lose an H atom at smaller sizes. For example, only [Ca(H₂O)₁₄]⁺ is observed upon EC of [Ca(H₂O)₂₄]²⁺ and not [Ca(H₂O)₁₃]⁺, which would dissociate by loss of an H atom if formed with sufficient internal energy. Similarly for M = Mg, BIRD experiments indicate that loss of a water molecule from [Mg(H₂O)_n]⁺ occurs for n>17, whereas [MgOH(H₂O)_n]⁺ formation is favored for the smaller clusters.[48] This is consistent with no pathway I products being formed by EC of [Mg(H₂O)₂₄]²⁺, because these products are unstable with respect to hydrogen-atom loss at smaller cluster sizes. Because EC by [M(H₂O)₃₂]²⁺, M = Mg, Sr, Ca, and Ba, results in formation of only [M(H₂O)₂₁]⁺ and [M(H₂O)₂₂]⁺,[33] we conclude that the HA of [MOH(H₂O)₂₃]⁺ is slightly greater than the binding energy of a water molecule (8.6 kcal mol⁻¹).

Hydrogen-atom loss upon EC could occur by several different mechanisms.[34] A salt-bridge within the cluster, M²⁺-OH⁻-H₃O⁺, may be transiently formed,[49] possibly facilitated by the incoming electron. Reduction of H₃O⁺ would form the reactive H₃O radical, which should dissociate through loss of H. The electron may attach directly to an outer-shell water molecule to form H₂O⁻, which, as an isolated ion, dissociates by loss of H.[50] Results from electronic structure computational methods support this latter mechanism.[51] The metal ion may be directly reduced and followed by an intracluster reaction to form the hydrated metal hydroxide and hydrogen-atom elimination, similar to that proposed for thermal dissociation of [Mg(H₂O)_n]⁺.[48]

Relating nanocalorimetry measurements to bulk hydrolysis

The value for E(II) can be directly related to bulk hydrolysis by using the Scheme 3 thermodynamic cycle, in which ΔH_solv(2+) and ΔH_solv(1+) are the cluster ion solvation energies of [M(H₂O)₂₄]²⁺ and [MOH(H₂O)₂₄]⁺, respectively, and ΔH_at(½H₂), ΔH_hyd(M²⁺), and ΔH_abs(SHE) are the enthalpies of H₂ atomization, the first M²⁺ hydrolysis reaction in aqueous solution, and the absolute SHE versus a free electron, respectively.

Scheme 3.

As an approximation, the surface-potential contribution to the −E(II) values measured for these nanodrops is estimated to be equal to the surface potential of bulk water. Recent results from infrared multiple-photon dissociation spectroscopy of [Ca(H₂O)_n]²⁺ with n ranging from 4 to 69 indicate that the coordination number of Ca²⁺ changes from a value of 6 at cluster sizes below 12 to a value of 8 at larger sizes.[52, 53] Eight-coordinate solvation is consistent with results from many solution-phase studies.[54–58] The bonded OH regions in the spectra of the larger clusters are similar to, but blue-shifted from, that of bulk water.[53] The free-OH regions are well resolved and indicate that the surfaces of the clusters are well ordered with a structure approaching that at the bulk air–water interface. For the intermediate size clusters in this study, the coordination number of Ca²⁺ is likely the same as that in bulk water and the majority of surface water molecules accept two hydrogen bonds, donate a single hydrogen bond to adjacent water molecules, and have a free OH. These results indicate that the water structure at the surface of these intermediate size nanodrops should be similar to that of the bulk air–water interface and this should be increasingly true for larger nanodrops.

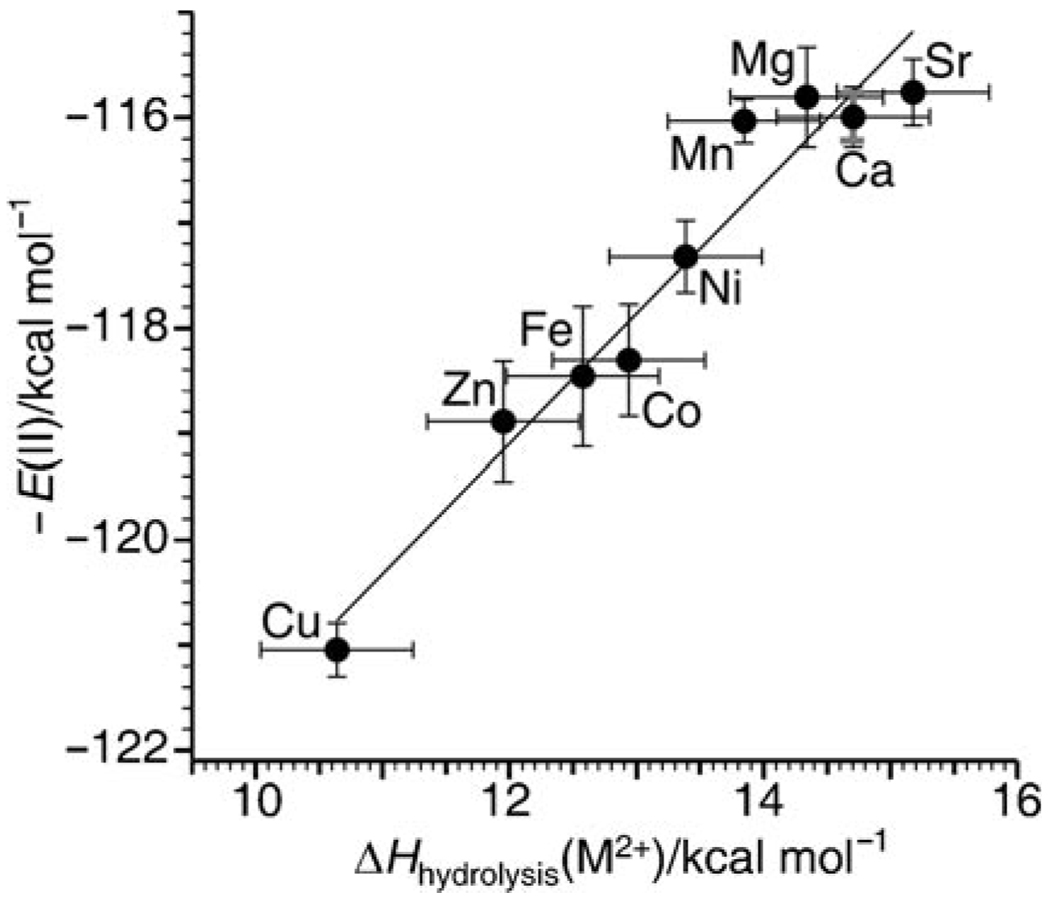
Because the enthalpies of solvation of the different metal ion containing nanodrops should not depend appreciably on the metal ion identity at this cluster size, and because ΔH_at(½H₂) and ΔH_abs(SHE) are constant, there should be a direct correspondence between E(II), obtained from these nanocalorimetry experiments, and bulk ΔH_hyd(M²⁺) values as a function of metal-ion identity. Bulk hydrolysis Gibbs free energies, ΔG_hyd(M²⁺), are known for the divalent metal ions studied here.[59, 60] To obtain ΔH_hyd(M²⁺), an entropy value calculated from an empirical formula for each M²⁺ ion is combined with measured free-energy values.[59] The estimated standard deviation in TΔS_hydrolysis is ±0.6 kcal mol⁻¹, but TΔS is only an average of 2.3% of the hydrolysis enthalpy value (ΔH = ΔG + TΔS) for the transition-metal ions and 16% for the alkaline-earth-metal ions; that is, ΔH_hyd(M²⁺) values are obtained predominantly from experimental free energies.[59] Values of −E(II) versus the ΔH_hyd(M²⁺) (Table 1) for each metal ion are shown in Figure 4. A linear regression results in a slope of 1.2±0.1 and an R² value of 0.94. This slope is slightly higher than the predicted value of 1.0, but the general relationship between these nanocluster measurements and solution values is excellent especially when considering that the range in enthalpy values is only ≈5 kcal mol⁻¹ and the uncertainty in the solution phase hydrolysis entropy correction is relatively large.

Figure 4.

The negative of E(II), from gas-phase nanocalorimetry measurements, versus enthalpy of solution-phase hydrolysis. The black vertical error bars reflect the uncertainty in the average number of water molecules lost propagated from the signal-to-noise level in the electron capture dissociation mass spectra for each metal ion. The vertical grey error bars for Ca represent the standard deviation in the number of water molecules lost from three replicate measurements made over 18 months. The horizontal error bars correspond to one standard deviation in the entropy correction.[59]

Absolute SHE from gas-phase cluster measurements and solution hydrolysis

The Scheme 3 thermodynamic cycle provides a unique route to obtain the absolute SHE enthalpy from a single cluster measurement that does not require the use of metal ions that have known one-electron reduction potentials in solution; see Equation (7) in which the difference in ΔH_solv(1+) and ΔH_solv(2+) can be obtained from a modified Born equation,[61] resulting in a ΔΔH_solv value of 89.9 kcal mol⁻¹.

$$\mathrm{\Delta }{H}_{\text{abs}}(\text{SHE})=\mathrm{\Delta }\mathrm{\Delta }{H}_{\text{solv}}-\mathrm{\Delta }{H}_{\text{hyd}}({\mathrm{M}}^{2+})-E(\text{II})-\mathrm{\Delta }{H}_{\text{at}}(\raisebox{1ex}{$1$}\!\left/ \!\raisebox{-1ex}{$2$}\right.{\mathrm{H}}_2)$$ (7)

Although these nanoclusters are smaller than those used in our previous method,[29] they are still sufficiently large that a continuum solvation model should account for the vast majority of the energy for M(H₂O)₂₄^z+(g)→M^z+(aq). The value of ΔH_at(½H₂), 52.10 kcal mol⁻¹,[62] is accurately known. Values for the absolute ΔH_abs(SHE) versus a free electron for each individual metal ion calculated from Equation (7) are given in Table 1. The absolute entropy term (TΔS) of the SHE at 298 K (0.260 eV)[63] has been obtained from temperature-dependent measurements of common half-cell reactions and is consistent with another value (0.262±0.002 eV)[64] obtained from experiments in which effects of junction potentials were investigated. The absolute SHE free-energy values are obtained from ΔH_abs(SHE) and this absolute entropy term. The average value of ΔG_abs(SHE) obtained for the nine different metal ions is −4.29 eV or +4.29 V (ΔG = −nFE), and the standard deviation in these values is ±0.02 V.

Reproducibility and uncertainty

The standard deviation in three replicate measurements of EC by [Ca(H₂O)₂₄]²⁺ made over the course of 18 months is ±0.02 water molecules or ±0.3 kcal mol⁻¹ (less than 0.2%). In addition, recent experiments done on this instrument show that the energy deposited upon EC does not depend on the cathode voltage or the trapping potentials over a wide range of experimental conditions used.[32] Experiments done in ion storage rings, in which the relative ion and electron velocities are carefully controlled, demonstrate that EC cross sections increase by many orders of magnitude when the relative ion and electron velocities approach zero.[65–69] In our EC experiments, there is a wide spread of electron kinetic energies, but some fraction of these electrons can have near zero relative ion and electron kinetic energies, owing to effects of electron–electron repulsion, inelastic collisions that do not result in electron capture, and emission of electrons from long-lived Rydberg states formed by EC of more energetic electrons. It is the electrons for which the relative ion and electron kinetic energy is near zero that should be captured most efficiently.

Although the precision of this method is good, the absolute uncertainty is higher owing to possible systematic deviations in the energy lost per water molecule, calculated cluster solvation energies, and any differences in the surface potential of these nanodrops and bulk water. The value of ΔG_abs(SHE) versus a free electron obtained with this method is lower than the value of +4.45 V that we obtained using a similar but largely independent method.[29] The majority of the absolute uncertainty can be attributed to the calculated water binding energies. In our previous study, as many as 19 water molecules were lost upon reduction of [Ru(NH₃)(H₂O)₅₅]³⁺ and predominantly divalent ions were formed upon EC. Here, fewer water molecules are lost and monovalent ions are formed upon EC. Because of these two factors, the uncertainty in the RE values reported here should be less. However, the uncertainty in the solvation energy and the energy partitioned into translational and rotational modes of the products is greater for smaller clusters.

The slightly lower ΔG_abs(SHE) value obtained with this method may be partially attributable to small differences in the sequential water binding energies to a hydrated M⁺ versus an MOH⁺ cluster. Because of the large number of water molecules lost, even small differences can be significant. Electronic structure calculations indicate that the sequential hydration energies for CaOH⁺ are higher than for Ca⁺;[31] for n = 1 and 5, the hydration energy of the hydroxide ion is 4.2 and 1.2 kcal mol⁻¹ higher, respectively.[31] If the hydroxide-ion-containing clusters have systematically higher binding energies than the M⁺-containing clusters, this would result in E(II) values that are systematically low; only a ≈0.4 kcal mol⁻¹ higher water molecule binding energy to MOH⁺ versus M⁺ containing clusters could account for the 0.16 V difference in the absolute SHE potential obtained by these two nanocalorimetry methods. There may also be a slight difference in the surface potentials for the different-sized clusters used in the two different methods, although IRMPD spectra indicate that the orientation of water at the nanodrop surface does not change very significantly in this size range. The similar absolute SHE values obtained by these two largely independent methods indicate that the absolute uncertainty in both methods is less than ±10%. In principle, binding energies can be accurately measured for the clusters relevant to these and previous nanocalorimetry experiments, which would improve the absolute accuracy of these methods.

Real proton solvation free energy

From the absolute SHE potential, the real proton solvation free energy can be obtained by using the Scheme 1 thermodynamic cycle.[70] A ΔG_abs(SHE) value of +4.29 V obtained here or +4.45 V obtained with the previous nanocalorimetry method[29] corresponds to values for α(H⁺,aq) of −264.7 or −261.2 kcal mol⁻¹ (−11.5 or −11.3 eV), respectively. These values are close to the value reported by Farrell and McTigue (−260.0 kcal mol⁻¹),[16] which is obtained by using Boltzmann statistics for the integrated heat capacity of the electron for the ΔG_ion(H) value. Taking into account the fact that the electron is a fermion by using Fermi–Dirac statistics for the integrated heat capacity of the electron,[71] using updated values for ΔG_ion(H) and ΔG_at(½H₂),[62] and using the standard state convention of Kelly et al,[8] results in a revised value of −261.3 kcal mol⁻¹ for α(H⁺,aq) reported by Farrell and McTigue. A value of −260.7 kcal mol⁻¹ for α(H⁺,aq) was recently reported by Fawcett[9] from experimental data[72] and updated thermodynamic data. Our nanocalorimetry values are slightly more negative than these earlier values, but are generally in good agreement.

Conclusions

The value for the absolute SHE potential obtained from these nanocalorimetry experiments does not include effects of counterions (or other solute effects), nor do they include effects related to the solid/liquid interface between a metal electrode and solution, because these effects are absent in the nanocalorimetry measurements. However, these measurements are more direct and have several other potential advantages, including the ability to investigate counterion effects by carefully controlling the content of the nanodrop, or investigating individual electron-transfer events for redox active couples, for which transfer of multiple electrons is spontaneous. In solution, measuring hydrolysis energies can be challenging when multiple forms of the reduced ion may exist, as is the case with Cu²⁺ hydrolysis, or when the chemical form of the products are ambiguous. These gas-phase measurements could be used to provide thermodynamic values of bulk hydrolysis in such cases. Although the absolute uncertainty in the value of the absolute SHE potential obtained from these measurements is difficult to evaluate, the high precision of the method indicates that possible systematic errors could be identified by investigating different size clusters and clusters containing additional metal ions. By carefully evaluating and eliminating potential sources of systematic error, an absolute electrochemical redox scale that bridges gas-phase and solution-phase electrochemistry could be established using these methods.

Experimental Section

Nanocalorimetry

Experiments were performed on a 2.75 T Fourier transform ion cyclotron resonance mass spectrometer with an ion cell cooled to −140°C by using a regulated flow of N₂(l).[31, 32, 73] Hydrated metal ions were generated from 1 to 10 mm aqueous solutions of metal sulfate or chloride salts by means of nanoelectrospray. A potential of ~600 V relative to the heated (≈80°C) entrance capillary of the mass spectrometer was applied to a platinum wire that was in direct contact with the solution contained in a borosilicate capillary with an inner tip diameter of ≈1 µm. Ions were guided into the ion cell through five stages of differential pumping and accumulated for 4–6 s during which time dry N₂(g) was introduced to a pressure of ≈10⁻⁶ Torr to enhance thermalization and trapping of the ions. A 4–6 s delay prior to ion isolation ensured that the ions reached a steady-state internal energy distribution and allowed the cell pressure to return to <10⁻⁸ Torr prior to EC experiments. Precursors were isolated and after a 50 ms delay, electrons that were thermally generated by using a resistively heated barium–scandate impregnated cathode were introduced into the ion cell for 120 ms by pulsing the cathode housing to −1.5 V. A potential of +10 V was applied to the cathode at all other times to prevent electrons from entering the cell.

Data analysis

The average number of water molecules lost from the reduced precursor was obtained from a weighted average of the observed product-ion distribution and corrected for minor dissociation of up to 0.1 water molecules due to the absorption of blackbody infrared radiation from the ion cell, cell jacket, and from the heated cathode located 20 cm from center of the cell. Internal energies were calculated as described previously[29] by using calculated harmonic frequencies for a B3LYP/LACVP**++ energy-minimized structure of [Ca(H₂O)₁₄]²⁺. The internal energies for clusters of interest were obtained by linearly scaling the degrees of freedom of these clusters by the degrees of freedom of [Ca(H₂O)₁₄]²⁺.