Dynamics and stability of muscle activations during walking in healthy young and older adults

Abstract

To facilitate stable walking, humans must generate appropriate motor patterns and effective corrective responses to perturbations. Yet most EMG analyses do not address the continuous nature of muscle activation dynamics over multiple strides. We compared muscle activation dynamics in young and older adults by defining a multivariate state space for muscle activity. Eighteen healthy older and 17 younger adults walked on a treadmill for 2 trials of 5 minutes each at each of 5 controlled speeds (80 – 120% of preferred). EMG linear envelopes of v. lateralis, b. femoris, gastrocnemius, and t. anterior of the left leg were obtained. Interstride variability, local dynamic stability (divergence exponents) and orbital stability (maximum Floquet multipliers; FM) were calculated. Both age groups exhibited similar preferred walking speeds (p = 0.86). Amplitudes and variability of individual EMG linear envelopes increased with speed (p< 0.01), in all muscles but gastrocnemius. Older adults also exhibited greater variability in b. femoris and t. anterior (p < 0.004). When comparing continuous multivariate EMG dynamics, older adults demonstrated greater local and orbital instability of their EMG patterns (p < 0.01). We also compared how muscle activation dynamics were manifested in kinematics. Local divergence exponents were strongly correlated between kinematics and EMG, independent of age and walking speed, while variability and max FM were not. These changes in EMG dynamics may be related to increased neuromotor noise associated with aging and may indicate subtle deterioration of gait function that could lead to future functional declines.

Introduction

Falls pose serious risks to older adults (Fuller, 2000), and most falls occur during walking (Niino et al., 2000; Berg et al., 1997). Gait disorders also lead to disability in older adults (Alexander, 1996; Alexander and Goldberg, 2005). Preventing these outcomes requires a better understanding of gait dynamics. Facilitating stable walking kinematics requires generating appropriate motor patterns and effective corrective responses to perturbations. Yet how the muscle activation patterns produced by the nervous system are then reflected in the observed kinematics, or how these relationships change with aging, are not well understood.

Since muscles generate the forces that drive walking, the dynamics observed in the kinematics presumably reflect that of muscle activation patterns. However, since kinematics are much less variable than EMG patterns during gait (Winter and Yack, 1987), kinematics appear more tightly controlled than muscle activations. This could be due to inertial and damping properties of body segments that smooth individual muscle force fluctuations. Muscle activation dynamics also reflect the need to respond to perturbations and maintain stability during walking more than producing consistent kinematics. Thus, muscle activation dynamics may not be reflected in kinematics. Because each kinematic degree of freedom is controlled by multiple muscles, walking kinematics result from the coordination of many muscles. Therefore, one cannot meaningfully compare the dynamics of individual joint angles to those of individual muscles.

Gait dynamics evolve over multiple strides, where each stride depends (explicitly or implicitly) on multiple previous strides (Hausdorff et al., 2001). The local dynamic stability of walking kinematics have been well characterized (Dingwell and Kang, 2007; Granata and Lockhart, 2008; Kang and Dingwell, 2008a). However, EMG has not been characterized in this manner. Mean EMG patterns change with aging (Winter and Yack, 1987), function and pathology (Abel et al., 2005), and also exhibit walking speed-related changes in both amplitudes and timing (Shiavi, 1985; Shiavi et al., 1987; Chung and Giuliani, 1997). However, these studies did not quantify EMG dynamics over consecutive strides. Also, by using self-selected speeds, these studies did not adequately control for walking speed, which greatly influences gait dynamics independently of aging (Kang and Dingwell, 2008a; Kang and Dingwell, 2008b). Variability measures do not describe how EMG fluctuations change from one stride to the next, or how multiple muscles coordinate during walking. Clustering or principal component analysis methods quantify multivariate muscle activation patterns (Ivanenko et al., 2004; Jansen et al., 2003), but not across consecutive strides.

Dynamical systems come in many types, from a wide range of scientific disciplines (Strogatz, 1994). Mathematically, all of these systems can be analyzed using the same general set of tools, regardless of how their governing state variables are defined. For biomechanical kinematic data, various different state space definitions can yield similar final conclusions (Gates and Dingwell, 2009). Continuous EMG linear envelopes exhibit strongly periodic, but slightly a-periodic dynamics during walking, similar to those seen in walking kinematics. Thus, methods previously used to characterize the dynamic stability of walking kinematics can also be validly used to characterize the dynamic stability of muscle activations (i.e., EMG).

In this study, we measured age- and speed-related changes in interstride variability of muscle activations. We also used state-space descriptions that account for both multivariate and multi-stride dynamics. From these, local and orbital stability (Dingwell and Kang, 2007) of EMG amplitudes were quantified to describe how multiple muscles coordinate over consecutive strides. Leg muscle activations were measured in young and older adults walking at multiple controlled speeds. Thus, the effects of age were quantified independently of walking speed (Kang and Dingwell, 2008b; Kang and Dingwell, 2008a). Finally, we determined whether the dynamics of EMG patterns during walking were reflected in the associated dynamics of walking kinematics, which we reported previously (Kang and Dingwell, 2008b; Kang and Dingwell, 2008a).

Methods

Eighteen healthy older adults (age 65–85) and 17 height-, weight-, and gender-matched young adults (age 18–28), participated after providing informed consent as approved by the local institutional review board (Table 1). We excluded those who reported recent lower extremity injuries, visible gait asymmetries or disabilities, or those who were on medications that may influence gait.

Table 1.

Subject Characteristics

	Young adults	Older Adults	p-value
Gender (M/F)	12/5*	12/6	0.55**
Age (years)	23.3 ± 2.6	72.1 ± 6.0	<0.0001
Height (m)	1.73 ± 0.094	1.70 ± 0.104	0.36
Body Mass (kg)	71.1 ± 9.86	73.2 ± 12.3	0.58
Preferred Walking Speed (PWS) (m/s)	1.30 ± 0.10	1.29 ± 0.15	0.86
PWS Range (m/s)	1.16 – 1.56	0.93 – 1.52

^*Reflects the number after the data for one young subject were discarded

^**Fisher’s Exact Test (χ²)

Details of data collection are presented elsewhere (Kang and Dingwell, 2008b; Kang and Dingwell, 2008a). Subjects walked on a treadmill (Desmo S model, Woodway USA, Waukesha WI) while wearing a safety harness (Protecta International, Houston TX). Each subject’s preferred walking speed (PWS) was determined using an established protocol (Dingwell and Marin, 2006; Kang and Dingwell, 2008b; Kang and Dingwell, 2006), allowing treadmill acclimation. Subjects completed two 5-minute walking trials each at 5 different speeds (0.8×−1.2×PWS), with 2 minutes of in-between rest. The order of presentation was randomized while preventing two consecutive fast speed trials to avoid fatigue. All data from one young subject (not counted above), and 1 trial from one older subject were discarded due to technical problems (Table 1). A second older subject could not complete one 1.2×PWS trial, so this trial was also discarded. Subjects were instructed to look straight ahead and avoid extraneous movements. Kinematics were measured using Vicon 612 (Oxford Metrics, UK). Kinematic analyses are presented elsewhere (Kang and Dingwell, 2008b; Kang and Dingwell, 2008a).

Muscle activation patterns during walking were recorded using surface electromyography (EMG) (Delsys, Boston MA), using bipolar electrodes from 4 muscles of the left leg: vastus lateralis (VL), biceps femoris (BF), medial head of gastrocnemius (GA), and tibialis anterior (TA) according to the SENIAM conventions (Hermens et al., 2000). The EMG signals were sampled at 1080 Hz, bandpass filtered (passband 20–300 Hz), notch-filtered at 60 Hz using a Butterworth filter, and demeaned (MATLAB 7.04, Mathworks, Natick MA). Then, signals were normalized to the peak amplitude during the preferred walking speed trial of each person, to allow for better comparison between subjects. These normalized signals were then rectified, and low-pass filtered using a Hamming averaging window (bell-shaped curve) of 100 ms, equivalent to a low-pass filter with 10Hz cutoff (Granata et al., 2004). Once smoothed, the signal was down-sampled to 60Hz to determine the EMG linear envelopes used in subsequent analyses. Noisy sections of the signals due to static discharge, electrode dys-adhesion, etc. as identified via visual inspection were not used in subsequent analyses. In some subjects, the VL muscle was mostly inactive during slow walking speeds (Ivanenko et al., 2006). Such trials (15 out of 349 collected) were not included in the variability analysis for VL, because they would excessively lower the observed variability. Likewise, several individual trials for BF (17/349), GS (8/349), and TA (7/349) muscles were excluded due to poor signal quality. Any walking trials with any unusable EMG signal(s) (total 29/349) were not used in the stability analyses because the state-space could not be defined similarly as other trials.

For each trial, the data for each stride were normalized from 0 to 100% gait cycle. Means and standard deviations of EMG linear envelopes were calculated at each percentage of gait cycle. To determine the variability of each EMG linear envelope over the entire gait cycle, MeanSD’s were determined (Dingwell and Marin, 2006; Dingwell and Cavanagh, 2001; Kang and Dingwell, 2008b):

$$\mathit{\text{MeanSD}}={\langle \mathit{\text{SD}}(i)\rangle }_i,i\in \{0-100\%\text{gait}\text{cycle}\}$$ (1)

where SD(i) indicates the standard deviation of a measure at ith % gait cycle, and 〈 〉_i denotes the average over all i. MeanSD and average peak amplitude values were each calculated for each muscle of each trial (Figure 1).

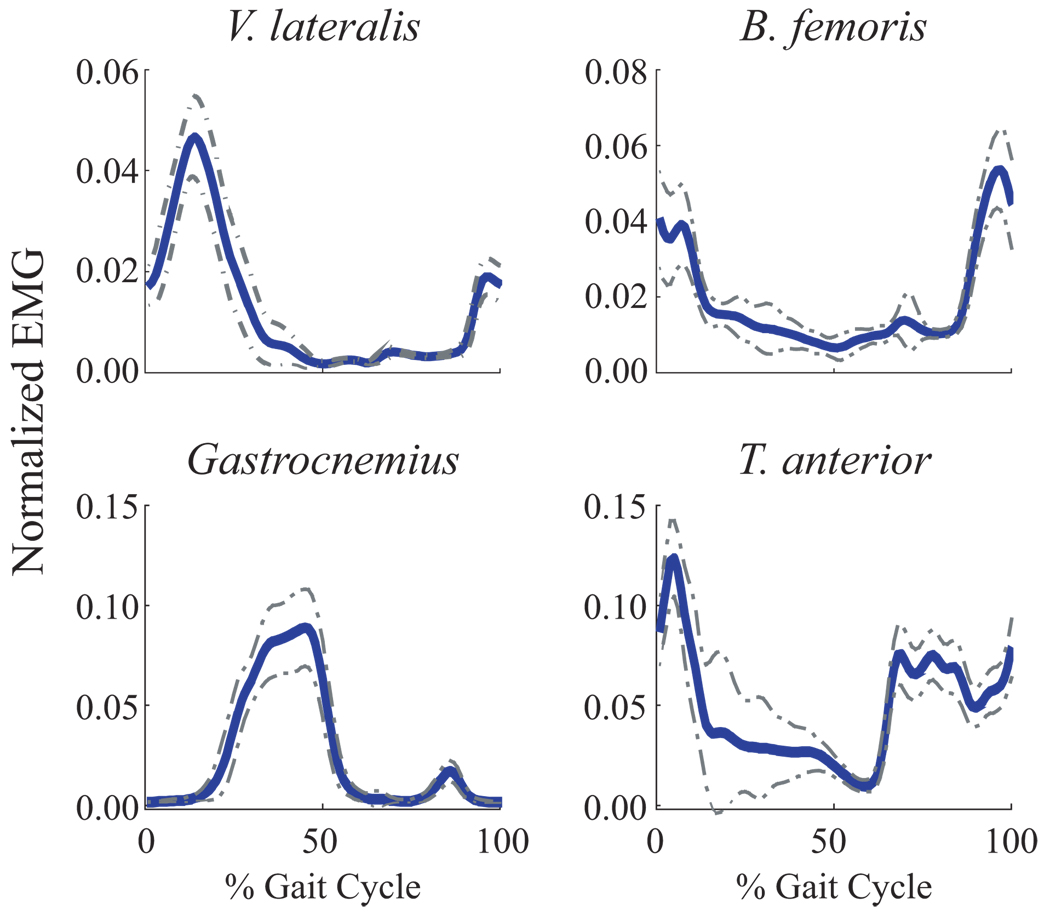
Figure 1.

Normalized (unitless) EMG Linear Envelopes from a single trial for a typical subject. The solid line represents the average and the dashed line represents ± 1 standard deviation (SD) across all strides within that trial. MeanSD was defined as the average thickness of the ± 1 SD band over the gait cycle.

Previous work showed that as few as 5 principal components can reconstruct most features of multiple EMG signals recorded during walking (Ivanenko et al., 2004; Ivanenko et al., 2006). This suggests that 5 or more state variables should be sufficient to describe the dynamics of the muscle activation patterns during walking. EMG dynamics were therefore described using the four normalized (now unitless) signals as processed above, as well as their time derivatives (Packard et al., 1980), which were non-dimensionalized by $\sqrt{l/g}$, where l = leg length (Hof, 1996). These defined an 8-dimensional unitless state-space (Figure 2A):

$$\mathbf{S}(t)=[{\mathrm{V}}_1(t){\mathrm{V}}_2(t){\mathrm{V}}_3(t){\mathrm{V}}_4(t){\dot{\mathrm{V}}}_1(t){\dot{\mathrm{V}}}_2(t){\dot{\mathrm{V}}}_3(t){\dot{\mathrm{V}}}_4(t)]\in {𝕽}^8$$ (2)

where V is the normalized linear envelope of EMG voltage, and V̇ corresponding time-derivative. Time derivatives of EMG signals were included to capture the rate of activation dynamics. A state-space of 8 dimensions is more than adequate to describe dynamics that occur in 5 dimensions (Ivanenko et al., 2004; Kennel et al., 1992).

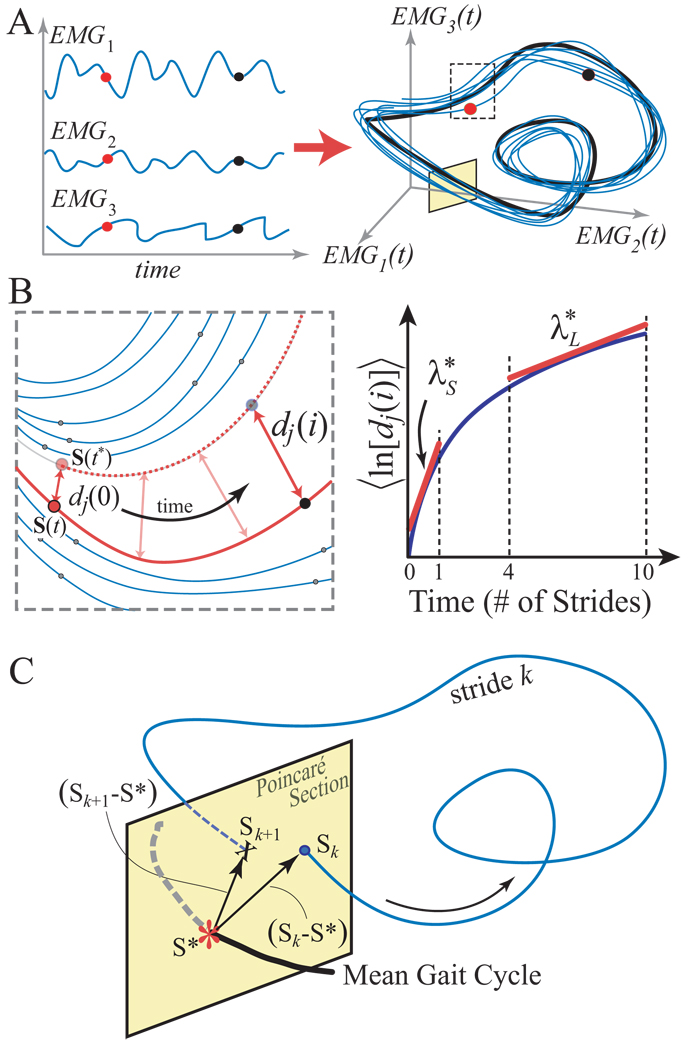
Figure 2.

Schematic representation of state space embedding and dynamic stability analyses of EMG signals. A: The original time series of each EMG signal and its derivative defined the states of the system (Eq. 2). These states were combined to form the system’s trajectory in state space (only 3 states are shown here used for illustrative purposes). B: Expanded view of a typical local region. A small perturbation moves the system at S(t) to its closest neighbor S(t^*). Local divergence is computed by measuring the Euclidean distances between the subsequent points, denoted d_j(i). The local dynamic stability is defined by how quickly, on average, the two trajectories diverge away from each other. Local rates of divergence, λ^*_s and λ^*_L , were calculated from the slopes of the mean log divergence curve (Eq. 3). C: Poincaré sections were defined to be orthogonal to the mean (i.e., limit) cycle. The system state, S_k, at stride k evolves to S_k+1 one stride later. Floquet multipliers quantify, on average, whether the distances between these states and the system fixed point, S^*, grow or decay after one cycle (Eq. 6).

The sensitivity of these multivariate EMG patterns to small inherent perturbations that naturally occur during walking were quantified in two ways. First, local dynamic stability (Figure 2B) was quantified (Dingwell and Cusumano, 2000; Kang and Dingwell, 2008a; England and Granata, 2007). Euclidean distances between neighboring trajectories in state space were computed as a function of time (Figure 2B) and averaged over many original pairs of initially nearest neighbors (Rosenstein et al., 1993). Local divergence exponents (λ^*) were estimated from the slopes of linear fits to these curves:

$$y(i)=\frac{1}{\mathrm{\Delta }t}\langle \text{ln}[d_j(i)]\rangle =[{\mathrm{\lambda }}^{*}]i+c$$ (3)

where d_j(i) was the Euclidean distance between the j^th pair of initially nearest neighbors after i discrete time steps (i.e. iΔt seconds) and 〈 · 〉 denotes the average over all values of j (Rosenstein et al., 1993). Positive exponents indicate local instability, with larger exponents indicating greater local instability, or greater sensitivity to small perturbations. Since the intrinsic time scales (i.e., average stride times) were different for each subject, the time axes of these curves were re-scaled by multiplying by the average stride frequency for each subject. Short-term exponents (λ^*_s) were calculated from the slopes of linear fits to the divergence curves between 0 and 1 stride. Long-term exponents (λ^*_L) were calculated as the slopes between 4 and 10 strides (Figure 2B) (Dingwell et al., 2000).

Second, orbital stability was quantified by calculating maximum Floquet Multipliers (FM) using established techniques (Hurmuzlu et al., 1996; Donelan et al., 2004). First, we defined a Poincaré section (Figure 2C) at each percentage of the gait cycle (0% to 100%), where 0% defined left heel strike. The system state S_k for each stride k at that Poincaré section evolved to a state at the following stride, S_k+1, according to the Poincaré map (Eq. 4):

$${\mathbf{S}}_{k+1}=\mathbf{F}({\mathbf{S}}_k)$$ (4)

We defined the limit cycle trajectory as the average trajectory across all strides within a trial. This limit cycle trajectory produces a single fixed point in each Poincaré section:

$${\mathbf{S}}^{*}=\mathbf{F}({\mathbf{S}}^{*})$$ (5)

We then computed the effects of small perturbations away from these fixed points, using a linearized approximation of Eq. (4):

$$[{\mathbf{S}}_{k+1}-{\mathbf{S}}^{*}]\approx J({\mathbf{S}}^{*})[{\mathbf{S}}_k-{\mathbf{S}}^{*}]$$ (6)

For S ∈ 𝕽⁸ , J(S *) ∈ 𝕽^8×8 had 8 eigenvalues. The first 7 eigenvalues of J(S*) defined the Floquet Multipliers (FM) that quantified how much small perturbations in the Poincaré section grew or diminished by the next cycle (Kang and Dingwell, 2008a). If these FM all have magnitude < 1, perturbations on average shrink by the next stride, and the system remains stable. We computed the magnitudes of the maximum FM for Poincaré sections at 0%, 25%, 50%, and 75% of the gait cycle, as we did previously (Kang and Dingwell, 2008a).

EMG peak amplitudes, MeanSD’s, local divergence exponents, λ^*_S, λ^*_L, and maximum FM at 0%, 25%, 50%, and 75% of the gait cycle were compared between age groups and across speeds using a general linear model analysis of variance (ANOVA) using SPSS 14 (SPSS, Chicago IL). To compare the variability and stability metrics derived from EMG and previously reported kinematics (Kang and Dingwell, 2008a), we used Pearson correlation (r), as well as general linear model analysis of covariance (ANCOVA) using SAS 9.1 (SAS Institute, Cary NC). ANCOVA was used to determine the correlation between kinematics– and EMG–derived stability metrics independent of the effects of age and speed. The ANCOVA model for each EMG–derived stability metric included age, speed, age×speed interaction, plus the corresponding kinematics-derived metric as a covariate.

Results

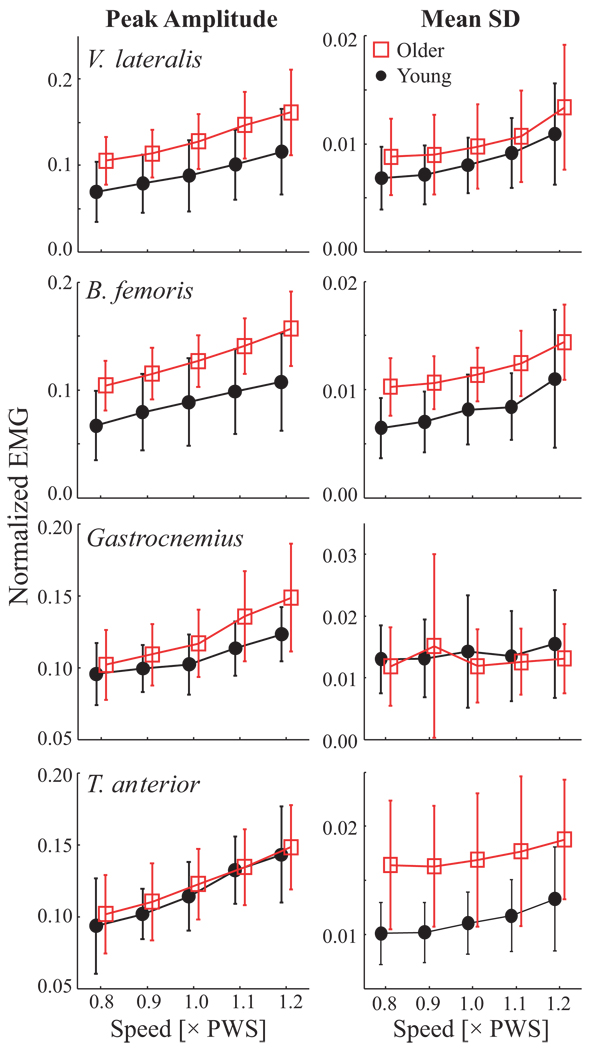
Peak EMG amplitudes increased with speed for all four muscles (p < 0.001). Older adults displayed higher amplitudes in v. lateralis (VL) (p <0.003), b. femoris (BF) (p < 0.001), and gastrocnemius (GS) (p < 0.03; Figure 2). Variability (MeanSD) of EMG increased with speed in VL, BF, and t. anterior (TA) muscles (p < 0.001; Table 2). The main effect for speed was also significant for gastronemius (p = 0.027; Table 2). However, post-hoc analyses revealed that only the 0.8×PWS and 1.2×PWS speeds were different and these differences were quite small (Fig. 3). Variability was also larger in older adults in BF (p = 0.003) and TA (p < 0.001) muscles. Interaction effects were not significant. However, MeanSD of GS was not different between age groups and speed effects were marginal (p = 0.03).

Table 2.

Effects of Age and Speed on EMG variability and dynamic stability (p-values)

		Age	Speed	Age × Speed
Interstride Variability	v. lateralis	0.18	<0.001	0.66
	b. femoris	0.003	<0.001	0.74
	gastrocnemius	0.407	0.027	0.54
	t. anterior	<0.001	<0.001	0.71
Local dynamic stability	λ* S	0.002	<0.001	0.76
	λ* L	0.98	<0.001	0.99
Orbital Stability	0%	<0.001	0.17	0.025
	25%	0.002	0.19	<0.001
	50%	<0.001	0.18	0.57
	75%	0.008	0.23	0.027

Figure 3.

Peak amplitudes and MeanSD of normalized (unitless) EMG linear envelopes vs. Age and Speed. Error bars denote between-subject standard deviations within each group. Left: Between-strides average of EMG linear envelope peak amplitudes. Amplitudes increased with speed for all four muscles (p < 0.001). Older adults displayed higher amplitudes in v. lateralis (p <0.003), b. femoris (p < 0.001), and gastrocnemius (p < 0.03). Right: MeanSD of EMG envelopes. EMG variability increased significantly with speed for v. lateralis, b. femoris, and t. anterior (all p <0.001). Older adults exhibited significantly greater variability in b. femoris (p = 0.003) and t. anterior (p < 0.001).

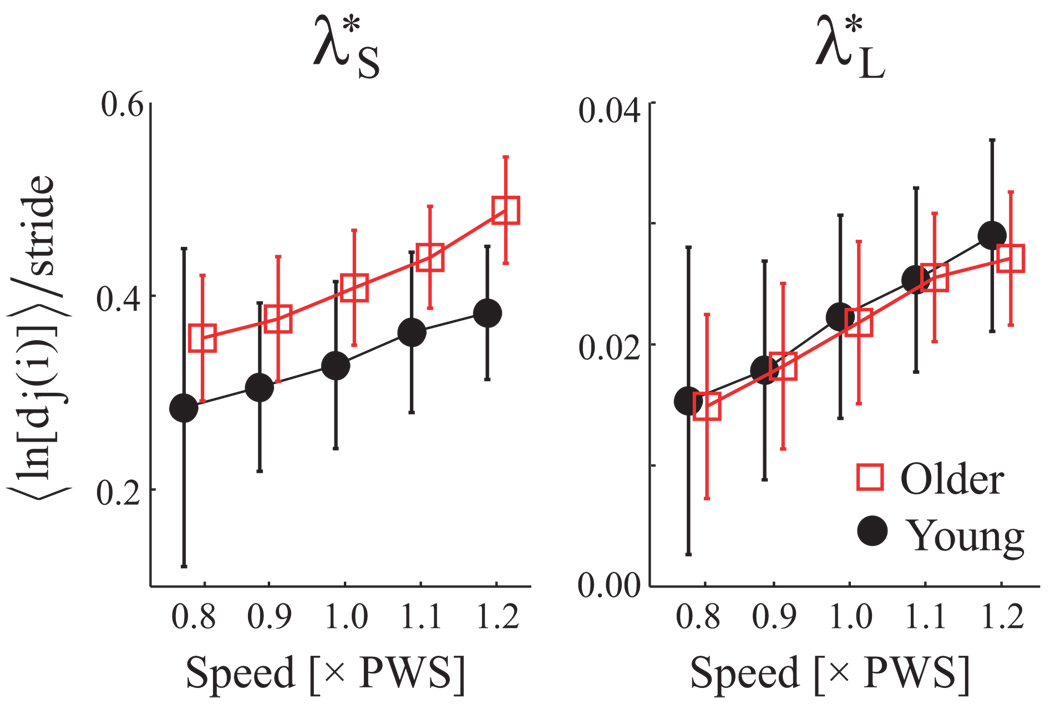
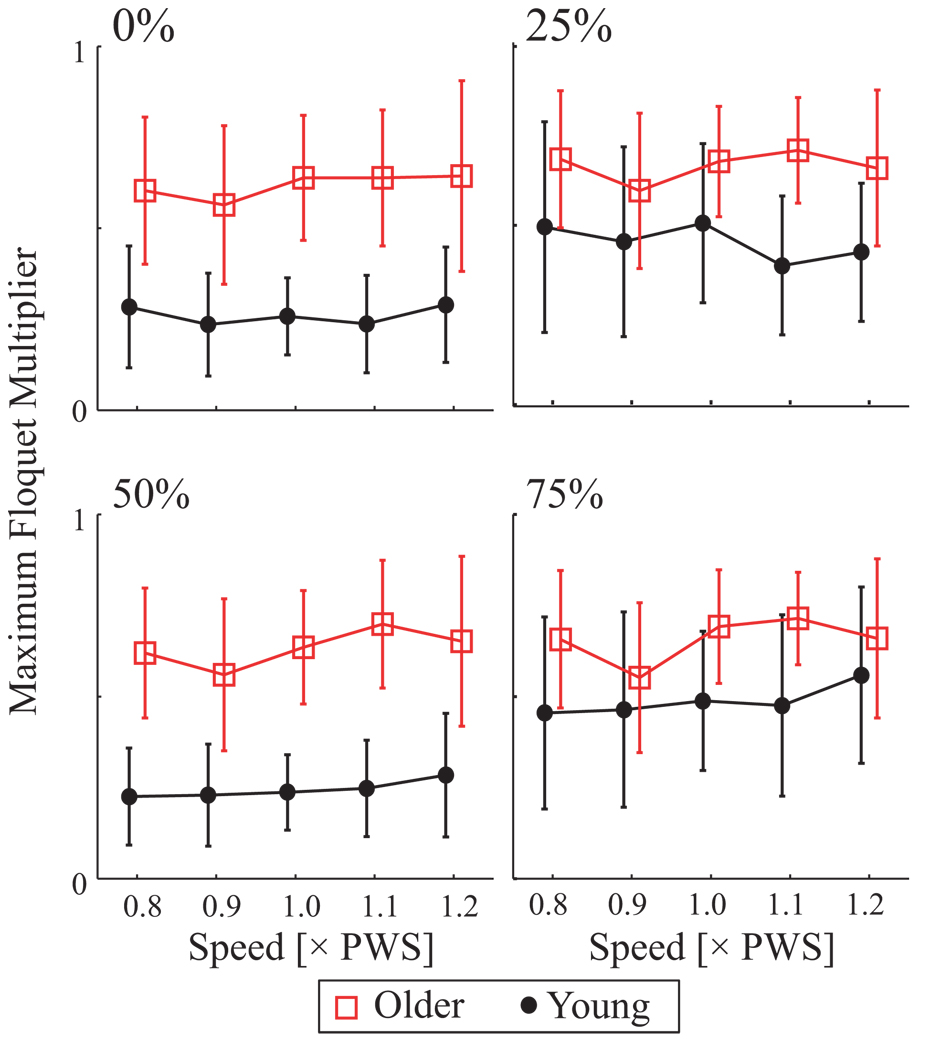
Both divergence exponents λ^*_s and λ^*_L increased with speed (p < 0.001), while λ^*_s was greater in older adults (p < 0.003; Fig 4; Table 2). Thus the EMG amplitude pattern was more sensitive to perturbations in older adults independently of speed. Maximum FM of older adults were larger at 0, 25, 50, and 75% of the gait cycle (p < 0.009; Figure 5). FM did not vary significantly with speed (p = 0.2), but interaction effects were significant at 25% (p < 0.001), where speed effects were seen only in young adults (Tukey’s LSD post-hoc p < 0.003).

Figure 4.

Short-term (λ^*_S) and long-term (λ^*_L) local divergence exponents (units = 1/stride) vs. Age and Speed. Error bars denote between-subject standard deviations within each group. All subjects became locally more unstable with increased speed (p < 0.001). Older adults exhibited larger short-term (λ^*_s) exponents relative to young subjects (p = 0.002), but no differences for long-term (λ^*_L) exponents (p = 0.980).

Figure 5.

Maximum Floquet Multipliers (FM; unitless) vs. Age and Speed for Poincaré sections taken at 0, 25, 50, and 75% of the gait cycle. Error bars denote between-subject standard deviations within each group. Older adults exhibited larger maximum FM values than Young adults (p ≤ 0.008). Maximum FM did not vary with walking speed (p ≥ 0.170). Qualitatively similar results were obtained for all Poincaré sections.

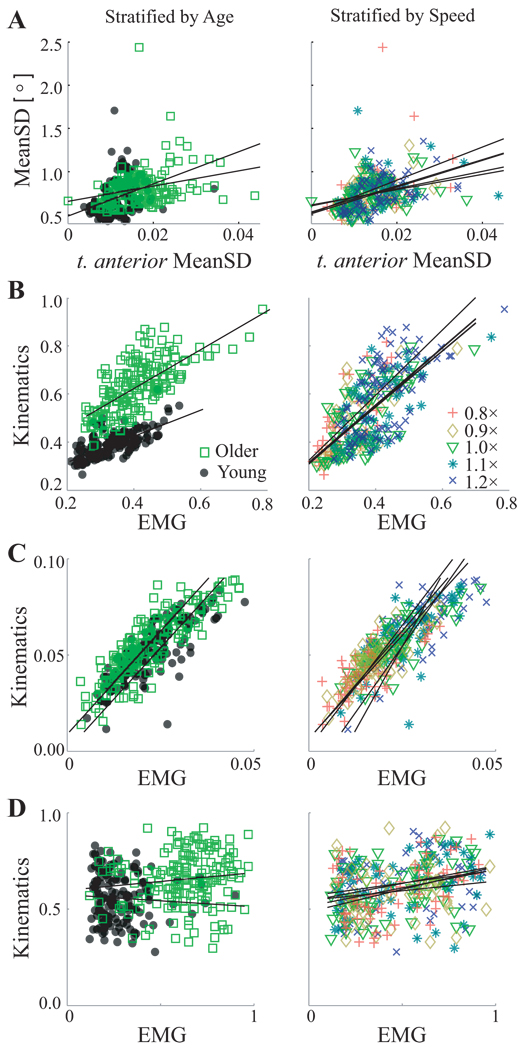
Among kinematic variability results published previously (Kang and Dingwell, 2008b), sagittal plane knee flexion/extension angle MeanSD was slightly correlated with EMG MeanSD’s for VL (r² = 0.04, p < 0.001, where r² is from Pearson r), BF (r² = 0.02, p = 0.02), and TA (r² = 0.14, p < 0.001; Fig. 6A) muscles. After accounting for age and speed in the ANCOVA model, EMG MeanSD’s for VL (R² = 0.03, p = 0.001, where R² is the proportion of variance explained by the covariate), and TA (R² = 0.07, p < 0.001), but not for BF (R² = 0.001, p = 0.5) were still significantly correlated to kinematic variability (not shown). However, these correlations were relatively weak (r² ≤ 0.14; R² ≤ 0.07). Ankle plantar/dorsiflexion angle MeanSD was also slightly correlated with EMG MeanSD’s of VL and GS (r² ≤ 0.015, p ≤ 0.026), and in the ANCOVA model, (R² = 0.014, p < 0.04).

Figure 6.

Correlations between primary dependent measures, stratified by both Age (left) and Speed (right). A: Sagittal plane knee flexion/extension variability and t. anterior variability were slightly correlated after accounting for Age and Speed effects (R² = 0.07; p < 0.001). B: Short-term (λ^*_s) local divergence exponents derived from kinematics (Kang and Dingwell, 2008a) and EMG (Fig. 4) were strongly correlated (R² = 0.38; p < 0.001). C: Longterm (λ^*_L) local divergence exponents derived from EMG and kinematics were also strongly correlated (R² = 0.52; p < 0.001). D: Maximum FM derived from kinematics (Kang and Dingwell, 2008a) and EMG (Fig. 5) were not correlated after accounting for Age and Speed effects (R² < 0.01; p = 0.41).

In contrast, both λ^*_s and λ^*_L derived from EMG-based and kinematics-based (Kang and Dingwell, 2008a) state spaces were strongly correlated (r² = 0.49 and 0.61; p < 0.001; Fig. 6). In the ANCOVA model, these relationships remained highly significant (R² = 0.38 and R² = 0.52, p < 0.001; Fig. 6). However, maximum FM measures were only slightly correlated between EMG and kinematics (r² ≤ 0.09; p < 0.001), and not correlated after accounting for age and speed effects (R² <0.01, p = 0.41).

Discussion

Older adults exhibited greater interstride variability of muscle activation patterns during gait (Fig. 3). However, motor system pathology affects gait timing dynamics over multiple strides (Hausdorff et al., 1997). Traditional EMG analyses fail to account for the continuous nature of muscle activation dynamics over multiple consecutive strides, or coordination across multiple muscles. By using novel state-space descriptions of multi-muscle activations over time, we found that older adults exhibit greater interstride dynamic instability of muscle activation patterns during gait (Fig. 4 & Fig 5). By comparing measures of EMG dynamics to those of kinematics (Fig. 6), we also demonstrate for the first time that multi-dimensional dynamics of muscle activations are reflected in that of kinematics, while interstride variability is not.

Variability of EMG patterns during gait increased with speed, except in the gastrocnemius (Fig. 3). Variability of gastrocnemius activation did not vary with age or speeds, perhaps because the activation of the plantarflexors is carefully managed, as these propulsive muscles (Neptune et al., 2007) add mechanical energy to the system. Age-related differences were seen only in b. femoris and t. anterior. This is unlike sagittal leg joint angles, which did not exhibit this speed or age relationship (Kang and Dingwell, 2008b), and showed only small correlations (r² ≤ 0.14; R² ≤ 0.07) with that of EMG. Thus, interstride variability of EMG patterns is only marginally reflected in that of kinematics. This validated the idea that comparing activation patterns of individual muscles with individual kinematic variables cannot account for the coordination and synergies of multiple muscles.

EMG patterns in older adults exhibited greater local (Fig. 4) and orbital (Fig. 5) instability, similar to their kinematics (Kang and Dingwell, 2008a). Thus, muscle activation patterns may be more easily perturbed in these older adults, which may explain the similar kinematics results. Older adults exhibit increased EMG response latencies to perturbations (Lin and Woollacott, 2002; Pijnappels et al., 2005). The increased λ^*_s and maximum FM observed during unperturbed walking likely reflect the slowed responses to perturbations.

Our state-space analyses also demonstrated that local instability of the multivariate dynamics of kinematics and EMG were strongly correlated (Fig. 6), even after accounting for age and speed differences. Thus, the local stability properties of multivariate EMG dynamics are manifested in the multivariate dynamics of kinematics. Howver, since muscle activations measured using EMG do not represent muscle forces, it is not yet clear how these muscle activation dynamics generate the muscle forces that lead to the observed kinematics. Dynamic simulation studies could help address these questions.

This study only included very healthy older adults. Therefore, our findings may not translate directly to understanding risk for falls. However, we found differences in muscle activation dynamics even in healthy older adults who had no prior history of falls and who did not exhibit slower walking speeds that might otherwise indicate functional decline (Alexander, 1996). Therefore, the observed changes in muscle activation dynamics may be a precursor to future functional declines. Detecting these changes early may help prevent further loss of gait function. This needs to be tested in a clinical outcomes study.

The mechanisms that generate muscle activations to produce normal gait appear to give rise to state-space attractor (Nayfeh and Balachandran, 1995). These mechanisms likely involve spinal central pattern generators (Shik and Orlovsky, 1976; Ivanenko et al., 2006) and sensory feedback. These neural structures may deteriorate with aging, and thus may not be able to respond as easily to perturbations to restore normal gait. This deterioration could arise from increased neuromotor noise (Dean et al., 2007; Faisal et 2008) or randomness (Hausdorff et al., 1997) that occurs with aging, and which could alter the internal dynamics of the attractor. Deteriorated brain function associated with diminished cognitive function or motor system diseases leads to gait problems in older adults (Allali et al., 2007; Atkinson et al., 2007; Ben-Itzhak al., 2008; Holtzer et al., 2006). Future work should investigate the roles of noise in the nervous system brain function in the gait of older adults.