Abstract
One key issue that must be addressed during the development of image segmentation algorithms is the accuracy of the results they produce. Algorithm developers require this so they can see where methods need to be improved and see how new developments compare with existing ones. Users of algorithms also need to understand the characteristics of algorithms when they select and apply them to their neuroimaging analysis applications. Many metrics have been proposed to characterize error and success rates in segmentation, and several datasets have also been made public for evaluation. Still, the methodologies used in analyzing and reporting these results vary from study to study, so even when studies use the same metrics their numerical results may not necessarily be directly comparable. To address this problem, we developed a web-based resource for evaluating the performance of skull-stripping in T1-weighted MRI. The resource provides both the data to be segmented and an online application that performs a validation study on the data. Users may download the test dataset, segment it using whichever method they wish to assess, and upload their segmentation results to the server. The server computes a series of metrics, displays a detailed report of the validation results, and archives these for future browsing and analysis. We applied this framework to the evaluation of 3 popular skull-stripping algorithms – the Brain Extraction Tool (Smith, 2002), the Hybrid Watershed Algorithm (Ségonne et al., 2004), and the Brain Surface Extractor (Shattuck et al., 2001) under several different program settings. Our results show that with proper parameter selection, all 3 algorithms can achieve satisfactory skull-stripping on the test data.
Index Terms: validation, segmentation, MRI, skull-stripping
I. Introduction
The development of computational approaches for medical image analysis requires appropriate validation methodologies to assess their performance. This validation is important so that algorithm developers can understand the ways in which existing algorithms could be improved, so that they can compare their own methods with those of others, and so that users of algorithms can understand the characteristics of algorithms that they may select for a particular data processing stream. There are several reasons why validation is of great importance in medical imaging, as these algorithms may ultimately be used in decisions that affect patient treatment. Even algorithms that are not used directly in clinical application may be used as part of processing sequences for studies that have implications for drug trials, public policy, or even legal arguments.
The importance of validation in medical image processing is well-recognized, and much effort has been undertaken to develop tools and methods related for it. One of the early standards used in medical image validation was the Shepp-Logan phantom, which was developed for computed tomography (CT) (Shepp and Logan, 1974). This phantom was constructed from a set of 10 overlapping ellipses that produced a 2D map of attenuation values, with each ellipse contributing a different attenuation constant. This image shares basic shape properties with those of a scan of a human brain, and was still described completely by a table with 6 numbers per ellipse. More recently in the MRI brain imaging community, datasets made publicly available via the Internet have had a large impact. The Internet Brain Segmentation Repository (IBSR)1 provides several datasets that have been delineated using manually-guided processes. The IBSR website also provides similarity metrics computed on the results produced by several algorithms, thereby providing developers of new algorithms with a basis for comparison. Another dataset that has emerged as a standard in brain imaging is the BrainWeb digital phantom 2, which was constructed based on a high-resolution image from one individual (Collins et al., 1998). The BrainWeb site provides several versions of this scan, at different resolutions, noise levels, and with various degrees of RF nonuniformity. The site was later extended to provide templates produced from 20 additional individuals (Aubert-Broche et al., 2006).
Both the IBSR and BrainWeb datasets have been used in several publications (e.g., Rajapakse and Kruggel, 1998; Pham and Prince, 1999; Zeng et al., 1999; Zhang et al., 2001; Shattuck et al., 2001; Marroquin et al., 2002; Tohka et al., 2004, 2007; Bazin and Pham, 2007) and have played a key role in the validation and improvement of image processing algorithms. One benefit of this has been that users can compare their results on the data with those that have been published previously. However, there may be cases where results are not directly comparable across publications. For example, studies may use different subsets of the available data.
There have been several studies performed to evaluate multiple medical image processing approaches. These have included registration comparisons, such as an evaluation of 4 different approaches performed by Strother et al. (1994). West et al. (1997) performed a large-scale study in which numerous registration algorithms were compared. The developers of each algorithm were invited to perform the registration of the test data, and then their results were evaluated independently. Arnold et al. (2001) performed an evaluation of 6 bias field correction algorithms, also with some interaction with the developers of the individual algorithms. Boesen et al. (2004) evaluated 4 different skull-stripping methods. That work also introduced a web-based evaluation service, termed Brain Extraction Evaluation (BEE)3, through which users could download the set of 15 test MRI volumes used in the paper and submit their segmented data for evaluation and have their results e-mailed to them. The Bioinformatics Resource Network (BIRN) sponsored an additional evaluation of skull-stripping algorithms, in which 4 publicly available methods were applied to 16 data volumes (Fennema-Notestine et al., 2006). For that study, the authors of each algorithm were invited to participate by suggesting parameters based on their own tests on practice data (3 of the 4 elected to participate). The data processing was then performed without further input from the developers.
At the 2007 conference on Medical Image Computing and Computer-Assisted Intervention (MICCAI), two segmentation competitions were held as part of a workshop (van Ginneken et al., 2007). Participants were able to segment test data for one of two problems: caudate segmentation or liver segmentation. For both segmentation problems, a training set and a test set were provided to interested participants prior to the conference. A second test set was provided on the day of the workshop and had to be segmented within 3 hours after it was made available. The results were ranked using a set of metrics. The life of this competition extends beyond the conference, as two websites4 have been established to provide access to the results from the competition. These sites also allow existing and new participants to submit new results for evaluation. Additional segmentation competitions were held during the 2008 MICCAI conference5.
We make a few observations based on some of the validation studies that have been performed. First, since researchers often struggle with identifying ways to validate their methods, the public availability of reference datasets is of clear benefit to the medical imaging community. Second, when researchers publish descriptions and comparisons of their own algorithms, the algorithm they are publishing typically performs the best in their evaluation. This could indicate an intentional bias on the part of the group performing the comparison; however, other possible explanations also exist. Researchers are unlikely to publish methods that don’t perform as well as the state of the art, as this would reduce their own motivation to publish as well as reduce the likelihood of acceptance by their peers during the review process. Additionally, researchers are most familiar with their own algorithms, and thus may not be sufficiently experienced with the existing methods to tune them appropriately to the test data. Third, metrics that are published in separate publications are not always comparable, as the testing procedures and assumptions may differ even when the same assessment metrics and data are used. Finally, evaluation methods such as the ones performed by BIRN or MICCAI, where each algorithm developer was allowed to participate in the parameter selection process or in the data processing, are likely to provide an opportunity for each algorithm tested to perform well. We note that these results may differ from what an actual end-user of the algorithm may experience in practice.
In this paper, we introduce a web-based resource that provides automatic evaluation of segmentation results, specifically for the problem of identifying brain versus non-brain in T1-weighted MRI. Skull-stripping is often one of the earliest stages in computational analysis of neuroimaging, and it can have an impact on downstream processing such as intersubject registration or voxel-based morphometry (Acosta-Cabronero et al., 2008). In spite of the many programs developed for skull-stripping, neuroimaging investigators often resort to manual cleanup or completely manual removal of non-brain tissues.
The online resource that we have developed works as follows. Registered users are allowed to download a set of 40 T1-weighted whole-head MRI that have been manually labeled, process the data according to their method of choice, and then upload the segmented data to the web-server. An application on the server then computes a series of metrics and presents these to the user through a series of navigable webpages. These results are also archived on the server so that results from multiple methods can be compared, and the archived results are provided on the webserver. To examine the utility of our new framework, we used it to perform an examination of 3 popular skull-stripping methods – Hybrid Watershed (Ségonne et al., 2004), Brain Extraction Tool (Smith, 2002), and our own Brain Surface Extractor (Shattuck et al., 2001).
II. Materials and Methods
A. Validation data set
We produced a ground truth data set based on MRI volumes from 40 normal research volunteers. For each subject MRI, we generated a manually edited brain mask volume, which labeled each voxel as being brain or non-brain, and a structure label volume, which identified 56 anatomical areas in the MRI on a voxel-by-voxel basis (see Table II for a list of structures that were labeled). Additionally, our validation data set included a nonlinear mapping from the native scan space of each subject volume to the ICBM452 5th-order warp atlas (Rex et al., 2003), which allowed us to map segmentation results between the native space of each scan and a canonical reference space. The test data were derived from data that we had used in previous studies, including the production of a brain atlas termed the LONI Probabilistic Brain Atlas (LPBA40) (Shattuck et al., 2008). We describe the data acquisition processing in greater detail below, including the relevant details of processing that occurred as part of other studies.
TABLE II.
Structure sensitivity metrics (mean + S.D.), shown for each of the 3 algorithms compared using the settings that produced the highest Jaccard similarity scores. With the exception of the brainstem, HWA had the highest sensitivity for all structures In reply to: the atlas.
| BET2.1 | BSE08a | HWA3 | |
|---|---|---|---|
| L. superior frontal gyrus | 0.9521 ± 0.0189 | 0.9753 ± 0.0208 | 0.9998 ± 0.0004 |
| R. superior frontal gyrus | 0.9496 ± 0.0216 | 0.9749 ± 0.0222 | 0.9998 ± 0.0005 |
| L. middle frontal gyrus | 0.9377 ± 0.0262 | 0.9645 ± 0.0248 | 0.9998 ± 0.0004 |
| R. middle frontal gyrus | 0.9346 ± 0.0256 | 0.9682 ± 0.0229 | 0.9996 ± 0.0008 |
| L. inferior frontal gyrus | 0.9381 ± 0.0242 | 0.9653 ± 0.0331 | 0.9997 ± 0.0005 |
| R. inferior frontal gyrus | 0.9430 ± 0.0252 | 0.9698 ± 0.0274 | 0.9997 ± 0.0004 |
| L. precentral gyrus | 0.9810 ± 0.0082 | 0.9825 ± 0.0112 | 0.9997 ± 0.0004 |
| R. precentral gyrus | 0.9811 ± 0.0071 | 0.9834 ± 0.0092 | 0.9996 ± 0.0006 |
| L. middle orbitofrontal gyrus | 0.9324 ± 0.0253 | 0.9249 ± 0.0598 | 0.9975 ± 0.0027 |
| R. middle orbitofrontal gyrus | 0.9296 ± 0.0299 | 0.9279 ± 0.0626 | 0.9971 ± 0.0045 |
| L. lateral orbitofrontal gyrus | 0.8856 ± 0.0529 | 0.9389 ± 0.0807 | 0.9962 ± 0.0034 |
| R. lateral orbitofrontal gyrus | 0.8893 ± 0.0561 | 0.9392 ± 0.0864 | 0.9958 ± 0.0043 |
| L. gyrus rectus | 0.8999 ± 0.0413 | 0.8780 ± 0.1311 | 0.9999 ± 0.0001 |
| R. gyrus rectus | 0.8881 ± 0.0487 | 0.8773 ± 0.1287 | 0.9999 ± 0.0002 |
| L. postcentral gyrus | 0.9661 ± 0.0178 | 0.9778 ± 0.0151 | 0.9993 ± 0.0008 |
| R. postcentral gyrus | 0.9707 ± 0.0135 | 0.9802 ± 0.0101 | 0.9993 ± 0.0008 |
| L. superior parietal gyrus | 0.9753 ± 0.0157 | 0.9789 ± 0.0121 | 0.9997 ± 0.0005 |
| R. superior parietal gyrus | 0.9750 ± 0.0174 | 0.9785 ± 0.0159 | 0.9997 ± 0.0005 |
| L. supramarginal gyrus | 0.9512 ± 0.0249 | 0.9716 ± 0.0190 | 0.9988 ± 0.0018 |
| R. supramarginal gyrus | 0.9554 ± 0.0194 | 0.9718 ± 0.0266 | 0.9986 ± 0.0019 |
| L. angular gyrus | 0.9516 ± 0.0251 | 0.9655 ± 0.0237 | 0.9996 ± 0.0008 |
| R. angular gyrus | 0.9561 ± 0.0234 | 0.9670 ± 0.0251 | 0.9995 ± 0.0007 |
| L. precuneus | 0.9944 ± 0.0103 | 0.9907 ± 0.0135 | 1.0000 ± 0.0000 |
| R. precuneus | 0.9950 ± 0.0080 | 0.9922 ± 0.0091 | 1.0000 ± 0.0000 |
| L. superior occipital gyrus | 0.9180 ± 0.0423 | 0.9663 ± 0.0254 | 1.0000 ± 0.0001 |
| R. superior occipital gyrus | 0.9155 ± 0.0577 | 0.9621 ± 0.0338 | 1.0000 ± 0.0001 |
| L. middle occipital gyrus | 0.9270 ± 0.0284 | 0.9646 ± 0.0235 | 0.9999 ± 0.0002 |
| R. middle occipital gyrus | 0.9335 ± 0.0258 | 0.9647 ± 0.0189 | 0.9998 ± 0.0005 |
| L. inferior occipital gyrus | 0.9728 ± 0.0204 | 0.9792 ± 0.0183 | 0.9999 ± 0.0001 |
| R. inferior occipital gyrus | 0.9749 ± 0.0176 | 0.9728 ± 0.0303 | 1.0000 ± 0.0001 |
| L. cuneus | 0.9519 ± 0.0298 | 0.9705 ± 0.0194 | 1.0000 ± 0.0001 |
| R. cuneus | 0.9543 ± 0.0299 | 0.9648 ± 0.0243 | 1.0000 ± 0.0002 |
| L. superior temporal gyrus | 0.9461 ± 0.0272 | 0.9603 ± 0.0472 | 0.9983 ± 0.0014 |
| R. superior temporal gyrus | 0.9364 ± 0.0299 | 0.9548 ± 0.0614 | 0.9984 ± 0.0014 |
| L. middle temporal gyrus | 0.9540 ± 0.0229 | 0.9607 ± 0.0538 | 0.9983 ± 0.0012 |
| R. middle temporal gyrus | 0.9548 ± 0.0213 | 0.9584 ± 0.0593 | 0.9982 ± 0.0013 |
| L. inferior temporal gyrus | 0.9195 ± 0.0440 | 0.9493 ± 0.0814 | 0.9984 ± 0.0018 |
| R. inferior temporal gyrus | 0.9183 ± 0.0455 | 0.9451 ± 0.0849 | 0.9986 ± 0.0011 |
| L. parahippocampal gyrus | 0.9864 ± 0.0125 | 0.9667 ± 0.0616 | 0.9998 ± 0.0012 |
| R. parahippocampal gyrus | 0.9883 ± 0.0114 | 0.9644 ± 0.0560 | 1.0000 ± 0.0001 |
| L. lingual gyrus | 0.9991 ± 0.0017 | 0.9932 ± 0.0198 | 1.0000 ± 0.0000 |
| R. lingual gyrus | 0.9994 ± 0.0019 | 0.9921 ± 0.0229 | 1.0000 ± 0.0000 |
| L. fusiform gyrus | 0.9761 ± 0.0149 | 0.9748 ± 0.0620 | 0.9998 ± 0.0004 |
| R. fusiform gyrus | 0.9712 ± 0.0183 | 0.9674 ± 0.0697 | 0.9998 ± 0.0004 |
| L. insular cortex | 1.0000 ± 0.0000 | 0.9877 ± 0.0721 | 1.0000 ± 0.0000 |
| R. insular cortex | 1.0000 ± 0.0000 | 0.9768 ± 0.1030 | 1.0000 ± 0.0000 |
| L. cingulate gyrus | 1.0000 ± 0.0000 | 1.0000 ± 0.0000 | 1.0000 ± 0.0000 |
| R. cingulate gyrus | 1.0000 ± 0.0000 | 1.0000 ± 0.0000 | 1.0000 ± 0.0000 |
| L. caudate | 1.0000 ± 0.0000 | 1.0000 ± 0.0000 | 1.0000 ± 0.0000 |
| R. caudate | 1.0000 ± 0.0000 | 1.0000 ± 0.0000 | 1.0000 ± 0.0000 |
| L. putamen | 1.0000 ± 0.0000 | 1.0000 ± 0.0000 | 1.0000 ± 0.0000 |
| R. putamen | 1.0000 ± 0.0000 | 1.0000 ± 0.0000 | 1.0000 ± 0.0000 |
| L. hippocampus | 0.9997 ± 0.0014 | 0.9744 ± 0.1092 | 1.0000 ± 0.0000 |
| R. hippocampus | 0.9996 ± 0.0019 | 0.9738 ± 0.1101 | 1.0000 ± 0.0000 |
| cerebellum | 0.9514 ± 0.0571 | 0.9443 ± 0.1578 | 1.0000 ± 0.0001 |
| brainstem | 0.9453 ± 0.0216 | 0.9973 ± 0.0071 | 0.9848 ± 0.0113 |
1) Subjects
40 volunteers were scanned with MRI at the North Shore - Long Island Jewish Health System (NSLIHS). Inclusion criteria for healthy volunteers included ages 16 to 40 and denial of any history of psychiatric or medical illness as determined by clinical interview. Exclusion criteria for all study participants included serious neurological or endocrine disorder, any medical condition or treatment known to affect the brain, or meeting DSM-IV criteria for mental retardation. The volunteer group was composed of 20 males and 20 females; average age at the time of image acquisition [mean ± S.D.] was 29.20yr±6.30 (min = 19.3, max = 39.5). The subjects had an average education level of 2.90 ± 1.04, on a scale from 1 (completed graduate school) to 7 (partial completion of elementary school), where a score of 2 reflects completing college (16 years of education) and a score of 3 reflects completing part of college (12–16 years of education) (Hollingshead and Redlich, 1958; Hollingshead, 1975). The subjects were ethnically diverse, as described by self-selected categories (‘Asian or Pacific Islander’: 4 subjects; ‘Black not of Hispanic Origin’: 7 subjects; ‘Hispanic’: 5 subjects; ‘White not of Hispanic Origin’: 23 subjects; ‘Other’: 1 subject).
2) Data acquisition
High-resolution 3D Spoiled Gradient Echo (SPGR) MRI volumes were acquired on a GE 1.5T system as 124 contiguous 1.5-mm coronal brain slices (TR range 10.0ms–12.5ms; TE range 4.22ms – 4.5ms; FOV = 220mm or 200mm; flip angle 20°) with in-plane voxel resolution of 0.86mm (38 subjects) or 0.78mm (2 subjects). Data were transmitted to the UCLA Laboratory of Neuro Imaging (LONI) for analysis following IRB approved procedures of both NSLIJHS and UCLA.
3) Cerebrum extraction
As part of an earlier study, the 40 subject MRI volumes were processed to extract the cerebrum and to align the brains rigidly to a canonical space; this processing was done in accordance with protocols used by LONI. To ensure unbiased anatomical decisions during the delineation process, each MRI volume was first aligned to the MNI-305 average brain (181 × 217 × 181 voxels; voxel size 1 × 1 × 1mm 3) (Evans et al., 1993) to correct for head tilt and alignment. The alignment was performed with a rigid-body rotation to preserve the native dimensions of the subject. Within each MRI volume, ten standard anatomical landmarks were identified manually in all three planes of section by a trained operator (see (Narr et al., 2002; Sowell et al., 1999) for details on this procedure). The landmarks for the subject were then matched with a set of corresponding point locations defined on the MNI-305 average brain; the landmarks were matched using a least-squares fit to produce a six parameter linear transformation (three-translation, three-rotation rigid-body, no rescaling). This computation was performed using the Register software package6 (MacDonald et al., 1994). Each image volume was then resampled into a common coordinate system using trilinear interpolation. The resampled image volumes had the same dimensions and resolution as the atlas. Magnetic field inhomogeneities were corrected using a non-parametric non-uniformity normalization method (nu_correct) (Sled et al., 1998). Extra-meningeal tissue in the resampled data was then removed using the Brain Extraction Tool (BET) (Smith, 2002). Errors in the automated segmentation of the brain were corrected manually; the cerebellum and brainstem were also removed manually to produce a cerebrum mask.
4) Structure labels
The MRI data were labeled during the development of the LPBA40 atlases (Shattuck et al., 2008). A group of 15 raters labeled a set of 56 structures in each of the 40 brain MRIs. The structures labeled included 25 cortical areas and 2 subcortical areas in each hemisphere, the cerebellum, and the brainstem (see Table II for a complete list). The delineation space for each subject was the subject’s MRI after alignment to the MNI-305 average brain.
5) Atlas transforms
As part of the LPBA40 construction, each brain volume was aligned to the ICBM452 5th-order warp atlas (Rex et al., 2003) using a 5th-order nonlinear transformation computed by the AIR 5.2.5 software package (Woods et al., 1998). For that alignment, brain-only masks were generated by performing mathematical morphology operations on the union of the cerebrum masks and the structure labels.
6) Manually-delineated whole brain masks
We produced manually-delineated whole brain masks for the 40 subject MRI. For each subject, we produced an initial brain mask by taking the union of the voxels that were contained in the cerebrum mask and structure label volumes. Since the protocols for performing the labeling emphasized grey matter, some areas of white matter and some CSF spaces such as the 4th ventricle were not included in this mask. Raters then used BrainSuite to fill brain areas that had not been included and also to exclude any additional voxels that were determined not to be brain. These operations were performed in the delineation space for each subject, and any remaining internal cavities in the brain masks were filled. The labels and brain masks were then resampled to the space of the subject’s original MRI using nearest-neighbor interpolation. Any internal cavities or disjoint brain voxels in the resampled brain masks were removed using a connected-components labeling program. These 40 brain masks constitute our gold standard data for our evaluation procedure; we used these in conjunction with the atlas transforms and the region labels as described below.
B. Evaluation metrics
We describe several metrics that are often used for evaluation of two binary segmentations of the same structure in an image. Let X be the set of all voxels in the image. We define the ground truth T ε X as the set of voxels that were labeled as brain by the expert. Similarly, we define S ε X as the set of voxels that were labeled as brain by the algorithm or method being tested.
1) Success and error rates
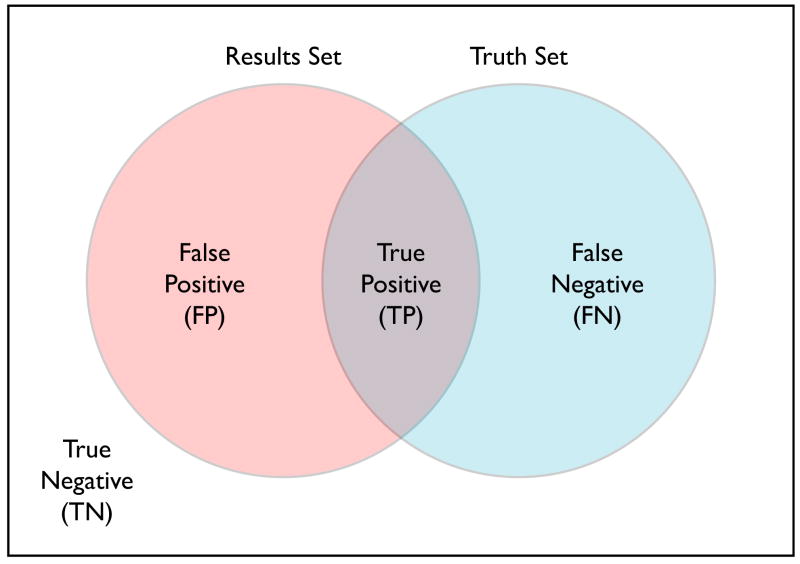
The true positive (TP) set is defined as TP = T ∩ S, i.e., the set of voxels common to T and S. The true negative set is defined as TN = T̄ ∩ S̄, i.e., the set of voxels that were labeled as non-brain in both sets. Similarly, the false positive set is FP = T̄ ∩ S̄ and the false negative set is FN = T ∩ S̄. We note that these sets are disjoint and cover X, i.e., X = TP ∪ FP ∪ FN ∪ TN. Figure 1 shows the relationship of these subsets of the image.
Fig. 1.
Set matching indicated are the true negative, false positive, false negative, and true positive areas.
From these sets, success and error rates can be computed:
| (1) |
| (2) |
| (3) |
| (4) |
where |A| is the size of a set A. Because of the simple relationships between sensitivity and false negative rate and between specificity and false positive rate, we computed only the sensitivity and specificity.
2) Set similarity metrics
Two additional metrics that are frequently used in set comparsion are the Jaccard similarity metric (Jaccard, 1912), also known as the Tanimoto coefficient, and the Dice coefficient (Dice, 1945), which has been shown to be a special case of the kappa statistic (Zijdenbos et al., 1994). The Jaccard similarity metric for two sets is defined as size of the intersection of the two sets divided by the size of their union, or
| (5) |
The Dice coefficient is defined as the size of the intersection of two sets divided by their average size, or
| (6) |
3) Sensitivity rates in subparcellated areas
Since the 40 volumes in the LPBA40 data were manually segmented into multiple anatomical structures, we computed success rates within each of these regions. We defined the label set Li as the set of voxels labeled as structure i in the ground truth data. We then computed metrics within the domain of Li, thus comparing the sets T ∩ Li and S ∩ Li.
We note that none of the voxels categorized as true negative or false positive were in the areas that have regional labels, since Li ε T, i.e., all of the labeled voxels were in the set of brain voxels in the ground truth brain. Thus, |FP ∩ Li| = 0 and |TN ∩ Li| = 0 and the Jaccard index is then represented by
| (7) |
which is equivalent to the sensitivity measure computed over Li. We used this to compute a regional sensitivity measure,
| (8) |
which represents the fraction of voxels within the labeled area that were included in S, the test mask. We emphasize that this measure did not include false positives, since these were not assigned anatomical labels in the atlas data.
4) Projection maps
As mentioned above, our test data included a set of non-linear transformations that align each subject MRI in its native space to the ICBM452 5th-order warp atlas. We applied these transformations to the FP, FN, TP, and TN sets to generate visual maps of the locations of segmentation errors and successes in the atlas space. For each test image, we computed a corresponding image where each voxel was labeled based on its membership in {TP, TN, FP, FN} using corresponding integer values, {1, 2, 3, 4}. We then resampled these labels using the native-to-ICBM452 transforms with nearest-label interpolation. For each of the four categories, we computed a volume by counting, at each voxel location, the number of subjects that had that label at that voxel. This produced spatial maps of the correctly and erroneously segmented regions of the brain for all 40 subjects, and thus provided a means to explore trends in the data. To provide a simple method of visualizing these volumes, we computed 2D images for axial, sagittal, and coronal views by summing the counts along the respective axis and dividing by the number of subjects. In our initial test, the images mapping the False Positive and False Negative counts provided the most utility, as they showed where the algorithms being tested were in error. Each pixel in these 2D images represents the number of error voxels (false positive or false negative) along a projected ray through that coordinate and perpendicular to the image plane, averaged across all subjects. We selected these two types of maps for use in our web-based system.
C. Web-based test environment
We implemented a web-based test environment using the data and metrics described above; this site is available at http://sve.loni.ucla.edu. The system was developed using Apache Server v.2.2 and Apache Tomcat v.5.0 running on a VMWare virtual linux installation sharing an 8-core physical machine. We developed the website with 3 levels of user access. Any visitor can access the documentation and see the archived results. Users who are registered for general access to the Laboratory of Neuro Imaging’s website are automatically granted download privileges. The registration process is automatic following submission of a web-based form providing the name, e-mail, institution and country of the user; this information is used for grant purposes. Additionally, users may request upload privileges, which requires specification of a screenname that will be associated with any uploaded results. Registered users may download the 40 subject MRI data set, which consists of the volumes in the native space without any pre-processing other than file-type conversion. The users may then perform skull-stripping on all of the 40 image volumes, and upload their segmentation results to the server along with a description of which program or method was used to process the data, any settings or parameters that were used, and additional comments. Upon upload of the data, the server uses a Tomcat servlet to execute a set of programs that compare the uploaded brain mask images to the hand-labeled masks. The first program computes the TP, TN, FP, FN, Sensitivity, Specificity, Jaccard, Dice and regional specificity measures for each uploaded image compared to the ground truth data. A second program applied the sets of warps to the images to produce the projection maps of TP, TN, FP, and FN. These results are then presented to the user. The uploaded data are archived on the server; the program parameters, values, product images, and the location of the archived data are stored in a MySQL database. The website also provides an interface to the results archive, allowing visitors to examine previously computed results. This facilitated comparison of different methods and parameter settings based on the different measures that were computed.
D. Testing of 3 skull-stripping algorithms
As a test of our validation framework, we performed an example comparison using 3 skull-stripping algorithms that are often used in neuroimaging studies. The methods tested were FSL’s Brain Extraction Tool (Smith, 2002), our own Brain Surface Extractor (BSE) (Shattuck et al., 2001), and FreeSurfer’s Hybrid Watershed Algorithm (HWA) (Ségonne et al., 2004).
1) Brain Extraction Tool
BET uses a deformable model to extract the brain. We used BET2.1, which is included as part of the FSL 4.1 package. The script for BET offers the following options that may improve the results:
-R: robust brain centre estimation (iterates BET several times)
-S: eye and optic nerve cleanup
-B: bias field and neck cleanup
We ran the command bet2 with its default settings, as well as each of the options listed above, which were described as mutually exclusive in the software’s documentation.
2) Brain Surface Extractor
BSE processes T1-weighted images using a sequence of anisotropic diffusion filtering, Marr-Hildreth edge detection, and mathematical morphology. We used version bse08a, which was an internal development version. This version included new features not previously described in our publications, including an optional post-processing morphological dilation. The parameters available included:
-n: the number of diffusion iterations applied
-d: the diffusion constant used
-s: the edge detection constant used
-p: post-processing dilation of the brain mask
The default values for BSE correspond to the settings: -n 3 -d 25 -s 0.64. We also applied settings of -n 3 -d 15 -s 0.7 -p based on an empirical evaluation of one test subject and prior experience with the algorithm. Based on additional results with this second set of parameters, we modified these settings slightly to use a higher constant (-n 3 -d 18 -s 0.7 -p), and then to apply more diffusion iterations (-n 5 -d 18 -s 0.7 -p).
3) Hybrid Watershed Algorithm
HWA combines a watershed algorithm with a deformable surface model. For this study, we used the version of the software mri_watershed distributed as part of FreeSurfer 3.0.5. We selected the following options to examine:
-atlas: use the atlas information to correct the segmentation
-less: shrink the surface
-more: expand the surface
We applied combinations of these three options to the downloaded test data.
The settings used for each program are summarized in Table I. We note that these are only a subset of the parameters available for the 3 programs, and each one can be tuned extensively for the data being processed.
TABLE I.
Metrics computed for the 3 skull-stripping approaches.
| method | parameters | Jaccard | Dice | sensitivity | specificity |
|---|---|---|---|---|---|
| BET 2.1 | |||||
| BETv2.1 | defaults | 0.8919 ± 0.0539 | 0.9420 ± 0.0320 | 0.9858 ± 0.0057 | 0.9804 ± 0.0140 |
| BETv2.1 | -B | 0.9400 ± 0.0089 | 0.9691 ± 0.0048 | 0.9627 ± 0.0117 | 0.9957 ± 0.0014 |
| BETv2.1 | -R | 0.9310 ± 0.0156 | 0.9642 ± 0.0085 | 0.9875 ± 0.0052 | 0.9892 ± 0.0036 |
| BETv2.1 | -S | 0.9016 ± 0.0464 | 0.9476 ± 0.0272 | 0.9834 ± 0.0062 | 0.9833 ± 0.0117 |
|
| |||||
| BSE08a | |||||
| BSEv08a | defaults | 0.5956 ± 0.2073 | 0.7272 ± 0.1495 | 0.9804 ± 0.0135 | 0.8538 ± 0.0941 |
| BSEv08a | -n 3 -d 15 -s 0.70 -p | 0.9242 ± 0.0386 | 0.9602 ± 0.0220 | 0.9489 ± 0.0437 | 0.9953 ± 0.0016 |
| BSEv08a | -n 3 -d 18 -s 0.70 -p | 0.9378 ± 0.0345 | 0.9675 ± 0.0196 | 0.9663 ± 0.0393 | 0.9947 ± 0.0016 |
| BSEv08a | -n 5 -d 18 -s 0.70 -p | 0.9394 ± 0.0330 | 0.9684 ± 0.0188 | 0.9725 ± 0.0382 | 0.9937 ± 0.0028 |
|
| |||||
| HWA3 | |||||
| HWA3 | defaults | 0.8531 ± 0.0179 | 0.9207 ± 0.0104 | 0.9992 ± 0.0003 | 0.9693 ± 0.0053 |
| HWA3 | -less | 0.8537 ± 0.0184 | 0.9210 ± 0.0107 | 0.9992 ± 0.0003 | 0.9695 ± 0.0053 |
| HWA3 | -more | 0.8520 ± 0.0179 | 0.9200 ± 0.0104 | 0.9993 ± 0.0003 | 0.9690 ± 0.0055 |
| HWA3 | -atlas | 0.8506 ± 0.0191 | 0.9191 ± 0.0111 | 0.9993 ± 0.0003 | 0.9687 ± 0.0058 |
| HWA3 | -less -atlas | 0.8508 ± 0.0190 | 0.9193 ± 0.0111 | 0.9993 ± 0.0003 | 0.9687 ± 0.0060 |
| HWA3 | -more -atlas | 0.8493 ± 0.0201 | 0.9184 ± 0.0118 | 0.9993 ± 0.0003 | 0.9683 ± 0.0062 |
III. Results
A. Implementation and computation time
The webserver implementation was developed as described above. The time required to upload a set of brain masks varied depending on the size of the compressed segmentation results and the internet connection used. Typically, the compressed segmentation files required 4MB or less of storage. The upload process required less than 1 minute over a residential broadband connection; on a local gigabit network within our laboratory, the upload required less than 1 second. The entire server-side processing sequence for a set of 40 brain segmentations required less than 2 minutes.
B. Skull-stripping results
We processed the 40 brains using BET, BSE, and HWA. We applied 4 settings for BET, 4 settings for BSE, and 6 settings for HWA; beyond the setting of the parameters, no additional manual intervention was performed. The combinations of program settings are detailed in Table I. For each setting, we uploaded the results to our web server, which processed the data and recorded it in the database. Table I shows the average Jaccard, Dice, sensitivity, and specificity metrics for each set of results for each algorithm.
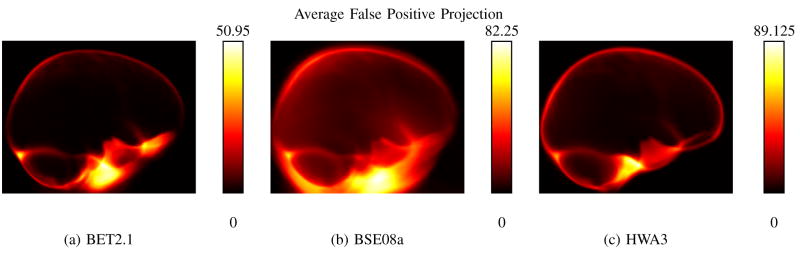
We first examine the cases for each algorithm which had the lowest average specificity, i.e., those that kept the most non-brain tissue. Corresponding sagittal projection maps of the average False Positive count for each method are shown in Fig. 2. Under its default settings, BET’s specificity averaged over the 40 volumes was 0.9804±0.0140 [mean ± s.d.]. The average FP map for BET (see Fig. 2.a.) showed large intensities below the frontal lobe, indicating that some of the brain masks produced with BET under these settings did not remove the skull and scalp completely. BSE, using its default parameters, produced an average specificity measure of 0.8538 ± 0.0941. We note that these settings also produced the lowest results for Jaccard and Dice scores, and these 3 measures were the lowest for the methods tested in this study. The False Positive projection map for BSE shows bright regions around the entire brain, with particularly bright areas below the frontal and temporal lobes, indicating that the neck was not removed for several subjects. HWA produced very little variation across the parameter settings used; while settings of “-less -atlas” produced HWA’s lowest specificity score, 0.9683 ± 0.0062, this is only slightly smaller than its best result of 0.9695 ± 0.0053. HWA also retains some extraneous tissue slightly anterior to the cerebellum. It is also worth noting that the settings that produced the lowest average specificity for the algorithms did not always produce the lowest measure for each individual subject.
Fig. 2.
Shown are sagittal projections of the False Positive results produced by the single set of parameters that produced the lowest average specificity rates for each algorithm. The False Positive maps from the 40 results were mapped using the LPBA40 transforms and averaged. Each pixel in the 2D images shows the total number of false positive voxels along a projected ray through that coordinate and perpendicular to the image plane, averaged across the 40 subjects. (a) BET using its default settings. This result produced the lowest specificity measure for BET, and the bright region below the brain indicates the presence of extraneous tissue in some of the brains. (b) BSE using its default settings. This result produced the lowest specificity measure of the methods tested, and the extraneous tissue is clearly visible in the inferior portion of the image, as well as around the perimeter of the brain. (c) HWA using options -more -atlas. HWA also exhibits a false positive region below the brain, though it does not extend as far as those of BSE or BET.
Changing parameters for BET and BSE produced improvements in several of their measures. BET’s best results for Jaccard, Dice, and specificity measures were achieved with the -B setting (bias field and neck cleanup); its results with highest sensitivity were produced using the -R setting (robust). BSE’s best average performance for Jaccard and Dice index was achieved with settings “-n 5 -d 18 -s 0.70 -p”; its best specifity result was achieved with “-n 3 -d 15 -s 0.70 -p”. Its best sensitivity result was its default settings, and as described above, the sensitivity result came at the expense of including large regions of the head that should have been excluded. HWA’s metrics changed slightly under the different parameter settings; the “-less” option produced its best result for Jaccard, Dice, and specificity measures; its sensitivity measures were the highest of the tested algorithms, and were all either 0.9992 ± 0.0003 or 0.9993 ± 0.0003. BET’s best Jaccard and Dice measures were also the highest of the algorithms tested (0.9400±0.0089 and 0.9691±0.0048, respectively), with BSE’s best results being a close second (0.9394 ± 0.0330 and 0.9684 ± 0.0188, respectively). BET also had the highest specificity score 0.9957 ± 0.0014. BSE’s highest specificity result (-n 3 -d 15 -s 0.70 -p) was second, at 0.9953 ± 0.0016, but this was achieved with settings that had lower sensitivity than its best settings, and examination of its false positive images indicated that portions of the cerebellum had been excluded for some subjects.
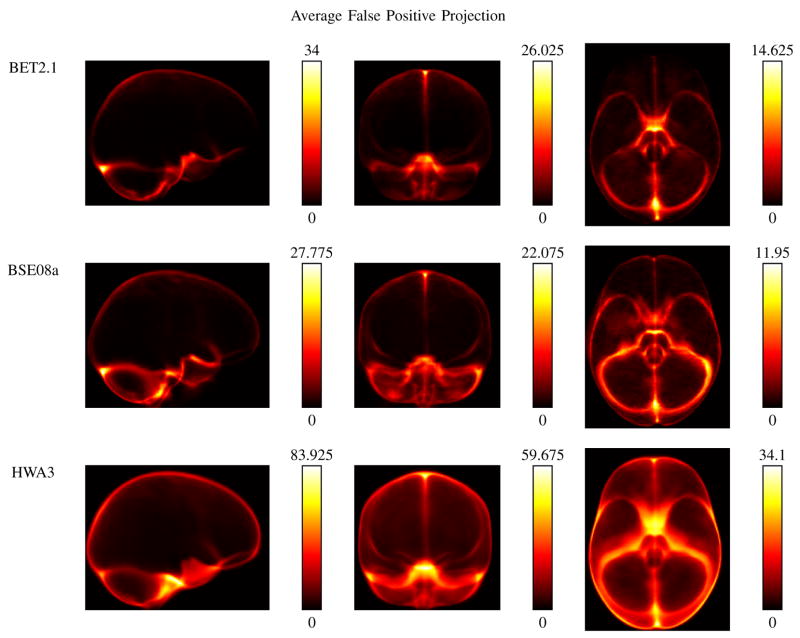
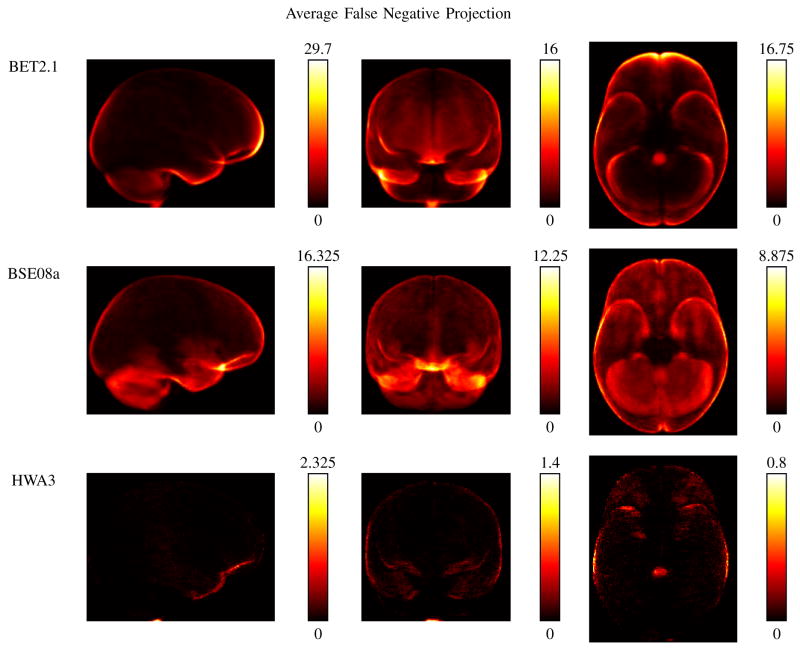
Figures 3 and 4 show the average false positive and false negative projection maps, respectively, for the parameter settings that produced the highest average Jaccard similarity measure for each of the 3 algorithms. One common trait exhibited by all 3 algorithms was an area of high false positive counts corresponding to the sagittal sinus. HWA, which emphasizes sensitivity over specificity, had the highest values for the false positive counts. BSE showed some high counts in regions of the cerebellum, though its pattern of false positive counts is similar to that of BET, which had the highest specificity of the 3. In Figure 4, the high sensitivity of HWA is evident with none of its false negative images showing an average FN count greater than 2.325 along any line of projection. For BET, the false positive voxels tended to be on the boundary of the brain, with a hotspot towards the frontal lobe. BSE shows a hotspot in the frontal lobe, near the gyrus rectus. These characteristics are confirmed by the regional sensitivity measures, as shown in Table II; again, the measures shown were computed using the results from each algorithm that had produced the highest Jaccard similarity measures. BET exhibited its lowest structure sensitivity measure for gyrus rectus and lateral orbitofrontal gyrus, while BSE received its lowest scores for the gyrus rectus and the cerebellum. HWA performed extremely well in the regional sensitivity measures. Its lowest measure was in the brainstem, and the FN projection maps indicate that the voxels not included correspond to the lowest slices of the brainstem. It should be noted that the FN map for BET also shows that the region of the brainstem that was not included was the lower portion of it. The choice of where to separate the brainstem may differ depending on the application, and changing this delineation would improve the scores for both HWA and BET. A similar argument could be made about the choice to include or exclude regions of extra-cortical CSF.
Fig. 3.
Comparison of false positive pixel counts. For each of the 3 algorithms, the images show the false positive pixel counts for the single set of parameters that produced the the best average Jaccard result. The false positive maps for all 40 subjects were aligned using the LPBA40 transforms, averaged across the 40 subjects, and then summed along each cardinal dimension (sagittal, coronal, and axial). These plots graphically illustrate some of the differences among the results of the 3 algorithms compared. BET, which produced the highest specificity in these tests, has fewer false positive voxels. HWA, which produced the lowest specificity of these 3 results, has more false positive voxels, but shows better results in Fig. 4
Fig. 4.
Comparison of false negative pixel counts. Shown are the false negative pixel counts corresponding to the best average Jaccard result for each of the 3 algorithms tested. The false negative maps for all 40 subjects were aligned using the LPBA40 transforms, averaged across the 40 subjects, and then summed along each cardinal dimension (sagittal, coronal, and axial). In this case, HWA had the highest sensitivity and the fewest false negative voxels.
IV. Discussion
We have presented a new online resource for performing validation studies of skull-stripping algorithms using a set of 40 manually labeled MRI. These results were computed in only a few minutes and archived on the server, providing a convenient and repeatable mechanism to evaluate and compare different methods. We applied our framework to evaluate 3 existing skull-stripping algorithms, BET, BSE, and HWA. Our results indicated that with proper parameter selection, all 3 could produce very good results for the skull-stripping problem for the 40 subject brains. It is important to recognize that different metrics may be appropriate for different applications. For example, BET with the ‘-B’ option achieved the highest average Jaccard score of all combinations of algorithms and settings used in these tests; however, this result had lower sensitivity than the HWA and BSE settings that produced the best Jaccard results for those algorithms. For some applications of skull-stripping, increased sensitivity may be more important than selectivity, particularly in specific regions of the brain. Also, the spatial maps of errors suggest that the false negative rates for HWA and BET would be improved if the ground truth labeling of the brainstem did not extend as far inferiorly as it does in these data, and increasing the ground truth brain masks to include more extra-cortical CSF would likely improve the specificity measures for the algorithms. The high sensitivy rate for HWA and the high specificity rate for BSE are consistent with the results of the study performed by Fennema-Notestine et al. (2006) on different data. We note that BET’s results achieved higher specificity in the present study, suggesting improvements to the algorithm compared to the version that was evaluated by Fennema-Notestine et al. (2006). This is one of the benefits of our proposed system. Software packages are frequently updated, and validation results can be recomputed rapidly and comparisons can be updated to reflect the current state of the art.
This new resource provides a potential standard reference set that other users could use for evaluating their own skull-stripping algorithms. They could potentially publish results computed with this system, and their results would be archived and readily compared with existing ones. Other users could compare their use of existing algorithms with the published results for those algorithms, or compare the use of an algorithm by a novice user to that of an expert. The method could also be used for the purpose of evaluating manual raters being trained to skull-strip the brain. Furthermore, since the segmentation results are all archived, new metrics could be added to the system in the future and computed for previously submitted data. Additionally, the results in the archive could be mined in order to design meta-algorithms that combine results from 2 or more skull-stripping methods, as has been described by Rehm et al. (2004) and Rex et al. (2004). We are also developing a user forum that will be part of the website, which will provide a space for the user community to discuss the use of the site, the results, and other aspects of segmentation problems. This forum will also be used by our laboratory to extend the support provided to users, which presently includes the use of a web-based form.
A possible limitation of the system we propose is that users could potentially adapt their algorithms to the 40 subject data or perform manual intervention in order to achieve more competitive results. This type of manipulation of results would also be possible in traditional evaluation methods. With our online resource, however, others users could attempt to repeat the results; this should encourage users to submit appropriately obtained results.
In future work, we will extend the framework to provide validation for segmentation of individual structures within the brain, as well as to provide validation for surface-based methods, such as those that identify the cerebral cortical surface. We will also be extending our test data set to include additional brains that were acquired with different protocols; this will potentially allow the examination of the segmentation algorithms on different demographics, such as performance on brains during different stages of development and aging. The system is accessible through the website http://sve.loni.ucla.edu/.
Acknowledgments
This work is funded by the National Institutes of Health through the NIH Roadmap for Medical Research, Grant U54 RR021813. Information on the National Centers for Biomedical Computing can be obtained from http://nihroadmap.nih.gov/bioinformatics. Funding was also provided under NIH Grants P41-RR013642 (PI: AW Toga) and R01-MH060374 (PI: RM Bilder).
Footnotes
online at http://www.nitrc.org/projects/ibsr/
online at http://www.bic.mni.mcgill.ca/brainweb/
online at http://www.cause07.org/ and http://www.sliver07.org/
online at http://grand-challenge2008.bigr.nl/
Publisher's Disclaimer: This is a PDF file of an unedited manuscript that has been accepted for publication. As a service to our customers we are providing this early version of the manuscript. The manuscript will undergo copyediting, typesetting, and review of the resulting proof before it is published in its final citable form. Please note that during the production process errors may be discovered which could affect the content, and all legal disclaimers that apply to the journal pertain.
References
- Acosta-Cabronero J, Williams GB, Pereira JMS, Pengas G, Nestor PJ. The impact of skull-stripping and radio-frequency bias correction on grey-matter segmentation for voxel-based morphometry. NeuroImage. 2008 Feb;39 (4):1654–1665. doi: 10.1016/j.neuroimage.2007.10.051. [DOI] [PubMed] [Google Scholar]
- Arnold JB, Liow JS, Schaper KA, Stern JJ, Sled JG, Shattuck DW, Worth AJ, Cohen MS, Leahy RM, Mazziotta JC, Rottenberg DA. Qualitative and quantitative evaluation of six algorithms for correcting intensity nonuniformity effects. NeuroImage. 2001 May;13 (5):931–943. doi: 10.1006/nimg.2001.0756. [DOI] [PubMed] [Google Scholar]
- Aubert-Broche B, Griffin M, Pike GB, Evans AC, Collins DL. Twenty new digital brain phantoms for creation of validation image data bases. IEEE Trans Med Imaging. 2006 Nov;25 (11):1410–1416. doi: 10.1109/TMI.2006.883453. [DOI] [PubMed] [Google Scholar]
- Bazin PL, Pham DL. Topology-preserving tissue classification of magnetic resonance brain images. IEEE Trans Med Imaging. 2007 Apr;26 (4):487–496. doi: 10.1109/TMI.2007.893283. [DOI] [PubMed] [Google Scholar]
- Boesen K, Rehm K, Schaper K, Stoltzner S, Woods R, Luders E, Rottenberg D. Quantitative comparison of four brain extraction algorithms. NeuroImage. 2004 Jul;22 (3):1255–1261. doi: 10.1016/j.neuroimage.2004.03.010. [DOI] [PubMed] [Google Scholar]
- Collins DL, Zijdenbos AP, Kollokian V, Sled JG, Kabani NJ, Holmes CJ, Evans AC. Design and construction of a realistic digital brain phantom. IEEE Trans Med Imaging. 1998 Jun;17 (3):463–468. doi: 10.1109/42.712135. [DOI] [PubMed] [Google Scholar]
- Dice. Measures of the amount of ecologic association between species. Journal of Ecology. 1945;26:297–302. [Google Scholar]
- Evans AC, Collins DL, Mills SR, Brown ED, Kelly RL, Peters TM. 3D Statistical neuroanatomical models from 305 MRI Volumes. Nuclear Science Symposium and Medical Imaging Conference, 1993., 1993 IEEE Conference Record.1993. [Google Scholar]
- Fennema-Notestine C, Ozyurt IB, Clark CP, Morris S, Bischoff-Grethe A, Bondi MW, Jernigan TL, Fischl B, Segonne F, Shattuck DW, Leahy RM, Rex DE, Toga AW, Zou KH, Brown GG. Quantitative evaluation of automated skull-stripping methods applied to contemporary and legacy images: effects of diagnosis, bias correction, and slice location. Hum Brain Mapp. 2006 Feb;27 (2):99–113. doi: 10.1002/hbm.20161. [DOI] [PMC free article] [PubMed] [Google Scholar]
- Hollingshead. Four Factor Index of Social Status. Yale University; New Haven: 1975. [Google Scholar]
- Hollingshead A, Redlich F. Social Class and Mental Illness. John Wiley; New York: 1958. [DOI] [PMC free article] [PubMed] [Google Scholar]
- Jaccard P. The distribution of the flora in the alpine zone. New Phytologist. 1912 Feb;11 (2):37–50. [Google Scholar]
- MacDonald D, Avis D, Evans AC. Multiple surface identification and matching in magnetic resonance images. In: Robb RA, editor. Visualization in Biomedical Computing 1994. Vol. 2359 of Proc. SPIE. 1994. pp. 160–169. [Google Scholar]
- Marroquin JL, Vemuri BC, Botello S, Calderon F, Fernandez-Bouzas A. An accurate and efficient bayesian method for automatic segmentation of brain MRI. IEEE Trans Med Imaging. 2002 Aug;21 (8):934–945. doi: 10.1109/TMI.2002.803119. [DOI] [PubMed] [Google Scholar]
- Narr KL, Cannon TD, Woods RP, Thompson PM, Kim S, Asunction D, van Erp TGM, Poutanen VP, Huttunen M, Lnnqvist J, Standerksjld-Nordenstam CG, Kaprio J, Mazziotta JC, Toga AW. Genetic contributions to altered callosal morphology in schizophrenia. J Neurosci. 2002 May;22 (9):3720–3729. doi: 10.1523/JNEUROSCI.22-09-03720.2002. [DOI] [PMC free article] [PubMed] [Google Scholar]
- Pham DL, Prince JL. Adaptive fuzzy segmentation of magnetic resonance images. IEEE Trans Med Imaging. 1999 Sep;18 (9):737–752. doi: 10.1109/42.802752. [DOI] [PubMed] [Google Scholar]
- Rajapakse J, Kruggel F. Segmentation of MR images with intensity inhomogeneities. Image and Vision Computing. 1998 March;16 (3):165–180. [Google Scholar]
- Rehm K, Schaper K, Anderson J, Woods R, Stoltzner S, Rottenberg D. Putting our heads together: a consensus approach to brain/non-brain segmentation in T1-weighted MR volumes. NeuroImage. 2004 Jul;22 (3):1262–1270. doi: 10.1016/j.neuroimage.2004.03.011. [DOI] [PubMed] [Google Scholar]
- Rex DE, Ma JQ, Toga AW. The LONI pipeline processing environment. Neuroimage. 2003 Jul;19 (3):1033–1048. doi: 10.1016/s1053-8119(03)00185-x. [DOI] [PubMed] [Google Scholar]
- Rex DE, Shattuck DW, Woods RP, Narr KL, Luders E, Rehm K, Stoltzner SE, Stolzner SE, Rottenberg DA, Toga AW. A meta-algorithm for brain extraction in MRI. NeuroImage. 2004 Oct;23 (2):625–637. doi: 10.1016/j.neuroimage.2004.06.019. [DOI] [PubMed] [Google Scholar]
- Ségonne F, Dale AM, Busa E, Glessner M, Salat D, Hahn HK, Fischl B. A hybrid approach to the skull stripping problem in MRI. NeuroImage. 2004 Jul;22 (3):1060–1075. doi: 10.1016/j.neuroimage.2004.03.032. [DOI] [PubMed] [Google Scholar]
- Shattuck DW, Mirza M, Adisetiyo V, Hojatkashani C, Salamon G, Narr KL, Poldrack RA, Bilder RM, Toga AW. Construction of a 3D probabilistic atlas of human cortical structures. NeuroImage. 2008 Feb;39 (3):1064–1080. doi: 10.1016/j.neuroimage.2007.09.031. [DOI] [PMC free article] [PubMed] [Google Scholar]
- Shattuck DW, Sandor-Leahy SR, Schaper KA, Rottenberg DA, Leahy RM. Magnetic resonance image tissue classification using a partial volume model. NeuroImage. 2001;13:856–876. doi: 10.1006/nimg.2000.0730. [DOI] [PubMed] [Google Scholar]
- Shepp L, Logan B. The Fourier reconstruction of a head section. IEEE Trans Nucl Sci. 1974;21(3):2134. [Google Scholar]
- Sled JG, Zijdenbos AP, Evans AC. A nonparametric method for automatic correction of intensity nonuniformity in MRI data. IEEE Trans Med Imag. 1998 Feb;:17. doi: 10.1109/42.668698. [DOI] [PubMed] [Google Scholar]
- Smith SM. Fast robust automated brain extraction. Hum Brain Mapp. 2002 Nov;17 (3):143–155. doi: 10.1002/hbm.10062. [DOI] [PMC free article] [PubMed] [Google Scholar]
- Sowell ER, Thompson PM, Holmes CJ, Batth R, Jernigan TL, Toga AW. Localizing age-related changes in brain structure between childhood and adolescence using statistical parametric mapping. NeuroImage. 1999 Jun;9 (6 Pt 1):587–597. doi: 10.1006/nimg.1999.0436. [DOI] [PubMed] [Google Scholar]
- Strother SC, Anderson JR, Xu XL, Liow JS, Bonar DC, Rottenberg DA. Quantitative comparisons of image registration techniques based on high-resolution MRI of the brain. J Comput Assist Tomogr. 1994;18 (6):954–962. doi: 10.1097/00004728-199411000-00021. [DOI] [PubMed] [Google Scholar]
- Tohka J, Krestyannikov E, Dinov ID, Graham AM, Shattuck DW, Ruotsalainen U, Toga AW. Genetic algorithms for finite mixture model based voxel classification in neuroimaging. IEEE Trans Med Imaging. 2007 May;26 (5):696–711. doi: 10.1109/TMI.2007.895453. [DOI] [PMC free article] [PubMed] [Google Scholar]
- Tohka J, Zijdenbos A, Evans A. Fast and robust parameter estimation for statistical partial volume models in brain MRI. NeuroImage. 2004 Sep;23 (1):84–97. doi: 10.1016/j.neuroimage.2004.05.007. [DOI] [PubMed] [Google Scholar]
- van Ginneken B, Heimann T, Styner M. 3D segmentation in the clinic: A grand challenge. Workshop at Medical Image Computing and Computer Assisted Intervention; MICCAI; 2007. pp. 7–15. [Google Scholar]
- West J, Fitzpatrick JM, Wang MY, Dawant BM, Maurer CR, Kessler RM, Maciunas RJ, Barillot C, Lemoine D, Collignon A, Maes F, Suetens P, Vandermeulen D, van den Elsen PA, Napel S, Sumanaweera TS, Harkness B, Hemler PF, Hill DL, Hawkes DJ, Studholme C, Maintz JB, Viergever MA, Malandain G, Woods RP. Comparison and evaluation of retrospective intermodality brain image registration techniques. J Comput Assist Tomogr. 1997;21 (4):554–566. doi: 10.1097/00004728-199707000-00007. [DOI] [PubMed] [Google Scholar]
- Woods RP, Grafton ST, Watson JDG, Sicotte NL, Mazziotta JC. Automated image registration: II. Intersubject validation of linear and nonlinear models. Journal of Computer Assisted Tomography. 1998;22:153–165. doi: 10.1097/00004728-199801000-00028. [DOI] [PubMed] [Google Scholar]
- Zeng X, Staib L, Schultz R, Duncan J. Segmentation and measurement of the cortex from 3-D MR images using coupled-surfaces propagation. IEEE Trans Med Imaging. 1999 Oct;18 (10):927–937. doi: 10.1109/42.811276. [DOI] [PubMed] [Google Scholar]
- Zhang Y, Brady M, Smith S. Segmentation of brain MR images through a hidden markov random field model and the expectation-maximization algorithm. IEEE Trans Med Imaging. 2001 Jan;20 (1):45–57. doi: 10.1109/42.906424. [DOI] [PubMed] [Google Scholar]
- Zijdenbos AP, Dawant BM, Margolin RA, Palmer AC. Morphometric analysis of white matter lesions in MR images: method and validation. IEEE Trans Med Imaging. 1994;13 (4):716–724. doi: 10.1109/42.363096. [DOI] [PubMed] [Google Scholar]