Regulation of ClC-1 and K_ATP channels in action potential–firing fast-twitch muscle fibers

Abstract

Action potential (AP) excitation requires a transient dominance of depolarizing membrane currents over the repolarizing membrane currents that stabilize the resting membrane potential. Such stabilizing currents, in turn, depend on passive membrane conductance (G_m), which in skeletal muscle fibers covers membrane conductances for K⁺ (G_K) and Cl⁻ (G_Cl). Myotonic disorders and studies with metabolically poisoned muscle have revealed capacities of G_K and G_Cl to inversely interfere with muscle excitability. However, whether regulation of G_K and G_Cl occur in AP-firing muscle under normal physiological conditions is unknown. This study establishes a technique that allows the determination of G_Cl and G_K with a temporal resolution of seconds in AP-firing muscle fibers. With this approach, we have identified and quantified a biphasic regulation of G_m in active fast-twitch extensor digitorum longus fibers of the rat. Thus, at the onset of AP firing, a reduction in G_Cl of ∼70% caused G_m to decline by ∼55% in a manner that is well described by a single exponential function characterized by a time constant of ∼200 APs (phase 1). When stimulation was continued beyond ∼1,800 APs, synchronized elevations in G_K (∼14-fold) and G_Cl (∼3-fold) caused G_m to rise sigmoidally to ∼400% of its level before AP firing (phase 2). Phase 2 was often associated with a failure to excite APs. When AP firing was ceased during phase 2, G_m recovered to its level before AP firing in ∼1 min. Experiments with glibenclamide (K_ATP channel inhibitor) and 9-anthracene carboxylic acid (ClC-1 Cl⁻ channel inhibitor) revealed that the decreased G_m during phase 1 reflected ClC-1 channel inhibition, whereas the massively elevated G_m during phase 2 reflected synchronized openings of ClC-1 and K_ATP channels. In conclusion, G_Cl and G_K are acutely regulated in AP-firing fast-twitch muscle fibers. Such regulation may contribute to the physiological control of excitability in active muscle.

INTRODUCTION

Excitation and propagation of action potentials (APs) are the hallmarks of excitable cells. Both of these cellular processes require that excitatory currents exceed the inhibitory currents that dampen cellular excitability via their stabilizing actions on the resting membrane potential. The magnitude of the inhibitory currents can be inferred from measurements of passive membrane conductance (G_m), which reflect the function of the ion channels that are open at the resting membrane potential. In resting skeletal muscle fibers, G_m represents the sum of conductances for K⁺ (G_K) and Cl⁻ (G_Cl), the latter accounting for 80–90% of G_m (Hutter and Noble, 1960; Bryant and Morales-Aguilera, 1971; Pedersen et al., 2005; Pierno et al., 2007). The roles of G_K and G_Cl for skeletal muscle excitability can be illustrated by considering two extreme conditions: at one extreme, loss of function mutations of the muscle-specific Cl⁻ channel, the ClC-1 channel, is the cause of greatly reduced G_m and hyperexcitable muscles in patients suffering from myotonia congenita (McComas and Mrozek, 1968; Bryant and Morales-Aguilera, 1971; Koch et al., 1992; Pusch, 2002). At the other extreme, muscle excitability is completely lost when metabolic poisoning was used to reveal that G_Cl and G_K have the capacity to increase ∼14-fold and ∼110-fold, respectively (Fink and Lüttgau, 1976). Although these extreme conditions reflect pathological or unphysiological conditions, they do demonstrate that regulation of Cl⁻ and K⁺ channels can cause very large changes in G_m of skeletal muscle fibers and have dramatic consequences for muscle excitability. However, it is not known whether this potential of Cl⁻ and K⁺ channels to modulate muscle excitability via G_m is exploited in the normal physiological regulation of the excitability of active AP-firing muscle fibers. This lack of knowledge about regulation of G_m in active muscles is likely to be ascribable mainly to the experimental difficulties associated with measuring G_m while muscle fibers are firing APs.

In this study, we establish a new technique that allows the determination of G_Cl and G_K with a temporal resolution of seconds in AP-firing muscle fibers. This approach is used to demonstrate that G_Cl and G_K are both highly dynamic in fast-twitch extensor digitorum longus (EDL) muscle fibers firing APs and, furthermore, that these changes in G_Cl and G_K are caused by regulation of ClC-1 and K_ATP ion channels. This study is followed by a companion study (see Pedersen et al. in this issue) that compares the highly dynamic nature of G_Cl and G_K in fast-twitch muscle fibers with the dynamics of G_Cl and G_K in fatigue-resistant slow-twitch muscle fibers.

MATERIALS AND METHODS

Animal handling and muscle preparation

All experiments were performed on isolated EDL muscles from 12–14-wk-old female wistar rats (∼230 g). Handling and killing of animals followed Danish animal welfare regulations. Most experiments were performed using standard Krebs-Ringer bicarbonate solution containing 122 mM NaCl, 25 mM NaHCO₃, 2.8 mM KCl, 1.2 mM KH₂PO₄, 1.2 mM MgSO₄, 1.3 mM CaCl₂, and 5.0 mM d-glucose. Total buffer [Cl⁻] was 127.4 mM (127 mM). In Cl⁻-free solutions, methylsulfate salts replaced NaCl and KCl. Ca(NO₃)₂ was used to replace CaCl₂. Solutions with lower Cl⁻ concentration were prepared by mixing standard and Cl⁻-free solutions. All solutions were maintained equilibrated with 5/95% of CO₂/O₂, pH 7.2–7.4, throughout experiments. All experiments were performed at 30°C.

Electrophysiological technique

Electrophysiological investigations were performed on superficial fibers of intact muscles using a previously described setup (Macdonald et al., 2005; Pedersen et al., 2005). To measure resting membrane conductance before (G_mS) and in between AP trains (G_m), two electrodes were inserted into the same fiber. One electrode was used to inject square current pulses, and the other electrode recorded the membrane potential. The protocols for injections of current pulses and the data sampling were controlled using Signal 2.09 software (Cambridge Electronic Design). Recordings were low-pass filtered at 10 kHz and sampled at 60 kHz. Electrodes were filled with 2 M K-citrate except for a few experiments in which 3 M KCl or 770 mM K-methanesulphonate was used to check for any influence on the results of the citrate ion. No effects of citrate except more stable resting membrane potentials were observed. Holding currents were not used in any of the experiments. Intracellular measurements of AP trains were achieved without interference from contractile activity by including 50 µM N-benzyl-p-toluene sulphonamide (BTS) in the perfusion solution. BTS is a specific inhibitor of fast-twitch myosin II (Cheung et al., 2002) that does not markedly affect the excitability of the muscle fibers (Macdonald et al., 2005). Importantly, it has been shown that despite the reduction in contractile force, BTS only reduces muscle energy turnover by ∼20% (Zhang et al., 2006). Fibers in which the resting membrane potential depolarized beyond −60 mV during electrophysiological assessments were disregarded.

Determination of the resting membrane conductance before AP firing, G_mS

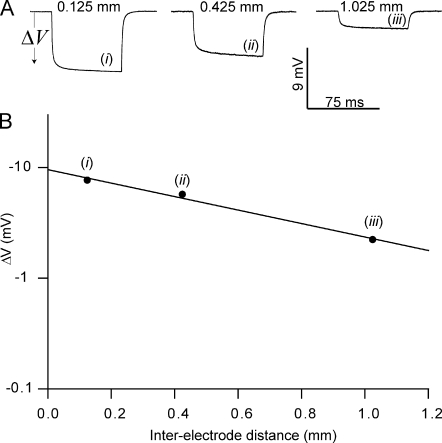
To calculate G_m in AP-firing fibers, it was necessary to know its value before AP firing (G_mS). This constant was measured in resting fibers using the classical technique for G_m determination in skeletal muscle fibers (Boyd and Martin, 1959; Pedersen et al., 2005) that relies on measurements of the membrane potential deflections (ΔV) in response to the injection of square current pulses at three to five locations along the muscle fibers (Fig. 1 A; Hodgkin and Rushton, 1946). After plotting the steady-state amplitudes of these deflections as a function of the interelectrode distance (x; Fig. 1 B), the input conductance (G_in) and the length constant (λ) of the fibers can be extracted by fitting the data to a two-parameter exponentially decaying function (r² ≥ 0.99; Eq. 1),

$$\begin{array}{l}\Delta V\left(x\right)=\Delta V_{x=0}\exp (-x{\lambda }^{-1})\\ \text{and\hspace{0.17em}}\Delta V\left(x\right)=I{G}_{in}^{-1}\exp (-x{\lambda }^{-1}),\end{array}$$ (1)

where Δ V_{x = 0} represents the steady-state membrane potential deflection at the point of current injection (x = 0) and I represents the amplitude of the square current. G_mS could then be calculated by adopting an internal resistivity, R_i, of 180 Ωcm from Albuquerque and Thesleff (1968), which they had calculated (R_i = a²πr_i) on the basis of an optically measured muscle fiber diameter (2a) and a measured intracellular resistance (r_i) that was similar to our observations:

$$G_{mS}={\lambda }^{-1.5}\sqrt{\frac{G_{in}}{8\pi R_i}}.$$ (2)

Table I provides the G_mS values for the different experimental conditions used in this study.

Figure 1.

Measurements of G_m using the classical technique. Two electrodes were inserted into the same fiber: one electrode was used for injection of square current pulses, and the other electrode penetrated the fiber at three locations (i, ii, and iii) to record the membrane voltage deflection associated with the current pulses. The steady-state amplitudes of these voltage deflections were then plotted against the distance between the electrodes and fitted to a two-parameter exponential decaying function whereby G_in and λ were obtained (Eq. 1). (A) Representative membrane potential deflections during current injections in a muscle fiber in the standard Krebs-Ringer solution. (B) A plot of the amplitude of the steady-state voltage deflection against the interelectrode distance of this fiber. The solid line illustrates the fit from which G_in and λ were extracted.

TABLE I.

G_m in EDL muscle fibers before AP firing

Experimental conditions	GmS	GmS,50	GKS	GClS	GClS,50
	µS/cm2	µS/cm2	µS/cm2	µS/cm2	µS/cm2
50 µM BTS	1,458 ± 70 (n = 26/7)	361 ± 21 (n = 15/4)	144 ± 16 (n = 13/6)	1,314 ± 72	217 ± 26
50 µM BTS + 10 µM glibenclamide	1,252 ± 42 (n = 24/4)	524 ± 27 (n = 11/2)	195 ± 32 (n = 6/2)	1,057 ± 53	329 ± 42
50 µM BTS + 100 µM 5-HD	1,609 ± 82 (n = 14/2)	ND	ND	NA	NA
50 µM BTS + 100 µM 9-AC + 0.01 µM TTX	143 ± 13 (n = 9/2)	ND	ND	NA	NA

The subscript S indicates values for G_m before AP firing under the various experimental conditions as determined using the classical technique (Fig. 1 and Eq. 1). G_mS,50 represents G_m before AP firing at 50 mM Cl⁻. G_KS and G_ClS represent component conductances of G_mS for K⁺ and Cl⁻, respectively, whereas G_ClS,50 represents the component conductance of G_mS,50 for Cl⁻. All data have been presented as means ± SEM. n represents fibers/muscles. NA, not applicable.

Determination of G_m between successive AP trains from measurements of G_in

The aim of this study was to determine changes in G_m in muscle fibers that were being activated intermittently to fire trains of APs. Clearly, the aforementioned classical technique for the determination of G_m in muscle fibers is too slow to allow G_m measurements in AP-firing skeletal muscle fibers. Instead, the two intracellular microelectrodes were inserted at close proximity (∼70 µm), whereby direct measurements of G_in became possible in between AP trains. The following equation was then used to relate G_in to G_m (Appendix 1 in supplemental text):

$$G_m=\frac{G_{in}^2}{G_{in0}^2}{G}_{mS}.$$ (3)

G_in0 refers to the input conductance of the investigated fiber before AP firing, and G_in represents the input conductance measured in between the AP trains. G_mS represents the mean resting membrane conductance measured in a subset of fibers that were not exposed to AP firing but kept under the same conditions as the fibers in which G_in was determined between the AP trains (Table I). The G_mS values for the different experimental conditions were obtained using the aforementioned classical technique and are presented in Table I (also see Fig. 1). Thus, G_m is the calculated membrane conductance between the AP trains for the fiber in question based on measurements of its G_in and measurements of G_mS in other fibers under similar conditions using the classical technique. Essentially, Eq. 3 provides a way to extract absolute values of G_m from G_in obtained during muscle activity, provided G_mS and G_in0 are known.

Determination of component conductances for K⁺ and Cl⁻

To elucidate the roles of K⁺ and Cl⁻ channels for the dynamics of G_m in AP-firing muscle fibers, G_K was calculated from G_m determinations in fibers incubated at 127 and 50 mM Cl⁻ using the following expression (Appendix 2 in supplemental text):

$$G_K=\frac{G_{m,50}{G}_{ClS,127}-G_{ClS,50}{G}_{m,127}}{G_{ClS,127}-G_{ClS,50}}.$$ (4)

Again, the subscript S indicates the mean conductance measured in fibers before muscle activation, whereas non-S subscripts indicate mean conductances determined in AP-firing muscle fibers at either 50 or 127 mM Cl⁻. G_Cl was subsequently determined by subtracting G_K from G_m at 127 mM Cl⁻.

Chemicals

All chemicals were of analytical grade. BTS was obtained from Toronto Research Chemicals, whereas all other chemicals were purchased from Sigma-Aldrich. Glibenclamide, BTS, and 9-anthracene carboxylic acid (9-AC) were dissolved in DMSO. The maximal concentration of DMSO in experimental solutions was 0.15%, which did not affect resting conditions in muscles. Muscles were incubated for at least 15 min with drugs before experiments were conducted.

Statistics

All mean data are presented as means ± SEM. Statistical significance between two data groups was ascertained using a Student's two-tailed t test for unpaired observations. Fisher's exact test was used for two categorical data groups. One-way ANOVA was used for comparisons of more than two data groups. Tukey's posthoc test was used to detect a significant difference between individual data groups. P < 0.05 was considered significant.

Online supplemental material

Part I of the supplemental text contains detailed derivations of Eqs. 3 and 4. Part II investigates the influence of the possible volume increase of muscle fibers or changes in R_i during AP firing for G_m determinations. Part III presents results from experiments in which the dynamics of G_m were elicited in AP-firing muscle fibers without inserted electrodes. These are compared with observations of G_m dynamics with inserted electrodes. Fig. S1 shows the estimated effect of muscle fiber swelling on G_m during AP firing. Fig. S2 shows that the regulation of ion channels underlying phase 1 is independent of inserted electrodes. Fig. S3 shows that the cellular mechanisms that triggered phase 2 were activated by APs independently of inserted electrodes. Online supplemental material is available at http://www.jgp.org/cgi/content/full/jgp.200910291/DC1.

RESULTS

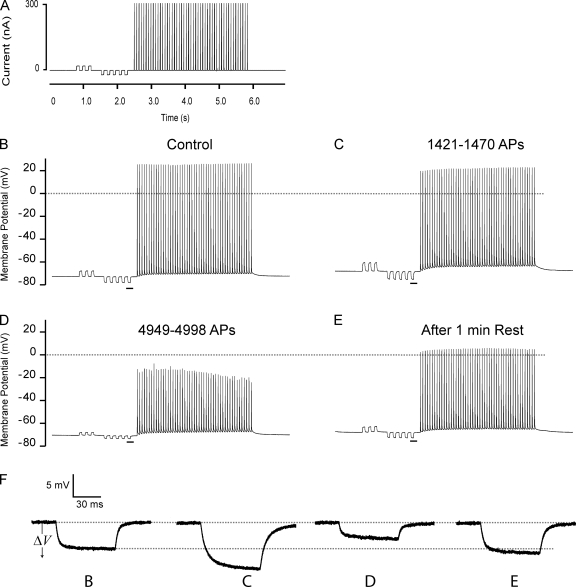
When G_m in skeletal muscle fibers is measured using the classical technique, one intracellular microelectrode is used for injection of square current pulses while another electrode records the resulting membrane potential change at several locations along the fiber (Fig. 1 A). From the decay of the steady-state amplitude of such voltage changes along the fiber (Fig. 1 B), G_in and λ are extracted and used to calculate G_m (Eq. 2). Although this classical technique is preferable in resting muscle fibers, it usually requires several minutes to extract the experimental observation required for each determination of G_m. This makes it highly unsuitable for determinations of fast changes in G_m as might occur in AP-firing muscles. Here, we have overcome this problem by developing a method in which G_m in AP-firing fibers is calculated from G_in, which can be measured directly if the electrodes are inserted into the fiber at sufficiently close proximity. In the standard experimental protocol, the current electrode was used to trigger 3.5-s trains of APs repeatedly every 7 s (Fig. 2 A). Currents of small amplitude were injected in between the successive AP trains, and from the ratio of these injected currents and the resulting steady-state deflection in membrane potential (ΔV), G_in was monitored in the AP-firing fibers.

Figure 2.

Representative recordings of successive AP trains in a fast-twitch EDL muscle fiber. Two electrodes were inserted in the fiber at close proximity (∼70 µm): one electrode was used for injection of square current pulses, and the other electrode recorded the membrane potential. (A) The current injection protocol consisted of low amplitude (±10–20 nA) 75-ms square pulses, which were used for G_in determinations. These were followed by a train of AP trigger pulses (for 3 ms at 300 nA), here delivered at 15 Hz. The protocol was repeated until 4,998 trigger pulses had been injected. Recovery of G_in was assessed 1 min after the stimulation ceased. (B–D) Recordings of the membrane potential during the 1st, the 32nd, and the 85th current injection protocol. (E) An AP train 1 min of recovery after the fiber had fired 4,998 APs. (F) Enlargement of the resting membrane voltage deflections (ΔV) that are underlined in B–E. Because G_in and G_m are inversely related to ΔV, an increase in ΔV reflects reduced G_in and G_m and vice versa.

Muscle activity is associated with biphasic G_m dynamics

Fig. 2 (B–D) shows the effect of repeated AP trains on ΔV in a representative fast-twitch rat EDL muscle fiber, and Fig. 2 F shows enlargements of the underlined ΔV recordings in Fig. 2 (B–D). Remarkably, AP firing was associated with the pronounced biphasic development of ΔV. Thus, at the onset of AP firing, ΔV was increased (Fig. 2, compare B with C), but as stimulation continued, a sudden drop in ΔV to less than half its value before AP firing was observed (Fig. 2, compare B with D). Fig. 2 E shows that when AP firing was stopped for 1 min after the fiber had fired 4,998 APs, ΔV fully recovered to its level before AP firing.

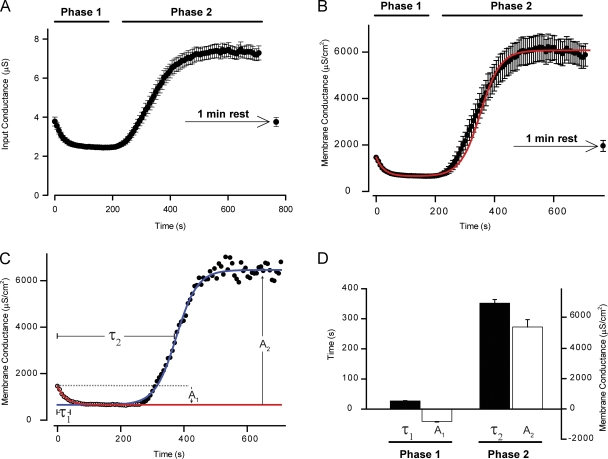
Next, G_in during AP firing was evaluated from the ratio of injected current and the recorded ΔV values during the muscle activity. The mean G_in during 18 experiments such as the one presented in Fig. 2 is shown in Fig. 3 A, and in Fig. 3 B the observations of G_in have been used to extract G_m in the AP-firing fibers (Eq. 3). Fig. 3 B shows that the onset of muscle activity led to a pronounced reduction in G_m that was maintained during the initial ∼1,800 APs. This phase of G_m regulation during muscle activity will be referred to as phase 1. When AP firing continued, G_m suddenly rose to around 400% of its level before AP firing, marking the beginning of the second phase. This phase of G_m regulation during muscle activity will be referred to as phase 2. If AP firing was stopped after 4,998 APs, at which point the second phase was fully developed, G_m recovered within 1 min (Fig. 3 B). This fast recovery showed that the elevated G_m during phase 2 was not caused by membrane damage. This was further supported by a repolarization from −69 ± 1 to −76 ± 1 mV during the development of phase 2 (18 fibers stimulated at 15 Hz), which would not occur under conditions of unspecific membrane damage (Clausen and Gissel, 2005). If AP firing was resumed after the 1 min of rest, G_m rapidly rose. This indicates that the cellular signaling that triggered phase 2 had not completely recovered in the 1-min resting period (unpublished data).

Figure 3.

Fast-twitch muscle fibers showed biphasic regulation of G_m during AP firing. The voltage deflections, ΔV, in AP-firing fibers associated with the small-amplitude current injections were used for calculation of G_in and G_m using Eq. 3. This approach resulted in a temporal resolution of G_in and G_m of 7 s. (A and B) The mean values of G_in (A) and G_m (B) from 18 experiments that were performed as described for the fiber in Fig. 2. To quantify the data, phase 1 was fitted to Eq. 5, and phase 2 was fitted to Eq. 6. (C) G_m from a representative experiment (black circles) in which Eq. 5 was fitted to phase 1 (red line) and extended beyond phase 1 to illustrate the starting value for the fit of phase 2 to Eq. 6 (blue line). (D) The mean parameters obtained by fitting Eqs. 5 and 6 to the individual observations in the 18 fibers whose mean, G_m, is shown in B. These mean parameters were subsequently used to calculate G_m during the firing of 5,000 APs using Eqs. 5 and 6. The outcome of this calculation has been included as a red line in B. All mean data have been presented as means ± SEM.

To further ascertain that the dynamics of G_m observed in the aforementioned experiments (Fig. 3 B) reflected the normal physiological behavior of active AP-firing muscle fibers, a series of experiments was conducted in which the APs were elicited either via motor nerve stimulation or via direct field stimulations. In these experiments, the electrodes were only inserted once the AP firing had ceased, and the recovery of G_in (Fig. S2) or its behavior upon resumed AP firing in the impaled fiber (Fig. S3) was compared with the G_in dynamics observed when all APs were elicited via the inserted electrodes (Fig. 3 A). These experiments confirmed that the G_m dynamics observed when the APs were triggered by the current electrode could also be induced when the whole muscle was stimulated by more physiological stimulation without inserted electrodes (Part III in supplemental text). Also, the derivation of Eq. 3 assumed that the volume of the fiber did not change during the AP firing, which may not be absolutely valid because it is well known that muscles swell during activity (Usher-Smith et al., 2009). However, when the observation of G_m in AP-firing fibers was corrected for volume changes of up to 30%, it was obvious that this could only marginally affect the G_m dynamics (Fig. S1 and Part II of supplemental text).

To quantify and characterize the dynamics of G_m in the AP-firing muscle fibers, the experimental observations were fitted to suitable functions. The dynamics of G_m during phase 1 fit very accurately to a single exponential function,

$$G_{m,\text{Phase}1}=G_{mS}+A_1(1-\exp (-t/{\tau }_1\left)\right),$$ (5)

whereas the dynamics of G_m during phase 2 were well described by a sigmoidal function,

$$G_{m,\text{Phase}2}=G_{mS}+A_1+\frac{A_2}{1+\exp \left(\frac{{\tau }_2-t}{\beta }\right)}.$$ (6)

Fig. 3 C shows experimental observations of G_m dynamics in a representative fiber and illustrates what was described by the five parameters in the fits (A₁, τ₁, A₂, τ₂, and β): phase 1 was characterized by an amplitude, A₁, that describes the magnitude of the reduction of G_m during this phase and a time constant, τ₁, that quantifies the time or the number of fired APs that was required from the beginning of the experiment to reach 63% of A₁. Phase 2 was also characterized by an amplitude, A₂, that describes the magnitude of the rise in G_m from the steady level during phase 1 to the steady level during phase 2 and by a time constant, τ₂, that quantifies the time or the number of fired APs that was required to reach half of A₂. In addition, phase 2 was described by β, which quantifies how rapidly G_m rose during the development of phase 2. The mean amplitudes and time constants from the 18 fibers summarized in Fig. 3 B are shown in Fig. 3 D. Note that A₁ is negative because G_m drops during phase 1, whereas A₂ is positive because G_m rises during phase 2. On average, G_m was reduced by 55 ± 3% during phase 1, whereas during phase 2, G_m rose by 372 ± 34% of G_m at the start of the experiment. In Fig. 3 B, the mean of the five parameters obtained by the fits was used to calculate G_m in AP-firing muscle fibers during the firing of 5,000 APs (solid red line).

Regulation of G_m depends most closely on the total number of APs fired

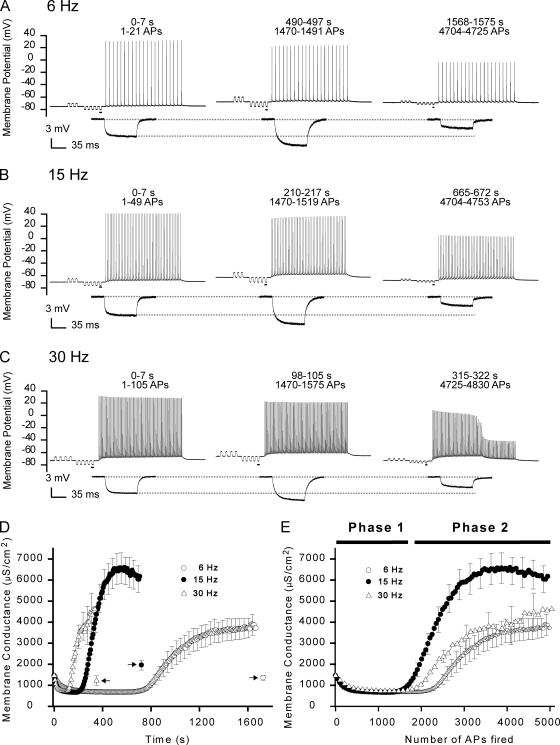
To examine the importance of the AP firing intensity for the regulation of G_m in AP-firing fibers, the development of G_m was compared in fibers in which the AP firing frequency in the pulse trains was either 6 (Fig. 4 A), 15 (Fig. 4 B), or 30 Hz (Fig. 4 C). At all frequencies, the increase of ΔV that characterized phase 1 was observed at the onset of AP firing, and with prolonged AP firing, ΔV suddenly dropped, marking the beginning of phase 2. In Fig. 4 (D and E), the measurements of ΔV have been converted to G_m, and the mean G_m for each of the three frequencies has been plotted against either the experimental time (Fig. 4 D) or the number of APs fired (Fig. 4 E). Interestingly, a comparison of Fig. 4 D with Fig. 4 E suggests that G_m dynamics in AP-firing fibers were more closely related to the number of APs elicited than to the experimental duration. To quantify this notion, the experimental observations at all frequencies were fitted to Eqs. 5 and 6, whereby the time constants for phase 1 (τ₁) and phase 2 (τ₂) were obtained both as functions of the number of APs fired and as functions of the experimental duration (Table II). Such quantification revealed that the 400% increase in AP firing frequency (6 to 30 Hz) was associated with 266% and 524% variations in τ₁ and τ₂, respectively, when these parameters were assessed as functions of experimental durations. In contrast, τ₁ and τ₂ only varied by 37 and 25% when assessed as functions of the number of APs fired. This confirmed that the G_m dynamics during phase 1 and phase 2 were most closely related to the number of APs fired and further suggested that the dynamics of G_m were elicited by mechanisms that, with the present experimental protocol, could sense and integrate the discrete AP events. However, note that the quantification showed that phase 2 did occur slightly later with 6-Hz AP trains than with the 15- and 30-Hz trains (3,264 ± 237 APs at 6 Hz vs. 2,466 ± 2,611 APs and 2,611 ± 129 APs at 15 Hz and 30 Hz, respectively; P < 0.05). The quantification also showed that the magnitudes of reductions in G_m during phase 1 (A₁) were similar at all frequencies (P > 0.31). Furthermore, it showed that the magnitude of the rise in G_m during phase 2 (A₂) was smaller at 6 Hz than when compared with the values of A₂ at 15 and 30 Hz (P < 0.05). In marked contrast to phase 1, in which all APs were well maintained at all frequencies of AP firing, phase 2 was characterized by the dropout of AP (i.e., loss of AP excitation with the 300-nA current injection, particularly at the highest frequency of AP firing). Thus, as exemplified in Fig. 4 C (right), AP dropout during phase 2 left only the passive responses from the injection of the AP trigger currents. Such dropout was observed in all fibers at 30 Hz (13 out of 13), in some fibers at 15 Hz (7 out of 18; P < 0.05, Fisher's exact test; 15 vs. 30 Hz), and was not observed at 6 Hz (eight fibers; P > 0.05 and P < 0.05 against 15 Hz and 30 Hz, respectively).

Figure 4.

The dynamics of G_m in AP-firing fibers were more closely related to the number of APs fired than to the experimental duration. Experiments were conducted similar to that presented in Fig. 2 except that the frequency of the AP trains was varied. (A–C) Recordings from representative fibers in which the APs were triggered using trains of 6 Hz (A), the usual 15 Hz (B), or 30 Hz (C). Enlargements of the underlined parts in the recordings of the membrane potential have been included below. (D) G_m at the three frequencies have been plotted against the experimental time. At all frequencies, ∼5,000 APs were fired, and the fibers were allowed to rest for 1 min before recovery of G_m was assessed. Arrows indicate G_m 1 min after cessation of AP firing. (E) G_m at the three frequencies have been plotted against the number of APs fired. (D and E) Mean data from eight fibers at 6 Hz, 18 fibers at 15 Hz, and 13 fibers at 30 Hz. For clarity of mean data, only every fifth error bar (SEM) has been included.

TABLE II.

Parameters obtained by fitting observations of G_m at 6, 15, or 30 Hz to Eqs. 5 and 6

AP firing frequency	A1	τ1	τ1 (APs)	A2	τ2	τ2 (APs)	β	β(APs)
	µS/cm2	s		µS/cm2	s		s
6 Hz (n = 8)	−779 ± 78	66 ± 8a	199 ± 24	3,400 ± 431b	1,088 ± 79a	3,264 ± 237b	79 ± 14	238 ± 43
15 Hz (n = 18)	−809 ± 39	27 ± 1a	189 ± 10	5,426 ± 494	352 ± 12a	2,466 ± 81	34 ± 2	237 ± 12
30 Hz (n = 13)	−706 ± 50	18 ± 1a	273 ± 14	4,157 ± 575	174 ± 9a	2,611 ± 129	26 ± 2	383 ± 37

Experimental observations of G_m in AP-firing fibers were fitted to Eq. 5 and Eq. 6 to obtain parameters that describe phase 1 and phase 2, respectively. A₁ describes the reduction in G_m during phase 1, and τ₁ describes either the time required or the number of APs fired before 63% of A₁ was observed. A₂ describes the magnitude of the increase in G_m during phase 2, and τ₂ describes the time or the number of APs that was fired before G_m had risen to half of A₂. β reflects the steepness of the rise of G_m during phase 2. All data has been presented as means ± SEM.

^aAll frequencies resulted in significantly different values.

^bSignificantly different from observations at 15 and 30 Hz.

Regulation of G_K and G_Cl during AP firing

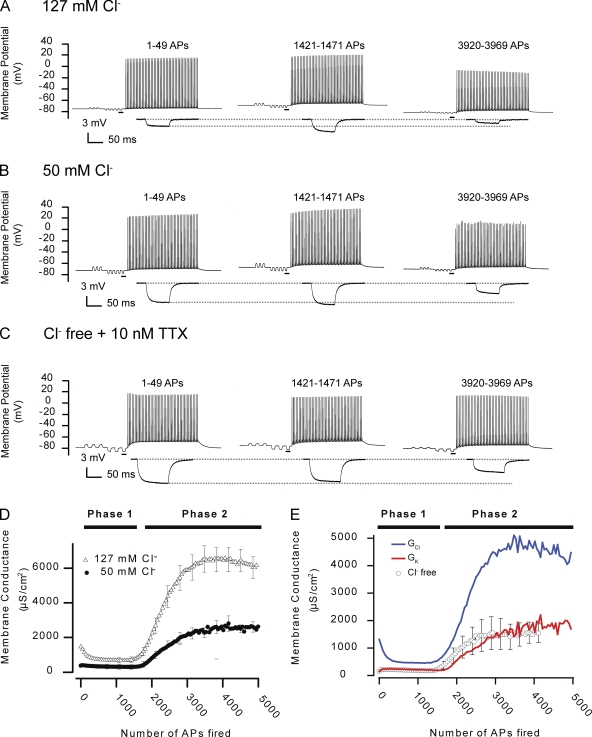
As a first approach in resolving which ion channels were involved in the regulation of G_m in AP-firing fibers, the composite conductances of G_m for K⁺ and Cl⁻ (G_K and G_Cl, respectively) were calculated. Such calculations required experimental determinations of composite conductances before AP firing (G_ClS, G_KS, and G_mS; Table I) and the dynamics of G_m at two different extracellular Cl⁻ concentrations (Eq. 4 and Appendix 2 in supplemental text). Thus, Fig. 5 shows AP trains and ΔV responses from representative fibers at 127 (Fig. 5 A) and 50 mM Cl⁻ (Fig. 5 B). Comparison of the middle traces in Fig. 5 (A and B) shows that the increase in ΔV, which was usually observed during phase I in fibers at 127 mM Cl⁻, was almost absent in the fiber at 50 mM Cl⁻. This indicated that increased ΔV during phase I was related to Cl⁻ channel inhibition. In contrast, after prolonged AP firing leading to phase 2 (Fig. 5, A and B, right), the ΔV responses were similarly reduced in both fibers, indicating an involvement of both K⁺ and Cl⁻ channels in phase 2. The mean G_m from fibers at 127 and 50 mM Cl⁻ showed that the reduction of G_m during phase 1 largely disappeared when extracellular Cl⁻ was reduced to 50 mM and that the rise in G_m during phase 2 was substantially reduced by the partial removal of Cl⁻ (Fig. 5 D). Indeed, quantification by fitting of the observations at 50 mM Cl⁻ to Eqs. 5 and 6 showed that the G_m dynamics during phase 1 no longer achieved reliable fits to Eq. 5, whereas G_m during phase 2 was still accurately described by Eq. 6. Analysis of phase 2 in the fibers at 50 mM Cl⁻ showed that neither the steepness of the rise in G_m during phase 2 (β) nor the number of APs that had to be fired before phase 2 appeared (τ₂) was affected by removal of Cl⁻ (compare Table II with Table III). However, the magnitude of the rise in G_m during phase 2 (A₂) was substantially reduced by partial removal of Cl⁻ (P < 0.05; Tables II and III). This indicated that Cl⁻ channels were involved in both phase 1 and phase 2. Accordingly, calculations of G_K and G_Cl (Eq. 4) showed that phase 1 was caused by a small activation of K⁺ channels and a more substantial inhibition of Cl⁻ channels with G_Cl decreasing by ∼70%, whereas the large increase in G_m during phase 2 was caused by a synchronized activation of both Cl⁻ and K⁺ channels as indicated by an ∼3-fold and ∼14-fold increase in G_Cl and G_K, respectively.

Figure 5.

AP-firing fast-twitch fibers display a biphasic G_m as a result of alterations in G_Cl and G_K. Experiments similar to that in Fig. 2 were conducted in muscle fibers incubated in solutions with reduced or no extracellular Cl⁻. (A–C) Recordings from a control fiber at 127 mM Cl⁻ (A) that was included for comparison with the representative fiber at 50 mM Cl⁻ (B) and the fiber in the Cl⁻-free solution (C). Note that in Cl⁻-free solutions, 10 nM TTX had to be included in the extracellular solution to prevent myotonic discharges when the electrodes were inserted. Enlargements of the underlined parts in the recordings of the membrane potential have been included below. (D) The mean G_m in fibers in the control solution of 127 mM Cl⁻ (n = 18) and in fibers at 50 mM Cl⁻ (n = 9). (E) The mean G_m in Cl⁻-free solution (n = 11) and the composite conductances, G_K and G_Cl, calculated from recordings in fibers at 127 and 50 mM Cl⁻ using Eq. 4. Mean data are presented with every fifth error bar (SEM).

TABLE III.

Parameters obtained by fitting observations of G_m at 50 mM Cl⁻, Cl⁻-free conditions, or with 9-AC to Eq. 6

AP firing frequency	A2	τ2 (APs)	β (APs)
	µS/cm2
50 mM Cl− (n = 9)	2,335 ± 248	2,559 ± 204	227 ± 29
Cl− free (n = 11)	1,601 ± 196	2,135 ± 189	206 ± 18
127 mM Cl− + 9-AC + TTX (n = 13)	1,558 ± 157	2,895 ± 237	251 ± 18

All data were obtained with 15-Hz AP trains. Experimental observations of G_m in AP-firing fibers at 50 mM Cl⁻, Cl⁻-free conditions, and with both 100 µM 9-AC and 10 nM TTX. Under these three conditions, G_m could only be fitted to Eq. 6 because phase 1 was not observed. A₂, τ₂, and β are the same as described in Table II. The values in the A₂ column were significantly different from observations at 127 mM Cl⁻ at the corresponding 15-Hz AP trains. All data have been presented as means ± SEM.

To verify the calculation of G_Cl and G_K in AP-firing muscle fibers, additional experiments were conducted in Cl⁻-free solution under which conditions G_K could be calculated directly from development in ΔV during the experiments. In these experiments, a small concentration of the Na⁺ channel inhibitor, tetrodotoxin (TTX; 10 nM), had to be included in the experimental solutions to avoid myotonic AP firing (Fig. 5 C). As shown in Fig. 5 E, there was a close agreement when G_K was measured directly in the Cl⁻-free solution and when G_K was calculated from the experimental observations at 127 and 50 mM Cl⁻. Indeed, quantification of the observations at Cl⁻-free conditions (Table III) showed that G_m reached a level during phase 2 (1,739 ± 197 µS/cm²) that differed <2% from the level reached by the calculated G_K during phase 2 (∼1,715 µS/cm²). Comparing the observations at 127 mM Cl⁻, 50 mM Cl⁻ and Cl⁻-free conditions showed that although the magnitude of the rise of G_m during phase 2 (A₂) was inversely related to the Cl⁻ concentration (P < 0.05), the numbers of APs fired to reach half of these increases (τ₂) were similar at all conditions (P > 0.11). Furthermore, under all conditions, the rise in G_m during phase 2 displayed similar steepness (β; P > 0.45). Thus, even though the removal of Cl⁻ eliminated the majority of the rise in G_m during phase 2, the parameters that characterized the kinetics of the rise of G_m during phase 2 (β and τ₂) were not affected. This suggested that the K⁺ and Cl⁻ ion channels that conveyed the rise in G_K and G_Cl during phase 2 were responding to a similar cellular signal.

Regulation of ClC-1 and K_ATP channels underlies the biphasic dynamics of G_m

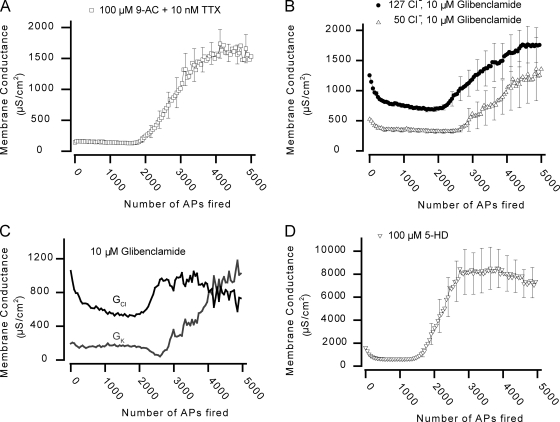
In the last part of this study, we investigated which ion channels underlie the dynamics of G_Cl and G_K during AP firing. Because ClC-1 is the dominant Cl⁻ channel in skeletal muscle fibers (Steinmeyer et al., 1991; Koch et al., 1992; Lueck et al., 2007), experiments were initially performed in the presence of a high concentration of the ClC-1 channel inhibitor 9-AC (100 µM; Palade and Barchi, 1977; Lueck et al., 2007). As expected, 9-AC reduced G_mS by ∼90% (Table I). Fig. 6 A shows the development of G_m in AP-firing fibers at 127 mM Cl⁻ in the presence of 9-AC and 10 nM TTX (added to avoid myotonic AP discharges). The decrease in G_m usually observed with the onset of AP firing was now replaced by a small increase. This was consistent with the observations in Cl⁻-free solutions (Fig. 5 E) and shows that the inhibition of ClC-1 channels underlies the reduction of G_m during phase 1. As AP firing continued, G_m suddenly increased substantially, reflecting the onset of phase 2, but the rise only represented ∼29% of the rise in G_m during phase 2 in the absence of ClC-1 inhibition (1,558 ± 157 vs. 5,426 ± 494 µS/cm²; Tables II and III). Interestingly, in the presence of 9-AC, G_m reached a level during phase 2 that was almost identical to the level reached at Cl⁻-free conditions (1,688 ± 158 vs. 1,739 ± 197 µS/cm²) and to the level reached by the calculated G_K (∼1,715 µS/cm²; Fig. 5 E). Together, this provides three independent ways of showing that both K⁺ and Cl⁻ channels contribute to phase 2 and further demonstrates that the dynamics of G_Cl in AP-firing fibers are being mediated entirely by ClC-1 channels.

Figure 6.

The dynamics of G_m during AP firing in rat EDL muscle fibers reflect regulation of ClC-1 and K_ATP ion channels. (A) Mean G_m from 13 fibers in the presence of 100 µM 9-AC and 10 nM TTX. (B) Mean G_m from experiments at 127 (n = 13) or 50 mM Cl⁻ (n = 16) in the presence of 10 µM of the K_ATP channel inhibitor glibenclamide. (C) From the recordings in B, G_K and G_Cl in the presence of glibenclamide were calculated using Eq. 4. (D) Mean G_m from six experiments in which the mitochondrial K_ATP channels were inhibited using 5-HD. Under all conditions, G_m recovered fully within 1 min after cessation of AP firing (not depicted). Mean data are presented with every fifth error bar (mean ± SEM).

To test for an involvement of K_ATP channels in the regulation of G_m in AP-firing fibers, experiments were performed in the presence of 10 µM of the K_ATP channel inhibitor glibenclamide (Cifelli et al., 2008). Fig. 6 B shows mean G_m dynamics in glibenclamide-treated fibers, 13 of which were at 127 mM Cl⁻ and 16 of which were at 50 mM Cl⁻. At 127 mM Cl⁻, phase 1 appeared to be largely unaffected by the inhibitor (A₁ = −579 ± 27 µS/cm²; τ₁ = 299 ± 27 APs), whereas phase 2 was substantially reduced and delayed. In 5 out of the 13 fibers at 127 mM Cl⁻, a clear phase 2 was never observed, even after firing ∼5,000 APs, and in the remainder of the glibenclamide-treated fibers, phase 2 was not accurately described by Eq. 6. Thus, the observations from the experiments with glibenclamide were not quantified by fitting. However, comparison of the maximum G_m during phase 2 in the absence and presence of glibenclamide suggested that glibenclamide blocked phase 2 more than would be expected if this inhibitor only blocked the rise in G_K during phase 2. Consequently, experiments with glibenclamide were also performed at 50 mM Cl⁻ whereby extraction of G_K and G_Cl in AP-firing fibers treated with glibenclamide became possible (Eq. 4). Fig. 6 C shows that elevations in both G_K and G_Cl during phase 2 were markedly reduced and delayed by glibenclamide. This demonstrates that in addition to preventing the opening of K_ATP channels during phase 2, the drug also prevented the reopening of ClC-1 channels during phase 2. In addition, phase 2 was usually associated with repolarization of the resting membrane potential in the absence of glibenclamide, whereas with glibenclamide, this repolarization was either not observed or was delayed in onset.

Because the involvement of K_ATP channels in phase 2 was assessed with glibenclamide, which is known to target the K_ATP channels in both the surface membrane of muscle fibers as well as in their mitochondria, a series of experiments was conducted using the inhibitor 5-hydroxydecanoate (5-HD), which predominantly targets the mitochondrial K_ATP channel (Moses et al., 2005). In experiments with six fibers, both phase 1 (A₁ = −992 ± 51 µS/cm²; τ₁ = 125 ± 12 APs) and phase 2 (A₂ = 7,686 ± 1,464 µS/cm²; τ₂ = 2,440 ± 275 APs) were fully developed (Fig. 6 D). This indicated that the effect of glibenclamide on G_K during phase 2 reflected direct interference with the surface membrane K_ATP channels rather than interacting with phase 2 via some indirect effect that involved the mitochondria.

DISCUSSION

This study demonstrates for the first time that G_m is acutely regulated in AP-firing muscle fibers. We report that modulation of the functions of ClC-1 and K_ATP ion channels underlies biphasic dynamics of G_m in AP-firing rat EDL muscle fibers: at the onset of AP firing, inhibition of ClC-1 channels conveys a reduction in G_m, whereas with continued AP firing, reopening of ClC-1 channels and activation of K_ATP channels massively elevate G_m.

G_K and G_Cl can be determined on a time scale of seconds in AP-firing muscle fibers

With the classical technique of measuring G_m, muscle fibers must be penetrated multiple times, making it an unsuitable approach for determinations of rapid regulation of G_m in AP-firing fibers. To determine G_m with a temporal resolution of seconds in AP-firing fibers, an alternate method was developed in this study that extracts G_m during muscle activity from on-line measurements of G_in. However, this approach only provides a relative measure of G_m, and to obtain absolute values for G_m, the value of the resting membrane conductance before AP firing, G_mS, had to be determined in a separate group of fibers under similar experimental conditions using the classical technique. Thus, a full description of G_m in AP-firing fibers relies on observations obtained with both techniques. The massive benefit of combining the two techniques is witnessed by the possibility of separating G_m dynamics into its G_K and G_Cl components from experiments conducted at two different Cl⁻ concentrations. In this way, the involvement of K⁺ and Cl⁻ channels for G_m dynamics may be assessed. In AP-firing EDL muscle fibers, we observed that upon the onset of AP firing, a substantial reduction in G_Cl and a minor increase in G_K summed to give the substantial reduction in G_m during phase 1. With prolonged AP firing leading to phase 2, G_Cl and G_K rose to stable levels corresponding to ∼3-fold and ∼14-fold of their initial values, respectively.

Reduced G_m during phase 1 reflects inhibition of ClC-1 channels

When experiments were performed in Cl⁻-free conditions or the ClC-1 channels were blocked by 9-AC, G_mS was reduced by almost 90%, and the normal reduction in G_m during phase 1 in AP-firing fibers was absent. This suggests that during early stages of physical activity, AP firing in muscle initiates a cellular signaling pathway that leads to inhibition of ClC-1 channels and, consequently, to a reduction in G_Cl. Interestingly, G_m during phase 1 was well described by a single exponential function, which suggests that inhibition of the ClC-1 channels during phase 1 proceeds via a cellular signaling system that has a single rate-limiting step.

The physiological role of reduced G_Cl for the excitability and contractile properties of working muscle have been investigated previously using intact muscle and mechanically skinned muscle fibers. Because it is well documented that exercise is associated with marked elevation in the extracellular K⁺ concentration (for review see Sejersted and Sjøgaard, 2000), several of these studies have focused on the role of Cl⁻ channels for the effect of elevated K⁺ on muscle function. These studies show that under conditions of elevated K⁺, muscle excitability becomes substantially depressed, but if ClC-1 channels are inhibited via intracellular acidification, 9-AC, or by removal of Cl⁻ from the extracellular solution, the muscle fibers substantially regain excitability and function (Nielsen et al., 2001; Pedersen et al., 2004, 2005; van Emst et al., 2004; de Paoli et al., 2007). This could indicate that loss of excitability in working muscles can be counteracted if ClC-1 channels are inhibited. This study demonstrates for the first time that the onset of muscle activity is indeed associated with an inhibition of ClC-1 channels, and, consequently, it can be speculated that this reduction in G_m would assist in the maintenance of muscle excitability in working muscle.

ClC-1 and K_ATP channels open synchronously during phase 2

A remarkable characteristic of phase 2 was its consistent appearance after firing roughly ∼1,800 APs irrespective of whether the APs were fired in trains of 6, 15, or 30 Hz. This suggests that the recovery of the pathway that signals phase 2 was slow compared with the difference in experimental time with the different stimulation frequencies. Experiments showed that after the fibers had fired ∼5,000 APs, G_m achieved full recovery if the fibers rested for 1 min. However, upon resumed AP firing, phase 2 rapidly reoccurred. From the full recovery of G_m during the 1-min resting period and the fast reappearance of phase 2 upon resumed AP firing, it can be envisaged that phase 2 relies on a cellular signaling system that has a distinct threshold such that once this threshold is crossed, it leads to the opening of Cl⁻ and K⁺ channels. If this cellular signal behind phase 2 recovers below the threshold in the 1 min of rest, G_m should fully recover. However, upon resumed AP firing, the cellular signal starts to increase again, but this time from a much higher level. Therefore, the threshold is crossed much faster in the second round of AP firing. Indeed, such a system should be well represented by a sigmoidal function, which typically describes systems that can alternate between two states.

Experiments with reduced extracellular Cl⁻, Cl⁻-free solutions, and 9-AC (a) showed that reopening of ClC-1 channels caused the rise in G_Cl during phase 2 and (b) demonstrated that the elevations in G_K and G_Cl during phase 2 appeared after the same number of APs and rose with similar steepness. This indicated that the reopening of ClC-1 channels and the rise in G_K were temporally very closely synchronized and suggested that the ClC-1 and K⁺ channels that mediated the elevations in G_Cl and G_K during phase 2 responded to similar cellular signaling. To this end, three lines of evidence suggest that this common signal may be a substantial reduction in the cellular energetic state of the muscle fibers: (1) Fink and Lüttgau (1976) showed that metabolic poisoning of frog skeletal muscle causes enormous elevations in both G_K (110-fold) and G_Cl (14-fold). Importantly, these elevations in G_K and G_Cl occurred almost synchronously, as occurs during phase 2. Furthermore, such elevations occurred without alterations in the resting membrane potential, which indicates that the cellular integrity of the poisoned muscle fibers was conserved. Such observations with metabolic poisoning have been linked to opening of K_ATP channels in mammalian muscle (Allard et al., 1995). Collectively, the experiments with metabolic poisoning demonstrate that skeletal muscle fibers are equipped with Cl⁻ and K⁺ ion channels that are sensitive to the metabolic state of the cell and that these channels appear to open at the same level of metabolic depression. However, the present study provides the first direct evidence that similar regulation of K⁺ and Cl⁻ channels may be involved in physiological regulation of ion channels in active skeletal muscle fibers. (2) Experiments performed in this study demonstrate that the dramatic elevation of G_K in phase 2 is significantly reduced and delayed by the K_ATP channel inhibitor glibenclamide. These channels are generally considered to constitute a link between the metabolic state and excitability of cells because they open when the energy level becomes low (Nichols, 2006). Thus, the experiments with glibenclamide indicate that the rise in G_K during phase 2 was initiated by the depressed metabolic state of the fibers that caused K_ATP channels to open. (3) The synchronicity of ClC-1– and K_ATP-channel opening in phase 2 suggests that ClC-1 channels should also be sensitive to the metabolic state of the cells.

Bennetts et al. (2005) have recently demonstrated in expression systems that conditions of low cellular energy levels increase the opening probability of ClC-1 channels. This important contribution to the understanding of ClC-1 channels has now been further developed to show that the sensitivity of ClC-1 channel to the metabolic state of cells is inversely related to the intracellular proton activity (Bennetts et al., 2007; Tseng et al., 2007) and is completely lost upon cell oxidation (Zhang et al., 2008). However, one study has raised doubt that ClC-1 channels are sensitive to the metabolic state of the cells (Zifarelli and Pusch, 2008). All of these observations on the regulation of ClC-1 channels were obtained using various expression systems, and whether native ClC-1 channels are sensitive to the metabolic state of muscle fibers has not been explored. In the present study, we demonstrate that ClC-1 channels open after prolonged AP firing, and the synchronicity of opening of ClC-1 and K_ATP channels strongly suggests that ClC-1 channels do respond to depressed metabolic conditions in native skeletal muscle fibers. Because the metabolic state can be severely depressed in fast-twitch fibers during physical exertions (Esbjörnsson-Liljedahl et al., 1999), it is possible that such openings of ClC-1 and K_ATP channels occur in fatigued muscles in vivo.

Until now, our understanding of the regulation of G_m in working muscles has been limited to extrapolations from knowledge obtained in resting muscles. Using a new technical approach, however, we here identify significant activity-induced regulation of G_m in fast-twitch skeletal muscle fibers that provides new perspectives on the roles of ClC-1 and K_ATP channels for muscle function. We demonstrate that at the onset of muscle activity, ClC-1 channels are rapidly inhibited. Such inhibition of ClC-1 channels may assist working muscle in their maintenance of excitability. The data further implicate ClC-1 channels in a mechanistic alliance with K_ATP channels such that at times of low cellular energy levels, opening of these channels generates a large G_m. Because such an increase in G_m tends to lower fiber excitability, we suggest that elevation of G_m in response to the reduced metabolic state of the muscle fibers may switch off further muscle fiber activation and thus prevent complete depletion of the energetic state of the fibers that otherwise might result in loss of cellular integrity. This scenario is supported by the loss of AP excitation when G_m became elevated during phase 2 and by observations of severe muscle damage in K_ATP channel knockout mice after treadmill running (Thabet et al., 2005; Cifelli et al., 2007).