Trabeculae carneae as models of the ventricular walls: implications for the delivery of oxygen

Abstract

Trabeculae carneae are the smallest naturally arising collections of linearly arranged myocytes in the heart. They are the preparation of choice for studies of function of intact myocardium in vitro. In vivo, trabeculae are unique in receiving oxygen from two independent sources: the coronary circulation and the surrounding ventricular blood. Because oxygen partial pressure (PO₂) in the coronary arterioles is identical in specimens from both ventricles, whereas that of ventricular blood is 2.5-fold higher in the left ventricle than in the right ventricle, trabeculae represent a “natural laboratory” in which to examine the influence of “extravascular” PO₂ on the extent of capillarization of myocardial tissue. We exploit this advantage to test four hypotheses. (1) In trabeculae from either ventricle, a peripheral annulus of cells is devoid of capillaries. (2) Hence, sufficiently small trabeculae from either ventricle are totally devoid of capillaries. (3) The capillary-to-myocyte ratios in specimens from either ventricle are identical to those of their respective walls. (4) Capillary-to-myocyte ratios are comparable in specimens from either ventricle, reflecting equivalent energy demands in vivo, driven by identical contractile frequencies and comparable wall stresses. We applied confocal fluorescent imaging to trabeculae in cross section, subsequently using semi-automated segmentation techniques to distinguish capillaries from myocytes. We quantified the capillary-to-myocyte ratios of trabeculae from both ventricles and compared them to those determined for the ventricular free walls and septum. Quantitative interpretation was furthered by mathematical modeling, using both the classical solution to the diffusion equation for elliptical cross sections, and a novel approach applicable to cross sections of arbitrary shape containing arbitrary disposition of capillaries and non-respiring collagen cords.

INTRODUCTION

Cardiac ventricular trabeculae carneae are naturally arising “strands” of axially arranged cardiac tissues present in both ventricles of the heart. They are minute, seldom >3 mm in length and 50–500 µm in diameter. Because of these features, they are much favored by experimentalists for the study of the ionic, mechanical, and metabolic function of cardiac muscle. Those most favored arise from the free wall and insert into the atrioventricular ring, but they can be found in almost any location within either ventricle. For studies of myocardial function, specimens that are free-running from origin to insertion are sought. Implicit in their use is the assumption that their tissues are homologous with those of the ventricular free walls and septum. An obvious index of homology is the extent of capillarization. Curiously, and despite the implicit assumption, the literature lacks an explicit test of homology for specimens from either ventricle.

However, in an extensive series of investigations over the past two decades, H.F. Downey and co-workers have quantified striking differences in coronary blood flow and oxygen supply between the right ventricle (RV) and left ventricle (LV). Their review (Zong et al., 2005) provides the following summary statements germane to resting conditions. (1) When normalized per gram of tissue, the rate of oxygen consumption of the RV is about one half that of the LV. (2) Despite identical coronary perfusion pressures, coronary blood flow to the RV is less than that to the LV. (3) The external work of the RV is much less than that of the LV, reflecting its proportionately lower afterload. (4) The lesser rate of oxygen consumption of the RV is consistent with its lower work output. (5) The lesser rate of oxygen consumption of the RV reflects its lower peak wall stress developed during systole. Although we do not concur with the latter assertion, we nevertheless consider that the preceding four statements provide justification for an examination of the difference in extent of capillarization between RV and LV tissues. Our particular focus is on trabeculae carneae. Because all specimens are supplied by coronary blood at the same oxygen partial pressure (PO₂), but they are situated in chambers whose ambient PO₂ differs by some 2.5-fold, trabeculae represent a naturally occurring “laboratory” in which to examine the extent to which capillarization is responsive to the PO₂ of extravascular blood.

Thus, the aim of our study was to compare capillary density between RV and LV trabeculae on the basis of quantifying their respective capillary-to-myocyte ratios. The considerations above led us to propose four experimentally testable hypotheses. (1) Because oxygen can diffuse directly from the ventricular blood into a freely running trabecula (i.e., one that is unattached to the wall throughout its extent), we predict that an outer annulus of cells will be unperfused by the coronary circulation. (2) An obligatory corollary of this prediction is that trabeculae of sufficiently small diameter will also be completely devoid of capillaries, receiving their oxygen entirely by diffusion from blood in their respective ventricular chambers. (3) The capillary-to-myocyte ratios of trabeculae from either ventricle will be found to be identical to those in the walls from which they arise, reflecting the presumed comparability of structure alluded to above. (4) The capillary-to-myocyte ratios will be comparable in specimens from either ventricle, reflecting the fact that they experience equivalent energy demands in vivo, driven by identical frequencies of contraction and comparable peak systolic stresses. Note that the latter implication (based on the assumption that the higher afterload pressure seen by the LV is met by its thicker wall, rather than by development of higher peak systolic wall stress) is diametrically opposite to that of Zong et al. (2005), given in item 5 of our précis of their summary above. As will be seen, our predictive success was somewhat better than would be expected from tossing a coin.

Because diffusive oxygen supply plays a central role in the formulation of our hypotheses, we pay particular attention to this issue, using the analytical solution to the diffusion equation for elliptical cross sections and developing an innovative method of solution for trabecula cross sections of arbitrary shape containing arbitrary dispositions of capillaries and non-respiring collagen cords.

MATERIALS AND METHODS

Ethical approval

The experiments reported here were approved by the Animal Ethics Committee of the University of Auckland. Male Wistar rats (n = 13) weighing 290–340 g were deeply anaesthetized using either halothane or isoflurane. After cervical spinal dislocation and thoracotomy, the heart was exposed and 1 ml of heparin solution was injected into the left ventricular lumen. After waiting a few beats to allow circulation of the anticoagulant through the coronary vasculature, the heart was rapidly excised and placed in ice-cold saline to induce arrest. The distal stump of the aorta was then attached to the perfusion catheter, and Langendorff perfusion commenced under a hydrostatic pressure of 100 mm Hg. The Krebs-Henseleit perfusate comprised 118 mM NaCl, 4.75 mM KCl, 1.18 mM MgSO₄, 1.18 mM KH₂PO₄, 24.8 mM NaHCO₃, and 2.54 mM CaCl₂. It was equilibrated with 95% O₂-5% CO₂ at room temperature.

Shortly after beating had recommenced (thereby ensuring that the heart was viable), the heart was rearrested using St. Thomas's (cardioplegic) solution. Immediately upon induction of arrest, the perfusion medium was switched to Bouin's solution to fix the tissue and to provide an acidic environment to aid the staining of collagen by picrosirius red (PSR). After 50 ml of Bouin's solution had traversed the coronary circulation, 50 ml PSR was slowly perfused (at a rate of ∼1 drop per second).

Variations of perfusion protocol

The above procedures allowed us to produce cross-sectional images of trabeculae in which individual myocytes, capillaries, collagenous structures, and extracellular space could readily be identified and quantified in RV trabeculae. Such was not the case, however, for trabeculae dissected from the LV. Preliminary experiments (n = 3 hearts) using identical perfusion, fixation, and staining procedures failed to reveal the presence of capillaries in LV preparations. On the presumption that the standard Langendorff perfusion procedure, described above, was incapable of perfusing the LV vasculature, we examined five variations of protocol, as follows. During the period of PSR infusion, we increased the perfusion pressure to 250 mm Hg. This was done in both the absence (n = 2) and presence (n = 4) of 1 mM adenosine, a coronary vasodilator. In a separate series of experiments, we ligated the right coronary artery on the presumption that it had been receiving a disproportionate fraction of the flow under standard perfusion conditions. Once again, this was done in both the absence (n = 2) and presence (n = 4) of adenosine. None of these four techniques was successful in revealing the presence of capillaries in preparations from the LV, despite each being successful in the RV. In the fifth variation of the standard protocol (n = 6), we omitted the Bouin's perfusion step on the hunch that its function to cross-link proteins might differentially affect capillaries in the LV and RV, causing the former to shrink or even to collapse completely. This, indeed, appears to have been the case because capillaries were now clearly evident in specimens dissected from the LV. Thus, LV trabeculae were immersion-fixed in Bouin's fixative after perfusion staining with PSR. In contrast, RV trabeculae were successfully prepared by all five procedures.

Isolation of trabeculae

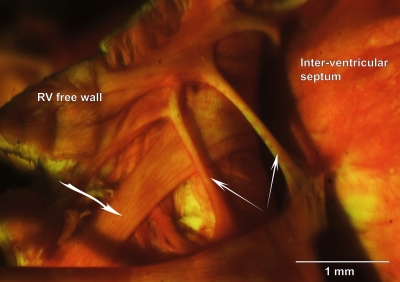
Upon completion of a perfusion process, the heart was disconnected from the catheter and placed in cold saline (0.9% NaCl). The LV lumen was carefully exposed, and un-branched, free-running trabeculae (n = 13) were excised, leaving a small block of ventricular wall tissue at each end. The same procedure was repeated in the RV (n = 9). A portion of RV with a particularly generous choice of specimens is shown in Fig. 1. Regardless of the perfusion technique, excised trabeculae were placed in Bouin's fixative for about a week, thereby providing sufficient time for PSR to bind to collagenous structures.

Figure 1.

Rat right ventricular trabeculae in situ. Photomicrograph of a Bouin's-fixed, PSR-stained rat RV in which the free wall has been reflected to reveal the presence of trabeculae. The two narrow arrows point to thin, free-running preparations of the sort sought by experimentalists. The heavier arrow points to a wider, apparently strap-like, specimen.

Tissue processing

Fixed and stained trabeculae were processed for resin embedding by dehydration through a graded ethanol series (10-min steps). Dehydrated trabeculae were then placed in a resin–propylene oxide mixture (1:1; epon 812; ProSciTech) for 2 h, followed by pure resin for 4 h.

The well of a silicone mold was half-filled with resin and placed in an oven at 60°C for 3 h, after which it was removed and allowed to cool. A resin-infiltrated trabecula was placed on the surface of the partially cured resin, aligned parallel to the long axis of the mold. The well was then filled with resin and cured for an additional 4 h.

Embedded trabeculae were selected for imaging using two criteria. A trabecula had to be longitudinally oriented within its block, and it had to be free from any evidence of damage. Resin blocks containing trabeculae meeting these criteria were epoxy-mounted onto individual aluminum plates with the trabecula oriented vertically. The aluminum plates provide for the secure attachment of the blocks on the viewing stage so that they are held firmly during imaging and milling processes.

Imaging of trabeculae in cross section

The imaging system has been described previously in detail (Sands et al., 2005). In brief, it comprises a laser-scanning confocal microscope (TCS 4D; Leica), a high-precision (0.1 µm resolution) three-axis translation stage (ALS5000; Aerotech), and an ultra-mill (SP2600; Leica) mounted on an anti-vibration table (Newport Corporation). Excitation at 568 nm was provided by a laser (Omnichrome Kr-Ar; Melles Griot).

Images of 512 × 512 pixels (150 × 150 µm) were acquired at ∼0.3-µm pixel resolution. For many trabeculae, cross sections could be imaged in a single field captured by a 20× (0.7 NA) water-immersion objective. Larger trabeculae required the acquisition of multiple, overlapping images.

Image processing

Confocal images were background-corrected for uneven illumination. Deconvolution with a theoretical point-spread function was performed using a Richardson-Lucy algorithm. When necessary, a cross-correlation technique was used to align overlapping images to form a single montage.

3-D reconstruction from 2-D images

Extended volume imaging was performed on a single, small RV trabecula of the sort commonly chosen for functional studies. The trabecula was dissected such that its distal (valvular) end retained tissue from the atrioventricular ring, whereas its proximal end retained tissue from the right ventricular free wall. The trabecula was <150-µm wide at its distal end, but it increased in diameter somewhat toward the wall. By commencing distally, the entire cross section was initially captured in a single image slice. This considerably reduced the time required for acquisition of an image because the montaging step was obviated. However, as the imaging and milling process continued, the cross-sectional area of the trabecula increased progressively. When the cross section became larger than the field of view, the montage facility was adopted.

A series of 90 confocal optical sections at 0.3-µm z-steps was acquired as a 27-µm “stack.” The top 25 µm of the specimen was then removed by the ultra mill before imaging the next 27 µm. The 2-µm regions of overlap between adjacent stacks were required to achieve registration in the z-direction. This imaging–milling cycle was repeated 35 times, thereby allowing 3-D reconstruction of 875 µm of the trabecula. The volume fraction occupied by blood vessels in a 270-µm segment was computed.

Processed image planes were imported into ImageJ (National Institutes of Health) to form a 3-D image stack. Using Voxx software (Clendenon et al., 2002), the reconstructed 3-D image could be rotated and re-sliced in any desired orientation.

RV wall, LV wall, and septal tissues

To test hypothesis 3, we applied comparable techniques to tissues excised from the ventricular free walls and the interventricular septum. The standard method of perfusion, fixation, and staining of tissues was as described above. Dissection criteria necessarily differed, inasmuch as regions of the septum and free walls were arbitrarily selected, from which blocks of tissue were dissected. Care was taken that the blocks were oriented on the microscope stage such that vessels and myocytes were imaged perpendicular to their longitudinal axes. For each block, five images (containing some 100–250 myocytes) were arbitrarily selected, and the numbers of myocytes and blood vessels were counted.

Quantification

The numbers of vessels and myocytes were counted in two 2-D cross-sectional images from each trabecula. The number of vessel lumens was given automatically by a segmentation program (see Results). Vessels whose diameters exceeded 5 µm were classified as “distribution vessels.” Smaller vessels were classified as capillaries (Bassingthwaighte et al., 1974; Tomanek et al., 1982; Hossler et al., 1986). In contrast with blood vessels, myocytes had to be counted manually because there was insufficient difference of fluorescence intensity between myocytes per se and their endomysial surroundings. For trabeculae, but not for either wall or septal tissues, the fractional area occupied by blood vessels was also determined.

The long and short axes of the trabecula cross section were measured, with the latter being taken at right angles to the midpoint of the former to determine eccentricity. The eccentricity (ε) of cross sections of trabeculae was calculated as follows:

$$\epsilon =\sqrt{1-\frac{b^2}{a^2}},$$ (1)

where a and b are, respectively, the lengths of the long and short axes of the trabecula cross section. Note that this index varies between 0 (for a circle) and 1 (for an elongated ellipse).

Statistical analyses

Statistical analyses were performed using Statistica software (StatSoft Pacific Pty Ltd.). ANOVA was used to test the significance of differences of eccentricity and of the fractional areas occupied by vessels between LV and RV trabeculae. The difference of capillary-to-myocyte ratios arising from RV trabeculae dissected under different Langendorff perfusion protocols was tested using one-way ANOVA. The dependence of the number of capillaries on the number of myocytes was assessed by linear regression. Homogeneity of slopes among confocally imaged RV trabeculae, confocally imaged LV trabeculae, and surface-imaged RV trabeculae was assessed using analysis of covariance. Variation of the capillary-to-myocyte ratios between trabecula (RV and LV) and ventricular wall sites (RV, LV, and septum) was examined using one-way ANOVA (treating data from separate images as “replications”), followed by the application of three mutually orthogonal vectors of post hoc contrast coefficients. To ensure that the “strength of evidence” was in the “moderate-to-strong” range, for each of the preceding statistical decisions we chose a minimum Bayes factor of 0.036, corresponding to a conventional p-value of 0.01 (Goodman, 1999). Numeric values are presented in the text as the mean ± SEM.

RESULTS

Identification of capillaries and myocytes

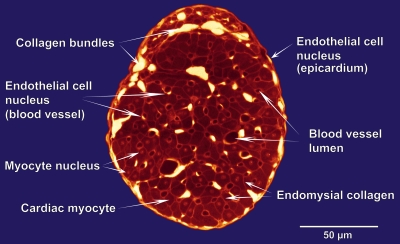
A confocal cross-sectional image from a typical RV trabecula is shown in Fig. 2, with its intracellular and extracellular components labeled. The trabecula shown is roughly elliptical in cross section (ε = 0.66). Collagen bundles are identified as the brightest (yellow-white) regions. Myocytes appear in the range of medium intensity as dull red. Blood vessel lumens are roughly circular regions displayed as dark red to black. Individual myocytes are distinguished from their neighbors by brighter red endomysial collagen. Some myocytes show a nucleus, a region of brighter red than its surroundings, enclosed within the cell boundary. Nuclei of other cell types, endothelial cells of blood vessels and on the trabecula surface, are also occasionally visible. They typically show strong fluorescence signals that are almost at the same level of intensity as the extracellular collagen bundles, distinguishable only by their intracellular locations. Although the existence of these various nuclei is helpful for identification purposes, their presence is ignored henceforth as we restrict our focus to blood vessels and myocytes.

Figure 2.

Cross-sectional confocal image (false-colored) of a Bouin's-fixed, PSR-stained RV trabecula prepared under the standard perfusion protocol.

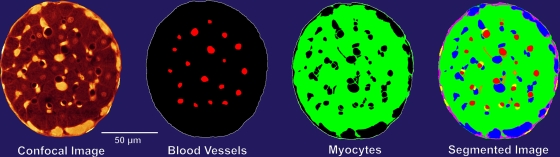
Image segmentation

Custom-written software was used to segment the images according to brightness and feature extraction (Fig. 3). Roughly circular regions of low intensity were segmented as the lumens of blood vessels. Collagen generated a strong fluorescence signal because it bound PSR strongly (it appears white in Fig. 2). The staining of endomysial collagen readily allowed for visual identification of individual myocytes. This identification step was enhanced by the fact that myocytes per se yielded regions of low-to-moderate intensity as a consequence of the nonspecific binding of PSR. The various segmentation components are shown in Fig. 3, where the colors represent regions of different fluorescence intensity.

Figure 3.

Cross-sectional confocal image of a right ventricular trabecula and its segmented regions. Note that “Myocytes” includes both the cells and their surrounding endomysial collagen, which could not be separately distinguished on the basis of fluorescence intensity. In the “Segmented Image,” blood vessels appear red and collagen cords appear blue.

3-D reconstruction from 2-D images

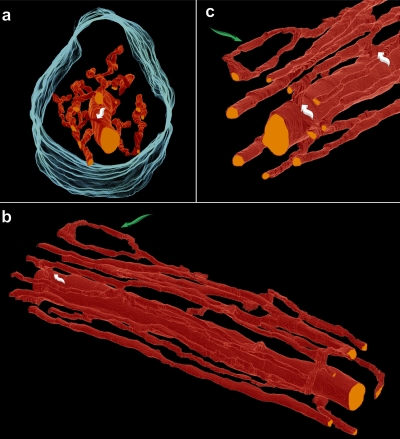
A sequence of cross-sectional images from an RV trabecula was used for 3-D reconstruction. A stack of 2,900 individual confocal optical sections was assembled in the z-direction. The vascular components of these segmented images were then assembled to reconstruct the blood vessel network in 3-D. The network is shown in “end-on” view in Fig. 4 a. The relatively large central vessel (possibly a venule) is surrounded by a network of capillaries to which it is occasionally anastomosed. The capillary network is complex, even demonstrating a “ring” structure (Fig. 4 c), but nevertheless it is predominantly in parallel with the long axis of the trabecula, as is shown more clearly in Fig. 4 b. In this particular example, the vasculature occupied 4.01% of the volume. Although this proportion is of inherent interest, it does not allow determination of the capillary-to-myocyte ratio. To accomplish that objective, we reverted to segmented 2-D images in cross section.

Figure 4.

3-D reconstruction of the proximal 270 µm of the 2,900-slice dataset. (a) Vessels (red) and trabecula surface (cyan). Note the absence of vessels in the outer annulus. (b) The blood vessel network shown in longitudinal aspect. (c) A segment of the vessel network. White arrows show anastomoses between a capillary and the large central vessel (bottom arrow), and between two capillaries (top arrow). Green arrows indicate the splitting and subsequent reconvergence of a capillary (also shown in b).

Quantification of capillaries, myocytes, and trabecula dimensions

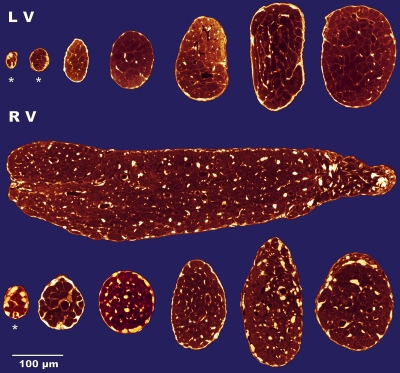
We selected un-branched, free-running trabeculae. The number available in either chamber was highly variable. In general, specimens were more abundant and of more varied shapes and sizes in the RV. A sense of the extreme variability in size and eccentricity of trabeculae is conveyed by the cross sections shown in Fig. 5.

Figure 5.

Cross-sectional images of seven LV (top row) and seven RV (bottom two rows) trabeculae. The specimen in the bottom right-most corner is the same as in Fig 2. Note the absence of blood vessels in the three smallest specimens (*).

Trabecula eccentricity.

The smallest trabecula examined (1,350 µm²) was from the LV (Fig. 5, top left specimen). It was moderately elliptical in cross section (ε = 0.64; with semimajor and semiminor axes of ∼24 and 18 µm, respectively). In contrast, the largest preparation (∼340 by ∼100 µm; 0.11 mm²) was from the RV (Fig. 5, middle row) and was decidedly elliptical (ε = 0.96). There was no difference of average eccentricity between specimens from the LV and RV (0.75 ± 0.014 and 0.77 ± 0.017, respectively).

Blood vessels and myocytes.

Within trabeculae from the RV, blood vessels were patent and readily recognizable, regardless of the method of perfusion. In the LV, in contrast, vessels were not observed unless the Bouin's perfusion step had been eliminated (the specimens being subsequently “immersion-fixed”). In consequence, the proportion of cross-sectional area occupied by RV vessels (3.7 ± 0.22%) was nearly twice that of LV samples (2.1 ± 0.21%). We suspect that this is a fixation artifact, reflecting more constricted (and, consequently, less circular) vessels (of any diameter) observed in sections from the LV (contrast the images in the top and bottom panels of Fig. 5). There was no difference in the proportion of cross-sectional area occupied by myocytes between specimens arising from the RV (83.4 ± 1.37%) and those selected from the LV (84.3 ± 0.98).

Capillary-to-myocyte ratios

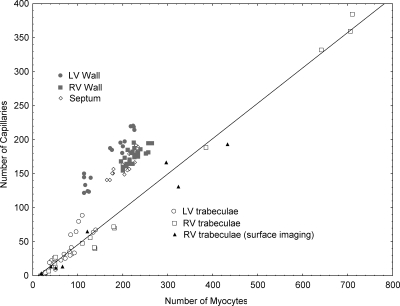
In addition to the capillary-to-myocyte ratios calculated here, arising from confocal fluorescence microscopy, we had available ratios from an earlier study in which eight RV trabeculae had been examined using surface imaging microscopy. Because these earlier results have been published only in abstract form (Joshi, P., G. Sands, D. Gerneke, I. LeGrice, and D. Loiselle. 2006. Proceedings of the Physiological Society. Abstr. C25:15P; Joshi, P., Q. Dollie, D.A. Gerneke, G.B. Sands, I.J. LeGrice, and D.S. Loiselle. 2007. International Society for Heart Research, Australasian Section, Annual Scientific Meeting. Abstr. S216), and because the microscopy technique was fundamentally different (Gerneke et al., 2007), we considered it instructive to compare the values obtained in the two studies. To that end, we separately regressed the number of capillaries on the number of myocytes for the three separate sets of data: (1) RV trabeculae examined by surface-imaging microscopy (Joshi, P., G. Sands, D. Gerneke, I. LeGrice, and D. Loiselle. 2006. Proceedings of the Physiological Society. Abstr. C25:15P; Joshi, P., Q. Dollie, D.A. Gerneke, G.B. Sands, I.J. LeGrice, and D.S. Loiselle. 2007. International Society for Heart Research, Australasian Section, Annual Scientific Meeting. Abstr. S216); (2) RV trabeculae examined by confocal fluorescence microscopy (this study); and (3) LV trabeculae, also examined confocally in this study. Analysis of covariance showed no statistically significant differences of regression parameters among the three groups, so we pooled the data and subjected them to linear regression, with the following result:

$${\text{n}}_{\text{capillary}}=\left(0.\text{52}\pm 0.0\text{1}\right)*{\text{n}}_{\text{myocyte}}-\text{6}.\text{46}\pm \text{2}.\text{4}0$$ (2)

We are thus confident of two facts: (1) in trabeculae from either ventricle, each capillary services roughly two myocytes, and (2) trabeculae of sufficiently small diameter lack capillaries.

Given the results for trabeculae, in which a single regression line (Eq. 2) fitted the observations from two distinct datasets (Fig. 6), it was of interest to contrast them with the capillary-to-myocyte ratios arising from the ventricular free walls and the septum. These data are also shown in Fig. 6, where, in each case, they lie above and to the left of the regression line fitted to the trabecula data. There was no difference of average ratios between the RV wall (0.79 ± 0.01) and the septum (0.80 ± 0.01), both of which differed from the LV free wall (1.06 ± 0.03).

Figure 6.

Scatterplot of the number of capillaries as a function of the number of myocytes arising from: LV free wall, RV free wall, septum, and trabeculae (LV and RV by two different microscopy procedures). Data fitted by linear regression analysis to trabeculae data only: n_capillaries = 0.52 × n_myocytes − 6.46; r² = 0.988; s_y.x = 13.52.

DISCUSSION

To our knowledge, this is the first study to examine quantitatively the microstructure of cardiac trabeculae—preparations that have been used for some four decades to study the electrical, ionic, mechanical, and metabolic aspects of cardiac function. Our study was designed to test four hypotheses. But before addressing them, we consider the methodological limitations of the study.

Methodological limitations

Whole heart Langendorff perfusion.

For reasons that are not entirely clear, we found it nearly impossible to detect capillaries in LV trabeculae that had been perfused with Bouin's fixative. Even when the perfusion pressure was increased 2.5-fold, the right coronary artery was ligated and/or adenosine was present in the coronary perfusate. Only by perfusing directly with PSR, in the absence of Bouin's fixative, could we visualize blood vessels in the subsequently Bouin's-fixed preparations. And, even then, we suspect that the capillaries were not fully patent in trabeculae dissected from the LV. We emphasize that, although this undoubtedly accounts for the lesser proportion of total cross-sectional area occupied by vessels in the left- vis-à-vis the right-ventricular preparations, it has no effect on capillary-to-myocyte ratios because these are based on integers rather than proportions. We have some, admittedly circumstantial, evidence that capillaries in LV trabeculae are more responsive than those in the RV to the acidic nature of fixatives. In the earlier study (Joshi, P., G. Sands, D. Gerneke, I. LeGrice, and D. Loiselle. 2006. Proceedings of the Physiological Society. Abstr. C25:15P; Joshi, P., Q. Dollie, D.A. Gerneke, G.B. Sands, I.J. LeGrice, and D.S. Loiselle. 2007. International Society for Heart Research, Australasian Section, Annual Scientific Meeting. Abstr. S216), we also perfusion-fixed Langendorff-circulated rat hearts, but we used a solution of 3% formalin in phosphate buffer. Although that procedure left RV capillaries fully expanded, we were unable to detect any capillaries in preparations dissected from the LV. But we are at a loss to offer any explanation for the interventricular difference in responsiveness of trabecular capillaries to common histological fixatives.

Combination of microscopy methodologies.

As alluded to earlier, our original intention had been to use the procedures of surface-imaging microscopy. However, we abandoned that approach because of our inability to detect capillaries in LV specimens. Nevertheless, we have opted to include the results arising from RV samples in that study because they are in remarkable accord with those acquired using confocal fluorescence techniques. Specifically, the regression equation relating the number of capillaries to the number of myocytes was (Joshi, P., G. Sands, D. Gerneke, I. LeGrice, and D. Loiselle. 2006. Proceedings of the Physiological Society. Abstr. C25:15P):

$${\text{n}}_{\text{capillary}}=0.\text{48}0*{\text{n}}_{\text{myocyte}}-\text{6}.\text{37},$$ (3)

which predicts avascularity of trabeculae containing fewer than 13 myocytes. The similarity of slope and intercept between Eqs. 2 and 3 is noteworthy and, we consider, provides ample justification for combining the results of two fundamentally different microscopy methodologies.

Tests of hypotheses

Hypothesis 1: When a trabecula is viewed in cross section, an outer annulus of cells will be seen to be unperfused by the coronary circulation.

Support for this hypothesis can be seen in several specimens shown in Fig. 5, but it is best revealed in the preparation shown as a series of segmented images (Fig. 3) or in 3-D reconstruction (Fig. 4 a). This characteristic is also clearly evident (although not given commentary) in Fig. 1 B of Hanley et al. (1999).

Hypothesis 2: Trabeculae of sufficiently small diameter will be completely devoid of capillaries.

The three cross sections indicated by asterisks in Fig. 5 provide visual support for this prediction. Comparably convincing evidence is supplied by the nonzero intercept on the abscissa of Fig. 6, the value of which implies that a trabecula will be avascular if its cross section contains not more than about a dozen myocytes.

Hypothesis 3: The capillary-to-myocyte ratios of trabeculae from either ventricle will be found to be identical to those in the walls from which they arise.

On the basis of the quantitative data presented above and shown graphically in Fig. 6, we must reject this hypothesis. Trabeculae from either ventricle had capillary-to-myocyte ratios of ∼0.5, indicating that each capillary delivers oxygen to two cells. In stark contrast, the capillary-to-myocyte ratio was double this value in the LV wall, where each capillary services a single myocyte. The discrepancy between trabeculae and wall tissues also prevailed with respect to both the RV free wall and the septum, where, in both cases, the capillary-to-myocyte ratio was 0.8.

The extent of capillarization of myocardial tissue, in health and under a wide range of environmental and pathological conditions, has been extensively reported in the literature. These are commonly expressed as “capillary density” or “intercapillary distance” (for reviews see Rakusan, 1999, 2004), from which it is not possible to extract capillary-to-myocyte ratios. Most useful for our purposes are those papers in which capillary-to-myocyte ratios are presented explicitly. Exemplary in this regard is the seminal paper by Wearn (1928), in which the number of capillaries per 1,000 fibers in the hearts of rabbits, cats, and humans range from 1,031 to 1,075, with no difference between LV and RV. More recently, Koyama et al. (1997) found a capillary to myocyte ratio of 1.09 ± 0.05 in the LV of Wistar rats. This value is in remarkable accord with ours of 1.06 ± 0.03, but it is discordant with the finding by Panisello et al. (2007) of 1.46 ± 0.06. The literature appears to be silent on the capillary-to-myocyte ratios of trabeculae from either ventricle. Likewise, we are not aware of any reports of differing ratios between the LV and either the RV or the interventricular septum.

Hypothesis 4: The capillary-to-myocyte ratios will be found to be comparable in specimens from either ventricle.

Although the data of Fig. 6 bear out this prediction convincingly, it is undercut somewhat by the difference of the ratios between the ventricular walls per se. We had anticipated that, had the data supported the hypothesis, it could be taken as evidence that the peak stresses (and, hence, demand for oxygen) experienced by myocytes in the walls of the LV and RV are comparable (as has long been averred as a result of the application of the law of Laplace to thick-walled structures). But given the difference of capillary-to-myocyte ratios that we observed between the RV (0.8) and LV (1.0), it is difficult to sustain this argument. In fact, the lesser ratio in the RV wall is qualitatively consistent with the claim by Zong et al. (2005) that the lower rate of oxygen consumption by RV tissues reflects lower peak systolic wall stress vis-à-vis that of the LV. The lower ratios in trabeculae are certainly consistent with our basic claim that trabecula tissue is privileged inasmuch as it has two independent supplies of oxygen: from the coronary capillaries and from the ventricular blood. This leads us to further considerations of oxygen supply by diffusive means.

Cross-sectional eccentricity enhances the diffusive supply of oxygen

Experimentalists strive to ensure that isolated (unperfused) trabeculae do not risk development of anoxic cores. To that end, preparations of small diameter are preferred (see Fig. 1). These are typically bathed in solutions of high PO₂ (p) and driven at modest rates of energy demand. Historically, most considerations of the adequacy of diffusive oxygen supply to isolated tissues have been based on solutions of the diffusion equation applied to cylindrical preparations of circular cross section (Murray, 1974; van Ouwerkerk, 1977; Loiselle, 1982, 1985, 1987; Daut and Elzinga, 1988; Barclay, 2005; van der Laarse et al., 2005). We now consider the advantage conferred on preparations of elliptical vis-à-vis circular cross section.

Eq. 4 gives the steady-state solution of the partial differential equation describing the diffusion of oxygen into a long cylinder of tissue of elliptical cross section (Hill, 1965). The elliptical cylinder has semimajor and semiminor axes a and b, respectively. Its perimeter is held at a constant PO₂, p = p_o, whereas it respires at a constant metabolic rate, m_o. K is Krogh's diffusion constant, the product of the diffusivity and the solubility of oxygen in tissue, and represents the volume of oxygen (cm³) diffusing across a surface of 1 cm² in 1 min, under a partial pressure gradient of 1 atmosphere per cm (Hill, 1928). At room temperature, its numeric value is assumed to be 2.37 × 10⁻⁵ (Barclay, 2005).

$$p(x,y)=p_o-\frac{m_o}{2K}\frac{\left(1-\frac{x^2}{a^2}-\frac{y^2}{b^2}\right)}{\left(\frac{1}{a^2}+\frac{1}{b^2}\right)},$$ (4)

where x and y are the coordinates of a point in the cross section, the center of which (0, 0) defines the origin of the rectangular coordinate system.

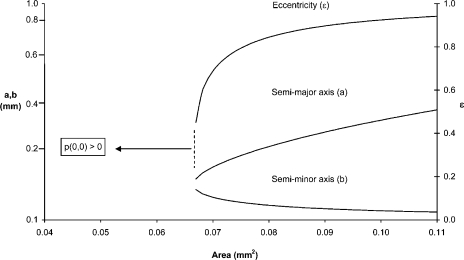
Interest focuses on the maximum dimensions that will just avoid anoxia on the central axis. These dimensions are determined by setting p(0, 0) = 0 and solving Eq. 4 for a as a function of cross-sectional area (πab). This produces an equation, quartic in a, the positive real root of which is plotted as the middle curve in Fig. 7. For the selected values of p_o (0.95 atm) and m_o (4.25 cm³ O₂ cm⁻³ min⁻¹), all trabeculae (whether circular or elliptical in cross section) whose cross-sectional areas are <0.067 mm² will have nonzero axial values of PO₂. Eccentric preparations of a larger area can avoid the development of an anoxic core, but only at the expense of increased eccentricity. Hence, the midmost specimen in Fig. 5 would avoid anoxia at the specified metabolic rate, despite its improbably large cross-sectional area (0.11 mm²), because its eccentricity is ε = 0.96.

Figure 7.

Eccentricity (ε) and lengths of semimajor (a) and semiminor (b) axes of trabeculae of elliptical cross-sectional area such that the partial pressure of oxygen (p) would just fall to zero on the central axis (0, 0) when bathed in a solution equilibrated with 95% oxygen and respiring at a rate of 4.5 ml O₂ g⁻¹ min⁻¹. Note the logarithmic scale on the left-hand ordinate, where a and b have units of mm; ε (right-hand ordinate; see Eq. 1) is dimensionless.

Thus (and in accord with intuition), for any given cross-sectional area that is metabolically reliant on a diffusive supply of oxygen from the periphery, an advantage is conferred by an elliptical profile (Fig. 7).

Simultaneous diffusion of oxygen from two sources: capillaries and ventricles

To investigate further how a common capillary-to-myocyte ratio can apply to trabeculae from both ventricles, despite the fact that their ambient levels of PO₂ vary by some 2.5-fold (at rest), we expanded the scope of diffusion modeling. That is, we (G. Sands) developed a novel method of solving the diffusion equation for a trabecula cross section of arbitrary configuration (i.e., size, shape, and location of capillaries and collagen cords). Both simple and myoglobin-facilitated diffusion of oxygen are incorporated. Oxygen consumption is assumed to be of the Michaelis-Menten form (Loiselle, 1987; Barclay, 2005) with a value for P₅₀ (the PO₂ at which oxygen consumption is half-maximal) of 1.5 mm Hg. The value of this and all other parameters are taken from Barclay (2005). Oxygen is presumed to be freely diffusible through collagen (Androjna et al., 2008). The method of solution is described in the Appendix.

Our approach was to select a particular trabecula cross section, the length of whose major and minor axes (200 and 175 µm) correspond to those commonly encountered experimentally. For this purpose, we chose the specimen used for 3-D reconstruction of the network of blood vessels (Fig. 4). Ventricular chamber PO₂ (i.e., the black region lying outside the cyan-colored trabecula boundary in Fig. 4 a) was set to either 100 or 40 mm Hg to mimic resting conditions in the LV and RV, respectively. To mimic PO₂ at the arterial end of a capillary bed in trabeculae from either ventricle, capillary PO₂ was set to 100 mm Hg. To mimic conditions at the venous end of the capillary bed, PO₂ was set to 40 mm Hg. To mimic extreme conditions under intense exercise, the RV chamber value was reduced to 20 mm Hg and the capillary value at the venous end to 15 mm Hg. Interest is focused on whether the low capillary-to-myocyte ratio of trabeculae renders them prone to anoxia, particularly in the non-perfused annulus between the capillaries and the boundary (Fig. 4 a), and especially under conditions of extreme oxygen demand.

Simulated PO₂ profiles across the observed cross section of the selected trabecula depend critically on the simulated rate of oxygen consumption, as well as on the PO₂ values in the ventricular chambers and capillaries. The metabolic rate of actively contracting trabeculae has been scantily reported (Daut and Elzinga, 1989; Schramm et al., 1994; Loiselle et al., 1996; Han et al., 2009). We have chosen to use a simulation value calculated from the heat–stress relation reported for a single rat trabecula contracting at 10 Hz at 37°C (Loiselle et al., 1996). This yields a value of 300 mW/g_dry, corresponding to ∼3 μLO₂ g⁻¹ s⁻¹ (assuming a wet weight/dry weight ratio of 4.5 and an energetic equivalent of oxygen of 20 kJ L⁻¹). A value for the rate of basal metabolism (1 μLO₂ g⁻¹ s⁻¹) was taken from Table I of Loiselle et al. (1996).

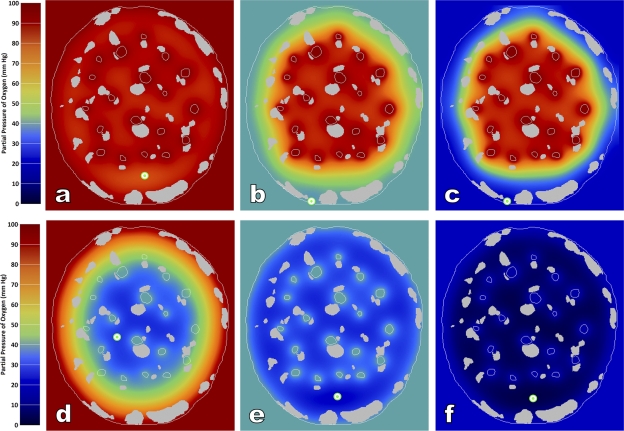
The results of six simulations are shown in Fig. 8. Recalling that the simulated rate of oxygen consumption is extreme (100 mW/g is well above any value recorded for papillary muscles resting on a thermopile or for isolated, Langendorff-perfused isovolumetrically contracting whole rat hearts at 37°C), it is remarkable that the lowest value of PO₂ calculated in myocytes located at the arterial end of the capillary bed is 81.1 mm Hg (Fig. 8 a). Even at the venous end of the capillary bed, the lowest value (indicated by the bull's-eye) is 26.6 mm Hg (Fig. 7 d), an order of magnitude higher than the P₅₀ for mitochondrial oxygen consumption. It is clearly seen that the annular region of the cross section, which is poorly endowed with capillaries, is nevertheless richly supplied with oxygen diffusing directly from the ventricle.

Figure 8.

Simulated PO₂ profiles in the cross section of a selected trabecula (same specimen as in Figs. 3 and 4). The silver-colored regions (including the boundary) indicate collagen. The region outside the cross section represents the respective ventricle. In a and d, its color is red, indicating a PO₂ of 100 mm Hg. In b and e, its color is azure, indicating 40 mm Hg, the PO₂ of RV blood at rest. In c and f, the color blue indicates extremely low PO₂ (20 mm Hg) of blood in the RV during exhausting exercise. The top row shows the simulated PO₂ profiles at the arterial ends of the capillary beds, and the bottom row shows them at the venous ends. Note the extensive penetration of O₂ from the ventricle into the avascular annulus of peripheral tissue in each case, but especially in d. The bull's-eyes indicate PO₂ minima under each condition.

Matters are scarcely different in the RV, where the minimum PO₂ values in tissues at the arterial and venous ends of the capillary bed are computed to be 38.9 and 21.3 mm Hg, respectively (Fig. 8, b and e). But perhaps the most counterintuitive result is that found for the RV during simulated intense exercise when the chamber PO₂ has fallen to 20 mm Hg and the venous end of the capillary bed to 15 mm Hg (Fig. 8, c and f). These simulated conditions are probably unrealistically harsh. Nevertheless, the minimal value of PO₂ (2.7 mm Hg) is still twice the P₅₀ value for oxygen uptake by mitochondria. These simulations demonstrate that, even during extreme exercise, provided that systemic (i.e., coronary vascular) arterial PO₂ remains near 100 mm Hg, then the presence of “assisted diffusion” directly from ventricular blood ensures adequacy of oxygen supply to vigorously respiring myocytes, despite a capillary-to-myocyte ratio of only 0.5 and the absence of capillaries in the peripheral annulus.

A final comment concerning cross-sectional shape is warranted. In the trabecula literature, it is not uncommon for authors to describe their specimens as being “slab-shaped” in cross section (ter Keurs et al., 1980; Mulder et al., 1989; de Tombe and ter Keurs, 1990; Loiselle et al., 1996; Raman et al., 2006). Perhaps we have been unduly influenced by the original Latin nomenclature (“little plank”), but Fig. 5 shows scant justification for continued use of the term, at least as applied to the 30 rat ventricular trabeculae that we have examined.

Conclusions

Our investigation has shown that the “capillary density” of trabeculae is the same in specimens from either ventricle, but it is only about one-half that of the ventricular walls or interventricular septum. This raises the intriguing question as to how myocardial tissue “knows” that it is resident in a trabecula and not in the immediately adjacent wall. Does the diffusion of oxygen and nutrients inward from the ventricular blood (as distinct from their movement outward from the capillaries) inhibit angiogenesis? Such a notion would be consistent with the observation that very thin preparations show a complete absence of capillaries. In any case, it can no longer be presumed that trabeculae are strictly homologous with the ventricular myocardium.

A second issue suggests further caution. To report stress development, experimentalists commonly divide the observed force production of a trabecula by its estimated cross-sectional area. When the radial dimension of a trabecula is measured in only a single view, a circular cross section is necessarily assumed. When two orthogonal half-diameters (a and b) are measured, a slab-shaped cross section is commonly assumed and its area calculated as 4ab. If, however, the true cross section is elliptical, as we have found consistently to be the case, then the cross section should be approximated as πab. The resulting error in the estimation of cross-sectional area would thus be 100 (4/π − 1) = 27%, independent of the aspect ratio of the trabecula. Of course, the error risks being much greater if a circular cross section is presumed. We suspect that some of the remarkable variability of peak stress development reported in the literature may reflect errors-of-estimation of cross-sectional area.

APPENDIX

We developed a finite difference–based diffusion equation solver that incorporated both simple and myoglobin-facilitated diffusion of oxygen in a 2-D trabecula cross section. The model geometry was automatically constructed from a segmented image (Fig. 3) that described the tissues, collagen, and capillary structures, forming a 176 × 196–µm finite difference grid with 0.6-µm grid resolution. The governing diffusion equation is:

$$\frac{\partial }{\partial \text{t}}\sigma \text{P}(\text{t})=\text{D}·\sigma ·{\nabla }^2\text{P}(\text{t})+{\text{D}}_{\text{Mb}}·{\text{C}}_{\text{Mb}}·{\nabla }^2\text{S}(\text{P})-\text{m}(\text{P},\text{t}),$$ (A1)

where t = time (s); P(t) = partial pressure of oxygen (Pa); σ = solubility of oxygen in tissue (14.63 µmol m⁻³ Pa⁻¹); D = diffusion constant for oxygen in tissue (1.09 × 10⁻⁹ m² s⁻¹); D_Mb = diffusion constant for myoglobin in tissue (12.5 × 10⁻¹² m² s⁻¹); C_Mb = total concentration of myoglobin plus oxymyoglobin in tissue (0.4 mol m⁻³); S(P) = saturation of myoglobin (M) with oxygen:

$$\text{S}(\text{P})=\frac{\text{P}{(\text{t})}^{{\text{n}}_{\text{M}}}}{\text{P}{(\text{t})}^{{\text{n}}_{\text{M}}}+{\text{P}}_{{\text{M}}_{50}}^{{\text{n}}_{\text{M}}}},$$ (A2)

where n_M = Hill coefficient for myoglobin diffusion (1.5); P_M50 = pressure at which myoglobin saturation is half-maximal (300 Pa [2.2 mm Hg]); m(P,t) = metabolic rate of oxygen consumption (O; mol m⁻³ s⁻¹):

$$\text{m}(\text{P},\text{t})=\frac{\text{P}\rho }{\text{RT}}{(\text{m}}_{\text{a}}+{\text{m}}_{\text{b}})\frac{\text{P}{(\text{t})}^{{\text{n}}_{\text{o}}}}{\text{P}{(\text{t})}^{{\text{n}}_{\text{o}}}+{\text{P}}_{{\text{o}}_{50}}^{{\text{n}}_{\text{o}}}},$$ (A3)

where P = atmospheric pressure (101.3 kPa); ρ = tissue density (1,060 kg m⁻³); T = temperature (310 K or 37°C); m_a = active rate of oxygen consumption in tissue (mol s⁻¹ kg); m_b = basal rate of oxygen consumption in tissue (mol s⁻¹ kg); n_O = Hill coefficient for metabolic oxygen consumption (1.5); and P_O50 = pressure at which oxygen consumption is half-maximal (200 Pa [1.5 mm Hg]).

Oxygen was provided from the surrounding chamber (at 100, 40, or 20 mm Hg, corresponding to 13.3, 5.33, or 2.67 kPa, respectively) and from the capillaries (at 100, 40, or 15 mm Hg, corresponding to 13.3, 5.33, or 2.00 kPa) and presumed to diffuse freely through collagen, without consumption (Androjna et al., 2008). The diffusion operator ∇² was computed at each pixel using finite differences, and the solver was written using LabVIEW (National Instruments).

The diffusion equation was discretized in the time domain using a simple Euler forward-differencing method with a stable time step (Δt = 50 µs), and each combination of source parameters was solved iteratively until reaching a steady state.