A comparison of bounded diffusion models for choice in time controlled tasks

Abstract

The Wiener diffusion model (WDM) for 2-alternative tasks assumes that sensory information is integrated over time. Recent neurophysiological studies have found neural correlates of this integration process in certain neuronal populations. This paper analyses the properties of the WDM with two different boundary conditions in decision making tasks in which the time of response is indicated by a cue. A dual reflecting boundary mechanism is proposed and its performance is compared with a well-established absorbing boundary in the cases of the WDM, the WDM with extensions, and the WDM with prior probability. The two types of boundary influence the dynamics of the model and introduce differential weighting of evidence. Comparisons with Ornstein-Uhlenbeck models are also done, and it is shown that the WDM with both types of boundaries achieves similar performance and produce similar fits to existing behavioural data. Further studies are proposed to distinguish which boundary mechanism is more consistent with experimental data.

1 Introduction

Making choices is a frequent and critical element of human and animal lives. This problem has been studied by psychologists under two types of 2-alternative-forced-choice (2AFC) paradigms, in which subjects must decide between two available alternatives. The information controlled (IC) paradigm allows subjects to respond whenever they feel confident (Luce, 1986). Alternatively, subjects can be required to report their choice immediately after a cue to respond (Yellott, 1971; Swensson, 1972), under the time controlled (TC) paradigm (sometimes referred to as the response signal paradigm, see Dosher, 1984).

Over the last half century several sequential sampling models have been proposed to describe experimental results as well as underlying decision-making mechanisms in 2AFC tasks (for reviews, see Townsend and Ashby, 1983; Luce, 1986). The Wiener diffusion model (WDM) - the focus of this paper - assumes that subjects integrate partial information representing the relative support for the two alternatives over time (Stone, 1960; Laming, 1968; Ratcliff, 1978), and has been shown to be the statistically optimal method for choosing between two alternatives on the basis of noisy evidence. For a fixed set of stimulus conditions, the WDM minimizes the reaction time for given accuracy, or maximizes the accuracy for given reaction time (Wald, 1947; Edwards, 1965; Laming, 1968; Gold and Shadlen, 2001, 2002). The WDM successfully describes reaction times distribution and accuracy in various cognitive decision tasks in the IC paradigm (Stone, 1960; Laming, 1968; Link, 1975; Link and Heath, 1975; Ratcliff, 1978; Ratcliff et al., 1999; Ratcliff and Smith, 2004). However, in the TC paradigm, the earlier version of the model (Ratcliff, 1978) allows integrator states to take arbitrary values. It leads to the prediction that the accuracy always increases over time if the drift of the process is in the correct direction. This is contrary to the finding that accuracy in the paradigm grows over time to an asymptote. To avoid this shortcoming, the model needs to assume that drift values are normally distributed across trials (Ratcliff, 1978) or that the integration range is bounded (Ratcliff, 1988). With one of these elaborations, the model correctly predicts the time-accuracy curves found in the IC condition.

This paper introduces a reflecting boundary mechanism to model 2AFC tasks in the TC paradigm. We compare the dynamics and performance of the WDM with reflecting and absorbing boundaries (Feller, 1968) and assess their ability to account for published behavioural data from 2AFC experiments. We also compare them with an Ornstein-Uhlenbeck (O-U) model (Busemeyer and Townsend, 1992, 1993; Diederich, 1995, 1997; Smith, 1995, 2000; Ratcliff and Smith, 2004). Analytical and numerical results show that both boundary types lead to similar performance and produce similar fits, but we identify some differences between them. Further studies are proposed that might distinguish which type of boundary better describes the decision making process.

The paper is organized as follows. Section 2 reviews neurophysiological evidence of decision making, and describes the WDM and alternative boundary mechanisms. More detailed reviews are available elsewhere (Glimcher, 2001; Schall, 2001; Smith and Ratcliff, 2004; Bogacz et al., 2006; Gold and Shadlen, 2007). Section 3 compares the dynamics and the performance of models with the two types of boundaries. Section 4 compares fits of bounded models with behavioural data. Finally, Section 5 discusses further experimental studies that could distinguish between the boundary mechanisms. Mathematical details are provided in Appendices A and B.

2 The biology of decision and the sequential sampling models

2.1 The neural basis of 2AFC tasks

Recently, neuronal activity from awake animals has been recorded in choice experiments. For example, in the motion discrimination task, visual stimuli comprise arrays of random moving dots, a proportion of which move coherently to the left or right. Subjects (monkeys) are required to indicate their decision regarding the coherent direction by making a saccade to a left or right target (Shadlen and Newsome, 2001; Roitman and Shadlen, 2002).

The activity of neurons in the middle temporal (MT) area has been shown to correlate with the motion coherence (Britten et al., 1993). However, since these neurons are highly noisy and poorly correlated with choices, area MT is less likely to be a “decision maker” than to provide temporal information for a further process. It has been suggested that the lateral interparietal (LIP) area may interpret raw information from MT neurons. Shadlen and Newsome (1996) reported that LIP neurons gradually build up or attenuate their activity within a trial, and exhibit persistent activity in the absence of stimuli (Shadlen and Newsome, 2001). The time course of LIP neuronal activity suggests that area LIP integrates inputs from MT neurons (Roitman and Shadlen, 2002; Huk and Shadlen, 2005; Hanks et al., 2006). Similar discharge patterns are also found in the frontal eye field (FEF) (Schall, 2002) and the superior colliculus (SC) (Basso and Wurtz, 1998).

These results indicate a general decision mechanism manifested in different brain regions in which certain neuronal populations integrate sensory information over time to increase the accuracy of selection between alternatives (Gold and Shadlen, 2007; Schall, 2001). Gold and Shadlen (2001, 2002) formalize the decision process in 2AFC tasks as following two processes: two populations of sensory neurons (e.g., in MT) generate continuous noisy information streams (Y₁(t) and Y₂(t)) for each of two alternatives Y₁ and Y₂ at time t. For simplicity, we assume that Y₁(t) and Y₂(t) have constant means μ₁ and μ₂ during each trial, with the same constant standard deviation, σ. The goal of the second process, (reflected in LIP activities), is to successfully identify which input population has higher mean based on sample sequences Y₁(t) and Y₂(t). This framework is the basis for several sequential sampling models in behavioural studies, including the WDM (Ratcliff, 1978), the O-U model (Busemeyer and Townsend, 1992), and the leaky-competing-accumulator (LCA) model (Usher and McClelland, 2001).

2.2 The Wiener diffusion model (WDM)

The Wiener diffusion or Brownian motion is a continuous limit of the random walk (Stone, 1960; Laming, 1968; Ratcliff, 1978). It implies a leak-free integrator that accumulates the difference Y₁(t) - Y₂(t) between noisy evidence streams for the two alternatives. Let X(t) denote the accumulated difference at time t: the value of the integrator state, with initial state X₀ = X(0). If there is no prior bias towards either choice, the process starts at baseline X₀ = 0, and is described by a stochastic differential equation:

$$dX\left(t\right)=\mu dt+\sigma dW\left(t\right),\text{with}{X}_0=0,$$ (1)

where dX(t) denotes the evidence obtained during time step dt. μ is a constant drift (the accumulation rate), representing the average of evidence difference μ₁ - μ₂. On a given trial, μ > 0 (μ₁ > μ₂) implies that Y₁ is the correct choice, while μ < 0 (μ₁ < μ₂) if Y₂ is correct. For consistency we hereafter set μ > 0 unless indicated specifically and hence assume Y₁ is the correct choice. The magnitude of μ reflects the difficulty level of the task: for small μ (μ₁ ≈ μ₂), it is difficult to distinguish which evidence samples have higher mean. The second term σ dW(t) denotes Gaussian noise with mean 0 and variance σ²dt. In the absence of noise (σ = 0), X(t) changes at rate μ and always reaches a correct decision. Noisy inputs cause the X(t) to fluctuate and hence induce incorrect choices on some trials.

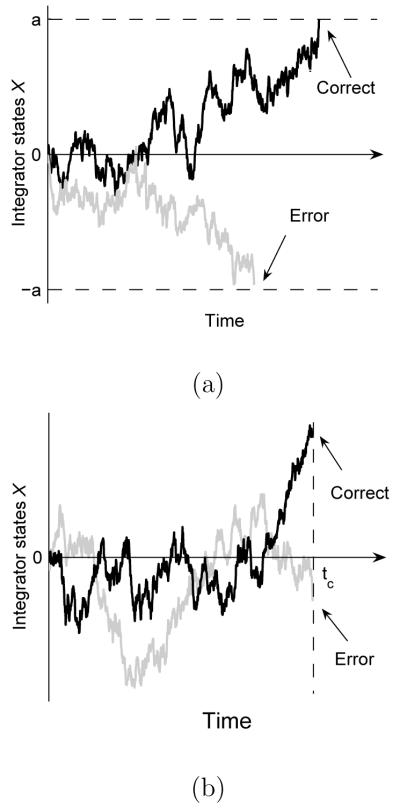
Figure 1 shows the growth of X(t) in the two paradigms. For the IC paradigm, the decision time is unrestricted and two thresholds ±a are introduced to indicate termination states. Once X(t) reaches a threshold, the corresponding alternative is chosen. For the TC paradigm, the decision process is interrupted by a response cue, and a response is immediately required. We hereafter denote the time delay from stimulus onset to response cue by t_c. The alternatives are selected by locating the final integrator state X(t_c) and selecting Y₁ if X(t_c) > 0, and Y₂ if X(t_c) < 0.

Fig. 1.

Evolutions of integrator states after stimulus onset for the WDM, showing correct trials (black) and error trials (grey). The model was simulated with μ = σ = a = 1 and time-step dt = 0.01s, and hence X(t) > 0 corresponds to the correct alternative. a) IC paradigm: choices are made on first reaching one of the two thresholds. b) TC paradigm: choices are determined by the sign of the integrator state X(t_c) at time t_c.

Performance can be measured by the error rate: the probability of making an incorrect choice in a block of trials¹, hereafter denoted by P. The error rate is a function of model parameters μ, σ, and threshold setting, a, or response signal, t_c, depending on the paradigm. For unbiased initial conditions X₀ = 0, the error rate of the WDM in the IC and TC paradigms are given by Eqs. 2 and 3, respectively (Bogacz et al. 2007; cf. Gardiner 1985; Ratcliff 1978):

$$P\left(a\right)=\frac{1}{1+e^{\frac{2\mu a}{{\sigma }^2}}},\text{and}$$ (2)

$$P\left(t_c\right)={\int }_{-\infty }^{-\frac{\mu }{\sigma }\sqrt{t_c}}\frac{1}{\sqrt{2\pi }}{e}^{-\frac{u^2}{2}}du.$$ (3)

Two extensions have been proposed to improve fits to experimental data (Ratcliff et al., 1999). They allow certain parameters to vary randomly across trials. First, drift rate $\tilde{\mu }$ is assumed to have a Gaussian distribution across trials with mean μ* and variance ${\sigma }_{\mu }^2$, which might reflect the variability of difficulty between trials, the subject’s attention level, or other variable inter-trial factors. On each trial, $\tilde{\mu }$ can take either positive or negative values, promoting accumulation towards different alternatives. The correct choice is determined by the mean drift μ*, even if the sampled value $\tilde{\mu }$ has opposite sign in some trials. This is motivated by the fact that, in difficult situations, stimulus distributions corresponding to the two alternatives often overlap (Ratcliff et al., 1999). Even after long training, perfect performance in such tasks is impossible. Drift variability is also necessary to ensure that the asymptotic accuracy of the WDM in the IC paradigm is not infinite in the absence of boundaries (Ratcliff, 1978). Second, the theory of premature sampling assumes that subjects start to integrate noise before sensory information is available. Hence the starting point is not at 0 when stimuli onset (Laming, 1968). Instead, On each trial X₀ is chosen from a uniform distribution ² on the interval [-σ_X, σ_X].

The extended WDM produces different reaction times on correct and error trials in the IC paradigm (Ratcliff et al., 1999). We assume that the same variability sources also operate in the TC paradigm; their effects on the decision process will be evaluated in the next section.

2.3 Boundary mechanisms

In the TC paradigm, the fact that integrator states X(t) are unbounded implies that the error rate of the WDM with no variability in drift rate diminishes to zero for large t_c (cf. Eq. 3). To eliminate this contradiction, absorbing boundaries can be introduced at X = ±b. This mechanism was originally used to model tasks in which IC and TC paradigms were intermixed (Ratcliff, 1988). Such tasks promote subjects to respond as fast as possible before a predetermined deadline. Under this condition the proposed model, also called the internal deadline model, assumes that the decision process is terminated when the accumulated evidence reaches one of the three possible boundaries, whichever comes first. The three boundaries are: top and bottom absorbing boundaries in the state domain, and a deadline boundary in the time domain (Diederich and Busemeyer, 2006; Ratcliff and Rouder, 2000).

In this work, we consider a pure TC paradigm in which subjects are only allowed to respond after the deadline t_c (Roitman and Shadlen, 2002). If the decision process reaches one of the absorbing boundaries before t_c, the accumulation process stops and the activity X(t) = ±b is maintained until the end of the trial. For sufficiently large t_c, X(t) will almost surely reach one of the boundaries before t_c (cf. Section 3.1). Absorbing boundaries have the same effect as the decision threshold in the IC paradigm. Hence the error rate of the absorbing WDM with infinite t_c can be analytically obtained as (cf. Eq. 2):

$$\underset{t_c\to \infty }{\lim }{P}_{\left(abs\right)}\left(t_c\right)=\frac{1}{1+e\frac{2\mu b}{{\sigma }^2}},$$ (4)

where the subscript abs stands for the WDM with absorbing boundary. For b < ∞, the error rate does not decrease to zero as t_c increases, which is consistent with experimental observations (Meyer et al., 1988; Usher and McClelland, 2001).

In contrast with the absorbing boundary mechanism, since no time pressure exists in the pure TC paradigm, subjects may use the deadline alone to terminate the decision process. In this case two reflecting boundaries may be more suitable to constrain the accumulation process, because they allow the preferred choice to change even if X(t) reaches a boundary. Here the boundaries restrict the amount of evidence that can be represented (much as a sigmoidal function provides cutoffs at high and low activation). Some previous studies (Diederich, 1995; Diederich and Busemeyer, 2003) use a lower reflecting and an upper absorbing boundary to model the simple reaction time task in which subjects respond immediately after a stimulus is detected. The reflecting boundary in their model and the one proposed here share similar motivations but there is a major difference. In the simple reaction time task, the accumulated sensory information directly represents the absolute evidence to make a response. Sinece the integrated information cannot drop below a certain baseline, one reflecting boundary is required to model the minimum level of absolute evidence. Single reflecting boundaries have also been used to represent a lower bound on the integration process (see Usher and McClelland, 2001; Smith and Ratcliff, 2009; Ratcliff and Smith, 2004).

In the TC paradigm of 2AFC tasks, the integrator in the WDM represents the relative evidence supporting the alternatives. The preferred alternative at time t is determined by the sign of X(t). A value of X(t) > 0 means that the first alternative is the provisional choice, whereas X(t) < 0 means that the second alternative is currently preferred. If we also assume that a minimum activity baseline exists and that decision preferences may switch during the trial, two reflecting boundaries are required to restrict the relative evidence of two alternatives within a certain range. Details of the model are given in Section 3.

2.4 The Ornstein-Uhlenbeck (O-U) model

Another widely applied sequential sampling method is the O-U model (Busemeyer and Townsend, 1992, 1993; Busemeyer and Diederich, 2002). It introduces a new parameter λ to the WDM to represent decay (λ < 0) or growth (λ < 0) of accumulated information, its evolution being described by:

$$dX\left(t\right)=(\lambda X\left(t\right)+\mu )dt+\sigma dW,X_0=0,$$ (5)

where the notations are as in Eq. 1. In the O-U model the accumulation rate depends not only on drift μ but also on the current state of the integrator X(t). This allows the error rate of the O-U model to approach a finite asymptote for large t_c even without boundaries.

The O-U model can account for the primacy and recency effects observed in decision making tasks: some subjects paying more attention to initial evidence (primacy) while others focus on later evidence (recency) (Wallsten and Barton, 1982). To illustrate this, note that Eq. 5 has a fixed point X = -μ/λ. For λ > 0, the fixed point is unstable. After X(t) has been driven to one side or other of the fixed point, subsequent evidence has little effect on the final choice due to repulsion, indicating a primacy effect. For λ < 0, the fixed point is an attractor. Information decays over time so that early evidence is partially lost, indicating a recency effect. A proof is available in Busemeyer and Townsend (1993).

The O-U model has been applied to a variety of tasks (Diederich, 1995, 1997; Smith, 1995) and also been extended to multi-alternative tasks (Usher and McClelland, 2001; McMillen and Holmes, 2006). As it is similar to the WDM, we include the O-U model in our subsequent comparative study.

3 Comparison of properties of bounded WDMs

3.1 The WDM with reflecting boundaries

Motivated by the discussion in Section 2.3, we now propose reflecting boundary conditions. In the simplest cases, the boundaries ±b are still symmetric about X₀ but they differ from absorbing boundaries in that once X(t) reaches ±b, it cannot exceed this value, but it may move back due to noise, as specified by:

$$\{\begin{array}{cc}X(t+dt)=b,\hfill & \text{if}X\left(t\right)+dX\left(t\right)\ge b,\hfill \\ X(t+dt)=-b,\hfill & \text{if}X\left(t\right)+dX\left(t\right)\le -b,\hfill \\ X(t+dt)=X\left(t\right)+dX,\hfill & \text{otherwise}\hfill \end{array}\phantom{\}}$$ (6)

where dX(t) is given by Eq. 1. In contrast to absorbing boundaries, reflecting boundaries allow information from any time period to contribute to the final choice, which is not determined until the end of t_c. Figure 2 shows sample paths of integrator states in the WDM with both types of boundaries, over one trial.

Fig. 2.

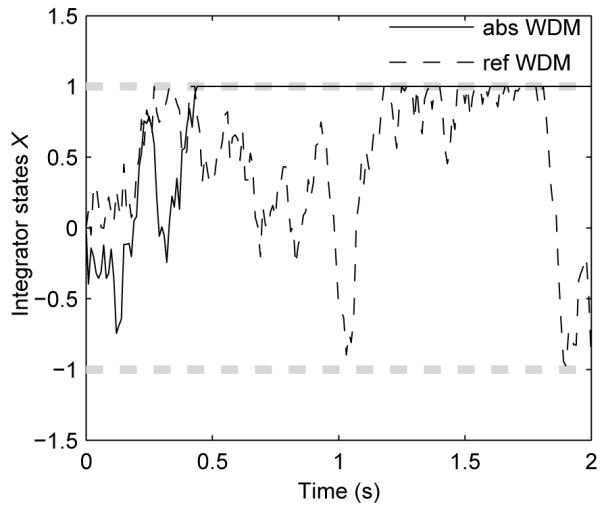
Examples of trajectories of the WDM with absorbing and reflecting boundaries. Models were simulated with μ = 1, σ = 1, dt = 0.01 s, and symmetric boundaries ±b = ±1, indicated by thick grey dashed lines. For the absorbing WDM (solid), the choice is determined when the state first hits a boundary (at 0.5s); for the reflecting WDM (dashed), the preferred choice may change throughout the decision process.

The solid line shows that for reflecting boundaries, even if X(t) reaches the upper boundary, X(t) continues to evolve until t_c and it may “backtrack” to subsequently reach the lower boundary.

Note that, unlike the absorbing WDM in which boundary contact induces a decision, the reflecting WDM requires an external criterion to stop (e.g., a response cue at time t_c), so it cannot be applied to the IC paradigm to tasks in which IC and TC paradigms are intermixed. Hence we will only consider the TC paradigm in the rest of this paper.

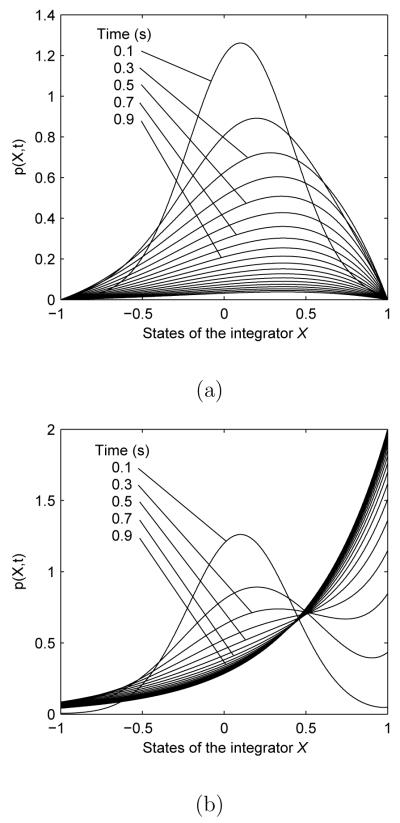
The first step in investigating the bounded WDM is to compute the probability density p(X, t) of Eq. 1 with appropriate boundary conditions, i.e., the probability of finding a sample path at state X at time t. Explicit expressions for p(X, t) of absorbing and reflecting WDMs are given in Eqs. B.5 and A.9 of the Appendix. Figure 3b illustrates the distribution of the reflecting WDM at several time instants. Comparing with that of the absorbing WDM in Figure 3a, we may distinguish properties of p(X, t) for the two types of boundaries. Initially both are approximately Gaussian (note the curves marked t = 0.1s), with means close to X₀ and shifted towards the upper boundary (the correct choice for μ > 0), but they become significantly different as t grows. For the absorbing WDM, p(X, t) collapses to 0 as t → ∞, since every decision process is absorbed by one of the boundaries after sufficiently large t_c. In contrast, no paths terminate in the reflecting WDM, but p(X, t) remains of unit mass and approaches the equilibrium distribution:

$$\underset{t\to \infty }{\lim }p(X,t)=\frac{2\mu e^{\mu (b+X)}}{e^{4\mu b}-1}.$$ (7)

The error rate of the reflecting WDM can be computed by integrating p(X, t) from -b to 0 (cf. Eq. A.16 of Appendix A), and as t_c increases, it converges to:

$$\underset{t_c\to \infty }{\lim }{P}_{\left(\mathit{ref}\right)}\left(t_c\right)=\frac{1}{1+e^{\frac{2\mu b}{{\sigma }^2}}},$$ (8)

were ref stands for reflecting WDM. Note that arbitrarily small P_(ref)(t_c) can be achieved for b < ∞ only if the signal-to-noise ratio μ/σ → ∞, and that the expression of P is identical to Eq. 4.

Fig. 3.

Probability densities of integrator states in bounded WDMs. State values are shown on horizontal axes. Densities are shown for parameters μ = σ = 1 and boundaries ±b = ±1. Different curves show densities at different time instants from 0.1s to 2s. The probability density functions p(X, t) are calculated via Eqs. B.5 and A.9 in the Appendix. All solutions start at X₀ = 0. (a) Absorbing WDM; (b) reflecting WDM.

3.2 Primacy and recency effects

Since the updating rule in Eq. 1 is independent of the current state X(t), the unbounded WDM implicitly assumes that the influence of sensory evidence on the final choice does not depend on the timing of its occurrence. This assumption is contrary to the primacy and recency effects discussed before. Here we show that by applying the two types of boundary, the WDM can also represent primacy and recency effects.

For the absorbing WDM, once X(t) hits the boundary, the preferred decision is determined and maintained. Only inputs prior to the first boundary hit contribute to the decision process, so the probability that incoming evidence at time t contributes to the final choice (denoted by P(dX(t) ≠ 0)) is equal to the probability that neither boundary has been reached before t, i.e.,:

$$P(dX\left(t\right)\ne 0)=P(G\left(X\right)>t)=1-{\Phi }_{G\left(X\right)}\left(t\right),$$ (9)

where the random variable G(X) is the time required for X(t) to frist reach either boundary (the first-passage time (Feller, 1968) and Φ_G(X) is the cumulative distribution of G(X). Since Φ_G(X) is a monotonically increasing function, P(dX(t) ≠ 0) is monotonically decreasing. Thus on average the decision is more likely based on earlier inputs, indicating a primacy effect.

For the reflecting WDM, each boundary hit results in a loss of information, since the model does not fully integrate the increment that carries it to the boundary. To illustrate this, assume that, at time τ, the incoming evidence dX(τ) drives the integrator to reach one of the boundaries. Compared with the unbounded WDM, hitting the reflecting boundary leads to a loss of information |X(τ) + dX(τ) - b| (cf. Eq. 6). On average, evidence presented earlier in the trial results in more boundary hits. Thus, information arriving earlier is partially lost and the final choice depends to a greater extent on later inputs, producing a recency effect. The reflecting WDM can also (repeatedly) change the preferred alternative within a trial, e.g., in Figure 2 the state of the reflecting WDM drops below zero, changing its choice in the last 0.2 s.

Primacy and recency effects can be illustrated by showing how the two models weight noisy inputs during the decision process. A sequence of trials was simulated and the noisy inputs recorded (right side of Eq. 1) only for trials resulting in correct choices. These inputs were then averaged to indicate the correlation between the mean inputs and the final choice, and this averaged input was shown in Figure 4. For absorbing boundaries, larger inputs at early times contributed more to the final decision (primacy), while for reflecting boundaries, larger inputs before the response led to the correct choice (recency).

Fig. 4.

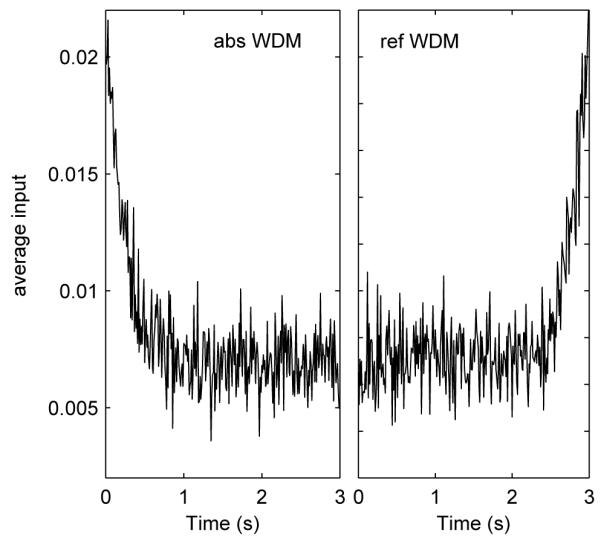
Primacy and recency effects for the WDM with absorbing (left) and reflecting (right) boundaries. The bounded WDM is simulated for 10,000 trials. For all correct trials the input to the WDM (μdt + σdW, cf. Eq. 1) at every time step is recorded and averaged. Curves illustrate averaged inputs plotted against time. Parameter values are μ = 0.71, b = 0.47, σ = 1, which are obtained by fitting behavioural data from subject S1 in a 2AFC task (Usher and McClelland (2001), Table 1 and see Section 4) and t_c = 3s.

3.3 Performance of bounded WDMs

Recall that the error rate expressions for the reflecting and absorbing WDM coincide when t_c → ∞ (Eqs. 4 and 8). In appendix B we prove that such an equality holds in general: given the same parameter set (μ, σ, b) and no prior bias (i.e., boundaries equidistant from the starting point X₀ = 0), the error rates for the two bounded WDMs are identical for any t_c:

$$P_{\left(abs\right)}\left(t_c\right)=P_{\left(\mathit{ref}\right)}\left(t_c\right).$$ (10)

Hence both bounded models achieve the same accuracy under the TC paradigm, as illustrated in Figure 5: the two curves coincide for any given t_c. Thus, although the different boundaries profoundly influence the dynamics of the decision process, their performances are indistinguishable. For given experimental observations (P(t_c) in TC paradigm) and the same parameter set, the two types of bounded models can always provide the same fitting ability, as we shall illustrate in Section 4.

Fig. 5.

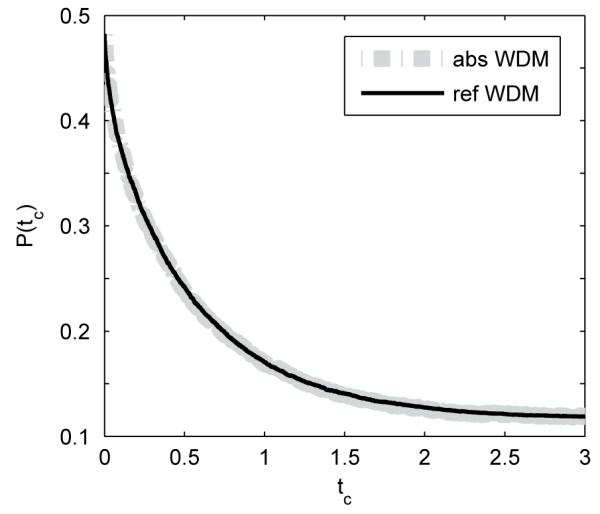
Error rates of the WDM with reflecting (solid) and absorbing (thick dashed) boundaries at different time t_c. Model parameters are μ = σ = b = 1 and data are averaged over 100,000 trials.

3.4 Performance of bounded WDM with extensions

We now consider the extended WDM described in Section 2.2.

3.4.1 Variability of drift rate

Figure 6 compares P(t_c) at different t_c for the bounded WDM with drift rates sampled from a normal distribution, with P(t_c) for the bounded WDM with constant drift rate. Drift variability increases the error rate for all t_c. The figure also shows that reflecting and absorbing boundaries still produce identical error rates for any t_c. This is not surprising since while drift differs across trials in the extended model, within each trial the sampled drift $\tilde{\mu }$ remains fixed. Hence both bounded models produce the same error rate, according to Section 3.3.

Fig. 6.

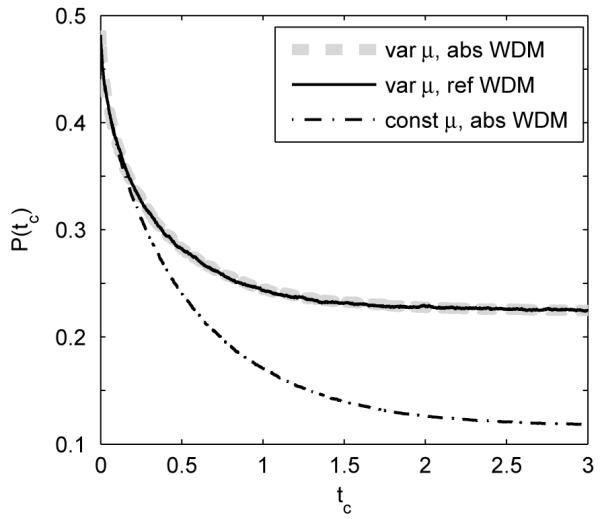
Error rates of the bounded WDMs at different t_c with variable drift rates across trials sampled from a normal distribution $\mathcal{N}$(1,1) (solid and thick dashed), compared with the error rate of the bounded WDM with constant drift rate μ = 1 (dash-dotted). Other model parameters are σ = b = 1. Data are averaged over 100,000 trials.

3.4.2 Variability of starting point

Figure 7 shows the performance of the bounded WDM with starting points X₀ sampled from a uniform distribution. This produces higher error rates than models with constant X₀. Also, since starting points are not equidistant from the boundaries, the error rates differ for the two types of boundary. One interesting result is that the reflecting WDM with variable and constant X₀ can achieve the same error rate for large t_c (the dashed and dash-dotted curves converge after 2s). This follows from the recency effect discussed in Section 3.2: initial condition variability is attenuated by reflecting boundaries as t_c increases. In contrast, the performance of the absorbing WDM is highly sensitive to starting points.

Fig. 7.

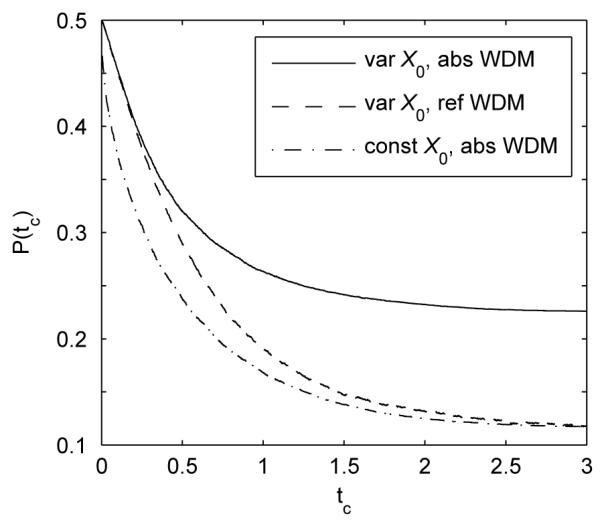
Error rates of absorbing (solid) and reflecting (dashed) WDMs at different t_c with variable starting point across trials, sampled from a uniform distribution between [1, 1], compared with the error rate for the bounded WDM with starting point X₀ = 0 (dash-dotted). Model parameters are μ = σ = b = 1. Data are averaged over 100,000 trials.

3.5 Prior probability and biased starting points

In this section we investigate how boundaries affect performance if the starting point X₀ depends on the prior probability of the alternatives.

If the subject knows that one of the alternatives is more probable, performance can be improved by moving the starting point towards that alternative (Edwards, 1965; Link, 1975). Such starting point biases have been observed in behavioural experiments (Laming, 1968; Link, 1975; Ratcliff et al., 1999). We now compare the performance of bounded WDMs in this situation. We denote the probability that the first alternative is correct by p₊, and that the second is correct by p_- = 1 - p₊, so that on each trial drift μ > 0 occurs with probability p₊ and μ < 0 with probability p_-.

Link (1975) proved that to minimize the error rate under the IC paradigm, the starting point should be set to:

$$X_0=\frac{{\sigma }^2}{4\mid \mu \mid }\ln \frac{p+}{p-}.$$ (11)

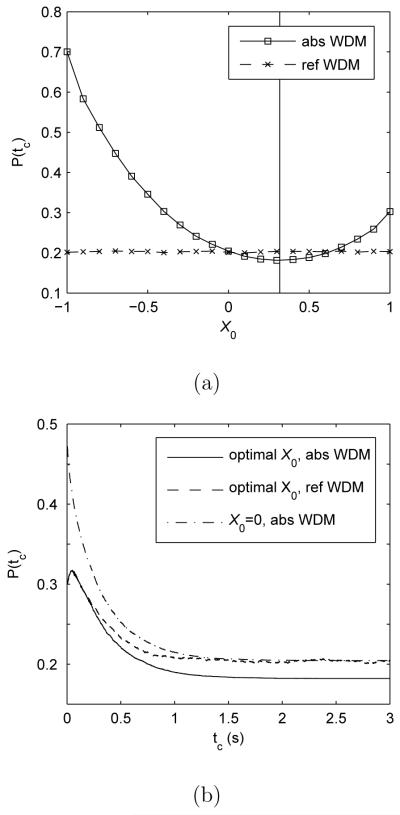
Thus, as the difference in prior probabilities increases, X₀ moves towards the boundary which is more likely to be correct. Recall that in Section 2 we proposed that absorbing boundaries in the TC paradigm act like decision thresholds in the IC paradigm. Hence Eq. 11 also specifies the optimal starting point of the absorbing WDM for large t_c under the TC paradigm. Figure 8a illustrates this prediction by stimulating bounded models with several starting points. The theoretically optimal X₀ (vertical solid line) of Eq. 11 can minimize the error rate of the absorbing model (solid curve). Note that the correct choice in the simulation is still defined by the sign of the drift rate. Hence a biased starting point close to the error boundary (X₀ < 0) induces P(t_c) larger than 0.5. In contrast, the reflecting boundary model achieves the same error rate for different X₀ for large t_c, because the recency effect attenuates the influence of starting point on final choices.

Fig. 8.

Error rates of bounded WDMs for stimuli with unequal prior probabilities. Models are stimulated with μ = σ = b = 1, and probability of the positive alternative being correct p₊ = 0.9. Data are averaged over 10,000 trials. (a) Error rates as functions of starting point X₀ for large t_c = 3s: solid vertical line indicates the optimal starting point predicted by Eq. 11. (b) Error rates as functions of t_c for the starting point of Eq. 11, compared with the error rate for unbiased starting point X₀ = 0. Note that error rates of the reflecting WDM with biased starting points approach that for X₀ = 0 at large t_c.

Figure 8b compares the performance of bounded WDMs with starting points given by Eq. 11. Biased starting points produce lower error rates for all t_c than X₀ = 0. As expected from Figure 8a, for large t_c the reflecting WDM with the starting points of Eq. 11 has similar error rate to the bounded WDM with X₀ = 0 because of the recency effect, while the absorbing boundary model with biased starting points of Eq. 11 achieves superior performance, since it can profit from starting point adjustments. For small t_c (< 0.3s), the two bounded models with biased starting points exhibit similar performances, since early in the decision process most integrator states |X(t)| are distant from the boundaries, so the models approximate an unbounded WDM and hence produce similar error rates.

4 Fitting the models to experimental data

An interesting debate has recently taken place between Ratcliff and Usher and McClelland regarding which model best describes data from the TC paradigm. We briefly recall this to place our results in context.

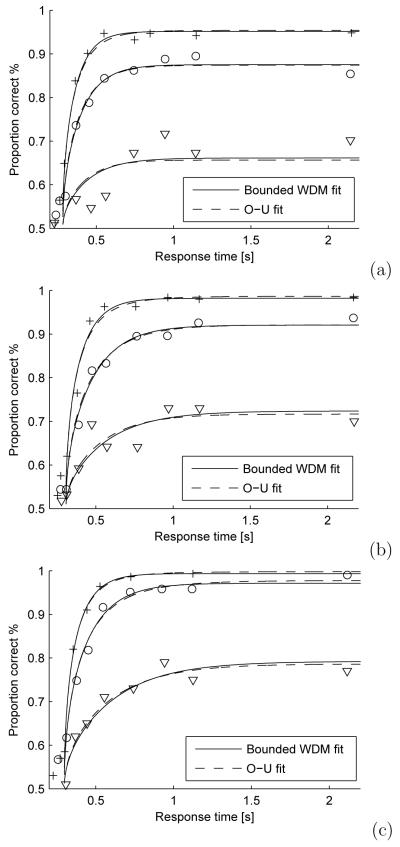
Eq. 3 predicts that the error rate of the unbounded WDM under the TC paradigm converges to zero as t_c → ∞ if the sign of μ represents the correct choice, so that subjects can achieve arbitrarily small error rate even for difficult tasks (small μ). However, it is known that humans cannot produce 100% accuracy even for large t_c. For example, Usher and McClelland (2001) performed an experiment in which subjects were required to decide whether a rectangle is tilted to the left or to the right and to respond within 200 ms of a cue (approximating the TC paradigm). Three subjects were tested with ten different viewing times (lags) and three levels of difficulty, 190 trials being administered for each combination of lag and difficulty. For no subject did error rate in the most difficult condition approach zero, even at the longest t_c: see Figure 9.

Fig. 9.

Accuracies as a function of reaction time for three subjects in the TC paradigm, from Usher and McClelland (2001). Different symbols indicate different difficulty levels; solid and dashed lines show fits of bounded WDM and O-U models for the three difficulty levels. Estimated parameters used to generate the curves are given in Table 1.

The unbounded WDM can be extended to account for these data by adding variability of drift, which predicts that the error rate does not decrease to zero for large t_c (see Section 2.3). However, Usher and McClelland (2001) have shown that it is inferior to an O-U model in describing the shape of the error rate as a function of t_c Ratcliff (2006) then proposed that the poor fit of the WDM is due to the absence of boundaries and showed that the absorbing WDM fitted the data from a combined IC and TC experiment better or equally well than alternative models.

We now provied further support for Ratcliff’s claim that boundaries allow the WDM to account for TC data. In Figure 9 we compare fits of the O-U model and bounded WDM to the data of Usher and McClelland (2001). To fit the O-U model, each subject is characterized by five parameters: drifts μ₁, μ₂, μ₃ under three difficulty conditions, the coefficient λ, and the component T₀ of t_c not due to the decision process (analogous parameters were used by Usher and McClelland (2001)). For simplicity and without loss of generality, the noise level is set to σ = 1. To allow fair comparison, we fit bounded WDMs that are also characterized by five parameters: drifts in three difficulty conditions, the boundary level ±b, and the non-decision part of the t_c (T₀). Since WDMs with absorbing and reflecting boundaries produce the same error rate under the TC paradigm (see Section 3.3), their data fits are also the same. Hence we do not specify the boundary types in Figure. 9.

We estimated the above parameters using a maximum likelihood approach, computing the likelihood of subjects’ accuracy under each experimental condition (corresponding to each data point in Figure 9) from a binomial distribution (Usher and McClelland, 2001). The likelihood of accuracy under condition i in which the subject made n_i correct decisions in N (N = 190) trials is equal to:

$$Pr(n_i\mid \text{model})=\frac{N!}{n_i!(N-n_i)!}{p}_i^{n_i}{(1-p_i)}^{N-n_i}.$$ (12)

In Eq. 12, p_i denotes the probability of a correct choice predicted by the model for the mean t_c of a given subject under condition i. The probability p_i is equal to 1 - P(t_c) in condition i. P(t_c) is calculated from Eq. A. 16 in the Appendix A for the bounded WDM, while for the O-U model it is equal to (Busemeyer and Townsend, 1992):

$$P\left(t_c\right)=\Phi \left(-\frac{\mu }{\sigma }\sqrt{\frac{2(e^{\lambda t_c}-1)}{\lambda (e^{\lambda t_c}+1)}}\right).$$ (13)

where Φ is the normal standard cumulative distribution function. The total likelihood of the model for a given subject is equal to the product of likelihoods of the accuracies in all 30 (10 lags × 3 difficulty levels) experimental conditions:

$$Pr(\text{data}\mid \text{model})=\prod _{i=1}^{30}Pr(n_i\mid \text{model}).$$ (14)

We used the Subplex optimization algorithm (Rowan, 1990) to maximize this total likelihood over the five free parameters in both the O-U and bounded WDM. The values of the estimated parameters and the likelihood ratios of experimental data given the models are listed in Table 1. The curves in Figure 9 show accuracies predicted by the O-U model and the ounded WDM. The fits are very similar and cannot differentiate between the models. Although the likelihood ratios imply that overall the data are about 3.5 times more likely to have been produced by the bounded WDM than by the O-U model, this preference was not consistent among subjects as the bounded WDM fits two subjects better, and the O-U model better fits the third subject.

Table 1.

Estimated parameters of bounded WDMs and O-U models, and likelihood ratios of experimental data given the models. Estimated parameters for the O-U model are very close to those given in the left part of Table 2 in Usher and McClelland (2001)

Subject	$\frac{P(\text{data}\mid WDM)}{P(\text{data}\mid O-U)}$	Parameters of O-U model					Parameters of bounded WDMs
		μ1	μ2	μ3	λ	T0	μ1	μ2	μ3	b	T0
S1	4.91	3.21	2.19	0.77	7.30	284	3.17	2.08	0.71	0.47	283
S2	1.34	3.29	2.10	0.85	4.41	307	3.29	2.01	0.79	0.61	306
S3	0.52	3.66	2.59	1.02	3.33	297	3.64	2.56	0.97	0.69	297
ALL	3.42

In summary, Usher and McClelland (2001) showed that the O-U model fits the data shown in Figure 9 much better than an unbounded WDM. Here we have shown that bounded WDM fit the data at least as well as the O-U model, and the WDM with absorbing and reflecting boundaries fit the data equally well.

5 Discussion

The present study compared the performance and consistency of WDMs with absorbing and reflecting boundaries with existing experimental data, as summarized in Table 2. We first showed that both boundary types introduce differential weighting of evidence within trials, yielding a primacy effect for absorbing boundaries and a recency effect for reflecting boundaries (Figure 4; we return to these effects below in discussing experimental predictions).

Table 2.

Comparison of properties of bounded WDMs. ‘+’ denotes superiority of model in a given criterion (better fit to data), ‘-’ denotes inferiority, and ‘=’ denotes equality

		Absorbing	Reflecting
Weighting of inputs		primacy effect	recency effect
Error rate	pure	=
	variable μ	=
	variable X0	-	+
	biased X0	+	-
Fit data		=
Unification of IC & TC		+	-

We then showed that, in spite of the different probability densities of their solutions (Figure 3), the absorbing and reflecting WDMs produce the same error rates under the TC paradigm with and without variability of drift rate (Figure 5 and 6). Thus, simple comparisons of performance between bounded WDMs cannot provide clear evidence in support of either model. However, for starting point variability resulting from premature sampling, the reflecting WDM yields lower error rate due to the recency effect, while if starting points reflects estimates of prior probabilities, the absorbing WDM is superior (Figures 7 and 8).

Finally, we compared model fits to existing experimental data, showing that both absorbing and reflecting WDMs produce the same fit to behavioural data from TC experiments (Figure 9). A bounded WDM produces as good fit as the O-U model on the given data set. We claim that both absorbing and reflecting WDMs should be considered as useful models in the TC paradigm.

Boundary mechanisms are not limited to the WDM, but can also be applied to decision making models based on absolute evidence. Bogacz et al. (2007) analyse the LCA model (Usher and McClelland, 2001) with one reflecting and one absorbing boundary in both IC and TC paradigms. They show that the reflecting boundary can improve performance in the IC paradigm as the number of choice-alternatives increases. Although whether the decision is rendered based on relative or absolute information is still an open question, the concept of boundary modification is versatile and important to both categories of models.

Nevertheless, we feel that the existing experimental data is insufficient to differentiate between the two types of bounded models and that further studies are required. We have shown that the two types of boundaries introduce different weighting of evidence, so it seems that this should provide clear experimental predictions. Unfortunately, the primacy and recency effects are also predicted by the O-U model (Busemeyer and Townsend, 1993). Hence even if such effects are detected, it will be unclear whether they are caused by the boundaries or by the linear term in the O-U model.

One limitation of the WDM with dual reflecting boundaries is its deficiency in describing the IC paradigm, while the absorbing WDM provides an account of performance in both IC and TC paradigms (Ratcliff, 2006, and cf. Table 2). However, since the state variable of the integrator of the WDM only reflects abstract evidence accumulated from sensory information, rather than a specific quantity directly encoded by neural systems (Ratcliff et al., 2003), it is possible that the boundaries of the WDM would change for different paradigms. To illustrate this, we compare the neural recording data from experiments under the IC (Huk and Shadlen, 2005; Churchland et al., 2008) and TC (Shadlen and Newsome, 2001; Kiani et al., 2008) paradigms and notice an interesting regularity: the firing rate of integrator neurons after stimulus onset is much lower in TC than IC paradigm (for comarison, see Figure 7 and 9 in Roitman and Shadlen, 2002). This is consistent with the idea that there are differences in the neural implementation of these two paradigms, so it seems reasonable to propose different models for the two paradigms.

The two types of boundary might be differentiated by considering their possible neural implementations. As mentioned before, accumulating sensory information is a common mechanism observed in many brain functions, including decision making. Accumulation up to a threshold is equivalent to applying an absorbing boundary to the integrating process. Some previous studies show that absorbing boundaries can be explicitly implemented in neural circuits (Mazurek et al., 2003; Lo and Wang, 2006), or implicitly achieved by attractor dynamics (Wang, 2002; Wong and Wang, 2006; Wong et al., 2007). On the other hand, Zhang and Bogacz (2008) proposed that a reflecting boundary can be implemented by a network including area LIP, the basal ganglia, and SC.

Most recently, Kiani et al. (2008) provided support for absorbing boundaries when monkeys performed the motion discrimination task under TC paradigm. In their experiment, neuronal activity in the LIP area was maintained after a certain latency, even when stimulus was still available, suggesting the influence of a boundary. Further, they observed the primacy effect (Kiani et al., 2008, figure 4c), which is consistent with an absorbing boundary. Nevertheless, as Kiani et al. (2008) also pointed out, in their experiment t_c varied widely (80 ms - 1500 ms) between trials which might have encouraged the animal to make choices quickly and be ready to respond, thus adopting a strategy that can be modelled by absorbing boundaries. There is as yet no neurophysiological study supporting the reflecting boundary or recency effect. However, given its complementary characteristics and similar performance to the absorbing boundary, we think it is necessary to test the existence of such boundary mechanism, e.g., in tasks in which t_c is not varied within a block of trials.

A version of the TC paradigm in which, on some trials, the stimulus changes within a trial could also distinguish between the types of boundaries. One approach is to perturb the stimulus during decision process by introducing informative background texture, as used by Huk and Shadlen (2005). Another approach is to consider time varying stimulus (Rouder, 2000; Smith, 1995). For example, in the motion coherence task (see Section 2.1) initially the coherent dots could move left, and then right (as proposed by Wang, 2002). Stimuli would have to be carefully constructed to ensure that the integrator hits a boundary before the change in the stimulus, but such a condition is hard to guarantee in the classical moving-dots paradigm. One alternative would be to employ sequences of different geometrical shapes, with each shape carrying a certain amount of information, as in the weather prediction task (Yang and Shadlen, 2007). The shapes could first be evaluated under the IC paradigm to determine which sequence induces a boundary hit, and then the sequence can be manipulated to serve as the stimulus under the TC paradigm (e.g., by adding or changing individual shapes). Under these conditions, the two types of boundaries would lead to different predictions: choices being dominated by information before the change in the case of absorbing boundaries and by information after it for reflecting boundaries. Recordings of neuronal firing rates during such an experiment would further illuminate underlying mechanisms.

A The probability density function for reflecting boundaries

Here we derive the probability density function p(X, t) for the WDM with reflecting boundaries. To simplify the calculations, we fix unit noise variance (σ=1) and boundaries at 0 and 2b and (symmetric) initial condition:

$$dX=\mu dt+dW,\text{with}X\left(0\right)=b.$$ (A.1)

As shown in (Bogacz et al., 2006, Appendix), only the parameter ratios μ/σ and b/μ influence the following expressions, so we may set σ = 1 without loss of generality.) To obtain expressions for the case ±b and X(0) = 0 treated in the main text, one replaces X by X + b. We note that a Laplace-transformed version of the solution to this problem appears in Khantha and Balakrishnan (1983), but explicit expressions such as those given below do not appear to be readily available.

The probability distribution p(X, t) for solution of (A.1) satisfies the forward Kolmogorov or Fokker-Planck equation (Gardiner, 1985):

$$\frac{\partial p(X,t)}{\partial t}=-\mu \frac{\partial p(X,t)}{\partial X}+\frac{1}{2}\frac{{\partial }^{2}p(X,t)}{\partial X^2},$$ (A.2)

and reflecting boundaries imply the following no-flux boundary conditions:

$$-\mu p(X,t)+\frac{1}{2}\frac{\partial p(X,t)}{\partial X}=0\text{at}X=0\text{and}X=2b.$$ (A.3)

To solve (A.3) we separate variables (Boyce and DiPrima, 1997) and seek a solution of the form:

$$p(X,t)=\sum _{j=1}^{\infty }{\omega }_j\left(t\right){\varphi }_j\left(X\right),$$ (A.4)

obtaining the following eigenvalue problem

$$\frac{1}{2}{\varphi }^{″}-\mu {\varphi }^{\prime }+\lambda \varphi =0;-2\mu \varphi \left(0\right)+{\varphi }^{\prime }\left(0\right)=0=-2\mu \varphi \left(2b\right)+\varphi \prime \left(2b\right),$$ (A.5)

and ODEs for the time-dependent coefficients ω_j(t):

$${\stackrel{.}{\omega }}_j=-{\lambda }_j{\omega }_j\Rightarrow {\omega }_j\left(t\right)={\omega }_j\left(0\right)e^{-{\lambda }_{j}t}.$$ (A.6)

Applying the boundary conditions (A.3) to the general solution

$$\varphi =e^{(\mu \pm \sqrt{{\mu }^2-2\lambda })X}$$ (A.7)

of (A.5), we find a single eigenvalue λ₀ = 0 with eigenfunction ϕ₀(X) = e^2μX and an infinite set of the form

$${\lambda }_j=\frac{j^2{\pi }^2}{8b^2}+\frac{{\mu }^2}{2},{\varphi }_j\left(X\right)=e^{\mu X}\left[\cos \left(\frac{j\pi X}{2b}\right)+\frac{2\mu b}{j\pi }\sin \left(\frac{j\pi X}{2b}\right)\right],$$ (A.8)

for j = 1,2, . . .. Hence, from (A.4), the general solution of the Fokker-Planck equation may be written as an infinite series

$$p(X,t)={\omega }_0\left(0\right)e^{2\mu X}+\sum _{j=1}^{\infty }{\omega }_j\left(0\right)e^{-{\lambda }_{j}t}{e}^{\mu X}\left[\cos \left(\frac{j\pi X}{2b}\right)+\frac{2\mu b}{j\pi }\sin \left(\frac{j\pi X}{2b}\right)\right];$$ (A.9)

this may be computed with arbitrary accuracy by summing finitely many terms.

The coefficients ω_j(0) in (A.9) are obtained from the initial probability distribution p(X, 0) = p₀(X). To compute them, it is convenient to use a weighted inner product with respect to which the (non-normalized) eigenfunctions (A.8) are orthogonal. Upon multiplication by e^-2μX the non self-adjoint boundary value problem (A.5) becomes a regular Sturm-Liouville problem (Boyce and DiPrima, 1997):

$${\left(e^{-2\mu X}{\varphi }^{\prime }\right)}^{\prime }+2\lambda e^{-2\mu X}\varphi =0,$$ (A.10)

and hence the eigenfunctions are pairwise orthogonal with respect to the weighted inner product:

$${({\varphi }_j,{\varphi }_k)}_{\mu }={\int }_0^{2b}{\varphi }_j\left(X\right){\varphi }_k\left(X\right)e^{-2\mu X}dX=c_k{\delta }_{jk},\text{for}j,k=0,1,2,\dots ,$$ (A.11)

with normalization constants

$$c_0=\frac{e^{4\mu b}-1}{2\mu },\text{and}{c}_k=b\left(1+\frac{4{\mu }^2{b}^2}{k^2{\pi }^2}\right)\text{for}k\ge 1.$$ (A.12)

Equating (A.9) to p₀(X) at t = 0, and taking inner products, we obtain

$${\omega }_j\left(0\right)=\frac{{(p_0,{\varphi }_j)}_{\mu }}{c_j},\text{for}j\ge 0.$$ (A.13)

As t → ∞, the terms in the sum of (A.9) all decay to zero and p(X, t) approaches the equilibrium probability distribution p_∞(X) = ω₀(0)e^2μX, so for normalized initial data $\int p_0\left(X\right)dX=1$ it must follow that

$${\int }_{2b}^0{\omega }_0\left(0\right)e^{2\mu X}dX=1\Rightarrow {\omega }_0\left(0\right)=\frac{1}{c_0}=\frac{2\mu }{e^{4\mu b}-1}.$$ (A.14)

For the delta function initial condition p₀(X) = δ(X - b), the remaining coefficients for j ≥ 0 may be computed directly from (A.13) as:

$$\begin{array}{c}\hfill {\omega }_j\left(0\right)=\frac{e^{-\mu b}\left[\cos \left(\frac{j\pi }{2}\right)+\frac{2\mu b}{j\pi }\sin \left(\frac{j\pi }{2}\right)\right]}{b\left(1+\frac{4{\mu }^2{b}^2}{j^2{\pi }^2}\right)}\hfill \\ \hfill =\frac{e^{-\mu b}\left[{(-1)}^{\frac{j}{2}}\left(\frac{1+{(-1)}^j}{2}\right)+\frac{2\mu b}{j\pi }{(-1)}^{\frac{j-1}{2}}\left(\frac{1-{(-1)}^j}{2}\right)\right]}{b\left(1+\frac{4{\mu }^2{b}^2}{j^2{\pi }^2}\right)}.\hfill \end{array}$$ (A.15)

Substituting (A.14) and (A.15) in (A.9), we obtain an explicit series representation of p(X, t).

The error rate P(t_c) at given t_c is computed by integrating p(X, t_c) between the left boundary and the starting point:

$$P\left(t_c\right)={\int }_0^{b}p(X,t_c)dX=\frac{1}{1+e^{2\mu b}}+\sum _{j=1}^{\infty }{\omega }_j\left(0\right)e^{{\lambda }_j{t}_c}\frac{2b{e}^{\mu b}\sin \frac{j\pi }{2}}{j\pi }.$$ (A.16)

As t increases, p(X, t_c) converges to the equilibrium distribution

$$\underset{t_c\to \infty }{\lim }p(X,t_c)=\frac{2\mu e^{2\mu X}}{e^{4\mu b}-1},$$ (A.17)

and the P(t_c) approaches

$$\underset{t_c\to \infty }{\lim }P\left(t_c\right)=\frac{1}{1+e^{2\mu b}}.$$ (A.18)

B Equality of the error rate for the bounded WDMs

Here we show that the error rates of the reflecting and absorbing WDM are the same for arbitrary t_c. We again set σ=1, and take boundaries at 0 and 2b with X₀ = b. Since the error rate for absorbing boundaries cannot be evaluated analytically, we consider fluxes across the starting point b (Goel and Dyn, 2003):

$$F={\phantom{\mid }-\mu p(X,t)+\frac{1}{2}\frac{\partial p(X,t)}{\partial X}\mid }_{X=b}.$$ (B.1)

For reflecting boundaries, the derivative of p(X, t) at X = b is:

$$\begin{array}{cc}\hfill {\phantom{\mid }\frac{\partial p}{\partial X}\mid }_{X=b}=\frac{4{\mu }^2{e}^{2\mu b}}{e^{4\mu b}-1}+\sum _{j=1}^{\infty }& \frac{\exp (-{\lambda }_{j}t)}{b\left(1+\frac{4{\mu }^2{b}^2}{j^2{\pi }^2}\right)}\left[\cos \left(\frac{j\pi }{2}\right)+\frac{2\mu b}{j\pi }\sin \left(\frac{j\pi }{2}\right)\right]\times \hfill \\ \hfill & \left[2\mu \cos \left(\frac{j\pi }{2}\right)+\left(\frac{2{\mu }^{2}b}{j\pi }-\frac{j\pi }{2b}\right)\sin \left(\frac{j\pi }{2}\right)\right],\hfill \end{array}$$ (B.2)

where (cf. equations) (A.8-A.9))

$${\lambda }_j=\left(\frac{j^2{\pi }^2}{8b^2}+\frac{{\mu }^2}{2}\right).$$ (B.3)

Hence from (B.1) the flux across b is:

$$\begin{array}{cc}\hfill F_{\mathit{ref}}=\sum _{j=1}^{\infty }\frac{\exp (-{\lambda }_{j}t)}{b\left(1+\frac{4{\mu }^2{b}^2}{j^2{\pi }^2}\right)}\left[\cos \left(\frac{j\pi }{2}\right)+\frac{2\mu b}{j\pi }\sin \left(\frac{j\pi }{2}\right)\right]& \left(-\frac{{\mu }^{2}b}{j\pi }-\frac{j\pi }{4b}\right)\sin \left(\frac{j\pi }{2}\right)\hfill \\ \hfill & =-\sum _{j=1}^{\infty }\left[\frac{\mu \exp (-{\lambda }_{j}t)}{2b}\right]{\sin }^2\left(\frac{j\pi }{2}\right).\hfill \end{array}$$ (B.4)

For absorbing boundaries, the probability density p(X, t) with boundary at ±b is (Feller, 1968):

$$p(X,t)=\frac{1}{b}{e}^{\mu X∕{\sigma }^2}\sum _{j=1}^{\infty }\sin \left(\frac{j\pi }{2}\right)\sin \left[\frac{j\pi (X+b)}{2b}\right]\exp \left[-\left(\frac{j^2{\pi }^2{\sigma }^2}{8b^2}+\frac{{\mu }^2}{2{\sigma }^2}\right)t\right].$$ (B.5)

Upon replacing X by X - b to adapt for absorbing boundaries at X = 0 and X = 2b, the probability density function (B.5) becomes (Goel and Dyn, 2003)

$$p(X,t)=e^{\mu (X-b)}\sum _{j=1}^{\infty }\frac{\exp (-{\lambda }_{j}t)}{b}\sin \left(\frac{j\pi }{2}\right)\sin \left(\frac{j\pi X}{2b}\right),$$ (B.6)

and its derivative at X = b is:

$${\phantom{\mid }\frac{\partial p}{\partial X}\mid }_{X=b}=\sum _{j=1}^{\infty }\frac{\exp (-{\lambda }_{j}t)}{b}\sin \left(\frac{j\pi }{2}\right)\left[\mu \sin \left(\frac{j\pi }{2}\right)+\frac{j\pi }{2b}\cos \left(\frac{j\pi }{2}\right)\right].$$ (B.7)

Using (B.1) again, the flux for absorbing boundaries is therefore

$$\begin{array}{cc}\hfill F_{abs}=\sum _{j=1}^{\infty }\frac{\exp (-{\lambda }_{j}t)}{b}\sin \left(\frac{j\pi }{2}\right)& \left[-\frac{\mu }{2}\sin \left(\frac{j\pi }{2}\right)+\frac{j\pi }{4b}\cos \left(\frac{j\pi }{2}\right)\right]\hfill \\ \hfill & =-\sum _{j=1}^{\infty }\left[\frac{\mu \exp (-{\lambda }_{j}t)}{2b}\right]{\sin }^2\left(\frac{j\pi }{2}\right).\hfill \end{array}$$ (B.8)

Since the fluxes (B.4) and (B.8) are identical as functions of t, the error rates of the WDM with symmetric reflecting and absorbing boundaries are also equal. Note the remarkable simplicity of the final flux formula, due to cancellation of terms.