A state-mutating genetic algorithm to design ion-channel models

Abstract

Realistic computational models of single neurons require component ion channels that reproduce experimental findings. Here, a topology-mutating genetic algorithm that searches for the best state diagram and transition-rate parameters to model macroscopic ion-channel behavior is described. Important features of the algorithm include a topology-altering strategy, automatic satisfaction of equilibrium constraints (microscopic reversibility), and multiple-protocol fitting using sequential goal programming rather than explicit weighting. Application of this genetic algorithm to design a sodium-channel model exhibiting both fast and prolonged inactivation yields a six-state model that produces realistic activity-dependent attenuation of action-potential backpropagation in current-clamp simulations of a CA1 pyramidal neuron.

The importance of modeling ion channels has been understood since Hodgkin and Huxley's seminal work with the squid giant axon (1). Subsequently, the development of the patch-clamp method (2) enabled the characterization of the properties of a wide range of channels, and intensive efforts followed to produce quantitative models that could predict and explain specific ion-channel behavior (3–7). Such efforts have led to two broad classes of models: those describing single-channel and gating currents, and those describing macroscopic currents.

Models of single-channel and gating currents can be used to analyze properties such as open-channel probabilities, dwell times, and activation kinetics; they therefore facilitate an improved understanding of channel biophysics (3–5, 7–9). By contrast, models of macroscopic currents are usually intended as empirical tools as part of larger compartmental models of neurons. Such a macroscopic model may not necessarily describe the actual molecular state changes of the channel; the goal is rather for it to function as a “black-box” that reproduces the mean behavior of a population of channels. Hodgkin and Huxley's (1) original formulation of sodium- and potassium-channel models is a prime example of this case, and its basic formalism continues to be widely used to generate empirical ion-channel models.

An alternative to the Hodgkin–Huxley formalism is the state-dependent modeling approach (3). In reality, state-dependent models subsume Hodgkin–Huxley models because the latter can be recast as the former (3). State-dependent models are more general, however, because they can describe certain behaviors more easily than Hodgkin–Huxley type models, such as having widely different transition rates into and out of a given state (10). In general, the gold standard for the use of state-dependent models is single-channel recording (3, 5, 11), but the state-dependent formalism is also often employed in models of macroscopic currents (12–15) because of the generality and flexibility it affords.

Methods to make empirical state-dependent models conform to data have been studied extensively and have involved a multitude of techniques such as hand fitting (12–14, 16), principal-axis fitting (17), maximum-likelihood estimation (5, 7, 17, 18), and genetic algorithms (15), among others. Here, we present a new fitting technique based on a topology-mutating genetic algorithm. Genetic algorithms have a number of useful characteristics: First, they have been shown to explore a large area of parameter space with relatively quick convergence, especially for problems with many parameters (19). Second, they are easily parallelizable. Third, they have been successfully applied to neuronal modeling, both for Hodgkin–Huxley-type ion-channel parameters and for compartmental neuronal models with voltage-activated conductances (15). Here we show that if the ion-channel model is formulated properly, genetic algorithms provide a natural way to incorporate changes in model topology as mutations.

The algorithm presented here has several key features. Most notably, whereas other published optimization algorithms fix the model topology and optimize the rate constants, our algorithm searches over the space of model topologies and the space of rate parameters simultaneously. In order to design such an algorithm appropriate for state-dependent ion-channel models, we formulated an automated, computationally efficient method to satisfy the principle of microscopic reversibility, an equilibrium condition that imposes constraints on topologies with loops (20, 21). Finally, our algorithm uses a sequential approach, also known as goal programming (22), to optimize multiple protocols without the need to assign weights to each of the objective functions. The ability of this genetic algorithm to select and examine topologies not previously explored demonstrates its flexibility in developing working empirical models.

We applied this genetic algorithm to devise a sodium-channel model that exhibits both fast and slow inactivation. Fast inactivation refers to a nonconducting channel state that follows quickly after depolarization and activation (within milliseconds) and from which channels recover quickly when the voltage is restored to resting levels (1). In response to either sustained depolarization (23, 24) or a train of depolarizing pulses (16, 25), however, the fraction of sodium channels available for activation also decreases rapidly, but in this case recovery occurs much more slowly, on the order of seconds rather than milliseconds. This form of inactivation has therefore been called “prolonged” or “slow” (16, 25). The presence of such widely disparate time scales makes the creation of state-dependent models of these channels a challenge. At the same time, the effect of prolonged inactivation on processes such as action-potential backpropagation (26, 27), transitions from bursting to spiking (28), and dendritic spiking (29, 30) makes the development of accurate models of prolonged inactivation important for computational simulations of neuronal function.

Results

To ensure the generation of a model with proper behavior over a wide range of time scales and voltages, we required it to fit macroscopic current data from voltage-clamp experiments detailing the voltage-dependence of peak activation and steady-state inactivation (31), the voltage-dependence of the activation and fast-inactivation time constants (14), the time course of entry into and recovery from prolonged inactivation (16), and the two-phase recovery from a single depolarizing pulse (16), in that order. Starting with a population of 100 randomly generated models with different topologies and numbers of states, we ran the algorithm with 3,000 generations per protocol by using a goal-programming approach with an error tolerance of 10% (see Materials and Methods). The algorithm took approximately two weeks of run time to converge on a parallel cluster with 16 processors; during this time, more than two million models with varying topologies were examined.

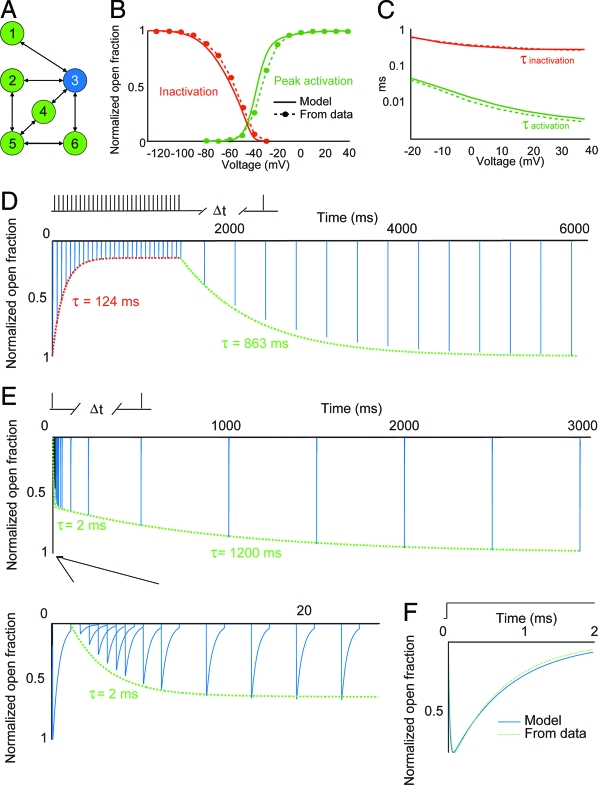
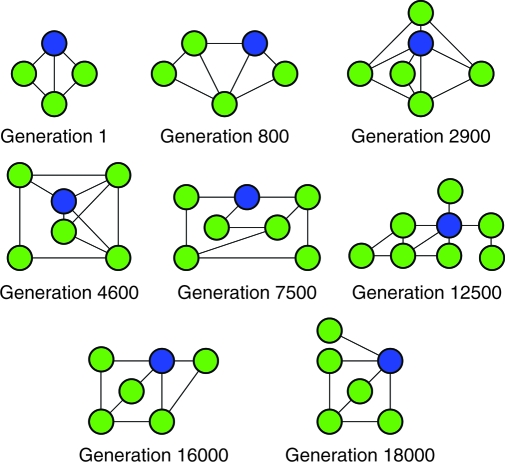
The model to which the algorithm converged consisted of six states and seven pairs of directed edges (Fig. 1A), with rate parameters given in Table 1. This model reproduced the experimental data for all the protocols (Fig. 1 B–F) with an average error of 1.8%. This six-state topology has not been proposed in any previous studies. In addition, analysis of the topologies of intermediate best-fit models (Fig. 2 and Movie S1 in the SI Appendix) shows that the algorithm generated models with between four and eight states at various points throughout the optimization process. This finding demonstrates that the algorithm is not confined to optimizing the parameters of one or two topologies but does indeed evaluate a wide range of possible model structures.

Fig. 1.

Summary of voltage-clamp simulation behavior for the optimal model under the various fitting protocols. (A) Topology of the optimal model. The blue state (state 3) corresponds to the open conductance state. (B) Voltage-dependent activation and inactivation curves for the model (solid lines) and from experiments (31) (points and dashed lines). (C) Activation and inactivation time-constant curves for the model (solid lines) and from experiments (14) (points and dashed lines). (D) Entry into and recovery from prolonged inactivation induced by a train of 20 Hz depolarizing pulses. The first 1,000 ms show the decline in peak open fraction resulting from the 20 Hz train. The remaining points represent the peak open fraction during depolarizing test pulses delivered at various intervals and comparison with experimental data (16) (dashed line). (E) Two-phase recovery from inactivation induced by a single depolarizing pulse. The lower frame is a close-up of the first 20 ms, showing the initial phase of the two-phase recovery from a single pulse and comparison with experimental data (16) (dashed line). (F) Model response (solid line) to a single-step depolarization from −70 mV to −1 mV, showing agreement with the experimentally observed time course of activation and inactivation (14) (dashed line).

Table 1.

Rate parameters for the optimal six-state model

rij	a	b
r31	5.218	0.1066
r32	2.187	0.04433
r52	6.863	0.2200
r43	−11.53	0.03047
r63	0.5124	0.005264
r54	−2.802	0.05300
r65	−3.671	0.04366
r13	−5.018	−0.1773
r23	−2.819	−0.1498
r25	−4.085	−0.05757
r34	−18.68	−0.000002500
r36	14.85	0.2956
r45	−1.599	0.0000
r56	16.61	0.4175

The topology of this model is given in Fig. 1A of the main text. Rate constants are in the from r_ij = exp(a + bV), where r_ij is the rate from state j to state i.

Fig. 2.

Intermediate topologies. The best-performing topologies at various intermediate generations during the genetic algorithm optimization routine.

The fitting of the first few protocols was accompanied by a rapid reduction of the error in the initial generations; later protocols took longer to fit, due to the larger number of constraints imposed by the goal-programming approach (see Fig. S1 in the SI Appendix). The presence of error fluctuations in the earlier protocols during later generations indicates that the algorithm makes use of the leeway afforded by the 10% tolerance constraint (see Materials and Methods).

In order to qualitatively assess the robustness of this algorithm to initial conditions, we performed three additional runs with different random initial populations. All runs generated models with identical topology to the optimal model presented here, but one of the three contained an extra edge (see Tables S1 and S2 in the SI Appendix for the results of two of these runs). In all three alternate models the rate parameters were slightly different, but the overall behavior of the models was qualitatively similar to the optimal model. Thus, the algorithm reproducibly converged to a six-state topology as providing the best fit to the experimental data.

To test the ability of models with fewer states to fit the data, we conducted a run with a fixed four-state topology with all-to-all connectivity. This optimization procedure generated a model (data not shown) that could reproduce either fast or slow kinetics, but not both simultaneously, suggesting that a four-state topology is insufficient to characterize the observed range of behaviors on both the fast and slow time scales. A similar procedure with a five-state topology improved the fits of the channel kinetics, but resulted in poorer fits to the voltage-activation curve.

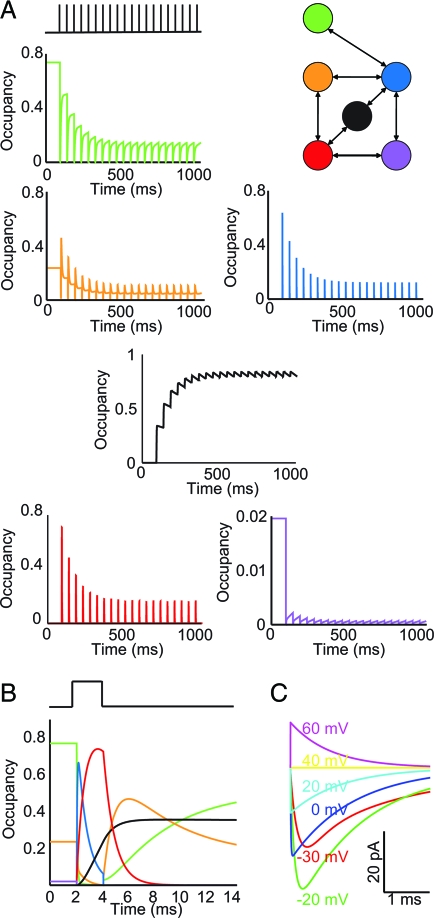
Because the algorithm generated a model with a unique topology (Fig. 3A Upper Right), the pathways corresponding to activation and the two types of inactivation were not immediately evident. By examining the state occupancies during the induction of prolonged (Fig. 3A) and fast (Fig. 3B) inactivation, it is clear that this model contains a slow-inactivated state, where channel occupancy accumulates during the induction protocol. This state is mainly accessed through the fast-inactivated state. Apart from these two states and the open state, there are two identifiable closed states that the channel occupies at rest, and a transition state that never achieves a high degree of occupancy in the protocol shown here but is occupied more substantially at larger depolarizing steps. The existence of this transition state improves fits of the voltage-activation curve at voltages beyond 0 mV. Thus, a model with a five-state topology fits the data well at most voltages, but a sixth state improved the overall accuracy of the model because of better fits at larger depolarizations. As a final check, the model behaves properly in response to a range of voltage-step pulses (Fig. 3C).

Fig. 3.

Dynamics of the optimal model. (A) State occupancies during entry into prolonged inactivation in response to a train of 2-ms, 50-mV amplitude pulses at 20 Hz. Topologies of the optimal six-state model are shown at the upper right. The channel accumulates in the prolonged-inactivation (black) state upon successive depolarizing pulses. (B) Occupancies of the various states during a single 2-ms, 50-mV amplitude depolarizing step, and for a 10-ms recovery period. During the depolarization, the channel opens (blue line) and then enters the fast-inactivated state (red line), through which it accesses the prolonged-inactivation state (black line). Upon repolarization, the channel starts to recover into the two closed (green and orange lines) states. The sixth state (purple) is a transition state. (C) Current traces for a channel with 1-nS peak conductance in response to a range of step pulses, assuming a sodium-reversal potential of 40 mV.

Although the analysis of state occupancies does not necessarily provide a prediction of actual channel conformational changes, the identification of an appreciable fast-to-prolonged-inactivation pathway suggests that this model will reproduce experimental observations beyond those used in the fitting protocols. Specifically, the existence of this pathway has been posited to explain the experimental observation that slow inactivation is induced fully by long depolarizations (16). Simulation of this protocol (see Fig. S2 in the SI Appendix) shows that our model reproduces the proper behavior. It is reassuring that this behavior emerged despite not being a fitting constraint, as the goal is to use the model in simulations other than those tested during the optimization. On a similar note, the removal of the slow-inactivated state and its connecting edges from the six-state model resulted in a five-state topology exhibiting only fast inactivation. (See Table S3 in the SI Appendix for the rate constants after an additional fixed-topology optimization to improve accuracy.)

We also tested models with additional states. In particular, we added two additional states to a previously-developed 12-state sodium-channel model (12), fixed the topology, and used the genetic algorithm to optimize the rate constants. The resulting 14-state model, as shown in Fig. S3 and Table S4 of the SI Appendix, did not produce a significantly better fit than the six-state model. Simulations with the 14-state model, of course, require more than twice the amount of computational effort than the six-state model.

Given that the ultimate purpose of this algorithm is to devise models that can be used in compartmental simulations of neurons with branching dendrites and multiple conductances, we incorporated our sodium-channel model into a model of a CA1 pyramidal neuron (32). We examined the activity-dependent attenuation of backpropagating action potentials (26, 27, 33). Because prolonged inactivation of sodium channels has been implicated in this phenomenon (25, 34), we inserted a combination of sodium-channel models having fast inactivation alone and having both fast and prolonged inactivation, with the latter comprising a larger fraction of the total in the dendrites (see Materials and Methods), as suggested by experimental observations (16).

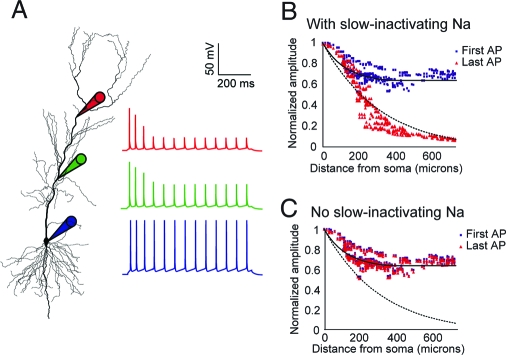
The simulations (Fig. 4 A and B) showed that this model produced accurate action-potential firing and backpropagation on both the fast (during individual action potentials) and slow (over the course of multiple backpropagating action potentials) time scales. In addition, eliminating the prolonged inactivation of the sodium conductance abolished the activity dependence of action-potential backpropagation (Fig. 4C). Further simulations showed that prolonged inactivation of sodium channels resulted in experimentally observed inhibition of dendritic spikes by prior local depolarization (29, 30) (see Fig. S4 in the SI Appendix).

Fig. 4.

Compartmental simulation using the ion-channel model. The optimal model was incorporated into current-clamp simulations to examine the distance-varying degree of activity-dependent attenuation of a train of backpropagating action potentials (bAPs). (A) Morphology of reconstructed CA1 pyramidal neuron showing attenuation of the bAP train at the soma and two different apical dendritic locations. (B) Normalized amplitudes of the first and last spike in a train of bAPs at various locations throughout the dendritic tree, in a simulation with a mixture of fast-only and slow-inactivating sodium channels. The fraction of total sodium conductance contributed by the slow-inactivating type is 100% in the distal dendrites and decreases linearly with distance to 0% in the soma. The somatic current injection was 0.15 nA for 800 ms. The solid and dashed lines represent fits of the experimental data for the first and last APs respectively, extrapolated from data (27). (C) Same as B, but using only sodium conductance with fast inactivation.

Discussion

A standard approach for the development of empirical state-dependent models has been to select a topology (usually based on or pieced together from single-channel studies) and optimize the transition-rate parameters (12–17, 35, 36). This inverse channel-fitting problem (37) has been extensively studied, and a number of different optimization techniques have been used (37). A common theme that runs through the published techniques, however, is that the model topology is constrained at the start.

The results from the algorithm presented here show that optimization of channel models does not require the a priori constraint of fixing the topology, and the burden of doing so can be shifted to the computer. One problem with fixing the topology, of course, is that one may have insufficient transitions to capture the range of experimental behavior. A topology with a large number of states and edges can be selected beforehand, but this can result in more transitions and rate parameters than necessary, which in turn can lead to slower computation, which is a disadvantage when performing large-scale simulations. Although we have not performed a systematic analysis of whether the topology-mutating genetic algorithm generates a minimally complicated model, the fact that the final model contains only six states (and five states without prolonged inactivation), as opposed to the eight- or 12-state sodium-channel models found in the literature (12, 13), suggests that the models it develops are not overly complicated.

In addition to the topology-mutating aspect, the automatic satisfaction of microscopic reversibility allows for the computationally efficient generation of models which satisfy equilibrium constraints. For optimization of fixed topologies, the selection of independent rate constants based on microscopic reversibility can be done by hand. This approach is not convenient for an algorithm that needs to explore multiple topologies in an efficient manner, however. Alternative methods to ensure microscopic reversibility have been devised, including the identification of ordered cycles and spanning trees (21). Our approach, however, recasts the free parameters not as the individual rates themselves, but as the sums and differences of the logarithms of the rates (see Materials and Methods); in this way, model-rate parameters for any given topology can be made to satisfy microscopic reversibility automatically with minimal computational effort.

A second important characteristic of the algorithm described here is the goal-programming approach. To generate a model that captures several distinct behaviors, one must by definition have multiple experimental protocols covering a range of voltages and time scales. A standard approach is to assign weights to the errors associated with the different protocols and to balance the performance of the model under one protocol with its behavior under the others. A difficulty with this approach, however, can arise when combining the errors; in particular, the minima associated with each protocol's error can appear in the weighted sum, and thus the total error can have many local minima. The goal-programming approach, on the other hand, optimizes the error for each protocol individually while merely constraining the error associated with previously optimized protocols to not increase beyond some set tolerance (22). Thus, with goal programming at each step of the sequential optimization one is only dealing with minima of the individual protocol being examined.

Although one does not need to assign weights when goal programming is used, one does need to assign a sequential order to the protocols. In general, this ordering could remain arbitrary, but in the present case we have found that to a certain extent the protocols have an implicit hierarchy. For example, in order to exhibit proper fast- and slow-inactivation kinetics, the model must have the correct amount of activation. Similarly, the model must exhibit the correct degree of prolonged inactivation before its recovery profile can be fit. As a result, for this example we found the goal-programming approach to be more straightforward than choosing protocol weights. Nevertheless, selecting the protocol order is crucial to the optimization process; indeed, an alternate run of the algorithm with a random protocol order resulted in unacceptable fits.

The model generated by this algorithm captures all the channel activation and inactivation kinetics throughout the range of experimental voltages and time scales more accurately than previously published sodium-channel models. A prior qualitative Hodgkin–Huxley-based slowly inactivating model (38) reproduced peak activation, steady-state inactivation, and entry into slow inactivation but did not accurately model the recovery from slow inactivation. Previous state-dependent models reproduced the kinetics of entry into and recovery from prolonged inactivation (16, 25) but did not exhibit proper peak activation, steady-state inactivation, and kinetics of activation and entry into fast inactivation. In contrast, this model reflects the kinetics of activation, entry into and recovery from fast inactivation (Fig. 1 C and F) as closely as other six-state, non-slow-inactivating models (14), in addition to capturing the kinetics associated with prolonged inactivation. Improvements could potentially be realized, of course, by re-running the fitting algorithm with additional experimental data from new protocols to further constrain the model.

We emphasize that the topologies generated by this algorithm are not intended to reflect molecular reality. Examination of the optimal model (Fig. 3) shows that recovery into one of the closed states necessitates a transition through the open state. If this transition took place in actual channels, brief channel openings would be evident in single-channel recordings during the recovery phase, an observation which has not been made experimentally. In the model, the transition from the open to the closed state during the recovery phase is much faster than entry into the open state, so on the macroscopic scale no appreciable accumulation in the open state (and hence no appreciable current) is observed during recovery from prolonged inactivation (Figs. 1 and 3).

A remaining question is the effect of various parameters on algorithm performance. First, the optimization of the first few protocols (Fig. S1) is much more rapid than the later protocols, suggesting that a hard limit on the number of generations could be replaced by a dynamic criterion. In addition, the sensitivity of our algorithm to the probabilities of mutation, the goal-programming tolerance, and the penalty factor imposed on more complex models, has not been explored systematically. Although values for these parameters are somewhat arbitrary, qualitative analysis during the prototyping phase of this algorithm suggested that the present values for these parameters result in rapid, but not premature, convergence. Optimizing these parameters for the full algorithm would no doubt result in a more efficient search process, although it is unlikely that the resulting algorithm would perform drastically better than the one presented here as there is such good agreement between the final model and the experimental data.

Finally, this genetic algorithm can be easily modified to design ion-channel models exhibiting any specified behavior; the only required external specifications are the fitting protocols themselves. To model a different ion channel, therefore, it is only necessary to change these protocols, and not the state-dependent model topology and formulation. In fact, this algorithm should not be limited merely to ion-channel models, but should be applicable to any system representable by a Markov process with unknown underlying topology. The broad applicability of this algorithm, combined with its topology-mutating feature, makes it an ideal candidate for optimizing ion-channel models given any set of macroscopic data.

Materials and Methods

All programs will be made available on the ModelDB database, http://senselab.med.yale.edu/ModelDB/.

Generation of Q matrix.

A state-dependent model can be characterized by its rate matrix Q, which determines the system of ordinary differential equations describing flow into and out of the various states (3),

Here $\overrightarrow{s}$ is a column vector whose components s_j indicate the fraction of channels in state j. Element Q_ij, for i ≠ j, represents the transition rate from state j to state i.* In addition, Q_jj is the total rate at which state j is exited, and ∑_i Q_ij = 0.

The connectivity information of a state-dependent model can be represented by an incidence matrix I_a. I_a is an M-by-N matrix, where M is the number of states and N is the number of directed edges. Each column represents a single edge, with a −1 for the originating or source state, and a 1 for the final, or target, state (39). Given the incidence matrix I_a and an ordered vector of rate constants $\overrightarrow{r}$, Q can be constructed as follows (40):

Here {$\overrightarrow{r}$} is a matrix with the components of $\overrightarrow{r}$ along the diagonal (and zeros elsewhere), and I_k is the transpose of the incidence matrix I_a with all the −1s and 1s replaced by 1s and 0s, respectively.

Microscopic Reversibility.

For the most general case, the rate parameters $\overrightarrow{r}$ can all be specified independently of one another. For systems that must satisfy microscopic reversibility, however, a topology containing P cycles must have P dependent rate constants (21). Alternatively, because a graph with N/2 edges (or N directed edges) and M nodes must have (N/2)−M+1 cycles, the number of free rate parameters must equal M+(N/2)−1 (21).

The algorithm outlined here relies on the structure of the equations and the connection between microscopic reversibility and detailed balance (20). The latter is based upon the requirement that in the steady-state, the forward and backward fluxes between any two states must be equal,

If fluxes are equal pairwise, then the fluxes around closed loops in opposite directions must also be equal, i.e., these transitions are reversible. The detailed balance equations can be rewritten in terms of logarithms as

for all nonzero values of Q_ij and Q_ji. If the directed edges in the incidence matrix I_a are ordered pairwise, with the lower-numbered of the two states as the source in the first of the two edges, then the full set of difference equations can be written as a matrix equation connecting the logarithms of the rate constants (in the same order as in the vector $\overrightarrow{r}$) with the logarithms of the equilibrium state variables,

Here D is a rectangular diagonal matrix with D_i,2i−1 = −1 and D_i,2i = 1, the rows of I_e consist of the even columns of the incidence matrix I_a, and ln ($\overrightarrow{r}$) and ln ($\overrightarrow{s}$) are vectors formed by taking logarithms componentwise of $\overrightarrow{r}$ and $\overrightarrow{s}$.

For a fully connected network topology, the matrix I_e has a single null vector consisting of all 1's (39). Thus, there are M − 1 independent parameters (where M is the number of states) in ln $\overrightarrow{s}$; because the equations only involve the ratios of the state occupancies, an overall scaling constant is omitted.

The constraints imposed by detailed balance generate N/2 equations. There are a total of N rates that need to be specified, however, because each directed edge has its own corresponding rate. The additional N/2 equations needed to completely determine each rate can be found by specifying the sum of the logarithms for each pair of forward and backward rate constants,

where abs (D) is the matrix D with −1's replaced by 1's. The components of $\overrightarrow{k}$ are constants representing the products of the forward and backward rates for each edge.

Therefore, with this approach the free parameters for any given model are the logarithms of the steady-state occupancies of each state, less one, and the sums of the logarithms of each pair of rates. For each pair of rates, there is one equation for the difference of their logarithms and one for their sum, so obtaining the rates from the free parameters is straightforward.

Voltage Dependence.

To incorporate voltage dependence into the rates, all of the independent parameters, i.e., ln $\overrightarrow{s}$ and ln $\overrightarrow{k}$, should depend upon the voltage. The simplest choice is to use a linear function, $\overrightarrow{a}$ + $\overrightarrow{b}$V. In this case, both the rates and the equilibrium-state occupancies become exponential functions of the voltage. This basic formulation is essentially a version of the one-ion symmetrical barrier pore model (41). We also tested two alternative formulations, the first being a quadratic function, $\overrightarrow{a}$ + $\overrightarrow{b}$V + $\overrightarrow{c}$V², and the second a piecewise linear function, with different constants $\overrightarrow{b}$ for positive and negative voltages. The quadratic formulation did not yield significantly better models and so is not discussed here. The piecewise linear model reduced the matrix stiffness at higher voltages. This model's optimal rate constants are given in Table S5 in the SI Appendix.

Genetic Algorithm.

Models were ranked according to the squared error between the experimental data and the simulation results for the six different protocols described in the text. A final protocol was added to reduce the stiffness of the Q matrix by decreasing the ratio of the largest and smallest nonzero eigenvalues. A more complete description of the fitting protocols is provided in the supporting information online. In addition, the error value for a given model under the protocol being optimized was multiplied by 1 + (N/100), where N represents the number of directed edges; this penalty factor is used to favor models with simpler topologies in order to keep the size from growing without bound.

The genetic algorithm follows the goal-programming approach (22) to address the multiobjective nature of this optimization. Protocols are optimized sequentially; for any given run, only the error from a single protocol is optimized, with the constraint that the error from each previously optimized protocol remains within a certain tolerance. This tolerance was set at a value 10% above the lowest error found for each protocol.

After the population of models is ranked, some fraction of the worst models is replaced by “offspring” of existing models. To generate an offspring model, two parents are chosen by using tournament selection (42). If the parents have identical topologies, the offspring model is created by using a two-point cross-over on the parents' parameter vectors (42). If the parent topologies are different, new parents are selected until two with identical topologies are found. If 20 successive attempts to select parents are unsuccessful, the model is mutated instead of being replaced by an offspring model.

The remaining models in the population, with the exception of the best model, are mutated. Mutation consists of four possibilities:

1. Addition of an edge: Two existing states are randomly selected, and an edge is created between them. A pair of values (corresponding to the voltage-independent and -dependent portions of the sum of the logarithms of the transition rates) is drawn from a normal distribution and appended to the parameter vector. If the states happen to be connected already, then the algorithm adds a new state, as described below.

2. Subtraction of an edge: Two connected states are selected, and the edge between them is deleted. If, after edge subtraction, the topology consists of a disconnected graph, the segments not containing the open state are deleted. The corresponding pair(s) of values from the parameter vector are also removed.

3. Addition of a state: A new state is created and randomly connected to an existing state. Two pairs of values are drawn from a normal distribution and are added to the parameter vector: one set after the 2(M − 1 )th parameter (corresponding to the new state) and another set at the end of the parameter vector (corresponding to the new connecting edge).

4. Change of parameters: The topology is unchanged, but each parameter is altered with some mutation probability. This is the default mutation operation.

The genetic algorithm was run for 3,000 generations per protocol for seven different protocols by using the goal-programming approach, with a population size of 100 models per generation. The initial population was generated randomly and contained model topologies with between three and eight states. In each generation, the best model was carried over unchanged, 80% of the population was replaced by offspring, and the remaining models were mutated. The probabilities of edge addition, subtraction, and parameter mutation were 5%, 10%, and 7%. Parameters were mutated by using the formula p_new = p_old(1 + Z), with Z being a standard Gaussian random variable. We used 16 processors in a parallel cluster to speed up the optimization algorithm by having 15 slave processors evaluate the error for multiple individuals in the population.

Neuronal Simulations.

Multicompartmental simulations were carried out by using the NEURON software package (43). Two types of sodium conductance were used: the optimal channel model exhibiting prolonged-inactivation, and the model with only fast recovery from inactivation obtained by eliminating the prolonged-inactivation state. The amount of slowly inactivating sodium as a proportion of total sodium conductance varied from 0% at the soma to 100% in distal dendrites, reflecting the experimentally observed gradient of sodium channels exhibiting prolonged inactivation (16). Additional details associated with the compartmental models are provided in the SI Appendix.