Abstract
Study Design
Nondestructive displacement-controlled dynamic testing of cadaver material, with repeated measures design and randomized sequence of tests.
Objective
To determine whether the frequency-dependent changes in disc stiffness and phase angle between load and displacement differ between the 6 principal directions of displacement, and whether these differences are greater in deformation directions associated with greater intradiscal fluid flow.
Summary of Background Data
Prior studies of time-dependent behavior of discs have focused on compression. Comparing different deformation directions allows effects of fluid flow to be distinguished from effects of the solid phase viscoelasticity.
Methods
Vertebra-disc-vertebra preparations (N = 9) from human lumbar spines were subjected to each of 3 displacements and 3 rotations (6 degree of freedom) at each of 4 frequencies (0.001, 0.01, 0.1, and 1 Hz) after equilibration overnight under a 0.4 MPa preload in a bath of phosphate buffered saline at 37°C with protease inhibitors. The forces and torques were recorded along with the applied translation or rotation. The stiffness (force/displacement or torque/rotation) and the phase angle (between each force and displacement) were calculated for each degree of freedom from recorded data.
Results
Disc stiffness increased linearly with the log-frequency. The increases over the four decades of frequency were 35%, 33%, and 26% for AP shear, lateral shear, and torsion respectively, and were 45%, 29%, 51%, and 83% for compression, lateral bending, flexion, and extension. The phase angle (a measure of energy absorption) averaged 6.2, 5.1, and 5.1 degrees in AP shear, lateral shear, and torsion, respectively, and 7.0, 7.0, and 8.6 degrees for compression, lateral bending, and flexion-extension. There were no consistent variations of phase angle with frequency.
Conclusion
The stiffness increase and phase angle decrease with frequency were greater for deformation modes in which fluid flow effects are thought to be greater.
Keywords: intervertebral disc, biomechanics, frequency, six degree of freedom, poroelasticity, viscoelasticity
The intervertebral disc is a complex, composite structure that possesses both elastic (energy storing) and energy-absorbing properties.1,2 The time-dependent behavior may result from interactions between the solid phase and fluid flow (poroelasticity) and from intrinsic viscoelasticity in the solid phase itself. It is well established that the time-dependent behavior of articular cartilage derives from both the fluid-solid interactions (poroelasticity) and from intrinsic viscoelasticity in the solid phase.3–6 The strain-rate dependence of rabbit, human medial collateral, anterior cruciate, and human anterior longitudinal ligaments have been demonstrated.7–10 The time-dependent behavior of intervertebral disc and the relative contributions of the solid and fluid phases are less well understood.
The nucleus pulposus possesses both fluid and solid behavior,11–13 and anulus samples show nonlinear, anisotropic, and viscoelastic behavior.14–20 These findings for isolated disc tissue support the notion that the time-dependent behavior is highly dependent on the fluid content of tissue, and is likely to be determined by proteoglycan-proteoglycan and proteoglycan-collagen interactions that are strain-rate dependent. The resulting fluid flow promotes the transport of nutrients and solutes, and also provides shock absorption characteristics. However, there is little information in the literature regarding the strain-rate dependent effects on disc tissues. A study on the tensile mechanics of isolated human lamellas reported a small stiffening effect with increasing strain rate (0.1–10 mm/min).19 For whole discs, the compressive modulus of bovine discs was found to increase significantly with increasing loading rate (3 kPa/s–3 MPa/s),21 and the tensile and compressive modulus of young baboon cervical functional spinal units increased by at least 60% between slow and fast displacement rates (0.5–5000 mm/s).22,23 Cervical discs of pigs loaded to failure in compression over a range of loading rates (100, 1000, 3000, 10,000, and 16,000 N/s) significantly increased in stiffness at faster loading rates.24 Human discs showed increased compressive stiffness with increasing strain rate (6.8, 13.5, and 72.7 strain per second).25 However, compressive sinusoidal loading of human discs at 1 and 10 Hz indicated no difference in hysteresis loss energy.26
Although disc compressive stiffness increases with increasing strain rate, no studies reporting strain-rate dependency in other degrees of freedom (DOFs) were identified. Furthermore, there is very little information on how energy loss (hysteresis etc.) depends on the rate of loading or of deformation. The relative contributions of the fluid-solid phase effects (poroelasticity) and intrinsic solid phase viscoelasticity to this behavior are not known. Certain modes of deformation of the disc (such as compression and bending) are associated with internal pressure gradients producing fluid flow and poroelastic material behaviors, whereas others (such as torsion and shear) would have time-dependent behavior associated primarily with solid-phase deformation because volume change is small or negligible. Hence, by comparing the time-dependent deformation properties of the disc, one can identify the relative contributions of poroelasticity and solid matrix viscoelasticity in these time-dependent behaviors. An understanding of the nature of these contributions may be used to design/engineer intervertebral disc implants/tissue that behave more physiologically than current implants/tissue over a broad range of applied frequencies.
The overall purpose of this study was to measure the frequency-dependent stiffness and the phase angle between cyclic load and deformation (a measure of energy absorption) of human lumbar intervertebral discs in each of the 6 DOFs, and to determine whether these properties differ in those DOFs thought to be dominated by fluid-flow dependent behavior, relative to those DOFs thought to be dominated by solid-phase intrinsic viscoelastic behavior. We hypothesized that stiffness and phase angle would be significantly affected by cyclic frequency, and that there would be greater frequency dependence of these properties for those DOFs thought to exhibit predominantly poroelastic behavior, compared with those DOFs thought to be dominated by intrinsic viscoelastic behavior.
Materials and Methods
Specimen Preparation
Nine vertebra-disc-vertebra motion segments from 7 lumbar human spines were used in this study [5 males, 2 females, mean (SD) age: 41.9 (18.4) years, range: 16–60 years, levels: L1/L2 × 3, L2/L3 × 3, L3/L4 × 3, weight: 84.5 (20.8) kg). According to Thompson’s criteria for disc grade27 modified for transverse sections, 2 discs were grade 1, 5 were grade 3, and 1 each were grades 4 and 5 degeneration. Lumbar spines were thawed overnight at room temperature, after which all soft tissue was removed and carefully dissected around the disc and vertebral bodies. The transverse and spinous processes and zygapophysial joints were removed, while preserving the posterior and anterior longitudinal ligaments. Vertebral bodies were then embedded in cups using polymethylmethacrylate cement. A jig was used to align the axis of each specimen with the parallel cups. Axial, anteroposterior, and lateral radiographs were taken of each embedded specimen to identify the location of the center of the disc relative to the cups. This point was used as the center of rotation for the rotational tests described below. The embedded specimens were then sprayed with saline, wrapped in saline-soaked gauze and plastic wrap, sealed in air-tight plastic bags, and frozen at −80°C. On the day before testing, each specimen was removed from the freezer and thawed for a minimum of 3 hours at room temperature, while still in its sealed bag. The anteroposterior (AP) and lateral (LAT) major dimensions of the superior and inferior disc end-plates were measured 3 times each using a Vernier caliper and averaged, from which disc area was estimated using the formula: Area = 0.84 × AP × LAT.28
Testing Protocol
For testing, each specimen was placed in an acrylic fluid-filled bath and attached to the platens of a custom-made 6 DOF hexapod robot.29 The vertebra-disc-vertebra segment was aligned with the hexapod’s axes (+x = anterior, +y = left lateral, and +z = superior). The bath was filled with 0.15 M phosphate buffered saline with protease inhibitors added to reduce putrefaction and tissue autolysis (1 mmol/L ethylenedia-minetetraacetic acid (EDTA), 1 mmol/L iodoacetamide, 1 μg/mL pepstatin-A, and 1 mmol/L benzamadine). An axial compressive external preload of 0.4 MPa30,31 was then applied to the disc and maintained using load control for approximately 16 hours overnight in a saline bath at 37°C to allow the disc fluid content to reach equilibrium.32 The saline bath at 37°C was used throughout testing because studies have shown that viscoelastic tissue properties differ with temperature26,33–35 and differ with fluid immersion.21,36
After overnight equilibration, each vertebra-disc-vertebra segment was subjected to dynamic sinusoidal displacements/rotations in each of 6 DOF in random sequence. The amplitudes of the displacements were: axial compression ±0.25 mm; anteroposterior/lateral shear ±0.6 mm; flexion-extension ±2 degrees; lateral bending ±3 degrees; and axial rotation ±2 degrees. Each was applied at each of 4 frequencies (0.001, 0.01, 0.1, and 1 Hz). Ten cycles were applied for the 1 and 0.1 Hz tests, 5 cycles for the 0.01 Hz test, and 2 cycles for the 0.001 Hz test. Four decades of frequencies were applied to cover the most likely range of physiologic displacement/rotation rates at the same time promoting fluid-flow behavior or intrinsic viscoelastic behavior. The 2 faster frequencies (0.1 and 1 Hz) represent approximate physiologic walking speeds. The 2 slower frequencies (0.001 and 0.01 Hz) represent sitting/office work activities, employing quasistatic frequencies, aimed at elucidating poroelastic tissue behavior where fluid flow mechanisms are thought to dominate disc behavior over intrinsic viscoelastic behavior. An initial axial preload of 0.4 MPa was applied during all tests. A period of re-equilibration with the 0.4 MPa preload was included after the slower frequency tests in loading directions thought to induce large fluid-flow (axial compression, flexion/extension, and lateral bending). The duration of the recovery period was 30 minutes after axial compression at 0.001 Hz, 10 minutes for the 0.01 Hz frequency, and 5 minutes after the 0.1 Hz tests. Five minutes of recovery were allowed for the remaining DOFs and frequencies. Pilot studies showed that 5 minutes of creep recovery at 0.4 MPa in compression were sufficient to return the disc to its original equilibrium hydration level. The data sampling rate was 128 Hz for the 1 Hz test, 32 Hz for the 0.1 Hz test, and 2 Hz for the 2 slowest frequencies. The testing order for each DOF and frequency was randomized for each specimen. The total duration for the equilibration and testing was approximately 44 hours for each disc.
Data and Statistical Analyses
All data were analyzed using custom programs written in Matlab R2007a (The Mathworks Inc., Natick, MA). Recorded data were imported into Matlab as columns representing time, 3 displacements (Tx, Ty, Tz), 3 rotations (Rx, Ry, Rz), 3 forces (Fx, Fy, Fz), and 3 moments (Mx, My, Mz). Recordings were first partitioned into cycles representing the applied sinusoidal displacements/rotations. Data from the second to final cycles were analyzed. Data for DOFs not symmetrical about the coronal plane, i.e., anterior/posterior shear (±Tx), compression (−Tz), flexion (+Ry), and extension (−Ry), were analyzed separately for each direction. Data for symmetrical DOFs, i.e., lateral shear (Ty), lateral bending (Rx), and axial rotation (Rz) were not separated.
Stiffnesses for each frequency were calculated using linear regression over the entire load/unload cyclic data for the symmetrical DOFs and separately for the load/unload sections of the recorded data for the asymmetrical DOFs. Phase angles for each frequency were calculated between the input displacements/rotations and measured forces/moments using the cross spectral density estimate function (Matlab: CSD m) for each of 6 DOFs (Tx, Ty, Tz, Rx, Ry, and Rz).
To address the hypothesis that poroelastic DOFs exhibit significantly greater frequency-dependent effects compared with intrinsic viscoelastic DOFs, the DOFs were divided into 2 groups. Group 1 represented those expected to have large poroelastic (fluid flow) effects (compression, lateral bending, flexion, and extension), and group 2 represented those DOFs that were expected to exhibit primarily intrinsic (solid phase) viscoelastic behavior (anterior/posterior/lateral shear and axial rotation). For comparisons between different DOFs, stiffnesses and phase angles for each DOF were normalized and expressed as percentage change relative to 0.001 Hz for the other frequencies.
Separate repeated measures ANOVAs were performed for each DOF, and then between group 1 and group 2 each for stiffness and phase angle. Significant differences were accepted when P < 0.05 (2-tailed), and a Bonferroni adjustment was used for all statistical post hoc pairwise multiple comparisons.
Results
Loss of some recordings because of technical errors during testing reduced the repeated measures dataset to between 6 and 9 specimens (Table 1). No obvious signs of tissue putrefaction were noticed, and the disc tissue appeared to be in good condition at the end of the testing period.
Table 1.
Mean (95% Confidence Interval) Stiffnesses for Each Degree of Freedom and Frequency
| Freq. (Hz) | Ant. Shear (N = 7) | Post. Shear (N = 7) | Lat. Shear (N = 9) | Compr. (N = 7) | Lat. Bend (N = 7) | Flex. (N = 6) | Ext. (N = 6) | Ax. Rot. (N = 9) |
|---|---|---|---|---|---|---|---|---|
| 0.001 | 127 (42) | 151 (56) | 252 (162) | 3513 (612) | 3.4 (1.5) | 2.3 (2.2) | 2.1 (1.6) | 2.3 (0.6) |
| 0.01 | 148 (45) | 171 (59) | 284 (172) | 4306 (836) | 3.8 (1.5) | 2.8 (2.4) | 2.8 (2.0) | 2.6 (0.7) |
| 0.1 | 157 (47) | 181 (62) | 299 (183) | 4737 (1008) | 4.1 (1.6) | 3.0 (2.5) | 3.0 (2.1) | 2.7 (0.7) |
| 1 | 171 (49) | 190 (61) | 318 (189) | 5141 (1106) | 4.6 (2.1) | 3.3 (2.9) | 3.5 (2.4) | 2.9 (0.8) |
| P | 0.002 | <0.001 | 0.002 | <0.001 | 0.025 | 0.043 | 0.094 | <0.001 |
P from repeated measures ANOVA analyses for the overall effect of frequency on each degree of freedom are also shown. Units for translation stiffnesses are N/mm, and Nm/degree for rotation stiffnesses.
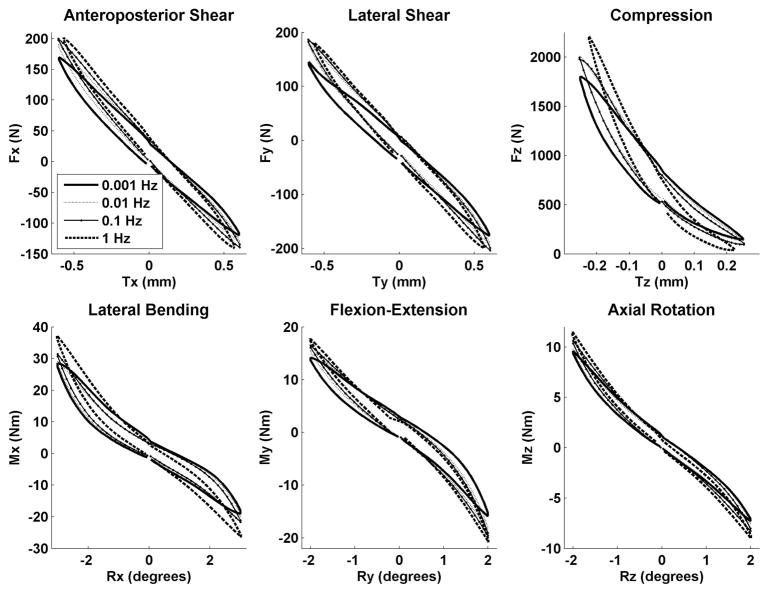
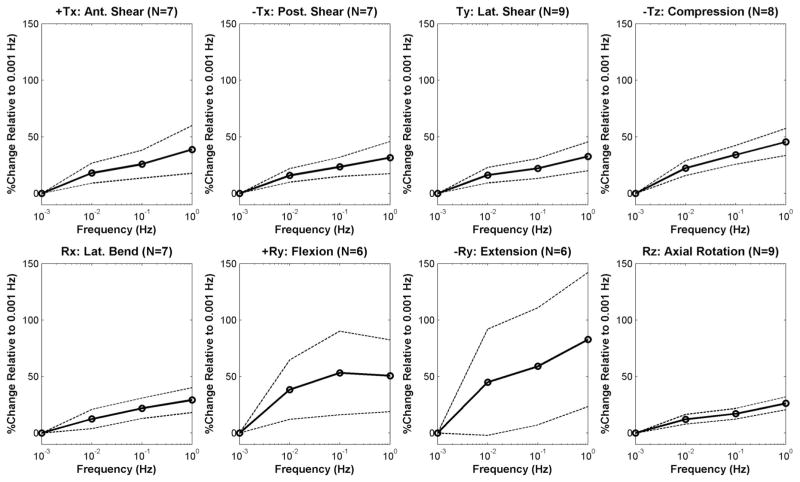
Nonlinear and frequency-dependent behavior was evident in all degrees of freedom (Figure 1). The mean stiffnesses increased monotonically with frequency in most cases relative to 0.001 Hz for each DOF and frequency, with mean percentage stiffness increases at 1 Hz, compared with 0.001 Hz between 26% and 39% for the shear translations and axial rotation, and between 29% to 83% for compression and bending (Figures 2 and 3 and Table 1). The stiffness significantly increased with increasing frequency in almost all DOFs (P < 0.04), apart from extension (P = 0.09, Table 1). Significant post hoc differences existed between all frequencies for anterior and posterior shear (P < 0.05), and the majority of frequency permutations for lateral shear (P < 0.03, apart for between 0.1 and 0.01 Hz, P = 0.2), and compression (P < 0.05, apart for between 0.1 and 1 Hz, P = 0.5). Despite having a significant overall main effect due to frequency, no significant post hoc differences existed between frequency permutations for flexion (P > 0.1), axial rotation (P < 0.04), and lateral bending (P > 0.1, except for between 0.001 and 0.1 Hz, P = 0.02).
Figure 1.
Recorded data for 1 typical specimen for each frequency and each of 6 DOFs smoothed and averaged by fitting to a third-order polynomial to several cycles of data.
Figure 2.
Mean percentage change in stiffness relative to 0.001 Hz values, plotted as a function of frequency for each DOF (dashed lines = 95% confidence interval).
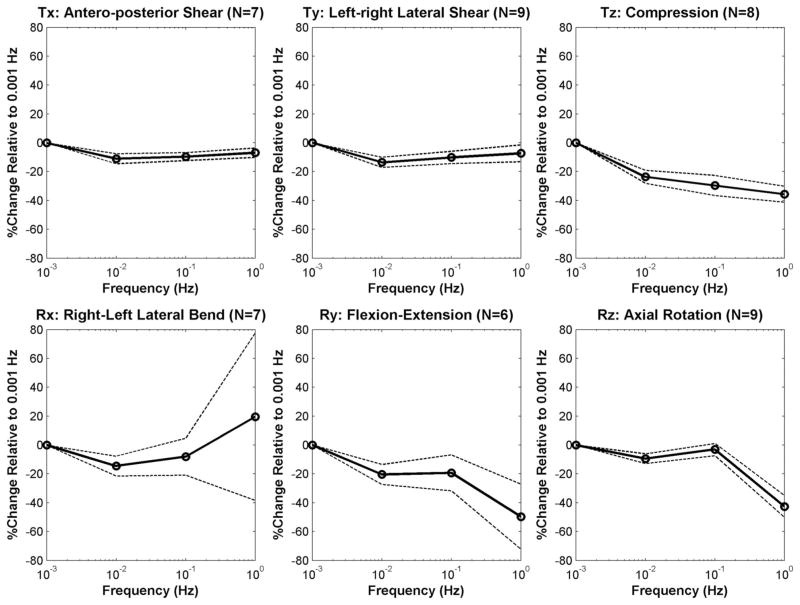
Figure 3.
Mean percentage change in phase angle relative to 0.001 Hz values, plotted as a function of frequency for each DOF (dashed lines = 95% confidence interval).
The phase angle significantly decreased overall with increasing frequency in all DOFs (P < 0.01), except for lateral bending (P = 0.4, Table 2). Mean percentage decreases in phase angle over the 4 decades were approximately 7% for lateral and anteroposterior shears, 43% for axial rotation, 20% for lateral bending, 50% for flexion-extension, and 36% for compression. In compression, significant (P < 0.01) differences were identified by post hoc tests between most frequency permutations (exceptions were between 0.1 and 0.01 Hz/1 Hz, P > 0.06). Similarly, in axial rotation, there were significant differences (P < 0.01) except for between 0.1 and 0.001 Hz (P = 1). In flexion-extension, no significant differences were found between frequency permutations (P > 0.07), and in shear DOFs, there were no significant differences between most frequency permutations except between 0.001 and 0.01 Hz/0.1 Hz (P < 0.03).
Table 2.
Mean (95% Confidence Interval) Phase Angles for Each Degree of Freedom and Frequency
| Freq. (Hz) | Ant. Post. Shear (N = 7) | Lat. Shear (N = 9) | Compr. (N = 8) | Lat. Bend (N = 6) | Flex-Ext. (N = 6) | Ax. Rot. (N = 9) |
|---|---|---|---|---|---|---|
| 0.001 | 6.6 (2.4) | 5.5 (1.7) | 9.0 (1.3) | 7.5 (2.1) | 11.2 (2.7) | 5.9 (0.9) |
| 0.01 | 5.9 (2.1) | 4.8 (1.4) | 6.8 (1.0) | 6.3 (1.6) | 8.8 (1.8) | 5.4 (0.9) |
| 0.1 | 6.0 (2.2) | 5.0 (1.6) | 6.3 (0.9) | 6.6 (1.0) | 8.8 (1.8) | 5.7 (1.0) |
| 1 | 6.1 (2.2) | 5.2 (1.8) | 5.7 (0.6) | 7.7 (1.8) | 5.4 (2.5) | 3.4 (0.6) |
| P | 0.001 | 0.005 | <0.001 | 0.426 | 0.008 | <0.001 |
P from repeated measures ANOVA analyses for the overall effect of frequency on each degree of freedom are also shown. Units for phase angle are in degrees.
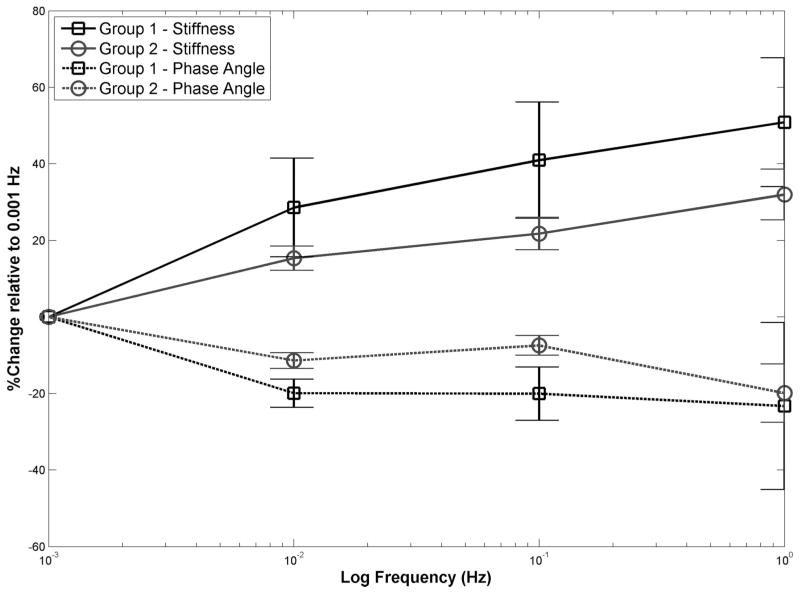
Comparison of stiffness and phase angle for those DOFs thought to exhibit predominantly poroelastic behavior (group 1) with those DOFs thought to be dominated by intrinsic viscoelastic behavior (group 2) revealed a significant groupwise difference for stiffness (P = 0.02) but only marginally significant differences for phase angle (P = 0.08) (Figure 4). For stiffness, post hoc multiple comparisons between the 2 groups at each frequency revealed that group 1 exhibited larger percentage changes compared to group 2 (P < 0.04). Post hoc multiple comparisons for phase angles revealed that the group 1 percentage changes were significantly larger than group 2 changes at 0.01 and 0.1 Hz (P < 0.002) but not at 1 Hz (P = 0.8).
Figure 4.
Mean stiffnesses and phase angles plotted as a percentage of those at 0.001 Hz as a function of frequency for group 1 DOFs (those thought to be dominated by poroelastic behavior) and group 2 DOFs (those thought to be dominated by intrinsic viscoelastic behavior) (error bars = 95% confidence interval).
Discussion
The stiffness of the vertebra-disc-vertebra specimens significantly increased with increasing frequency, and phase angle significantly decreased for most DOFs. Those DOFs, believed to be responsible for poroelastic (fluid-flow) behavior (group 1), had significantly greater increase in stiffness than those DOFs thought to be dominated by intrinsic viscoelastic solid matrix behavior (group 2). This supports the contention that both poroelasticity and viscoelasticity contribute to the time-dependent behavior in the tested frequency range. It is not possible to distinguish between the relative contributions of the poroelastic and viscoelastic effects by examination of the variations with frequency in a single degree of freedom.
The greater apparent stiffness and lesser energy loss at higher frequencies were demonstrated to result from both fluid flow effects and solid phase viscoelastic effects to a degree that depends on the amplitude of the relative solid/fluid flow velocity and the solid strains, respectively, and the associated physical properties and time constants. The distinct relationship defining the mechanism for viscoelasticity is degree of freedom dependent, but the normalized changes allow general distinction between the poroelasticity and solid matrix viscoelasticity mechanisms. In these displacement-controlled experiments, a first-order approximation for complex loading conditions (e.g., bending and twisting) may be obtained through superposition.
Despite substantial decreases with increasing frequency of 23% to 50%, the phase angle was always less than 12 degrees, indicating that the disc behaves predominantly as an elastic material across all frequencies tested.
The deformation mechanics of discs is very complex. Internal pressure produces stresses that cause bulging of endplates and anulus, and fluid flow within the disc tissue, and across the boundaries at the endplates and around the periphery of the disc. The exact pattern of relative fluid/solid displacement cannot be readily determined, especially when considering the complex composite materials and unique geometry of the disc. However, some simplifications are relevant, and in this study, it was assumed that minimal pressure gradients are produced in pure shear and in torsion; hence, the flow effects would be very small at all frequencies for those degrees of freedom. Conversely, compression, lateral bending, flexion, and extension were expected to produce pressure gradients and fluid flow particularly as frequency increased. This simplifying assumption was generally supported because poroelastic degrees of freedom had the largest increases in stiffness with frequency (83% for extension, 51% for flexion, and 45% for compression).
Prior studies of time-dependent properties of the intervertebral disc have focused on compression behavior only. Some report cyclic load, others ramp loading at differing rates. For the compression DOF, some qualitative comparisons can be made by transforming the frequencies used in the present study to a loading rate (N/s), stress rate (MPa/s), displacement rate (mm/s), and strain-rate (strain/s), as listed in Table 3. The apparent compressive moduli of bovine discs tested from 3 kPa/s to 3 MPa/s by Race et al21 were greater than that at 3 kPa/s by 104%, 196%, and 256%. The slowest rate was comparable to the 0.001 Hz frequency in the present study, but the stiffness increases were approximately 6 times larger than those observed here. One possible reason for this 6-fold difference may be the higher loads used by Race et al because nonlinear elasticity and strain-dependent permeability effects would both increase stiffness with preload.37 We used a preload of 0.4 MPa and applied no more than 1 MPa of stress to the discs, whereas Race et al21 used a preload of 1 MPa and applied compression up to 1.5 MPa. Geometric and species differences may also contribute to the differences.
Table 3.
Estimated Conversion of Sinusoidal Frequencies From the Compression Test Data of the Present Study to Loading-, Stress-, Displacement-, and Strain-Rates Used for Comparison With Other Studies
| Freq. (Hz) | Average Max. Applied Compressive Load (N) | Average Max. Applied Stress (MPa) | Average Modulus (MPa) | Loading Rate (N/s) | Stress Rate (kPa/s) | RMS Displ. Rate (mm/s) | RMS Strain Rate (strain/s) |
|---|---|---|---|---|---|---|---|
| 0.001 | 878 | 0.59 | 23.6 | 3.5 | 2.3 | 0.0011 | 0.00011 |
| 0.01 | 1077 | 0.72 | 28.8 | 43.1 | 29 | 0.011 | 0.0011 |
| 0.1 | 1184 | 0.78 | 31.2 | 474 | 316 | 0.111 | 0.011 |
| 1 | 1285 | 0.86 | 34.4 | 5140 | 3430 | 1.11 | 0.111 |
Compressive stiffnesses from Table 1 were used to estimate the average maximum applied compressive load at a compressive displacement of 0.25 mm. An average disc area of 1500 mm2 was assumed for average maximum applied stress calculations, and an average disc height of 10 mm after overnight preload equilibration was used for strain calculations. Root mean square (RMS) values are presented as approximations for displacement and strain rates because the strain rate for a sine wave is not constant.
A relative percentage change of 9% in stiffness of porcine cervical discs subjected to compressive loading at rates of 100 and 1000 N/s by Yingling et al24 compares closely to the finding from the present study (8.5%). These rates were equivalent in magnitude to our frequencies of 0.1 and 1 Hz (Table 3). Yingling et al24 also tested at loading rates of 3000, 10,000, and 16,000 N/s to simulate injury rates and found a 54% increase in stiffness at 3000 N/s compared with 100 N/s, but no further increases in stiffness as loading rate continued to increase.
The testing conditions were intended to simulate in vivo conditions. Discs were hydrated in a physiologic phosphate buffered saline bath with protease inhibitors added to minimize autolysis and putrefaction; the disc fluid content was kept constant by the application of a 0.4-MPa preload that is within the in vivo measured range; the disc fluid content was allowed to re-equilibrate between tests. Testing was performed at the temperature of 37°C in a physiologic saline bath. The tested discs were relatively young discs that were disease free, but most discs had moderate degeneration and 2 discs had very severe degeneration. The testing was performed under displacement control with ranges of motion that were known to be well within physiologic limits to avoid damaging the discs.
This study provides substantial data on frequency-dependent behaviors of human discs under 6 DOF loading conditions and demonstrated that DOF was more important than loading frequency in determining stiffness and phase angle behaviors. This study also demonstrated that both poroelastic and solid matrix viscoelasticity exist in the disc under simulated physiologic loading and suggests their relative contributions may be partly distinguished based on general degree of freedom considerations. This information is important in understanding normal function and disease processes, and in designing synthetic and engineered tissues for treating diseased or injured discs. The clinical significance of this work becomes apparent when one considers the application of this knowledge to tissue engineering, implant design (nucleus replacement), and future repair/regeneration therapies. The stiffening effect with increasing frequency in each of the 6 DOFs, and the fluid-flow frequency-dependent behavior, which is more predominant in compression and bending DOFs, should be taken into account to engineer and design more “disc-like” materials and implants.
Key Points
The time-dependent energy storage and energy absorption by intervertebral discs results from both flow-dependent solid-fluid interactions (poroelasticity) and intrinsic (solid phase) viscoelasticity.
Prior studies of time-dependent behavior of discs have focused on compression alone. Comparing different deformation directions allows effects of fluid flow to be distinguished from effects of the solid phase viscoelasticity.
Deformational degree of freedom was more important than loading frequency in determining stiffness and phase angle of the disc.
The stiffness increase and phase angle decrease with frequency found in this study were greater for deformation modes in which fluid flow effects are thought to be greater.
Acknowledgments
The authors thank Jake R. Lubinski for technical assistance and National Disease Research Interchange (NDRI) for supply of human cadaver lumbar spines. The authors also thank the National Institutes of Health for providing funding (R01 AR049370), the National Disease Research Interchange (NDRI) for supply of human cadaver lumbar spines, and Jake R. Lubinski for technical assistance.
Supported by National Institutes of Health Grant R01 AR049370. The manuscript submitted does not contain information about medical device(s)/drug(s).
Federal funds were received in support of this work. No benefits in any form have been or will be received from a commercial party related directly or indirectly to the subject of this manuscript.
References
- 1.Huyghe JM, Houben GB, Drost MR, et al. An ionised/non-ionised dual porosity model of intervertebral disc tissue. Biomech Model Mechanobiol. 2003;2:3–19. doi: 10.1007/s10237-002-0023-y. [DOI] [PubMed] [Google Scholar]
- 2.Iatridis JC, Laible JP, Krag MH. Influence of fixed charge density magnitude and distribution on the intervertebral disc: applications of a poroelastic and chemical electric (PEACE) model. J Biomech Eng. 2003;125:12–24. doi: 10.1115/1.1537190. [DOI] [PubMed] [Google Scholar]
- 3.Hayes WC, Bodine AJ. Flow-independent viscoelastic properties of articular cartilage matrix. J Biomech. 1978;11:407–19. doi: 10.1016/0021-9290(78)90075-1. [DOI] [PubMed] [Google Scholar]
- 4.Mow VC, Huiskes R, editors. Basic Orthopaedic Biomechanics and Mechano-Biology. 3. Philadelphia: Lippincott Williams & Wilkins; 2005. [Google Scholar]
- 5.Mow VC, Kuei SC, Lai WM, et al. Biphasic creep and stress relaxation of articular cartilage in compression? Theory and experiments. J Biomech Eng. 1980;102:73–84. doi: 10.1115/1.3138202. [DOI] [PubMed] [Google Scholar]
- 6.Mak AF. The apparent viscoelastic behavior of articular cartilage–the contributions from the intrinsic matrix viscoelasticity and interstitial fluid flows. J Biomech Eng. 1986;108:123–30. doi: 10.1115/1.3138591. [DOI] [PubMed] [Google Scholar]
- 7.Woo SL, Peterson RH, Ohland KJ, et al. The effects of strain rate on the properties of the medial collateral ligament in skeletally immature and mature rabbits: a biomechanical and histological study. J Orthop Res. 1990;8:712–21. doi: 10.1002/jor.1100080513. [DOI] [PubMed] [Google Scholar]
- 8.Danto MI, Woo SL. The mechanical properties of skeletally mature rabbit anterior cruciate ligament and patellar tendon over a range of strain rates. J Orthop Res. 1993;11:58–67. doi: 10.1002/jor.1100110108. [DOI] [PubMed] [Google Scholar]
- 9.Bonifasi-Lista C, Lake SP, Small MS, et al. Viscoelastic properties of the human medial collateral ligament under longitudinal, transverse and shear loading. J Orthop Res. 2005;23:67–76. doi: 10.1016/j.orthres.2004.06.002. [DOI] [PubMed] [Google Scholar]
- 10.Neumann P, Keller TS, Ekstrom L, et al. Effect of strain rate and bone mineral on the structural properties of the human anterior longitudinal ligament. Spine. 1994;19:205–11. doi: 10.1097/00007632-199401001-00016. [DOI] [PubMed] [Google Scholar]
- 11.Iatridis JC, Weidenbaum M, Setton LA, et al. Is the nucleus pulposus a solid or a fluid? Mechanical behaviors of the nucleus pulposus of the human intervertebral disc. Spine. 1996;21:1174–84. doi: 10.1097/00007632-199605150-00009. [DOI] [PubMed] [Google Scholar]
- 12.Iatridis JC, Setton LA, Weidenbaum M, et al. The viscoelastic behavior of the non-degenerate human lumbar nucleus pulposus in shear. J Biomech. 1997;30:1005–13. doi: 10.1016/s0021-9290(97)00069-9. [DOI] [PubMed] [Google Scholar]
- 13.Leahy JC, Hukins DW. Viscoelastic properties of the nucleus pulposus of the intervertebral disk in compression. J Mater Sci Mater Med. 2001;12:689–92. doi: 10.1023/a:1011212425029. [DOI] [PubMed] [Google Scholar]
- 14.Ebara S, Iatridis JC, Setton LA, et al. Tensile properties of nondegenerate human lumbar anulus fibrosus. Spine. 1996;21:452–61. doi: 10.1097/00007632-199602150-00009. [DOI] [PubMed] [Google Scholar]
- 15.Acaroglu ER, Iatridis JC, Setton LA, et al. Degeneration and aging affect the tensile behavior of human lumbar anulus fibrosus. Spine. 1995;20:2690–701. doi: 10.1097/00007632-199512150-00010. [DOI] [PubMed] [Google Scholar]
- 16.Elliott DM, Setton LA. Anisotropic and inhomogeneous tensile behavior of the human anulus fibrosus: experimental measurement and material model predictions. J Biomech Eng. 2001;123:256–63. doi: 10.1115/1.1374202. [DOI] [PubMed] [Google Scholar]
- 17.Galante JO. Tensile properties of the human lumbar annulus fibrosus. Acta Orthop Scand. 1967;(suppl 100):1–91. doi: 10.3109/ort.1967.38.suppl-100.01. [DOI] [PubMed] [Google Scholar]
- 18.Fujita Y, Duncan NA, Lotz JC. Radial tensile properties of the lumbar annulus fibrosus are site and degeneration dependent. J Orthop Res. 1997;15:814–9. doi: 10.1002/jor.1100150605. [DOI] [PubMed] [Google Scholar]
- 19.Holzapfel GA, Schulze-Bauer CA, Feigl G, et al. Single lamellar mechanics of the human lumbar anulus fibrosus. Biomech Model Mechanobiol. 2005;3:125–40. doi: 10.1007/s10237-004-0053-8. [DOI] [PubMed] [Google Scholar]
- 20.Skaggs DL, Weidenbaum M, Iatridis JC, et al. Regional variation in tensile properties and biochemical composition of the human lumbar anulus fibrosus. Spine. 1994;19:1310–9. doi: 10.1097/00007632-199406000-00002. [DOI] [PubMed] [Google Scholar]
- 21.Race A, Broom ND, Robertson P. Effect of loading rate and hydration on the mechanical properties of the disc. Spine. 2000;25:662–9. doi: 10.1097/00007632-200003150-00003. [DOI] [PubMed] [Google Scholar]
- 22.Nuckley DJ, Hertsted SM, Eck MP, et al. Effect of displacement rate on the tensile mechanics of pediatric cervical functional spinal units. J Biomech. 2005;38:2266–75. doi: 10.1016/j.jbiomech.2004.09.021. [DOI] [PubMed] [Google Scholar]
- 23.Elias PZ, Nuckley DJ, Ching RP. Effect of loading rate on the compressive mechanics of the immature baboon cervical spine. J Biomech Eng. 2006;128:18–23. doi: 10.1115/1.2133767. [DOI] [PubMed] [Google Scholar]
- 24.Yingling VR, Callaghan JP, McGill SM. Dynamic loading affects the mechanical properties and failure site of porcine spines. Clin Biomech (Bristol, Avon) 1997;12:301–5. doi: 10.1016/s0268-0033(97)00009-0. [DOI] [PubMed] [Google Scholar]
- 25.Kemper AR, McNally C, Duma SM. The influence of strain rate on the compressive stiffness properties of human lumbar intervertebral discs. Biomed Sci Instrum. 2007;43:176–81. [PubMed] [Google Scholar]
- 26.Koeller W, Meier W, Hartmann F. Biomechanical properties of human intervertebral discs subjected to axial dynamic compression. A comparison of lumbar and thoracic discs. Spine. 1984;9:725–33. doi: 10.1097/00007632-198410000-00013. [DOI] [PubMed] [Google Scholar]
- 27.Thompson JP, Pearce RH, Schechter MT, et al. Preliminary evaluation of a scheme for grading the gross morphology of the human intervertebral disc. Spine. 1990;15:411–5. doi: 10.1097/00007632-199005000-00012. [DOI] [PubMed] [Google Scholar]
- 28.Nachemson AL, morris JM. In vivo measurements of intradiscal pressure. Discometry, a method for the determination of pressure in the lower lumbar discs. J Bone Joint Surg Am. 1964;46:1077–92. [PubMed] [Google Scholar]
- 29.Stokes IA, Gardner-Morse M, Churchill D, et al. Measurement of a spinal motion segment stiffness matrix. J Biomech. 2002;35:517–21. doi: 10.1016/s0021-9290(01)00221-4. [DOI] [PubMed] [Google Scholar]
- 30.Wilke HJ, Neef P, Caimi M, et al. New in vivo measurements of pressures in the intervertebral disc in daily life. Spine. 1999;24:755–62. doi: 10.1097/00007632-199904150-00005. [DOI] [PubMed] [Google Scholar]
- 31.Nachemson A. Towards a better understanding of low-back pain: a review of the mechanics of the lumbar disc. Rheumatol Rehabil. 1975;14:129–43. doi: 10.1093/rheumatology/14.3.129. [DOI] [PubMed] [Google Scholar]
- 32.Pflaster DS, Krag MH, Johnson CC, et al. Effect of test environment on intervertebral disc hydration. Spine. 1997;22:133–9. doi: 10.1097/00007632-199701150-00003. [DOI] [PubMed] [Google Scholar]
- 33.Hasberry S, Pearcy MJ. Temperature dependence of the tensile properties of interspinous ligaments of sheep. J Biomed Eng. 1986;8:62–6. doi: 10.1016/0141-5425(86)90032-4. [DOI] [PubMed] [Google Scholar]
- 34.Woo SL, Lee TQ, Gomez MA, et al. Temperature dependent behavior of the canine medial collateral ligament. J Biomech Eng. 1987;109:68–71. doi: 10.1115/1.3138645. [DOI] [PubMed] [Google Scholar]
- 35.Lam TC, Thomas CG, Shrive NG, et al. The effects of temperature on the viscoelastic properties of the rabbit medial collateral ligament. J Biomech Eng. 1990;112:147–52. doi: 10.1115/1.2891165. [DOI] [PubMed] [Google Scholar]
- 36.Costi JJ, Hearn TC, Fazzalari NL. The effect of hydration on the stiffness of intervertebral discs in an ovine model. Clin Biomech (Bristol, Avon) 2002;17:446–55. doi: 10.1016/s0268-0033(02)00035-9. [DOI] [PubMed] [Google Scholar]
- 37.Gardner-Morse MG, Stokes IA. Physiological axial compressive preloads increase motion segment stiffness, linearity and hysteresis in all six degrees of freedom for small displacements about the neutral posture. J Orthop Res. 2003;21:547–52. doi: 10.1016/S0736-0266(02)00199-7. [DOI] [PubMed] [Google Scholar]