Protein Dynamics from NMR: The Slowly Relaxing Local Structure Analysis Compared with Model-Free Analysis

Abstract

¹⁵N-¹H spin relaxation is a powerful method for deriving information on protein dynamics. The traditional method of data analysis is model-free (MF), where the global and local N-H motions are independent and the local geometry is simplified. The common MF analysis consists of fitting single-field data. The results are typically field-dependent, and multi-field data cannot be fit with standard fitting schemes. Cases where known functional dynamics has not been detected by MF were identified by us and others. Recently we applied to spin relaxation in proteins the Slowly Relaxing Local Structure (SRLS) approach which accounts rigorously for mode-mixing and general features of local geometry. SRLS was shown to yield MF in appropriate asymptotic limits. We found that the experimental spectral density corresponds quite well to the SRLS spectral density. The MF formulae are often used outside of their validity ranges, allowing small data sets to be force-fitted with good statistics but inaccurate best-fit parameters. This paper focuses on the mechanism of force-fitting and its implications. It is shown that MF force-fits the experimental data because mode-mixing, the rhombic symmetry of the local ordering and general features of local geometry are not accounted for. Combined multi-field multi-temperature data analyzed by MF may lead to the detection of incorrect phenomena, while conformational entropy derived from MF order parameters may be highly inaccurate. On the other hand, fitting to more appropriate models can yield consistent physically insightful information. This requires that the complexity of the theoretical spectral densities matches the integrity of the experimental data. As shown herein, the SRLS densities comply with this requirement.

I. Introduction

NMR is currently the most powerful method for studying protein dynamics at the residue level.^1-3 The commonly used dynamic probe is the ¹⁵N-¹H bond. The relaxation parameters ¹⁵N T₁, T₂ and ¹⁵N-¹{H} NOE are measured experimentally at one or several magnetic fields. Their expressions are given by the spectral densities, J(ω), and the relevant magnetic interactions (¹⁵N-¹H dipolar and the ¹⁵N CSA).^4,5 The functions J(ω) are determined by the dynamic model used, and the local geometry at the N-H site.

The traditional method of data analysis is the model-free (MF) approach.^6-8 MF assumes that the global motion of the protein (R^C = 1/6τ_m) and local motion of the N-H bond (R^L = 1/6τ^L) are ‘independent’ or ‘decoupled’, by virtue of the former being much slower than the latter (τ_m ≫ τ^L). The local ordering is measured by a squared generalized order parameter, S², and the rate of local motion is evaluated by an effective correlation time, τ_e. Both parameters represent mathematical properties of the spectral density. The local geometry is simplified, with the ordering and magnetic tensor frames axial and collinear.

Three point (¹⁵N T₁, T₂ and ¹⁵N-{¹H} NOE) data acquired at a single magnetic field pertaining to structured regions of the protein backbone can be usually analyzed with optimization (data fitting) methods using the original MF formula.^6,7 Flexible residues residing in loops and mobile domains required the development of the extended MF formula.⁸ The latter features a fast effective local motion, τ_f, associated with a generalized squared order parameter, S_f², and a slow effective local motion, τ_s, associated with a generalized squared order parameter, S_s². All the modes are assumed to be independent, i.e., τ_m ≫ τ_f, τ_m ≫ τ_s, and τ_s ≫ τ_f.

The MF order parameters including the global motion correlation time, τ_m, are typically found to be field-dependent. This means that combined multi-field data sets cannot be fit with standard fitting schemes unless some data are excluded.⁹ Small anisotropies in the global diffusion tensor were found to have a very large effect on the analysis.¹⁰ Non-normal t-distribution of NOE's was detected.¹¹ The temperature-dependence of MF order parameters was found to be unduly small.^12,13 The local motion was found to be practically independent of temperature and/or experimentally measured viscosity,^14-16 contrary to expectations based on typical activation energies for motions in flexible molecules. In some cases experimental relaxation parameters exceeded the extreme theoretical values.^13,17 Combined analysis of N-H bond dynamics and C′-C^α bond dynamics yielded inconsistent results.^13,18 We found that known functional dynamics in adenylate kinase from E. Coli is not detected with MF analysis.^19,20 Similar observations were made by other workers in the field.²¹

These shortcomings are usually rationalized by invoking data imperfection. Alternatively the simplicity of the MF analysis may be the main underlying reason. This option can be tested by analyzing the same data with an improved version of the theory, where the simplifying MF assumptions related to liquid dynamics and local geometry are no longer invoked. This was accomplished by applying to spin relaxation in proteins²² the Slowly Relaxing Local Structure (SRLS) approach of Freed et al.^23-25 which can be considered a generalized version of MF. Rather than assuming mode-independence SRLS accounts rigorously for mode-mixing through a local potential. The latter represents the spatial restrictions on N-H motion which in MF are expressed by a squared generalized order parameter. Genuine axial and rhombic order parameters are defined in SRLS in terms of the local potential. Unlike MF, SRLS allows for a full range of time scale separation between the local and global motions (e.g., they can be comparable). The magnitude, symmetry and orientation of the ordering, diffusion and magnetic tensors are all allowed to vary. In general SRLS features pure and mixed local and global dynamic modes. In the appropriate asymptotic limit it yields the pure-mode (or mode-independent) MF formulae.

Experimental ¹⁵N relaxation data were subjected in parallel to SRLS (exact solution) and MF (asymptotic solution) analyses.^{19,20,22,26,27} Significant improvement on many of the issues mentioned above was obtained with SRLS analysis. The goodness of fit was similar to, but the best-fit parameters significantly different from, the MF counterparts. Given that the more general SRLS contains MF as a special case, this indicates that the experimental data correspond to the general SRLS solution rather than the asymptotic MF solution. It also indicates that it is the simplicity of MF, rather than experimental imperfections, that underlie the inconsistencies mentioned above. That a similar quality of fit was obtained is related to the fitting process involving specific values of J(ω) which enter the expressions for T₁, T₂ and the NOE.^4,5 The process whereby an oversimplified spectral density yields inaccurate best-fit parameters with good statistics is called ‘force-fitting’.

Let us point out the asymptotic nature of the MF approach. The original MF formula represents the SRLS solution in the Born-Oppenheimer (BO) asymptotic limit defined by R^L ≫ R^C, where the local motion, characterized by the rate R^L, can be treated for frozen global motion, measured by the rate R^C.^27,28 In this limit the total time correlation function, C(t), may be expressed within a good approximation as the product of the time correlation function for global motion, C^C(t), and the time correlation function for local motion, C^L(t). When C^C(t) = exp(t/τ_m) and the local ordering is high then the S² from MF is a good approximation to the squared axial SRLS order parameter (S²₀)², and the effective local motion correlation time, τ_e, is given by the ‘renormalized’ local motion correlation time, τ_ren.²⁷ The concept of renormalization was used in early work²⁹ to characterize significant reduction in τ^L = 1/6R^L by strong local potentials. It was shown²⁹ that τ_ren ≅ 2 τ^L/c²₀, where c²₀ evaluates the strength of the local axial potential. Clearly τ_ren ⪡ τ^L when c²₀ is large. Typical values are c²₀ = 10 – 40 (which is to be multiplied by k_BT) for squared order parameters of 0.8 – 0.95. Equation A4 of reference ⁶, based on the wobble-in-a-cone model, is also appropriate for relating τ_e to τ^L and S² provided the ordering is high.²⁷

We determined quantitatively over what range the conditions R^L ≫ R^C and (S²₀)² ∼ 1 apply by comparing SRLS and MF results.²⁷ The original MF formula often yields best-fit parameters which do not fulfill these requirements. These are cases where the experimental spectral density comprises mixed modes, which are incompatible with the simplified MF formula. S² and τ_e can no longer be associated with the relevant physical quantities. Instead they just become fitting parameters, which have absorbed the discrepancies between the experimental and oversimplified theoretical spectral densities. Moreover, we found that often the symmetry of the local ordering at the N-H site is rhombic.²⁶ In these cases the original MF formula is not a good approximation to the experimental spectral density even when S² is high and R^C/R^L is small, because a single order parameter no longer suffices.

The extended MF formula was obtained in early work as a perturbational expansion of the SRLS solution in rhombic local ordering in the R^L ≫ R^C limit.³⁰ For a 90° tilt between the (axial) magnetic frame and the main local ordering/local diffusion frame (M),²⁷ this means that the N-H bond experiences fast diffusive local motion in the presence of very small ordering exerted by the immediate protein environment around, say, the C^α_i-1-C^α_i axis, or the N_i-C^α_i bond. The components of the diffusion tensor are R^L_∥ = 1/6τ^L_∥ and R^L_⊥ = 1/6τ^L_⊥ and of the ordering tensor, S²₀ and S²₂. The protein surroundings reorient at a rate R^C = 1/6τ_m much slower than R^L_∥ and R^L_⊥. The extended MF formula⁸ was offered to represent the mathematical scenario where the N-H bond experiences both fast and slow isotropic local motions with eigenvalues and squared order parameters 1/τ_f + 1/τ_m and S_f², and 1/τ_s + 1/τ_m and S_s², respectively. These motions are assumed to be decoupled from one another, and from the global motion, implying the conditions τ_f ⪡ τ_s ⪡ τ_m. In practice the extended MF formula is used when τ_s ∼ τ_m. The coefficients of the local and global motion terms in the extended MF formula are formally expressible in terms of (S²₀)² and (S²₂)². However, the MF parameters are totally different in implication from the SRLS parameters.

Typical best-fit values obtained with MF fitting of flexible protein residues are S_s² ∼ 0.55, S_f² ∼ 0.8, τ_s ∼ τ_m and τ_f ⪡ τ_m, which are just fitting parameters. This is implied by the presence of mixed modes which dominate the spectral density when τ_s is on the order of τ_m (which is typically the case for flexible residues in proteins). It should be pointed out that even if the perturbational conditions would prevail at the N-H site the MF physical picture would be puzzling, requiring two independent isotropic but restricted local motions associated with different ordering scenarios (S_s² and S_f²) imposed by the very same protein environment reorienting with correlation time τ_m ∼ τ_s while being at the same time decoupled from τ_s. On the other hand, an N-H bond may reorient almost independently around C^α_i-1-C^α_i (i.e., mixed modes can be ignored) in the limit where R^L ≫ R^C when the restricting local potential is very small. In this case the physical properties of axial local diffusion and rhombic local ordering are properly described by the simplified spectral density given by eq 19 below.

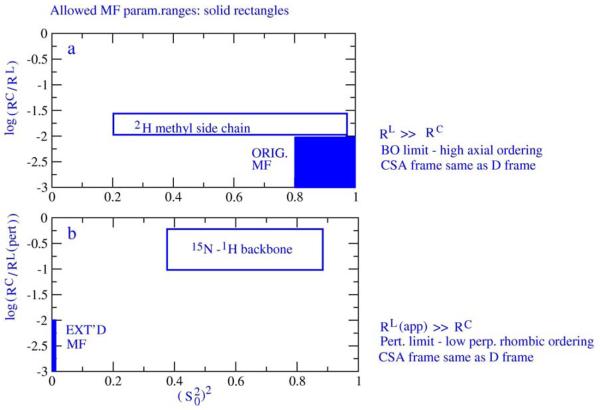
The validity ranges of the MF formulae are illustrated in Figs. 1a and 1b. The ordinates represent the logarithm of the time scale separation between the global and local motions and the abscissas represent squared order parameters. The original MF formula is applicable to a good approximation within the solid box on the right-hand side of Fig. 1a. This range is often exceeded in MF studies. We found that typical usage of the original MF formula involves discrepancies on the order of 7-8% between the squared SRLS order parameter, (S²₀)², and squared generalized MF order parameter, S², implied by limited mode-mixing effects, and by the simplified MF assumption that the ¹⁵N-¹H dipolar and ¹⁵N CSA magnetic frames are collinear.²⁷ If the effective correlation time for local motion, τ_e, is taken to represent the bare correlation time for local motion, τ^L, the latter will be underestimated five-, to twenty-fold.²⁷ The ²H spin relaxation of side chain methyl groups is analyzed mainly with the original MF formula (e.g., refs. ³¹ and ³²). The parameter range covered by typical best-fit parameters is shown in Fig. 1a by the rectangle labeled ‘²H methyl side chain’, which clearly digresses from the solid box in this Figure. Thus, in this application the original MF formula is mostly used outside of its validity range. The solid box in Fig. 1b shows the parameter range in which the extended MF formula is valid. In this case the abscissa represents both the axial, (S²₀)², and the rhombic, (S²₂)², squared order parameters which are very small. The rectangle labeled ‘¹⁵N-¹H backbone’ shows the parameter range in which the extended MF formula is applied in N-H bond dynamics studies. Here the abscissa represents both S_s² and S_f². Clearly in this application the extended MF formula is used outside of its validity range. We found that the MF parameters τ_s and S_s² exceed their formal SRLS analogues, τ^L_⊥ and (S²₀)², up to four-fold and twelve-fold, respectively.^19,20,22 Significantly larger disagreements between SRLS and MF are expected when the SRLS analyses are carried out allowing for rhombic potentials. Illustrative calculations based on a recently developed fitting scheme featuring rhombic potentials are provided below.

Figure 1.

Schematic illustration of the range of validity of the original (Fig. 1a) and the extended (Fig. 1b) model-free formulae. R^C (R^L) represents the diffusion rate for isotropic global (local) motion. The solid rectangles delineate the valid ranges. The empty rectangles delineate the parameter ranges where these formulae are typically applied in protein dynamics research. The conditions under which the MF formulae are valid are specified on the right-hand side of Figs. 1a and 1b.

Force-fitting will also occur with SRLS versions which are over-simplified as compared to the experimental spectral densities. Therefore investigating the mechanism of force fitting with the goal of elucidating the SRLS version, which satisfactorily matches the experimental data as implied by their integrity is important. This is the subject of the present study. It is shown that model-free force-fits the experimental data because mode-mixing, rhombic potentials and general features of local geometry are not accounted for. When possible the various effects mentioned above are estimated quantitatively. Our general conclusions imply that the dynamic picture yielded by MF analysis is often distorted. We show cases where qualitatively erroneous conclusions were drawn, fictitious phenomena were detected, and known functional dynamics was missed. Conformational entropy and other thermodynamic quantities derived from MF order parameters^33-36 may be inaccurate. Reliable fitting occurs with SRLS when the rhombicity of the local potential is accounted for and the local diffusion is allowed to be axial without limitations on the ratio N = R^L_∥/R^L_⊥. At this level of complexity the SRLS spectral density matches the integrity of currently available experimental data.

II. Theoretical background

1. The Slowly Relaxing Local Structure (SRLS) model

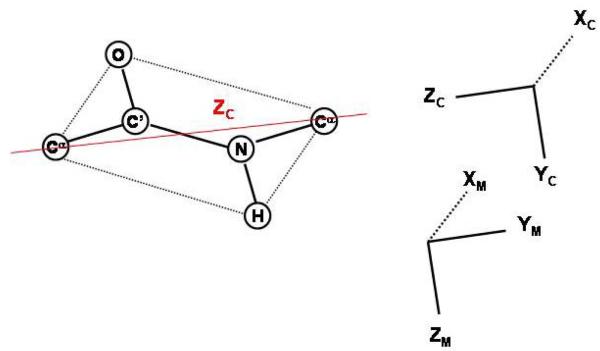
The fundamentals of the stochastic coupled rotator slowly relaxing local structure (SRLS) theory as applied to biomolecular dynamics including protein NMR were outlined recently.^22,25,37 We summarize below key aspects. The various reference frames, which define the SRLS model, and their relation to N-H sites in proteins, are shown in Fig. 2. A segment of the protein backbone comprising the atoms C^α_i, N_i, HN_i, C′_i-1, O_i-1 and C^α_i-1, the equilibrium positions of which are traditionally taken to lie within the peptide plane defined by N_i, HN_i, C′_i-1 and O_i-1, is illustrated in Fig. 2b. The orientation of the N-H bond with respect to the magnetic field is modulated by its local motions and by the global motion of the protein. Thus, in the SRLS model we are dealing with at least two dynamic modes which we can represent by two bodies (N-H bond and protein) whose motions are coupled or mixed.^23,24 For each motion two frames need to be introduced. The first is the local ordering/local diffusion frame, M, which is fixed in body 1 (in this case the N-H bond) and is usually determined by its geometric shape in the context of its motionally restricting environment. The second is the director frame, C′, whose axes represent the preferred orientation of the N-H bond (Fig. 2b) and which is fixed within the protein framework. The motion of body 1 is coupled to, or mixed with, the motion of body 2 (in this case the protein) by a local coupling or orienting potential which seeks to bring the N-H bond into alignment with the director frame. There are no limitations on the relative rates of motion of the two bodies, or the symmetry and strength of the coupling potential.

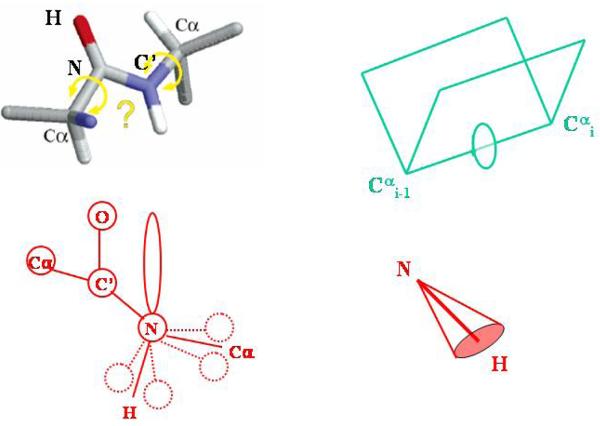
Figure 2.

(a) Various reference frames which define the Slowly Relaxing Local Structure (SRLS) model: L – laboratory frame, C – global diffusion frame associated with protein shape, C′ – local director frame associated with the stereochemistry of the local protein structure at the N-H site, M – local ordering/local diffusion frame fixed at the N-H bond, D – magnetic ¹⁵N-¹H dipolar frame, CSA - magnetic ¹⁵N chemical shift anisotropy frame. (b) Z_D, X_D, Z_M and Y_M reside within the peptide plane, Z_D lies along the N-H bond and Y_D is perpendicular to the peptide plane.⁴⁴ The uniaxial local director (C, assuming isotropic global diffusion) is taken to lie along the equilibrium C^α_i−1−C^α_i axis. The main ordering axis is taken along C^α_i−1−C^α_i. This implies perpendicular Y_M ordering with β_MD = 101.3°. ‘Nearly planar Y_M-X_M ordering’, i.e., positive ordering along X_M and almost no ordering along Z_M (for brevity we will denote this ordering symmetry below as ‘nearly planar Y_M-X_M ordering/symmetry’), implies β_MD = 101.3° and γ_MD = 90°. For high ordering the Y_M axis is aligned preferentially along C. The axes X_CSA, Y_CSA and Z_CSA (not shown) are defined to be aligned with the most shielded (σ₁₁), intermediate (σ₂₂) and least shielded (σ₃₃) components of the ¹⁵N shielding tensor, respectively⁴⁴ (information on chemical shielding and local geometry for the C′-C^α bond appears in ref. 45). The polar angle between Z_D and Z_CSA was set equal to 17° in our study.³ Y_CSA is perpendicular to the peptide plane (i.e., parallel to Y_D).⁴⁴

The reorientation of the N_i-H_i bond is restricted due to limited bond oscillations, conformational reorientations about the adjacent dihedral angles (Φ_i, Ψ_i-1), the crankshaft motion (anti-correlated rotations about Φ_i and Ψ_i-1),³⁸ nitrogen pyramidalization,³⁹ peptide-plane motion around C ^α_i-1-C^α_i, etc., and any interactions with the local environment. In general, these processes imply effective Euler angles Ω_MD = (α_MD, β_MD, γ_MD) which define the relative orientation of the local ordering/local diffusion frame, M, and the magnetic ¹⁵N-¹H dipolar frame, D (which lies along the N-H bond). In particular, taking C ^α_i-1-C^α_i as local director, C′, and as main local diffusion axis, one has Y_M along the instantaneous orientation of the C ^α_i-1-C^α_i axis (i.e., ‘Y_M ordering’), and C′ along the equilibrium orientation of the C ^α_i-1-C^α_i axis. In this case Ω_MD = (0°, 101.3°, 90°). This geometry is implicit in the 3D Gaussian Axial Fluctuations (GAF) model⁴⁰ (the difference in the γ_MD values − 180° in 3D GAF and 90° in SRLS – is implied by the different definitions of the X_M and Y_M axes). Similar values of Ω_MD are obtained by replacing the C^α_i-1-C^α_i axis with the N_i-C^α_i bond. The N-H bond experiences an increasing orienting potential when Y_M deviates from C′. The global motion of the protein (body 2) is frequently approximated as that of a cylinder, with its long axis taken to be the z-axis of the global diffusion (C) frame. For spherical (or globular) proteins the C and C′ frames are the same.

1a Geometry and observables

The various frames of the SRLS model, as applied to amide ¹⁵N spin relaxation in proteins, are shown in Fig. 2a. A formal definition, as compared to the physically descriptive presentation given above, of the various frames follows. The laboratory L frame is space-fixed, both C and C′ are protein-fixed, and the M, D (¹⁵N-¹H dipolar) and CSA (¹⁵N CSA) frames are fixed with respect to the N-H bond. The L frame is considered an inertial frame with respect to which all moving frames are defined. The M frame represents both the local ordering and the local diffusion frame, which for convenience are taken to be the same. The Euler angles Ω_LM are modulated by the local motion and the global motion, whereas the Euler angles Ω_LC are only affected by the latter. These angles are referred to the fixed lab frame to properly describe the diffusion. The local ordering frame M tends to align with respect to a local director C′. The relative orientations of M with respect to C′ and C are defined by Ω_CM and Ω_C′M, respectively. The local director C′ is tilted at Euler angles Ω_CC′ with respect to the cage (i.e., protein) frame C (tilted with respect to the laboratory frame at Euler angles Ω_LC). The Euler angles Ω_CC′ are time-independent. It is reasonable to assume that only the polar angle β_C′C is important. Note that Ω_LM involves the sum of rotations Ω_LC + Ω_CC′ + Ω_C′M [here and in the following we shall employ a shorthand notation for indicating sequences of rotations; namely, for a generic rotation Ω₁₂ = Ω_2′ + Ω₁, resulting from first applying Ω₁ and then Ω_2′ we can write the explicit relation among Wigner rotation matrices as D^j_mk(Ω₁₂) = Σ_m′ D^j_mm′(Ω₁) D^j_m′k(Ω₂)]. The time dependence of the Euler angles Ω_C′M is governed by the local orienting potential, which couples the two modes of motion. Through the time dependence of Ω_C′M the locally reorienting N-H bond follows the slower motion of the protein.

The magnetic¹⁵ N-¹ H dipolar tensor frame, D, and the magnetic ¹⁵N CSA tensor frame CSA, are also shown in Fig. 2a. The Euler angles specifying the rotation from M to D are Ω_MD, and the rotation from D to CSA is given by Ω_CSA. The Euler angles Ω_MD and Ω_D–CSA are time independent. The D frame is axially symmetric. If the M frame is also axially symmetric, then Ω_MD = (0, β_MD, 0), where β_MD is known as ‘diffusion tilt’.

The diffusion tensor R^L describing the rotational diffusion properties of the probe (N-H bond in this case) is diagonal in M, while the diffusion tensor R^c describing the rotational diffusion properties of the cage is diagonal in C. We start by assuming Smoluchowski dynamics for the coupled set of orientational coordinates Ω_LM and Ω_LC, according to the slowly relaxing local structure or SRLS approach. Namely, the system consists of two Brownian rotators (or ‘bodies’) -the amide group and the rest of protein - linked by an interaction potential which depends on their relative orientation. Their motions are characterized by slow diffusive changes, controlled by suitable rotational diffusion parameters. Formally the diffusion equation for the coupled system is given by:

$$\frac{\partial }{\partial t}P(X,t)=-\widehat{\Gamma }P(X,t)$$ (1)

where X is a set of coordinates completely describing the system:

$$\begin{array}{cc}\hfill X& =({\Omega }_{\mathit{LM}},{\Omega }_{\mathit{LC}})\hfill \\ \hfill \widehat{\Gamma }& =\widehat{J}\left({\Omega }_{\mathit{LM}}\right){\mathbf{R}}^L{P}_{\mathrm{e}q}\widehat{J}\left({\Omega }_{\mathit{LM}}\right)P_{\mathrm{e}q}^{-1}+\widehat{J}\left({\Omega }_{\mathit{LC}}\right){\mathbf{R}}^c{P}_{\mathrm{e}q}\widehat{J}\left({\Omega }_{\mathit{LC}}\right)P_{\mathrm{e}q}^{-1},\hfill \end{array}$$ (2)

where Ĵ(Ω_LM) and Ĵ(Ω_LC) are the angular momentum operators for the probe and the cage, respectively.

Changing to different coordinates is straighforward.²⁸ We select the set defined by Ω_C′M and Ω_LC′. The Euler angles Ω_C′M describe the N-H-bond--fixed M frame orientation relative to the protein-fixed C′ frame, and the Euler angles Ω_LC′ the C′ frame orientation with respect to the lab frame. In the new coordinate frame one has:

$$\begin{array}{cc}\hfill X& =\left({{\Omega }_{C^{\prime }M}}^{,}{\Omega }_{{\mathit{LC}}^{\prime }}\right)\hfill \\ \hfill \widehat{\Gamma }& =\widehat{J}({\Omega }_{C^{\prime }M}){\mathbf{R}}^L{P}_{\mathrm{e}q}\widehat{J}\left({\Omega }_{C^{\prime }M}\right)P_{\mathrm{e}q}^{-1}+[\widehat{J}\left({\Omega }_{C^{\prime }M}\right)-\widehat{J}\left({\Omega }_{{\mathit{LC}}^{\prime }}\right)]{\mathbf{R}}^c{P}_{\mathrm{e}q}[\widehat{J}\left({\Omega }_{C^{\prime }M}\right)-\widehat{J}\left({\Omega }_{{\mathit{LC}}^{\prime }}\right)]P_{\mathrm{e}q}^{-1}\hfill \end{array}$$ (3)

The Boltzmann distribution P_eq = exp[−U(Ω_LM)/k_BT]/〈exp[−U(Ω_LM)/k_BT]〉 is defined with respect to the probe-cage interaction potential given by:

$$u\left({\Omega }_{C^{\prime }M}\right)=\frac{U\left({\Omega }_{C^{\prime }M}\right)}{k_{B}T}=-c_0^2{D}_{0,0}^2\left({\Omega }_{C^{\prime }M}\right)-c_2^2[D_{0,2}^2\left({\Omega }_{C^{\prime }M}\right)+D_{0,-2}^2\left({\Omega }_{C^{\prime }M}\right)].$$ (4)

This represents the expansion in the full basis set of Wigner rotation matrix elements, D^L_KM(Ω_MC), with only lowest order, i.e. L = 2, terms being preserved. The coefficient c²₀ is a measure of the orientational ordering of the N-H bond with respect to the local director whereas c²₂ measures the asymmetry of the ordering around the director. Here we follow historical convention by using L = 2 terms as the leading terms, rather than L = 1. This is sufficient for many purposes, as we have previously shown, because NMR involves second-rank (i.e., L = 2) magnetic tensors. But the SRLS theory can readily be modified to include L = 1 terms. The current approach is in the spirit of keeping the number of parameters to a minimum.

The SRLS equation can be solved in terms of the time dependent distribution P(Ω_C′M,Ω_LC′,t), which describes the evolution in time and orientational space of the system. Alternatively, it is convenient to directly calculate time correlation functions $C_{M,{\mathrm{KK}}^{\prime }}^J\left(t\right)=\langle {D_{M,K}^J}^{\ast }\left({\Omega }_{\mathit{LM}}\right)\left|\exp (-\widehat{\Gamma }t)\right|D_{M,K^{\prime }}^J\left({\Omega }_{\mathit{LM}}\right)P_{\mathit{eq}}\rangle$, which for proper values of the coefficients J,M,K,K′ determine the experimental NMR relaxation rates. Actually, the Fourier-Laplace transforms of $C_{M,{\mathrm{KK}}^{\prime }}^J\left(t\right)$ are needed, and they are obtained as the spectral densities at a given frequency ω:

$$j_{{\mathit{KK}}^{\prime }}^M\left(\omega \right)=\langle {D_{M,K}^J}^{\ast }\left({\Omega }_{\mathit{LM}}\right)\left|{(i\omega +\widehat{\Gamma })}^{-1}\right|D_{M,K^{\prime }}^2\left({\Omega }_{\mathit{LM}}\right)P_{\mathit{eq}}\rangle$$ (5)

As stated here, the model has eleven parameters: c₀, c₂ (potential parameters), $R_i^L$ (probe diffusion i =1,2,3 principal values), $R_i^c$ (global diffusion i =1,2,3 principal values) and Ω_CC′ = (α_CC′,β_CC′,γ_CC′ (global diffusion tilt angles). For the sake of simplicity, we shall limit our analysis to axial probe $R_1^L=R_2^L=R_{\perp }^L\ne R_3^L=R_{\parallel }^L$, axial cage $R_1^c=R_2^c=R_{\perp }^c\ne R_3^c=R_{\parallel }^c$, and α_CC′ = γ_CC′ = 0. The orientation of the magnetic tensors is specified by Ω_MD and Ω (defined in Fig. 2a). In the past work^{19,20,22,26,27} we made use of eq 2 involving Ω_LM and Ω_LC. In the present study we have used eq 3 involving Ω_LC′ and Ω_C′M. The primary reason is that the use of the relative orientation of the N-H bond in the protein specified by the Ω_C′M is the more natural one in terms of conventional intuition. One can simply think of the Euler angles Ω_C′M as just being modulated by the local motion, whereas Ω_LC′ is just modulated by the overall tumbling of the protein. Also, as we have already noted, the Ω_C′M are the natural coordinates for expressing the potential energy given by eq 4 (This does, however, render the Γ̂ operator somewhat more complicated). Of course, the two forms are mathematically equivalent. The global diffusion tensor assumes the form in the C′ frame:

$${\mathbf{R}}^c=\left(\begin{array}{ccc}\hfill R_{\perp }^c{\cos }^2{\beta }_{{\mathrm{CC}}^{\prime }}+R_{\parallel }^c{\sin }^2{\beta }_{{\mathrm{CC}}^{\prime }}\hfill & \hfill 0\hfill & \hfill \frac{1}{2}(R_{\perp }^c-R_{\parallel }^c)\sin 2{\beta }_{{\mathrm{CC}}^{\prime }}\hfill \\ \hfill 0\hfill & \hfill R_{\perp }^c\hfill & \hfill 0\hfill \\ \hfill \frac{1}{2}(R_{\perp }^c-R_{\parallel }^c)\sin {\beta }_{{\mathrm{CC}}^{\prime }}\hfill & \hfill 0\hfill & \hfill R_{\perp }^c{\sin }^2{\beta }_{{\mathrm{CC}}^{\prime }}+R_{\parallel }^c{\cos }^2{\beta }_{{\mathrm{CC}}^{\prime }}\hfill \end{array}\right)$$ (6)

The probe diffusion tensor, defined in the M frame, is diagonal. Note that for β_CC′ = 0 or R^c_⊥ = R^c_∥ the global diffusion tensor is diagonal and invariant in both the C and C′ frames.

1b Numerically exact treatment

We address here the problem of devising an efficient procedure for evaluating numerically accurate spectral densities. We adopt a variational scheme, based on a matrix vector-representation of eq 5, followed by an application of the Lanczos algorithm in its standard form developed for Hermitian matrices. It is convenient to express the generic correlation function as the linear combination of normalized auto-correlation functions. Defining $2A_{M,{\mathrm{KK}}^{\prime }}^J=D_{M,K}^J+D_{M,K^{\prime }}^J$, the spectral densities of the normalized auto-correlation functions of interest are:

$$j_{M,{\mathrm{KK}}^{\prime }}^S\left(\omega \right)=\langle {A_{M,{\mathrm{KK}}^{\prime }}^J}^{\ast }\left({\Omega }_{\mathit{LM}}\right)P_{\mathit{eq}}^{1∕2}\left|{(i\omega +\tilde{\Gamma })}^{-1}\right|A_{M,{\mathrm{KK}}^{\prime }}^J\left({\Omega }_{\mathit{LM}}\right)P_{\mathit{eq}}^{1∕2}\rangle ∕\langle |A_{M,{\mathrm{KK}}^{\prime }}^J\left({\Omega }_{\mathit{LM}}\right){|}^2{P}_{\mathit{eq}}\rangle ,$$ (7)

and the generic spectral densities are:

$$j_{M,{\mathrm{KK}}^{\prime }}\left(\omega \right)=[2(1+{\delta }_{K,K^{\prime }})j_{M,{\mathrm{KK}}^{\prime }}^S\left(\omega \right)-j_{M,{\mathrm{KK}}^{\prime }}^S\left(\omega \right)-j_{M,K^{\prime }{K}^{\prime }}^S\left(\omega \right)]∕2\left[J\right],$$ (7a)

where J = 2 and M = 0 in our case. We use the shorthand notation [J ] = 2J +1. A numerical calculation is then performed by choosing a basis set of functions, representing in matrix form the transformed operator $\widehat{\Gamma }=P_{\mathit{eq}}^{-1∕2}\widehat{\Gamma }{P}_{\mathit{eq}}^{1∕2}$, and evaluating eq 7 directly by employing a standard Lanczos approach. The latter is reviewed here for completeness in accordance with the standard technique of Moro and Freed.^41,42 Let us suppose that we are interested in calculating the Fourier-Laplace transform of the normalized auto-correlation function of an observable f (q) for a diffusive symmetrized (i.e. Hermitian) operator Γ̃ acting on coordinate q, in the form $j\left(\omega \right)=\langle \delta f^{\ast }{P}_{\mathit{eq}}^{1∕2}\left|{(i\omega +\widehat{\Gamma })}^{-1}\right|\delta f{P}_{\mathit{eq}}^{1∕2}\rangle ∕\langle |f{|}^2{P}_{\mathit{eq}}\rangle$, where δf = f − 〈fp_eq〉 is the observable redefined to yield an average value of zero. In the present case we consider only rotational motion in an isotropic fluid, so the relevant 〈fp_eq〉 = 0. The Lanczos algorithm is a recursive procedure to generate orthonormal functions which allow a tridiagonal matrix representation of Γ̃ in terms of the coefficients α_n, β_n, which form the main and secondary diagonal of the tridiagonal symmetric matrix T, and the spectral density can be written in the form a continued fraction^41,42. The calculation of the tridiagonal matrix elements can be carried out in finite precision by working in the vector space obtained by projecting all the functions and operators on a suitable set of orthonormal functions |λ〉. One only needs to define the matrix operator, Γ, and starting vector elements, v₁, given by Γ_λλ′ = 〈λ|Γ̃|λ′〉, respectively.

In the case under study the SRLS diffusion operator is given by eq 3 and the starting vector is given by $\phantom{\langle }|1\rangle =A_{M,{\mathrm{KK}}^{\prime }}^J\left({\Omega }_{\mathit{LM}}\right)P_{\mathrm{e}q}^{1∕2}∕\langle |A_{M,{\mathrm{KK}}^{\prime }}^J{|}^2{P}_{\mathrm{e}q}\rangle =\sqrt{\frac{2\left[J\right]}{1+{\delta }_{K,K^{\prime }}}}{A}_{M,{\mathrm{KK}}^{\prime }}^J\left({\Omega }_{\mathit{LM}}\right)P_{\mathrm{e}q}^{1∕2}$. A natural choice for a set of orthonormal functions is the direct product of normalized Wigner matrices. What is left is the calculation of the matrix elements Γ_λ,λ′ and the vector elements 〈λ|1〉. The algebraic intermediate steps are relatively straightforward and based on properties of the Wigner rotation matrices, angular momentum operators and spherical tensors; we skip the technical details and list the resulting expressions.^23,24,28

1c Observables

In order to interpret ¹⁵ N-¹ H dipolar and ¹⁵ N CSA auto-correlated relaxation rates we only need spectral densities with J = 2 and M = 0. Dependence upon K, K′ is slightly more complex and it discussed in detail in the following section.

According to standard analysis for the motional narrowing regime⁴³ we can define the observable spectral density for two magnetic interactions μ and ν as the real part of the Fourier-Laplace transform of the correlation function of the second rank Wigner functions in the orientation of the magnetic tensors in the laboratory frame, (here μ,ν = D or CSA and Ω^D = Ω_MD,Ω^CSA = Ω_MD + Ω, cf. Fig. 2a):

$$J_M^{\mu \nu }\left(\omega \right)={\int }_0^{\infty }{e}^{-i\omega t}\langle {D_{M,0}^2}^{\ast }[{\Omega }^{\mu }+{\Omega }_{\mathit{LM}}\left(t\right)]{D_{M,0}^2}^{\ast }[{\Omega }^{\nu }+{\Omega }_{\mathit{LM}}\left(0\right)]\rangle ,$$ (8)

and relying on standard properties of the Wigner functions, in the form:

$$J_M^{\mu \mu }\left(\omega \right)={\int }_0^{\infty }{e}^{-i\omega t}\underset{{\mathrm{KK}}^{\prime }}{\Sigma }{D_{K,0}^2}^{\ast }\left({\Omega }^{\mu }\right)D_{K^{\prime },0}^2\left({\Omega }^{\mu }\right)\langle {D_{M,K}^2}^{\ast }\left[{\Omega }_{\mathit{LM}}\left(t\right)\right]{D_{M,K^{\prime }}^2}^{\ast }\left[{\Omega }_{\mathit{LM}}\left(0\right)\right]\rangle .$$ (8a)

Based on the symmetry relation $j_{M,{\mathrm{KK}}^{\prime }}^J=j_{M,K^{\prime }K}^J$ (cf. eq 7a) we obtain:

$$\Re \left[J_M^{\mu \mu }\left(\omega \right)\right]=\underset{K}{\Sigma }|D_{K,0}^2\left({\Omega }^{\mu }\right){|}^2\Re \left[j_{M,\mathit{KK}}\left(\omega \right)\right]+2\underset{K<K^{\prime }}{\Sigma }\Re \left[{D_{K,0}^2}^{\ast }\left({\Omega }^{\mu }\right)D_{K^{\prime },0}^2\left({\Omega }^{\mu }\right)\right]\Re \left[j_{M,{\mathrm{KK}}^{\prime }}\left(\omega \right)\right],$$ (9)

where ℜ stands for the real part. Note that for axial potentials ($c_2^2=0$) the second term goes to zero and we are left with standard expressions. The coefficients $D_{K,0}^2\left({\Omega }^D\right)$ are readily evaluated, while $D_{K,0}^2\left({\Omega }^{\mathit{CSA}}\right)$ can be calculated in terms of Ω_MD and Ω, as in the expression: $D_{K,0}^2\left({\Omega }^{\mathit{CSA}}\right)={\displaystyle {\Sigma }_L}{D}_{K,L}^2\left({\Omega }_{\mathit{MD}}\right)D_{L,0}^2\left(\Omega \right)$.

The spectral densities for ¹⁵N-¹H dipolar and ¹⁵N CSA auto-correlation are then obtained as $J^{\mathit{DD}}\left(\omega \right)=\Re \left[J_0^{D,D}\left(\omega \right)\right]$ and $J^{\mathit{CC}}\left(\omega \right)=\Re \left[J_0^{\mathrm{CSA},\mathrm{CSA}}\left(\omega \right)\right]$, respectively. The measurable ¹⁵N relaxation quantities ¹⁵N T₁, T₂ and ¹⁵N-{¹H} NOE are calculated as functions of J^DD (ω_i) and J^CC (ω_i), with ω_i = 0,ω_H, ω_N, ω_H − ω_N and ω_H + ω_N, using standard expressions for NMR spin relaxation.^4,5 Note that due the additional symmetry j_M,K,K′ = j_{M,−K,−K′}, only the nine distinct couples (K, K′) = (−2, 2), (−1,1), (−1, 2), (0,0), (0,1), (0, 2), (1,1), (1, 2), (2, 2) need to be considered. For dipolar auto-correlation, where Ω_MD = (0,β_MD,0), one has the explicit expression (denoting $j_{{\mathrm{KK}}^{\prime }}=\Re \left[j_{0,{\mathrm{KK}}^{\prime }}^2\left(\omega \right)\right]$ for brevity):

$$\begin{array}{cc}\hfill & J^{\mathit{DD}}\left(\omega \right)=J^{\mathit{CC}}\left(\omega \right)=\hfill \\ \hfill & ={\mathrm{d}}_{00}^2{\left({\beta }_{\mathit{MD}}\right)}^2{j}_{00}+2{\mathrm{d}}_{10}^2{\left({\beta }_{\mathit{MD}}\right)}^2{j}_{11}+2{\mathrm{d}}_{20}^2{\left({\beta }_{\mathit{MD}}\right)}^2{j}_{22}\hfill \\ \hfill & +4{\mathrm{d}}_{00}^2\left({\beta }_{\mathit{MD}}\right){\mathrm{d}}_{20}^2\left({\beta }_{\mathit{MD}}\right)j_{02}+2{\mathrm{d}}_{-10}^2\left({\beta }_{\mathit{MD}}\right){\mathrm{d}}_{10}^2\left({\beta }_{\mathit{MD}}\right)j_{-11}+2{\mathrm{d}}_{-20}^2\left({\beta }_{\mathit{MD}}\right){\mathrm{d}}_{20}^2\left({\beta }_{\mathit{MD}}\right)j_{-22}\hfill \end{array}$$ (10)

with only six couples (K, K′) = (0,0), (1,1), (2, 2), (0, 2), (−1,1) and (−2, 2) involved.

A convenient measure of the orientational ordering of the N-H bond is provided by the order parameters, $S_0^2=\langle D_{00}^2\left({\Omega }_{C^{\prime }M}\right)\rangle$ and $S_2^2=\langle D_{02}^2\left({\Omega }_{C^{\prime }M}\right)+D_{0-2}^2\left({\Omega }_{C^{\prime }M}\right)\rangle$, which are related to the orienting potential (eq 4), hence $c_0^2$ and $c_2^2$, via the ensemble averages:

$$\langle D_{0n}^2\left({\Omega }_{C^{\prime }M}\right)\rangle =\int d{\Omega }_{C^{\prime }M}{D}_{0n}^2\left({\Omega }_{C^{\prime }M}\right)\exp [-\mu \left({\Omega }_{C^{\prime }M}\right)]∕\int d{\Omega }_{C^{\prime }M}\exp [-\mu \left({\Omega }_{C^{\prime }M}\right)]$$ (11)

One may convert to Cartesian ordering tensor components according to $S_{\mathit{zz}}=S_0^2,S_{\mathit{xx}}=\left(\sqrt{3∕2}{S}_2^2-S_0^2\right)∕2,S_{\mathit{yy}}=-\left(\sqrt{3∕2}{S}_2^2+S_0^2\right)∕2$. Note that S_xx + S_yy + S_zz = 0.

In case of zero potential, $c_0^2=c_2^2=0$, and axial diffusion, the solution of the diffusion equation associated with the time evolution operator features three distinct eigenvalues:

$$1∕{\tau }_K=6{R^L}_{\perp }+K^2({R^L}_{\parallel }-{R^L}_{\perp })\text{for}K=0,1,2,$$ (12)

where R^L_∥ = 1/(6τ_∥) and R^L_⊥ = 1/(6τ_⊥) = 1/(6τ₀). Only diagonal j_K(ω) ≡ j_KK(ω) terms are non-zero and they can be calculated analytically as Lorentzian spectral densities, each defined by width 1/τ_K. When the ordering potential is axially symmetric, $c_0^2\ne 0,c_2^2=0$, again only diagonal terms survive, but they are written as infinite sums of Lorenzian spectral densities, which are defined in terms of eigenvalues 1/τ_i of the diffusion operator and weighing factors c_K,i such that:

$$j_K\left(\omega \right)=\underset{i}{\Sigma }\frac{c_{K,i}{\tau }_i}{1+{\omega }^2{\tau }_i^2}$$ (13)

The eigenvalues 1/τ_i represent modes of motion of the system, in accordance with the parameter range considered. Note that although in principle the number of terms in eq 13 is infinite, in practice a finite number of terms is sufficient for numerical convergence of the solution. Finally when the local ordering potential is rhombic, $c_0^2\ne 0,c_2^2\ne 0$, both diagonal j_K(ω) and non-diagonal j_KK′(ω) terms are different from zero and need to be evaluated explicitly according to expressions analogous to eq 13.

Details of the implementation of SRLS in a data fitting scheme featuring axial potentials and isotropic global diffusion were outlined previously.²² For practical reasons this fitting scheme is based on pre-calculated 2D grids of spectral densities, j_K(ω). The coordinates of these grids are c²₀ and R^C. The structural parameters β_MD and γ_MD are used to assemble J^DD(ω) out of j_K(ω). The set of free variables includes c²₀, R^C and β_MD. The angle γ_MD was fixed at 90° based on stereo-chemical considerations, and R^L_∥≫R^L_∥ (in analogy with the MF requirement that τs ≫ τ_f) was imposed. This scheme is computationally as fast as the commonly used MF fitting schemes.^46,47

We developed recently a fitting scheme where the functions j_KK′(ω) are calculated on the fly. In this case the set of free variables includes c²₀, c²₂, R^L_∥/R^L_⊥, R^C and β_MD. Clearly the local potential is allowed to be rhombic and the local diffusion, axial. This scheme is currently rather demanding computationally and efforts to improve its efficiency are underway. A number of conditions can be employed, however, to simplify the analysis. If the local geometry is assumed to be known, as in the 3D GAF model,⁴⁰ β_MD can be fixed at 101.3°. If the symmetry of the local ordering is known c²₂/c²₀ can be fixed. Note that in SRLS the global diffusion rate, R^C, is determined in the same fitting process as the site-specific parameters, as is appropriate when the modes R^C and R^L are ‘mixed’. The next stage will be to allow the global diffusion tensor to be axially symmetric. This requires a complex fitting scheme where the R^C tensor is global whereas all the other parameters are local. Instead of a single variable for global motion, R^C, three variables, R^C(app), R^C_∥/R^C_⊥ β_CC′ will be featured. Note that R^C and R^C(app) define the time scale separation between the global and local motions as rates are given in SRLS in units of R^L_⊥.

When the local potential is axially symmetric in SRLS then formal (but not necessarily physical) analogies with the MF formulae can be specified. In this case the number of formally analogous free parameters, hence the minimum number of data points required, is the same in SRLS and MF.²² Model-free data fitting was carried out in this study with the computer programs Modelfree 4.0 (ref. ⁴⁶) and Dynamics (ref. ⁴⁷).

Thus, the spectral densities j_K(ω) (j_KK′(ω) for rhombic potentials) are the building blocks for a given dynamic model relative to the local diffusion frame, and the spectral densities J^x(ω) are the building blocks for a specific geometric implementation of this dynamic model relative to the frames of the magnetic tensors. The measurable quantities are J^x(0), J^x(ω_N), J^x(ω_H), J^x(ω_H + ω_N) and J^x(ω_H − ω_N). Together with the magnetic interactions they determine the experimentally measured relaxation rates according to standard expressions for NMR spin relaxation.^4,5 If the equilibrium orientations of N-H and C^α-C′ are assumed to reside within the peptide plane then the functions j_KK′(ω) for N-H bond dynamics can also be used to treat C^α-C′ bond dynamics. Different local geometry, specific to the C^α-C′ bond, determines the J^x(ω) functions and different magnetic interactions enter the calculation of the relaxation rates measured experimentally.

2. The model-free approach

A brief summary of the model-free approach, as formulated by its developers, is outlined below.

2a. Original MF spectral density.^6,7

The basic premise is that the global motion of the protein is much slower than the local motions of the N-H bond. Consequently the global and local motions are ‘independent’, and the total time correlation function, C(t), can be expressed as:

$$\mathrm{C}\left(\mathrm{t}\right)={\mathrm{C}}^{\mathrm{C}}\left(\mathrm{t}\right)\times {\mathrm{C}}^{\mathrm{L}}\left(\mathrm{t}\right).$$ (14)

The global motion is assumed to be isotropic, with C^C(t) = exp(−t/τ_m). C^L(t) is given by:

$${\mathrm{C}}^{\mathrm{L}}\left(\mathrm{t}\right)={\mathrm{S}}^2+(1-{\mathrm{S}}^2)\exp (-\mathrm{t}∕{\tau }_{\mathrm{e}}),$$ (15)

where τ_e is the effective correlation time for local motion defined as the area of C^L(t) divided by (1 − S²), and τ_e << τ_m. The parameter S², which represents the plateau value of C^L(t) at long times (t ≫ τ_e), is taken as the square of a generalized order parameter. This definition of S² (eqs 14-16 of ref. 6) involves the spherical harmonic functions of rank 2, whereas C^L(t) at shorter times is given in terms of the Legendre polynomial of rank 2 (eqs 4 and 12 of ref. 6). All of the equations cited involve the equilibrium probability distribution function, P_eq(Ω_CM) where C denotes the local director fixed in the protein (called ‘molecular axis’ in ref. 6), and M the local diffusion frame (taken in MF to lie along the N-H bond). Equations 4 and 12 feature P_eq(0, β_CM, 0) (p_eq(θ) in the notation of ref. 6), whereas eqs 14-16 feature P_eq(0, β_CM, γ_CM) (p_eq(θ,φ) in the notation of ref. 6). Thus, there is inconsistency in the symmetry of C^L(t) at short and long times, implied by M considered axial in eqs 4 and 12 and rhombic in eqs 14-16. Fourier transformation of eq 14 with eq 15 inserted for C^L(t) yields:

$$\mathrm{J}\left(\omega \right)={\mathrm{S}}^2{\tau }_{\mathrm{m}}∕(1+{\omega }^2{{\tau }_{\mathrm{m}}}^2)+(1-{\mathrm{S}}^2){{\tau }_{\mathrm{e}}}^{,}∕(1+{\omega }^2{{\tau }_{\mathrm{e}}}^{,2}),$$ (16)

where 1/τ_e′ = 1/τ_e + 1/τ_m.

2b. The original MF formula as SRLS asymptote

It was shown in early work³⁰ that in the limit where R^L≫ R^C the following equation is valid in the perturbation limit, i.e., for very small local ordering:

$${\mathrm{j}}_{\mathrm{K}}\left(\omega \right)={\left({{\mathrm{S}}^2}_{\mathrm{K}}\right)}^2[{\tau }_{\mathrm{m}}∕(1+{\omega }^2{{\tau }_{\mathrm{m}}}^2)+(1-{\left({{\mathrm{S}}^2}_{\mathrm{K}}\right)}^2){\tau }_{\mathrm{K}}∕(1+{\omega }^2{{\tau }_{\mathrm{K}}}^2)\phantom{]},$$ (17)

with τ_K given by eq 12. S²_K denotes the principal values of the ordering tensor in irreducible tensor notation (where S²₁ = 0.) When the symmetry of the local potential/local ordering is axial ten S²₂ is zero. In this case j₀(ω) is given by the first term of eq 17, whereas j_K≠0(ω) are given by 2τ_K/(1 + ω²τ_K²).⁴⁸

The function C₀(t) corresponding to j₀(ω) is shown by the dashed curve in Fig. 3a, with the plateau value given by (S²₀)² 2 and the decay to it by τ₀ = 1/6R^L. The final decay of C₀(t) to zero is given by τm = 1/6R^C. However, the local ordering at an N-H bond is never as low as required by the perturbation limit in the local ordering, but rather quite high. Using the full SRLS solution we showed in previous work²⁶ that for high enough (S²₀)² and low enough R^C/R^L (see ref. 26 for quantitative evaluation of validity ranges) eq 16 is valid with S² ∼ (S²₀)² and the initial decay of C₀(t) given by:

$${\tau }_{\text{initial}}={\tau }_{\mathrm{e}}~{\tau }_{\mathrm{ren}}=2{\tau }_0∕{{\mathrm{c}}^2}_0,$$ (18)

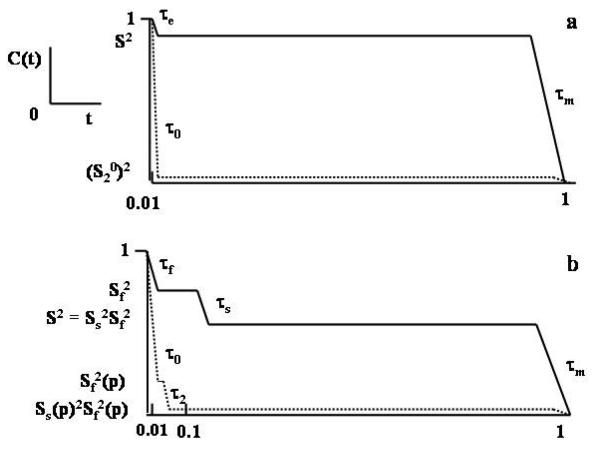
where τ_ren is the renormalized correlation time for local motion.²⁹ The parameter 1/6τ_ren is the rate at which the distribution of orientations is restored to equilibrium when a spin-bearing particle reorients rapidly in the presence of a strong orienting potential.^29,49 τ_ren is reduced significantly relative to τ₀, in accordance with the strength, c²₀, (and symmetry) of the local potential. The expression given by eq 18 is valid in SRLS in the asymptotic limit (R^L ≫ R^C)²⁷ when the local potential is axial and high. In this case eq 16 is a good approximation of the SRLS solution with S² representing (S²₀)² and τ_e representing τ_ren. The time correlation function corresponding to eq 16 is shown by the solid curve in Fig. 3a.

Figure 3.

(a) Time correlation function, C(t), corresponding to j₀(ω) of eq 17 (and eq 16 applied in the perturbation limit) with (S²₀)² → 0 and τ₀/τ_m << 1 (dashed curve). Time correlation function, C(t), corresponding to eq 16 with (S²₀)² ∼ 0.8 and τ_e/τ_m << 1 (solid curve). (b) Time correlation function, C(t), corresponding to eq 20 (and eq 19 applied in the perturbation limit) with (S²₀)² → 0 and (S²₂)² → 0 (S_f² ∼ 0.25 and S_s² ∼ 0) and τ₀, τ₂ << τ_m (τ_f, τ_s << τ_m) (dashed curve). Time correlation function, C(t), corresponding to eq 19 as applied to treat flexible residues in proteins with S_f² ∼ 0.75, S² ∼ 0.55, τ_s/t_f ∼ 10 and τ_f/τ_m << 1 (solid curve). The index ‘p’ stands for ‘perturbational limit’. The abscissas in Figs. 3a and 3b are given in units of τ^L/τ_m. Note that τ_e and τ_f are significantly smaller than displayed (for visibility), as they represent renormalized correlation times.

The range of validity of eq 16 depends on τ_m and the experimental uncertainties. It can be determined by comparing results with SRLS. For example, we showed previously that for τ_m = 15 ns and typical experimental errors, eq 16 may be considered valid when S² ≥ 0.8 and τ/τ_m ≤ 0.01 (ref. ²⁷). When these conditions are fulfilled (see below) S² and τ_e are physically meaningful. Otherwise they become parameterizing entities.

When S² is high, the angle β_CM is restricted to small values, hence the cosine squared potential of the cone model is a good approximation to U/k_BT = −c²₀ P₂cos²(β_CM), where P₂ denotes the Legendre polynomial of rank 2. This represents the first term of eq 4. In this case τ_e determined with the wobble-in-a-cone model agrees with τ_ren, the wobbling rate, D_w, of the cone model represents R^L_⊥ and D_∥ = R^L_∥ → ∞. Other models, such as the Woessner model, or jumps between symmetry-related sites,⁶ yield τ_e values which can disagree with τ_ren (eq18). The quantity S², taken as the square of a generalized order parameter, is in actual fact an approximation to (S²₀)² when the time scale separation between the global and local motions is large enough, and the ordering high enough for the solution for the local motion to be given solely in terms of the D^L_MK (When (S²₀)² is not very high additional local motion eigenmodes emerge. Their presence requires a more complex description of how the correlation functions of the D^L_MK relate to the eigenmodes of a rotor in a fairly restricted (even static) potential). Quantitative evaluations of validity ranges appear in reference ²⁶.

The order parameter S²₀ is obtained in terms of U/k_BT = −c²₀ P₂cos²(β_CM) based on P_eq(β_CM) ∝ exp(−U/k_BT) (eq 4 with c²₂ = 0, and eq 11). Likewise conformational entropy (or any other thermodynamic quantity based on P_eq) is obtained directly in SRLS. In MF the local potential has to be derived from S² to calculate thermodynamic properties, notably residual configurational entropy. This is appropriate only when S² is a good approximation to (S²₀)², i.e., when the conditions specified in the previous paragraph are fulfilled. Since this is often not the case the MF-derived residual configurational entropy is likely to be inaccurate. The form of the potential is clearly ambiguous. As pointed out in the previous paragraph, other forms may not be compatible with the meaning of τ_e as given by eq 18, which can complicate their interpretation. In SRLS the potential given by eq 4 represents the leading terms in a complete expansion, and the parameters varied are the potential coefficients. The latter procedure is a general one.

For high rhombic ordering there is no analytical expression for C(t), so the ensuing spectral density, even in the R^L ≫ R^C (BO) limit, requires the full SRLS solution. We found that the actual local potential at N-H sites in proteins is rhombic. Note that in SRLS the conformational entropy can still be calculated based on P_eq using the rhombic form of the potential (eq 4) with c²₀ and c²₂ determined with data fitting.

For rigid residues, where the fast local fluctuations at the N-H site can be considered harmonic (i.e., cos²β_CM), rhombic local ordering can be treated with the 3D GAF model.⁴⁰ The local geometry is pre-determined in 3D GAF by selecting C^α_i−1−C^α_i as the principal ordering axis (z), with x perpendicular to it within the peptide plane. Contrary to 3D GAF, the SRLS approach is applicable to arbitrary local geometry and arbitrary rates of local motion.^22-25 Rhombic symmetry of the local ordering is outside the scope of MF. Taking the D and ¹⁵N CSA frames collinear in MF introduces further inaccuracies (see below).

Single-exponential approximation, τ_e; the effect of additional local motion eigenmodes

It was shown in early work that a single exponent, τ_e, is a good approximation for the multi-exponential time correlation function of the wobble-in-a-cone model.^50,51 Moreover, an analytical formula which relates τ_e to S² and the wobbling rate, D_w, was developed.⁵¹ This result is based on the assumption that eq 14 is valid, which implies the neglect of additional local motion eigenmodes. Table 1 shows the SRLS eigenvalues (and corresponding weights) which contribute to C(t) for a time scale separation τ^L/τ_m = 0.01 and potential strength decreasing from c²₀ = 20 ((S²₀)² = 0.901) to c²₀ = ((S²₀)² = 0.507). As benchmark we show the eigenvalues and associated weights when a single local motion eigenmode prevails. These include 1/τ_m (column 3) and (S²₀)² (column 1) for the global motion, and 1/τ_ren (column 2, calculated with eq 18) and (1 − (S²₀)²) (numbers in parenthesis in column 6) for the local motion. Column 7 shows the percent deviation of the correlation function for local motion from its solely D^L_KM-determined single-local-motion-eigenmode form (see above). Namely, for each value of c²₀ the numbers in column 7 (in fractional units) have to be added to wt^L (numbers without parenthesis) and wt^C to obtain the total weight of 1.

Table 1.

SRLS eigenvalues 1/τ_m (1/τ^L) of the global motion term (the main local motion term, i.e., the largest 1/τ(i) value of eq 13 with weight near to (1 – (S²₀)²), and associated weights wt^C (wt^L), as a function of c²₀ in units of k_BT (and corresponding (S²₀)² values) calculated for τ^L/τ_m = 0.01. The eigenvalues are given in units of R^L, hence 1/τ^L = 6 and 1/τ_m = (τ^L/τ_m×6). The parameter 1/τ_ren represents the renormalized local motion eigenvalue calculated with eq 18. The numbers in parentheses in column 6 show (1 – (S²₀)²). Column 7 shows the percent deviation of the correlation function for local motion from its solely D^L_KM-determined single-local-motion-eigenmode form (see above).

1	2	3	4	5	6	7
c20 ((S20)2)	1/τren	1/τm	wtC	1/τL	wtL	wMM, %
20 (0.901)	60	0.06	0.903	58.5	0.093(0.099)	0.4
10 (0.803)	30	0.06	0.800	27.9	0.172 (0.197)	2.8
8 (0.754)	24	0.06	0.757	21.6	0.202 (0.246)	4.1
6 (0.671)	18	0.06	0.676	15.4	0.239 (0.329)	8.5
4 (0.507)	12	0.06	0.512	10.0	0.294 (0.493)	19.4

It can be seen that for 4 ≤ c²₀ ≤ 20 the global motion eigenvalue is given by 1/τ_m = 0.06 and its weight, wt^C, is given within a good approximation by (S²₀)². The main local motion eigenvalue, 1/τ^L, decreases relative to 1/τ_ren with decreasing c²₀. The difference is 2.5% for (S²₀)² = 0.901 (c²₀ = 20), 10% for (S²₀)² = 0.803 (c²₀ = 10) and 16.7% for (S²₀)² = 0.507 (c²₀ = 4). The deviation of the correlation function for local motion from its solely D^L_KM-determined single-local-motion-eigenmode form is 0.4% when (S²₀)² = 0.901, 2.8% when (S²₀)² = 0.803, and 19.4% when (S²₀)² = 0.507. A typical (S²₀)² value for rigid N-H bonds is 0.8, implying 10% error in τ_e calculated with the cone model and 2.8 % error in assuming that the weight of the local motion term is (1 − (S²₀)²). This implies 3.1% error in S² which should be taken into consideration when the accuracy and precision of S² are estimated in MF studies.^11,13 The estimates given above are based on direct calculation. When S² is determined with data fitting the errors can be larger.

The time scale separation between the global and local motion is evaluated in MF based on the τ_e/τ_m ratio, which is substantially smaller than the true measure, τ^L/τ_m, and which is S²-dependent. For example, for τ^L/τ_m = 0.01 the ratio τ_e/τ_m is 0.002 for (S²₀)² = 0.8 (c²₀ = 10) and 0.003 for (S²₀)² = 0.75 (c²₀ = 7.9). As noted above for τ^L/τ_m ≥ 0.01 mixed modes (see below) contribute significantly to the spectral density. Tables 2 and 3 show the effect of τ^L/τ_m exceeding 0.01 for (S²₀)² assuming the values of 0.75 and 0.8. The numbers in parenthesis are the values corresponding to an ‘accurate’ MF formula where S² = (S²₀)² and τ_e = τ_ren. It can be seen that the errors are significant for τ_e/τ_m values which might be considered in MF analyses as representing large time scale separations. For example, while the true time scale separation is τ^L/τ_m = 0.1, MF would report on τ_e/τ_m = 0.02 (0.025) for (S²₀)² = 0.8 (0.75), corresponding to 5.3% (6.8%) mixed-mode contribution, implying increase in wt^C and decrease in wt^L, as shown in Table 2. As pointed out above, the error in the compromise value of S² determined by data fitting may be larger than the estimates of Tables 2 and 3 which are based on direct calculations. Further inaccuracies will be implied by the MF assumption that the dipolar and ¹⁵N CSA frames are collinear, and by simultaneously (S²₀)² being lower, and τ^L/τ_m being higher, than the relevant threshold values.

Table 2.

Eigenvalue (1/τ_m) and weight (wt^C) of the global motion, eigenvalue (1/τ^L) and weight (wt^L) of the main local motion mode, and contribution of additional local motion eigenmodes modes (w^MM) to C(t) as a function of τ^L/τ_m. The last column shows τ_e/τ_m corresponding to τ^L/τ_m in column 1 (eq 18). An axial potential with coefficient c²₀ = 10, corresponding to (S²₀)² = 0.8, was used. The terms in parenthesis represent the case in which the local motion is given by the eigenvalue 1/τ_ren and the weight (1 – (S²₀)²), and the global motion by the eigenvalue 1/τ_m and the weight (S²₀)².

τL/τm	1/τm	wtC	1/τL	wtL	wMM, %	τe/τm
0.01	0.06(0.06)	0.805(0.803)	27.9(30.0)	0.172(0.2)	2.8	0.002
0.030	0.18(0.18)	0.813	28.5	0.167	3.3	0.006
0.050	0.29(0.30)	0.819	29.1	0.161	3.9	0.01
0.100	0.55(0.60)	0.833	30.7	0.147	5.3	0.02
0.200	1.00(1.20)	0.858	33.8	0.119	8.1	0.04

Table 3.

Same as the title of Table 2 except that c²₀ = 7.9, corresponding to (S²₀)² = 0.75, was used.

τL/τm	1/τm	wtC	1/τL	wtL	wMM, %	τe/τm
0.01	0.06(0.06)	0.755(0.75)	21.30(23.7)	0.234(0.25)	1.6	0.003
0.030	0.18(0.18)	0.763	21.81	0.201	4.9	0.008
0.050	0.29(0.30)	0.770	22.32	0.196	5.4	0.013
0.100	0.55(0.60)	0.788	23.61	0.182	6.8	0.025
0.200	1.00(1.20)	0.818	26.23	0.158	9.2	0.051

2c. The extended MF formula.⁸

When eq 16 cannot fit the experimental data the extended MF spectral density, given by:

$$\mathrm{J}\left(\omega \right)={{\mathrm{S}}_{\mathrm{f}}}^2[{{\mathrm{S}}_{\mathrm{s}}}^2{\tau }_{\mathrm{m}}∕(1+{\omega }^2{{\tau }_{\mathrm{m}}}^2)+(1-{{\mathrm{S}}_{\mathrm{s}}}^2){{\tau }_{\mathrm{s}}}^{,}∕(1+{\omega }^2{{\tau }_{\mathrm{s}}}^{,2})]+(1-{{\mathrm{S}}_{\mathrm{f}}}^2){{\tau }_{\mathrm{f}}}^{,}∕(1+{\omega }^2{{\tau }_{\mathrm{f}}}^{,2}),$$ (19)

has been used. The parameter τ_f is taken as the effective correlation time for the fast local motion, τ_s as the effective correlation time for the slow local motion, and S_s² and S_f² as squared generalized order parameters associated with these motions. 1/τ_f′ = 1/τ_f + 1/τ_m and 1/τ_s′ = 1/τ_s + 1/τ_m. No effort is made to define any geometric relationships between the axes of fast and slow local motions. Although eq 19 requires that τ_f << τ_s << τ_m, in practice this formula is used when τ_s is on the order of τ_m.

2d. The extended MF formula as a SRLS asymptote

As shown previously, an expression similar to equation 19 was obtained in early work as a perturbational expansion of the SRLS solution in rhombic local ordering in the R^L >> R^C limit for β_MD ≠ 0° (ref. ³⁰) Let us reiterate the basics of this derivation. J^DD(ω) is given by eq 10, the functions j_K(ω) are given by eq 13, and setting β_MD = 90° implies A = (1.5cos²β_MD − 0.5)² = 0.25, B = 3 cos²β_MD sin²β_MD = 0 and C = 0.75 sin⁴β_MD = 0.75 (A, B and C represent (d²₀₀)², 2 (d²₀₁)² and 2 (d²₀₂)², respectively, where ‘d’ denotes reduced Wigner rotation matrix elements). The function J^DD(ω) is then given by:

$$\begin{array}{cc}\hfill {\mathrm{J}}^{\mathrm{DD}}\left(\omega \right)=& [0.25{\left({{\mathrm{S}}^2}_0\right)}^2+0.75{\left({{\mathrm{S}}^2}_2\right)}^2]{\tau }_{\mathrm{m}}∕(1+{\omega }^2{{\tau }_{\mathrm{m}}}^2)+0.25[1-{\left({{\mathrm{S}}^2}_0\right)}^2]{\tau }_0∕(1+{\omega }^2{{\tau }_0}^2)+0.75[1-{\left({{\mathrm{S}}^2}_2\right)}^2]\hfill \\ \hfill & {\tau }_2∕(1+{\omega }^2{{\tau }^2}_2).\hfill \end{array}$$ (20)

Assuming that J(ω) = J^DD(ω) = J^CC(ω) eq 20 is formally analogous to the extended MF formula⁸ (eq 19) with τ_s formally equivalent to τ₀, τ_f to τ₂, and the squared generalized order parameters, S_s² and S_f², related to (S²₀)² and (S²₂)² as:

$${{\mathrm{S}}_{\mathrm{f}}}^2=0.25+0.75{\left({{\mathrm{S}}^2}_2\right)}^2$$ (21)

and

$${{\mathrm{S}}_{\mathrm{s}}}^2=({{\mathrm{S}}_{\mathrm{f}}}^2-0.25)∕{{\mathrm{S}}_{\mathrm{f}}}^2+0.25{\left({{\mathrm{S}}^2}_0\right)}^2∕{{\mathrm{S}}_{\mathrm{f}}}^2.$$ (22)

The equivalence outlined above is only formal. Equation 19 is a physically vague mathematical formula whereas eq 20 is a physically precise geometric model based on SRLS. Note also that other SRLS models, such as one, which features an additional mode of internal motion, would yield the form of eq 19 in a perturbational limit.

For τ_f, τ_s << τ_m (representing the R^L >> R^C limit) and very low local ordering ((S²₀)² → 0 and (S²₂)² → 0 implied by the perturbation limit) one obtains S_f² ∼ 0.25 and S_s² ∼ 0 when eqs 21 and 22 are used. The corresponding time correlation function is shown by the dashed curve in Fig. 3b. However this C(t) function is never used to analyze N-H bond dynamics in proteins since the local ordering at the N-H site is significantly higher than S_f² ∼ 0.25 and S_s² → 0, and τ_s is on the order of τ_m rather than being much smaller than τ_m. A typical parameter set obtained with MF analysis for flexible residues in proteins is given by τ_f ∼ 20 ps, τ_s ∼ 10 ×τ_f, τ_m ≥ 10×τ_s, S_f² ∼ 0.75 and S_s² ∼ 0.55. The corresponding time correlation function C(t) is shown by the solid curve in Fig. 3b. Table V of reference ²³ (where the SRLS theory has been fully developed) shows quantitatively that mode-mixing dominates the time correlation function when τ_m ≥ 10×τ_s and the ordering is (S²₀)² ∼ 0.55 (corresponding to c²₀ ∼ 4.4). In this case the spectral densities given by eq 13 instead of spectral densities given by eq 17 are to be used. For rhombic ordering not only diagonal terms, j_KK(ω), but also cross-terms, j_KK′(ω), need to be considered. J^x(ω) obtained from j_KK′(ω) by frame transformations (determined by the specific local geometry) are therefore complex functions. In the MF formulation J(ω) = J^DD(ω) = J^CC(ω) is the Fourier transform of the simple function shown by the solid line in Fig. 3b, with the plateau values determined by S_f² and S² = S_s²×S_f² and the step between them monitored by τ_s. Therefore when force-fitting is successful, i.e., the statistical requirements are fulfilled this can be only accomplished with highly inaccurate best-fit parameters which constitute parameterizing entities. The latter are field-dependent since parameterization by force-fitting depends on which J(ω) values are to be reproduced. The fitting of larger data sets obtained by combining multi-field data is likely to fail when standard fitting schemes are used. The trends in the values of the best-fit parameters upon changing environmental conditions such as temperature and complex formation are devoid of physical meaning, and may show abrupt changes, which are not associated with genuine physical phenomena. These features are illustrated below.

Table 5.

Results of fitting with SRLS and MF the experimental data of eight VHHS residues fit with model 1 by Vugymeyster et al.¹¹ Squared SRLS order parameters, (S²₀)², obtained from the best-fit c²₀ values using eq 4 with c²₂ =0, and eq 11, and best-fit MF S² values, are shown. The corresponding χ² values are also given. The data in parentheses were obtained with the SRLS program where the ¹⁵N-¹H dipolar and ¹⁵N CSA tensors were set deliberately collinear. %diff is the percent difference between the MF and SRLS squared order parameters divided by the SRLS value. The last two columns show the experimental NOE error and the percent difference (%D_max) between the experimental NOE and the maximum NOE obtained for a rigid sphere.

	SRLS	MF		SRLS	MF	NOE
res	(S20)2	S2	%diff		χ2	%err	%Dmax
45	0.842	0.804 (0.803)	−4.5	6.44	1.7 (1.7)	2.1	1.4
49	0.853	0.817 (0.815)	−4.2	2.1	2.2 (2.2)	1.9	0.0
57	0.887	0.847 (0.845)	−4.5	6.6	1.7 (1.8)	2.2	2.1
58	0.908	0.869 (0.860)	−4.3	34.0	15.5 (20.0)	2.2	7.7
59	0.898	0.855 (0.853)	−4.8	19.0	12.6 (14.2)	2.4	3.5
60	0.849	0.810 (0.810)	−4.6	27.0	18.7 (19.0)	3.3	16.0
69	0.853	0.815 (0.814)	−4.5	15.6	7.7 (7.9)	2.2	4.5
71	0.841	0.803 (0.803)	−4.5	12.0	3.1 (3.3)	1.9	3.1

The extended MF formula is based on the theory of moments, which is a mathematical approach that ignores physical details for convenience. The physical principles underlying NMR spin relaxation in locally orienting environments have been set forth previously.^52a The important structural/electronic/charge-related information one can extract when the restrictions on the local motion are properly treated as potentials or ordering tensors have been illustrated amply in the literature (e.g., ref 52b). Within the scope of these established approaches the solution offered by the extended MF formula to N-H bond motion in proteins is physically not reasonable. The very same entity (the cylindrical N-H bond) cannot be involved in two separate motions which are isotropic (as manifested by the scalar quantities τ_s and τ_f) and at the same time restricted (as manifested by S_s² and S_f²). The simplification to isotropic local motion, is certainly not justified for the restricted slow motion, τ_s, as τ_s ∼ τ_m. It is not reasonable to have no geometric relationship whatsoever between the fast and slow local motions. The very same (internal) protein environment cannot exert multiple different restrictions on the same body. The global motion (τ_m) cannot occur on the same time scale as the slow local motion (τ_s) and at the same time not lead to mixed modes. A restricted motion can be nearly ‘decoupled’ from the slowly relaxing environment, which exerts the spatial restrictions, only when these processes occur on very different time scales (R^L_∥/R^L_⊥ >> 1) and the ordering (S²₀ and S²₂) is so small that it constitutes a perturbation on the free motion, or so large that the local motion correlation times become renormalized by the strong local potential. Only in this case can mode-mixing be ignored. Accounting for the correct local geometry (β_MD on the order of 90° in the present case) one may use the analytical function given by eq 20, which is assembled from the simplified functions j_K(ω) given by eq 17. In this case eq 20 describes properly an axially diffusing N-H bond in the presence of a weak rhombic potential. Note that even in this limit the global and local modes are only nearly ‘independent’ since the terms (S²_K)² (τ^L_K)/(1 + ω²(τ^L_K²), K = 0 and K = 2, actually represents statistical interdependence.⁴⁸

A numerical example, which illustrates the distorted picture obtained by using the extended MF formula outside the perturbation limit is shown in Table 4.

Table 4.

Squared axial ((S²₀)²) and rhombic ((S²₂)²) SRLS order parameters in irreducible tensor notation, corresponding order parameters (S_xx, S_yy and S_zz) in Cartesian tensor notation, and corresponding squared generalized MF order parameters (S_f² and S_s², based on using eqs 21 and 22). The coefficients c²₀ and c²₂ determine the potential U/k_BT in terms of which S²₀ and S²₂ are defined (eq 11).

c20	c22	(S20)2	(S22)2	Ss2	Sf2	Sxx	Syy	Szz
2	3	0.008	0.327	0.50	0.50	0.306	−0.394	0.088

The coefficients c²₀ = 2 and c²₂ = 3 represent rhombic Y_M ordering with ‘nearly planar Y_M-X_M′ symmetry, which we found previously to prevail at the N-H site.²⁶ This symmetry is reflected clearly in the principal values, S_xx, S_yy and S_zz, of the Cartesian tensor. In irreducible tensor notation one has S²₀ = 0.089 and S²₂ = 0.572 (Table 4 shows the squared values of S²₀ and S²₂, which appear in eq 20). The corresponding MF parameters are S_s² = 0.50 and S_f² = 0.50. The physical picture of two independent isotropic local motions of the N-H bond associated with squared generalized order parameters (incidentally) equal to 0.5 is certainly different from the physical picture associated with an axial N-H bond diffusing in a well-defined rhombic local potential associated with a well-defined ordering tensor with its Y_M axis aligned preferentially along the C^α_i-1-C^α_i axis (or the N_i-C^α_i bond).

In practice a reduced form of eq 19, where τ_f′ is set equal to zero, is used in MF studies. The reason for this simplification is that standard MF fitting schemes can typically only fit three-point single-field data sets, precluding the variation of τ_f as a free parameter in addition to S_s², S_f² and τ_s. Values of S_f² are typically in the range of 0.8-0.9. The weight of the last term of eq 19 is (1 – S_f²). Hence a 20-10% contribution is being ignored when the reduced extended MF formula is used, implying further inaccuracies in the best-fit parameters. This can also be realized noticing that formally the reduced extended MF formula is given by J(ω) = S_f²×j₀(ω), where j₀(ω) = S_s² τ_m/(1 + ω²τ_m²) + (1 – S_s²) τ_s′/(1 + ω²τ_s′²) has the form of the K = 0 perturbational expansion (eq 17) featuring the squared order parameter S_s² and local motional correlation time τ_s′. This is analogous to J^DD(ω) = A j_K(0) in SRLS, with the K = 1 and K = 2 terms set equal to zero in eq 10. We call this form of J^DD(ω) (and ensuing J^CC(ω)) ‘combination 5’, in analogy with model 5 MF (the term ‘combination’ is used instead of ‘model’ since the hierarchy consists of different parameter combinations within the scope of the same model). Setting B j₁(ω) = C j₂(ω) = 0 in eq 10 was considered justified based on the relation R^L_∥ >> R^L_⊥ (implicit in the calculation) which is analogous to τ_s >> τ_f in MF.

The fact that the coefficient A is returned by the fitting scheme as 0.8 – 0.9 instead of unity means that in the presence of significant mode-mixing the K = 1 and K = 2 terms will still contribute to J^DD(ω) even though RL_∥ >> R^L_⊥. This has been verified by us with relevant calculations.¹⁹ While SRLS combination 5 is certainly a better spectral density than MF model 5, since j₀(ω) SRLS accounts for mode-mixing while j₀(ω) MF does not, it still misses 10-20% contributions, to be absorbed by the best-fit parameters. As shown below, a consistent physical picture is only obtained with rhombic instead of axial ordering, and arbitrary instead of very high local diffusion anisotropy, R^L_∥/R^L_⊥.

In summary, the mathematical model-free formulae were introduced as parameterizing spectral densities.^6-8 Independently the stochastic SRLS model has been developed first in the perturbation limit for certain simplified geometries,^48,30 in the BO limit for axial ordering and isotropic local motion,²⁸ and in its general form.^23,24 It turned out that (1) the original MF formula is given by the SRLS solution in the BO limit and the extended MF formula is given by the perturbational expansion of ref. 30, (2) N-H bond dynamics exceeds the perturbation limits and in most cases the BO limit, (3) mode-coupling and general features of local geometry, ignored in both limits, are important, and (4) MF analysis does not stop at the stage of parameterization but proceeds by interpreting the parameterizing quantities in terms of physical quantities (order parameters, correlation times) inherent to the SRLS model. This justifies the assessments associated with the implications of interpreting the MF parameters in terms of physical quantities.

2. Practical implementation of the theoretical premises of SRLS and MF

The basic idea underlying the MF approach is to reproduce the spectral density assuming statistical independence (decoupling) between the mobility of the probe and the mobility of the protein.^6-8 This requires large time scale separation between these motions. Based on the theory of moments analytical expressions for the spectral density were suggested. The price paid for simplicity becomes relevant when the parameters obtained by data fitting^46,47 are interpreted within the scope of specific models. The MF formulae only agree with high symmetry of the various physical quantities featured, and accommodate only simplified local geometry, besides requiring mode-decoupling. Hence the usage of MF is prone to overextension.

A different but related idea is to envision the overall system to be composed of two bodies, probe and protein, with mobilities coupled by a phenomenological potential energy function. An established set of dynamic variables is modulated according to an explicit model, typically based on stochastic operators. Contrary to MF there is no pretence for generating a universal tool. Instead there is an attempt to treat the experimentally relevant situations within the scope of rigorous formal frameworks. The computational burden is greater than that of the analytical model-free formulation.

The SRLS model features such a framework. It is based on a Smoluchowski equation representing the rotational reorientation of two interacting rotors (bodies).^23,24 SRLS was applied earlier to molecular probes in complex fluids and ESR spin relaxation in bio-macromolecules.^25,27 Recently we applied SRLS to NMR spin relaxation in proteins.^{19,20,22,26,27} In this application the two rotors are represented by the locally reorienting spin-bearing moiety (e.g., the N-H bond), and the globally reorienting protein. The global and local motions are described at the diffusive level, hence characterized by two distinct diffusion tensors. The coupling potential, which expresses the spatial restrictions imposed by the immediate protein surroundings at the site of the motion of the probe, depends upon the mutual orientation of the coupled rotors. The physical quantities may be asymmetric, and features of general local geometry are accommodated. Obviously mode-coupling is accounted for rigorously.

Results were compared with MF. SRLS is clearly the generalization of MF, yielding the latter in asymptotic limits. We found that the MF formulae are poor approximations of the experimental spectral density. On the other hand, the SRLS solution appears to match the integrity of currently available experimental data.

The practical problem with SRLS is computational efficiency, as in some cases the (numerical) calculation of the SRLS spectral densities is significantly more demanding than the instantaneous calculation of the simple analytical MF formulae. Otherwise the SRLS and MF fitting schemes are similar. In our first implementation of SRLS in a fitting scheme we pre-calculated 2D grids of spectral density values which were then used as look-up tables. This program is comparable in speed with the MF programs, and is operated in the same way. The best-fit parameters are formally (but not physically) analogous to the parameters of the extended MF formula. The deficiencies of this scheme are that (1) the global motion is isotropic and determined separately from the local motion (similar to the MF strategy), and (2) the symmetry of the local restrictions is axial, as in MF. We found that these limitations must be eliminated. To this end we developed recently a fitting program for SRLS where the generic spectral densities (eq 13) are calculated on the fly. In terms of operating it the only extra requirement on the part of the user is to determine a truncation parameter which controls the number of terms which need to be taken into account for convergence of the solution (given by eq 13 or similar equations). Several trial and error calculations carried out for typical cases suffice. Some aspects of this program are still under development. It is expected that this effort will be brought to completion shortly, at which time this general fitting scheme will be made available to the community. The 2D-grid-based fitting scheme, as well as and the 2D grids, are available upon request. The ‘Theoretical background’ section of this paper comprises all the information needed for ab initio programming.

III. Results and Discussion

1. SRLS versus MF analysis in the asymptotic limit

1a. Geometric effects: the D → CSA frame transformation

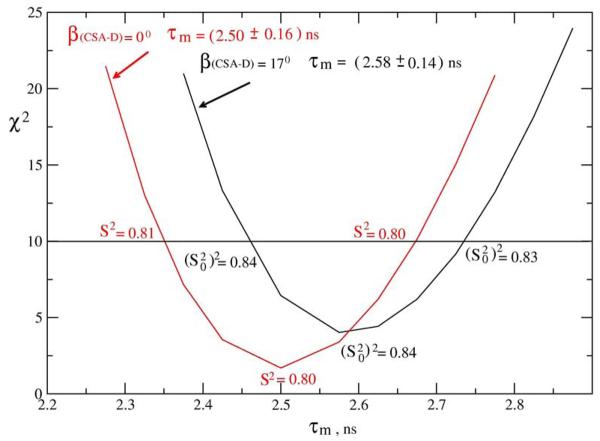
When τ_e is very small the second term in the MF formula (eq 16) can be ignored, yielding the so-called MF ‘model 1’. In this limit the difference between SRLS and MF consists solely of the D-CSA transformation carried out in SRLS and omitted in MF. The implications of this approximation are illustrated below using the experimental data obtained at 295 K, 11.7 T, by Vugmeyster et al.¹¹ for eight out of the 35 residues of the Villin Headpiece Helical Subdomain (VHHS) which were analyzed with MF model 1. τ_m = 2.5 ns was determined based on T₁/T₂ ratios.⁵³ We subjected these data to model 1 MF analysis using the program Modelfree 4.0,⁴⁶ and to combination 1 SRLS analysis using our fitting scheme for axial potentials.²² From S² MF we calculated c²₀ using eq 4 with c²₂ =0, and eq 11. In SRLS we varied c²₀ and calculated (S²₀)² using eq 4 with c²₂ =0, and eq 11. The results are shown in Table 5.

The data in parentheses, obtained by setting D and CSA deliberately collinear in the fitting program for SRLS, are practically identical with the corresponding MF data. This indicates that the two programs perform identically when the D and CSA frames coincide. Thus, the differences between corresponding data in columns 2 and 3 are due solely to the D-to-CSA frame transformation which was carried out for a tilt angle θ =17° (ref. ³) in SRLS and omitted in MF. Underestimation of (S²₀)² by MF on the order of 4.5% is not negligible given that currently reported precision in S² is, in some cases, on the order of 1% (ref. ¹¹) and the precision in the average value of S² on the order of 0.2% (ref. ¹³). The error in S² has severe implications for conformational entropy calculations (see below). Recently θ = 21.4° was determined with an extensive Ubiquitin data set.⁵⁴ The larger angle θ implies even greater inaccuracies than shown in Table 5.

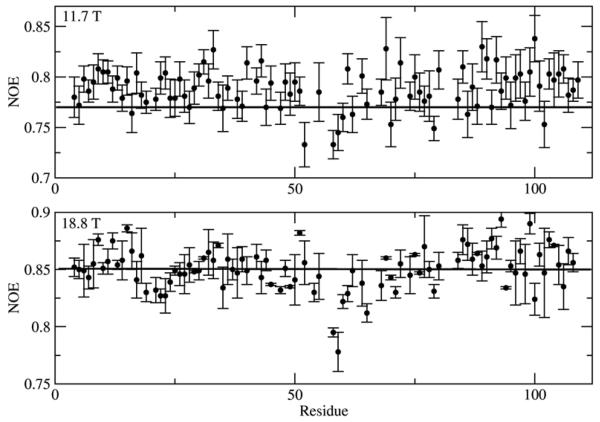
MF is clearly force-fitting the experimental data yielding S² and corresponding c²₀ values which are too low. Table 6 illustrates this using the experimental data of residue 49 of VHHS. Back-calculated ¹⁵N T₁, T₂ and ¹⁵N-{¹H} NOE relaxation parameters obtained with the best-fit SRLS and MF order parameters of Table 5 are shown in Table 6a aside the experimental data. Table 6b shows the specific J(ω) values associated with the back-calculated T₁, T₂ and NOE data of Table 6a. It can be seen that the MF spectral density can fit the experimental data as well as the SRLS spectral density (Table 6a) by compensation of the individual J(ω) values (Table 6b). In particular, MF yields smaller J^DD(ω) values and larger J^CC(ω) values than their correct SRLS counterparts. Note the significantly different values of J^DD(0) and J^DD(ω_N) versus J^CC(0) and J^CC(ω_N) in SRLS, implied by carrying out the D-to-CSA frame transformation. Also note that (with one exception) the experimental NOE exceeds the maximum NOE as shown by %D_max > 0 (Table 5). This feature will be discussed below in detail.

Table 6a.

Experimental and back-calculated SRLS and MF ¹⁵N T₁, T₂ and ¹⁵N-{¹H} NOE values obtained with the best fit squared order parameters shown in Table 5 for residue 49. In this Table, and in all of the Tables and Figures below where T₁, T₂ and NOE were calculated, we used ¹⁵N CSA of σ_∥ – σ_⊥ = −170 ppm, r_NH = 1.02 Ǻ (e.g., ref 11) and θ = 17° (ref. ³).

	T1 [ms]	T2 [ms]	NOE
Exp	381.2±6.1	251.5±3.1	0.565±0.011
SRLS	387.8	250.9	0.5533
MF	386.7	249.5	0.5758

Table 6b.

J(ω) values for ω = 0, ω_N, ω_H+ω_N, ω_H and ω_H−ω_N for dipolar auto-correlation and ¹⁵N CSA auto-correlation. The c²₀ values (and the corresponding (S²₀)² values from Table 5) used in these calculations are given under the heading ‘Input’. τ_m = 2.5 ns was used. The units of J(ω) are ns/rad.

Input			Output
	(S20)2	c20	JDD(0)	JDD(ωN)	JDD(ωH+ωN)	JDD(ωH)	JDD(ωH−ωN)	JCC(0)	JCC(ωN)
SRLS:	0.853	13.5	0.854	0.523	0.0168	0.0130	0.0113	0.651	0.398
MF:	0.817	10.8	0.817	0.500	0.0161	0.0130	0.0108	0.817	0.500

1b. Local motion effects

The ¹⁵N relaxation data of 21 VHHS residues were fit by Vugmeyster et al.¹¹ with model 2, where the complete original MF formula (eq 16) is used. We subjected 15 out of 21 residues to SRLS analysis using combination 2 and repeated the calculations of Vugmeyster et al.¹¹ using the same computer program (Modelfree 4.0). The average results obtained for the squared order parameters and the associated c²₀ values are shown in Table 7 under the heading ‘model 2’. For comparison the average results of Table 5, including c²₀ corresponding to the squared order parameters, are also shown under the heading ‘model 1’.

Table 7.

Average c²₀ and corresponding (S²₀)² best-fit SRLS parameters. Average S² and corresponding c²₀ best-fit MF parameters. %diff represents 100×[param(MF) − param(SRLS)]/param(SRLS).

	Model 1			Model 2
	SRLS	MF	%diff	SRLS	MF	%diff
(S20)2	0.87	0.83	−4.5	0.73	0.78	+6.8
c20	15.4	11.7	−23	7.5	9.0	+20

The differences featured by the ‘model 1’ SRLS and MF results stem solely from the geometric D → CSA frame transformation. The differences featured by the ‘model 2’ SRLS and MF results stem from the D → CSA frame transformation, and from the effect of additional local motion eigenmodes on the form of the local motion correlation function, accounted for in SRLS and ignored in MF. SRLS yielded <τ^L/τ_m> = 0.1 whereas MF yielded <τ_e/τ_m> = 0.02 (data not shown). If τ^L would be derived from τ_e according to eq 18 then the MF time scale separation would have been 0.09, which is close to its SRLS counterpart (differing by only 10%).

Table 7 shows that S² over-estimates (S²₀)² by nearly 7% in model 2 and under-estimates it by approximately 4.5% in model 1. As already mentioned, this has implications for the precision of S² MF. Most importantly, it affects the accuracy of thermodynamic parameters calculated from potentials derived from S² MF.^33-36 The coefficient c²₀ of the general form of the potential (eq 4 with c²₂ = 0) is very sensitive to changes in (S²₀)² when (S²₀)² is high, as shown in Fig. 4 which is the graphical representation of eq 4 with c²₂ = 0. Because of the asymptotic form of the (S²₀)² versus c²₀ curve as (S²₀)² → 1, relatively small uncertainty in (S²₀)² imply large uncertainty in c²₀. For example, in Table 5 the S² errors cover the range between −4.5% and 6.8% whereas the c²₀ errors cover the range between −23% and 20%. Note that these large errors in the strength of the potential, hence in the probability distribution function P_eq = exp(-U/_BT), stem solely from the geometric effect of omitting the D-to-CSA frame transformation. Significantly larger inaccuracies are implied by also disregarding the possibility that the correlation function for local motion has a more complex form implied by the presence of additional eigenmodes, and over-simplifying the symmetry of the local ordering.

Figure 4.

Squared order parameter, (S²₀)² as a function of the potential coefficient, c²₀ (in units of k_BT) determined with eq 4 with c²₂ = 0, and eq 11.

As discussed above, the effective correlation time, τ_e, typically reported in MF studies as a ‘correlation time for local motion’, is actually a composite, approximately given by 2τ^L/c²₀ (eq 18). For S²=0.8, 0.9 and 0.95, corresponding to c²₀ = 10, 20 and 40, respectively, the parameter τ_e is 5, 10 and 20 times smaller than τ^L = 1/6R^L. The ratio τ_e/τ_m grossly over-estimates what is considered to represent the time scale separation between the rate of global reorientation (R^C) and the rate of local reorientation (R^L) (note that 1/τ_m and 1/τ_e are global motion mode and main local motion mode eigenvalues, respectively, whereas R^C = 1/6τ_m and R^L=1/6τ^L are ‘bare’ diffusion constants for global and local motion, respectively). This may lead to inclusion of non-rigid residues into data sets used to determine τ_m from T₁/T₂,⁵³ and improper usage of the Reduced Spectral Density^55-57and model-independent⁵⁸ approaches which are only valid when the local motion correlation time, τ^L, is very fast. It was observed by several authors^14-16 that τ_e is nearly invariant as a function of temperature. This is not surprising since τ_e ∝ τ^L/c²₀, with both the numerator and the denominator decreasing with increasing temperature. While τ^L may exhibit Arrhenius-type temperature dependence, τ_e might not.

1c. General considerations

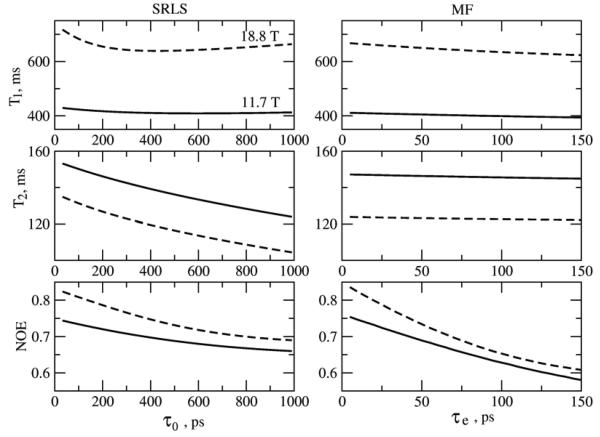
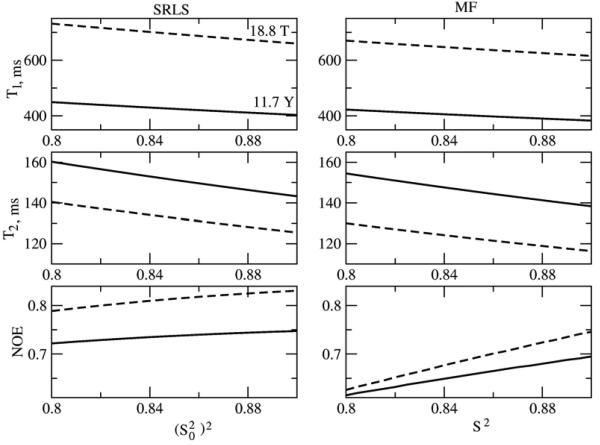
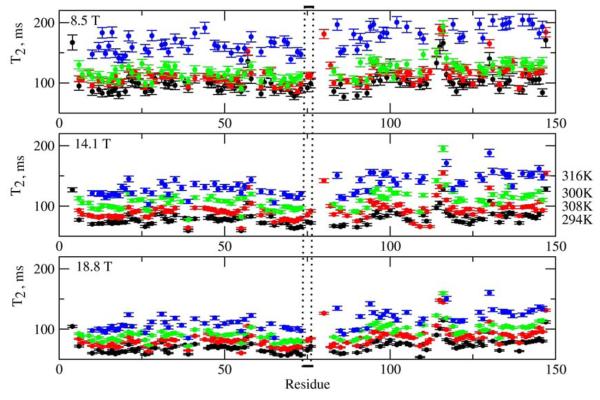
Illustrative simulated SRLS and MF T₁, T₂ and NOE values are shown in Figs. 5-8 for the parameter range where the original MF formula is typically applied. High ordering ((S²₀)² = 0.85) and large time scale separation (τ_e/τ_m = 0.015 when τ_m = 5 ns, and τ_e/τ_m = 0.005 when τ_m = 15 ns) were used. In Figs. 5 and 7 c²₀ is fixed at 13.2, corresponding to (S²₀)² = 0.85. In the SRLS calculations the local motion correlation time, τ^L = 1/6R^L, is varied from 0 to 1000 ps (curves on the left). The corresponding MF effective local motion correlation time, τ_e = 2τ^L/c²₀ = τ^L/6.6, is varied from 0 to 150 ps (curves on the right). The global motion correlation times are τ_m = 5 and 15 ns, and the magnetic fields are 11.7 and 18.8 T. For fixed τ_m the parameter τ^L (τ_e) represents the time scale separation τ^L/τ_m (τ_e/τ_m). The SRLS and MF relaxation parameters in Figs. 5 and 7 were calculated using the same physical input (i.e, τ^L = 1/6R^L in SRLS and τ_e = 2 τ^L/c²₀ in MF, with all the other parameters the same). It can be seen clearly that all the SRLS relaxation parameters depend significantly on τ^L/τ_m in ways which differ for low and high fields and small and large proteins (or high and low temperatures). On the other hand, in the parameter range considered, the MF T₁ and T₂ values vary to a small extent as a function of τ_e/τ_m, whereas the MF NOE's vary significantly in ways which differ from the variations in the SRLS NOE's.

Figure 5.

¹⁵N T₁, T₂ and NOE calculated with SRLS (J^DD(ω) was calculated according to eq 10, and J^CC(ω) as explained after eq 9) and MF (eq 16) for τ_m = 5 ns, 11.7 and 18.8 T, as a function of τL = τ₀ = 1/6R^L (left - SRLS) and corresponding τ_e = 2τ₀/c²₀ (right – MF). The potential coefficient c²₀ = 13.2, corresponding to (S²₀)² = 0.85, was used.

Figure 8.

¹⁵N T₁, T₂ and NOE calculated for τ_m = 15 ns, 11.7 and 18.8 T, as a function of the squared order parameter, (S²₀)² (left - SRLS), and the generalized squared order, S² (right - MF). The potential coefficient c²₀ = 13.2, corresponding to (S²₀)² = 0.85, and was used. τ₀ = 75 ps in SRLS, and τ_e = 75 ps in MF, were used.

Figure 7.

¹⁵N T₁, T₂ and NOE calculated for τ_m = 15 ns, 11.7 and 18.8 T, as a function of τ^L = τ₀ = 1/6R^L (left - SRLS) and corresponding τ_e = 2τ₀/c²₀ (right - MF). The potential coefficient c²₀ = 13.2, corresponding to (S²₀)² = 0.85, was used.

Table 8 shows the percent difference between 1/T₁, 1/T₂ and NOE shown in Figs. 5 and 7 calculated with SRLS for τ^L = 495 ps and MF for τ_e = 75 ps. These data illustrate clearly the field-dependence of the best-fit MF parameters. In this example the features which are likely to yield different results at different fields are the opposite trends in the 1/T₁ discrepancy between SRLS and MF at 11.7 and 18.8 T for τ_m = 5 ns, and the very large field-dependence of the NOE discrepancy for τ_m = 15 ns. Clearly, fitting of combined multi-field data is expected to be problematic and in most cases impossible with MF, as often encountered in practice.

Table 8.

Percent difference ((var_MF-var_SRLS)/var_SRLS), where ‘var’ represents 1/T₁, 1/T₂ or NOE from Figs. 5 and 7 for τ^L = 495 ps and the corresponding value of τ_e = 75 ps. The potential coefficient c²₀ = 13.2 ((S²₀)² = 0.8) was used. The τ_m values and the magnetic field strengths are given in the Table.

%diff versus SRLS	1/T1,1/s	1/T2, 1/s	NOE
5 ns, 11.7 T	+0.8	−6.2	−4.3
5 ns, 18.8 T	−1.3	−5.2	−6.8
15 ns, 11.7 T	−5.9	0.0	−4.8
15 ns, 18.8 T	−18.2	+4.4	−16.7

Another feature illustrated in Table 8 is the field-dependence of the deviation of the MF T₁/T₂ value from the SRLS T₁/T₂ value implying field-dependent τ_m values, as often encountered in MF analyses. The relaxation parameters shown in Figs. 5 and 7 were calculated with the proper analogy between SRLS and MF local motion correlation times, i.e., τ^L SRLS corresponds to τ_e = 2τ^L/c²₀ MF. The relaxation parameters shown in Figs. 6 and 8 were calculated with the improper analogy, i.e., τ^L SRLS the same as τ_e MF. This is done to show how misleading it is to consider τ_e as representing a bare (i.e., 1/6R^L) local motion correlation time, although Lipari and Szabo⁶ indicated that this quantity is a composite. For example, one expects Arrhenius-type temperature dependence of τ_e, and obtains typically near temperature independence. Within the scope of the wobble-in-a-cone model τ_e depends on D_w and S² (ref. ⁶). The physical parameter is the wobbling rate, D_w. If τ_s and S_s², obtained from data dominated by mode-coupling, are used in this context the implications can be detrimental, as shown in section 5d.

Figure 6.

¹⁵N T₁, T₂ and NOE calculated with SRLS and MF for τ_m = 5 ns, 11.7 and 18.8 T, as a function of the squared order parameter, (S²₀)² (left - SRLS) and the generalized squared order, S² (right - MF). The potential coefficient c²₀ = 13.2, corresponding to (S²₀)² = 0.85, and was used. τ₀ = 75 ps in SRLS, and τ_e = 75 ps in MF, were used.

Figs. 5 and 7 show that SRLS relaxation rates calculated with τ^L agree reasonably with MF relaxation rates calculated with τ_e = 2τ^L/c²₀ for τ^L < 200 when τ_m = 5 ns, and for τ^L < 100 ps when τ_m = 15 ns. On the other hand, when τ_e = τ^L (Figs. 6 and 8) the agreement between the T₁ and T₂ values is reasonable (since in MF T₁ and T₂ depend only to a small extent on τ_e - see Figs. 5 and 7) but the NOE's differ significantly. This is precisely the empirical observation, which motivated the development of the extended MF formula⁸ commonly used in its reduced version. In the reduced extended MF formula a slow effective correlation time, τ_s, adjusts the NOE, whereas a scaling factor, S_f², adjusts 1/T₁ and 1/T₂. This is related intimately to the ‘mode-independent’ form of this formula, with τ_m affecting predominantly the global motion term, τ_s affecting exclusively the local motion term, and neither affecting the weights of these terms. On the other hand, in SRLS the motional rates and the potential coefficients determine the weights of the various modes contributing to the spectral density, and the eigenvalues of the solution differ from the pure ‘mode-independent’ eigenvalues 1/τ_m and 1/τ^L. The MF parameterization of the spectral density impairs statistical properties of genuine fitting. For example, Vugmeyster et al.¹¹ reported on a non-normal t-distribution in NOE values back-calculated using best-fit MF parameters obtained with models 1 and 2.

1d. τ_m determination

In MF the determination of the global diffusion tensor⁵³ is implicitly based on the ‘Born-Oppenheimer’ type approximation inherent in factoring C(t) into C^L(t)×C^C(t) (eq 14). When C^C(t) = exp(-t/τ_m), i.e., the protein is spherical, and C^L(t) is given by the first term of eq 16 (model 1, where τ^L = 0), then deriving τ_m from T₁/T₂ is appropriate in SRLS, but in MF it is as inaccurate as implied by the omission of the D-to-CSA frame transformation. The various filtering procedures devised to extract from the complete data set the sub-set used for R^C determination⁵³ do not eliminate data, which correspond to the original MF formula (eq 16) (‘model 2’, where τ^L ≠ 0). The high sensitivity to τ^L of T₁ and T₂ for small proteins (Fig. 5), and T₁ for large proteins (Fig. 7), indicates that significant errors will be introduced by including ‘model 2‘ data in the process of R^C determination. When C^C(t) corresponds to axial global diffusion and/or C^L(t) corresponds to eq 19, the full SRLS time correlation function is to be used. Very precise τ_m values were reported recently by an MF study¹⁵ where C(t) was used in the fitting process, with C^C(t) corresponding to axial global diffusion and C^L(t) given by eqs 16 and 19. For the reasons outlined above the accuracy and precision of these results should be reassessed.

As shown below, when axial potentials are used model 1 is often selected instead of model 2 by force-fitting, yielding unduly high (S²₀)² values. This has been documented in the literature by a recent SRLS application to nitroxide-labeled biomacromolecules which showed that force-fitting by using model 1 on a set of synthetic data which correspond to model 2, generates (S²₀)² values which are too high and τ_m values which are too low.²⁵ The discrepancies increase with increasing magnetic field.²⁵ These are precisely the trends observed with MF analyses - higher S² and lower τ_m at higher fields.

We found that a useful method for estimating the precision of τ_m is to first determine it from T₁/T₂ ratios (desirably acquired at low magnetic fields) of combination 1 fits, where τ^L → 0, and then scan the vicinity of this value. Illustrative calculations were carried out for residue 45 of VHHS acquired at 11.7 T, 295 K, fit by Vugmeyster et al.¹¹ with MF model 1. The T₁/T₂-derived τ_m value is 2.5 ns. χ² values obtained as a function of τ_m within a ±0.5 ns range centered at τ_m = 2.5 ns, using SRLS (black curve) and MF (red curve) are shown in Fig. 9. Let us assume that χ² = 10 is the threshold (Vugmeyster et al.¹¹ set χ² = 25 as threshold for the site-specific fitting). It can be seen that in both cases practically identical (S²₀)² (S²) values are obtained for τ_m within a range of 5-6% from the 2.58 (2.50) ns minimum. We believe that this is a realistic estimate of the precision with which τ_m can be currently determined in the BO limit for axial local ordering. Precision estimates of 0.2% (ref. ¹⁵) are highly over-rated. As shown in Fig. 9 about 4% accuracy is gained in this case by using SRLS instead of MF.

Figure 9.

χ² probability distribution as a function of the global motion correlation time calculated with combination 1 SRLS (blue) and model 1 MF (red) for residue 45 of VHHS. The MF calculations used the same spectral densities as the SRLS calculations, except that the frame transformation D-to-CSA was omitted.

2. SRLS versus MF analysis in the mode-mixing regime

One of the greatest benefits of SRLS lies in the treatment of flexible residues where mode-mixing dominates the spectral density, as a consequence of local and global motions occurring on similar time scales. Allowing for rhombic local ordering shown previously to prevail at the N-H bond,²⁶ and accounting for general features of local geometry,^22-27 constitute additional significant advantages over MF. As pointed previously^22,27 and mentioned above, the reduced extended MF formula is formally equivalent to J^DD(ω) = A j₀(ω), with SRLS fitting yielding A ∼ S_f² ∼ 0.8 – 0.9. These spectral densities are typically inaccurate because terms, which contribute 10 – 20% have been omitted. Let us illustrate this quantitatively. The value of A = (1.5 cos²β_MD - 0.5)² = 0.8 is obtained for β_MD = 15.4°, and A = 0.9 obtains for β_MD = 10.7°. The values of B = 3 sin²β_MD cos²β_MD (C = 0.75 sin⁴β_MD) corresponding to these angles are 0.20 (0.004) and 0.1 (0.0009), respectively. B is clearly not very small, but B j₁(ω) could become negligible if j₁(ω) were much smaller than j₀(ω), in view of the imposed condition that R^L_∥ >> R^L_⊥. This is not borne out by the SRLS analysis of the experiment, since if it were, the fitting scheme would have returned A = 1, corresponding to β_MD = 0°. By analogy, the validity of ‘reducing’ the extended MF formula, based on the condition that τ_s >> τ_f, is not borne out by the experiment, since if it were, the MF fitting scheme would have returned S_f² = 1.

The values of j₁(ω) and j₂(ω) are, indeed, much smaller than j₀(ω) for all ω values when R^L_∥ >> R^L_⊥, in the absence of mode-mixing. The presence of mode-mixing invalidates the relations j₁(ω) << j₀(ω) and j₂(ω) << j₀(ω) in the high ω regime. This is illustrated in Fig. 10, where we show the SRLS functions j_K(ω) calculated using as input the best-fit parameters obtained by fitting with SRLS the ¹⁵N relaxation data of residue 124 of RNase H, acquired at 11.7 T, 300K. This residue pertains to the flexible loop α_D/β₅ and was fit previously with model 5 by Mandel et al.¹² It can be seen that in the low frequency region j₀(ω) >> j₁(ω) and j₂(ω). However, in the frequency range comprising the ω values relevant for the NOE (ω_H + ω_N and ω_H - ω_N) the j₁(ω) values exceed the corresponding j₀(ω) and j₂(ω) values. Clearly even when R^L_∥ >> R^L_⊥ (or τ_s >> τ_f in MF) the term B j₁(ω) cannot be ignored in eq 12 for the β_MD = 10 - 20° geometry when mode-mixing is important. For the very same reason the incorrect eq 19 is further impaired when its last term is omitted.

Figure 10.

j_K(ω) functions obtained with c²₀ = 3.2 ((S²₀)² = 0.4), τ₀/τ_m = 0.45, β_MD = 16.3° and N = R^L /R^L∥ ⊥ = 916. The high-frequency region is shown in panel ‘a’ and the low-frequency region in panel ‘b’.

In principle setting B j₁(ω) and C j₂(ω) equal to zero implies the β_MD = 0° geometry which corresponds to A = 1. In practice the fitting schemes returns A ≠ 1, indicating that force-fitting has occurred. The β_MD = 90° geometry (which is approximately correct as the angle between N-H and C^α_i-1-C^α_i is 101.3°) corresponds to A = 0.25, B = 0 and C = 0.75. As shown below, this materializes by fitting when the potential is allowed to be rhombic and R^L_∥/R^L_⊥ is allowed to be arbitrary instead of being forced to be very high.

In the perturbation limit the ordering is very small. Motion about Z_M is prohibited physically as the N-H bond is attached to the protein backbone. The highly plausible local diffusion/local ordering axes C^α_i−1-C^α_i and N_i-C^α_i are tilted at approximately 90° from the N-H bond. Therefore the β_MD = 90° geometry is actually implied in this limit. Outside the perturbation limit, Z_M may be tilted with respect to the N-H bond. In order to assign physical meaning to the tensor R^L we will assume, based on stereo-chemical considerations, that the β_MD = 90° is preserved in the general case.

The experimental data of residue 124 of RNase H are further used for illustrative purposes as follows. They are shown in Table 9a along with the NMR relaxation data back-calculated with MF and SRLS using the best-fit parameters (given in Table 9b) obtained with the respective fitting processes. Clearly both SRLS and MF reproduce the experimental data. The specific J(ω) values entering the expressions for T₁, T₂ and NOE are shown in Table 9b. It can be seen that MF can fit the experimental data as well as SRLS, but this requires that the relevant J^DD(ω) values be under-estimated, and the relevant J^CC(ω) values over-estimated. This is a clear example of force-fitting. The different best-fit parameters can be further rationalized by examining Table 9c, where we show the dominant eigenvalues and their weights, which are clearly different in SRLS and MF. Thus, a fictitious physical situation characterized by MF eigenvalues and weights of C(t) and best-fit parameters of J(ω) obtained with force-fitting can reproduce technically very well the experimental data.

Table 9a.

Best-fit T₁, T₂ and NOE values corresponding to the best-fit parameters shown in Table 9b under the heading ‘input’. The χ² values were practically zero for both SRLS and MF.

	T1 [ms]	T2 [ms]	NOE
EXP	633.8±10.1	112.3±3.1	0.5343±0.031
SRLS	633.8	112.3	0.5344
MF	633.8	112.3	0.5343

Table 9b.

Best-fit J(ω) values corresponding to the best-fit parameters listed under the heading ‘input’, used to calculate the data of Table 9a. The SRLS input set includes R^C = 0.47 (τ^L_⊥ = 4.36 ns, τ_m = 9.28 ns)), c²₀ = 3.04 ((S²₀)² = 0.37) and (β_MD = 16.6° (formally S_f² = 0.770). N = R^L_∥/R^L_⊥ was fixed at the value of 1000. The MF input set includes τ_s/τ_m = 0.114, c²₀ = 10.2 derived from S_s² = 0.806 (eqs 4 and 11), S_f² = 0.809 and τ_f = 0. The formally²²,²⁷ analogous SRLS parameters are R^C, c²₀, A = (P₂(cos(β_MD)))² and R^L_∥ >> R^L_⊥, respectively. The units of J(ω) are ns.

Input				Output
c20	(S20)2	βMD	RC	JDD(0)	JDD(ωN)	JDD(ωH+ωN)	JDD(ωN)	JDD(ωH+ωN)	JCC(0)	JCC(ωN)
3.01	0.368	16.6	0.47	2.61	0.318	1.09	0.0093	0.0081	1.96	0.241
10.2	0.806	15.0	0.11	2.48	0.303	1.08	0.0087	0.0074	2.48	0.303

Table 9c.

Significantly contributing SRLS eigenvalues and associated weights, and corresponding ‘independent’ MF eigenvalues and associated weights. The eigenvalues are given in units of R^L, hence the ‘independent’ local motion eigenvalue is 6.

	SRLS				MF
Eigenvalue	2.13	10.12	24.52	14.13	0.678	6
weight	0.61	0.325	0.042	0.019	0.652	0.157

Note that the weights of the local and global motion terms in Table 9c, yielded by the reduced extended MF formula (eq 19 with the last term set equal to zero), do not sum up to unity. There is no requirement in the MF fitting schemes for normalization in the so-called ‘model 5’, which uses this formula. This is yet another aspect of the MF treatment which implies force-fitting of the experimental data. Additional confusion with regard to what the parameter τ_s represents is implied by the phenomenon of renormalization, which is important when the local potential is high. Since some S_s² values are low and others are high, this complicates further the comparison among the τ_s values of different N-H sites. Finally, conformational entropy is often calculated from S² instead of S_s². The parameter S_s² is formally equivalent to (S²₀)², whereas S² taken as S_f²×S_s² includes the parameter S_f² which is formally analogous to a geometric factor, P₂(cos(β_MD))²).²² S_s² is highly inaccurate;^19,20,22 S² is qualitatively problematic.

We conclude this section by discussing the limit N = R^L_∥/R^L_⊥ >>1, which is the analogue of the MF restriction τ_s >> τ_f. The j_K(ω) functions in Fig. 10 were obtained with N ∼ 1000. We show in Fig. 11 SRLS j_K(ω) functions obtained with N = 1. Except for the value of N, the parameters used to calculate the Fig. 11 functions - R^C = τ^L_⊥/τ_m = 0.57, c²₀ = 4.04 ((S²₀)² = 0.51), β_MD = 20° and R^L_∥ >> R^L_⊥ - are quite similar to those used to calculate the Fig.10 functions. It can be seen that for a small time scale separation (τ^L_⊥/τ_m = 0.57), moderate ordering ((S²₀)² = 0.51) and the β_MD = 20° geometry, the functions j₁(ω) and j₂(ω) are comparable in magnitude to j₀(ω) over the entire range of ω values when N = 1 (Fig. 11). On the other hand, j₀(ω) >> j₁(ω), j₂(ω) in the low frequency regime, whereas j₁(ω) > j₀(ω), j₂(ω) in the high frequency regime when N >> 1 (Fig. 10). Thus, the parameter N affects the analysis significantly.

Figure 11.

SRLS spectral densities j_K(ω) obtained with c²₀ = 4.04 ((S²₀)² = 0.51), τ^L_⊥/τ_m = 0.57, β_MD = 20° and R^L_∥/R^L_⊥ >> 1 (blue curves). Reduced extended MF spectral density calculated with S_s² = 0.51, S_f² = 0.68 and τ_s′/τ_m = 0.57 (red curve). The coefficients of the SRLS j_K(ω) functions shown in the expression of J^DD(ω) are 0.68, 0.31 and 0.01 for K = 0, 1 and 2, respectively.

The restriction to high N = R^L_∥/R^L_⊥ was imposed in our first fitting scheme for SRLS (ref. ²²) for practical reasons. R^L_∥ and R^L_⊥ represent the principal values of the diffusion tensor of ‘body 1’, i.e., the N-H bond. The inequality R^L_∥/R^L_⊥ >> 1 is clearly a simplifying approximation. As shown below, only by removing this restriction, and allowing for rhombic potentials, is a consistent physical picture obtained with data fitting. In SRLS the principal values of the local diffusion tensor comprise information on physically meaningful variations among the various N-H sites (examples of such variations among nitroxide-labeled sites in proteins appear in ref. 37). This information is lost when the restriction that N >> 1, whereby R^L_∥ is forced to be in the extreme motional narrowing limit, is imposed.

Within the scope of the formal (definitely not physical) analogy between SRLS and MF, R^L_∥/R^L_⊥ >> 1 in SRLS corresponds to τ_s/τ_f >> 1 in MF. Based on the results presented below, which indicate that R^L_∥/R^L_⊥ >> 1 is not to be imposed, the mathematical MF inequality τ_s/τ_f >> 1 constitutes an inappropriate oversimplification.

For comparison we also show in Fig. 11 the reduced extended MF spectral density obtained with the analogous parameters - τ_s′/τ_m = 0.57, S_s² = 0.51, S_f² = 0.68 ( S_f² = A = 1.5 cos²(20°) - 0.5) and τ_f' = 0 (red curve). This function is clearly a poor approximation of J^DD(ω) assembled according to eq 12 from the j_K(ω) functions of Fig. 11, with the coefficients A = 0.68, B = 0.31 and C = 0.01, corresponding to the β_MD = 20° geometry. This illustrates clearly the limited capabilities of MF, which cannot reproduce physical situations where R^L_∥/R^L_⊥ ∼ 1.

3. Conformational entropy derived in MF from S².

In recent years squared generalized MF order parameters have been used extensively to derive thermodynamic quantities, notably configurational entropy.^33-36 The logic behind this approach is as follows. S² is determined with data fitting. Subsequently it is assumed that P_eq is axially symmetric. Thereby the squared generalized order parameter becomes the square of an axial order parameter. This enables the derivation of the strength of an axial potential, the form of which must be guessed, based on equations similar to our eq 11. Since MF is an SRLS asymptote, the potential form given by eq 4 (with c²₂ set equal to zero) is appropriate. Employing other potential forms^33-36 may increase the inaccuracy in the configurational entropy derived from the already inaccurate S² value.

Large errors in the strength of the potential U/k_BT = –c²₀ P₂cos²β_MD are illustrated in Table 7 in the best-case scenario where S² is determined with models 1 or 2. As pointed out above, the errors in c²₀ are significantly larger than the errors in S² due to the functional form of the (S²₀)² versus c²₀ dependence (Fig.4). Table 7 shows that within the context of model 1 (or combination 1) the potential coefficient (c²₀) derived from S² MF underestimates the SRLS potential coefficient on average by 23%, whereas in the context of model 2 (or combination 2) the potential coefficient derived from S² MF overestimates the SRLS potential coefficient on average by 20%. Much larger inaccuracies in the potential underlying the calculation of configurational entropy are expected in the extended MF regime, where S_s² MF and (S²₀)² SRLS differ by factors of 3 - 4 (refs. ^{19, 20} and ²²). When the local potential is rhombic, as it turns out to be at the N-H site,²⁶ MF cannot provide the equilibrium probability distribution function, P_eq = exp(U/k_BT), since only one parameter, S², is available while a rhombic potential is defined by at least two coefficients.

Contrary to MF, in SRLS the general rhombic form of the potential is implicit in the theory and its coefficients (c²₀ and c²₂) can be obtained directly with data fitting. The SRLS theory also emphasizes the relevance of the Euler angles Ω_C′M. P_eq, and therefore the thermodynamic quantities, are obtained straightforwardly in SRLS. Order parameters are thus not required to infer the potential in order to derive conformational entropy. They can be calculated independently, if so desired, using eqs 6-9.

4. Rhombic symmetry of the local potential/local ordering

4a. The rhombicity of the local ordering and the axiality of the global diffusion

A very large effect on the analysis not accounted for in MF is the rhombicity of the potential U/k_BT(Ω_CM). This is illustrated below in quantitative terms. The symmetry of the potential depends on the symmetry of local diffusion/local ordering frame, M, and the symmetry of the local director frame, C. In SRLS the local director is taken to be uniaxial for simplicity but the M frame is in general allowed to be rhombic. We found previously that the particular rhombic symmetry of the M frame is of the ‘nearly planar Y_M-X_M’ type.²⁶ Fig. 12 illustrates these frames in the context of the stereo-chemistry of the peptide plane. The C axis is considered to lie along the equilibrium C^α_i−1-C^α_i axis. The main ordering axis, Y_M, is parallel to the instantaneous orientation of the C^α_i−1-C^α_i axis. Z_M is perpendicular to Y_M within the peptide plane and X_M is perpendicular to both Y_M and Z_M, i.e., perpendicular to the peptide plane. The axis X_M lies along the symmetry axis of the lone electron pair of the nitrogen, assigning clear meaning to the ‘nearly planar Y_M-X_M ordering’ symmetry, where |S_xx|, |S_yy| >> |S_zz|, S_yy > 0 and |S_yy| is slightly larger than |S_xx|. In the original MF formula, and in the extended MF formula as presented by its developers, C lies implicitly along the equilibrium N-H orientation. In a high ordering scenario the implied motion around N-H is not viable. On the other hand, motion around C^α_i−1-C^α_i, is definitely viable. Note that taking the local director to lie along the C^α_i−1-C^α_i axis within a presumed rigid peptide plane sets the angle β_MD close to 90° for the N-H bond and close to 0° for the C′-C^α bond.

Figure 12.

Schematic illustration of high ‘nearly planar Y_M-X_M ordering’ prevailing at the NH site, with Y_M as main ordering axis. The M frame denotes the rhombic local ordering/local diffusion frame. Y_M lies along the instantaneous orientation of the C^α_i−1-C^α_i axis (or the N_i-C^α_i bond). X_M lies along the symmetry axis of the lone pair of the nitrogen. The C frame denotes the uniaxial local director frame with Z_C along the equilibrium orientation of the C^α_i−1-C^α_i axis (or the N_i-C^α_i bond). Within the scope of high ordering Y_M is aligned preferentially along the C axis.

The rhombicity of the local ordering tensor, S, is outside the scope of MF. Since the above geometric considerations imply that rhombicity affects the experimental data, it must be absorbed by the best-fit MF parameters. We showed previously²⁶ that the conformational exchange parameter, R_ex, can absorb S rhombicity in the data fitting process. Another likely candidate, in particular in the BO limit where mode-mixing is limited, is R^C axiality, as explored below.

The large effect of the symmetry of the local potential on the analysis is illustrated in Table 10 which shows NMR relaxation rates calculated for R^C = 0.01, β_MD = 0°, τ_m = 15 ns and axial or rhombic potentials on the order of 10×k_BT. In the axial case c²₀ = 8 ((S²₀)² = 0.754), whereas in the rhombic case c²₀ = 8 and c²₂ = 4. This is moderate rhombicity, corresponding to (S_xx - S_yy)/S_zz = 8.6%, where S_xx = −0.382, S_yy = −0.454 and S_zz = 0.836 are the principal values of the Cartesian ordering tensor. As shown in Table 10, potential (or ordering) rhombicity affects the NOE to a very large extent, amounting to 31.6 % (46.3 %) difference from the axial case at 11.7 T (18.8 T). The parameters used in Table 10 for the axial potential case are also used in Table 11 to illustrate the effect of global diffusion axiality with R^C_∥/R^C_⊥ = 1.2, which is a typical value for globular proteins.¹⁰ ‘%diff’ denotes the percent difference between corresponding variables calculated with β_CC′ = 0° and β_CC′ = 90°, where β_CC′ denotes the angle between the (uniaxial) local director frame, C′, and the (axial) global diffusion frame, C. The effect illustrated in Table 11 is small relative to the large effect of moderate potential rhombicity on the NOE illustrated in Table 10. It is very likely that in many cases the rhombicity of the ordering tensor, S, was absorbed in the MF analyses by introducing R^C axiality, in particular when the total time correlation function, C(t), rather than the time correlation function for global motion, C^C(t), is used to determine R^C. In the former case ¹⁵N T₁, T₂ and ¹⁵N-{¹H} NOE enter the analysis, whereas in the latter case only ¹⁵N T₁ and T₂ enter the analysis.

Table 10.

Percent difference [var(axial) − var(rhombic)]/var(axial)×100 between ¹⁵N T₁, T₂ and NOE calculated with τ_m = 15 ns, R^C = 0.01, and an axial (c²₀ = 8 and c²₂ = 0) or a rhombic (c²₀ = 8 and c²₂ = 4) potential. Calculations are shown for magnetic fields of 11.7, 14.1 and 18.8 T.

	11.7 T	14.1 T	18.8 T
T1	−2.4	−1.0	+1.5
T2	−7.6	−7.5	−7.6
NOE	+31.6	+39.3	+46.3

Table 11.

Percent difference [var(β_CC'=0°) − var(β_CC'=90°)]/var(β_CC'=0°) ×100 between ¹⁵N T1, T₂ and NOE calculated with τ_m(app) = 15 ns, R^C(app) = 0.01, an axial potential given by c²₀ = 8, and a global diffusion anisotropy R^C_∥/R^C_⊥ = 1.2. Calculations are shown for magnetic fields of 11.7, 14.1 and 18.8 T.

	11.7	14.1	18.8
T1	+7.4	+7.1	+6.1
T2	−9.0	−9.0	−9.2
NOE	−2.7	−3.5	−4.0

The data shown in Table 11 were obtained for a time scale separation of 0.01, which is quite large, and a potential strength of c²₀ = 8, which corresponds to the relatively high ordering of (S²₀)² = 0.754. In this parameters range the effect of additional local motion eigenmodes on the correlation function is not very large.²⁷ However, not accounting for it, and oversimplifying the local geometry, render the MF-based T₁ and T₂ values inaccurate by 7% and 9%, respectively. Interestingly, the field dependence of these discrepancies is small. This indicates that in those cases where MF analysis yields significantly field-dependent τ_m values either mode-mixing is pervasive in the experimental data, or the latter feature rhombic potentials.

It should be noted that in general all the parameters entering the J^x(ω) functions, including the global diffusion tensor, are to be determined in the same fitting process. The separate determination of R^C in MF is implied by the mode-independence concept, the applicability of which to N-H bond dynamics we challenge herein.

4b. ‘Nearly planar Y_M-X_M’ rhombic ordering

As pointed out above the ‘nearly planar Y_M-X_M’ ordering symmetry with Y_M as main ordering axis represents realistic stereochemical and electronic properties of the N-H site in proteins. Let us investigate this symmetry in further detail. For convenience we use c²₀ = 2, and allow c²₂ to increase from 0 to 6, scanning thereby over a range of symmetries.

Table 12 shows potential coefficients and corresponding ordering tensor components in spherical tensor notation, S²₀ and S²₂, and in Cartesian tensor notation, S_xx, S_yy and S_zz. The numerical values of the Cartesian tensor components indicate clearly that the entry with c²₂ = 0 represents positive axial Z_M ordering; the entry with c²₂ = 2.45 represents negative axial Y_M ordering; the entry with c²₂ = 3 represents rhombic negative Y_M ordering with ‘nearly planar Y_M-X_M symmetry’; the entry with c²₂ = 4 represents positive rhombic X_M ordering with ‘nearly planar Y_M-X_M symmetry’; the entry c²₂ = 6 represents positive X_M ordering and substantial negative Y_M ordering. The angle γ_MD was fixed in the calculations of this study, and all our previous studies, at 90°, in agreement with stereochemical considerations (Fig. 2b).

Table 12.

Potential coefficients c²₀ and c²₂ (eq 4) and corresponding principal values of the ordering tensor in spherical tensor notation, S²₀ and S²₂ (eq 11), and in Cartesian notation, according to ${\mathrm{S}}_{\mathrm{xx}}=(1∕2)\sqrt{3∕2}{{\mathrm{S}}^2}_2-0.5{{\mathrm{S}}^2}_0;{\mathrm{S}}_{\mathrm{yy}}=-(1∕2)\sqrt{3∕2}{{\mathrm{S}}^2}_2-0.5{{\mathrm{S}}^2}_0$; and S_zz = S²₀. Note that reversing the sign of c²₂ will cause the values of S_xx and S_yy to be exchanged.

c20	c22	S20	S22	Sxx	Syy	Szz
2	0	+0.440	0.000	−0.220	−0.220	+0.440
2	2	+0.265	+0.368	+0.093	−0.358	+0.265
2	2.45	+0.188	+0.460	+0.188	−0.376	+0.188
2	3	+0.088	+0.572	+0.306	−0.394	+0.088
2	4	−0.082	+0.750	+0.500	−0.418	−0.082
2	6	−0.183	+0.878	+0.739	−0.446	−0.293

The high sensitivity of the analysis to the symmetry of the local ordering (local potential) is illustrated in Fig. 13. We show the functions j_KK′(ω) for all the relevant combinations of quantum numbers K and K′, as determined by the symmetry of the local potential. The potential is axial in Fig. 13a, with c²₀ = 1.5, and of the ‘nearly planar Y_M-X_M ordering’ type in Figs. 13b (c²₀ = 2 and c²₂ = 3) and 13c (c²₀ = 2 and c²₂ = 3.25). To calculate the j_KK′(ω) functions we used R^C = 0.001, and to further calculate T₁, T₂ and NOE we used β_MD = 0° in Fig. 13a and β_MD = 90° in Figs. 13b,c, and the value of τ_m = 5.5 ns.

Figure 13.

Functions j_K(ω) = j_KK(ω) (Fig. 13a) and j_K(ω) = j_KK(ω) and j_KK′(w) (Figs. 13b,c) calculated for R^C = 0.001, and c²₀ and c²₂ as depicted in Figs. 13a-13c. The potential coefficients correspond to axial symmetry with c²₀ = 1.5 (Fig. 13a), and ‘nearly planar Y_M-X_M symmetry’ with c²₀ = 2 and c²₂ = 3 in Fig. 13b and c²₀ = 2 and c²₂ = 3.25 in Fig. 13c. The black, red and green curves represent the functions j_K(ω) with K = 0, 1 and 2, respectively. The blue, yellow and indigo curves in Fig. 13b and 13c represent the functions j_KK′(ω) with KK′ = (2, 0) = (0, 2), KK′ = (2, −2) = (−2, 2) and KK′ = (1, −1) = (−1, 1), respectively. The NMR relaxation rates were calculated for β_MD equal to 0° (Fig. 13a) or 90° (Figs. 13b, c), τ_m = 5.5 ns and a magnetic field of 11.7 T. Note that for β_MD = 90° the contributions cross-terms include j₂₀(ω) = j₀₂(ω) and j_2-2(ω) = j₋₂₂(ω)).

There are significant differences between the axial and rhombic potential scenarios. First of all, rhombic symmetry requires the cross terms j_2-2(ω) = j₋₂₂(ω), j₂₀(ω) = j₀₂(ω) and j_1-1(ω) = j₋₁₁(ω) in addition to the diagonal terms j₀(ω), j₁(ω) and j₂(ω) required for axial symmetry. The NOE generated with the rhombic potential given by c²₀ = 2 and c²₂ = 3.25 (cf. Fig. 13) can also be reproduced with an axial potential given by c²₀ = 1.5 (with all the other input parameters being the same). However, T₁ and T₂ differ substantially indicating that a completely different set of input parameters featuring an axial potential would be required to reproduce satisfactorily the T₁, T₂ and NOE of Fig. 13c. This illustrates the need for force-fitting, with Fig.13c representing “model” experimental data. Figs. 13b and 13c show that the NMR relaxation rates are altered substantially when the rhombicity of the potentials changes moderately. Thus, an 8% increase in c²₂/c²₀ implies a 53% increase in the NOE, pointing out the very high sensitivity of the analysis to the precise form of the local potential.

The examples shown in Fig. 13 pertain to the large time scale separation regime where mode-mixing is limited. The effect of potential symmetry on the experimental variables for R^C = 0.5, where mode-mixing is important, is illustrated in Fig. 14. The other parameters used include τ_m = 6.1 ns and c²₀ = 2. Isotropic R^L (N = 1) and β_MD = 0° were used in Figs. 14a - c, and axial R^L (with N = 10) and β_MD = 90° were used in Figs. 14d - f. The rhombic potential coefficient, c²₂, was varied from 0 to 6. Positive axial Z_M ordering corresponds to c²₂ = 0 (S_zz = 0.440, S_xx = S_yy = −0.220), negative Y_M corresponds to c²₂ = 2.45 (S_yy = −0.376, S_xx = S_yy = 0.188), ‘nearly planar Y_M-X_M ordering’ with Y_M as main (negative) ordering axis corresponds to c²₂ = 3 (S_xx = 0.306, S_yy = −0.394 and S_zz = 0.088), and rhombic X_M ordering corresponds to c²₂ = 6 (S_xx = 0.629, S_yy = −0.446 and S_zz = −0.184).

Figure 14.

¹⁵T₁, T₂ and ¹⁵N-{¹H} NOE calculated with τ_m = 6.1 ns, R^C = 0.5 and a magnetic field of 11.7 T. Isotropic R^L and β_MD = 0° were used in panels a-c, and axial R^L with N= R^L_∥/R^L_⊥ = 10 and β_MD = 90° were used in panels d-f. The potential used was given by c²₀ = 2, with the rhombic coefficient, c²₂, varied from 0 to 6.

The ‘nearly planar Y_M-X_M’ ordering symmetry with Y_M as main (but negative) ordering axis, which corresponds to c²₀ = 2 and c²₂ = 3, has unique features. For β_MD = 0° the NOE and T₂ assume their maximum values, whereas T₁ assumes its minimum value for this symmetry. For β_MD = 90°, T₁ goes through a shallow minimum, whereas T₂ and the NOE exhibit a maximum slope for this symmetry in the c²₂ range shown. Particularly noteworthy is the fact that the NOE is significantly higher when the symmetry of the local potential is rhombic instead of axial. By analogy with Fig. 14, the maximum NOE corresponding to rhombic ‘nearly planar Y_M-X_M ordering’ is expected to be higher than the maximum NOE corresponding to axial ordering of similar magnitude. This turns out to be an important issue, discussed below in detail.

5. Examples of misleading force-fitting with MF

5a. ‘Missing’ contribution to ¹⁵N 1/T₂.

Lee and Wand,⁹ who carried out a comprehensive MF analysis of multi-field Ubiquitin data acquired at 300K, reported on an apparently missing contribution to 1/T₂ which led to large τ_m values despite having allowed for variations in the ¹⁵N CSA interaction. Only when T₂ was excluded from the analysis was the expected value of τ_m = 4.1 ns recovered. As shown in Fig. 5, for τ_m = 5 ns mixed modes contribute to 1/T₂ significantly already for τ_e on the order of 20 ps for S² = 0.85 (Fig. 5). Quantitative estimates given in Table 8 show that even when the contribution of mixed modes is relatively small, the 1/T₂'s obtained with MF are 5-6% lower than the 1/T₂'s obtained with SRLS. Lower time scale separation and lower ordering, which imply larger effects of additional eigenmodes for local motion on the correlation functions, will increase further the difference between 1/T₂ obtained with SRLS and 1/T₂ obtained with MF. The data shown in Table 8 were obtained with axial potentials. For rhombic potentials the 1/T₂ differences will be significantly larger since SRLS and MF differ, in general, to a larger extent when the potential is rhombic in SRLS and axial in MF (e.g., see Table 10).

Since MF does not account either for mode-mixing or potential rhombicity, the only way to render the fitting feasible is to exclude T₂ from the analysis. SRLS-based data fitting with rhombic potentials and arbitrary R^L_∥/R^L_⊥ is expected to make more insightful fitting of complete multi-field data from Ubiquitin and other proteins.

5b. Low performance of the N-H bond as dynamic probe

The commonly used probe for studying protein backbone dynamics is the N-H bond. The experimental auto-correlated relaxation rates ¹⁵N T₁, T₂ and ¹⁵N-{¹H} NOE are analyzed with data fitting. Recently the ¹³C′-¹³C^α bond has been suggested as a complementary dynamic probe (ref. ¹³ and papers cited therein). In this case the ¹³C′-¹³C^α dipolar-¹³C′ CSA cross-correlated relaxation rate, Γ, is measured. Since only a single relaxation rate is measured only model 1 cases, which feature τ_m and S²(C′-C^α) as free variables, can be treated. In such cases one can calculate S²(C′-C^α) from the expression of Γ using τ_m determined with ¹⁵N spin relaxation. Hence within the scope of MF combined N-H and C′-C^α analysis is relevant for rigid proteins where model 1 applies, assuming that the peptide plane is rigid.

The ribonuclease binase was studied earlier with ¹⁵N spin relaxation at 11.7 and 18.8 T,²¹ and recently with combined ¹⁵N-¹H and C′-C^α spin relaxation at 11.7 T.¹³ In the earlier study the 18.8 T data could not be fit with MF, and the 11.7 T data yielded an altogether rigid backbone although other methods (X-ray crystallography, molecular dynamics and ¹³C′-¹³C^α cross-relaxation) indicated that the catalytic loops L2 and L5 are flexible.²¹ In reference ¹³ it was found that at 278 K S²(N-H) and S²(C′-C^α) are practically the same, in agreement with nearly rigid N-H and C′-C^α bonds. However, when the temperature was increased to 303 K, S²(C′-C^α) decreased by 10%, whereas S2(N-H) decreased by only 2%. This was considered contrary to the expectation that at the higher temperature the N-H bond should be more sensitive than the C′-C^α bond to the crankshaft motion³⁸ occurring about an axis close to the N_i-C^α_i bond, since N-H is perpendicular to this axis whereas C′-C^α is parallel to it. Similar results were obtained for Ubiquitin.

The unexpected temperature-independence of S²(N-H) is actually imprinted in the raw data. Fig. 15 shows the experimental NOE's obtained at 303 K, 11.7 and 18.8 T. The horizontal lines show the maximum ‘rigid sphere’ NOEs corresponding to τ_m values determined with T₁/T₂ analysis. It can be seen that most NOE's exceed the ‘rigid sphere’ value. This feature necessarily imposes on the fitting scheme model 1, where the ‘rigid sphere’ NOE value is obtained. The latter is independent of S². T₁ and T₂ assume minimum values for S² = 1. As shown in Table 13 the difference between the average experimental and minimum T₁ and T₂ values is approximately 8% at 278 K and 10% at 303 K. The S² values yielded by the MF analysis are 0.903 at 278 K and 0.884 at 303 K, which differ from 1 by 10 and 12%, respectively. Hence the unexpectedly small temperature-dependence of S²(N-H) is to be assigned to issues related to the analysis, rather than issues related to the experimental data. A plausible interpretation is outlined below.

Figure 15.

Experimental NOE's of the ribonuclease binase acquired at 11.7 and 18.8 T, 303 K.²¹ The horizontal lines show the maximum NOE for 6.1 ns (11.7 T) and 5.5 ns (18.8 T), with the global motion correlation times determined based on T₁/T₂ ratios.

Table 13.

Maximum NOE (obtained with model 1) and minimum T₁ and T₂ (obtained with model 1 and S² = 1) values corresponding to 11.7 T and 13. 44 (5.5) ns at 278 (303 K) (row 1); average experimental T₁ and T₂ and NOE values from ref. 13 (row 2); percent difference between corresponding data in rows 1 and 2 (row 3).

	303 K
T1, ms	T2, ms	NOE
368.5	117.2	0.771
408.2 ± 6.5 (1.6%)	129.4 ± 2.5 (1.9%)	0.771
10.8%	10.4%	0
	278 K
T1, ms	T2, ms	NOE
720.4	55.0	0.816
781.3 ± 18 (2.3%)	59.2 ± 2.1 (3.6%)	0.816
8.5%	7.7%	0

The maximum theoretical NOE value is determined for axial local potentials. However, we found previously that ‘nearly planar Y_M-X_M ordering’ prevails at the N-H bond. Fig. 16 shows the effect of potential symmetry on the NOE. Calculations were performed for τ_m = 6.1 ns, τ^L_⊥/τ_m = 0.5, R^L_∥/R^L_⊥ = 0.5, c²₀ = 2 and β_MD = 0°. The rhombic potential coefficient, c²₂, was varied from 0 to 6, scanning thereby over the various symmetries of the coupling potential and the corresponding ordering tensor. As pointed out earlier c²₂ = 0 corresponds to axial Z_M ordering; c²₂ = 2 corresponds to rhombic Z_M ordering; c²₂ = 2.45 corresponds to axial perpendicular Y_M ordering; c²₂ = 3 corresponds to rhombic ‘nearly planar Y_M-X_M ordering’ with Y_M as main ordering axis; c²₂ ~ 5 corresponds to rhombic X_M ordering. It can be seen that the largest NOE value is obtained for c²₂ = 2 and c²₂ = 3, i.e., rhombic ‘nearly planar Y_M-X_M ordering’, with Y_M as main ordering axis.

Figure 16.

¹⁵N-{¹H} NOE calculated with τ_m = 6.1 ns, R^C = 0.5, R^L_∥/R^L_⊥ = 0.5 and c²₀ = 2. The rhombic potential coefficient, c²₂, was varied from 0 to 6.

Figure 16 shows clearly that rhombic potentials can yield higher NOE's than axial potentials. Therefore if the theoretical spectral density used in the fitting scheme yields maximum NOE's corresponding to ‘nearly planar Y_M-X_M ordering’, the experimental NOE's may not exceed the maximum NOE, and model 1 should not be imposed on the fitting scheme. Instead model 2, which yields significantly lower S² values than model 1 (Table 7), may be selected at 303K.

Yet another illustrative example is presented in Table 14 which shows high c²₀ and c²₂ values, corresponding to high order parameters, S²₀ and S²₂, as appropriate for model 1. For the expected β_MD= 90° geometry corresponding to the ‘nearly planar Y_M-Z_M ordering’, the term τ_m/(1 + ω²τ_m²) in the combination 1 spectral density is multiplied by the coefficient [0.25 (S²₀)² + 0.75 (S²₂)²], since (d²₀₀)² = 0.25 and 2×[d²₂₀)²] = 0.75 (eq 20). Let us assume that this expression is mimicked by (S²₀)axial2 in an axial potential scenario. We calculated S²₀ and S²₂ in terms of the potential of eq 6 with c²₀ = 10 and c²₂ varied from 16 to 22. These potentials correspond to ‘nearly planar Y_M-X_M ordering’. Table 14 also shows c²0(axial), corresponding to (S²₀)axial2. It can be seen that for c²₂/c²₀ ≥ 1.6 the axial mimic (S²₀)axial2 corresponds to very high potentials. This agrees with the high S²(N-H) values obtained in reference ¹³ at the higher temperatures for binase and Ubiquitin.

Table 14.

Order parameters S²₀ and S²₂, and (S²₀)_axial² = 0.25 (S²₀)² + 0.75 (S²₂)², for c²₀ and c²₂ as given in the Table.

c20	c22	S20	S22	(S20(axial))2	c20(axial)	c22/c20
10	16	−0.305	1.034	0.825	11.3	1.6
10	18	−0.381	1.100	0.943	34.9	1.8
10	20	−0.412	1.130	0.971	> 50	2.0
10	22	−0.432	1.147	1.005	very high	2.2

Combined analysis of N-H and C′-C^α bond dynamics can be carried out when the peptide plane is assumed to be rigid. The local ordering (associated with the M frame) is then a common property. Since the magnetic dipolar frames of ¹⁵N-¹H and ¹³C′-¹³C^α differ, the local geometry (Ω_MD) differs. However, for axial local ordering model 1 (combination 1) S² ((S²₀)²) represents the mean square amplitude of all the local motions.²⁵ In this case the angle β_MD does not enter the model. For that a rhombic M frame is required (eq 20). Hence one cannot expect differential sensitivity of the N-H and C′-C^α bonds to the crankshaft motion unless the local ordering is allowed to be rhombic in the theoretical spectral density. As pointed out previously²⁶ this ordering symmetry actually prevails at the N-H site. As shown herein, it can be treated with SRLS.

Unlike S²(N-H), which is determined with combined fitting of the relaxation quantities ¹⁵N T₁, T₂ and ¹⁵N-{¹H} NOE, S²(C′-C^α) is calculated directly from the expression for the cross-correlated relaxation rate, Γ. This can be accomplished assuming that model 1 is valid, i.e., the spectral density is given by the first term of eq 16, and that τ_m is determined with N-H bond dynamics analysis. In this case S²(C′-C^α) is the only unknown parameter. The maximum Γ value for 11.7 T is −2.395 (−1.194) for τ_m = 13.44 ns (5.5 ns) whereas the corresponding experimental value is −1.992 (−0.885). Hence limitations implied by the experimental values exceeding maximum values implied by axial potentials, as in the N-H case, do not exist in this case. For rigid residues the ¹³C′-¹³C^α dipolar - ¹³C′ CSA cross-correlated relaxation rate depends to a large extent on J^DD(0) and J^CC(0). Therefore local motion effects are small, justifying the use of model 1. Since β_MD is approximately 0° for C′-C^α, (S²₀)axial2 is approximately equal to (S²₀)². For this reason at the higher temperatures the relatively accurate S²(C′-C^α) MF value is smaller than the force-fitted S²⁽N-H) MF value.

The 3D Gaussian Axial Fluctuations (GAF) model⁴⁰ accounts quantitatively for the different geometric features at the N-H and C′-C^α sites. In this approach the S² MF is expressed in terms of harmonic fluctuations around the C^α_i-1-C^α_i axis (σ²_γ) and perpendicular to it (σ²_αβ). 3D GAF was applied to Ubiquitin at 300 K.⁴⁰ Molecular dynamics simulations showed that σ²_γ > σ²_αβ. MF fitting of the ¹⁵N relaxation data showed the same trend with even larger absolute magnitudes of σ²_γ and σ²_αβ. The S²(N-H) values obtained with the usual MF analysis were reproduced by the S²(N-H) values calculated with the 3D GAF model when (relatively small) contributions, which are usually ignored in ¹⁵N spin relaxation of ¹⁵N,¹³C-labeled proteins, were taken into account. S²(C′-C^α) values calculated with the 3D GAF model were found to higher than S²(N-H) as N-H senses the σ²_γ fluctuations, which can be considered to represent the crankshaft motion, whereas C′-C^α senses the σ²_αβ fluctuations. Thus, accounting for the asymmetry of the local ordering with 3D GAF yields S²(N-H) < S²(C′-C^α), as expected.

Instead of harmonic fluctuations σ²_γ and σ²_αβ (applicable to ‘rigid’ residues only) and a predetermined geometry, which is implicit in 3D GAF, SRLS allows for a rhombic ordering tensor with principal values S²₀ (eq 7) and S²₂ (eq 8) defined in terms of a rhombic potential (eqs 6 and 9). The SRLS treatment is not limited to ‘rigid’ residues, and the orientation of the M frame is not fixed. The perpendicular orientations are not considered equivalent and the magnitude of the local asymmetry is quantified through c²₀ and c²₂, or S²₀ and S²₂. The local motion is treated as diffusive, which is reasonable (although improved modeling can be introduced to account for any inertial effects).²³

Calculations using our fitting scheme for SRLS, which allows for rhombic ordering, were carried out for the average values of ¹⁵N T₁, T₂ and NOE acquired at 303K and 11.7 T, and for combined 11.7 and 18.8 T data of residue 16 acquired at 303 K. In the former case we fixed the ratio R^L_∥/R^L_⊥ at 1000 and the angle β_MD at 90°, allowing c²₀, c²₂ and R^C to vary. In the latter case we allowed c²₀, c²₂, R^C, R^L_∥/R^L_⊥ and β_MD to vary. The results are shown in Table 15. S²(C′-C^α) = 0.806 was derived in ref. 13 from the experimental cross-correlated relaxation rate, Γ, measured at 11.7 T and 303 K, as outlined above. Based on eq 11 S²(C′-C^α) = 0.806 corresponds to c²₀ = 10.2. The components of the Cartesian ordering tensor are S_xx = S_yy = −0.449, S_zz = 0.898. It can be seen that the magnitude of the local potentials at N-H and C′-C^α sites is similar. The local geometry is different with β_MD = 90° for the N-H bond and β_MD = 0° for the C′-C^α bond. Since R^L_∥/R^L_⊥ and β_MD were fixed in the fitting of the average ¹⁵N relaxation data (as only 3 data points were available), and rhombic potentials could not be used to treat C′-C^α bond dynamics (as only one data point was available), we regard the data in Table 15 as interim results. However, they can be used for illustrative purposes. If the peptide plane is rigid it is expected to determine the same tensor components permuted from Z_M ordering for C′-C^α to Y_M ordering for N-H. Thus, S_zz = 0.898 is to be compared with S_yy = 0.761 (results for the average data). If (S_yy)² is considered to represent the crankshaft fluctuations then 0.58 for N-H is to be compared with 0.20 for C'-C^α. Clearly proper analysis bears out the higher sensitivity of N-H bond dynamics as compared to C′-C^α bond dynamics to the crankshaft fluctuations.

Table 15.

Best-fit parameters for N-H site dynamics obtained with rhombic potentials for the average experimental data of binase at 11.7 T, 303 K (ref. ¹³) and for the combined 11.7 and 18.8 T data of binase residue 16 at 303 K (data from ref. 21 kindly provided by Prof. E. Zuiderweg). τ_m = 5.5 ns was used.

	c20	c22	RC	βMD°	RL∥/RL⊥	Sxx	Syy	Szz
Av	5.5	9.7	0.97	90_fixed	1000_fixed	−0.470	0.761	−0.291
res 16	5.0	10.0	1.0	90.0	30.0	−0.65	0.75	−0.10

It is concluded that the effects of potential rhombicity, mixed modes and the D-to-CSA tilt must be accounted for in the theoretical spectral density in order to obtain physically insightful information. This is outside the scope of model-free and can only be accomplished with SRLS. As shown above, combined ¹⁵N and ¹³C spin relaxation analysis is expected to be useful within the scope of SRLS analysis. As shown below, binase is not a singular case but a representative case.

Figure 17 shows the experimental NOE's of oxidized flavodoxin acquired at 11.7 T, 300 K.¹⁷ Similar to binase, most NOE's exceed the maximum NOE calculated for axial potentials, depicted by the horizontal line. ¹⁵N spin relaxation data of oxidized flavodoxin data could not be fit with the standard MF fitting scheme. Fitting became possible only after reducing the experimental NOE's globally by 10%, rendering them smaller than the maximum NOE. Even then model 1 was used predominantly, the S² values were very high, and τ_m was 7.6 ns, which is about 2 ns shorter than expected for a bare sphere with a molecular weight of nearly 20 kDa, corresponding to oxidized flavodoxin. Clearly the experimental data were force-fitted similar to the binase case. SRLS-based fitting with axial potentials gave similar results, in support of the assessment that rhombic potentials are to be used.

Figure 17.

Experimental NOE's of oxidized flavodoxin acquired at 11.7, 303K (ref. ¹⁷). The horizontal line shows the maximum NOE for 7.6 ns, with the global motion correlation time determined based on T₁/T₂ ratios.

The enzyme ribonuclease H (RNase H) was studied with ¹⁵N spin relaxation at 285, 300 and 310 K, 11.7 T.¹² The experimental NOE's are shown in Fig. 18. It can be seen that quite a few NOE's exceed the maximum NOE values depicted by horizontal lines. The average slope d(1–S)/dT determined with MF analysis was 5.9×10⁻⁴ K⁻¹, to be compared to 8×10⁻⁴ K⁻¹ for binase, considered to be low. Analysis with SRLS, using the equivalents of the MF models 1-5 (ref.⁴⁶) as implemented in our 2D grid-based fitting scheme for SRLS featuring axial potentials,²² yielded 6.4×10⁻⁴ K⁻¹ for the β₂ strand of RNase H. Thus, the detrimental features of model 1 analysis with axial potentials outlined for binase recur with RNase H.

Figure 18.

Experimental NOE's of Ribonuclease H acquired at 285, 300 and 310 K, 11.7 T.¹² The horizontal lines show the maximum NOE for the τ_m values shown, which were determined based on T₁/T₂ ratios.

¹⁵N relaxation data of RNase H were also acquired at 11.7, 14.1 and 18.8 T, 300 K (ref 57). The NOE's obtained for the rigid part of the protein backbone are shown in Fig. 19. NOE's exceeding the maximum NOE are pervasive at 18.8 T, where the local motion contributes significantly to the spectral density. Hence valuable information will be lost with force-fitted MF analysis.

Figure 19.

Experimental NOE's of RNase H acquired at 11.7, 14.1 and 18.8 T, 300 K.⁵⁹ The horizontal lines show the maximum NOE for the τ_m = 9.28 ns determined based on T₁/T₂ ratios.

A small value of d(1–S)/dT was also reported for Ubiquitin. The experimental NOE's acquired for Ubiquitin by Lee and Wand⁹ are shown in Fig. 20. It can be seen that similar to binase and RNase H, many NOE's exceed the maximum NOE.

Figure 20.

Experimental NOE's of Ubiquitin acquired at 11.7, 14.1 and 18.8 T, 298 K.⁹ The horizontal line shows the maximum NOE's for 4.1 ns.

Figures 15 - 20, as well as the last column of Table 5, indicate that in many cases MF fitting schemes select model 1 by force-fitting, yielding inaccurate S² values. When the main effect is the omission of the D-to-CSA frame transformation, as for the Villin Headpiece (Table 5), (S²₀)² is underestimated by S². When the main effect is over-simplified symmetry of the local ordering, (S²₀)² is overestimated by S² (Table 14). Thus, the S² profile over the protein backbone may become qualitatively inaccurate.

5c. Limited information on main-chain conformational entropy from N-H bond dynamics

Similar to its low sensitivity to temperature variations, S²(N-H) was also found to exhibit low sensitivity to ligand binding. The parameters S²(N-H) and S²(C′-C^α) of ligand-free and ligand-bound Ca²⁺-Calmodulin (CaM) were derived in reference ¹⁸. The experimental data were acquired at 11.7 T, 308K, and the MF analysis used predominantly model 1. Except for the central linker and several loops, S²(N-H) changed very little whereas S²(C′-C^α) changed significantly upon ligand binding. As in the temperature-dependent study, it was concluded that the N-H bond does not sense (in this case ligand-binding-dependent) backbone fluctuations sensed by the C′-C^α bond. This is important for conformational entropy derivation from S² MF in the context of complex formation.

Similar to the apparently low sensitivity of S²(N-H) of binase, RNase H and Ubiquitin to temperature changes, the apparently low sensitivity of S²(N-H) to ligand binding to CaM stems from force-fitting the experimental data with axial potentials, instead of physically sounder rhombic potentials. Proper interpretation requires a very efficient SRLS fitting scheme featuring rhombic potentials, which is currently being developed. We illustrate below the need for model generality using our SRLS fitting scheme featuring axial potentials. Table 16 features results obtained for the domain residues 30, 100 and 135 of CaM (associated with high experimental NOE's) and for the central linker residues 77 and 80 (associated with low experimental NOE's). τ_m = 7.5 ns for the free form and τ_m = 8.3 ns for the bound form were used.^35,60 SRLS combinations 1 and 2, which correspond to MF models 1 and 2, did not yield acceptable results. SRLS combination 5, with N fixed at the value of 1, gave the results shown in Table 16. This combination differs from model 2 MF in allowing the orientation of the ordering tensor, β_MD, to vary (recall that (1.5 cos²β_MD - 0.5)² is formally equivalent to S_f² in MF). For all the residues examined the local potential and the local ordering are high for both Calmodulin forms, as found in reference ⁶⁰, whereas β_MD is small for the free form and on the order of 25° for the bound form. Thus, ligand binding changes the orientation of the ordering tensor preserving the magnitude of its principal value. This could not be determined with MF because in models 1 and 2 the angle β_MD is zero.

Table 16.

Best-fit parameters obtained by subjecting the domain residues 30, 100 and 135, which feature high experimental NOE's, and residues 77 and 80 of the central linker region which feature low experimental NOE's, to SRLS analysis using combination 5 ((S²₀)², R^C and β_MD varied) with N = R^L_∥/R_⊥ = 1. The symbols ‘f’ and ‘b’ denote the ligand-free and ligand-bound forms, respectively.

	c20	(S20)2	RC	βMD°	χ2*
30_f	19.3	0.897	0.05	0.01	4.9
30_b	18.3	0.892	0.06	20.0	5.0
100_f	16.4	0.879	0.07	2.6	0.016
100_b	15.7	0.874	0.05	22.5	25.2
135_f	21.4	0.907	0.01	0.03	0.3
135_b	16.4	0.879	0.06	22.2	13.1
77_f	8.6	0.771	0.06	8.0	0.0
77_b	8.4	0.765	0.03	24.8	7.9
80_f	8.7	0.773	0.06	0.0	18.2
80_b	8.2	0.760	0.03	28.0	21.6

^*Note that a threshold value of χ² = 25 was also used by Vugmeyster et al.¹¹

As shown in Fig. 11 MF does not have the capability to fit flexible N-H sites where N ∼ 1 because it does not consider the spectral density components j₁(ω) and j₂(ω). The fact that the MF scheme converged to models 1 and 2 instead of model 5 is therefore assignable to force-fitting. Residues 77 and 80 of the central linker are associated with an average c²₀ value of 8.5 (corresponding to an average (S²₀)² value of 0.77), whereas residues 30, 100 and 135 are associated with c²₀ ∼ 17.9 ((S²₀)² ∼ 0.9). Hence axial-potential-based SRLS fitting differentiates between the central linker and the domains of CaM. These results will change when the potential will be allowed to be rhombic and N will be allowed to vary. However, Table 16 illustrates clearly the fact that sensitivity to ligand binding can be borne out by properties of the ordering tensor other than S², which is the only property measured when models 1 or 2 MF are used. The local ordering is characterized by a tensor, not merely by a scalar, S².

5d. Calmodulin: the detection of an incorrect phenomenon

Ca⁺²-ligated Calmodulin is made of an N-terminal domain and a C-terminal domain connected by a helical linker, which is flexible in the middle. In the crystal CaM adopts an elongated dumb-bell structure⁶¹ with the N-, and C-terminal regions of the helical linker parallel to one another (Figs. 21 and 22). Since the middle linker region is flexible the N-, and C-domains may adopt various relative orientations in solution. The helical target peptide, essential for CaM recognition and regulation, binds in-between the domains. Hence molecular shape, linker flexibility, and domain mobility are related to function, and deriving a reliable dynamic picture is important.

Figure 21.

Ribbon diagram of Ca²⁺-ligated Calmodulin reproduced from reference ⁶⁴. The coordinates of the crystal structure of Babu et al.⁶¹ (PDB accession number 3CLN) were used. The data depicted define the global diffusion tensor as determined in ref. 64. ‘N’ and ‘C’ denote the N-, and C-terminal domains of Ca²⁺-ligated Calmodulin.

Figure 22.

Ribbon diagram of the crystal structure of Babu et al.⁶¹ (PDB accession number 3CLN) and corresponding inertia frame, I. The global diffusion frame, D, shown in Fig. 21 is also depicted.

Several experimental and theoretical methods, including NMR spin relaxation, have been used to study CaM flexibility. The NMR-based dynamic picture changed as data were acquired at an increasing number of magnetic fields and temperatures. The first ¹⁵N spin relaxation study of Ca⁺²-saturated Drosophila CaM data acquired at 11.7 T, 35°, was carried out in 1992.⁶² These data were analyzed with the original MF formula. The assumption that Ca²⁺-CaM is nearly spherical in solution (also found in references 18 and 60) was corroborated by comparing N-H orientations in solution and in the crystal structure,⁶¹ and by the nearly flat T₁/T₂ profile. Somewhat different isotropic correlation times on the order of 6-8 ns were assigned to the N-, and C-domains. Except for the flexible residues 78-81 of the central linker and two loops, the CaM backbone was found to be quite rigid, with S² ∼ 0.85 and τ_e < 100 ps.

At low magnetic fields the local motion makes a relatively small contribution to the spectral density. If the spectral density used to calculate the NMR variables is appropriate, the addition of higher field data will merely increase accuracy and precision. If it is not, then inconsistencies will arise because local motion effects will be parameterized in different ways at different magnetic fields. The Ca⁺²-free Xenopus CaM study of Tjandra et al.⁶³ identified such inconsistencies when 11.7 T and 14.1 T data were analyzed in concert. The inconsistencies detected could be reconciled by using the reduced extended MF formula (eq 19 with τ_f′ set equal to zero) instead of the original MF formula (eq 15). With S_f² fixed at 0.85 and uniform parameters within each domain, the fitting yielded τ_m = 12 ns, S_s² ∼ 0.7 and τ_s ∼ 3 ns. The parameters S_s² and τ_s were interpreted within the scope of wobble-in-a-cone motions of the two domains. The vertex angle of the cones was approximately 30°, which is incompatible with isotropic τ_m. Semi-quantitative arguments in support of an elongated solution structure with N = R^C_∥/R^C_⊥ ∼ 1.6 were invoked.

¹⁵N spin relaxation data of Ca⁺²-saturated Xenopus CaM were acquired by Baber et al.⁶⁴ at 8.5 (except for NOE's), 14.1 and 18.8 T, 308 K. The analysis was similar to that of Tjandra et al.⁶³ The larger data set available made possible determination of the global diffusion tensor, R^C, and removal of the restrictions that τ_f = 0 and S_f² = 0.85. Chang et al.⁶⁵ extended the experimental data set of Baber et al.⁶⁴ so that ¹⁵N T₁, T₂ and NOE's became available at 8.5, 14.1 and 18.8 T, at 294, 300, 308 and 316 K. These data were analyzed in concert assuming that (1) S_f², τ_f and N = R^C_∥/R^C_⊥ are the same for all the residues within a given domain and are independent of temperature, and (2) the temperature dependence of τ_m(app) (with τ_m(app) = 1/6D(app), D(app) = 1/3(2D_⊥ + D_∥)) is controlled by the Stokes-Einstein formula. A sudden decrease (increase) in S_s² (τ_s) was observed when the temperature was increased from 308 to 316 K, interpreted as ‘melting’ of residues 74-77 of the central linker, considered important from a biological point of view.

Since data acquired at several magnetic fields and several temperatures are analyzed in concert, the analysis is particularly prone to force-fitting. It will be shown below that qualitatively erroneous results are obtained in the case of Ca²⁺-Calmodulin.

Global diffusion

The axial global diffusion tensor, R^C, was determined together with the site-specific parameters using the total time correlation function, C(t) (eq 13), with C^L(t) given by the extended MF formula, and the coordinates of the elongated dumb-bell shaped crystal structure.⁶¹ In most MF studies R^C is determined separately based on C^C(t). The C(t)-based fitting of the combined multi-field multi-temperature data yielded Θ = 68°, as shown in Fig. 21, with the global diffusion axis, C, along the symmetry axis of the molecule. Accordingly, the principal axis of the inertia tensor, I, must be tilted at 68° from C. This disagrees with the orientation of the inertia tensor in the crystal structure, shown in Fig. 22. Clearly the latter orientation of the inertia tensor is correct, hence the orientation of the global diffusion tensor is likely in error.

Fig. 23 shows the experimental T₁/T₂ data acquired at 8.5, 14.1 and 18.8 T, and 294 and 316 K and filtered according to traditional criteria.^64,65 The width of the distribution divided by the average error is 6 (4), 8.5 (9.0) and 13.0 (14.0) for 8.5, 14.1 and 18.8 T at 294 K (316 K). It is obvious that the distribution in T₁/T₂ is significantly smaller at 8.5 T, in agreement with the 11.7 T data of Barbato et al.⁶² and Wand and co-workers.^18,60 Isotropic global diffusion analysis with the program QUADRIC⁶⁶ yielded the τ_m values depicted in Fig. 23. The shape of the distribution in T₁/T₂ values is both field-, and temperature-dependent, although it has been assumed that R^C is temperature-independent except for τ_m(app), which does not affect the shape of the T₁/T₂ distribution. It is very likely that the structured T₁/T₂ profiles at the higher fields represent mixed-mode contributions and unaccounted for geometric effects. If this is not the case then analyses based on single-field data and the concerted analysis should yield the same results. This test is carried out below.

Figure 23.

Experimental T₁/T₂ ratios at 8.5, 14.1 and 18.8 T, 294 and 316 K, from reference ⁶⁵. The isotropic global diffusion correlation times, τ_m, determined with the program QUADRIC,⁶⁶ are also shown.

Using the filtered T₁/T₂ data of Chang et al.⁶⁵ we determined the axial global diffusion tensor R^C at each magnetic field and temperature separately with the program QUADRIC.⁶⁶ This corresponds to using C^C(t) instead of C(t). In Fig. 24 we show D(app) = 1/3 (D_∥ + 2 D_⊥) (R^C(app) in our notation) as a function of P₂(cos(β_CC′)) at 8.5, 14.1 and 18.8 T, and at the temperatures of 294 and 316 K.

Figure 24.

Analysis of the experimental data shown in Fig. 23 with the program QUADRIC⁶⁶ assuming axial global diffusion (R^C). The resulting parameters, which define the R^C tensor, are also shown.

The spread of points about the theoretical straight lines (obtained with linear regression) in Fig. 24 is invariably large, indicating that theory and data are incompatible. There are very few points corresponding to β_CC′ = 0, in disagreement with the purported solution structure (Fig. 21). The largest spread of points is obtained for 8.5 T, 316 K, although χ² assumes the smallest value (χ² = 2) in this case. This is certainly not expected for models matching the data to which they are applied, but can occur when force-fitting sets in. All four parameters defining the global diffusion tensor are field-dependent. In all the cases except for 8.5 T, 316 K, the angle Θ of the individual analyses is much closer to 0° (coincident inertia and diffusion frames) than to the non-physical angle of 68° yielded by the concerted multi-field multi-temperature MF analysis. The contradictions between the raw data, the single-field analysis and the concerted MF analysis are substantial. For example, the raw T₁/T₂ profile at 8.5 T, 316 K is nearly flat (Fig. 23), while the R^C tensor illustrated in Fig. 24 is closest to the axial tensor yielded by the concerted analysis. As shown in Fig. 23, isotropic R^C analysis also yielded inconsistent τ_m values. Inaccuracies in C^L(t) must have been clearly absorbed by C^C(t). Therefore the local motion parameters must be highly inaccurate, as demonstrated below.

Local motion

Fig. 25 reproduces the S_s² and τ_s temperature-dependent profiles obtained by Chang et al.⁶⁵ The squared generalized order parameter S_s² shows very limited temperature dependence between 294 and 308 K and decreases abruptly upon increasing the temperature to 316 K. The slow local motion correlation time, τ_s, is temperature-independent between 294 and 308 K and increases abruptly upon increasing the temperature to 316 K. Within the scope of the cone model used by Chang et al.⁶⁵ the correlation time for slow local motion, τ_s, depends analytically on S_s² and D_w. The respective expression is used to show that the abrupt increase in τ_s is due to the abrupt decrease in S_s², while D_w increases with temperature. However, inspection of the absolute values of D_w shows that 1/6D_w is equal to 8.3 (6.8) ns for the N-domain (C-domain), while the apparent global motion correlation time is 6.88 ns. This is not tenable physically, nor consistent with the basic MF mode-independence assumption of time scale separation between the global and local motions.

Figure 25.

Best-fit S_s² and τ_s values obtained with the extended MF formula as outlined in ref. 65 for the N-domain (open squares) and C-domain (solid circles). Additional best fit parameters are S_f² ∼ 0.86, τ_f ∼ 15 ps and global diffusion parameters D_∥/D_⊥ = 1.62, Θ ∼ 68°, Φ ∼ 94° for the N-domain and 146° for the C-domain. The τ_m(app) values are 11.55, 9.87, 8.12 and 6.88 ns at 294, 300, 308 and 316 K.

The discontinuities in S_s² and τ_s between 308 and 316 K in Fig. 25 results from the force-fitting process veering into a different region of the parameter space at 8.5 T and 316 K. Inspection of the experimental data presented in Figures 26-28 shows that the T₂'s at 8.5 T, 316 K, are outliers. Fig. 24 shows that the graph obtained for 8.5 T, 316 K is an outlier. Inspection of Figs. 5-8, where SRLS and MF are compared for corresponding parameter values near the BO limit, shows that for τ_m = 15 ns the corresponding NMR variables are comparable in magnitude. On the other hand, for τ_m = 5 ns T₂ obtained with MF is significantly higher than T₂ obtained with SRLS. This supports the assertion that artificial results can be obtained by force fitting large data sets covering extensive parameter ranges. In the case under consideration the experimental data acquired at low fields and high temperatures do not accommodate the force-fitted parameters, which fit all the other data. Therefore discontinuities in S_s² and τ_s, which are merely technical in nature, ensue.

Figure 26.

Longitudinal ¹⁵N T₁ relaxation times of Ca²⁺-calmodulin at 294 K (black), 300 K (red), 308 K (green) and 316 K (blue), and 8.5, 14.1 and 18.8 T.⁶⁵ The vertical dashed lines depict the central linker (residues 74 – 78).

Figure 28.

Steady-state ¹⁵N-{¹H} NOE's of Ca²⁺-calmodulin at 294 K (black), 300 K (red), 308 K (green) and 316 K (blue), and 8.5, 14.1 and 18.8 T.⁶⁵ The vertical dashed lines depict the central linker (residues 74 – 78).

SRLS analysis

The Calmodulin data were analyzed separately for each temperature and magnetic field using our fitting scheme for SRLS based on axial potentials. We assumed that in view of large-amplitude domain motion R^C is on average isotropic, and used the τ_m(app) values of Chang et al.⁶⁵ Isotropic R^C is consistent with the Calmodulin studies of Barbato et al.⁶² and Wand and co-workers,^18,60 and with other ¹⁵N spin relaxation studies of proteins exhibiting large-amplitude domain motion.^19,21 As mentioned above, this SRLS fitting scheme assumes implicitly that R^L_∥≫R^L_⊥, in analogy with τ_s ≫ τ_f in MF. The SRLS fitting scheme selected primarily combination 5, which corresponds to model 5 MF. The average (S²₀)² (the formal analogue of S_s² in MF) and τ^L_⊥ (the formal analogue of τ_s in MF) values for each magnetic field are shown as a function of temperature in Fig. 29.

Figure 29.

Best-fit (S²₀)² and τ^L_⊥ values obtained with combination 5 SRLS by averaging over the results obtained for the individual residues using τ_m values of 11.55, 9.87, 8.12 and 6.88 ns at 294, 300, 308 and 316 K. β_MD was on average 15°. Experimental data from ref. 65 were used.

It can be seen that τ^L_⊥ SRLS differs in magnitude from τ_s MF (cf. Fig. 25). While τ_s shows the non-physical temperature dependence illustrated in Fig. 25, τ^L_⊥ shows physically reasonable temperature dependence illustrated in Fig. 29. (S²₀)² SRLS is approximately half of S_s² MF and decreases monotonically with increasing temperature. No sudden change is observed between 308 and 316K in either parameter. The inconsistencies among (S²₀)² and τ^L_⊥ values obtained at different magnetic fields are expected to be eliminated in future work, where rhombic potentials will be used.

Dynamic picture according to MF.⁶⁵

CaM is an elongated dumb-bell shaped molecule. The N-, and C-terminal domains wobble within cones with vertex angles increasing suddenly from 22.5° (27°) to 27° (37°) for the N-domain (C-domain) when the temperature is increased from 308 to 316 K. This corresponds to a squared generalized order parameter, S_s², decreasing from 0.77 (0.68) to 0.68 (0.53) for the N-domain (C-domain). The average wobbling rate, D_w, is 1.7×10⁷ (2.0 10⁷) s⁻¹ at 295 (316 K) for the N-domain, which translates into correlation times, 1/6D_w, of 9.8 (8.3) ns. The value of D_w is 2.0 10⁷ (2.45 10⁷) s⁻¹ at 295 (316 K) for the C-domain, which translates into correlation times of 8.3 (6.8 ns). The correlation time for global motion is 11.55 (6.88) ns at 295 (316 K). Hence, at 316 K the correlation time for local motion, 1/6D_w, is larger than the correlation time for global motion, τ_m, for the N-domain, and equal to τ_m for the C-domain. Motion about the N-H bond is on the order of 20 ps and S_f² is on the order of 0.85 throughout the temperature range investigated.

The abrupt change in best-fit parameters values upon increasing the temperature from 308 to 316 K is interpreted as ‘melting’ of residues 74-77. This process is purported to have biological implications for target peptide binding by prolonging the flexible part of the central linker by 50%. Note that the experimental data of residues 74-77 (as well as many other CaM residues) are not observed experimentally at 316 K (Figs. 26-28, residues demarcated by the dashed vertical lines).

Dynamic picture according to the current SRLS analysis

CaM is on average spherical in solution due to large-amplitude nanosecond segmental motions of its N-, and C-terminal domains. This is physically plausible, consistent with the T₁/T₂ profiles at 11.7 T which are determined predominantly by the global motion, and the quantitative analysis by Barbato at al.⁶² and Wand and co-workers.^18,60 Average spherical shapes in solution were also determined with ¹⁵N spin relaxation for AKeco¹⁹ and Binase,²¹ which similar to CaM, feature large-amplitude domain or loop motions in solution. Both AKeco and Binase have elongated shapes in the crystalline state, similar to CaM..

Domain motion is expected to occur on the same time scale as the global motion, implying mode-mixing. This is accounted for by the SRLS analysis, which yields τ^L_⊥ on the order of 3 – 6 ns in the temperature range of 294 – 316 K. As expected, τ^L_⊥ decreases monotonically with increasing temperature. (S²₀)² is on order of 0.2-0.35 in this temperature range and decreases monotonically with increasing temperature. No discontinuity is exhibited by either the τ^L_⊥ or the (S²₀)² temperature profiles.

The results shown in Fig. 29 are interim results because the analysis used oversimplified axial symmetry for the local orienting potential/local ordering, and assumed implicitly that R^L_∥/R^L_⊥ ≫ 1. The implication of removing these restrictions are illustrated and discussed in the next section.

6. Reliable fitting; the mixed mode concept

The SRLS approach is a general one, although we have implemented it with several simplifying assumptions. In our current fitting scheme the local and global diffusion tensors are allowed to be axially symmetric, and the local ordering tensor (or local coupling/mixing/orienting potential) is allowed to be rhombic. The magnetic tensors have arbitrary symmetry and orientation. If one starts with the original MF limit, where the magnetic tensors are collinear, their frame is the same as the local ordering frame, and the global and local diffusion tensors are isotropic, one can then systematically lower symmetries until the complexity of the model matches the integrity of the data. In this case reliable fitting, which extracts the dynamic information inherent in the experimental data, can be accomplished. Table 17 illustrates the last part of such a process, where SRLS spectral densities are upgraded to include more detailed features in a stepwise fashion.

Table 17.

Best-fit parameters obtained with the SRLS combination 5 (SRLS_5) and SRLS combination 6 (SRLS_6) using the axial-potential 2D grid-based fitting scheme. SRLS_rh represents the calculation carried out with the fitting scheme allowing for rhombic potentials and arbitrary N = R^L_∥/R^L_⊥ values, with the j_KK'(ω) functions calculated on the fly. The combined ¹⁵N relaxation data of residue 124 of RNase H acquired at 11.7, 14.1 and 18.8 T, 300 K, were used. τ_m = 9.28 ns was used. R^C is the same as τ_L/τ_m, and N = R^L_∥/R_L⊥. S_xx, S_yy and S_zz are the components of the Cartesian ordering tensor.

	RC	c20	c22	Sxx	Syy	Szz	βMD°	N
SRLS_5	0.44	3.2	0.0	−0.315	−0.315	0.63	16.1	1000(fixed)(χ2 = 15.9)
SRLS_6	0.45	3.2	0.0	−0.315	−0.315	0.63	16.3	916(χ2 = 15.8)
SRLS_rh	0.23	4.8	10.1	−0.469	0.799	−0.330	99.5	40.0(χ2 = 12.3)

The example considered is residue 124 of RNase-H, which pertains to the flexible loop α_D/β₅. The ¹⁵N relaxation data acquired at 11.7 T, 300 K, were fit previously with MF model 5.¹² The global motion correlation time of RNase H was determined to be τ_m = 9.28 ns at 300 K, and it has been ascertained that the protein is spherical within a good approximation. We subjected the combined 11.7, 14.1 and 18.8, 300K, data of this residue (kindly provided by Prof. A. G. Palmer III of Columbia U.), to SRLS analysis.

The first row of Table 17 shows the best-fit parameters obtained with SRLS combination 5 (SRLS_5), which is formally analogous with MF model 5. In this scenario the local ordering is axially symmetric and N = R^L_∥/R^L_⊥ ≫1. The potential is small (c²₀ = 3.2), the corresponding squared order parameter is small ((S²₀)² = 0.47), the D-to-M tilt is small (β_MD = 16.1°), and there is only a modest time scale separation between the global and perpendicular component, R^L_⊥ (i.e., R^C = 0.44 in units of R^L_⊥). Similar values were obtained previously for the flexible residues of a large number of proteins and can be considered typical. This modest time scale separation between the global and local motion (R^C) is expected. Quite unexpectedly, the local potential is weak (c²₀ = 3.2) for the tightly packed globular proteins, i.e., the local ordering is low ((S²₀)² = 0.40). Also, the diffusion tilt is on the order of 16° instead of being on the order of 90°, corresponding to preferred ordering around C^α_i−1-C^α_i of N_i−C^α_i. No improvement was achieved by allowing N to vary (SRLS_6), indicating that N ≫ 1 is not the main reason for these difficult-to-reconcile results. On the other hand, significant improvement was achieved by allowing the potential to be rhombic, in addition to allowing N to vary, as shown by the last row of Table 17.

Let us compare the results obtained for axial (SRLS_6) and rhombic (SRLS_rh) potentials. The value of N = 40 corresponds to τ^L_∥ = 53 ps whereas N = 916 corresponding to τ^L∥ ∼ 0. The ordering is high in the rhombic case, as implied by c²₂ = 10.1, and low in the axial case. The ratio c²₂/c²₀ obtained with SRLS_rh corresponds to ‘nearly planar Y_M-X_M ordering’, as expected This is borne out clearly by the values of the components of the Cartesian ordering tensor shown in Table 17. The diffusion tilt is β_MD ∼ 90° in the rhombic case, compatible with crankshaft fluctuations³⁸ or peptide-plane reorientation about the C^α_i−1-C^α_i axis or the N_i-C_i bond, small-amplitude N-H wobbling motion and/or nitrogen pyramidalization,³⁹ which are illustrated in Fig. 30. The rate of this motion, R^L_⊥ = 0.23×9.23 = 2.1 ns, shows that, as expected, loops move on the same time scale as the entire molecule. Unlike the axial scenario the rhombic scenario is consistent and physically appropriate.

Figure 30.

Various local motion modes including the anti-correlated Φ_i and Ψ_i−1 crankshaft motion (upper left), peptide-plane motion about C^α_i−1-C^α_i (upper right), nitrogen pyramidalization (lower left) and fast small-amplitude fluctuations (lower right).

Data fitting with rhombic potentials was also carried out for residues 45 and 47 of Adenylate kinase from E. coli (AKeco), which are representative of the mobile domain AMPbd of AKeco. The results are shown in Table 18. The symmetry of the rhombic potential is of the same type as found for residue 124 of RNase H, and the angle β_MD is also close to 90°. However, R^C is on the order of 0.8 for the AKeco residues 45 and 47 as compared to 0.2 for residue 124 of RNase-H, and τ^L_∥ ∼ 1.5 ns for the AKeco residues 45 and 47 as compared to τ^L_∥ = 75 ps for residue 124 of RNase-H. This indicates significantly stronger dynamical coupling and smaller local diffusion anisotropy for mobile domains than for flexible loops.

Table 18.

Best-fit parameters obtained with the SRLS combination 6 featuring rhombic potentials using Adenylate kinase data acquired at 14.1 and 18.8 T, 303 K.¹⁹ τ_m = 15.1 ns was used. R^C = τ^L_∥/τ_m. S_xx, S_yy and S_zz are the components of the Cartesian ordering tensor.

res	c20	c22	RC	Sxx	Syy	Szz	βMD°	N
46	5.7	10.5	0.82	−0.465	0.827	−0.361	101.4	9.6
47	4.3	10.3	0.73	−0.470	0.761	−0.291	100.7	6.3

The SRLS version which allows for rhombic potentials and axial local diffusion clearly yields a consistent physical picture. It appears that this is as much as one can extract from ¹⁵N relaxation data in proteins. Note that nine data points, acquired at three magnetic fields were used in these calculations. The rhombic potential coefficient, c²₂, is the only extra parameter in SRLS as compared to extended MF. On the other hand, for flexible residues which are typically of biological interest, SRLS features a single local motion while MF features two local motions (fast and slow), so the MF concept is actually a more compounded one.

The meaning of mixed modes

Let us consider a cylinder diffusing freely in an isotropic medium. The diffusion rates are R^L_∥ and R^L_⊥, with N = R^L_∥/R^L_⊥ determined by its shape. The solution of the diffusion equation yields eigenvalues τ_K⁻¹ = 6 R^L_⊥ + K² (R^L_∥ – R^L_⊥), with K = 0, 1 and 2. Let us now consider the same cylinder diffusing in the presence of a locally orienting potential. This is a reasonable model for an N-H bond attached physically to the protein, with the local potential representing the restrictions imposed on its motion by the immediate protein environment. The protein itself is reorienting at a slower rate with respect to a fixed lab frame. When the local and global motions do not occur on a greatly separated time scale, and the local potential is neither very low nor very high, the potential couples or mixes the motions of the N-H bond and the protein. The local ordering can be expressed (as usually done for restricted motions in liquids) in terms of an ordering tensor with principal values defined in terms of the orienting potential.

This is the two-body problem solved by the SRLS model. A Smoluchowski equation of the form of eq 1 is solved where the SRLS diffusion operator Γ̂ can be written in either of the two equivalent forms given by eq 2 or eq 3. In eq 2 the orientation of each body is referred to the lab (inertial) frame, but with a potential coupling them, which depends on their relative orientations. Simple products of basis functions of the two rotators (N-H body and protein), corresponding to their free diffusion (i.e., zero potential coupling them), are utilized to provide a matrix representation of Γ̂. This is a convenient basis set when the potential is relatively small, i.e., weak coupling. In eq 3 only the global motion of the protein is referred to the lab frame, whereas the local motion of the N-H bond is referred to the local director frame in the protein. This latter scenario thus describes the local motion in relative coordinates. Then product basis functions for the overall motion and the relative motion are used to provide the matrix representation of Γ̂. This is a more natural choice when the potential coupling is large. Since these two approaches are mathematically equivalent, one may use either choice. In our past work we have utilizes eq 2, whereas in the newer work we have reported in this paper we utilized eq 3.

The eq 2 perspective on mixed modes means that as a coupling potential is added, the new eigenmodes of Γ̂ become linear combinations of the product functions of the two free rotors. This is a point of view where there are two sources of “mixed-modes”: the first results from the coupling between the two rotors, so that the motion of the internal rotor becomes more that of its motion relative to the protein. This is a feature that exists even when there is time-scale separation, i.e., R^C/R^L ⪡ 1. The second arises when R^C/R^L ∼ 1, so there is no longer a significant time-scale separation. In that case the diffusive reorientation of the internal rotor becomes a mixture of the global and local motions. That is, an observer that detects just the ¹⁵N label on a particular N-H bond can no longer distinguish between a local and a global mode of motion. Thus, these modes become mixed. In the case, wherein eq 3 and its convenient basis set are used, the intuitive picture changes somewhat, but the final analysis must remain equivalent. In simple mathematical terms, this means that the eigenvalues of Γ̂ are unchanged, but the eigenmodes are represented in (or referred to) the different basis sets, and appear different, although (again) they must be equivalent. Here, for very high ordering and R^C/R^L ⪡ 1, the eigenmodes can be represented by the overall motion and by the relative internal motion with eigenvalues given (for axial potentials) by eq 18, and eigenfunctions given elsewhere (refs. ²⁹ and ⁴⁸), yielding simple limiting correlation functions. As the coupling potential is reduced (but R^C/R^L ⪡ 1), then the correlation functions for the relative motion (i.e., for the D²_MK(Ω_CM)) become more complex, involving several eigenmodes of this motion. Again, as R^C/R^L_⊥ → 1, there must be “mixed modes” of the two coupled dynamic processes.

We illustrate some of these concepts with a relevant computational study presented by Polimeno and Freed.²³ This was performed using the basis set appropriate for eq 2, i.e., the global and internal rotors both referred to the lab frame. Table 19 shows the eigenvalues (in units of R^L) and corresponding weights of the two isotropic rotors coupled by an axial potential whose strength is given by c²₀. Values of R^C/R^L of 1.0, 0.1 and 0.01 are considered, and c²₀ ranges from 0 to 4. When c²₀ = 0, the motions are uncoupled, so only the motion of the local rotor relative to the lab frame is relevant. It corresponds to eigenvalue 6 (or more precisely 6R^L) with weight 1.00, independent of R^C/R^L. For the case of R^C/R^L = 0.01 there is good time-scale separation of the motions. Thus, as c²₀ is increased the global motion retains the eigenvalue 0.06, but its relative weight in the correlation function C₀(t) increases roughly according to (S²₀)². The local motion is represented by several eigenvalues with the (typically two) major ones given in Table 19. The results for R^C/R^L = 0.1 are qualitatively similar. For R^C/R^L = 1 the results are quite different. As c²₀ is increased from 0, two main mixed modes appear, one of which decreases from the value of 6.00, while the other increases from this value, and the former becomes relatively more important in C₀(t). We can intuitively suggest that the former represents a mixed mode, wherein as the protein reorients in one sense (e.g., clockwise), the internal rotor is attempting to reorient in the opposite (e.g., counterclockwise) sense; the latter mixed mode would correspond to more additive reorientational diffusion (i.e., both are in the same sense).

Table 19.

Dominant eigenvalues and respective weights (given in parenthesis) in the C₀(t) correlation function for two isotropic rotators, R^C and R^L = 1, mixed by an axial potential of strength 0 ≤ c²₀ ≤ 4, and time scale separation given by R^C = 1.0, 0.1 and 0.01. The (S²₀)² values corresponding to the c²₀ values are also presented.

			RC
c20	(S20)2	1.0	0.1	0.01
0	0	6.00(1.00)	6.00(1.00)	6.00(1.00)
1	0.049	4.79(0.60)	0.59(0.06)	0.06(0.05)
		7.57(0.39)	5.94(0.65)	5.57(0.32)
			7.33(0.15)	6.04(0.27)
2	0.193	3.90(0.71)	0.58(0.23)	0.06(0.19)
		10.0(0.27)	6.55(0.57)	6.04(0.26)
			8.10(0.11)	6.68(0.36)
3	0.366	3.41(0.79)	0.56(0.41)	0.06(0.37)
		13.43(0.17)	7.95(0.37)	7.20(0.15)
			9.47(0.12)	8.02(0.33)
4	0.506	3.19(0.85)	0.55(0.56)	0.06(0.51)
			10.06(0.22)	10.0(0.30)
			11.54(0.14)

Finally, a comment on the tensors R^C and R^L which constitute input values in a given SRLS calculation, or best-fit parameters in fitting actual experiments, is in order. These quantities may represent more complex local and global rotators, and not just the R^C and R^L tensors corresponding to simple rotators. One can suggest tentative interpretations, as was done in a recently published SRLS application to nitroxide-labeled T4 Lysozyme.³⁷ In that paper R^L_∥ was interpreted as motion around a specific bond of the nitroxide tether, whereas R^L_⊥ was associated with motion around the symmetry axis of the helix comprising the nitroxide-labeled residue. For N-H bond motion we associated at this stage of our studies R^L_⊥ with motion around the C^α_i−1-C^α_i axis and R^L_∥ with motion around an axis perpendicular to C^α_i−1-C^α_i within the peptide plane.

Table 20 illustrates the high sensitivity of the eigenvalues and weights comprised in the time correlation functions C_KK′(t) to the symmetry of the coupling potential. The parameters used include R^C = 0.001 and c²₀ = 2, with c²₂ = 0 for axial ordering and 3 for rhombic ‘nearly planar Y_M-X_M ordering’. For axial ordering only C₀(t) is relevant. For the β_MD = 90° geometry only the correlation functions C₀(t), C₂(t) and C_2–2(t) = C₋₂₂(t) contribute to the measurable spectral density. The dominant eigenvalues and their eigenmode composition depend to a large extent on the symmetry of the coupling potential. The individual Lorentzians in a given function j_K1K1(ω), obtained by Fourier transformation of the corresponding time correlation function, are multiplied by d²_KK′ to yield the measurable spectral density. The d²_KK′ values are also presented in Table 20. The additional contributions, comprising a large number of eigenvalues with small individual weights, are not shown. It can be seen clearly that potentials of similar magnitude but different symmetry are associated with a different composition of dynamic modes. Obviously potential symmetry is a very influential component, to which the experimental data are highly sensitive.

Table 20.

Dominant eigenvalues and respective weights (given in parenthesis) of the C_K(t) and C_KK'(t) components which contribute to the measurable spectral density for β_MD = 0° in the axial case given by R^C = 0.001, c²₀ = 2 and c²₂ = 0, and β_MD = 90° in the rhombic case given by R^C = 0.001, c²₀ = 2 and c²₂ = 3. The respective irreducible ordering tensor components, S²₀ and S²₂, are also presented.

c22	S20	S22	eigenvalue(weight)	K	K'	d2KK'
0.0	0.439	0.0	6.58(0.415)	0	0	1.0
			0.006(0.193)
			5.95(0.193)
			8.52(0.161)
			..............
3.0	0.088	0.572	5.40(0.349)	0	0	0.25
			4.44(0.237)
			4.36(0.232)
			8.31(0.114)
			0.006(0.008)
			...............
			4.36(0.214)	2	2	0.75
			1.85(0.209)
			5.70(0.184)
			0.006(0.098)
			...............
			4.36(0.428)	2	−2	0.75
			0.006(0.163)
			14.40(0.125)
			5.40(0.120)
			4.44(0.08)
			...............

As indicated, we have developed recently a fitting scheme for SRLS where the spectral densities j_K(ω) and j_KK′(ω) are calculated on the fly. This fitting scheme allows for rhombic potentials, and arbitrary axiality of the local and global diffusion tensors. Efforts to improve the computational efficiency of this scheme are underway.

IV. Conclusions

Model-free is a very simplified approach for analyzing spin relaxation data in proteins, such that the quality of the experimental data and their variations (e.g., with magnetic field) are frequently beyond its capabilities. Small data sets (three data points at a given field in the case of N-H bond dynamics) can usually be force-fitted with good statistics but inaccurate best-fit parameters, which are obtained through parameterization of the experimental spectral densities. When larger data sets acquired at several magnetic fields, temperatures, states of complex formation, etc., are subjected to MF analysis, or when N-H and C′-C^α bond dynamics are analyzed in concert, force-fitting is so pervasive that functional dynamics may be missed, qualitatively erroneous results may be derived, and incorrect phenomena may be detected. Conformational entropy derived from parameterizing entities is inaccurate. Entropy profiles over the protein backbone may even be qualitatively inaccurate.

On the other hand, the experimental data can be analyzed significantly more reliably with SRLS spectral densities, which constitute generalized forms of the MF formulae. The main aspects which greatly improve the analysis include non-symmetric (e.g., axial) local motion, rhombic local ordering, rigorous account of mode-coupling, and proper treatment of general features of local geometry. The dynamic picture emerging, which differs significantly from the MF picture, is physically insightful, consistent and comprehensive. Conformational entropy can be derived with SRLS in a straightforward manner from experimentally determined local potentials of arbitrary symmetry.

Figure 27.

Transverse ¹⁵N T₂ relaxation times of Ca²⁺-calmodulin at 294 K (black), 300 K (red), 308 K (green) and 316 K (blue), and 8.5, 14.1 and 18.8 T.⁶⁵ The vertical dashed lines depict the central linker (residues 74 – 78).