Diffusion in Model Networks as Studied by NMR and Fluorescence Correlation Spectroscopy

Abstract

We have studied the diffusion of small solvent molecules (octane) and larger hydrophobic dye probes in octane-swollen poly(dimethyl siloxane) linear-chain solutions and end-linked model networks, using pulsed-gradient nuclear magnetic resonance (NMR) and fluorescence correlation spectroscopy (FCS), respectively, focusing on diffusion in the bulk polymer up to the equilibrium degree of swelling of the networks, that is, 4.8 at most. The combination of these results allows for new conclusions on the feasibility of different theories describing probe diffusion in concentrated polymer systems. While octane diffusion shows no cross-link dependence, the larger dyes are increasingly restricted by fixed chemical meshes. The simple Fujita free-volume theory proved most feasible to describe probe diffusion in linear long-chain solutions with realistic parameters, while better fits were obtained assuming a stretched exponential dependence on concentration. Importantly, we have analyzed the cross-link specific effect on probe diffusion independently of any specific model by comparing the best-fit interpolation of the solution data with the diffusion in the networks. The most reasonable description is obtained by assuming that the cross-link effect is additive in the effective friction coefficient of the probes. The concentration dependences as well as the data compared at the equilibrium degrees of swelling indicate that swelling heterogeneities and diffusant shape have a substantial influence on small-molecule diffusion in networks.

I. Introduction

Molecular transport of penetrants through swollen networks is a key process that critically determines the material performance in a variety of polymer applications such as separation membranes, conductive layers in battery and fuel cell applications, as well as drug-release systems. Despite many decades of research on diffusion of differently sized molecules through polymer networks, solutions and melts, there is as yet no coherent picture of the appropriate model(s) that could describe or even predict penetrant mobility in systems with different local structures over large ranges of polymer concentration.¹⁻²⁶ For reviews on the topic see refs (27), (28). While geometric obstruction models have successfully been used to describe transport in highly swollen, often stiff-chain hydrogels,^12,20,22 free-volume concepts,^{1−8,10,13−15,19,29} and hydrodynamic theories^9,11,17,18 were more successful in covering also the range of semidilute to very concentrated systems. Even less clear is the effect of permanent cross-links,^{2,6−8,10,12,17−24,26} where the situation is complicated by the fact that the majority of studies has been performed either at swelling equilibrium or at the polymer concentration at which the networks are formed, thus mixing effects of cross-links with simple concentration effects, and that the theories used to analyze the data often do not distinguish between permanent network meshes and an interchain correlation length that is essentially determined by concentration only. As a rough classification, the literature suggests a qualitative difference between heterogeneous, phase-separated, stiff-chain hydrogels, such as agarose gels, and homogeneous networks and gels composed of flexible chains.^{12,17,20,22,24,27}

This study is intended to establish new insights for the case of homogeneous, amorphous model networks composed of flexible chains with well-defined and largely different mesh size, studied at different solvent concentrations, ranging from the unswollen state, where the polymer is still mobile and far above its T_g, to the equilibrium degree of swelling. To minimize secondary effects such as H-bonded solvation shells and long-range dipolar or even ionic interactions around hydrophilic or ionic polymers, we focus on an unpolar polymer, poly(dimethyl siloxane), swollen in an unpolar, good solvent, octane.(30) We compare the diffusivity of the solvent, measured by pulsed-field-gradient (PFG) nuclear magnetic resonance (NMR), with the diffusion of larger dye molecules, measured by fluorescence correlation spectroscopy (FCS), in solutions of linear polymer and different networks, and use different models to analyze the effect of cross-linking on probe diffusion. By using FCS, we are taking advantage of the very low penetrant concentration, at which “trace” diffusion coefficients (defined for the limit of zero penetrant concentration) are directly obtained.

Since FCS has been conceived in the early 1970s,(31) it has become an important method in molecular biology.³²⁻³⁷ Its advantages as a very direct and robust technique for the study of diffusion of dye-labeled synthetic polymers have already been noted in 1984,(38) yet significant activity of this kind has not started until the current decade.³⁹⁻⁴⁴ Other important areas of application are the investigation of micelle formation and size in amphiphilic systems, using either labeled amphiphiles⁴⁵⁻⁴⁹ or phase-specific dyes,^47,50−52 the study of polymer diffusion on surfaces(53) and interfaces,(54) and the internal dynamics of multiply labeled polymers with large persistence length.^55,56 The mobility of single fluorophores as a probe of local dynamics in polymeric systems(57) has been studied in melts far above(58) as well as around the glass transition.(59)

Important in the context of the present work are FCS diffusion studies of probes of various sizes (single dye molecules, labeled polymers, labeled particles) in polymer solutions(25) and hydrogels.²²⁻²⁴ The latter studies have shown that only a combination of obstruction and hydrodynamic effects can model the diffusion data. We here extent this work to well-defined networks and higher polymer concentrations. By combining NMR and FCS, yielding information on the mobility of the solvent and different dye molecules as penetrants, respectively, and comparing diffusion in linar polymers as well as cross-linked networks at different concentrations, we are able to test different established models describing diffusion of small to medium-sized molecules in such a model system. Importantly, we draw conclusions on the appropriate way to incorporate effects of permanent cross-links, which in the simplest picture constitute an upper limit to the mesh size that is available to penetrant motion. Our data further suggest that swelling heterogeneities play an important role.(30)

II. Theoretical Background

Free-volume theories appear to be the most successful approach to quantitatively describe diffusion in polymeric systems.^1−4,29 While the Vrentas-Duda formulation(4) is a quantitative and predictive theory, however, with an unwieldily large number of parameters, the mere concentration dependence of the diffusion coefficient in a two-component polymer solution is captured to a good approximation(3) by the much simpler earlier version of Fujita(1)

The concentration enters in the form of the degree of volume swelling Q = 1/ϕ_p = V/V₀ = (V_s + V_p)/V_p. The penetrant (trace) diffusion coefficient in the solution, D_soln, here given relative to the diffusion coefficient D₀ in the pure solvent, depends primarily on the molar (or molecular) free volumes of the solvent and the polymer, f_s and f_p, respectively, and the parameter B_d that is related to the displacement volume of the penetrant for an elementary jump. Note that, in particular, for two-component systems it is not uncommon to measure D relative to the diffusion coefficient in the pure polymer, which results in a different functional dependence.^5,14

Closer inspection of eq 1 reveals that it has only two truly independent parameters(14)

where the now dimensionless parameters B_d′ = B_d/f_s and f′ = f_p/f_s are the respective unprimed quantities in units of the free volume of the solvent.

An important extension is due to Yasuda et al.,(2) who has established the use of the above equation for the case of a three-component system (polymer, solvent, penetrant), recognizing that the penetrant size only enters in the parameter B_d, which may then be related to its cross sectional area ∼R² times the jump length. Yasuda et al. have also first introduced a multiplicative correction factor P_x(R,ξ) that describes the topological “sieving” effect of a network in the form of a jump probability that may be related to the cross-sectional area ∼R² of the penetrant and the mesh size ξ. The mesh size in turn depends on the network topology, as determined by the functionality of the cross-links and the network chain molecular weight M_c, and Q. Below, we will attempt to determine the functional form of P_x experimentally by comparing probe diffusion in a solution of a high molecular weight linear polymer, for which the probe diffusion is independent of molecular weight, with the diffusion in the swollen network,

Such a multiplicative sieving factor to incorporate the topological effect via a probabilistic argument has been used by a variety of authors. Peppas and co-workers have given different (and mutually exclusive) formulations of P_x as a function of the network parameters,^6−8,10 and the concept has also been extended to the combination of obstruction and hydrodynamic effects.^17,24,27 One of the purposes of this work is to collect general evidence for the feasibility of the multiplicative approach to describe the network effect.

Hydrodynamic theories represent an alternative to modeling penetrant motion. One of the most recognized approaches is due to Phillies,^9,11 who found that the reduced diffusion coefficient follows a stretched exponential function

The parameter α should primarily depend on the size of the diffusant, while the scaling exponent ν depends on the specific polymer system and also on diffusant molecular weight in certain cases. It should be noted that stretched exponential forms of this kind appear to fit data from very different systems very well and that many different theoretical treatments lead to the same functional dependence.^27,28 This obscures the meaning of the parameters α and ν and suggests that they should be treated as phenomenological parameters unless more specific experiments are performed to clarify their dependence on additional variables of the system.

Petit et al. developed an interesting alternative model based on the correlation length ξ of entangled polymer solutions and networks in relation to penetrant size.(16) The central argument rests on the use of the Stokes−Einstein equation, D = kT/ζ, and the assumption that the friction coefficient ζ is additive in the contributions from the mere polymer concentration effect and the effect due to the mesh size, ζ_ξ. Similar arguments have also successfully been used to describe polymer diffusion in dense melts, where competing relaxation mechanisms (Rouse and reptation) with additive contributions to the effective ζ determine the overall mean-square displacement.(13) In the Petit model, the influence of ξ on ζ_ξ is described by de Gennes’ scaling theory, and the result of this treatment is

Here, in agreement with scaling theory, the exponent ν′ should only depend on the solvent quality of the specific system, and a contains information on the penetrant size, following a picture of an activated jump through a network mesh.

Notably, similar to the free-volume model, the Phillies and Petit models (as many others) do not distinguish between a fluctuating mesh size ξ in a solution of linear chains and permanent meshes ξ_x determined by cross-links in a swollen network. We will therefore also test whether eqs 4 and 5, as applied to linear-chain solutions, can be combined with eq 3, which assumes that the effect due to cross-links is the multiplicative factor P_x. As an alternative, we take up the concept behind the Petit model and will also test whether a more consistent explanation of the data might be provided by assuming that the network effect is also additive in the effective friction coefficient, ζ_net = ζ_soln + ζ_x. This leads to the following relation between the diffusion coefficients of the probe in the solution and the network

where ζ₀ is the effective friction coefficient for the probe in the pure solvent. Essentially, the primary goal of this work is to shed light into the question whether probe diffusion in networks as compared to linear-chain melts is better described by eq 3 or 6.

III. Experimental Section

Samples

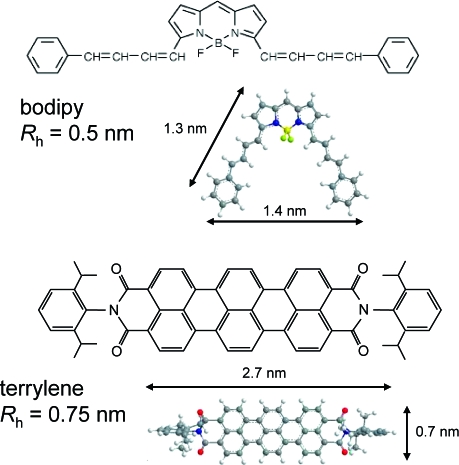
The probe molecules studied are the solvent octane itself (using NMR) and two different dye molecules studied by FCS, namely bodipy B3932 (Invitrogen, Inc.), and a terrylene diimide, which was synthesized as described previously.(60) Solvents (UVASOL grade) were purchased from Aldrich. Both dyes are efficient for fluorescence excitation at 639 nm, and they differ in size and shape, as shown in Figure 1. The room-temperature hydrodynamic radii R_h of octane, bodipy and terrylene are approximately 0.2, 0.5 ± 0.05, and 0.75 ± 0.05 nm, respectively, as estimated from their diffusion coefficients (2, 0.8, and 0.5 × 10⁻⁹ m²/s) and the Stokes−Einstein relations. The absolute diffusion coefficients were determined by PFG NMR (see below) in deuterated solvent, and the error intervals arise from systematic errors due to the low solubility and aggregation tendency of the dyes, leading to additional components in the decay functions. Note that also due to pronounced aggregation, bodipy in octane required the addition of 10% toluene, and the diffusion coefficient of terrylene could only be measured in pure toluene, where the given R_h and D in octane were transformed using the viscosity ratio of the solvents.

Figure 1.

Molecular structures and dimensions of the dye probes.

We study diffusion in octane solutions of linear PDMS with M_n = 47.2 kg/mol and in end-linked model networks, where precursors of different molecular weight were cross-linked with a tetrafunctional cross-linker (tetraethoxysilane) using a tin catalyst. Details on these samples are provided in ref (30), where the same samples, also swollen in octane, were studied with respect to swelling heterogeneities, as detected by multiple-quantum NMR. We note in passing the swelling heterogeneities have a characteristic length scale below 100 nm, whereas diffusion is studied on the μm length scale, which means that we observe averaged quantities. The sample denominations are net47k, net5k, net800, with precursor MW and, thus, network chain molecular weights M_c of 47.2, 5.2, and 0.8 kg/mol, respectively.

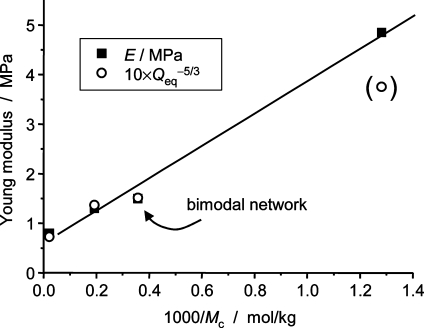
The fourth sample is a bimodal network with 30 wt % short chains (0.8k) and 70 wt % long chains (47k), termed net47k30. Such a network is known to mainly consist of nanoscale phase-separated short-chain clusters in a matrix of long chains,(61) and its averaged network chain MW is about 2.8 kg/mol. Despite its nanoscopic heterogeneity, its modulus and swelling properties are well described by the average M_c, as demonstrated in Figure 2, where the known cross-link density 1/M_c is compared to macroscopic sample properties, specifically the modulus E ∝ (1/M_c + 1/M_e) and the scaled equilibrium degree of swelling Q^−5/3_eq in octane. The y-intercept arises from the entanglement contribution to the modulus. The scaling exponent corresponds to Flory’s well-known relation between the expected bulk modulus and Q_eq for swelling in good solvent and in the limit of large degrees of swelling.(62) The deviation for the most highly cross-linked sample (net800, Q_eq = 1.8, point in brackets) is therefore easily explained.

Figure 2.

Properties of the studied PMDS end-linked model networks. Correlation of the chemically predetermined cross-link density 1/M_c with the modulus and the scaled equilibrium degree of swelling (data from ref (30)). The line is a linear fit to E.

For FCS measurements, the dyes were initially dissolved in toluene (due to the better solubilìty) and then diluted 3−4 times by a factor of 10 into octane. A dry piece of network was then infiltrated with a drop of dye solution and swollen to equilibrium in a octane vapor in a closed desiccator. Lower degrees of swelling were realized by controlled evaporation in ambient atmosphere and monitored on a scale, and stopped by encasing the sample in a closed cell. The sample dimensions were finally controlled by a stereo microscope, and the estimated error in Q as derived from the geometric measurement is reflected in the error bars along the corresponding axes in the plots below. For linear polymer, the components were simply mixed by weight.

NMR Spectroscopy

Pulsed field-gradient (PFG) stimulated-echo NMR diffusion experiments(63) were performed on a Bruker Avance 500 spectrometer equipped with a Micro5 imaging system. All details are given in ref (30), where the NMR data shown in Figure 4 was already published. The data is here mainly analyzed to delineate a possible description of the data by free-volume theory. In this earlier study, the largest error was due to the difficult control of the degree of swelling (below equilibrium, or more precisely, in equilibrium with the given vapor pressure of the solvent), explaining the scatter.

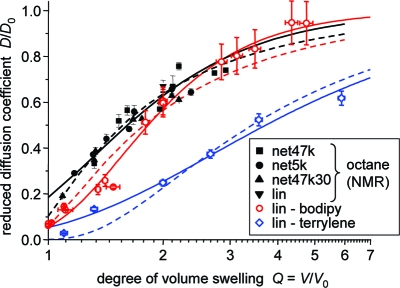
Figure 4.

Results for the reduced diffusion coefficient of the three probes in octane solution of linear PDMS 47k. The NMR data on octane diffusion are taken from ref (30). The dashed lines are fits to the free-volume model, eq 2, and the solid lines are fits to the Phillies model, eq 4.

FCS Apparatus

Fluorescence correlation spectroscopy³¹⁻³⁶ was performed on a home-built apparatus with pulsed excitation (80 MHz) using a red laser diode with λ = 639 nm (PDL 800-B, Picoquant, Berlin) and a detection system consisting of an avalanche photo diode (APD SPCM-AQR-14-FC, Perkin-Elmer) attached to a time-correlated single-photon counting system,(64) TimeHarp200 (Picoquant, Berlin), as well as an ALV 5000/60X0 correlator (ALV, Langen, Germany). Data acquisition, autocorrelation, and confocal scanning was performed with the SymphoTime software (Picoquant, Berlin), and autocorrelation functions (ACF) were also taken from the ALV software. The ACFs from the two systems were found to be identical.

Our apparatus is based on fiber optics, with the advantage of facile and robust setup and well-defined beam profiles.(65) The output of the laser diode, coupled into a single-mode fiber by the manufacturer, is expanded using a telescope arrangement to a parallel beam of about 0.5 cm diameter (1/e² intensity), roughly filling the back aperture of a Zeiss Plan Neofluar NA = 0.9 multi-immersion objective. Fluorescent light passes a dichroic beam splitter and a cleanup filter and is collected by a tube lens with f = 160 mm, coupling the light into a detection fiber with 50 μm diameter, with the latter being attached to the APD.

We chose the Zeiss NA = 0.9 objective for its correction ring, which is meant to adjust the objective to different immersion media ranging from oil to water. We used oil immersion and used the ring to correct for distortions due to the nonstandard (organic) sample medium.(39) The setup was optimized for molecular brightness (counts per molecule per second), based on the initial value of the ACF (∼1/N) and the overall count rate. Conveniently, PDMS and octane have almost the same refractive index (1.41), such that the focal volume does not change as a function of the degree of swelling. The objective is mounted on a PIFOC piezo z-positioner (P-725.1CL, Physik Instrumente, Karlsruhe, Germany), and the closed sample cell (a plastic cylinder, covered with circular 2 cm diameter, 150 μm thick coverslips at top and bottom, sealed with O-rings) is mounted on a piezo x/y positioner (P-733.2CL, Physik Instrumente), enabling 3D confocal imaging over 100 μm in all directions, as controlled by the SymphoTime software. With this setup, the z-position of the focus was accurately controlled (as it has an influence on the confocal volume), and the homogeneity of the samples on a scale of the optical resolution (∼0.7 μm full focal with at 1/e² intensity laterally, ∼3 μm along z) was assured by confocal scanning at larger dye concentrations.

FCS Data Analysis

Using FCS as a quantitative method is difficult due to effects of nonideal (non-Gaussian) focal-volume optics.^66,67 We therefore refrain from reporting absolute diffusion coefficients, and rather report D/D₀ in terms of the ratio of diffusion times τ_D0/τ_D obtained from fits to the ACF(34)

N is the number of independently diffusion dye molecules in the focus (typically around 5), and f_T and τ_T are the triplet fraction and triplet lifetime, respectively. Typical values for bodipy are 30% and 350 ns, respectively. We used a laser power on the order of 50−100 μW, such that systematic errors of the triplet parameters related to APD afterpulsing effects cannot be fully excluded. The axial ratio of the confocal volume, ω = z/x ≈ 4.6, was obtained from a fit to a measurement of the dye in pure octane and fixed in the fits to the polymer-containing systems. The focal dimensions were roughly confirmed by scanning of small fluorescent spheres embedded in a polymer film cast from aqueous solution.

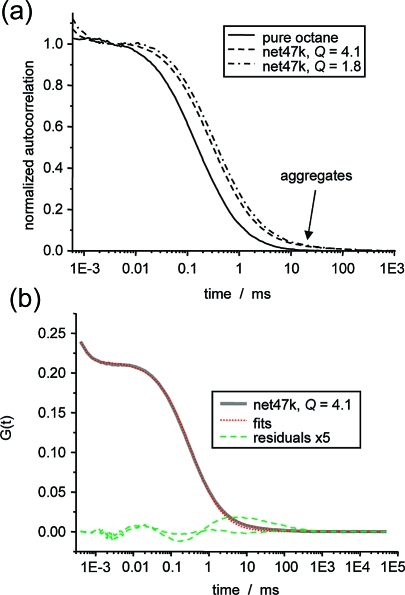
Examples of ACFs for bodipy in pure octane and a network at two different degrees of swelling are shown in Figure 3a. The slow-down in the polymer-containing systems is immediately apparent. In addition, in all polymer-containing samples, we observed a minor component of G(t) at longer diffusion times, which we attribute to aggregates. Their contribution was always on the order of a few percent, with irreproducible diffusion times in excess of 10 ms. This component was accounted for by a two-component fit (assuming a single triplet process), and due to its low fraction, the result for τ_D for the single free dye is affected by less than 10%. As can be seen in Figure 3b, even with the two-component fit the residuals indicate small systematic errors at early times, possibly related to nonideal focal-volume optics.(66) These deviations between experimental results and best fits were qualitatively the same for dyes in pure solvent, polymer solutions, and swollen networks, confirming the assumption (no aggregates were observed in pure solvent).

Figure 3.

Autocorrelation functions from FCS experiments and analysis. (a) Normalized ACFs for bodipy in octane solution and net47k at two different degrees of swelling. (b) Fitting of the ACFs and residuals, using one or two components. The one-component fit yields τ_D = 333 μs for the majority component, and the two-component fit yields 304 μs, with lower overall residuals.

Importantly, we did not observe any anomalies in the shape of the experimental G(t) in any of the polymer-containing samples, which indicates the absence of complications due to non-Gaussian (sub)diffusion and heterogeneities on the length scale of the focal size.(68) Effects of heterogeneities due to the cross-linking process or swelling, if important, would either arise on length scales much below 100 nm, and would then be detected in terms of a modified average τ_D, or would be reflected in the differences found on a larger scale. In fact, the accuracy of the measurements, reflected by error bars in the plots below, is mainly challenged by nonsystematic changes of the ACFs, which are quantified and averaged over by scanning the focus to different positions in the sample. The variations are, after all, not too large (on the order of 10−20%), and pronounced larger scale heterogeneities, as identified in terms of a spatially varying dye distribution in earlier confocal imaging studies of networks close to their phase separation temperature,(69) could not be found.

IV. Results and Discussion

Diffusion in Linear PDMS Solutions

Results for D_soln/D₀ for all three probes are plotted in Figure 4. Note that the NMR data for octane combines results from PDMS solutions as well as networks.(30) Within the limits posed by the relatively large scatter, no significant deviations between solution and network data are observable, suggesting that octane (R_h ≈ 0.2 nm) is a probe too small to be significantly influenced the network meshes. This is in agreement with recent NMR results of solvent diffusion in natural rubber with different cross-link densities.(70) Therefore, for octane diffusion we include all these data points in our ensuing analysis. Results of the fits to be discussed below are tabulated in Table 1.

Table 1. Results from Fits to D_soln/D₀ of the Three Probes in Linear PDMS Solution^a.

model		octane	bodipy	terrylene
free-volume,	Bd′	0.75 ± 0.1	0.96 ± 0.06	2.48 ± 0.2
eq 2	fp′b	→	0.25 ± 0.05	←
Phillies,	α	1.7 ± 0.1	2.9 ± 0.2	2.9 ± 0.3
eq 4	ν	1.85 ± 0.1	2.4 ± 0.1	1.1 ± 0.1
Petit,	a	3.3 ± 0.3	9.4 ± 1.3	10.3 ± 3.2
eq 5	ν′	1.2 ± 0.1	1.8 ± 0.1	0.87 ± 0.1

^aNote that all results are dimensionless.

^bObtained from a simultaneous fit of all three data sets using a common f_p′ and a probe-specific B′ .

The dashed lines are fits to the free-volume model, eq 2, where we have simultaneously fitted all three data sets, noting that the parameter f_p′ only depends on the polymer/solvent system and not on the probe. Table 1 lists results for the parameters. We see that B_d increases systematically but not linearly with probe dimensions. Notably, the value for bodipy is only slightly larger than for octane. Accepting the validity of the free-volume model, this may hint at additional effects due to the probe shape.

Better overall fits are provided by the Phillies and Petit models. Figure 4 only shows the Phillies fits, and we merely note that the fitting quality of the Petit model is only slightly inferior, with very similar curves and a tendency for somewhat lower fitted D_soln/D₀ at large Q. The fitting results (Table 1) for both models are not particularly instructive and do not allow any specific conclusions. In particular, the large and nonmonotonic variation of the scaling exponents suggests that the parameters of neither model should be interpreted in any depth. We emphasize again that, with this work, we do not wish to elaborate on the applicability of either model. For this purpose, a study of more diffusants of largely different size and shape would be required to better evaluate the parameter variations in Table 1.

In our view, the free-volume model is probably capturing the underlying physics of these semidilute to concentrated solutions best. Of course, the fitting quality is inferior for the simple free-volume model, yet we note that Vrentas and Duda have already pointed out that the simplified Fujita model for two-component systems only holds within the limit of a few assumptions that are not necessarily met.(3) Additional complexities arise when a third component (penetrant) is added, and penetrant shape effects cannot be excluded. We have not tried fits based on the complicated multiparameter theory of Vrentas and Duda,(4) but improved fitting quality can certainly be expected. In the following, we take advantage of the good fitting quality of the Phillies model and use the corresponding fits merely as empirical interpolations of our data to be able to compare data from solutions and swollen networks, which could not be measured at identical degrees of swelling.

Diffusion in Swollen PDMS Networks

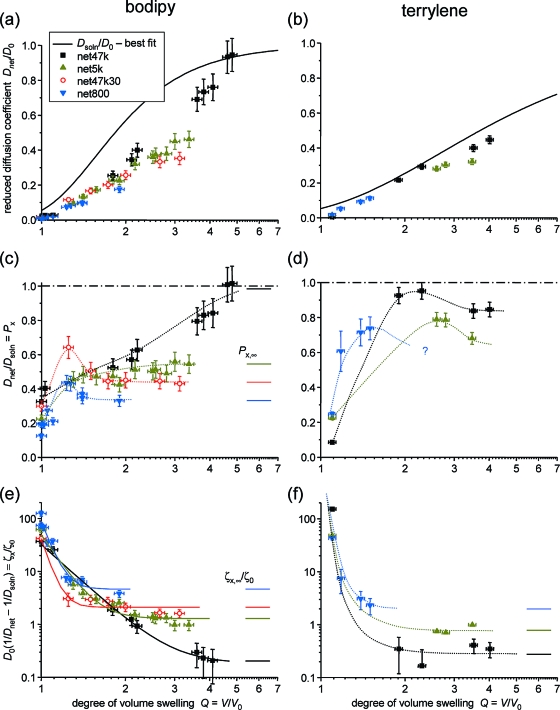
The main results of this work are collected in Figure 5. In (a) and (b), we plot D_net/D₀ for the two different dyes as a function of Q, and compare the data with the best-fit function to the diffusion data in linear PDMS solution. An important immediate conclusion is that now significant differences among the different networks are observed, indicating a decisive influence of cross-link density on the diffusion of the bigger dye molecules. Obviously, the constrained chain modes, now significantly influenced by the permanent links as opposed to fluctuating entanglements, pose additional restrictions to probe motion.

Figure 5.

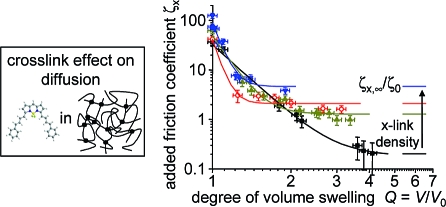
Results for diffusion of the two dye probes in the swollen PDMS networks as a function of Q. (a,b) Reduced diffusion coefficients. For comparison, the solid lines are again the best fits of the solution data to the Phillies model. (c,d) Translational probability P_x as evaluated from eq 3. The dotted lines are guides to the eye and, in (c), estimated plateau values are indicated as solid lines. (e,f)Effective relative friction coefficients due to cross-links, ζ_x/ζ₀, as evaluated from eq 6. The solid lines in (e) are fits to a power-law function, and the dotted lines in (f) are guides to the eye.

We now turn to analyzing the cross-link effect in terms of the multiplicative and additive approaches, represented by eqs 3 and 6. Combining linear-chain and network data according to eq 3 yields the sieving factor P_x plotted in (c) and (d). Rather nonmonotonic behavior is observed for both dyes. For the bodipy data, we observe plateau values P_x,∞ for the networks at equilibrium swelling, which can be estimated from the graph and will be discussed further below. For terrylene, the sparsity of data does not allow any further conclusions, yet we note that the values for the highly cross-linked net800 appear unusually high and anomalous.

Much cleaner trends are obtained if the additive approach represented by eq 6 is taken to calculate effective friction coefficients ζ_x/ζ₀. The data in (e) and (f) display monotonic behavior for all samples, and the approach of well-defined plateau values ζ_x,∞/ζ₀ toward Q_eq, defined by the maximum attainable mesh size. While the terrylene data is again too sparse to draw any further conclusions beyond the estimation of plateau values, we have attempted power-law fits to the bodipy data according to

which are shown as solid lines in (e). Such a power law could well be expected on the basis of scaling arguments for the increase of the mesh size ξ_x in the networks, heuristically including a plateau value taking into account the finite mesh size at swelling equilibrium. Despite the fair quality of the fits, the results for the exponent ν_x given in Table 2 are unrealistically high, so apparently, addition of a little solvent removes restrictions to probe diffusion very efficiently at the early stages of swelling.

Table 2. Results from the Power-Law Fits to ζ_x/ζ₀ of the Bodipy Dye in PDMS Networks.

network	ζx,0/ζ0	νx	ζx,∞/ζ0
net47k	32.8 ± 3.5	4.8 ± 0.3	0.19 ± 0.03
net5k	49 ± 12	7.7 ± 0.9	1.3 ± 0.1
net47k3	40 ± 11	16 ± 4	2.1 ± 0.3
net800	86 ± 14	14 ± 2	5 ± 1

Of course, the mesh size evolution at concentrations ranging from pure network via the concentrated to the semidilute regime can well be expected to follow different power laws in different regimes, as recently shown for the hydrodynamic mesh size ξ_h of linear polystyrene in good solvent, as studied by dynamic light scattering and related techniques.(71) Equation 8 must therefore be considered much too simplified. This is readily apparent from the fact that experimental values exhibit a second, slower decrease at higher Q. However, experimental and theoretical exponents for ξ_h versus concentration never exceed the value of 2, suggesting that the very high values of ν_x have a different origin.

We favor an interpretation in terms of heterogeneities, which is corroborated by the behavior of the bimodal net47k30 shown in Figure 5c,e. This network behaves differently in that it presents less obstacles to dye diffusion at comparably lower degrees of swelling. We remind that this network has a special structure, that is, it consists of highly cross-linked nanosized clusters of net800 in a matrix of 47k chains.(61) The solvent preferably swells the more weakly cross-linked matrix, thus, opening up tortuous pathways at rather low Q. In fact, the comparably lower effective friction coefficient ζ_x,0/ζ₀ for the dry network listed in Table 2 points into the same direction. Consequently, this network has the largest apparent scaling exponent. The other three networks are chemically homogeneous, yet our previous work,(30) as well as earlier scattering work performed on different types of networks,⁷²⁻⁷⁵ indicates the presence of swelling heterogeneities on the scale of tens of nm. Such percolating heterogeneities in the local degree of swelling can well be expected to enhance diffusion, in particular, when only small amounts of solvent are added.

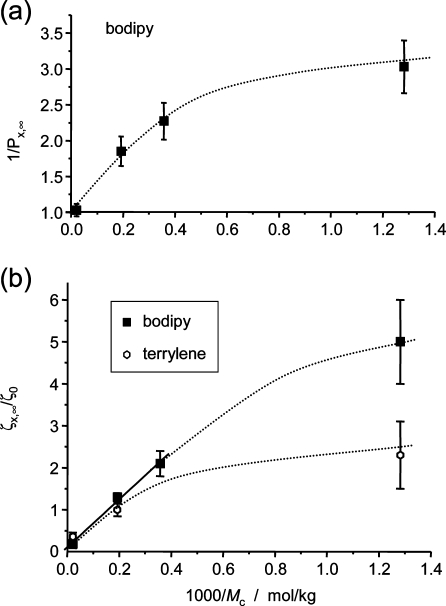
Finally, we plot the plateau results characterizing the cross-link effect at swelling equilibrium versus the cross-link density of the networks in Figure 6. Both the (less realistic) results on the (inverse) translational probability for bodipy in (a) as well as the results for the effective cross-link effect on the friction coefficient in (b) indicate a linear dependence on 1/M_c for the more lowly cross-linked networks. The latter results are in nice agreement with recent FCS observations on dye diffusion in water-swollen poly(vinyl alcohol) networks,(23) taken at much higher degrees of swelling in excess of 10 (corresponding to even lower 1/M_c).

Figure 6.

Results for the plateau behavior of the cross-link effect on probe diffusion at swelling equilibrium. (a) Inverse translational probability for bodipy derived from Figure 5c, and (b) effective friction contribution of cross-links for both dyes derived from Figure 5e,f. The solid line in (b) is a linear fit over the respective points.

For both dyes, the data for the most highly cross-linked network net800 indicate a transition to a weaker dependence, suggesting more effective diffusion than expected. Again, we hypothesize that this could be due to a more heterogeneous structure of such highly cross-linked network. This is again independently indicated by our first multiple-quantum NMR investigations of these samples,(61) which indicated a significantly broader distribution of local constraints (local apparent cross-link density) in net800. Another final point to note is that the dye with the larger R_h, terrylene, diffuses more slowly only in the least-cross-linked, most highly swollen network (of course as compared to its diffusion in the linear polymer, where it is overall less mobile). In the more highly cross-linked, less swollen networks it in fact diffuses faster (lower friction coefficient), which indicates an effect of diffusant shape. Note that for motion of the dyes along their longest axes (see Figure 1), the rod-like terrylene has a smaller cross sectional area than the disk-shaped bodipy.

V. Summary

We have shown that pulsed field-gradient NMR and in particular fluorescence correlation spectroscopy represent powerful tools for the investigation of probe diffusion in polymers solutions and networks. Combining diffusion data for different probes (octane, as well as bodipy and terrylene dyes) in octane-diluted PDMS, it is possible to evaluate the feasibility of different models describing diffusion in polymer systems.

For concentrated to semidilute solutions of long linear chains, the free-volume theory of Fujita provided the most meaningful parameters, while the phenomenologically best fits were provided by the hydrodynamic model of Phillies and the scaling model of Petit et al. The somewhat inferior fit of the simple free-volume expression is attributed to simplifications of this theory, as opposed to the more complete treatment of Vrentas and Duda.

For swollen networks, the situation is more complicated in that most theories do not account for cross-links explicitly. This contradicts our results taken in bulk networks with no or little solvent up to the equilibrium degrees of swelling (4.8 for our least-cross-linked network), which show that the small solvent molecule is not influenced by the cross-links, while the larger dye molecules feel additional restrictions. Rather than testing different theories, we chose a heuristic ansatz, comparing the interpolated linear-chain data with our network data and tested whether the cross-link effect is better described by a multiplicative “sieving factor” or an additive contribution to the effective friction coefficient. The latter approach proved to be more feasible in that monotonic behavior is observed over the whole range of concentrations.

The concentration dependence of the cross-link effect on diffusion is surprisingly strong, exceeding any realistic power law that may be expected on the basis of scaling theory. In combination with anomalies of a model-heterogeneous bimodal network, we suggest that the appearance of swelling heterogeneities can be made responsible for the strong dependence, leading to percolated tortuous pathways for probe diffusion already at moderate swelling. Finally, we observe a linear dependence of the cross-link effect on the effective friction coefficient when networks are compared at swelling equilibrium, with deviations for very high cross-link density, which are again interpreted as a possible consequence of more pronounced heterogeneities in their structure and characteristic differences between the two dyes that can be interpreted in terms of their shape.

Funding Statement

National Institutes of Health, United States