Abstract
Purcell (2002) proposed a bivariate biometric model for testing and quantifying the interaction between latent genetic influences and measured environments in the presence of gene-environment correlation. Purcell’s model extends the Cholesky model to include gene-environment interaction. We examine a number of closely-related alternative models that do not involve gene-environment interaction but which may fit the data as well Purcell’s model. Because failure to consider these alternatives could lead to spurious detection of gene-environment interaction, we propose alternative models for testing gene-environment interaction in the presence of gene-environment correlation, including one based on the correlated factors model. In addition, we note mathematical errors in the calculation of effect size via variance components in Purcell’s model. We propose a statistical method for deriving and interpreting variance decompositions that are true to the fitted model.
Keywords: Biometric model, Cholesky, identifiability, GxM, rGE, variance components, variance decomposition
1 Introduction
Gene-by-environment interaction (GxE) and gene-environment correlation (rGE) have long been of concern in the field of behavior genetics. Jinks and Fulker (1970), Eaves et al. (1977), and Plomin et al. (1977) describe the mechanisms by which rGE can arise, the effects of GxE and rGE in terms of bias and power in biometric modeling of data from twin and adoption designs, statistical approaches to testing GxE, and the role of measurement scale in the manifestation of GxE. In this foundational work, both genetic and environmental factors involved in GxE and rGE are unobserved.
Other work has considered designs in which both a measured aspect of the environment and the phenotype of interest are observed, but in which genetic factors are unobserved. Such designs provide an opportunity to test and model the interaction of latent genetic effects and measured environmental variables as a causal influence on the phenotype of interest. This is of great importance to the field of developmental psychopathology (Moffitt, 2005; Rutter, 2006) as current causal models do not adequately describe the gene-environment interactions that influence psychopathology (Lahey and Waldman, 2003). The motivation behind gene-by-measured environment (GxM) models is the possibility that some genes increase a person’s sensitivity to variation in environmental factors impacting the phenotype, or alternatively, that genetic variation impacting the phenotype is greater under certain environmental conditions than under others (Eaves et al., 2003).
Purcell (2002), in a seminal and already often-cited article, set out a modeling frame-work on which others have relied for testing and quantifying such GxM effects. In the first two of several models described by Purcell, the measured environment, or putative moderator1 (M) is both a regressor for the phenotype (P) and also interacts with additive genetic, and shared and nonshared environmental effects to explain phenotypic variance in the residual of P after regressing out the main effects of M. That is, these models test GxM in P residualized for M. These models have been widely applied (Jang et al., 2005; Kendler et al., 2004; Kremen et al., 2005; Rice et al., 2005).
As Purcell (2002, p.563) notes, his first two models are limited because they give a partial picture of the genetic and environmental variance in P. Purcell explains that these models could fail to detect GxM when it exists, and could under- or over-estimate heritability. This is because the genetic and environmental effects are being modeled on the residual from the regression of P on M. Therefore, any genetic or environmental effects that operate through—or are in common with—M are partialed out. Genetic effects on P that are common to M give rise to gene-measured environment correlation (rGM). The presence of rGM can therefore bias estimation of heritability and mask GxM.
These limitations motivated a new approach to modeling GxM while simultaneously allowing for rGM (Purcell 2002, p.563). Purcell’s new approach is based on a joint biometric model for the moderator and the phenotype which extends the classic Cholesky parameterization of the bi-variate biometric model to include interaction terms between the moderator and genetic and/or environmental effects. The model, described in § 2, yields a potentially powerful and widely-applicable approach to an important problem in behavior genetics, namely untangling the structure of gene-by-environment interplay. The range of possible fitted models has been described by Johnson (2007). Purcell’s new model has been used to test and quantify GxM in the possible presence of rGM in several recent papers (Burt et al., 2006; Johnson and Krueger, 2005a,b,c, 2006; Timberlake et al., 2006). These papers have examined the relation of phenotypes such as body mass index, physical health, and conduct disorder to moderators such as income, perceived life control, and age of menarche. It should be noted that, although Purcell’s model is important in its own right, it can also be seen as the simplest of a broad and flexible class of new approaches involving two or more observed variables in joint biometric structural models, a prominent example of which was recently proposed by Eaves et al. (2003).
Despite its potential power, Purcell’s new model requires care in its use for testing and quantifying GxM and rGM. Whereas this was clearly noted by Purcell (2002), the purpose of the present paper is to consider additional potential pitfalls of specification, identifiability, testing and interpretation of the parameters in this and related models for GxM that account for rGM. We consider equivalent and closely-related alternatives to Purcell’s model in § 3.1. These models are instances (sub-models) of a more general model containing multiplicative latent genetic and latent environmental effects. We describe some models that do not contain GxM but that may explain the data as well as Purcell’s GxM model. In § 3.2, we propose an alternative model for testing and quantifying GxM in the presence of rGM based on the correlated factors model (Loehlin, 1996), which we believe is simpler and avoids several pitfalls with the Cholesky model.
Purcell (2002) suggested computing separate genetic and environmental components of variance of P as functions of M while allowing for rGM. We show in § 4.1 that this idea is mathematically incorrect and we demonstrate via example in § 4.3 that it may yield incorrect conclusions about the true importance of GxM effects in certain contexts. The central problem lies in the difficulty of expressing the model for P in terms of uncorrelated effects and in quantifying the size of those effects in terms of components of variance. This derivation is more complicated in the presence of non-linear terms such as those required in models for GxM than in linear models such as the classical ACE biometric model. In § 4.2 we describe a method for deriving correct variance decompositions in the context of any structural model and apply this approach to obtain statistically meaningful decompositions in GxM with rGM models. We illustrate the ideas using two hypothetical examples in § 4.3.
2 Purcell’s GxM with rGM model
Purcell’s (2002) model for testing and quantifying GxM with rGM treats the measured putative moderating environmental variable and the response variable jointly in a bivariate model. This is an extension of the classical Cholesky parameterization of the bi-variate ACE model (Loehlin, 1996). In what follows, we restate the Purcell model in simplified form, leaving out the shared environmental component C for clarity of exposition. The key ideas advanced in the present paper do not depend on including or excluding C, but generalize to the full bivariate ACE model. We denote the “environmental” variable by M as a mnemonic both for measured environment and moderator in the GxM part of the model. The response variable is P, for phenotype. For example, M could be family income and P could be a measure of antisocial behavior.
The standard biometric model for M is given by
| (1) |
where AM and EM are each standard (mean 0, variance 1) normal latent random variables, uncorrelated with one another, μM is the mean of M, and, without loss of generality, aM ≥ 0 and eM ≥ 0. Here, AM and EM represent additive genetic and nonshared environmental influences on M, so that is the additive genetic variance component of the variance of M, is the nonshared environmental variance component of the variance of M, and the total variance of M is .
Purcell’s model for phenotype P which allows for rGM and GxM specifies
| (2) |
where AU and EU are again standard normal random variables independent of each other and of (AM, EM). Here, aC and αC represent additive genetic effects on P that are common with those on M (subscript C denoting common), eC and εC represent nonshared environmental effects on P that are common with those on M. Corresponding quantities aU, αU, eU and εU represent effects that are unique to P, i.e., unrelated to M. In (2), the Greek coefficients αC, εC, αU and εU capture the interaction of moderator M with the various genetic and environmental factors that act on P. In particular, the magnitude of αC (αU) captures the GxM interaction of M with common (unique) genetic factors AM (AU) in determining P. Models (1) and (2) together specify Purcell’s bivariate biometric GxM with rGM model (2002, pp. 563–566). Figure 1a contains a path diagram describing model (1) – (2), and Table I summarizes structural components and parameters figuring in the model.
Figure 1.
Path diagrams for several models which may or may not contain GxM. (a) Purcell’s (2002) model for testing and quantifying GxM in the presence of rGM. (b) Main effects model containing no AM-by-M or EM-by-M terms. (c) Alternative model containing main effects of M and M2 instead of AM-by-M terms. (d) Alternative model containing no multiplicative terms in M. (e) Correlated factors model for testing and quantifying GxM in the presence of rGM.
Note: All latent variables have mean 0 and variance 1. Dashed arrows pointing from a variable to a path indicate moderation of the indicated path by that variable.
Table I.
Components and parameters in structural GxM with rGM models.
| Model components | ||
|---|---|---|
| AM | additive genetic influences on M (standardized) | |
| EM | nonshared environmental effects on M (standardized) | |
| AU | additive genetic influences on P independent of AM (standardized) | |
| EU | nonshared environmental influences on P independent of EM (standardized) | |
| AP | additive genetic influences on P, possibly correlated with AM (standardized) | |
| EP | nonshared environmental influences on P, possibly correlated with EM (standardized) | |
| Model parameters (“main” effects) | ||
| aM | effect of AM on M | |
| eM | effect of EM on M | |
| effect of M on P | ||
| effect of M2 on P | ||
| aC | “main” effect of AM on P, i.e., additive genetic effects on P in common with M | |
| “main” effect of EM on P, i.e., nonshared environmental effects on P in common with M | ||
| aU | “main” effect of AU on P, i.e., additive genetic effects on P unique to P | |
| eU | “main” effect of EU on P, i.e., nonshared environmental effects on P that are unique to P | |
| aP | effect of AP on P | |
| eP | effect of EP on P | |
| Model parameters (interaction effects) | ||
| αC | interaction effect on P between M and AM, i.e., “common-genetic-by-environment” interaction | |
| interaction effect on P between M and EM | ||
| αU | interaction effect on P between M and AU, i.e., “unique-genetic-by-environment” interaction | |
| εU | interaction effect on P between M and EM | |
| αP | interaction effect on P between M and AP , i.e., “additive-genetic-by-environment” interaction | |
| εP | interaction effect on P between M and EP | |
| γJ | multiplicative effects on P of AM and EM, j = 1; 2; 3 | |
| δj | multiplicative effects on P of AM/EM with AU/EU, j = 1; 2; 3; 4 | |
| λj | multiplicative effects on P of AM/EM with AP /EP , j = 1; 2; 3; 4 | |
Notes: The terms “common” and “unique” refer to overlap (or lack thereof) in causal influences on M and P. The term “nonshared” refers to the fact that the effect is not shared across family members. The term “additive” refers to the fact that genetic effects are highly polygenic, allelic variation at each locus presumably making a small independent contribution to the overall variance.
Model (2) does not explicitly contain a “main effect” of M on P. Nonetheless, (2) does capture main effects of M on P indirectly through effects aC and eC on common genetic and environmental influences AM and EM. Additionally, the model contains as a sub-model a regression with direct effects of M on P. To see this, suppose that
| (3) |
Then, replacing aC, eC, αC, and εC with β1aM, β1eM, β2aM and β2eM respectively, (2) can be rewritten as
| (4) |
(Figure 1b). That is, in this sub-model the common factors AM and EM on P only operate through the manifest value M to influence P.
Before introducing model (1)–(2), Purcell (2002, pp. 555–560) presents model (4) with β2 = 0 for situations where one is interested in modeling the genetic and environmental contributions to P “controlling for” or “partialing out” M. A limitation of (4) is that genetic and environmental influences on P that are mediated through M are masked, potentially distorting the overall gene-environment picture. This issue directly motivated his GxM with rGM model given in (1) and (2).
Model (1)–(2) parameterizes the notions of rGM and GxM. The idea of rGM is that there are genetic influences on P that also impact the individual’s measured environment M. This is captured jointly by parameters (aC, αC) and can be examined by testing whether these quantities deviate significantly from zero. The notion of GxM is that genetic effects on P are moderated by environment M. This is captured jointly by parameters (αC, αU) and the presence of GxM can therefore be similarly tested in the context of model (2). The parameter αU is easier to interpret than αC: When αU ≠ 0, this indicates that the genes AU that influence P but do not influence M are more (or less) potent in the causation of P for larger values of M than they are for smaller values of M. This is one clear form of GxM. Interpretation of parameter αC is a bit more subtle: αC ≠ 0 indicates that the genes AM that influence both M and P are more (or less) potent in the causation of P for larger values of M. However, as will be seen in § 3.1, the interpretation of αC should be considered jointly with εC.
3 Specification and testing of GxM with rGM models
3.1 Sub-models and equivalent models
Here, we explore sub-models of, and alternative models equivalent to, Purcell’s model (1)–(2) that do not include GxM in the sense meant by Purcell. We also show that (1)–(2) is a restriction of a more general model containing multiplicative terms of genetic and environmental factors. The restrictions imposed yield GxM, but there are other restrictions that do not involve GxM that are equally parsimonious and scientifically plausible.2
3.1.1 Main effects model
We showed in § 2 that (4) is a sub-model of (2). A concern, therefore, is that a non-linear effect of M on P, parameterized by β2 in (4), could lead to an artifactual detection of common genetic (AM)-by-measured environment (M) interaction—i.e., αC ≠ 0—if the non-linear effect β2 is not specifically tested. Because (4) imposes constraints (3) on (2), this concern can be alleviated by testing (2) versus (4) via a likelihood ratio test (LRT). Rejection of the null hypothesis (4) in favor of the alternative (2) would provide support for the interaction of AM and M.
Simulated Example 1a
We simulated data on 1000 monozygotic (MZ) and 1000 dyzogotic (DZ) twins under models (1) and (4), setting μM = μP = 0.00, aM = eM = 1.00, β1 = 0.30, β2 = 0.20, , eU = 1.00, and αU = εU = 0.00. We fitted model (1)–(2) to these data and obtained estimates for GxM of α̂C = 0.18 and α̂U = 0.01. The LRT statistic for the GxM null hypothesis that αC = αU = 0.00 was χ2 = 29.9 which is highly significant on 2 degrees of freedom (df). Fitting instead model (4), we obtain β̂1 = 0.30, β̂2 = 0.20 and α̂U = 0.01. The LRT for model (2) versus (4) was χ2 = 0.11 on 2 df. If in (4) we test the GxM null hypothesis that αU = 0.00, we obtain χ2 = 0.20 on 1 df.
Simulated Example 1b
We simulated data as in Example 1a, but set β2 = 0.00 and αU = 0.20. Fitting model (1)–(2), we obtained GxM estimates of α̂C = 0.00 and α̂U = 0.21, with χ2 = 88.0 on 2 df for testing αC = αU = 0.00. Model (4) yielded β̂1 = 0.30, β̂2 = 0.00 and α̂U = 0.21. The LRT for model (2) versus (4) was χ2 = 0.07 on 2 df. Testing the GxM null hypothesis that αU = 0.00 in (4), we obtain χ2 = 87.9 on 1 df.
Simulated Example 1c
We then simulated data on 1000 monozygotic (MZ) and 1000 dyzogotic (DZ) twins under model (1)–(2), instead of under (4). We set μM = μP = 0.00, aM = eM = 1.00, aC = eC = 0.30, αC = 0.02, εC = 0.00, , eU = 1.00, and αU = εU = 0.00. Fitting model (1)–(2), we obtained GxM estimates of α̂C = 0.20 and α̂U = 0.02, with χ2 = 33.1 on 2 df for testing αC = αU = 0.00. Model (4) yielded β̂1 = 0.31, β̂2 = 0.09 and α̂U = 0.01. The LRT for model (2) versus (4) was χ2 = 13.0 on 2 df. Testing the GxM null hypothesis that αU = 0.00 in (4), we obtain χ2 = 0.27 on 1 df.
These three examples illustrate that (i) if model (4) is the true data generating mechanism for M and P, use of model (2) could lead to artifactual detection of GxM (Example 1a); (ii) it is possible to test (4) versus the more general (2) to provide support for true GxM over non-linear effects of M on P (Example 1c); and (iii) GxM can also be detected in model (4) by focusing on parameter αU (Example 1b).
In summary, model (2) distinguishes between moderation of A by M in the unique versus the common part of P. By contrast, in model (4), only GxM in the unique part of P is modeled, and any GxM in the common part is partialled out through β1 and β2. While use of (4) risks masking GxM, use of (2) risks mistaking non-linear effects of M for GxM. It therefore seems important to consider both complementary models when testing GxM.
3.1.2 Equivalent models without AM-by-M
A second concern with detecting AM-by-M interaction is that model (1)–(2) is equivalent to models containing no such effects. An equivalent model is an alternative model that is “indistinguishable from the original model in terms of goodness of fit to the data”; often these alternative models may offer substantively different interpretations of the data (MacCallum, Wegener et al., 1993). To see the equivalence, note that from (1) we can write AM = (M − μM − eMEM)/aM. Inserting this expression into (2) and re-arranging terms yields
i.e., (2) can be re-expressed as a model with a main and a quadratic effect of M and an nonshared environment (EM)-by-measured environment (M) interaction, with no AM-by-M interaction. That is, additive and multiplicative effects of M, AM and EM are not separately identifiable. Specifically, (2) can be rewritten as
| (5) |
(Figure 1c), where parameters in (5) replace parameters (μP, aC, αC, eC, εC) in (2). A one-to-one relationship between these two sets of parameters exists and is given in an online appendix.3 One key relation is that , so that when the true data generating mechanism is (5), and aM > 0 and , the analyst using (2) would incorrectly find that αC ≠ 0 and claim to have detected an AM-by-M interaction. This equivalence does not preclude testing for unique genetic (AU)-by-measured environment (M) interactions. Nonetheless, in the absence of a large AU-by-M term, it is impossible to unambiguously detect GxM because it cannot be distinguished from non-linear main effects of M and EM-by-M interaction.
Simulated Example 2
We again simulated data on 1000 MZ and 1000 DZ twins under models (1) and (5), setting μM = μP = 0.00, aM = eM = 1.00, , eU = 1.00, and αU = εU = 0.00. We fitted models (1) and (5) to these data and obtained the following estimates demonstrating that the fitted model is reflecting the true data generating mechanism. , âU = 0.98, âU = 0.01, êU = 1.00, and ε̂U = 0.00. Fitting model (1)–(2) to these data, we obtained estimates of α̂C = 0.21 and α̂U = 0.01, with a LRT statistic for the 2 df GxM null hypothesis that αC = αU = 0.00 of χ2 = 39.6. If we test the 1 df null hypothesis that αU = 0.00, we obtain a LRT statistic of χ2 = 0.36. Similarly, if instead we had fitted model (4) and tested αU = 0.00, we would have obtained χ2 = 2.52 on 1 df. This example illustrates how, (i) if model (5) is the true data generating mechanism, then fitting model (2) could lead to artifactual detection of GxM, and (ii) testing just αU = 0.00 in either model (2) or (4) yields a more robust test of GxM than tests including parameter αC.
3.1.3 Expanded structural model with GxM
We now examine a more general structural model for P as a function of additive and multiplicative effects of AM, EM, AU, EU. In this model, M is only indirectly represented by AM and EM, but the model contains (2) as a special case. For ease of exposition, we assume without loss of generality that μM = 0.00.
Beginning with (2) and replacing M with aMAM + eMEM, we obtain a model containing all multiplicative terms of AM, EM, AU, EU, except those composed only of a product of unique effects AU and EU. This more general model is given by
| (6) |
Here, the three γ parameters represent multiplicative or quadratic effects of common genes and common environment, and the four δ parameters represent multiplicative effects between common genes or environment and unique genes or environment. Model (2) is recovered through constraints on (6). Specifically, (2) holds if
| (7) |
in which case
Model (6) with constraints (7) conveys several important messages about (2). First, (2) is a special case of a model which contains non-linear effects of AM, EM, AU and EU. Second, the fit of (2) to the data can be tested by comparing it via LRT to (6) with only a 3-df test corresponding to the three constraints in (7). Third, the fact that model (2) imposes constraints (7) on (6) means that it is conceivable that in an analysis using (2), values of (αC, αU) significantly different than zero could arise spuriously as an artifact of effects of one or more of , AMAU, or EMEU, none of which are gene-by-environment interactions. This is because constraints (7) link effects of , AMAU, and EMEU with effects of AMEM, AUEM and AMEU.
This last point suggest directly testing (6) for GxM by testing whether
| (8) |
versus the alternative that one of them is different than zero. A significant result would suggest GxM. By contrast, if (8) holds, the resulting model is given by
| (9) |
(Figure 1d) which, because of (7) and (8), contains no GxM interactions in the sense of Purcell. Note that model (9) requires the same number of parameters as (2); in many settings, it may be equally parsimonious, easy to interpret and scientifically plausible as (2).4
Simulated Examples 3a and 3b
We simulated data on 1000 MZ and 1000 DZ twins under models (1) and (9). For Example 3a, we set μM = μP = 0.00, aM = eM = 1.00, aC = 0.30, , eC = 0.00, eU = 1.00, γ1 = 0.20, δ1 = 0.00, and γ2 = δ3 = 0.00. Fitting model (1)–(2) to these data, we obtained estimates for GxM of α̂C = 0.16 and α̂U = 0.01 with a LRT statistic for the 2 df GxM null hypothesis that αC = αU = 0.00 of χ2 = 26.9. For Example 3b, we simulated data as in Example 3a, but set γ1 = 0.00 and δ1 = 0.20. We obtained estimates of α̂C = 0.00 and α̂U = 0.21 with a likelihood ratio test statistic of χ2 = 85.4. These examples illustrate that, if the true data generating mechanism for P is model (9), this could lead to artifactual detection of GxM in model (2).
3.1.4 Summary: Identifiability and misspecification
The existence of models (4), (5) and (9) point out potential problems of identifiability and misspecification in using Purcell’s model (2) for testing GxM. Identifiability is a problem in many structural equations models, and is not specific to Purcell’s model. Our concern here is that these models are equally as or more parsimonious than (2), yet do not contain GxM in the sense of Purcell. For example, (9) and the non-unique parts of (4) and (5) are additive in the effects of genetic and environmental factors, even while allowing those effects to operate non-linearly. Such non-linear effects could easily arise if the scale on which genes contained in AM operate on P is different than the scale on which they operate on M. Those models do not contain gene-environment interaction terms, but may equally-well explain the observed associations between M and P.
3.2 Correlated factors model for GxM with rGM
Here, we question the Cholesky parameterization of the bivariate biometric model as a baseline for testing GxM, propose the correlated factors model as an alternative baseline model, and show how testing GxM is simpler in this model.
3.2.1 Cholesky parameterization
As noted above, model (1)–(2) extends the Cholesky parameterization of the classical bivariate AE model to allow for GxM interaction. As discussed by Loehlin (1996), the Cholesky is one of several equivalent bivariate biometric models, and, although the models are mathematically equivalent, the interpretation of the parameters is not. The Cholesky parameterization is most interpretable when there is a clear theoretical, causal, and/or temporal ordering of the variables M and P in the model (Johnson, 2007). In the absence of such ordering, it is incorrect to interpret AM as representing the shared genetic influences on M, as AM almost certainly contains genetic factors that are unique to M (Loehlin, 1996). For example, Johnson and Krueger (2005a) analyze data on income and body mass index (BMI) in a representative sample of adult twins. Their objective was to test whether “genetic variance associated with physical health decreases with increasing levels of income” (p.581). They provide a clear theoretical argument for treating income as the moderator M and measured body mass index (BMI) as the phenotype P of interest in their analysis. Nonetheless, income and BMI were measured concurrently in their sample and, as pointed out by Johnson (2007), the validity of their findings hinges on the validity of the ordering of these variables in the causal model. In situations without a clear causal ordering, Loehlin suggests using either a “common factor” or a “correlated factors” model. These models, which treat M and P on equal footing, might be simpler and more defensible base models for analyses of GxM. In the classical ACE model with no GxM moderation, the results of a Cholesky analysis can be transformed to yield an equivalent common factor analysis (Loehlin, 1996). This equivalence breaks down, however, when moderation by M is incorporated into the model.
3.2.2 Correlated factors model with GxM
Let AP and EP be the genetic and environmental influences on P. In a classical correlated factors (CF) model (Loehlin, 1996), AP is correlated with AM and EP is correlated with EM. This formulation suggests that an alternative to (2) be generated by extending the CF model to allow for GxM, viz,
| (10) |
Figure 1e presents a path diagram of this model. Here, AP and EP are standard normal random variables independent of each other, aP and αP represent additive genetic effects on P, eP and εP represent nonshared environmental effects on P, and ra and re represent the correlation in genetic and in environmental influences between M and P. When αP = εP = 0.00, (10) is the correlated factors parameterization of the bivariate biometric model. Additionally, (10) is a special case of model (2). To see this, suppose in (2) that
| (11) |
and define standard normal random variables
AP and EP are just Z-scores of the sums aCAM + aUAU and eCEM + eUEU. Replacing αC, αU, εC, εU with γaaC, γaaU, γeeC and γeeU, respectively, (2) becomes
from which (10) is recovered by setting .
We offer (10) as a more straightforward model in which to test and quantify GxM than (2) when M and P do not have a clear causal ordering. Model (10) allows for multiplicative effects with M with two fewer parameters than (2), and GxM can be tested in (10) with a single parameter αP , which could increase the power to detect GxM. Model (10) does not, however, permit differentiation of GxM effects into unique and common parts. Model (2) may be more appropriate where a causal ordering is justified, however, as when M and P are two longitudinal measurements. It is also possible to examine empirical support for (2) as an alternative to (10) via a likelihood ratio test, imposing constraints (11).
Simulated Example 4a
To investigate the performance of CF model (10), we simulated data on 1000 MZ and 1000 DZ twins under model (1)–(2), setting μM = μP = 0.00, aM = eM = 1.00, aC = 0.50, , eC = 0.10, , αC = 0.05, αU = 0.15, and εC = εU = 0.00. This specification comes close to satisfying constraints (11) so that model (10) holds approximately. Fitting model (1)–(2) to these data, we obtain estimates for GxM of α̂C = 0.05 and α̂U = 0.16 with a LRT statistic of χ2 = 59.4 for the 2 df GxM null hypothesis that αC = αU = 0.00. Alternatively, we might start out by testing the 2 df null hypothesis that (10) holds versus the more general (2); this yields χ2 = 4.50, so we do not reject the CF model in favor of the Cholesky model. In (10), we obtain a GxM estimate of α̂P = 0.16 with a 1 df LRT test statistic of χ2 = 56.5, which, given the lower df, is a stronger result for GxM than that obtained with model (2).
Simulated Example 4b
We again simulated data as in Example 4a, but set αC = −0.05 and αU = 0.15. This specification does not conform to CF model (10). Under model (1)–(2), we obtain α̂C = −0.05 and α̂U = 0.16 with LRT statistics of χ2 = 42.8 for αC = αU = 0.00 and χ2 = 41.8 for αU = 0.00. In (10), we obtain α̂P = 0.08 with a 1 df LRT test statistic of χ2 = 10.6, a substantially weaker result for detecting GxM than those obtained with model (2). Testing model (10) versus the more general (2), however, yields χ2 = 49.0, so, it is unlikely we would have proceeded to test GxM under model (10); rather ultimate GxM detection would be based on the test that αU = 0.00.
Simulated Example 4c
We again simulated data as in Example 4b, but set αC = −0.15 and αU = 0.05. As in that example, this specification does not conform to CF model (10), but here, αC (and not αU) is the larger source of GxM. Under model (1)–(2), we obtain α̂C = −0.16 and α̂U = 0.06 with a LRT statistic of χ2 = 24.7 for αC = αU = 0.00. In (10), we obtain α̂P = −0.11 with a 1 df LRT test statistic of χ2 = 22.5, an equally-strong result for detecting GxM than that obtained with (2). Testing (10) versus (2), yields χ2 = 77.1. Thus, whether one first tests (10) versus (2) and, having selected (2) proceeds to test GxM in (2), or rather tests GxM directly in (10), GxM would be correctly detected.
These three examples suggest that, when CF model (10) holds approximately, a test of (10) versus the Cholesky model (2) will lead us to choose (10). Under (10) the test for GxM is more powerful than that in (2). Alternatively, even when (10) does not hold, GxM sometimes can still be successfully tested in (10) or, when (10) is rejected in favor of (2), in the more exible model (2)
4 Variance decomposition in BG models
4.1 Misrepresentation of variance components in Purcell’s model
In order to quantify GxM in the context of (2), Purcell (2002, p. 564) and others (e.g., Johnson and Krueger, 2005a; Johnson, 2007) have described the total (unstandardized) variance in P due to genetic factors as given by
| (12) |
and, with parameter estimates for aC, αC, aU and αU, have plotted this quantity as a function of M.5 Expression (12) presumably arises from the assumption that AM and AU are independent standard normal variables in model (2). This expression is incorrect, however, because it presumes that for fixed M both AM and AU are freely varying quantities. Whereas this is true for AU, it is not for AM; when M is fixed the variance of AM is conditional on that fixed value of M. To formalize this point, note that M and AM are jointly bi-variate normal random variables with , var(AM) = 1 and . From standard bi-variate normal theory, given M,
which differ from the values E(AM) = 0 and var(AM) = 1 which hold marginally over M.
Additionally, statements such as “the variance of P due to additive genetic factors”, when attached to (12), carry an implicit presumption that genetic factors AM are independent of environmental factors EM. This is also incorrect; again due to conditioning on M, AM and EM are not independent as they are marginally over (i.e., averaging over) M. Rather, once M is fixed, EM is a deterministic function of AM. One can see this by writing EM = (M − μM − aMAM)/eM. Thus, conditional on M, AM no longer represents independent additive genetic effects on M, but rather the trade-off between genetic (AM) and environmental (EM) contributions to a given level of M.
For these reasons, (12) does not represent total additive genetic variance in phenotype P as a function of moderator M and, therefore, does not properly characterize the extent of GxM. Note, however, that, because AU and EU are independent of M, (aU + αUM)2 and (eU + εUM)2 do still represent the additive genetic and environmental contributions to the variance of P given M that are unique to P, and there is no loss of coherence in interpreting these quantities conditionally on M. In particular, (aU + αUM)2 does indeed capture the GxM that arises from genetic influences unique to P (i.e., with no influence on M).
A similar problem arises in obtaining rGM from (2). Purcell (2002, p. 564) quantifies rGM by
| (13) |
i.e., the signed square-root of the proportion of total genetic variance in P that is common to M. Johnson (2007, p. 428) correctly points out that rA in (13) is not so much rGM, which would be the correlation between M and the genetic effects on P, as it is the correlation between the genetic effects on P and the genetic effects on M. Nevertheless, whether one redefines rGM or renames rA, the interpretation assigned to it is incorrect. Again, the error is that one is attempting to condition on M while at the same time allowing AM to freely vary as if M were not fixed, which is not logical. Therefore, the expression (aC + αCM)2 appearing in (13) does not represent genetic variance in P that is common to M. Given M, not only is (aC + αCM)2 not the variance of (aC + αCM)AM, but it no longer represents purely genetic variance. Rather it is the variance in P due to the tradeoff between the genetic and environmental contributions to a given level of M.
4.2 A method for variance decomposition
If expressions (12) and (13) are not mathematically coherent, how then can one use the parameters of model (1)–(2) to quantify and summarize GxM and rGM? One straightforward answer to this question is to focus on the key structural parameters; specifically, (aC, αC) jointly capture rGM, while (αC, αU) capture GxM. However, there are strong and well-founded traditions in behavior genetics (BG) of interpreting models in terms of variance components and derivative quantities such as the proportion of common genetic variance between two traits. This approach has served BG research well because in traditional ACE and related models, the terms of interest are uncorrelated. Owing to the fact that model (2) contains multiplicative terms, however, it is not expressible in terms of uncorrelated effects on P due separately to factors AM, EM, AU and EU, even though these quantities are mutually independent.
Here, we propose an approach that does allow statistically meaningful variance decompositions to be obtained in structural models such as (2) for phenotype P. Our proposal involves re-expressing the model as a sum of uncorrelated additive terms. These terms represent average and partial effects of genetic and environmental factors AM, EM, AU and EU on P. Because the terms are uncorrelated, their variances are additive, and can therefore be used as measures of effect size of these factors. Unlike the ACE model, however, the decomposition of P into such terms is neither unique nor determined by the data.
4.2.1 The AE model revisited and expanded
Consider a general structural model for P as a function only of additive genetic effects A and independent environmental effects E.6 That is, P is a function of A and E, generally denoted P ≡ g(A, E), which may depend on A and E in a possibly non-linear way. The classical AE model is one such example, but is restricted to linear combinations of A and E.
When interest lies in isolating the effects of genes A on P, one might choose to write the model for P in one of two ways:
| (14) |
or, alternatively,
| (15) |
Note importantly that in both of these representations, the two additive components on the right-hand side are per force uncorrelated, the implication of which is that
i.e., the variances are additive. Therefore, representations (14) and (15) of the model for P yield valid decompositions of the variance of P.
The interpretation of decomposition (14) is as follows: The first term represents the average effect of A on P in the sense that it quantifies how the mean of P varies as a function of A ignoring (i.e., averaging over) E. It is what we would obtain if A were measured and we regressed P on A. The variance of this term is that part of the variance of P that is accounted for by the effect of A on P, i.e., that is explained by variability in A in the population, ignoring E.
The second term in (14) represents the partial or residual effect of E, removing or controlling for effects due to A in the sense that it quantifies how P varies with E for fixed values of A. The variance of this partial effect is that part of the variance in P that is accounted for by the partial effect given A of E on P, i.e., that is explained by variability in E holding A fixed.
Under an additive AE structural model for P, namely P = aA+eE, it can be shown that E(P|A) = {P − E(P|E)} = aA and E(P|E) = {P − E(P|A)} = eE, owing to the facts that A and E are (i) independent and (ii) figure additively into the model for P. Therefore, a2 = var(aA) represents both the average and the partial contribution of additive genetic effects to the variance of P, with a similar interpretation for e2.
Suppose now for sake of illustration that the structural model for P is given by
| (16) |
i.e., that independent factors A and E combine multiplicatively to yield the realized value of P. Using decomposition (14), we obtain
In this decomposition, the first term has var(aA) = a2 and the second has
| (17) |
The first variance component represents the part of the variance of P that is due to additive genes alone, ignoring variability in environmental factors, whereas the second one is that part due to variability in environment factors controlling for additive genetic effects. We make two remarks about this interpretation.
First, if P had been subjected to decomposition (15) rather than (14), different values and different interpretations would have obtained for the variance components due to A and E. This is analogous to what occurs with R2 and partial R2 in the multiple linear regression model. In that model, if two predictors X1 and X2 are correlated, then the total R2 can be expressed as the variance explained by X1, plus the variance explained by X2, controlling for X1. Reversing the order of the predictors yields a different interpretation.
Second, under decomposition (14), it is valid to view the variance of the partial effect of E controlling A both conditionally on—and marginally over—A. That is, given A, the conditional variance is
| (18) |
and this allows the analyst to interpret the relative contribution of E to P conditional on various levels of A. The unconditional (marginal) variance (17) of effects due to E controlling A is simply the average over A of (18). Expression (18) quantifies how the importance of the partial effect of E controlling A varies with levels of A.
4.2.2 Variance decomposition in Purcell’s model
As just shown in the simple AE model, the construction of partial effects and corresponding variance quantities provides a statistically coherent and defensible way to decompose the total variance in P and assign it to different factors contributing to P. We now apply this technique to the more complex GxM with rGM model (1)–(2). We propose two alternative variance decompositions, although there are others that one could construct. The first is based on the analytic aim of Purcell’s model, which is to evaluate interaction effects between genetic factors and a measured moderator M. The second ignores this aim, instead presenting variance due to all genetic influences followed by that due to partial effects of environment, controlling for and as a function of genetic effects. In the presentation below, the formulae for functions gj and hj and their corresponding variances are not critical for grasping the key ideas; in applications, such functions would simply be computed and, possibly, plotted using estimated parameters in model (1)–(2). Note that, because (10) is a special case of (2), the proposed decompositions apply equally well to the correlated factors model (10) as they do to (2).
For the first decomposition, we write
| (19) |
where we note that last two terms are valid because, given (AM, EM), partial effects due to AU and EU are uncorrelated with each other. These terms can be written as:
| (20) |
| (21) |
| (22) |
from which one can check that the sum is equal to P and that each gj is uncorrelated with the others.
The interpretation of these three terms is as follows: g1(AM, EM) is the (average) effect on P of genes and environment in common with M. Because M is a function of AM and EM, g1 also automatically includes effects of M as well. We combine the effects of AM and EM here into a single effect g1 because, as shown in § 3.1, effects of AM, EM and M are not separately identifiable. Regarding the other two terms, g2(AU;EM,AM) is the partial effect of unique genes, controlling for and as a function of common effects (AM, EM) and consequently M as well; finally, g3(EU;EM,AM) is the partial effect of unique environmental factors, controlling for and as a function of common effects (AM,EM) and M. Table II contains variance expressions for the the gj ’s, both conditionally on and marginally over M. These variances can be used as measures of effect size of (AM,EM), of AU and of EU.
Table II.
Conditional and marginal variance expressions for decomposition of GxM with rGM model according to common effects and unique effects (gj’s) and to genetic and environmental effects (hj’s).
| Effect | Conditional Variance | Marginal Variance | ||
|---|---|---|---|---|
| g1(AM,EM) | — | |||
| g2(AU;EM,AM) | (αU + αUM)2 | |||
| g3(EU;EM,AM) | (eU + εUM)2 | |||
| h1(AM,AU) | — | |||
| h2(EM,EU;AM,AU) | ||||
An alternative decomposition is given by
| (23) |
where
| (24) |
| (25) |
Conditional and marginal variance expressions are given in Table II. In (23), h1(AM,AU) is the average effect of all genetic factors on P, while h2(EM,EU|AM,AU) is the partial effect of all environmental factors on P, controlling for and as a function of genetic factors. Note that both AM and AU play a role in the conditional variance of h2. Note also that h1 could be further decomposed into an effect due to AM and an effect of AU controlling for and as a function of AM. Finally, decomposition (23) admits a complementary representation as average environmental effects plus residual effects due to genetics.
This latter variance decomposition provides a valid quantification of rGM as the correlation between the average genetic effect on M and the average genetic effect on P. I.e., rA = corr{E(M|AM,AU), E(P|AM,AU)}. As M and AU are independent, rA simplifies to rA = corr{E(M|AM), E(P|AM,AU)}, yielding
| (26) |
to replace (13). Note that (26) does not and should not depend on M because in order to compute it, we are required to average over M.
4.3 Hypothetical examples
We illustrate the variance decompositions in §§ 4.1–4.2 through two hypothetical examples.7 In the first, suppose that model (1)–(2) has been fitted to data and the following parameter estimates have been obtained: aM = eM = 1.00, aC = −0.40, , αC = 0.05, αU = 0.15, eC = 0.10, , and εC = εU = 0.00. This specification encodes a model wherein genes and environment contribute equally to M and approximately equally to P, the larger proportion of genetic contributions to P are unique to P (versus in common with M), and almost all of environmental contributions to P are unique to P.
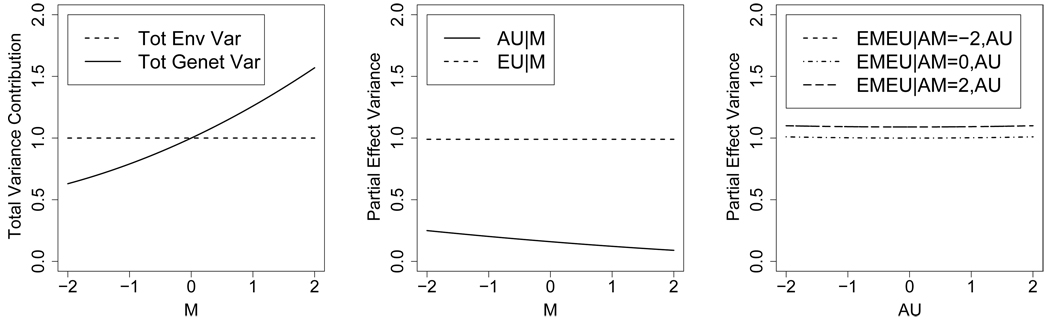
One might summarize such a fitted model via one of several variance decompositions. One decomposition for these hypothetical data is presented in the left panel of Figure 2. This decomposition has been used a number of times in the behavior genetics literature (e.g., Johnson and Krueger, 2005a; Johnson, 2007). It displays variance components due to genetic factors and nonshared environmental factors as functions of M, using (12) and an analogous formula for total variance due to nonshared environment. Using these formulae, at M = 0.00, each of genes and environment have an effect variance on P of 1.00, accounting for 50% each of the variance of P in this example. Effect variance of AM at M = 0.00 is 0.16 (8.0% of the total), while that of EM is 0.01 (0.5%). We would conclude from this hypothetical analysis that common genes and environmental factors account for a relatively small portion of the overall variance of P, while unique genes and environmental factors predominate. Furthermore, the expression of unique genes is strongly moderated by M (GxM), with lower M values suppressing the expression of those genes. It remains to be seen if these conclusions are justified, however, because, for the reasons given in § 4.1, the plot and these effect variances are mathematically incorrect.
Figure 2.
Variance decompositions for first hypothetical gene-environment interaction model for P moderated by M, presented in § 4.3. Left: Incorrect variance decomposition according to formula (12). Center: Correct variance decomposition for unique effects g2 and g3 controlling M. Right: Correct variance decomposition for environmental effects h2 controlling genetic effects.
Note: For center panel, effect variance due jointly to AM and EM combined is 0.18 and is not shown in the plot because it is not a function of M. For right panel, effect variance due to all genetic effects AM and AU is 1.03 and is not shown in the plot because it is not a function of AM or AU.
A mathematically correct summary of the fitted model for these hypothetical data is obtained via decomposition (19)–(22) with variance formulae in Table II. Under that decomposition, AM and EM together yield an average effect variance of 0.18 (i.e., var(g1) = 0.18, Table II, column 3), accounting for 8.6% of the variance of P. The remaining two variance components are due to uncorrelated partial effects of unique genes AU (g2) and unique environment EU (g3) controlling (AM,EM). These partial effects yield marginal variance components of 0.89 and 0.99 (Table II, column 3), accounting for 43% and 48% of the total variance respectively. These last two effect variances can also be presented as functions of M (Table II, column 2), and we have done so in the center panel of Figure 2. Note that similar conclusions are reached in this hypothetical model whether the mathematically correct (middle panel) or incorrect (left panel) effect variances are used. This is because, in this example, the environmental and genetic effects on P are almost fully accounted for by unique rather than by common factors.
An alternative model summary is given by decomposition (23)–(25). Under that decomposition, AM and AU together yield an average genetic effect variance of 1.03, accounting for 50% of the variance of P, leaving 50% to environmental partial effect variance. Here, genes influence the sensitivity of P to EM and EU, so the partial effect variances for environmental factors can also be presented as a function of genetic factors (AM,AU); see the right panel of Figure 2. The three curves are very similar because they depend only very weakly on AM, and moderation of environmental effects EM and EU by AU is also very weak, as evidenced by the nearly at variance curve. This decomposition can also be used to obtain valid quantification of rGM according to (26); this correlation is −0.39. The conclusions one would reach from this decomposition with regard to GxM are complementary to those based on the decomposition presented in the middle panel of Figure 2, and equally valid based on the data alone. Whether the decompositions presented in the second or third panels, or whether other decompositions are more pertinent will ultimately depend on the research question motivating the analysis.
Use of the mathematically correct effect variances is more important under other circumstances. For example, consider a second hypothetical fitted model in which common genetic effects on P are more important than unique genetic effects. All parameter values are the same as in the first example except that, , aU = 0.40, αC = 0.15, and αU = −0.05. The incorrect variance decomposition (12) is exactly the same as that for the first example and is presented in the left panel of Figure 3. Under the variance decomposition generated by (19)–(22), AM and EM together have an average effect variance on P of 0.92, accounting for 44% of the variance. The remaining two variance components due to uncorrelated partial effects of unique genes AU and unique environment EU controlling (AM,EM) are 0.17 and 0.99, accounting for 8.0% and 48% of the total variance respectively. Presented as a function of M, these last two components yield the center panel of Figure 3. This figure shows a very weak effect of unique genes and a GxM effect in the opposite direction of that in the left panel. The very different results presented in the left panel are due to the fact that, in this hypothetical model, genetic effects on P are largely in common with M and are therefore inseparable from effects of M and EM on P. The plot on the left incorrectly assumes that they are separable and yields potentially misleading results. In the third panel of Figure 3 using (23)–(25), a similar picture for partial environmental effect variance is obtained as that in the first example because the latent genetic and environmental effects for P are similar in the two models, even though the sharing of those effects with M differs. This decomposition yields rGM of 0.90 according to (26).
Figure 3.
Variance decompositions for second hypothetical gene-environment interaction model for P moderated by M, presented in § 4.3. Left: Incorrect variance decomposition according to formula (12). Center: Correct variance decomposition for unique effects g2 and g3 controlling M. Right: Correct variance decomposition for environmental effects h2 controlling genetic effects.
Note: For center panel, effect variance due jointly to AM and EM combined is 0.92 and is not shown in the plot because it is not a function of M. For right panel, effect variance due to all genetic effects AM and AU is 1.05 and is not shown in the plot because it is not a function of AM or AU.
Purcell’s variance decomposition (12) is never justified mathematically. The hypothetical examples in § 4.3 show, however, that when the genetic components AM common to M and P make relatively small contributions to P, and when GxM primarily arises between unique genetic components AU and M, Purcell’s decomposition yields conclusions that are comparable to those of decomposition (19)–(22). One difference is that (12) attempts incorrectly to capture the total variance as a function of M, while (19)–(22) describes only the unique variance components as functions of M and presents the common components as constants with respect to M. When the unique components dominate the common components, the two decompositions will yield very similar model interpretations. This was the case, for example, in the analysis presented by Johnson and Krueger (2005a) and in the primary analysis driving Johnson’s (2007) elegant paper based on Purcell’s model (Johnson, 2007, Figures 4 and 5).
By contrast, when GxM arises primarily between common genetic components AM and M, Purcell’s decomposition (12) could be quite misleading. This is illustrated by the difference between the left and center panels of Figure 3. This is a problem in a hypothetical model presented by Johnson (2007) based on Purcell’s decomposition. Figure 6 in Johnson (2007) yields inaccurate conclusions because it relies heavily on the incorrect expression (12) and on being able to separate multiplicative effects of M and EM from those of M and AM.
4.4 Choice of variance decomposition
In contrast to Purcell (2002), our proposal for obtaining statistically coherent variance decompositions in models such as (2) for phenotype P involves re-expressing the structural model as a sum of uncorrelated additive terms. In so doing, we have attempted to mimic a key feature of the ACE model, i.e., that it is specified as a sum of uncorrelated terms. Unlike the ACE model, however, the decomposition of P for a given fitted model is neither unique nor determined by the data. Many complementary decompositions exist and all are equally adequate representations of the data. Of these decompositions, which one should be used in a given analysis? There is no single answer to this question. An empirical option is to examine separately the total effects due to a variety of sources and to present the one with the largest variance first, as being the most important. Other sources of variance could then be presented as being due to partial effects.
A second option is to choose decompositions based on substantive theory in the context of the research question driving the analysis. This latter approach is similar to the analyst choosing the order of predictors in a multiple regression model to reflect the scientific questions of interest, and then reporting as effect measures successive partial R2 values for each regressor, controlling for all other regressors already entered in the model. The choice of decomposition depends on which factors should be controlled when examining each effect, and which factors are of theoretical interest as moderators of other effects. For example, decomposition (19)–(22) would be appropriate if unadjusted effects of moderator M and its components are of interest, and/or if M is of interest as an effect modifier of genetic and environmental factors. By contrast, decomposition (23)–(25) is relevant if total average genetic effects are of interest and/or if interest is on whether genetic factors moderate environmental effects.
5 Discussion
We revisited Purcell’s (2002) model for testing and quantifying GxM in the presence of rGM. We pointed out several problems with identifiability, specification, and testing in that model, showing how apparent GxM effects may arise spuriously due to alternative data generating mechanisms that are similar to but not the same as Purcell’s model. These misleading circumstances involve quadratic or multiplicative effects of solely genetic or solely environmental influences, but do not contain GxM. The issue of spurious moderator effects arising in the presence of untested quadratic effects has been discussed for structural equation models in general (MacCallum and Mar, 1995; Lubinski and Humphreys, 1990).
We have shown how to test some of these alternative models and also have proposed an alternative GxM model based on an extension of the CF model. The availability of main effects model (4) and CF model (10) and the ability to test them each versus Purcell’s Cholesky model (2) expands the tools available to model and test GxM. Using the main effects model instead of Purcell’s model will help prevent spurious detection of GxM due to non-linear effects of M on P and help focus attention on GxM parameter αU for moderation of unique genetic effects versus αC, which captures moderation of common genetic effects. The CF model provides for a more powerful test and more parsimonious quantification of GxM than does the Cholesky model and is not subject to the same problems of spurious GxM detection due to non-linear effects of M on P. We hope that the ability to fit quadratic effects models such as (9) and analogous varations of the CF model in the future will further expand the toolbox for flexible GxM testing and modeling.
We also have discussed the calculation of effect sizes via components of variance in Purcell’s and related structural models. We pointed out flaws in the current definitions and proposed alternative calculations based on the decomposition of the model into uncorrelated terms, yielding average and partial effects of latent factors AM, EM, AU, and EU. These decompositions provide additional and complementary tools for modeling GxM. As shown via example, the proposed decompositions are constructed to automatically avoid spurious GxM detection due to non-linear effects of common genetic or common environmental factors. Additionally, the proposed decomposition method provides more than one complementary set of effects which can be used alone or in combination depending on which factors are to be controlled, which are of interest, and/or which are putative moderators in a given analysis.
Acknowledgments
The authors thank Wendy Johnson and Robert F. Krueger for insightful comments on the first draft of this paper, which dramatically improved subsequent drafts.
Footnotes
The candidate moderator need not be an “environmental” variable in the narrow sense of the word. It could represent an environmental variable such as parenting practices or neighborhood crime, or it could also represent another phenotype being modeled as a precursor to the phenotype of interest.
Models for the simulated examples were fitted and tested in Mplus v.4.21 (Muthén and Muthén, 2006). Scripts and output files are available for download from the first author’s web site at http://health.bsd.uchicago.edu/rathouz/GxM/.
Currently-available structural equations modeling software such as Mplus (Muthén and Muthén, 2006) or Mx (Neale et al., 2003) does not permit estimation of models (6) or (9) owing to non-linearity of the A and E terms and difficulties of high-dimensional numerical integration. Development of specialized software to fit these models is an area for future development.
This formula is not explicitly stated but is unambiguously implied by Purcell’s formula for rGE given below in (13).
Recall that we omit shared environmental effects C only for simplicity of exposition; these models can be expanded to include C.
R (R Development Core Team, 2005) scripts and output files for obtaining the results in this section are available for download from the first author’s web site at http://health.bsd.uchicago.edu/rathouz/GxM/.
References
- Burt SA, Mcgue M, DeMarte JA, Krueger RF, Iacono WG. Timing of menarche and the origins of conduct disorder. Arch. Gen. Psychiatry. 2006;63:890–896. doi: 10.1001/archpsyc.63.8.890. [DOI] [PMC free article] [PubMed] [Google Scholar]
- Eaves LJ, Last K, Martin NH, Jinks JL. A progressive approach to non-additivity and genotype-environmental covariance in the analysis of human differences. Br. J. Math. Statist. Psychol. 1977;30:1–42. [Google Scholar]
- Eaves L, Silberg J, Erkanli A. Resolving multiple epigenetic pathways to adolescent depression. J. Child Psychol. and Psychiatry. 2003;44:1006–1014. doi: 10.1111/1469-7610.00185. [DOI] [PubMed] [Google Scholar]
- Jang K, Dick D, Wolf H, Livesley W, Paris J. Psychosocial adversity and emotional instability: An application of gene-environment interaction models. Eur. J. Personality. 2005;19:259–272. [Google Scholar]
- Jinks JL, Fulker DW. Comparison of the biometrical genetical, mava, and classical approaches to the analysis of human behavior. Psychol. Bull. 1970;73:311–349. doi: 10.1037/h0029135. [DOI] [PubMed] [Google Scholar]
- Johnson W. Genetic and environmental inuences on behavior: Capturing all the interplay. Psychol. Rev. 2007;114:423–440. doi: 10.1037/0033-295X.114.2.423. [DOI] [PubMed] [Google Scholar]
- Johnson W, Krueger RF. Genetic effects on physical health: Lower at higher income levels. Beh. Genet. 2005a;35:579–590. doi: 10.1007/s10519-005-3598-0. [DOI] [PubMed] [Google Scholar]
- Johnson W, Krueger RF. Higher perceived life control decreases genetic variance in physical health: Evidence from a national twin study. J. Personal. Soc. Psychol. 2005b;88:165–173. doi: 10.1037/0022-3514.88.1.165. [DOI] [PubMed] [Google Scholar]
- Johnson W, Krueger R. Predictors of physical health: Toward an integrated model of genetic and environmental antecedents. J. Gerontol. 2005c;Series B 60:42–52. doi: 10.1093/geronb/60.special_issue_1.42. [DOI] [PubMed] [Google Scholar]
- Johnson W, Krueger R. How money buys happiness: Genetic and environ-mental processes linking finances and life satisfaction. J. Personal. and Soc. Psychol. 2006;90:680–691. doi: 10.1037/0022-3514.90.4.680. [DOI] [PubMed] [Google Scholar]
- Kendler K, Aggen S, Prescott C, Jacobson K, Neale M. Level of family dysfunction and genetic influences on smoking in women. Psychol. Med. 2004;34:1263–1269. doi: 10.1017/s0033291704002417. [DOI] [PubMed] [Google Scholar]
- Kremen W, Jacobson K, Xian H, Eisen S, Waterman B, Toomey R, Neale M, Tsuang M, Lyons M. Heritability of word recognition in middle-aged men varies as a function of parental education. Beh. Genet. 2005;4:417–433. doi: 10.1007/s10519-004-3876-2. [DOI] [PubMed] [Google Scholar]
- Lahey BB, Waldman ID. A developmental propensity model of the origins of conduct problems during childhood and adolescence. In: Lahey BB, Moffitt TE, Caspi A, editors. Causes of conduct disorder and juvenile delinquency. New York: Guilford Press; 2003. pp. 76–117. [Google Scholar]
- Loehlin JC. The Cholesky approach: A cautionary note. Beh. Genet. 1996;26:65–69. [Google Scholar]
- Lubinski D, Humphreys LG. Assessing spurious “moderator effects”: Illustrated substantively with the hypothesized (“synergistic”) relation between spatial and mathematical ability. Psychol. Bull. 1990;107:385–393. doi: 10.1037/0033-2909.107.3.385. [DOI] [PubMed] [Google Scholar]
- MacCallum RC, Mar CM. Distinguishing between moderator and quadratic effects in multiple regression. Psychol. Bull. 1995;118:405–421. [Google Scholar]
- MacCallum RC, Wegener DT, Uchino BN, Fabrigar LR. The problem of equivalent models in applications of covariance structure analysis. Psychol. Bull. 1993;114:185–199. doi: 10.1037/0033-2909.114.1.185. [DOI] [PubMed] [Google Scholar]
- Moffitt TE. The New Look of Behavioral Genetics in Developmental Psychopathology: Gene-Environment Interplay in Antisocial Behaviors. Psychol. Bull. 2005;131:533–554. doi: 10.1037/0033-2909.131.4.533. [DOI] [PubMed] [Google Scholar]
- Muthén LK, Muthén BO. Mplus User's Guide. 4th Ed. Los Angeles, CA: Muthén & Muthén; 2006. [Google Scholar]
- Neale MC, Boker SM, Xie G, Maes HH. Mx: Statistical Modeling. 6th Ed. VCU Box 900126, Richmond, VA 23298: Department of Psychiatry; 2003. [Google Scholar]
- Plomin R, DeFries JC, Loehlin JC. Genotype-environment interaction and correlation in the analysis of human behavior. Psychol. Bull. 1977;84:309–322. [PubMed] [Google Scholar]
- Purcell S. Variance component models for gene-environment interaction in twin analysis. Twin Res. 2002;5:554–571. doi: 10.1375/136905202762342026. [DOI] [PubMed] [Google Scholar]
- Rice F, Gordon H, Shelton K, Thapar A. Family conflict interacts with genetic liability in predicting childhood and adolescent depression. J. Am. Acad. Child and Adolesc. Psychiat. 2006;45:841–848. doi: 10.1097/01.chi.0000219834.08602.44. [DOI] [PubMed] [Google Scholar]
- R Development Core Team. R: A language and environment for statistical computing. Vienna, Austria: R Foundation for Statistical Computing; 2005. ISBN 3-900051-07-0, URL http://www.R-project.org. [Google Scholar]
- Rutter M. Genes and behavior: Nature-nurture interplay explained. Blackwell: Malden, MA; 2006. [Google Scholar]
- Timberlake D, Rhee S, Haberstick B, Hopfer C, Ehringer M, Lessem M, Smolen A, Hewitt J. The moderating effects of religiosity on the genetic and environmental determinants of smoking initiations. Nicotine and Tobacco Res. 2006;8:123–133. doi: 10.1080/14622200500432054. [DOI] [PubMed] [Google Scholar]