Functional Energetic Landscape in the Allosteric Regulation of Muscle Pyruvate Kinase III: Mechanism

Abstract

Mammalian pyruvate kinase exists in four isoforms with characteristics tuned to specific metabolic requirements of different tissues. All of the isoforms, except the muscle isoform, exhibit typical allosteric behavior. The case of the muscle isoform is a conundrum. It is inhibited by an allosteric inhibitor, Phe, yet it has traditionally not been considered as an allosteric enzyme. In this series of study, an energetic landscape of rabbit muscle pyruvate kinase (RMPK) was established. The phenomenon of inhibition by Phe is shown to be physiological. Furthermore, the thermodynamics for the temperature fluctuation and concomitant pH change as a consequence of muscle activity were elucidated. We have shown that: 1. The differential number of protons released or absorbed with regards to the various linked reactions adds another level of control to shift the binding constants and equilibrium of active⇆inactive state changes; the latter controls quantitatively the activity of RMPK. 2. ADP plays a major role in the allosteric mechanism in RMPK under physiological temperatures. Depending on the temperature, ADP can assume duel and opposite roles of being an inhibitor by binding preferentially to the inactive form and a substrate. 3. Simulation of the RMPK behavior under physiological conditions shows that the net results of the twenty one thermodynamic parameters involved in the regulation are well tuned to allow maximal response of the enzyme to even minute changes of temperature and ligand concentrations.

Pyruvate kinase, an important glycolytic enzyme, catalyzes a transfer of a phosphate group from phosphoenolpyruvate (PEP) to ADP. This process yields a molecule of pyruvate and ATP. The enzyme has been extensively reviewed by Kayne (1). Mammalian PK exists in four isoforms with characteristics tuned to specific metabolic requirements of different tissues (2, 3). All of the isoforms, except the muscle isoform, exhibit typical allosteric behavior. The case of the muscle isoform is a conundrum. It is inhibited by an allosteric inhibitor, Phe, yet it has traditionally not been considered as an allosteric enzyme because the concentration required to elicit demonstrable inhibitory effect is too high to be considered physiological. In this series of study the goal is to establish an energetic landscape of rabbit muscle pyruvate kinase (RMPK) in order to resolve this issue of whether the phenomenon of inhibition by Phe is physiological. Furthermore, there is a long standing interest in the temperature fluctuation and concomitant pH change as a consequence of muscle activity (4–6). RMPK is being employed as a model system to address the consequences of temperature and pH changes in muscle enzymes.

In the previous two papers we have investigated the tetrameric RMPK (7, 8). Simultaneous analysis of isothermal titration calorimetry (ITC) data and fluorescence data acquired at different temperatures allowed for thorough thermodynamic characterization of the allosteric regulation of the enzyme within the frame of the two-state concerted model (9). According to this model the RMPK population equilibrates between two states with highly different enzymatic activities. Then the allosteric regulation is achieved by transitions of the RMPK tetramer between the active R and the inactive T state. These concerted conformational transitions of the RMPK subunits can be shifted to favor one state or another by temperature and ligand binding. Besides the thermodynamic characterization of the R↔T equilibrium we also quantified the binding of both RMPK substrates, PEP and ADP, as well as binding of the allosteric inhibitor, Phe.

It was shown that it requires 21 thermodynamic parameters to adequately describe the model for RMPK regulation. These include binding enthalpies and entropies, linked proton reactions, changes of the isothermal heat capacity, ligand interaction parameters, etc. (8). Due to a large amount of information, it is difficult to envision behavior of RMPK which is the resultant of the fine interplay among these parameters. In this paper we present a graphical summary of the previously obtained results with emphasis on the RMPK allosteric regulation. Simulation of the RMPK behavior under physiological conditions shows that all parameters involved in the regulation are well tuned to allow maximal response of the enzyme to even minute changes of temperature and ligand concentrations.

RESULTS AND DISCUSSION

The foundation of the regulatory mechanism of RMPK is the rapid equilibrium between the two structural states, namely, the active R-state and inactive T-state. One of the roles of the intricate network of linked reactions is to shift that equilibrium with the exception of a coupling between Phe and ADP bindings. The ability of effectors to regulate the activity is related to their ability to influence the R↔T equilibrium. The ability of a ligand to shift the R↔T equilibrium is dependent on the existence of a differential affinity of the ligand for the two states – the larger the difference, the greater the ability to shift the distribution of states. The direction of the shift is dependent on the state to which the ligand binds stronger.

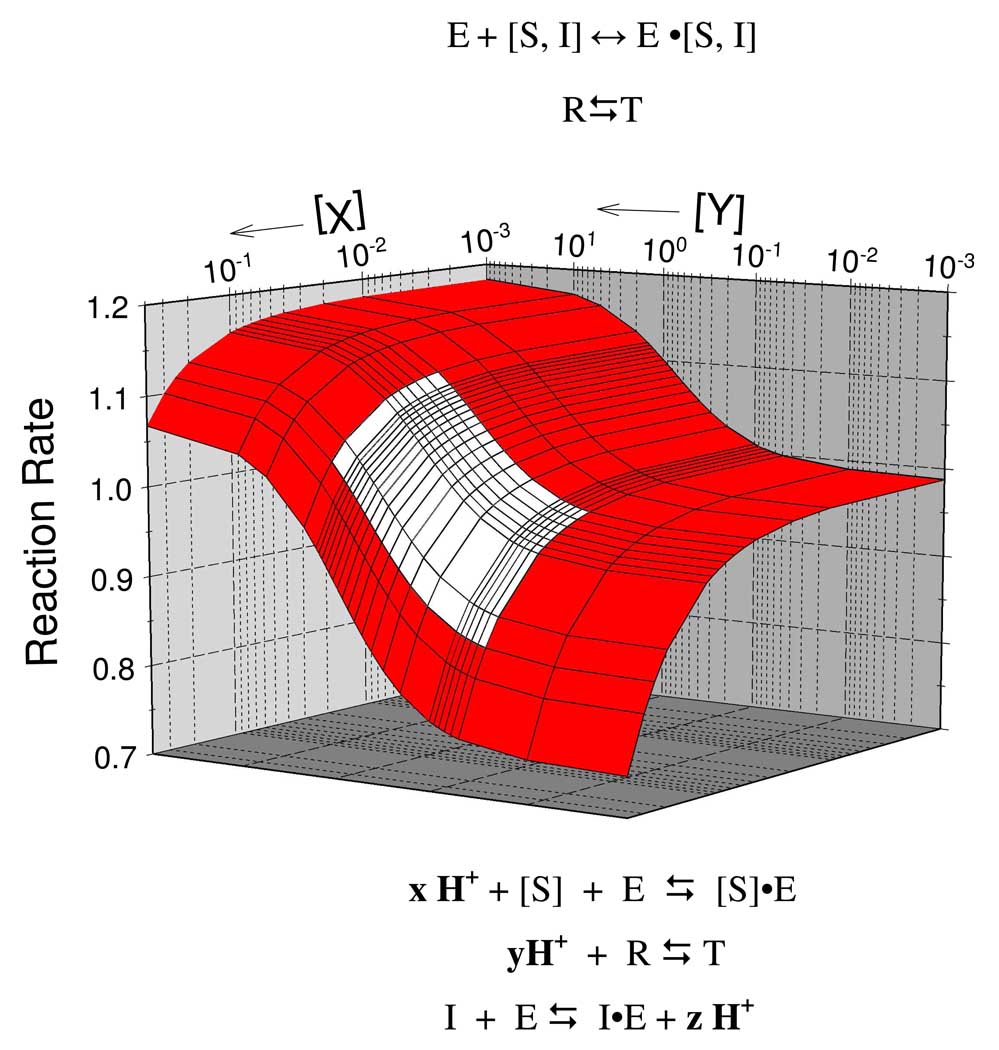
Fig. 1 presents a functional energetic landscape of the allosteric regulatory mechanism of RMPK. The landscape is defined by the relationship between two ligands, X and Y, as a function of temperature. The various reactions listed above the landscape represent the reactions that define the function of RMPK, namely, all the reactions of the enzyme with metabolites pertaining to the function of RMPK. The various reactions listed below the landscape indicate the linkage of proton release or absorption to these reactions. Let’s review the evidence in support of the mechanism shown in Fig. 1.

Fig. 1.

Functional energetic landscape of the allosteric regulation of RMPK.

R↔T equilibrium

A better insight to the apparently complex allosteric regulatory mechanism of the RMPK can be gleaned from a graphical representation of results obtained in the two previous papers by calorimetry and fluorescence techniques (7, 8). Based on the globally fitted thermodynamic parameters (8) the temperature dependence of equilibrium constants underlying the RMPK regulation was calculated. Figure 2A shows the temperature dependence of the R⇆T equilibrium constant, L₀ = [T₀]/[R₀] i.e. ratio of the concentration of inactive T₀ and active R₀ state of the unliganded RMPK. L₀ and its relation with the thermodynamic parameter can be expressed by

$$L_0=\text{exp}[-(1/RT)(\mathrm{\Delta }{H}_{R\leftrightarrow T}-T\cdot \mathrm{\Delta }{S}_{R\leftrightarrow T})]$$ (1)

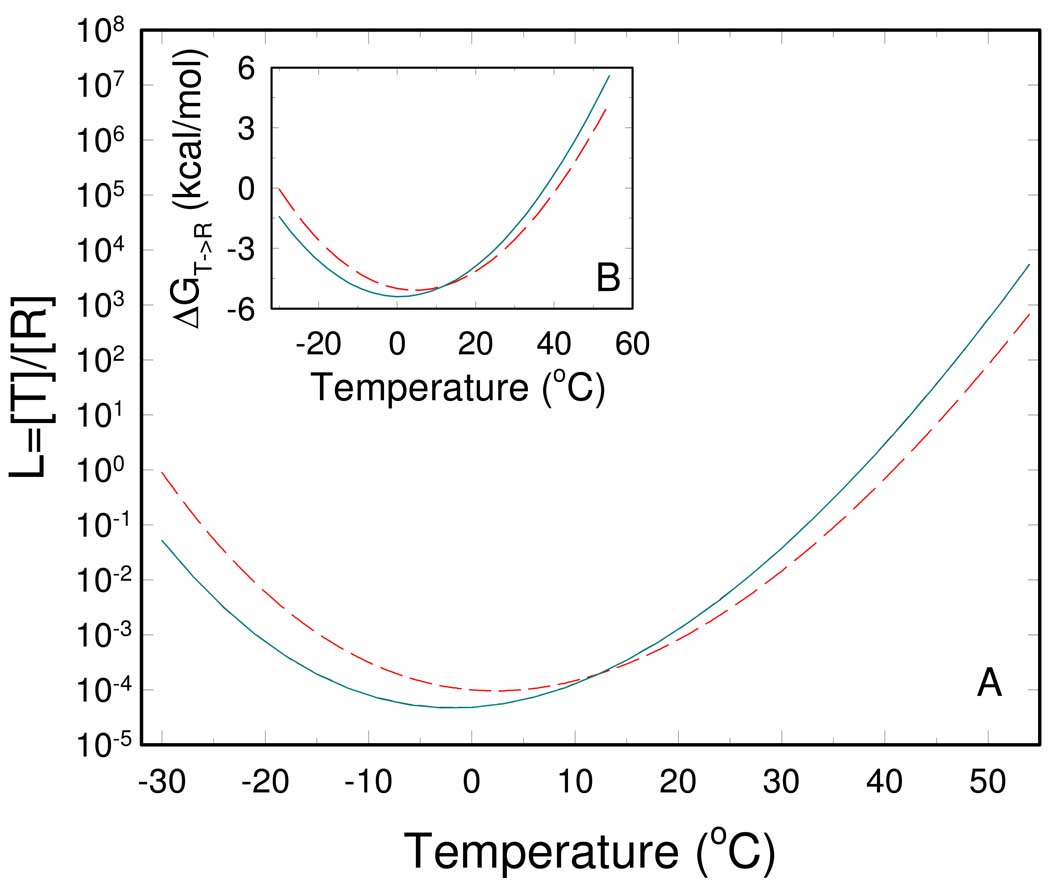
where ΔH_R↔T = ΔH_0,R↔T + ΔC_p,R↔T · (T−T₀) and ΔS_R↔T ΔS_{0, R↔T} + ΔC_{p, R↔T} · ln(T/T₀) ; R and T are the universal gas constant and the absolute temperature, respectively. Fig. 2A shows a bell-shaped relation between temperature and L₀, exhibiting a minimum near 0 °C. The observed minimum stems from a positive isobaric heat capacity change of ΔC_{p, R↔T} = 2.2 kcal/mol. The consequence of the bell-shaped relation is to ensure that L₀ is more sensitive to fluctuations of temperature at physiologically relevant temperatures. In turn the activity of RMPK is most responsive to temperature since the enzyme activity is directly related to the distribution of the active R- and inactive T-states.

Fig. 2.

Temperature dependence of the R ⇆ T equilibrium of RMPK. (A) - The equilibrium constant between the unliganded R and T state in the absence of ligands (cyan solid line) and the apparent one in the presence of 10 mM ADP (red dashed line). (B) –The free energy of the T → R transition in the absence of ligands (cyan solid line) and in the presence of 10 mM ADP (red dashed line).

Under temperatures where L₀ assumes the minimum value it means that there is a negligible amount of RMPK in the inactive T-state i.e. essentially all of RMPK is in the R-state at low temperature. As temperature increases, the value of L₀ increases indicating that the distribution between the R and the T-state becomes more towards the T-state. The favorable shift towards the R-state at low temperature is the basis for the observation that RMPK exhibits a hyperbolic kinetic behavior in the absence of inhibitor at temperatures below room temperature (10).

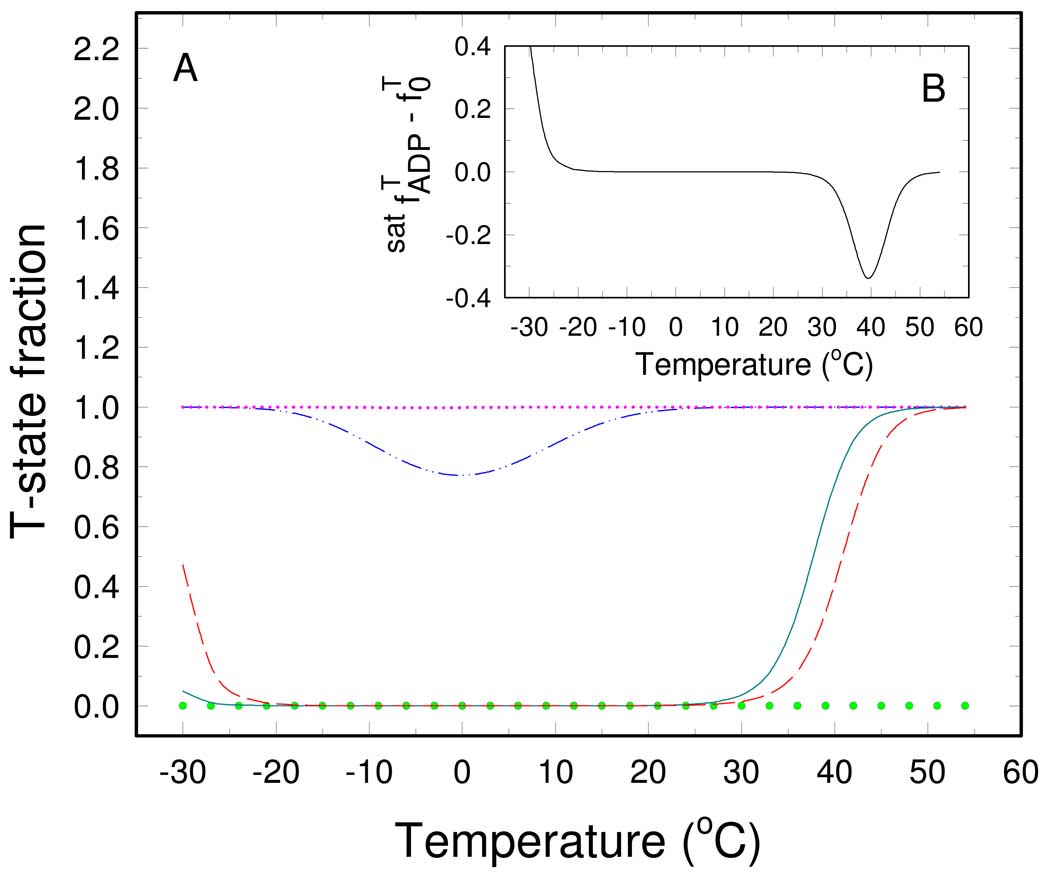
In order to better understand the influence of temperature on the RMPK regulation it is practical to visualize temperature induced changes of the fraction of inactive state f^T in the absence and in the presents of ligands. The fractions, as shown in Figure 3A, were calculated from the corresponding equilibrium constants between the R and T-states as

$$f^T=L/(1+L)$$ (2)

where L is equal to L₀ or L_0,lig for the unliganded or RMPK saturated by the ligand lig (7), respectively. The value of f^T for unliganded RMPK is bell-shaped with a negligible fraction of the inactive state between −25°C and 25 °C. The shape of the curve is governed by the temperature dependence of L₀ , as shown in Figure 2. Above 30 °C the value of f^T starts to sharply increase and the R→T transition is almost completed at 40 °C.

Fig. 3.

Temperature dependence of the T-state fraction of RMPK. (A) – The T-state fraction for unliganded RMPK - (cyan solid line), for RMPK saturated by 10 mM ADP (red dashed line), 12 mM Phe (pink dotted line), 2 mM PEP (green small circles), and for RMPK in the presence of both 12 mM Phe and 10 mM ADP (blue dash-dot-dot line). (B) - Difference between the T- state fraction of RMPK in the presence of 10 mM ADP and the T-state fraction of the unliganded RMPK.

PEP binding

Values for $K_{\mathit{\text{lig}}}^R\text{or}{K}_{\mathit{\text{lig}}}^T$ , the microscopic binding constant of ligand, lig, to the R- or T-state, respectively, can be calculated according to the equation

$$\text{ln}(K_{\mathit{\text{lig}}}^{\mathit{\text{state}}})=1/R\cdot (\mathrm{\Delta }{H}_{\mathit{\text{lig}}}^{\mathit{\text{state}}}/T-\mathrm{\Delta }{S}_{\mathit{\text{lig}}}^{\mathit{\text{state}}})$$ (3)

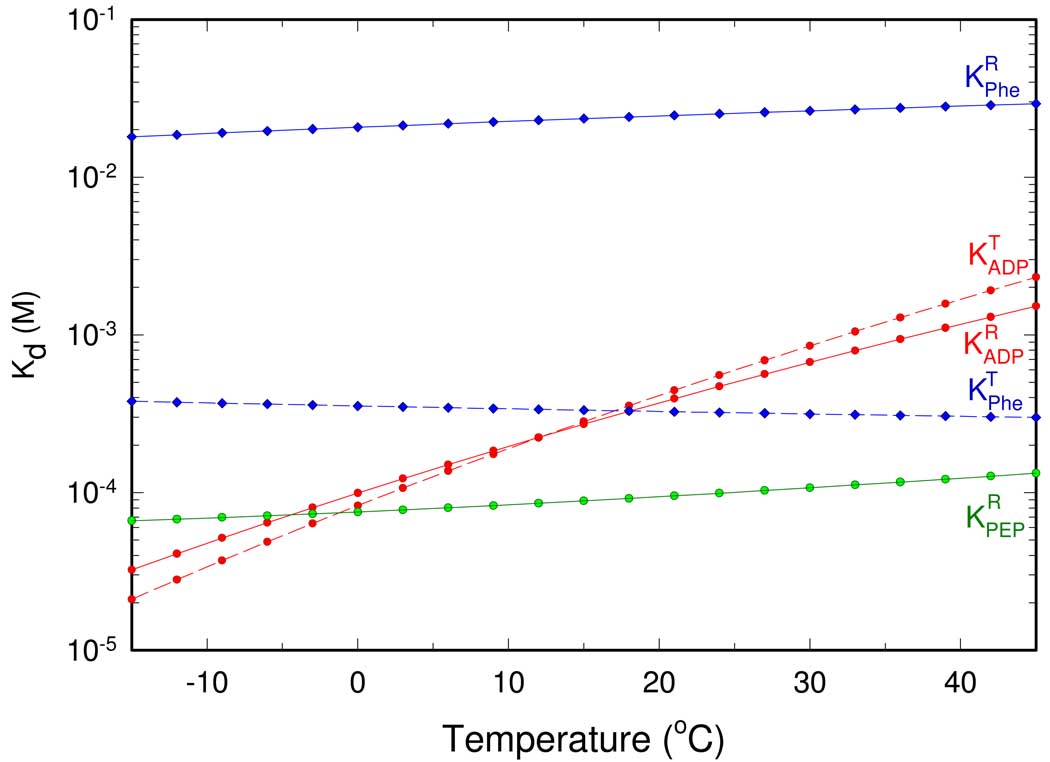
where binding enthalpies $\mathrm{\Delta }{H}_{\mathit{\text{lig}}}^{\mathit{\text{state}}}$ and entropies $\mathrm{\Delta }{S}_{\mathit{\text{lig}}}^{\mathit{\text{state}}}$ are results of the global fitting presented in the previous paper (8). Fig. 4 shows the K_d values of RMPK for PEP as a function of temperature. Binding of PEP to the R-state shows only slight temperature dependence due to a $\mathrm{\Delta }{H}_{\mathit{\text{PEP}}}^R=-2.1\text{kcal}/\text{mol}$. Negative enthalpy terms indicate weaker binding of the ligand at elevated temperatures. The binding of PEP to the T-state is significantly weaker, so much so that no accurate value can be derived from this series of study, although results based on steady-state kinetics imply at least a greater than ten fold weaker affinity (10).

Fig. 4.

Temperature dependence of dissociation constants for PEP (green line), ADP (red lines), and Phe (blue lines). The solid and dashed line represents binding to the R and T-state of RMPK, respectively.

Differential binding affinities of a ligand towards the R- and T-state, $K_{\mathit{\text{lig}}}^R$ and $K_{\mathit{\text{lig}}}^T$ , respectively, result in a shift of the R↔T equilibrium as a consequence of the relationship

$$L_{0,\mathit{\text{lig}}}=L_0{\left(K_{\mathit{\text{lig}}}^R/K_{\mathit{\text{lig}}}^T\right)}^4$$ (4)

where L_0,lig is L₀ in the presence of saturating amount of ligand, lig (4, 5). Furthermore, a differential temperature dependence of these affinities causes the shift to be temperature dependent as well. Since $K_{\mathit{\text{PEP}}}^R<K_{\mathit{\text{PEP}}}^T$ in all temperatures, binding of PEP will always shift RMPK towards the active R-state, a prediction substantiated by the results of steady-state kinetics (10).

We also investigated a temperature dependence of the T-state fraction of RMPK in the presence of a saturating amount of PEP. The calculated temperature dependence is depicted in Figure 3A by the opened circles $(f_{\mathit{\text{PEP}}}^T)$. It is seen that at all investigated temperatures the presence of saturating amount of PEP keeps the entire RMPK population in the active R-state.

Phe binding

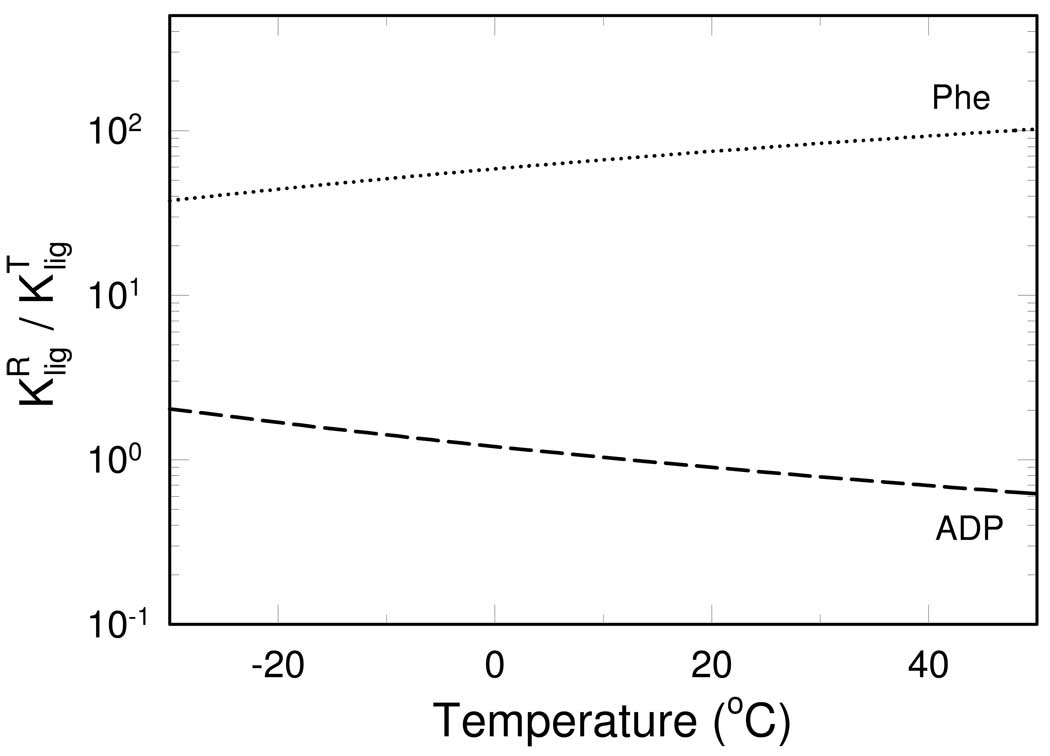
Temperature dependence of dissociation constants for Phe is shown in Figure 4. Phe binding to both states exhibits only weak temperature dependence that is characterized by a relatively small binding enthalpy change $\mathrm{\Delta }{H}_{\mathit{\text{Phe}}}^R=-1.4\text{kcal}/\text{mol}\text{and}\mathrm{\Delta }{H}_{\mathit{\text{Phe}}}^T=0.65\text{kcal}/\text{mol}$. The differential binding affinity as a function of temperature can be expressed as the ratio of $K_{\mathit{\text{Phe}}}^R/K_{\mathit{\text{Phe}}}^T$ , as shown in Fig. 5. The affinity of Phe to the T-state is greater than that to the R-state at all investigated temperatures, as shown in Fig. 4, thus, the ratio of $K_{\mathit{\text{Phe}}}^R/K_{\mathit{\text{Phe}}}^T$ is always larger than one. Since $K_{\mathit{\text{Phe}}}^T$ is more favored by higher temperature than $K_{\mathit{\text{Phe}}}^R$, the ratio increases with temperature, as shown in Fig. 5. Therefore, Phe always acts as an allosteric inhibitor by shifting RMPK population to the inactive T-state, particularly at higher temperatures.

Fig. 5.

Ratio $K_{\mathit{\text{lig}}}^R/K_{\mathit{\text{lig}}}^T$ between dissociation constants from the R and T-state of RMPK for ADP (dashed line) and Phe (dotted line) as a function of temperature.

The temperature dependence of the T-state fraction of RMPK in the presence of a saturating amount of Phe is shown in Fig. 3A as the dotted line $(f_{\mathit{\text{Phe}}}^T)$ . Similar to the case of PEP binding, saturation of RMPK by Phe in the absence of other ligands shifts the RMPK population fully to the inactive T-state regardless of temperature.

ADP binding

ADP appears to be an intriguing allosteric effector. The value of $K_{\mathit{\text{ADP}}}^R$ increases more than 10 times between 0°C and 40°C. $K_{\mathit{\text{ADP}}}^T$ is even more temperature sensitive, as shown in Fig. 4. At 23°C the value of $K_{\mathit{\text{ADP}}}^R=450\mathrm{\mu }\mathrm{M}$, a value in good agreement with a result obtained from steady-state kinetics (11). The strong increase of the ADP dissociation constants with increasing temperature is caused by significantly larger binding enthalpies for ADP, $\mathrm{\Delta }{H}_{\mathit{\text{ADP}}}^R=-10.5\text{kcal}/\text{mol}\text{and}\mathrm{\Delta }{H}_{\mathit{\text{ADP}}}^T=-12.8\text{kcal}/\text{mol}$, than for PEP or Phe. The R-state is therefore slightly disfavored by the ADP binding. The unfavorable free energy change was found to be 0.3 kcal/4 = 75 cal/monomer of RMPK, Fig. 1B.

According to the model described earlier (7, 8), the equilibrium constant in the presence of ADP can be calculated as

$$L_{0,\mathit{\text{ADP}}}=L_0{\left(1+[\mathit{\text{ADP}}]/K_{\mathit{\text{ADP}}}^T\right)}^4/{\left(1+[\mathit{\text{ADP}}]/K_{\mathit{\text{ADP}}}^R\right)}^4$$ (5)

where $K_{\mathit{\text{ADP}}}^T$ and $K_{\mathit{\text{ADP}}}^R$ are microscopic dissociation constants of ADP from the T and the R-state, respectively. The equation shows that any differential affinity of ADP to the R and T states, i.e. any difference in $K_{\mathit{\text{ADP}}}^R$ and $K_{\mathit{\text{ADP}}}^T$, will cause a shift of the R↔T equilibrium. Because both $K_{\mathit{\text{ADP}}}^T$ and $K_{\mathit{\text{ADP}}}^R$ are temperature dependent, i.e.

$$K_{\mathit{\text{lig}}}^{\mathit{\text{state}}}=\text{exp}[(1/\mathit{\text{RT}})(\mathrm{\Delta }{H}_{\mathit{\text{lig}}}^{\mathit{\text{state}}}-T\cdot \mathrm{\Delta }{S}_{\mathit{\text{lig}}}^{\mathit{\text{state}}})]$$ (6)

the shift of the equilibrium will depend on temperature as well.

The calculated temperature dependence of L_0,ADP is depicted in Figure 2A. It can be seen that in the presence of 10 mM ADP the minimum of L_0,ADP, shifts several centigrade to a higher temperature, compared to the equilibrium constant L₀ . As described above, this shift is caused by a difference between $K_{\mathit{\text{ADP}}}^R$ and $K_{\mathit{\text{Phe}}}^T$ .

As seen from Figure 5, the ratio of the dissociation constants, $K_{\mathit{\text{ADP}}}^R/K_{\mathit{\text{ADP}}}^T$ , decreases with increasing temperature. The ratio actually crosses over from >1 to <1 with increasing temperature i.e. the relative affinities to the R- and T-state are reversed. The ratio equals to one near 12 °C. At this temperature the presence of ADP does not influence the R↔T equilibrium. Above 12 °C ADP binds preferentially to the R-state and exerts activating effect on RMPK by shifting the enzyme population to the active R-state. Below 12 °C ADP acts as an allosteric inhibitor. In conclusion, depending on the temperature ADP induces either activation or inhibition of RMPK.

For RMPK saturated by ADP the transition from R- to T-state shifts about 3 °C to higher temperature, as shown in Fig. 3A. Figure 3A further suggests that the ADP-induced redistribution of the RMPK states becomes important mainly in two rather narrow temperature regions around −20°C and 40°C. Fig. 3B expresses the data as ${(}^{\mathit{\text{sat}}}{f}_{\mathit{\text{ADP}}}^T-f_0^T)$ , where ${}^{\mathit{\text{sat}}}{f}_{\mathit{\text{ADP}}}^T$ and $f_0^T$ are the T-state fractions in the presence and in the absence of ADP, respectively. The difference ${}^{\mathit{\text{sat}}}{f}_{\mathit{\text{ADP}}}^T-f_0^T$ is explicitly shown in Figure 3B. It is seen that the physiologically relevant region is located between 30°C and 45°C where the presence of ADP causes strong RMPK activation. Specifically, it is seen that around 40 °C almost 35 % of the RMPK population converts from the inactive to the active state in the presence of ADP. Interestingly, the rabbit physiological temperature of about 39°C falls into this temperature interval (12, 13). The second temperature region of the significant ADP effect can be found at subzero temperatures where ADP causes RMPK inactivation by an increase of the T-state fraction. At other temperatures ADP does not seem to significantly influence the allosteric regulation of RMPK. This observation is consistent with results of Consler et al. who had not detected any effect of ADP on the allosteric properties of RMPK at 23°C (11). Although the inhibition of RMPK by ADP at temperatures below −20°C is probably physiological irrelevant, the described mechanism of switching between activation and inhibition is general for any two-state concerted system. Depending on temperature and the associated thermodynamic parameters, ligands can activate or inhibit enzymes. Because the switching temperature between the activation and inactivation is determined by a fine interplay of the thermodynamic binding parameters, the described effect could be important for other allosteric proteins.

Our data presented in the previous paper (8) suggest that at low temperatures an addition of a saturating amount of ADP to RMPK, which is fully inhibited by Phe, would lead to an allosteric activation of RMPK. The activation is the result of a decrease of the fraction of T-state in the presence of both Phe and ADP. A calculated temperature dependence of the f^T under these conditions is shown in Figure 3A by the dash-dot-dot line. The presence of 10 mM ADP causes a decrease of f^T in the temperature range between −20 and 20 °C even in the presence of 12 mM Phe. In the absence of ADP it is predicted that at this Phe concentration RMPK is inactive as shown in Figure 3A.

Role of protonation and deprotonation

In this study of RMPK, it has been shown that protons are released or absorbed in these linked reactions, as shown in Fig. 1. These linked reactions of proton release or absorption may play an equally important role in modulating the allosteric behavior of RMPK. For the reactions which involve in proton release, lower pH would shift the equilibria to the left, as defined by the Le Chatelier’s principle. Thus, lower pH would increase the bindings of ADP, PEP and favors the T-state. The net result would be an expected change of cooperativity in substrate binding. This may be particularly relevant to the normal behavior of RMPK. It has long been reported that a development of acidosis is associated with intense exercise (14–17). Furthermore, intense exercise can lead to increase in temperature (22). An increase of muscle temperature causes stronger RMPK activation and the temperature decrease causes RMPK inactivation compared to the reference state without ADP. Thus, under intense exercise, the conditions would favor higher activity of RMPK to generate additional ATP.

RMPK regulatory behavior at physiological conditions

Having thermodynamically characterized the regulatory mechanism of RMPK it is of interest to simulate the state distribution at physiological conditions when both ADP and PEP are present in solution. It was shown that in a resting skeletal muscle the PEP and ADP concentration is close to 30 µM and 50 µM, respectively (18). At the rabbit physiological temperature of about 39 °C both values are significantly lower than their corresponding dissociation constants of $K_{\mathit{\text{PEP}}}^R=120\mathrm{\mu }\mathrm{M}\text{and}{K}_{\mathit{\text{ADP}}}^R=1.1\text{mM}$ (Fig. 4). Under these conditions only a small population of RMPK subunits binds simultaneously both substrates that are required for the enzymatic activity. As a consequence, only low reaction rates are observed. While the PEP concentration does not change significantly during muscle contraction, the ADP concentration increases primarily due to the shift of the following equilibrium

$$\text{ADP}+\text{creatine-P}\leftrightarrows \text{ATP}+\text{creatine}$$

that is maintained by creatine kinase. Because creatine phosphate is consumed during muscle contraction, the reaction equilibrium is displaced towards higher ADP concentrations. During intense muscle activity the ADP concentration can increase to almost 3 mM (19–21). According to the data from Figure 2 and Figure 3, the increased ADP concentration causes not only RMPK activation, it also changes the apparent cooperativity of the PK-catalyzed reaction. Both effects are a result of the ADP-induced shift of the R↔T equilibrium. To investigate the influence of temperature and ADP concentration on the state distribution, we plotted a change of the fraction of R-state, Δf^R , upon an addition of a variable amount of ADP $(\mathrm{\Delta }{f}^R=f_{\mathit{\text{ADP}}}^R-f_{\mathit{\text{withoutADP}}}^R)$ at different temperatures. The simulation was conducted in the presence of a physiological PEP concentration of 30 µM. The apparent equilibrium constant needed for calculation of f^R = 1/(1+L) in the presence of both PEP and ADP was calculated as

$$L_{0,\mathit{\text{ADP}},\mathit{\text{PEP}}}=L_0{\left(\frac{1+[\mathit{\text{ADP}}]/K_{\mathit{\text{ADP}}}^T}{1+[\mathit{\text{ADP}}]/K_{\mathit{\text{ADP}}}^R}\right)}^4\cdot {\left(\frac{1+[\mathit{\text{PEP}}]/K_{\mathit{\text{PEP}}}^T}{1+[\mathit{\text{PEP}}]/K_{\mathit{\text{PEP}}}^R}\right)}^4$$ (7)

Because binding of PEP to the T-state was found to be very weak (8), i.e. the physiological PEP concentration is always much lower than the value of $K_{\mathit{\text{PEP}}}^T$, the equation can be approximated by

$$L_{0,\mathit{\text{ADP}},\mathit{\text{PEP}}}=L_0{\left(\frac{1+[\mathit{\text{ADP}}]/K_{\mathit{\text{ADP}}}^T}{\left(1+[\mathit{\text{ADP}}]/K_{\mathit{\text{ADP}}}^R\right)\cdot \left(1+[\mathit{\text{PEP}}]/K_{\mathit{\text{PEP}}}^R\right)}\right)}^4$$ (8)

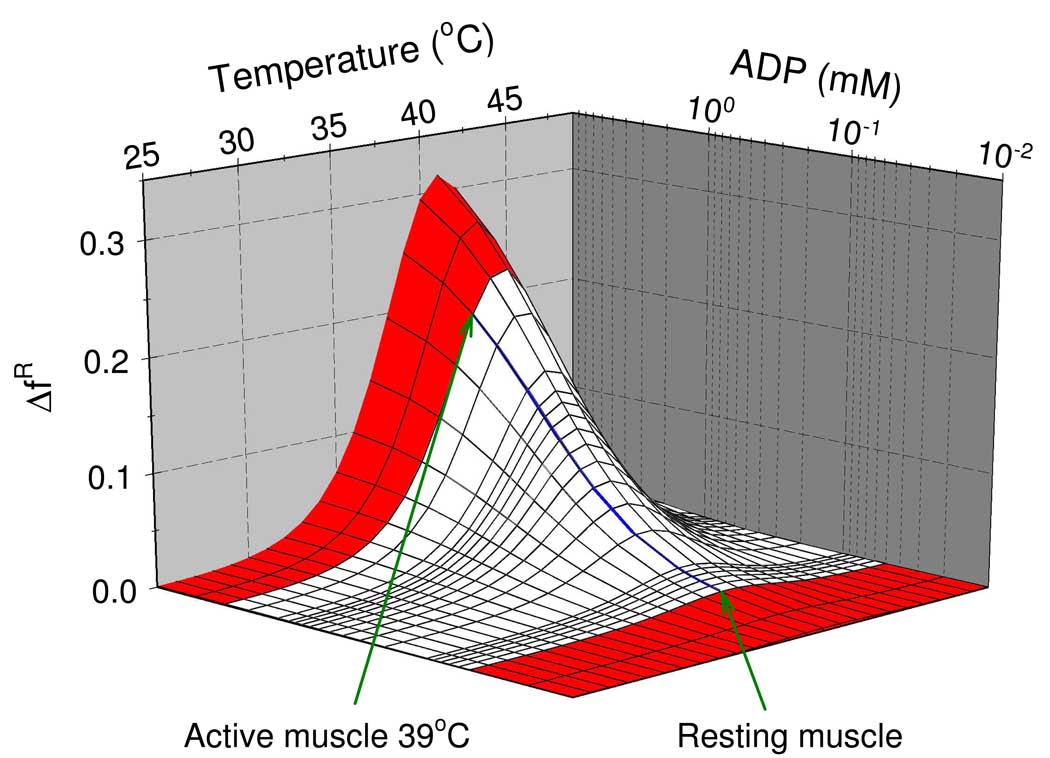
The result of the simulation is depicted in Figure 6 where the estimated region of the physiological ADP concentrations is marked by white color. Figure 6 reveals that near the physiological temperature of rabbit at 39 °C an intense muscle contraction would result in almost a peak of 3 mM ADP concentration which would induce about 20% increase of the fraction of active-state RMPK.

Fig. 6.

Predicted effect of ADP on the activation of the RM PK in the presence of a physiological concentration of PEP (30µM). $\mathrm{\Delta }{f}^R=f_{\mathit{\text{ADP}}}^R-f_{\mathit{\text{withoutADP}}}^R$ is an increase of the active R-state fraction upon the ADP addition. White color marks an approximate region of physiological ADP concentrations. The blue line is the isotherm at 39 °C.

In conclusion, we have shown that:

1. Equilibrium constants involved in the allosteric regulatory mechanism of RMPK are fine-tuned to facilitate maximal response of the enzyme to even minute changes of temperature and ligand concentrations.

2. The differential number of protons released or absorbed with regards to the various linked reactions adds another level of control to shift the binding constants and R↔T equilibrium, which controls quantitatively the activity of RMPK.

3. ADP was shown to be an important allosteric effector significantly affecting the allosteric regulation of RMPK. The ADP action was shown to be highly temperature dependent. Any ligand of any enzyme can behave like ADP in RMPK i.e. can under favorable conditions exert either an activating or inhibitory effect.