A Simple Mathematical Model of Cytokine Capture Using a Hemoadsorption Device

Abstract

Sepsis is a systemic response to infection characterized by increased production of imflammatory mediators including cytokines. Increased production of cytokines such as interleukin-6 (IL-6), interleukin-10 (IL-10), and tumor necrosis factor (TNF) can have deleterious effects. Removal of cytokines via adsorption onto porous polymer substrates using an extracorporeal device may be a potential therapy for sepsis. We are developing a cytokine adsorption device (CAD) containing microporous polymer beads that will be used to decrease circulating levels of IL-6, TNF, and IL-10. In this paper we present a mathematical model of cytokine adsorption within such a device. The model accounts for macroscale transport through the device and internal diffusion and adsorption within the microporous beads. The analysis results in a simple analytic expression for the removal rate of individual cytokines that depends on a single cytokine-polymer specific parameter, Γ_i. This model was fit to experimental data and the value of Γ_i was determined via nonlinear regression for IL-6, TNF, and IL-10. The model agreed well with the experimental data on the time course of cytokine removal. The model of the CAD and the values of Γ_i will be applied in mathematical models of the inflammatory process and treatment of patients with sepsis.

INTRODUCTION

Severe sepsis is defined as infection that results in systemic inflammation and organ failure and affects 750,000 patients annually in the United States, one third of whom die¹. In sepsis, an acute inflammatory reaction arises due to the host response to infection² and is characterized by the redundant release of multiple inflammatory mediators including cytokines into the bloodstream^{3, 4}. Increased production of pro-inflammatory cytokines such as tumor necrosis factor (TNF) and interleukin-6 (IL-6) and anti-inflammatory cytokines such as interleukin-10 (IL-10) can have deleterious clinical effects^{5, 6}. Increased expression of these cytokines in the circulation is strongly associated with death⁷. Drug therapies aimed at blocking single mediators have not been effective in attenuating the entire response^8-10.

One possible solution is hemofiltration, the removal of plasma solutes by the convective removal of plasma from blood using a semi-permeable membrane. Yet “renal dose” hemofiltration is relatively inefficient in removing cytokines¹¹, and one small phase II trial found that it does not result in improved outcome for patients with sepsis¹². The use of high-volume hemofiltration may be more effective but its use is technically demanding and still unproven¹³. Kellum and Dishart (2002) showed that adsorption on to the hemofiltration filter membrane appears to be the primary mechanism responsible for cytokine removal during high-volume hemofiltration¹⁴. They compared normal hemofiltration of an experimental model of sepsis in rats to hemofiltration with the ultrafiltrate being reintroduced into the animal and found that cytokine concentrations could be inhibited by hemofiltration whether or not the ultrafiltrate was reinfused. Accordingly, for many investigators, the focus of cytokine removal has shifted from hemofiltration to hemoadsorption^{15, 16}.

Some groups have shown that these mediators can be removed effectively with various polymer sorbents in a batchwise setting with a known mass of beads being continuously mixed in suspension with the cytokine solution¹⁷. Song et al. (2004) showed that circulating levels of TNF, IL-6, and IL-10 rapidly decreased when whole blood from lipopolysaccharide-challenged rats was circulated through a column containing a novel biocompatible polymer adsorbent¹⁸. Less than 50% of the initial concentrations of each cytokine remained after only one hour of treatment. These results were demonstrated in a circuit which more closely resembles that of actual extracorporeal blood purification by keeping the bead-filled cartridge separate from the reservoir.

In this paper we develop a model of cytokine adsorption within a cytokine adsorption device (CAD) which consists of microporous polymer beads packed within a cylindrical cartridge. Our model builds on existing models of transport in packed bed adsorbers. Garg and Ruthven (1973) published both an asymptotic analysis¹⁹ and a general isothermal solution²⁰ for molecular sieve adsorption columns under micropore diffusion control. Numerical solutions via Laplace transformation have been obtained for systems in which concentrations of sorbate are sufficiently small to operate entirely in a linear isotherm under the Langmuir model²¹. These solutions are particularly useful in predicting breakthrough curves for elution, frontal, and displacement chromatography applications²².

In this study we derived a simpler analytical capture rate expression by exploiting the high adsorption capacity of the beads and low relative affinity that exists under typical physiological concentrations of cytokines compared to an excess of potential adsorbing sites. This model captures the macroscale process of flow through the CAD and the microscale processes of internal diffusion and adsorption to the pore surfaces. The model predicts that a single cytokine-polymer specific parameter that can be estimated from experimental data determines the expected removal rates of cytokines using the CAD.

MATERIALS AND METHODS

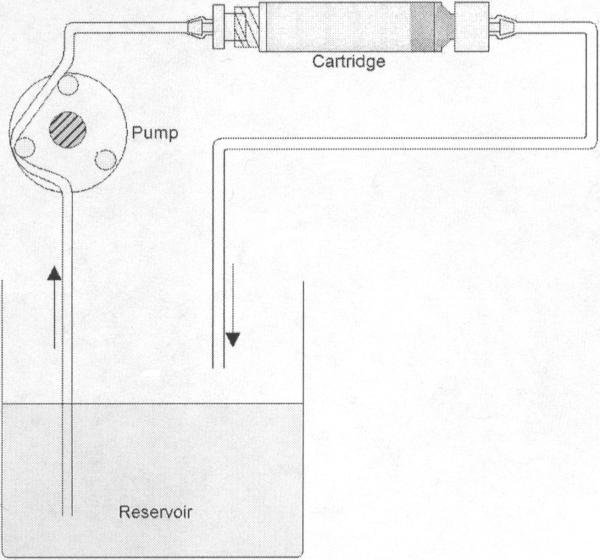
The cytokine adsorption device (CAD) consists of a cartridge filled with CytoSorb™ porous polymer beads (MedaSorb Technologies, LLC, NJ). The beads are made of a polystyrene divinylbenzene (PSDVB) copolymer and covered in a biocompatible polyvinylpyrrolidone coating. They are approximately 300-600 μm in diameter with a density of 1.02 g/cm³. A schematic of the CAD and recirculation loop can be seen in figure 1. The scaled-down CAD holds approximately 10g of CytoSorb™ beads and measures 3.25” long by 0.5” in diameter. The void fraction of the packed bead bed within the device is 0.31 while the porosity of the polymer is 67.6%.

Figure 1.

Typical set up of recirculation loop

Multiscale Transport Formulation

We describe the cytokine capture process using a multiscale transport approach. The macroscale follows the concentration of various cytokines, C_i (Z,t), as a function of time and axial position (Z) within the CAD. The microscale follows the concentration of the cytokines, c_i (r, Z,t) as a function of radial position (r) within the spherical adsorption beads at macroscale axial position Z.

A cytokine mass balance on a differential macroscale element ( ΔZ ) yields the governing macrotransport equation:

$${\epsilon }_c\frac{\partial C_i}{\partial t}+\frac{Q}{A}\frac{\partial C_i}{\partial Z}=-(1-{\epsilon }_c)\rho \frac{\partial {\stackrel{‒}{q}}_i}{\partial t}$$ (1)

where A is the cross-sectional area of the device, ε_c, is the device porosity (i.e. non-bead liquid volume), Q is the axial flowrate, ρ is the bead density, and $\stackrel{‒}{q}$ _i (Z,t) is the average mass concentration of adsorbed cytokines on the beads at axial location Z. Note that we have not included effects associated with the axial dispersion of cytokines in the CAD as the length of the CAD is assumed to be sufficient to render dispersion effects negligible ²³. A cytokine mass balance on a differential microscale element (Δr) yields the governing microtransport equation:

$$\rho \frac{\partial q_i}{\partial t}=D_i\frac{1}{r^2}\frac{\partial }{\partial r}\left(r^2\frac{\partial c_i}{\partial r}\right)$$ (2)

where q_i (r,t) is the mass of cytokine i adsorbed on the bead internal surfaces at radial position r on a per unit bead mass basis, D_i is the effective diffusion coefficient of the cytokine within the bead accounting for tortuosity of pores and bead porosity, and c_i (r, Z,t) is the mass concentration of cytokine in the liquid phase of the bead pores at location r. Here we assume that the biocompatible coating does not give rise to any additional mass transfer resistances and therefore that the surface and pore morphology are homogeneous.

Adsorption at the microscale is coupled to macrotransport through the boundary condition c_i (r = R, Z,t) = C_i (Z,t) based on the assumption that mass transfer is dictated by diffusion within the bead rather than film diffusion to the bead surface. Once the microscale transport solution is determined, adsorption at the macroscale is driven by temporal changes in the average adsorbed concentration:

$$\frac{\partial {\stackrel{‒}{q}}_i}{\partial t}=\frac{3}{R^3}\underset{0}{\overset{R}{\int }}\frac{\partial q_i}{\partial t}{r}^2\mathit{dr}$$ (3)

Microscale Transport Analysis

We assume that the rate of local adsorption within the bead is fast compared to diffusion so that local adsorption equilibrium applies^{21, 24}. Accordingly, adsorption onto the bead surface is described using the multicomponent Langmuir isotherm:

$$q_i=q_i^{\max }\frac{K_i{c}_i}{1+\sum _j{K}_j{c}_j}$$ (4)

where q_i is the adsorbed mass of the cytokine of interest and q_i ^max is the maximum adsorption of that cytokine on the bead surface in the absence of other adsorbing species. The parameters K_i and K_j correspond to the adsorption affinity constants of cytokine i and all other solutes, j, respectively. The Langmuir isotherm, in addition to being the simplest equilibrium adsorption model, is often used as a correlation for equilibrium adsorption data of proteins²².

A dimensional analysis of the microtransport equation can be performed to develop a solution for the microscale concentration profile (see Appendix A for further details). Cytokine concentration can be normalized using c^*_i ≡ c_i C ⁱⁿ_i where C ⁱⁿ_i is the concentration of cytokine in the solution flowing into the device. The properly scaled value for the dimensionless adsorbed cytokine concentration in our application is q^* ≡ q^max Kⁱⁿ_i, and the dimensionless Langmuir adsorption isotherm becomes:

$$q_i^{\ast }=\frac{c_i^{\ast }}{1+\sum _j{K}_j^{\ast }{c}_j^{\ast }}$$ (5)

where K ^*_i ≡ K_iC ⁱⁿ_i represents a dimensionless or relative affinity, which can also be expressed as

$$K_i^{\ast }\equiv \frac{C_i^{\mathit{in}}}{C_{50i}}$$ (6)

in which C_50i is the concentration of cytokine that would saturate half the polymer surface with that cytokine at equilibrium. The independent variables are normalized using

$$r^{\ast }\equiv r∕R;t^{\ast }\equiv t∕t_s$$ (7)

where R is the radius of the bead, and t_s is the time scale over which cytokine levels are being depleted from circulation in application of the therapy. The time scale t_s can be estimated using:

$$t_s\approx \frac{m_i^{\mathit{circ}}}{D_i\left(\frac{C_i}{R}\right)A_b}=\frac{m_i^{\mathit{circ}}\rho R^2}{m_b{D}_i{C}_i^{\mathit{in}}}$$ (8)

where A_b is the surface area of one bead, m^circ_i is the mass of circulating cytokine, and m_b is the mass of adsorbing beads in the device.

Substituting in the defined dimensionless variables, the dimensionless microtransport equation becomes

$${\delta }_i\frac{\partial q_i^{\ast }}{\partial t^{\ast }}=\frac{1}{r^{\ast 2}}\frac{\partial }{\partial r^{\ast }}\left(r^{\ast 2}\frac{\partial c_i^{\ast }}{\partial r^{\ast }}\right)$$ (9)

where the parameter δ_i is given by:

$${\delta }_i=\frac{m_i^{\mathit{circ}}}{m_b{K}_i^{\ast }{q}_i^{\max }}$$ (10)

Accordingly, two dimensionless parameters, δ_i and K_i, dictate cytokine diffusion and adsorption into the beads of the CAD. The approximate values of these parameters can be estimated straightforwardly. The C ⁱⁿ_i for cytokines in blood is approximately 10^-6-10^-4 mg/ml ¹⁸. The value of C_50i cannot be determined easily for cytokines of interest to us on the beads used in the current CAD because the material quantity required for measuring the Langmuir adsorption isotherm would be prohibitive. Generally, for proteins adsorbing on polymer surfaces C_50i is typically on the order of 10^-2-10^-1 mg/ml ¹⁸. For example, cytochrome C (12 kDa) adsorbing on the PSDVB beads used in our current CAD has a C_50i of 0.48 mg/ml. Thus, K ^*_i << 1 and the microtransport of cytokine corresponds to a low relative affinity regime. The dimensionless parameter δ_i represents the amount of circulating cytokine relative to the cytokine capture capacity of the device and is also a small parameter. For typical conditions of application:

$${\delta }_i\approx \frac{2.4\times {10}^{-4}\text{mg cytokine}}{\left(10\text{g beads}\right)\left({10}^{-3}\right)\left(370\text{mg cytokine/g bead}\right)}\cong 6.5\times {10}^{-5}$$ (11)

We performed an asymptotic analysis of the microtransport equation based on K ^*_i << 1 and δ_i << 1with the two dimensionless parameters properly scaled relative to one another (see Appendix B). The concentration profile predicted by the asymptotic analysis is:

$$c_i(Z,r,t)=C_i\left(Z\right)=C_i\left(Z\right)\left(1-\mathit{erf}\left[\sqrt{\frac{{\alpha }_i}{4t}}\left(1-\frac{r}{R}\right)\right]\right)$$ (12)

where

$${\alpha }_i=\frac{\rho q_i^{\max }{K}_i^{\ast }{R}^2}{D_i{C}_i^{\mathit{in}}}$$ (13)

and represents the characteristic time required to load a bead with a given cytokine i.

Macroscale Analysis and the Cytokine Removal Rate

In the following section we justify that the macrotransport equation is quasi-steady and as such the only relevant effects of time come in from the microtransport analysis. This justifies dropping the explicit time dependence from the macroscale concentration in the boundary condition for the microtransport equation. The macroscale average adsorption term (Eq. 3) can be determined from the microscale concentration profile using

$$\frac{\partial {\stackrel{‒}{q}}_i}{\partial t}=\frac{3}{R^3}{D}_i\frac{\partial c_i}{\partial r}{\mid }_{r=R}$$ (14)

By combining with Eq. 12, the macrotransport equation becomes:

$${\epsilon }_c\frac{\partial C_i}{\partial t}+\frac{Q}{A}\frac{\partial C_i}{\partial z}=-(1-{\epsilon }_c)\frac{3D_i}{R^2}\sqrt{\frac{{\alpha }_i}{\pi t}}{C}_i$$ (15)

An analysis of the first two terms in Eq. 15 provides the following relationship:

$$\frac{{\epsilon }_c\frac{\partial C_i}{\partial t}}{\frac{Q}{A}\frac{\partial C_i}{\partial z}}\approx \frac{\frac{{\epsilon }_c}{t_s}{C}_i^{\mathit{in}}}{\frac{Q}{\mathit{AL}}{C}_i^{\mathit{in}}}=\frac{V_c}{Q}\frac{{\epsilon }_c}{t_s}$$ (16)

Since 0 < ε_c < 1 and t_s >> V_c/Q, the first term in Eq. 15 can be neglected and the macroscale transport is quasi-steady. Integrating Eq. 15 with respect to the macroscale coordinate Z, and evaluating at Z = L gives

$$C_i(L,t)=C_i^{\mathit{in}}{e}^{-\frac{AL}{Q}(1-\epsilon )\frac{3D_i}{R^2}\sqrt{\frac{{\alpha }_i}{\pi t}}}$$ (17)

which can be further simplified since AL(1-ε_c)= m_b ρ. The overall mass removal rate, using Eq. 13 for α_i, is:

$${\stackrel{.}{m}}_i\left(t\right)=Q\left[C_i^{\mathit{in}}-C_i(L,t)\right]=Q{C}_i^{\mathit{in}}\left(t\right)\left[1-\exp \left(-\frac{3}{\sqrt{\pi }}\frac{m_b}{Q}\frac{1}{R}\sqrt{\frac{D_i{q}_i^{\max }{K}_i}{\rho t}}\right)\right]$$ (18)

The rate of removal depends on one unknown parameter, Γ_i, specific to cytokine i and its interaction with the bead micropores and polymer surface:

$${\Gamma }_i=D_i{q}_i^{\max }{K}_i$$ (19)

All the other parameters of the device and its operation are known or are easily determined.

Cytokine Capture During Recirculation

Using Eq. 18, a mass balance on a cytokine volume of distribution V_r within a reservoir (or patient in application) yields:

$$-\frac{d{C}_i}{dt}=\frac{Q}{V_r}\left[1-\exp \frac{-3}{\sqrt{\pi }}\frac{m_b}{Q}\frac{1}{R}\sqrt{\frac{{\Gamma }_i}{\rho t}}\right]C_i\left(t\right)$$ (20)

A dimensionless recirculation time, τ, can be defined as

$$\tau =\frac{t}{(V_r∕Q)}$$ (21)

and substituted into Eq. 20 to yield:

$$-\frac{d{C}_i}{d\tau }=\left[1-\exp \left(\frac{-G_i^{\ast }}{\sqrt{\tau }}\right)\right]C_i\left(\tau \right)$$ (22)

where

$$G_i^{\ast }\equiv \frac{3}{\sqrt{\pi }}\frac{m_b}{R}\sqrt{\frac{{\Gamma }_i}{\rho Q{V}_r}}$$ (23)

The dimensionless parameter G^*_i represents a relative diffusional conductance that ultimately determines whether cytokine clearance is diffusion limited, perfusion limited, or intermediate. Dimensionless clearance is given by:

$$\frac{\stackrel{.}{m}}{Q{C}_i}=\left[1-\exp \left(\frac{-G_i^{\ast }}{\tau }\right)\right]$$ (24)

Model Comparison to Experimental Data

The model was evaluated by comparing theoretical cytokine removal curves to experimental data. The cytokine concentration data from Song et al. (2004) was used as the experimental basis for comparison. For their experiments, Song et al. administered 20 mg/kg endotoxin intravenously to adult Sprague-Dawley rats. The animals were exsanguinated after either 2 or 4 h and blood from pairs of animals was pooled. The flow rate used was 0.8 mL/min and the reservoir volume was 24 mL. 500 μL samples of blood were taken over six hours of recirculation. TNF, IL-6, and IL-10 were assayed using enzyme-linked immunosorbent assays (ELISA).

The concentrations of TNF, IL-6, and IL-10 over time were normalized to the initial concentration of each cytokine. These data were fit to Eq. 20 using Matlab, subject to the initial condition that the percent of each cytokine at t=0 is 100. The finite change in reservoir volume of 500 μL per sample was taken into account for the value of V_r at each time point. The values of Γ_i found to most closely model cytokine removal in the device were obtained via nonlinear regression using Matlab. R² values were determined for best-fit curves to each data set.

RESULTS

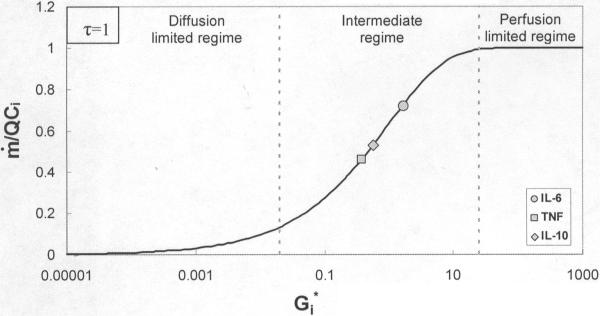
A plot of the dimensionless parameter G_i* against dimensionless clearance rate using Eq. 24 shows three distinct areas of cytokine clearance behavior within the cytokine adsorption device (CAD), as seen in figure 2. These three regions correspond to the diffusion limited, intermediate, and perfusion limited mechanisms of capture. The removal rate is independent of flow rate up to G_i* ≅ 0.02, which represents the diffusion limited regime. At G_i* ≅ 25, removal is perfusion limited and clearance becomes proportional to flow rate. Also shown on figure 2 are G_i* values for each of the three cytokines calculated from the Γ_i values obtained using the model. In figure 2, τ was set at 1 so that G_i* values could be plotted directly on the x-axis.

Figure 2.

Effect of increasing dimensionless relative conductance, ${\widehat{G}}_i^{\ast }$, on clearance

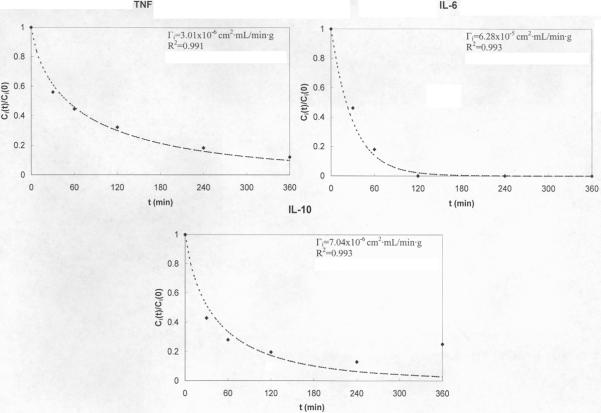
The Γ_i values for each cytokine and the results of the fits of Eq. 18 to experimental removal rate data are seen in figure 3. The best-fit value of Γ_i along with R² values are also indicated on each graph.

Figure 3.

Experimental data vs. model prediction for TNF, IL-6, and IL-10.

The values of Γ_i obtained for each cytokine from the simulation can be used to determine expected input values of the effective diffusion coefficient. Using Γ_i values predicted by the model and parameter values used in obtaining Γ_i, the effective diffusion coefficient for TNF, IL-6, and IL-10 can be estimated from a rearranged form of Eq. 19; these values are given in table I.

Table I.

Model results for conductance parameter and effective diffusion coefficient

Cytokine	Γi (cm2·mL/min·g)	Di (cm2/s)
TNF	3.01×10-6	4.07×10-9
IL-6	6.28×10-5	8.49×10-8
IL-10	7.04×10-6	1.45×10-8

DISCUSSION

The purpose of this study was to develop and validate a model describing cytokine capture in a hemoadsorption device containing porous polymer beads. Our goal was to predict removal rates of cytokines within the cytokine adsorption device (CAD) by determining the value of the cytokine specific parameter Γ_i that resulted in the best fit of the model to experimental data. Γ_i depends on the square root product of the diffusion coefficient and the two kinetic parameters of the Langmuir isotherm, the maximum adsorption capacity and Langmuir affinity constant (see Eq. 19).

The comparison of G_i* in figure 2 demonstrates that cytokine removal has both diffusion and perfusion limiting behavior. At very low flow rates (Q→0), the right hand side of Eq. 24 goes to 1 and removal rate is proportional to flow rate. This is the perfusion limit of capture which occurs for G_i* ≥25. For high flow rates (Q→∞), the right hand side of Eq. 24 goes to G_i* $G_i^{\ast }∕\sqrt{\tau }$ and clearance is independent of flow rate; any further increase in the capture rate would only be possible through a change in diffusion or adsorption parameters and hence a different Γ_i value. This regime represents diffusion limited capture and occurs at G_i* ≤0.02. At this limit, essentially all cytokines are removed from solution upon reaching the CAD. The values of G_i* calculated from the best-fit values of Γ_i show that removal of IL-6, IL-10, and TNF within the CAD falls into the intermediate region of clearance.

The effective diffusion coefficient accounts for porosity and tortuosity of the polymer and can be back-calculated from a rearranged form of Eq. 19 for each cytokine to assess the model predictions. Γ_i values predicted by the model and parameters used in obtaining Γ_i were used to estimate D_i for TNF, IL-6, and IL-10; these values are given in table I. The effective diffusion coefficient for pore sizes 8-50 Å, corresponding to those of the beads used in the experiments, is of the expected order of magnitude (10^-9-10^-8 cm²/s) for hindered diffusion into solvent filled pores ²⁵. Lewus and Carta (1999) report values of 9.0×10^-9cm²/s for similar proteins in porous polymer media ²⁶. The D_i values found are, as expected, lower than free diffusion coefficients given for these same proteins, approximately 1.0×10^-6cm²/s ^{27, 28}. Thus, Γ_i values obtained using the model appear to be reasonable for each of the three cytokines.

Another level of complexity lies in the presence of other cytokines and potential adsorbing molecules. This combination of solutes flowing through the CAD may give rise to competitive effects²⁹ which would further complicate transport within the CAD. In the low affinity regime relevant to the adsorption of cytokines, multicomponent adsorption effects like competitive binding and affinity-based displacement did not arise in our microtransport descrption of cytokine diffusion and adsorption within beads. The extremely large polymer adsorption capacity relative to the amount of circulating cytokine suggests multicomponent effects would not occur. However, if competitive adsorption behavior was suspected as the cause for deviations from the model, moving up to the next level of approximation in the asymptotic analysis would account for the effect on cytokine removal. Further validation of the model we have presented will include experiments that test for multicomponent effects by comparing data from single and multiple cytokine recirculation in the CAD and if changes to experimental parameters such as bead size and flow rate changes the predicted value of Γ_i for each cytokine.

CONCLUSION

The model of cytokine capture by a hemoadsorptive device that we have developed can be used to determine the cytokine removal capabilities of the CAD in application. The simplicity of the model allows for straightforward manipulations of operational parameters which will both expedite and confirm the design of the most efficient device. This model will be used in conjunction with an equation-based pathway model that describes the time course of major components of the inflammatory response. A mathematical model of the evolution of sepsis in a living organism is already being developed³⁰ and the CAD model will be integrated with this model to simulate the effect of blood purification therapy intervention during sepsis. Our ultimate goal is to use these models to develop a CAD device and intervention protocol which improves patient outcome in sepsis.

APPENDIX

A. Dimensional Analysis of Microtransport Equation

Normalizing the cytokine concentration using $c_i^{\ast }\equiv c_i∕C_i^{\mathit{in}}$, where $C_i^{\mathit{in}}$ is the concentration of cytokine in the solution flowing into the device, the Langmuir isotherm becomes

$$\frac{q_i}{q_i^{\max }}=\frac{K_i^{\ast }{c}_i^{\ast }}{1+\sum _j{K}_j^{\ast }{c}_j^{\ast }}$$ (A.1)

K_i*represents a dimensionless or relative affinity expressed as

$$K_i^{\ast }\equiv \frac{C_i^{\mathit{in}}}{C_{50i}}$$ (A.2)

in which C_50i is the concentration of cytokine that would saturate half the polymer surface with that cytokine at equilibrium. As described in the main text, K_i* ≈ 10^-1 -10^-3 and the microtransport of cytokine corresponds to a low relative affinity regime. In this regime the properly scaled value for the dimensionless adsorbed cytokine concentration is $q_i^{\ast }\equiv q_i∕\left(q_i^{\max }{K}_i{C}_i^{\mathit{in}}\right)$ and the dimensionless Langmuir adsorption isotherm becomes:

$$q_i^{\ast }=\frac{c_i^{\ast }}{1+\sum _j{K}_j^{\ast }{c}_j^{\ast }}$$ (A.3)

The cytokine microtransport equation can be put into a dimensionless form by also normalizing the independent variables:

$$r^{\ast }\equiv r∕R;t^{\ast }\equiv t∕t_s$$ (A.4)

where R is the radius of the bead,, and t_s is the time scale over which cytokine levels are being depleted from circulation in application of the therapy. The dimensionless microtransport equation is

$$\frac{{\alpha }_i}{t_s}\frac{\partial q_i^{\ast }}{\partial t^{\ast }}=\frac{1}{r^{\ast 2}}\frac{\partial }{\partial r^{\ast }}\left(r^{\ast 2}\frac{\partial c_i^{\ast }}{\partial r^{\ast }}\right)$$ (A.5)

where the parameter α_i is given by:

$${\alpha }_i=\frac{\rho q_i^{\max }{K}_i^{\ast }{R}^2}{D_i{C}_i^{\mathit{in}}}$$ (A.6)

and represents a characteristic time required to load a bead with a given cytokine i. Using Eqs. 8 and A.6, the time scale relative to the loading time is given by:

$${\delta }_i\equiv \frac{t_s}{{\alpha }_i}=\frac{m_i^{circ}}{m_b{K}_i^{\ast }{q}_i^{\max }}$$ (A.7)

The dimensionless parameter δ_i represents the amount of circulating cytokine relative to the cytokine capture capacity of the device. As described in the main text, δ_i is also a small parameter, with δ_i ≈ 10^-5.

B. Asymptotic Analysis of Dimensionless Microtransport Equation

Microscale transport is governed by the dimensionless Langmuir adsorption isotherm (Eq. A.3) and the dimensionless microtransport equation:

$${\delta }_i\frac{\partial q_i^{\ast }}{\partial t^{\ast }}=\frac{1}{r^{\ast 2}}\frac{\partial }{\partial r^{\ast }}\left(r^{\ast 2}\frac{\partial c_i^{\ast }}{\partial r^{\ast }}\right)$$ (A.8)

An asymptotic analysis of the microscale transport requires that we properly scale the two small dimensionless parameters relative to one another. The guiding principle of least degeneracy³¹ used in asymptotic analyses requires that we select ${\delta }_i~O\left(K_i^{\ast 2}\right)$. Accordingly, we define another dimensionless parameter ${\beta }_i\equiv {\delta }_i∕K_i^{\ast 2}~O\left(1\right)$ and recast the dimensionless microtransport equation as

$$\frac{1}{{\beta }_i{K}_i^{\ast 2}}\frac{\partial q_i^{\ast }}{\partial t^{\ast }}=\frac{1}{r^{\ast 2}}\frac{\partial }{\partial r^{\ast }}\left(r^{\ast 2}\frac{\partial c_i^{\ast }}{\partial r^{\ast }}\right)$$ (A.9)

In the asymptotic limit of $K_i^{\ast }$ <<1, Eq. A.9 indicates that the diffusion-adsorption process is confined to a boundary layer of dimensionless size $O\left(K_i^{\ast }\right)$ at the surface of each bead. Introducing a boundary layer coordinate given by $\eta \equiv K_i^{\ast -1}(1-r^{\ast })$ the microtransport equation, simplified in the limit as $K_i^{\ast }\to 0$, is:

$${\beta }_i^{-1}\frac{\partial q_i^{\ast }}{\partial t^{\ast }}=\frac{{\partial }^2{c}_i^{\ast }}{\partial {\eta }^{\ast 2}}$$ (A.10)

The temporal derivative term can be simplified using the dimensionless multicomponent adsorption isotherm (Eq. A.3):

$$\frac{\partial q_i^{\ast }}{\partial t^{\ast }}=\frac{\partial q_i^{\ast }}{\partial c_i^{\ast }}\frac{\partial c_i^{\ast }}{\partial t^{\ast }}+\sum _j\frac{\partial q_i^{\ast }}{\partial c_j^{\ast }}\frac{\partial c_j^{\ast }}{\partial t^{\ast }}=\frac{\partial c_i^{\ast }}{\partial t^{\ast }}+\sum _{j}O\left(K_j^{\ast }\right)\frac{\partial c_j^{\ast }}{\partial t^{\ast }}$$ (A.11)

Eq. A.11 indicates that in the low relative affinity regime effects related to multicomponent adsorption (e.g. affinity-based displacement) will appear, but only in the higher order correction terms for the c_i*. The boundary layer microtransport equation becomes:

$${\beta }_i^{-1}\frac{\partial c_i^{\ast }}{\partial t^{\ast }}=\frac{{\partial }^2{c}_i^{\ast }}{\partial {\eta }^{\ast 2}}+O\left(K_i^{\ast }\right)$$ (A.12)

which has the following solution for c_i*(η = 0) = 1:

$$c_i^{\ast }=1-erf\left(\frac{\eta }{\sqrt{4{\beta }_i{t}^{\ast }}}\right)$$ (A.13)