Skip to main content
PMC home page
The Journal of Neuroscience logoLink to The Journal of Neuroscience
. 2009 Jun 10;29(23):7497–7503. doi: 10.1523/JNEUROSCI.6044-08.2009

A Second Function of Gamma Frequency Oscillations: An E%-Max Winner-Take-All Mechanism Selects Which Cells Fire

Licurgo de Almeida 1, Marco Idiart 1,2, John E Lisman 3,✉
PMCID: PMC2758634  NIHMSID: NIHMS124500  PMID: 19515917

Abstract

The role of gamma oscillations in producing synchronized firing of groups of principal cells is well known. Here, we argue that gamma oscillations have a second function: they select which principal cells fire. This selection process occurs through the interaction of excitation with gamma frequency feedback inhibition. We sought to understand the rules that govern this process. One possibility is that a constant fraction of cells fire. Our analysis shows, however, that the fraction is not robust because it depends on the distribution of excitation to different cells. A robust description is termed E%-max: cells fire if they have suprathreshold excitation (E) within E% of the cell that has maximum excitation. The value of E%-max is approximated by the ratio of the delay of feedback inhibition to the membrane time constant. From measured values, we estimate that E%-max is 5–15%. Thus, an E%-max winner-take-all process can discriminate between groups of cells that have only small differences in excitation. To test the utility of this framework, we analyzed the role of oscillations in V1, one of the few systems in which both spiking and intracellular excitation have been directly measured. We show that an E%-max winner-take-all process provides a simple explanation for why the orientation tuning of firing is narrower than that of the excitatory input and why this difference is not affected by increasing excitation. Because gamma oscillations occur in many brain regions, the framework we have developed for understanding the second function of gamma is likely to have wide applicability.

Introduction

Gamma frequency oscillations were originally discovered in the field potential of visual cortex (Eckhorn et al., 1988; Gray and Singer, 1989) and have subsequently been observed in most brain regions (for review, see Jensen et al., 2007). Such oscillations are thus likely to be a fundamental aspect of neural processing. Analysis of the function of gamma oscillations has focused on the role of oscillations in synchronizing cell firing (Singer and Gray, 1995): rather than firing with a uniform probability over time, networks that display gamma oscillations show clustered firing of principal cells that tends to occur at a particular phase of each gamma cycle (Bragin et al., 1995; Penttonen et al., 1998; Csicsvari et al., 2003). Such synchronization is likely to be functionally important because it allows the detection of this group by coincidence detection in target cells (König et al., 1996). Gamma oscillations are thus thought to be an important aspect of neural processing that provides a way for a group of cells that represents a particular percept or memory to be distinguished from other groups.

Although neurons are synchronized by gamma oscillations, they do not generally fire on every gamma cycle. For instance, in the hippocampus, principal neurons fire during only 2–5% of the gamma cycles [Senior et al. (2008), their Fig. 6]. It is thus important to understand how excitation and inhibition interact to produce this selectivity. Importantly, inhibition itself is modulated at gamma frequency (Soltesz and Deschênes, 1993); indeed, gamma oscillations appears to arise through a feedback process in which principal cells excite interneurons, which then inhibit the principal cells (Miles, 1990; Fisahn et al., 1998; Bartos et al., 2007; Fries et al., 2007; Mann and Paulsen, 2007). This dynamic inhibition not only synchronizes cells but, through interaction with excitation, selects which cells fire.

Figure 6.

Figure 6.

Open in a new tab
Orientation tuning of firing is unaffected by increasing excitation (contrast) in an integrate-and-fire network with gamma frequency inhibition. A, Tuning of excitatory input as a function or orientation (same as in Fig. 5) at two different levels of contrast. B, Orientation tuning of firing in simulations. Curve fits to data show no effect of enhancing contrast on tuning. The responses were fit by
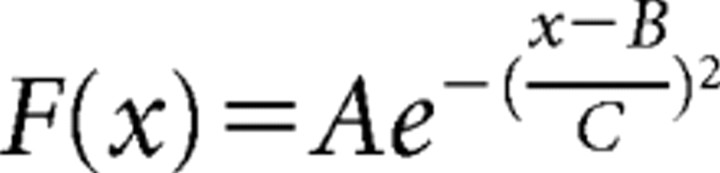graphic file with name zns02309-6566-m13.jpg
where x is the degree of orientation. For the lower level of contrast (filled squares), A = 0.19, B = 135, and C = 20.4; for higher contrast (open squares), A = 0.183, B = 134.9, and C = 19.74. The value of E%-max was 10%, based on results from hippocampus. The fact that the calculated tuning of spikes (16.5°) is narrower than observed experimentally (23°) could be because E%-max is higher in V1 or because noise levels are higher than we assumed (see Materials and Methods).

We have sought to determine whether there are any simple rules that describe this process. It has generally been thought that inhibition selects the most excited cells by performing a type of winner-take-all process. There is clearly more than one winner, and thus a commonly used assumption is that that there are k winners. We have examined this possibility and found that it is not robust. An alternative description (E%-max winner-take-all) is more robust: cells fire in a given gamma cycle if they have excitation (E) within E% of the cell that has maximal excitation. We show that the value E% can be estimated from easily measurable properties. Given how widespread gamma oscillations are in the nervous system, the role of these oscillations in determining which cells fire is of fundamental importance. This E%-max process is not a single-cell process, but rather a network process. In light of the present results, some standard ideas about what causes cells to fire may need to be revised.

Materials and Methods

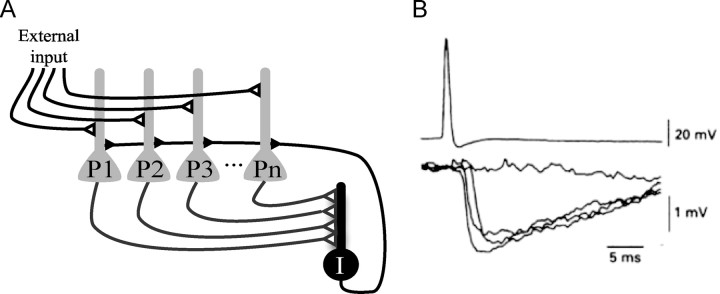
The network we simulate is shown in Figure 1 and involves a group of identical principal cells that converge onto an interneuron. The interneuron provides feedback inhibition to all principal cells. This inhibition occurs with a delay (d), relative to the spike in the principal cell. In most of the simulations, we adopted a delay period of 3 ms. This feedback inhibition is strong enough to prevent firing; firing can again occur after partial decline of the inhibition. This simple network creates gamma frequency inhibition.

Figure 1.

Figure 1.

Open in a new tab

A, Network structure showing interconnections of principal cells and an interneuron. Principal cells (P1 to Pn) receive external excitatory input. Principal cells excite an inhibitory interneuron (I) that provides feedback inhibition to all principal cells. B, An action potential (top trace) in a pyramidal neuron in the CA3 region of the hippocampus produces rapid disynaptic feedback inhibition in a nearby pyramidal neuron (bottom; several traces superposed). The entire process is very rapid: there is only a 2–3 ms delay between the action potential in the principal cell and the feedback inhibition of principal cells. Note: feedback inhibition probably also occurred in the cell that fired the action potential but is hard to detect because of the potassium conductances (and resulting hyperpolarization) activated by the action potential in that cell. Reprinted with permission from Miles (1990).

Different excitatory cells receive different excitation from an external source. Principal cells are modeled as simple integrate-and-fire neurons, which have excitatory input current (exc), inhibitory input current (GABA), and an afterhyperpolarization (AHP) current. The voltage Vj of neuron j is defined by the following equation:

graphic file with name zns02309-6566-m01.jpg

Here, we use as parameters the average input resistance of CA3 cells (∼Rm = 33 MΩ) (Turner and Schwartzkroin, 1983), the membrane time constant (τm = 30 ms), and the threshold for firing (T = −50 mV). After each spike, voltage is reset instantaneously to the resting potential (Vrest = −65 mV). We use the following parameters: the steady excitatory current Iexc is constant (Aexc = 2 nA); the afterhyperpolarization current (IAHP) has AAHP = −2 nA and τAHP = 17 ms (duration); the inhibitory current IGABA has AGABA= −20 nA and τGABA = 3 ms (duration).

For the simulation, we considered the excitatory input (Iexc) constant over time (see Results for rationale), whereas the other currents are modeled as an instantaneous rise followed by a linear decrease (for consideration of the case in which a component of excitation is rapid, see supplemental material, available at www.jneurosci.org).

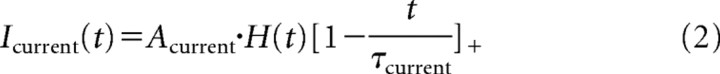graphic file with name zns02309-6566-m02.jpg

H(x) is the Heaviside function, where H(x) = 1 if x > 0 and 0 otherwise, and […]+ = xH(x) is the clipped linear function.

In the simulation of orientation selectivity, we consider that the excitatory current to a V1 neuron is given by the following:

graphic file with name zns02309-6566-m03.jpg

where Ibasal is an excitatory current strong enough to produce a suprathreshold potential in all neurons; Imax is related to the image contrast, such that the larger the contrast, the larger Imax; G(θ0,θ,σ) is the orientation selectivity function given by the following:

graphic file with name zns02309-6566-m04.jpg

where θ0 is the angle with the maximum response and σ is the width of the selectivity function. Finally, ζ is a Gaussian random variable with SD = 0.3 and clipped in the interval −1 and 1. This represents the noise in the system.

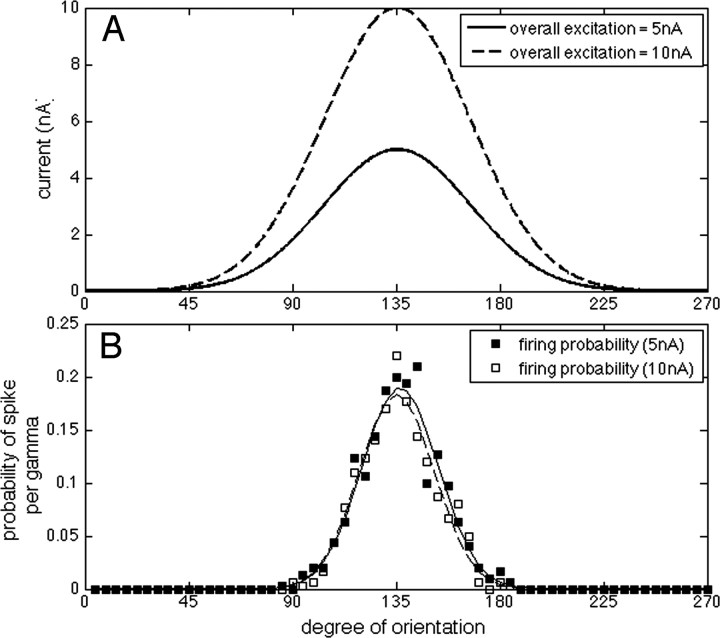
For these simulations, the width of the tuning curves is σ ≅ 32°, the values of Imax are 5 and 10 nA (as displayed in Fig. 6A), and Ibasal is 0.5 nA. All simulations and analysis here were made using Matlab (Mathworks).

Results

Our overall goal is to understand how networks with gamma frequency inhibition select which cells fire based on their varying excitatory drive. The simplified circuit that we consider here is shown in Figure 1A. Principal cells receive external input that is purely excitatory. When these cells fire, they excite an interneuron, which inhibits all the principal cells (feedback inhibition). When this inhibition declines sufficiently, firing again occurs. This process repeats indefinitely, thereby generating a gamma frequency oscillation. Experimental results (Miles, 1990) show that feedback inhibition is very rapid, as shown in Figure 1B (we use the value of 3 ms). The use of a single interneuron in our simulations is a reasonable approximation because of several properties of interneuron networks: there is enormous convergence of principal cells onto these interneurons, enormous divergence of the feedback connections from interneurons to principal cells and electrical coupling among the interneurons (Buhl et al., 1994; Cobb et al., 1995; Galarreta and Hestrin, 1999; Tamás et al., 2000; Meyer et al., 2002). Furthermore, interneurons are sensitive enough to fire in response to input from only a single principal cell (Miles, 1990; Gulyás et al., 1993; Marshall et al., 2002; Silberberg and Markram, 2007). The circuit of Figure 1A was simulated as an integrate-and-fire network (see Materials and Methods). The relevant currents are the excitatory input, the feedback inhibition and a brief AHP after each action potential.

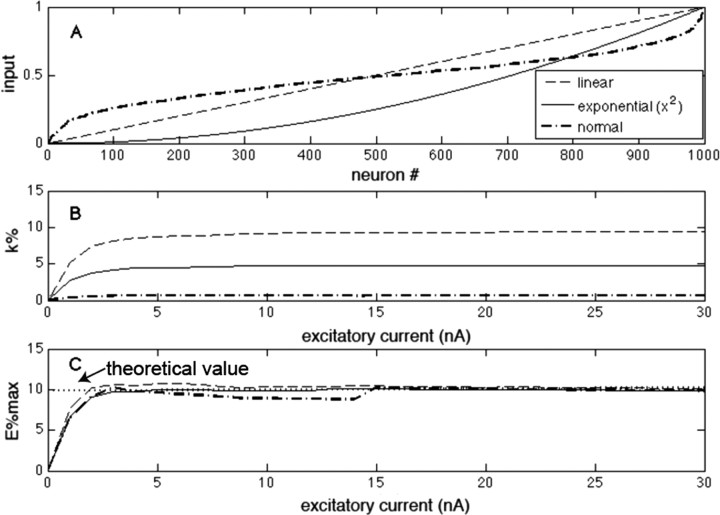
A common framework for describing networks with feedback inhibition is as a winner-take-all process. Because it is clear that there is more than one winner in biological networks, the term k-winner-take-all is often used to denote that there are k winners. Under a given set of conditions, this is certainly true, but to be a robust description of the network computation, k should be invariant not only for multiple values of excitation and inhibition but also for different distributions of input excitation (excitation is considered here to be constant over time) (for a similar analysis with time-varying excitation, see supplemental material, available at www.jneurosci.org). To examine whether this is the case, we changed the ratio of excitation and inhibition in our integrate-and-fire model; we also varied the distribution of inputs to different principal cells (Fig. 2A). We found that the number of winners (k) is invariant over a large range of excitation but varies strongly with the distribution of excitation (Fig. 2B). Thus, the concept that a network can robustly select a fixed number of winners is not correct.

Figure 2.

Figure 2.

Open in a new tab

Comparison of a k-winner-take-all description with an E%-max winner-take-all description. A, Graph of the input excitation of 1000 different neurons in the network. The minimum excitation is always zero, and the values are relative to the cell with maximal excitation (excitatory current). Neurons here are ranked in terms of increasing excitation. Several distributions are plotted (same legend for A–C). B, The number of winners (k%) as excitation is scaled up. C, E%-max as excitation is scaled up. The dotted line in C indicates the theoretical value derived in Results.

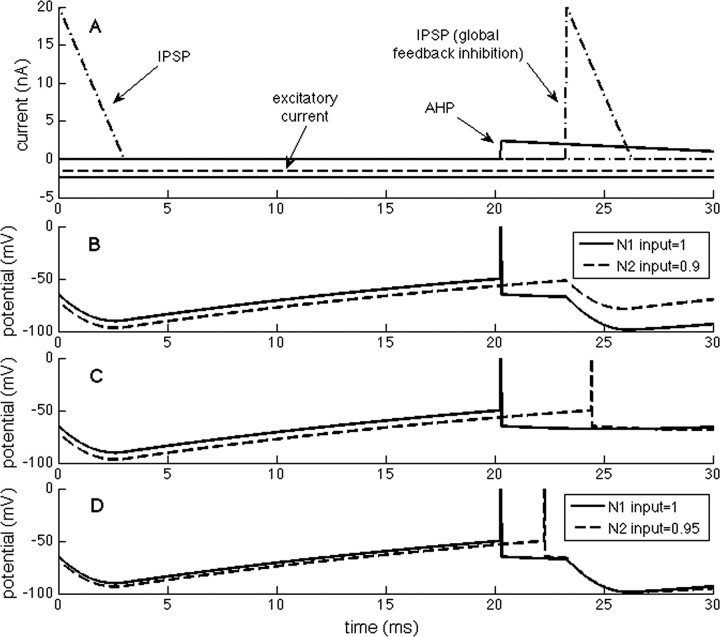
To identify a more robust description of the selection process, we considered two cells, N1 and N2, that have only slightly different (10%) excitatory input. The traces in Figure 3B start with the inhibition initiated during the previous gamma cycle. As the IPSP decays with the membrane time constant, N1 reaches threshold first and fires (resulting immediately in an AHP in N1). However, because the IPSP continues to decline, other cells may fire during the brief “vulnerable period” before feedback inhibition arrives. In the example shown in Figure 3, N2, which has only 10% less excitation than N1, continues to depolarize because of decay of the IPSP and almost reaches threshold. However, before it does so, feedback inhibition arrives and prevents N2 from reaching threshold. If feedback inhibition had not arrived, N2 would have fired after a short additional delay (Fig. 3C). However, if excitation of N2 was only 5% less than N1, the depolarization during the vulnerable period reaches threshold, and thus both cells fire (Fig. 3D). This simple example shows that the network can select which cells fire based on small (10%) differences in excitation and that understanding the events during the vulnerable period is crucial.

Figure 3.

Figure 3.

Open in a new tab

Events that govern the selection process in a network with feedback inhibition. One neuron (N2) receives 10% less excitation than the other (N1). A, The component currents of N1 and N2 (solid/dashed lines). At the left, there is onset of inhibition because of the previous gamma cycle (details not shown). B, As inhibition decays, threshold is reached in N1, causing an action potential. This is followed by an AHP in N1 and feedback inhibition in both cells (with a delay of 3 ms). During this delay, the decline of inhibition in N2 is not sufficient for that cell to reach threshold. C, If the feedback inhibition is prevented, N2 fires. D, If the excitation of N2 is only 5% less than N1, N2 fires.

To quantify the processes during the vulnerable period, we define the effective excitation (E) of a given cell as the excess of voltage above threshold (E = VE − T), where VE is the sum of the excitatory input and intrinsic afterpotentials that result from previous firing. If E < 0, a cell will never fire; if E > 0, cells may fire if the inhibition allows. The cell that fires first during a gamma cycles has excitation Emax; as inhibition declines during the gamma cycle, the last neuron to fire during the vulnerable period has lower excitation, Emin. E%-max is the percentage difference between this lower excitation and that of the maximal excitation. To examine the robustness of E%-max in defining which cells fire, we determined E%-max under various conditions in our integrate-and-fire network. Figure 2C shows that neither scaling the excitation (>10-fold) nor changing the distribution of excitation strongly affected E%-max. Thus, the E%-max description robustly captures a fundamental aspect of the computation.

Analytical estimation of E%-max and its determinants

We next sought to determine what properties of the network determine E%-max. As shown in Figure 1B, firing creates a feedback IPSP in all principal cells of the network. The fall of the IPSP occurs with the membrane time constant, creating a “ramp” in the membrane potential of the principal cell that interacts with synaptic excitation. As the ramp declines, the cell with maximal excitation fires and triggers feedback inhibition. At this moment (t*; defined relative to the onset of inhibition), the following condition is met relating the voltage threshold (T; defined relative to resting potential), the EPSP (VEmax) of the cell, and the IPSP (VGABA):

graphic file with name zns02309-6566-m05.jpg

Therefore, the condition to fire can be written as follows:

graphic file with name zns02309-6566-m06.jpg

where we define suprathreshold excitation “E” as the difference between the EPSP and threshold as follows:

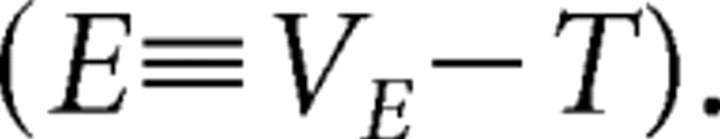graphic file with name zns02309-6566-m07.jpg

Our goal is to determine the minimal excitation (Emin) necessary for a second cell to fire in the same gamma cycle. Consider that the difference between excitations is

graphic file with name zns02309-6566-m08.jpg

Since the feedback inhibition takes d seconds to occur, the second cell will fire if at most

graphic file with name zns02309-6566-m09.jpg

Considering that the firing period t* is much larger than the delay (d), we can make a linear approximation as follows:

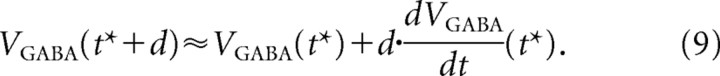graphic file with name zns02309-6566-m10.jpg

The inhibitory component of the potential is a consequence of the integration of the fast IGABA current across the membrane. We consider that IGABA(t) = 0 by the time the neurons are approaching to their thresholds; therefore, VGABA is decaying exponentially with the membrane time constant τm as follows:

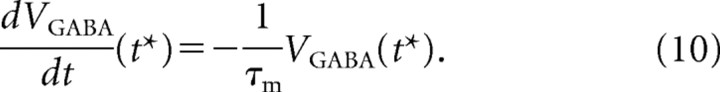graphic file with name zns02309-6566-m11.jpg

Combining Equation 6 with Equations 7, 9, and 10 results in the following:

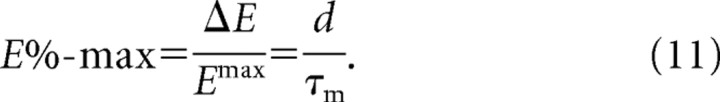graphic file with name zns02309-6566-m12.jpg

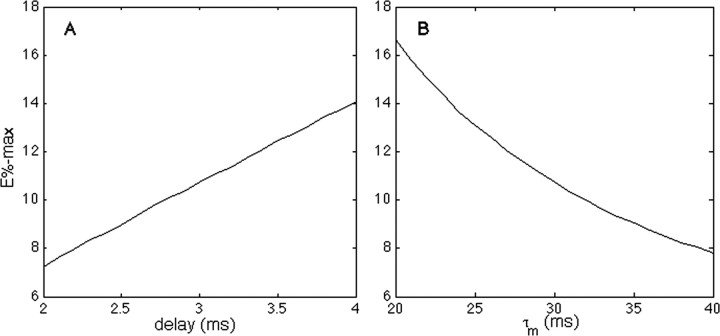
According to Equation 11, E%-max increases with d and decreases with the membrane time constant. Figure 2C, dotted line, shows that Equation 11 correctly predicts the magnitude of E%-max, as determined in our integrate-and-fire network. In Figure 4, the same network is used to verify that E% depends linearly on the delay of feedback inhibition and inversely on the membrane time constant, in accord with Equation 11.

Figure 4.

Figure 4.

Open in a new tab

The effect of the delay of feedback inhibition (A) and membrane time constant (B) on E%-max.

E%-max rule: application to excitation and firing tuning in V1

The process by which gamma oscillations perform an E%-max computation means that the selection of which cells fire is inherently a network process and implies that there is not a direct relationship between the excitatory input and cell firing. Rather, whether a cell fires will depend on the excitation to other cells in the network. In most brain regions, input excitation has not been measured and so the above ideas cannot be related to experimental data. However, in the case of orientation cells of V1, both the orientation tuning of excitation (measured intracellularly) and the orientation tuning of spiking have been measured (Anderson et al., 2000; Carandini and Ferster, 2000; Monier et al., 2003). The results show that the tuning of firing is considerably narrower than the tuning of excitation and that this difference is contrast invariant (unaffected by the increased excitation produced by enhancing the contrast of the stimulus). There has been considerable interest in understanding the mechanism of this invariance, and many models have been proposed (for review, see Ferster and Miller, 2000; Teich and Qian, 2006). However, although both intracellular and field recordings indicate the presence of gamma oscillations (Gray and Singer, 1989; König et al., 1996; Singer and Gray, 1995; Volgushev et al., 2003; Fries et al., 2007) in V1, the specific role of the dynamic inhibition provided by gamma has not previously been considered. It was thus of interest to ask whether an E%-max computation can account for the observed differences in the tuning of excitation and firing.

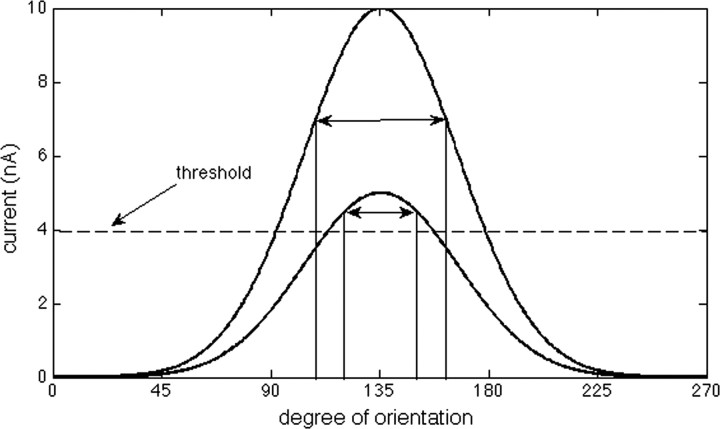
The tuning of excitation in V1 cells was studied by Carandini and Ferster (2000) and is illustrated in Figures 5 and 6A. Each cell responds maximally to some degree of orientation (around 135° for the graphs shown in Figs. 5, 6A), but the same cell also shows some level of excitation for a range of other orientations (between 45 and 225° for the examples here). Anderson et al. (2000) showed that the tuning of spiking is sharper than the tuning of excitation; specifically, the half-width at half-height of the tuning of spiking was around 23° compared with 38° for the EPSP. Importantly, this narrow tuning of spiking was not changed when the contrast of the visual stimuli was increased. As discussed by Carandini and Ferster (2000), feedforward models with fixed threshold are unable to reproduce this independence of contrast; in such models (Fig. 5), tuning can be sharpened because of a threshold for firing, a phenomenon termed the “iceberg” effect. However, an important property of this iceberg effect is that the sharpening is reduced by increasing the overall level of excitation (by increasing contrast).

Figure 5.

Figure 5.

Open in a new tab

Tuning changes produced by the iceberg effect. The bottom curve shows orientation tuning of excitation relative to threshold (dashed line). As shown in the bottom curve, the width of the tuning of firing (double arrow) can be quite narrow because only a few orientations are above threshold (the iceberg effect). However, if the overall level of excitation is scaled up (higher curve), as would occur if image contrast is enhanced, the tuning becomes broader, contrary to experimental observations.

To examine how gamma frequency inhibition affects orientation selectivity, we modified our integrate-and-fire network to have orientation-selective input to each principal cell. In these simulations, the network was composed of 100 neurons, each with slightly different optimal orientation (evenly spaced between 0 and 270°). E%-max was set at 10%. We ran the network for many gamma cycles using two levels of contrast (Fig. 6A). Figure 6B shows that the probability of spiking per gamma depended on stimulus orientation (300 trials). Similar to the experimental results (Anderson et al., 2000), the neurons in the simulated network displayed a sharper orientation tuning for spikes than for input excitation: the half-width at half-height of the excitation tuning is 37° (Fig. 6A), whereas the same measure for spike tuning is 16.5° (this value would be slightly higher if more noise was assumed). Importantly, the tuning of spikes was practically unchanged when the excitatory input was doubled (Fig. 6B). A selection process based on gamma frequency inhibition can thus account for the contrast invariance of orientation tuning.

We emphasize that we have kept this model as simple as possible to isolate the computational capabilities of feedback inhibition. Other forms of synaptic input (feedforward inhibition from both “on” and “off” cells; recurrent excitation) are necessary to account for the full complexities of the response of V1 cells, including the response to moving stimuli (Ferster and Miller, 2000).

Discussion

Almost all work to date on the functional role of gamma oscillations has focused on the production of synchronized firing (Bragin et al., 1995; Singer and Gray, 1995; Penttonen et al., 1998; Csicsvari et al., 2003). We argue that a second function of gamma, the selection of which cells fire, is equally important. It has been experimentally shown that only a fraction of cells fire on each gamma cycle (Senior et al., 2008), but the mechanism that determines which cells fire has been unclear. Our work indicates that this selection is a type of winner-take-all process that follows directly from the properties of the feedback inhibition that underlies gamma frequency oscillations.

We have sought to find a simple quantitative description of this winner-take-all process and have found that several descriptions are not correct. There is no single winner, and so the winner-take-all concept cannot be taken literally. Nor will a network determine a fixed number of winners, independent of the input distribution. We find, however, that a simple rule approximates the selection process: cells will fire if their suprathreshold excitation (E) is within E% of the cell that receives maximal excitation. We term this an E%-max winner-take-all-process. As shown in Figure 2C, E%-max holds over a considerable range as the excitatory inputs to the network are scaled relative to inhibition. Furthermore, E%-max is not altered by changing the distribution of excitation in the different cells (relative to the cell with maximal excitation). Thus, the E%-max computation is robust. Because E%-max rule does not depend on the exact ratio of excitation to inhibition, it can be applied to cases in which this ratio is not known. The companion study (de Almeida et al., 2009) applies the rule to calculate properties of hippocampal place fields. In contrast to previous work (Rolls et al., 2006), in which the percentage of cells with place fields was used as a way to arbitrarily set inhibition, the E%-max rule allows the calculation of this percentage from theoretical considerations (without knowing the exact value of inhibition), which can then be compared with the observed value.

Determinants of E%-max

We have shown by simulation and theory that E%-max is determined by the ratio of the delay of feedback inhibition (d) to the membrane time constant (τm). This functional dependence can be understood intuitively as follows (see also Fig. 3). When gamma-mediated inhibition is maximal, cells will be below threshold. The gradual decay of inhibition creates a ramp, which can be view as “searching” for the neuron with maximal excitation; this will be the first cell to fire and trigger feedback inhibition (Miles, 1990; Gulyás et al., 1993; Marshall et al., 2002). This inhibition occurs within 2–3 ms, and it is this delay that creates a vulnerable period during which cells with less than maximal excitation can fire. The more inhibition declines during the vulnerable period, the more likely it is that cells with less inhibition will fire: thus selectivity decreases as the delay increases. Selectivity is also decreased if the decay of inhibition (membrane time constant) becomes faster. Based on experimental values for d and τm in the hippocampus, we estimate that E%-max is in the range of 5–15%. This is a small fraction of excitation and indicates that the selection process can make fine discriminations.

We emphasize that the rules we have developed are meant only as a first-order approximation and that the operation of feedback networks will depend on additional factors that we have not taken into consideration. These include the variability of delays in feedback inhibition, the opening kinetics of inhibitory and excitatory channels, and the limited spatial spread of feedback inhibition in the network. Furthermore, the excitatory input to inhibitory cells may often be enhanced by convergent inputs from multiple principal cells, a summation process that we have not modeled. In most of our calculations, we have assumed that excitation varies slowly with respect to gamma. This assumption may be valid when the stimulus is slowly changing, but may be invalid when a network receives a brief pulse of synchronized input. In the supplemental material (available at www.jneurosci.org), we examine the case in which excitation has both steady and fast components and show that the E%-max rule and Equation 11 still apply. Another assumption in our calculations is the choice of a fast AHP. Different cell types have different duration afterpotentials, often depending on neuromodulatory state (Storm, 1987, 1989). Moreover, in some cells, the afterpotential can be depolarizaing rather than hyperpolarizing (Storm, 1989; Andrade, 1991; Araneda and Andrade, 1991; Caeser et al., 1993). These afterpotentials will contribute to the suprathreshold excitation of the cell. Under these conditions, E%-max can still be usefully applied to determine which cells fire, so long as it is understood that both internal and external processes contribute to the effective excitation. Indeed, afterpotentials may account for important properties of firing. For instance, a long AHP would prevent a cell from firing on sequential gamma cycles, even if the external excitatory drive stays constant. Alternatively, if there is an afterdepolarization, a cell that fired once would be particularly likely to fire again, a process that may underlie working memory (Lisman and Idiart, 1995; Klink and Alonso, 1997).

Implications for neural computation

Because analysis of spiking in functional circuits is generally done with extracellular recording, the tuning of the EPSP is usually not known. However, in the case of orientation-selective cells of V1, intracellular recordings have been achieved. Orientation selectivity appears to depend on two mechanisms: a process of connectivity, which makes the input EPSP somewhat orientation selective (Reid and Alonso, 1995), and a second process dependent on inhibition (Sillito, 1975; Troyer et al., 1998; Carandini and Ferster, 2000). This second mechanism makes the orientation tuning of spiking narrower than that of the EPSP. Moreover, this narrowing is not affected by scaling up the excitation, a finding inconsistent with models based on fixed inhibition. Consequently, the narrowing of tuning cannot be explained by the iceberg effect (Fig. 5). Intracellular recordings provide direct evidence for gamma frequency inhibition in orientation-sensitive V1 cells (Volgushev et al., 2003). We show here (Fig. 6) that an E%-max computation produced by such oscillations can explain why the orientation tuning of spiking is narrower than that of the EPSP and why this difference is contrast invariant. Thus, there will be orientations in which a cell receives substantial excitation (sufficient to make the cell fire in the absence of inhibition) but in which firing is suppressed by feedback inhibition triggered by cells that that are slightly more excited by the stimulus.

A second system in which the E%-max winner-take-all computation is likely to be important is the formation of place cells in the hippocampus (de Almeida et al., 2009). The input to place cells is from grid cells of the entorhinal cortex, which are active (with spatial periodicity), over broad regions of the environment. Nevertheless, hippocampal cells are active only in very restricted regions of the environment. We show in a companion study (de Almeida et al., 2009) that, despite the broad excitation, the E%-max mechanism can select winners that are only slightly more excited than other cells in the network and that cells are winners in a relatively small region of the environment, thereby accounting for their place cell properties.

More generally, the winner-take-all function (and the specific E%-max form considered here) requires a change in the conceptual understanding of how firing is controlled. According to textbook accounts, firing can be understood as a single-cell property; firing rate is determined by how far the net excitation is above threshold. Based on this, if excitation x causes firing, excitation 2x in another context should also cause firing. However, this is not necessarily correct in networks with feedback inhibition. If, for example there are other cells in the second context that have 3x excitation, the cell with 2x excitation may not be among the winners. This simple example demonstrates that firing in networks with winner-take-all gamma-frequency inhibition cannot be derived from the excitation of a given cell, but is rather a result of a competitive network computation in which all cells must be considered.

Footnotes

This work was supported by National Institute of Mental Health Grant MH060450, National Institute of Neurological Disorders and Stroke Grant NS27337, and European Commission Project 217148. M.I. and L.d.A. acknowledge partial financial support from Brazilian agencies Conselho Nacional de Desenvolvimento Científico e Tecnológico and Coordenação de Aperfeiçoamento de Pessoal de Nível Superior. We thank Ole Jensen and Sridhar Raghavachari for comments on this manuscript.

References

  1. Anderson JS, Lampl I, Gillespie DC, Ferster D. The contribution of noise to contrast invariance of orientation tuning in cat visual cortex. Science. 2000;290:1968–1972. doi: 10.1126/science.290.5498.1968. [DOI] [PubMed] [Google Scholar]
  2. Andrade R. Cell excitation enhances muscarinic cholinergic responses in rat association cortex. Brain Res. 1991;548:81–93. doi: 10.1016/0006-8993(91)91109-e. [DOI] [PubMed] [Google Scholar]
  3. Araneda R, Andrade R. 5-Hydroxytryptamine 2 and 5-hydroxytryptamine 1A receptors mediate opposing responses on membrane excitability in rat association cortex. Neuroscience. 1991;40:399–412. doi: 10.1016/0306-4522(91)90128-b. [DOI] [PubMed] [Google Scholar]
  4. Bartos M, Vida I, Jonas P. Synaptic mechanisms of synchronized gamma oscillations in inhibitory interneuron networks. Nat Rev Neurosci. 2007;8:45–56. doi: 10.1038/nrn2044. [DOI] [PubMed] [Google Scholar]
  5. Bragin A, Jandó G, Nádasdy Z, Hetke J, Wise K, Buzsáki G. Gamma (40–100 Hz) oscillation in the hippocampus of the behaving rat. J Neurosci. 1995;15:47–60. doi: 10.1523/JNEUROSCI.15-01-00047.1995. [DOI] [PMC free article] [PubMed] [Google Scholar]
  6. Buhl EH, Halasy K, Somogyi P. Diverse sources of hippocampal unitary inhibitory postsynaptic potentials and the number of synaptic release sites. Nature. 1994;368:823–828. doi: 10.1038/368823a0. [DOI] [PubMed] [Google Scholar]
  7. Caeser M, Brown DA, Gähwiler BH, Knöpfel T. Characterization of a calcium-dependent current generating a slow afterdepolarization of CA3 pyramidal cells in rat hippocampal slice cultures. Eur J Neurosci. 1993;5:560–569. doi: 10.1111/j.1460-9568.1993.tb00521.x. [DOI] [PubMed] [Google Scholar]
  8. Carandini M, Ferster D. Membrane potential and firing rate in cat primary visual cortex. J Neurosci. 2000;20:470–484. doi: 10.1523/JNEUROSCI.20-01-00470.2000. [DOI] [PMC free article] [PubMed] [Google Scholar]
  9. Cobb SR, Buhl EH, Halasy K, Paulsen O, Somogyi P. Synchronization of neuronal activity in hippocampus by individual GABAergic interneurons. Nature. 1995;378:75–78. doi: 10.1038/378075a0. [DOI] [PubMed] [Google Scholar]
  10. Csicsvari J, Jamieson B, Wise KD, Buzsáki G. Mechanisms of gamma oscillations in the hippocampus of the behaving rat. Neuron. 2003;37:311–322. doi: 10.1016/s0896-6273(02)01169-8. [DOI] [PubMed] [Google Scholar]
  11. de Almeida L, Idiart M, Lisman JE. The input–output transformation of the hippocampal granule cells: from grid cells to place fields. J Neurosci. 2009;29:7504–7512. doi: 10.1523/JNEUROSCI.6048-08.2009. [DOI] [PMC free article] [PubMed] [Google Scholar]
  12. Eckhorn R, Bauer R, Jordan W, Brosch M, Kruse W, Munk M, Reitboeck HJ. Coherent oscillations: a mechanism of feature linking in the visual cortex? Multiple electrode and correlation analyses in the cat. Biol Cybern. 1988;60:121–130. doi: 10.1007/BF00202899. [DOI] [PubMed] [Google Scholar]
  13. Ferster D, Miller KD. Neural mechanisms of orientation selectivity in the visual cortex. Annu Rev Neurosci. 2000;23:441–471. doi: 10.1146/annurev.neuro.23.1.441. [DOI] [PubMed] [Google Scholar]
  14. Fisahn A, Pike FG, Buhl EH, Paulsen O. Cholinergic induction of network oscillations at 40 Hz in the hippocampus in vitro. Nature. 1998;394:186–189. doi: 10.1038/28179. [DOI] [PubMed] [Google Scholar]
  15. Fries P, Nikolić D, Singer W. The gamma cycle. Trends Neurosci. 2007;30:309–316. doi: 10.1016/j.tins.2007.05.005. [DOI] [PubMed] [Google Scholar]
  16. Galarreta M, Hestrin S. A network of fast-spiking cells in the neocortex connected by electrical synapses. Nature. 1999;402:72–75. doi: 10.1038/47029. [DOI] [PubMed] [Google Scholar]
  17. Gray CM, Singer W. Stimulus-specific neuronal oscillations in orientation columns of cat visual cortex. Proc Natl Acad Sci U S A. 1989;86:1698–1702. doi: 10.1073/pnas.86.5.1698. [DOI] [PMC free article] [PubMed] [Google Scholar]
  18. Gulyás AI, Miles R, Sík A, Tóth K, Tamamaki N, Freund TF. Hippocampal pyramidal cells excite inhibitory neurons through a single release site. Nature. 1993;366:683–687. doi: 10.1038/366683a0. [DOI] [PubMed] [Google Scholar]
  19. Jensen O, Kaiser J, Lachaux JP. Human gamma-frequency oscillations associated with attention and memory. Trends Neurosci. 2007;30:317–324. doi: 10.1016/j.tins.2007.05.001. [DOI] [PubMed] [Google Scholar]
  20. Klink R, Alonso A. Muscarinic modulation of the oscillatory and repetitive firing properties of entorhinal cortex layer II neurons. J Neurophysiol. 1997;77:1813–1828. doi: 10.1152/jn.1997.77.4.1813. [DOI] [PubMed] [Google Scholar]
  21. König P, Engel AK, Singer W. Integrator or coincidence detector? The role of the cortical neuron revisited. Trends Neurosci. 1996;19:130–137. doi: 10.1016/s0166-2236(96)80019-1. [DOI] [PubMed] [Google Scholar]
  22. Lisman JE, Idiart MA. Storage of 7 ± 2 short-term memories in oscillatory subcycles. Science. 1995;267:1512–1515. doi: 10.1126/science.7878473. [DOI] [PubMed] [Google Scholar]
  23. Mann EO, Paulsen O. Role of GABAergic inhibition in hippocampal network oscillations. Trends Neurosci. 2007;30:343–349. doi: 10.1016/j.tins.2007.05.003. [DOI] [PubMed] [Google Scholar]
  24. Marshall L, Henze DA, Hirase H, Leinekugel X, Dragoi G, Buzsáki G. Hippocampal pyramidal cell-interneuron spike transmission is frequency dependent and responsible for place modulation of interneuron discharge. J Neurosci. 2002;22(RC197):1–5. doi: 10.1523/JNEUROSCI.22-02-j0001.2002. [DOI] [PMC free article] [PubMed] [Google Scholar]
  25. Meyer AH, Katona I, Blatow M, Rozov A, Monyer H. In vivo labeling of parvalbumin-positive interneurons and analysis of electrical coupling in identified neurons. J Neurosci. 2002;22:7055–7064. doi: 10.1523/JNEUROSCI.22-16-07055.2002. [DOI] [PMC free article] [PubMed] [Google Scholar]
  26. Miles R. Synaptic excitation of inhibitory cells by single CA3 hippocampal pyramidal cells of the guinea-pig in vitro. J Physiol. 1990;428:61–77. doi: 10.1113/jphysiol.1990.sp018200. [DOI] [PMC free article] [PubMed] [Google Scholar]
  27. Monier C, Chavane F, Baudot P, Graham LJ, Frégnac Y. Orientation and direction selectivity of synaptic inputs in visual cortical neurons: a diversity of combinations produces spike tuning. Neuron. 2003;37:663–680. doi: 10.1016/s0896-6273(03)00064-3. [DOI] [PubMed] [Google Scholar]
  28. Penttonen M, Kamondi A, Acsády L, Buzsáki G. Gamma frequency oscillation in the hippocampus of the rat: intracellular analysis in vivo. Eur J Neurosci. 1998;10:718–728. doi: 10.1046/j.1460-9568.1998.00096.x. [DOI] [PubMed] [Google Scholar]
  29. Reid RC, Alonso JM. Specificity of monosynaptic connections from thalamus to visual cortex. Nature. 1995;378:281–284. doi: 10.1038/378281a0. [DOI] [PubMed] [Google Scholar]
  30. Rolls ET, Stringer SM, Elliot T. Entorhinal cortex grid cells can map to hippocampal place cells by competitive learning. Network. 2006;17:447–465. doi: 10.1080/09548980601064846. [DOI] [PubMed] [Google Scholar]
  31. Senior TJ, Huxter JR, Allen K, O'Neill J, Csicsvari J. Gamma oscillatory firing reveals distinct populations of pyramidal cells in the CA1 region of the hippocampus. J Neurosci. 2008;28:2274–2286. doi: 10.1523/JNEUROSCI.4669-07.2008. [DOI] [PMC free article] [PubMed] [Google Scholar]
  32. Silberberg G, Markram H. Disynaptic inhibition between neocortical pyramidal cells mediated by Martinotti cells. Neuron. 2007;53:735–746. doi: 10.1016/j.neuron.2007.02.012. [DOI] [PubMed] [Google Scholar]
  33. Sillito AM. The contribution of inhibitory mechanisms to the receptive field properties of neurones in the striate cortex of the cat. J Physiol. 1975;250:305–329. doi: 10.1113/jphysiol.1975.sp011056. [DOI] [PMC free article] [PubMed] [Google Scholar]
  34. Singer W, Gray CM. Visual feature integration and the temporal correlation hypothesis. Annu Rev Neurosci. 1995;18:555–586. doi: 10.1146/annurev.ne.18.030195.003011. [DOI] [PubMed] [Google Scholar]
  35. Soltesz I, Deschênes M. Low- and high-frequency membrane potential oscillations during theta activity in CA1 and CA3 pyramidal neurons of the rat hippocampus under ketamine-xylazine anesthesia. J Neurophysiol. 1993;70:97–116. doi: 10.1152/jn.1993.70.1.97. [DOI] [PubMed] [Google Scholar]
  36. Storm JF. Action potential repolarization and a fast after-hyperpolarization in rat hippocampal pyramidal cells. J Physiol. 1987;385:733–759. doi: 10.1113/jphysiol.1987.sp016517. [DOI] [PMC free article] [PubMed] [Google Scholar]
  37. Storm JF. An after-hyperpolarization of medium duration in rat hippocampal pyramidal cells. J Physiol. 1989;409:171–190. doi: 10.1113/jphysiol.1989.sp017491. [DOI] [PMC free article] [PubMed] [Google Scholar]
  38. Tamás G, Buhl EH, Lörincz A, Somogyi P. Proximally targeted GABAergic synapses and gap junctions synchronize cortical interneurons. Nat Neurosci. 2000;3:366–371. doi: 10.1038/73936. [DOI] [PubMed] [Google Scholar]
  39. Teich AF, Qian N. Comparison among some models of orientation selectivity. J Neurophysiol. 2006;96:404–419. doi: 10.1152/jn.00015.2005. [DOI] [PubMed] [Google Scholar]
  40. Troyer TW, Krukowski AE, Priebe NJ, Miller KD. Contrast-invariant orientation tuning in cat visual cortex: thalamocortical input tuning and correlation-based intracortical connectivity. J Neurosci. 1998;18:5908–5927. doi: 10.1523/JNEUROSCI.18-15-05908.1998. [DOI] [PMC free article] [PubMed] [Google Scholar]
  41. Turner DA, Schwartzkroin PA. Electrical characteristics of dendrites and dendritic spines in intracellularly stained CA3 and dentate hippocampal neurons. J Neurosci. 1983;3:2381–2394. doi: 10.1523/JNEUROSCI.03-11-02381.1983. [DOI] [PMC free article] [PubMed] [Google Scholar]
  42. Volgushev M, Pernberg J, Eysel UT. Gamma-frequency fluctuations of the membrane potential and response selectivity in visual cortical neurons. Eur J Neurosci. 2003;17:1768–1776. doi: 10.1046/j.1460-9568.2003.02609.x. [DOI] [PubMed] [Google Scholar]

Articles from The Journal of Neuroscience are provided here courtesy of Society for Neuroscience

RESOURCES