Skip to main content
PMC home page
Proceedings of the National Academy of Sciences of the United States of America logoLink to Proceedings of the National Academy of Sciences of the United States of America
. 1998 May 26;95(11):6103–6107. doi: 10.1073/pnas.95.11.6103

Free energy of burying hydrophobic residues in the interface between protein subunits

Beatrice Vallone 1, Adriana E Miele 1, Paola Vecchini 1, Emilia Chiancone 1, Maurizio Brunori 1,*
PMCID: PMC27592  PMID: 9600924

Abstract

We have obtained an experimental estimate of the free energy change associated with variations at the interface between protein subunits, a subject that has raised considerable interest since the concept of accessible surface area was introduced by Lee and Richards [Lee, B. & Richards, F. M. (1971) J. Mol. Biol. 55, 379–400]. We determined by analytical ultracentrifugation the dimer–tetramer equilibrium constant of five single and three double mutants of human Hb. One mutation is at the stationary α1β1 interface, and all of the others are at the sliding α1β2 interface where cleavage of the tetramer into dimers and ligand-linked allosteric changes are known to occur. A surprisingly good linear correlation between the change in the free energy of association of the mutants and the change in buried hydrophobic surface area was obtained, after corrections for the energetic cost of losing steric complementarity at the αβ dimer interface. The slope yields an interface stabilization free energy of −15 ± 1.2 cal/mol upon burial of 1 Å2 of hydrophobic surface, in very good agreement with the theoretical estimate given by Eisenberg and McLachlan [Eisenberg, D. & McLachlan, A. D. (1986) Nature (London) 319, 199–203].

This paper deals with the experimental determination of the free energy change associated with modification of the surface buried in a protein–protein contact, a point of general interest in understanding stability and recognition in proteins. Since the pioneering work of Lee and Richards (1), a wealth of experimental and theoretical investigations have attempted to understand and quantify the forces stabilizing protein oligomers and complexes. After Chothia (2, 3) drew attention to the significance of the surface buried at an interface, other investigators emphasized shape complementarity (4), residue propensities (5), and the relative contribution of polar interactions and hydrophobic effects to the overall ΔG0 in protein–protein association (6–8). Experimental studies have used different proteins to understand the effect of a point mutation on enzyme–inhibitor (9, 10) or antibody–antigen complexes (11–13), as well as subunit interactions in mutants of human Hb (14). These studies led to the conclusion that both types of weak interactions play a role, and that Atom Solvation Parameters derived from partition coefficients can be used to evaluate the stabilization energy at protein interfaces (8, 15–17).

Questions arise whether the theoretical studies can be a guideline in the analysis and design of experiments with a resolution beyond the qualitative prediction of results and how far values obtained from physico-chemical considerations can be useful in protein engineering by mutagenesis. Although it is recognized that buried hydrophobic surface contributes to the stability of a protein–protein contact, theoretical estimates of the free energy gain associated with burial of 1 Å2 of hydrophobic surface are variable and range between 4 and 32.5 cal/mol (see ref. 16 for a recent review). We have addressed this point experimentally by using the dimer–tetramer association of human Hb mutants.

By analytical ultracentrifuge, we have determined the equilibrium constant for the 2αβ → (αβ)2 association for five single and three double mutants of human HbCO. The mutations are all at the α1β2 interface (Fig. 1) except one at the α1β1 interface, which has a larger number of contacts and is unchanged in the T → R allosteric transition (14, 18–20). The changes in association free energy relative to HbA have been correlated with changes in the buried surface area due to mutations, to dissect the contribution of the polar and hydrophobic contacts in the stabilization of the tetramer. Taking a +1.5 kcal/mol complementarity cost associated with each mutation, we found that the Δ(ΔG0) is linearly correlated for all of the mutants with the change in the buried hydrophobic surface area, yielding a value of −15 ± 1.2 cal/mol⋅Å2 for stabilization of the subunit interface. This experimental estimate is in good agreement with the work of Eisenberg and McLachlan (15) and provides a basis for further experiments on protein–protein interaction and stability.

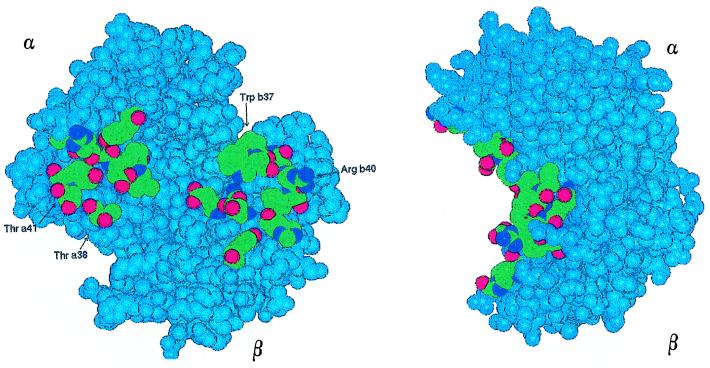
Figure 1.

Figure 1

Open in a new tab

Space filling model of HbA CO (25), with a view of the α1β2 interface in two orthogonal projections. α and β chains, colored in light blue, are respectively at the upper left and lower right of the left view. Amino acids belonging to the interface are indicated following their atom specification, i.e., C in green, O in red, and N in deep blue. Residues mutated in this work are labeled with their names. Hemes are not highlighted.

MATERIALS AND METHODS

Site-directed mutants of HbA were produced in Escherichia coli and were purified as described (21, 22). Reagents were of analytical grade. Ultracentrifuge experiments were carried out with a Beckman Optima XL-A instrument at 10°C in 0.1 M Bis–Tris⋅HCl buffer at pH 7.0 on proteins in the reduced-CO bound form. Sedimentation velocities were reduced to s20,w according to standard procedures. The value of s20,w, a weight average property, was used to calculate the weight fractions of tetramer and dimer because these species are in rapid equilibrium (23). Details of the calculations are given in ref. 24. The dimer–tetramer association constant (K2,4) was calculated from the mass law expression according to Gilbert and Gilbert (25).

Molecular modeling was performed by using the Discover/Insight and Brugel packages (26) on a Silicon Graphics workstation. We simulated the point mutation(s) starting from the known structure of the CO derivative of HbA (27). All of the side chains could be accommodated by using allowed rotamers, and only minor adjustments of surrounding amino acids were introduced by the subsequent minimization, with rms values ranging from 0.02 to 0.06 Å. We were confident on the very small movement of neighboring amino acids, even in the case of smaller to larger side chain replacement, because of the small Biso factor (<Biso> = 32) of these residues in the starting crystallographic structure (27). This mean value is really good, considering the position of the residues in an interface accessible to solvent. By using a probe with a radius of 1.4 Å (28), we computed, for the dimer and the tetramer, the water-accessible surface of the mutated side chain(s) and of the corresponding residue(s) in wild-type (wt) HbA, separating the contribution of the hydrophobic (C), polar (N/O), and charged (N+) atoms (Fig. 1). For each protein, we subtracted the value computed for the tetramer from that computed for the dimers, thereby obtaining an estimate of the contribution of that residue to the surface buried on tetramer formation. This information was used to compute the Δ(ΔSurface) in Å2 for each mutant. Computation of the atomic surface area was carried out with two programs: Survol (26) and Surface (CCP4 Suite; refs. 28 and 29). Both programs use an implementation of the Voronoi method with different sets of atomic radii. The outputs of the two simulations agreed within 10%.

RESULTS

Measurement of Dimer–Tetramer Equilibrium Constant.

The dimer–tetramer association constants of HbA and of the eight mutants were calculated from sedimentation velocity experiments carried out over the concentration range from 1 to 40 μM. The constants are summarized in Table 1, which also indicates the interface involved and, for the α1β2 interface, whether the mutation is at the “hinge” or “switch” region (18). All of the mutants displayed some perturbation in the stability of the tetramer compared with wt HbA, with Δ(ΔG0) values that ranged from −1 kcal/mol to ≥3 kcal/mol. In the case of Hb βW37T (largely dimeric up to 40 μM), we report in Table 1 and in our plots a value of +3 kcal/mol, obtained by subtracting the Δ(ΔG0) observed for Hb αT38W from that of the double mutant Hb αT38W+βW37T (Table 1). This calculation assumes additivity in the effects of mutations at C3 in the α and β chains, which seems reasonable given that they are beyond the threshold of 7 Å for interaction to occur between mutated amino acids (9, 30, 31).

Table 1.

Summary of the mutants studied in this work

Hemoglobin
Interface
K2,4* (M−1) × 10−4
Δ(ΔG0)† kcal/mol
HbA 100 ± 25 0 ± 0.28
1 α38Thr → Trp + α103His → Val α1β2 (switch) + α1β1 (stationary) 550  ±  130 −0.96  ±  0.27
2 α38Thr → Trp α1β2 (switch) 400  ±  100 −0.78  ±  0.28
3 α38Thr → Trp + α41Thr → Arg α1β2 (switch) 340  ±  90 −0.68  ±  0.29
4 α103His → Val α1β1 (stationary) 70  ±  30 +0.2  ±  0.38
5 α41Thr → Arg α1β2 (switch) 13  ±  3 +1.14  ±  0.27
6 β40Arg → Thr α1β2 (hinge) 2.4  ±  0.4 +2.1  ±  0.23
7 α38Thr → Trp+β37Trp → Thr α1β2 (switch + hinge) 2.0  ±  0.5 +2.2  ±  0.28
8 β37Trp → Thr α1β2 (switch) fully dimer (<40 μM) +3
Open in a new tab

We report the interface where the mutation is located and, for the α1β2 interface, the indication of the “switch” or the “hinge” region (2). 

*

K2,4 is given as mean ± SD. 

†

Δ(ΔGi0) = ΔGm0 − ΔGwt0, where m and wt stand for mutant and wild-type Hb, respectively. The errors in Δ(ΔG0) were calculated following the error propagation theory (42) and in particular the formulas: q(x) ± δq = q(xbest) ± |dq(x)/dx|δx and q ± δq = (x − y) ± (δx + δy), where q(x) is a function of a variable measured with errors, δq, δx, and δy are the errors associated to q(x), x, and y, respectively, and dq(x)/dx is the first derivative of the function q(x) with respect to the variable x. 

Isolated α chains from wt HbA have a very small tendency to associate into dimers (32, 33). Reconstitution of Hb with α chains mutants that are more associated than wt (22) leads to a heterotetramer with enhanced stability (1–5 in Table 1). This is the case for Hb αT38W, stabilized by −0.78 kcal/mol relative to wt HbA, and also for the double mutants Hb αT38W+αH103V (stabilized by −0.96 kcal/mol) and Hb αT38W+αT41R (stabilized by −0.68 kcal/mol). Of the two Hbs containing mutated α chains that are largely monomeric (like wt α chains), Hb αH103V is only marginally destabilized (Δ(ΔG0) = +0.22 kcal/mol), whereas Hb αT41R is destabilized by +1.1 kcal/mol compared with wt HbA.

Hbs containing mutated β chains that proved less associated than the wt ones (unpublished data from this Laboratory) also were destabilized as heterotetramers (6–8 in Table 1); namely by +2.1 kcal/mol (Hb βR40T) and +3 kcal/mol (Hb βW37T). An additive effect is seen in the double mutant Hb αT38W+βW37T, given that Trp at position α38 increases association of the heterotetramer (22) but cannot fully compensate for the destabilizing effect of the βW37T mutation, leading to a Δ(ΔG0) of +2.2 kcal/mol.

Accessible Surface Area Variations.

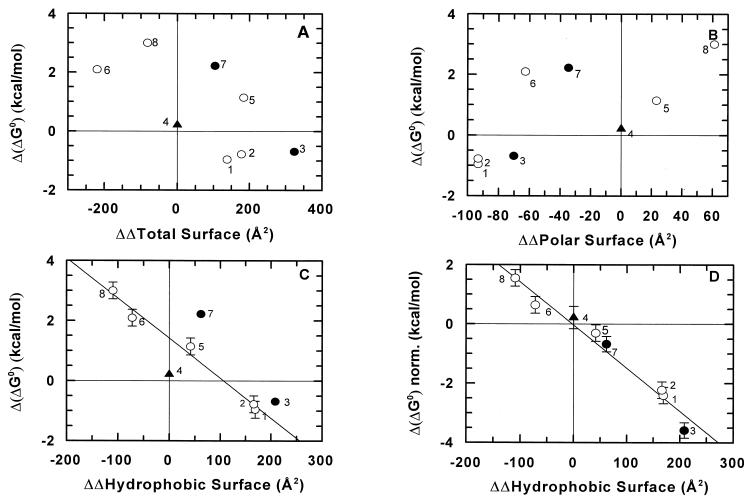
The Δ(ΔG0) values in Table 1 have been plotted against the calculated difference in buried surface (in Å2) at the α1β2 + α2β1 interface, according to polar/charged and hydrophobic components. The calculations, based on models of the mutants (see Materials and Methods), yielded the results shown in Fig. 2 A–C. Fig. 2 A and B show little or no correlation between the Δ(ΔG0) and the change in total or polar buried surface area. On the other hand, an approximate linear correlation may be seen in Fig. 2C for the single mutants of the α1β2 + α2β1 interface (1, 2, 5, 6, and 8 in Table 1) when the change in the hydrophobic buried surface area is considered.

Figure 2.

Figure 2

Open in a new tab

Plot of Δ(ΔG0) vs. ΔΔSurface calculated as detailed in the experimental section. The numbers in the four panels indicate the mutant to which they pertain (see Table 1). Open circles correspond to single mutants at the α1β2 interface (1, 2, 5, 6, and 8), and closed circles to double mutants (3 and 7); the filled triangle is the single mutant at the α1β1 interface (4). (D) A plot of Δ(ΔG0) vs. ΔΔ Surface calculated for the hydrophobic surface variation compared with wt HbA; these data were corrected for the complementarity cost of Δ(ΔG0) = +1.5 kcal/mol, taken twice for the mutants with two substitutions at the α1β2 interface (3 and 7). No complementarity cost correction was applied for the mutation at the α1β1 interface (mutant 1, second substitution, and mutant 4). Error bars correspond to the values given in Table 1.

No significant change in the dimer–tetramer equilibrium constant was expected upon mutating the α1β1 interface, given that this is a very stable contact and that dimerization involves disruption of the less extensive α1β2 interface (14, 19, 34, 35). It is therefore not surprising that mutation αH103V at α1β1 has essentially no effect within the limits of experimental errors (Table 1).

DISCUSSION

To estimate experimentally the free energy of burying hydrophobic surface in a protein–protein contact, we chose to modify the α1β2 interface of human Hb (Fig. 1), which is cleaved upon dissociation of the tetramer and which experiences large conformational changes associated to the allosteric transition (18–20). Examination of the natural human Hb variants (36) indicates that this contact is permissive with respect to a number of different amino acid substitutions associated with a perturbation of the dimer–tetramer equilibrium, without precluding protein folding and tetramer formation. Therefore, as expected, our interface mutants are synthesized and properly folded in a heterologous expression system. Determination of the equilibrium constant for dimer association of the carbon monoxide saturated derivative allows a quantification of the effect of each mutation on the stability of the surface.

As pointed out by several authors on the basis of analysis of the coordinates of proteins and protein complexes (3, 9, 37, 38), the parameter that dominates stabilization of molecular contacts is the hydrophobic surface buried within a given interface, without neglecting the role of salt bridges and hydrogen bonds, where present (19, 20). Hereby, we deal with the procedure followed to correlate the change in buried hydrophobic surface with the change in ΔG0 for the association of two αβ dimers into a Hb tetramer.

The plots in Fig. 2 A and B show that there is no simple correlation between the Δ(ΔG0) values for the α1β2 mutants and the change in the total or polar buried surface (ranging from −220 to +324 Å2 compared with wt HbA). Data on five single mutants at the α1β2 + α2β1 interface showed a linear correlation between Δ(ΔG0) for association and hydrophobic buried surface (Fig. 2C); the straight line through these points intercepts ΔΔSurface = 0 at Δ(ΔG0) = +1.5 kcal/mol. Therefore, we observed a destabilization of ≈1.5 kcal/mol for these mutants relative to wt Hb (without a change in the buried surface area); we assigned this value to the loss of complementarity, yielding a cost associated with each mutation at topological positions C3 or C6 in the two interfaces (α1β2 + α2β1). Examination of the HbCO model (18, 27) shows that three of the substitutions at C3 or C6 lead to the removal of one favorable electrostatic interaction per α1β2 interface, namely: (i) one between Nɛ of Trpβ37 and the carboxylate of Aspα94, (ii) one between the Argβ40 guanidinium group and the carbonyl oxygen of Thrα41; and (iii) one between the Thrα38 OH group and the carbonylic group of Hisβ97. In mutant αT41R, the mutated side chain is close to Argβ40, and we believe that, in this case, the complementarity cost reflects the introduction of one unfavorable interaction per α1β2 interface, rather than the loss of a favorable one.

It may be noticed that the complementarity cost as defined above is within the range of values (0.5–2 kcal/mol) attributed to the loss of one hydrogen bond in proteins (39). We are aware that cavity formation plays an important role in destabilization of proteins (40) and that estimating its contribution is not straightforward (38). In our mutants, the large to small substitutions seem to create open cavities accessible to the solvent; therefore, considering also the flexibility of the α1β2 and α2β1 interface (18, 19, 36), we presume that cavity formation in our mutants should not lead to a dramatic effect.

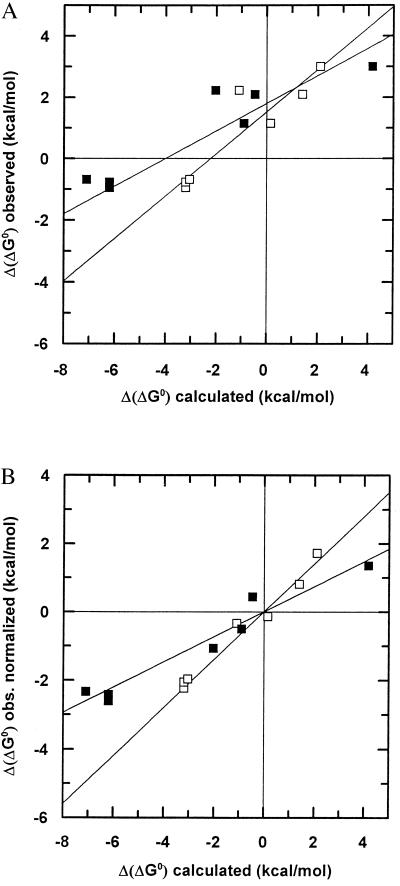
The observed Δ(ΔG0) for the mutants also was plotted as a function of the expected change in the free energy contribution calculated according to Eisenberg and McLachlan (15) or Pickett and Sternberg (17). Following these authors, the estimate was obtained multiplying the surface variations by the Atom Solvation Parameters, taking into consideration the contribution due to every type of atom; for the guanidinium group of arginines, the N+ value was divided by two. The resulting plots intercepted the y axis above 0 (respectively +1.6 and +1.3 kcal/mol; Fig. 3A), indicating that our estimate of the complementarity cost is not inconsistent with calculations based on Atom Solvation Parameters.

Figure 3.

Figure 3

Open in a new tab

(A) Plot of observed Δ(ΔG0) vs. calculated Δ(ΔG0) according to Eisenberg and McLachlan (empty squares) or Pickett and Sternberg (closed squares). (B) The same as A, corrected for the complementarity cost (see text).

If we subtract the complementarity cost of +1.5 kcal/mol from the Δ(ΔG0) values of all the mutants, underlying that in the double mutants this value should be doubled, we obtain a surprisingly good linear correlation of the stability data for all the mutants with the calculated changes in buried hydrophobic surface area (Fig. 2D). The slope yields a value of Δ(ΔG0) = −15 ± 1.2 cal/mol⋅Å2, which corresponds to the free energy gain upon burial of 1 Å2 of hydrophobic surface at this interface. A similar procedure may be applied to the results obtained by calculating the buried surface free energy change by using the parameters of Eisenberg and McLachlan (15) or Pickett and Sternberg (17), starting from the plot in Fig. 3A. In this case, we see from Fig. 3B of the same figure that a satisfactory linear relationship with the data for all eight mutants is obtained. With the parameters provided by Eisenberg and McLachlan (15), the slope is 0.75.

We therefore observed that the main free energy term that, in our mutants, controls variations in the association of αβ dimers into tetrameric HbCO is due to the change in solvent accessibility of the hydrophobic surface. The minor role of the polar contribution may be due to smaller variations in the exposure of polar/charged surface relative to the hydrophobic one, to smaller Atom Solvation Parameters associated with polar atoms as compared with hydrophobic atoms (15, 17), and/or to partial exposure of the polar/charged atoms in our mutants.

Concerning the quantitative agreement of our result with theoretical estimates, we noticed that the value of −15 ± 1.2 cal/mol⋅Å2 obtained from Fig. 2D for the hydrophobic surface variation is in excellent agreement with the value of −16.2 ± 2 cal/mol⋅Å2 estimated by Eisenberg and McLachlan (15) but is different from that reported by Pickett and Sternberg (17), which is −34.3 ± 3 cal/mol⋅Å2 per apolar C atom. In the latter work, a correction due to the different volume of solute and solvent was added (41). Moreover, it may be noticed that Juffer et. al (16) reported Eisenberg–McLachlan estimates to yield more consistent results.

In conclusion, we have observed that, in eight Hb mutants, perturbation of the stability of the α1β2 + α2β1 protein–protein interface is dominated by the hydrophobic component of nonbonding interactions. Our experimental estimate of −15 ± 1.2 cal/mol⋅Å2 of buried hydrophobic surface, in good agreement with calculations by Eisenberg and McLachlan (15), is taken as an experimental reference value to estimate stability in engineering protein–protein interfaces.

Acknowledgments

We express our thanks to Dr. K. Nagai (Medical Research Council, Cambridge, U.K.) for his learned advice in the preparation of the site-directed mutants and to Dr. W. A. Eaton (National Institutes of Health, Bethesda, MD) and Dr. P. Argos (European Molecular Biology Laboratory, Heidelberg, Germany) for their very useful suggestions. Dr. L. Nicolini and Mr. R. Dagai of the Istituto Superiore di Sanità (Rome, Italy) provided invaluable assistance in bacterial growth. We gratefully acknowledge Somatogen Inc. for permission to use the Hb expression system in E. coli. This work was partially supported by Ministero dell’Università della Ricerca Scientifica e Tecnologica of Italy (40%).

ABBREVIATION

wt

wild type

References

  • 1.Lee B, Richards F M. J Mol Biol. 1971;55:379–400. doi: 10.1016/0022-2836(71)90324-x. [DOI] [PubMed] [Google Scholar]
  • 2.Chothia C. Nature (London) 1974;248:338–339. doi: 10.1038/248338a0. [DOI] [PubMed] [Google Scholar]
  • 3.Janin J, Chothia C. J Biol Chem. 1990;265:16027–16030. [PubMed] [Google Scholar]
  • 4.Lawrence M C, Colman P M. J Mol Biol. 1993;234:946–950. doi: 10.1006/jmbi.1993.1648. [DOI] [PubMed] [Google Scholar]
  • 5.Jones S, Thornton J M. Proc Natl Acad Sci USA. 1996;93:13–20. doi: 10.1073/pnas.93.1.13. [DOI] [PMC free article] [PubMed] [Google Scholar]
  • 6.Xu D, Lin S L, Nussinov R. J Mol Biol. 1997;265:68–84. doi: 10.1006/jmbi.1996.0712. [DOI] [PubMed] [Google Scholar]
  • 7.Young L, Jernigan R L, Covell D G. Protein Sci. 1994;3:717–729. doi: 10.1002/pro.5560030501. [DOI] [PMC free article] [PubMed] [Google Scholar]
  • 8.Horton N, Lewis M. Protein Sci. 1992;1:169–181. doi: 10.1002/pro.5560010117. [DOI] [PMC free article] [PubMed] [Google Scholar]
  • 9.Schreiber G, Fersht A R. J Mol Biol. 1995;248:478–486. doi: 10.1016/s0022-2836(95)80064-6. [DOI] [PubMed] [Google Scholar]
  • 10.Laskowski M, Kato I, Ardelt W, Cook J, Denton A, Empie M W, Kohr W J, Park S J, Parks K, Schatzley B L. Biochemistry. 1987;26:202–221. doi: 10.1021/bi00375a028. [DOI] [PubMed] [Google Scholar]
  • 11.Walls P H, Sternberg M J E. J Mol Biol. 1992;228:277–297. doi: 10.1016/0022-2836(92)90506-f. [DOI] [PubMed] [Google Scholar]
  • 12.Chacko S, Silverton E, Kam-Morgan L, Smith-Gill S, Cohen G, Davies D. J Mol Biol. 1995;245:261–274. doi: 10.1006/jmbi.1994.0022. [DOI] [PubMed] [Google Scholar]
  • 13.Tulip W R, Varghese J N, Webster R G, Laver W G, Colman P M. J Mol Biol. 1992;227:149–159. doi: 10.1016/0022-2836(92)90688-g. [DOI] [PubMed] [Google Scholar]
  • 14.Ackers G K, Smith F R. Biophys J. 1986;49:155–165. doi: 10.1016/S0006-3495(86)83631-1. [DOI] [PMC free article] [PubMed] [Google Scholar]
  • 15.Eisenberg D, McLachlan A D. Nature (London) 1986;319:199–203. doi: 10.1038/319199a0. [DOI] [PubMed] [Google Scholar]
  • 16.Juffer A H, Eisenhaber F, Hubbard S J, Walter D, Argos P. Protein Sci. 1995;4:2499–2509. doi: 10.1002/pro.5560041206. [DOI] [PMC free article] [PubMed] [Google Scholar]
  • 17.Pickett S D, Sternberg M J E. J Mol Biol. 1993;231:825–839. doi: 10.1006/jmbi.1993.1329. [DOI] [PubMed] [Google Scholar]
  • 18.Baldwin J, Chothia C. J Mol Biol. 1979;129:175–220. doi: 10.1016/0022-2836(79)90277-8. [DOI] [PubMed] [Google Scholar]
  • 19.Perutz M F. Mechanisms of Cooperativity and Allosteric regulation in Proteins. Cambridge, UK: Cambridge Univ. Press; 1990. pp. 10–28. [DOI] [PubMed] [Google Scholar]
  • 20.Lesk A M, Janin J, Wodak S, Chothia C. J Mol Biol. 1985;183:267–270. doi: 10.1016/0022-2836(85)90219-0. [DOI] [PubMed] [Google Scholar]
  • 21.Hoffman S J, Looker D L, Roerich J M, Cozart P E, Durfus S L, Tedesco J L, Stetler G L. Proc Natl Acad Sci USA. 1990;87:8521–8525. doi: 10.1073/pnas.87.21.8521. [DOI] [PMC free article] [PubMed] [Google Scholar]
  • 22.Vallone B, Vecchini P, Cavalli V, Brunori M. FEBS Lett. 1993;324:117–122. doi: 10.1016/0014-5793(93)81375-a. [DOI] [PubMed] [Google Scholar]
  • 23.Chiancone E, Gilbert L M, Gilbert G A, Kellet G L. J Biol Chem. 1968;243:1212–1219. [PubMed] [Google Scholar]
  • 24.Gattoni M, Boffi A, Sarti P, Chiancone E. J Biol Chem. 1996;271:101130–10136. doi: 10.1074/jbc.271.17.10130. [DOI] [PubMed] [Google Scholar]
  • 25.Gilbert L M, Gilbert G A. Methods Enzymol. 1973;27:273–296. doi: 10.1016/s0076-6879(73)27014-3. [DOI] [PubMed] [Google Scholar]
  • 26.Delhaise P, Van Belle D, Bardiaux M, Alard P, Hamers P, Van Cutsem E, Wodak S. J Mol Graph. 1985;2:116–119. [Google Scholar]
  • 27.Baldwin J M. J Mol Biol. 1980;136:103–128. doi: 10.1016/0022-2836(80)90308-3. [DOI] [PubMed] [Google Scholar]
  • 28.Richards F M. Methods Enzymol. 1985;115:440–464. doi: 10.1016/0076-6879(85)15032-9. [DOI] [PubMed] [Google Scholar]
  • 29.CCP4-Collaborative Computational Project 4. Acta Crystallogr D. 1984;50:760–763. [Google Scholar]
  • 30.Horovitz A, Rigbi M. J Theor Biol. 1985;116:149–159. doi: 10.1016/s0022-5193(85)80135-1. [DOI] [PubMed] [Google Scholar]
  • 31.Wells J A. Biochemistry. 1990;29:8509–8517. doi: 10.1021/bi00489a001. [DOI] [PubMed] [Google Scholar]
  • 32.Bucci E, Fronticelli C, Chiancone E, Wyman J, Antonini E, Rossi Fanelli A. J Mol Biol. 1965;12:183–192. doi: 10.1016/s0022-2836(65)80292-3. [DOI] [PubMed] [Google Scholar]
  • 33.Valdes R, Ackers G K. J Biol Chem. 1977;252:74–81. [PubMed] [Google Scholar]
  • 34.Antonini E, Brunori M. Hemoglobin and Myoglobin in their Reactions with Ligands. Amsterdam: North Holland; 1971. pp. 150–180. [Google Scholar]
  • 35.Edelstein S J, Remar M J, Olson J S. J Biol Chem. 1970;270:4372–4382. [PubMed] [Google Scholar]
  • 36.Huisman T H J, Carver T H J, Efremov G A. Human Hemoglobin Variants. Atlanta, GA: The Sickle Cell Anemia Foundation; 1996. [Google Scholar]
  • 37.Rose G D, Geselowitz A R, Lesser G J, Lee R H, Zehfus M H. Science. 1985;229:834–838. doi: 10.1126/science.4023714. [DOI] [PubMed] [Google Scholar]
  • 38.Lee B. Protein Sci. 1993;2:733–738. doi: 10.1002/pro.5560020505. [DOI] [PMC free article] [PubMed] [Google Scholar]
  • 39.Serrano L, Kellis J T, Jr, Cann P, Matouschek A, Fersht A. J Mol Biol. 1991;224:783–804. doi: 10.1016/0022-2836(92)90562-x. [DOI] [PubMed] [Google Scholar]
  • 40.Hubbard S J, Argos P. Protein Sci. 1994;3:2194–2206. doi: 10.1002/pro.5560031205. [DOI] [PMC free article] [PubMed] [Google Scholar]
  • 41.Sharp K A, Nicholls A, Friedman R, Honig B. Biochemistry. 1991;30:9686–9697. doi: 10.1021/bi00104a017. [DOI] [PubMed] [Google Scholar]
  • 42.Taylor J R. An Introduction to Error Analysis: the Study of Uncertainties in Physical Measurements. Mill Valley, CA: Univ. Sci. Books; 1982. pp. 34–57. [Google Scholar]

Articles from Proceedings of the National Academy of Sciences of the United States of America are provided here courtesy of National Academy of Sciences

RESOURCES