Cataloguing the geometry of the human coronary arteries: a potential tool for predicting risk of coronary artery disease

Abstract

Background

The nonuniform distribution of atherosclerosis in the human vasculature suggests that local fluid dynamics or wall mechanics may be involved in atherogenesis. Thus certain aspects of vascular geometry, which mediates both fluid dynamics and wall mechanics, might be risk factors for coronary atherosclerosis. Cataloguing the geometry of normal human coronary arteries and its variability is a first step toward identifying specific geometric features that increase vascular susceptibility to the disease.

Methods

Images of angiographically normal coronary arteries, including 32 left anterior descending (LAD) and 35 right coronary arteries (RCA), were acquired by clinical biplane cineangiography from 52 patients. The vessel axes in end diastole were reconstructed and geometric parameters that included measures of curvature, torsion and tortuosity were quantified for the proximal, middle and distal segments of the arteries.

Results

Statistical analysis shows that (1) in the LAD, curvature, torsion and tortuosity are generally highest in the distal portion, (2) in the RCA, these parameters are smallest in the middle segment, (3) the LAD exhibits significant higher torsion than the RCA (P<0.005), and (4) >80% of the variability of coronary arterial geometry can be expressed in terms of two factors, one dominated by the curvature measures and tortuosity, and the other emphasizing the torsion parameters.

Conclusions

This study has comprehensively documented the normal arterial geometry of the LAD and RCA in end diastole. This information may be used to guide the identification of geometric features that might be atherogenic risk factors.

1. Introduction

It has been well documented through extensive epidemiological studies that human coronary atherosclerosis shows a non-uniform distribution in the coronary vasculature [1–4]. The discrepancy in disease occurrence exists not only among different coronary arteries [5], but along different sites of the same vessel as well [6]. This phenomenon cannot be explained by conventionally established risk factors, such as hypercholesterolemia, hypertension, diabetes, smoking, and male gender, which are all systemic and presumably influence the entire coronary vasculature and hence provide no mechanisms for disease localization.

The preferential disease distribution has led to a widespread speculation that local mechanical forces may play an important role in the initiation and localization of atherosclerosis. In fact, this speculation has been supported by ample evidence gathered from laboratory investigations that include in vivo or vitro experiments, cell culture studies and gene expression profiling. For instance, experiments on vessel wall cells in culture have demonstrated that they respond morphologically, functionally, metabolically, and at the molecular level to a variety of hemodynamic stresses (eg. [7–10]); these stresses vary regionally, and some of the responses they elicit are likely to be involved in the atherosclerotic process. Similar results have also been reported from in vivo studies (eg. [11–13]). It has also been argued that mechanical stresses in the vessel wall might act as mediators of the atherosclerotic process. Such stresses, which also vary from site to site, have been claimed to correlate with the location of atherosclerotic disease [14]. Furthermore, vascular wall cells in culture and in vivo have been shown to respond to imposed strains by activating signaling pathways and remodeling (eg. [15–18]). Therefore, it seems plausible that the non-uniformity in disease distribution is due, at least in part, to the presence of certain mechanical forces that vary spatially; these forces might mediate disease development in concert with some of the established systemic risk factors [19].

While the notion that biomechanics may be involved in the atherosclerotic process is by now widely accepted, to date the precise mechanism of its involvement remains unknown. The biomechanical factors that have been proposed to play a role in atherogenesis and atherosclerotic development include low fluid dynamic shear stress and impaired mass transfer, concentrations of mechanical stress in the wall, long near-wall residence times, oscillatory or reversing shear stress, high spatial or temporal gradients in shear, and an imprecisely defined "disturbed flow" characterized by oscillatory and low mean stress, and possibly including true turbulence.

Recognizing that vessel geometry has a major influence on the mechanical environment of the vessel wall, Friedman et al proposed the concept of “geometric risk factors” for the development of atherosclerosis [20]. It is hypothesized that certain geometric features of the human vasculature may be risk factors that increase vessel’s susceptibility to atherosclerotic disease by mediating an adverse mechanical environment in its vicinity. Indeed, this hypothesis has been supported by many studies based on in vivo observations or post-mortem examination [21–25]. One of the appealing aspects of the hypothesis is that it does not rely on any particular biomechanical mechanism of atherogenesis, since all of them depend quantitatively, and in some cases qualitatively, on the geometry of the conduit. Because the candidate mechanisms depend differently on geometry, the identification of geometric features that predispose to disease can help elucidate the mechanisms by which biomechanics participates in the pathological development of atherosclerosis.

To further evaluate the geometric risk factor hypothesis, it is necessary to understand the normal geometry of vascular regions of interest, and the variability, both along the vessel length and among different individuals, of geometric features that might affect the mechanical stress experienced by the wall. We begin here with a description of the static parameters of the human left anterior descending (LAD) and right coronary arteries (RCA), selected because of their clinical significance. Our long-term goal is to use these data and dynamic data to be derived subsequently, in relation to epidemiological data regarding the distribution of disease, to identify atherogenic geometric features that can predict risk and suggest mechanisms of atherogenesis. This work extends our earlier research on the dynamics of a limited number of coronary artery segments to include a larger number of cases, well defined arterial segments, and more comprehensive statistical analysis for the end diastolic geometry of the two coronary vessels.

2. Methods

2.1. Human subjects

Patients > 18 years of age undergoing elective coronary angiography at the cardiac catheterization laboratories of Duke University Medical Center and Vanderbilt University Medical Center were approached for enrollment in this study if they did not have a history or presence of acute or complicated myocardial infarction, renal insufficiency, uncontrolled hypertension, uncontrolled diabetes mellitus, or known severe coronary artery disease. Informed consent was obtained from each participating patient prior to angiography. The images were reviewed after acquisition, and those arteries with evident stenosis or unsatisfactory image quality, were excluded from further evaluation. Sixty-seven angiographically normal adult human coronary arteries (32 LADs and 35 RCAs) from 52 patients were finally selected for characterization of coronary geometry. The demographics of these patients are summarized in Table 1. The recruitment and study protocols were approved by the Institutional Review Boards of both medical centers.

Table 1.

Demographic Summary

		All Cases (n=52)	LAD (n=32)	RCA (n=35)
Gender	Male	20	12	15
	Female	32	20	20
	White	47	29	32
Race	Black	3	2	1
	Unknown	2	1	2
Age [Mean(SD), yr]		53.4(10.2)	52.4(10.5)	52.7(10.4)

2.2. Image acquisition and analysis

The imaging and analysis procedures are similar to those described previously [26,27] and are summarized as follows.

2.2.1. Image acquisition

Left or right coronary cineangiograms were obtained from recruited subjects using clinical biplane systems. Both anterior-posterior and lateral projections were used to image the vessel of interest. The projection angles were adjusted so that the entire vessel course was well visualized and imaged with minimal overlap with other vessels. The pixel dimensions were approximately 0.3×0.3 mm², and the rate of acquisition was 15 or 30 frames per second.

2.2.2. Calibration of imaging geometry

To allow reconstruction of the three dimensional (3-D) vessel course, the imaging geometry was derived from images of a Plexiglas calibration cube that were obtained subsequent to patient imaging. Embedded within the cube were twelve radio-opaque beads whose 3-D coordinates were known in relationship to one another. The calibration cube was placed approximately in the former position of the heart and imaged with the same imaging geometry as used with the patient. Based on the known spatial relationship of the 3-D coordinates of the beads and their corresponding 2-D coordinates in the image planes, two projection matrices, one for each projection direction, were derived. These matrices allow the coordinates of a 3-D point to be computed from those in the image planes.

2.2.3. Reconstruction of 3-D vessel axis

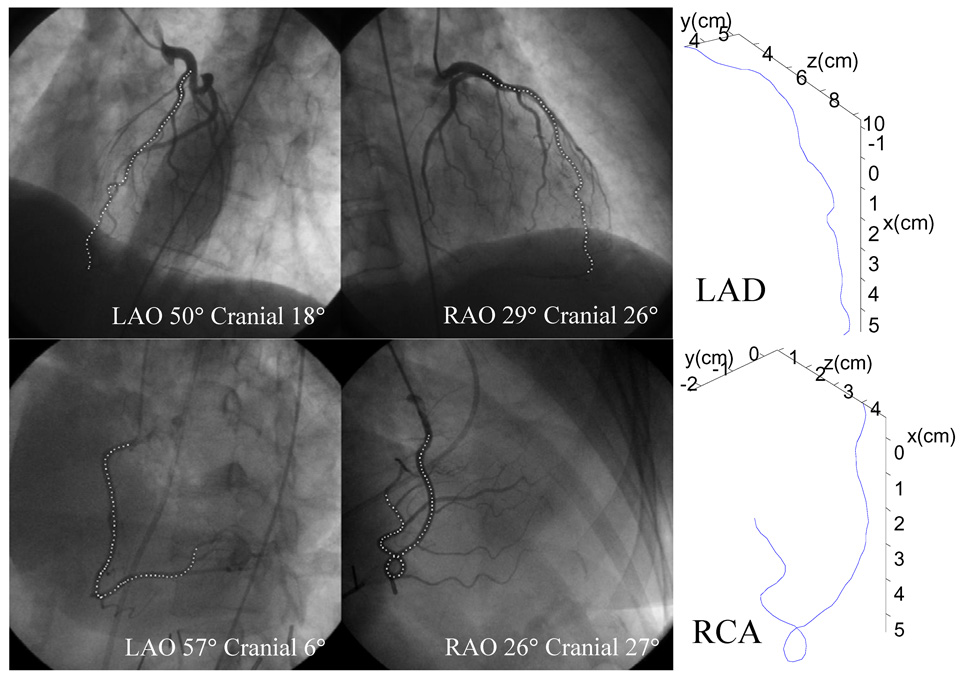
Three-dimensional reconstruction was performed using end diastolic images, with an epipolar line based technique (See [28] for technical details). Briefly, two paired cineangiographic frames, one from each projection and obtained at end diastole, were identified. Then, using the projection matrices obtained as described above and the epipolar line technique, the 3-D coordinates of several salient landmarks that could be well visualized in both projections were reconstructed. The initial reconstruction, including the landmarks and connecting "strings", was iteratively refined until a 3-D vessel axis that minimized a cost function was found. The refinement was based on an extension of the well established 2-D “snake” model [29] into 3-D space, with a smoothness constraint on the 3-D vessel axis and a requirement that the image intensity in both projections be simultaneously minimized [30]. Fig. 1 shows the reconstruction results for an LAD and an RCA.

Fig. 1.

3-D reconstruction of an LAD (top) and an RCA (bottom): left and middle, biplane angiograms; right, reconstructed 3-D vessel axes. L/RAO – Left/Right Anterior Oblique.

2.3. Characterization of geometric parameters

The geometry of the reconstructed 3-D vessel axis was characterized on the basis of curvature (κ), torsion (τ) and tortuosity. These measures were selected because they may be related to atherosusceptibility [22,26], and they are invariant under translation and rotation.

Curvature and torsion are defined according to the following equations [31]:

$$\kappa ={\left(\frac{{\mathit{(}y\prime z″-y″z\prime \mathit{)}}^{\mathit{2}}+{\mathit{(}z\prime x″-z″x\prime \mathit{)}}^{\mathit{2}}+{\mathit{(}x\prime y″-x″y\prime \mathit{)}}^{\mathit{2}}}{{\mathit{(}{x\prime }^{\mathit{2}}+{y\prime }^{\mathit{2}}+{z\prime }^{\mathit{2}}\mathit{)}}^{\mathit{3}}}\right)}^{\mathit{1}/\mathit{2}},$$ (1)

$$\tau =\frac{abs\left(\left|\begin{array}{ccc}x\prime \hfill & y\prime \hfill & z\prime \hfill \\ x″\hfill & y″\hfill & z″\hfill \\ x^{‴}\hfill & y^{‴}\hfill & z^{‴}\hfill \end{array}\right|\right)}{{\mathit{(}y\prime z″-y″z\prime \mathit{)}}^{\mathit{2}}+{\mathit{(}z\prime x″-z″x\prime \mathit{)}}^2+{\mathit{(}x\prime y″-x″y\prime \mathit{)}}^2},$$ (2)

where primes denote derivatives of the coordinates of the curve with respect to distance along the curve. The shape of a 3-D curve is uniquely determined by these two parameters. Curvature and torsion were calculated for each point on the vessel axis, using a cubic polynomial fitting method and derivatives that were computed algebraically [31]. Points close to the ends of the axis were excluded because there were too few adjacent points to permit reliable curve fitting.

The tortuosity between two points was defined as:

$$Tortuosity=1-\text{chord length}/\text{arc length}.$$ (3)

The tortuosity defined as above has a range between zero and unity. It is zero when the vessel is straight, and increases when the vessel is more tortuous. It is unity when the two endpoints of the curve are coincident.

As disease susceptibility varies from region to region, the geometry of each vessel axis was characterized on the basis of the three major segments commonly referred to at clinic and recommended by the American Heart Association [32]. The region of the LAD that we study here extends from its origin at the bifurcation of the left main coronary artery to the apex of the heart. This region is divided into the proximal, middle, and distal segments (LADp, LADm, and LADd) by two landmarks: the origins of the first septal perforator branch and the second diagonal branch. For the RCA, the study region extends from the RCA ostium to the posterior descending branch. It is also separated into three segments (RCAp, RCAm, and RCAd) by the ostia of the right ventricular and acute marginal branches. If there was more than one ventricular branch, the one closest to a point midway between the RCA ostium and the acute marginal branch was used. If there were no ventricular branches, the midpoint was used. For each major vessel segment, seven geometric parameters were calculated: the mean, maximum, and standard deviation (SD) of curvature (MeC, MaC, and SDC) and torsion (MeT, MaT, and SDT), and the tortuosity (TTS).

2.4. Statistical analysis

2.4.1. Basic statistics

The LAD and RCA data were analyzed separately. The distributions among the cases of all seven geometric parameters were skewed. Therefore, the median (M) and interquartile range [IQR, the range between the first (Q₁) and third quartile (Q₃)] were used to summarize the population data instead of the mean and standard deviation (SD). The variation of each parameter was measured by the coefficient of quartile variation (CQV), which is defined as (Q₃-Q₁)/(Q₃+Q₁). Paired t-tests were used to compare each parameter among the three segments of the LAD and the three segments of the RCA. The difference of these parameters between the LAD and RCA was examined by Wilcoxon rank-sum tests. A difference was considered statistically significant if P<0.05.

2.4.2. Factor analysis

Prior to multivariate analysis, the skewed distributions of the parameters were transformed to approximately normal distributions. A logarithmic transformation [to base 10, lg(1+x)] was applied to all parameters except tortuosity, for which a square root transformation was used. Accordingly, the transformed parameters were named LMeC, LMaC, LSDC, LMeT, LMaT, LSDT, and RTTS respectively. The correlation matrix R of the seven transformed geometric parameters indicated that they were not independent of one another. Therefore, exploratory factor analysis (FA) based on principal components analysis (PCA) was used to summarize the geometric parameters by a smaller number of independent factors; outliers identified on the basis of their Mahalanobis distance were excluded from the analysis. There were three steps for the FA [33]: first, PCA was applied to R, and principal components (PCs) with eigenvalues greater than unity were retained; second, these PCs were then orthogonally rotated by the varimax method to maximize high correlations and minimize low ones between each PC and the seven geometric parameters. The rotated PCs were the solution of the factors; last, to find out the factor scores for each case, the score coefficients which transformed raw scores to factor scores were calculated. The coefficients can be used (see Appendix) to calculate the score of a given case in the factor space and determine whether it is statistically consistent with the population of previously characterized cases.

All statistical analyses were performed using JMP 6.0 (SAS Institute Inc., Cary, NC).

3. Results

3.1. Basic statistics

The distributions of the seven geometric parameters (the mean, maximum, and SD of curvature and torsion, and tortuosity) of each of the three segments of the 32 LADs and 35 RCAs are summarized in Table 2, including the median, interquartile range, and coefficient of quartile variation. Pairwise comparisons of the geometric parameters among the three major segments of the LAD and among those of the RCA, using paired t-tests, are given in Table 3.

Table 2.

Summary of the Geometric Parameters: Median (M), Interquartile Range (Q₁ to Q₃), and Coefficient of Quartile Variation (CQV)

Parameter Statistics		LAD			RCA
		Proximal	Middle	Distal	Proximal	Middle	Distal
MeC	M(cm−1)	0.52	0.50	0.57	0.66	0.58	0.62
	Q1(cm−1)	0.37	0.39	0.44	0.55	0.42	0.45
	Q3(cm−1)	0.69	0.64	0.84	0.83	0.78	0.87
	CQV	29.9%	24.7%	31.5%	20.6%	29.9%	31.4%
MaC	M(cm−1)	0.87	1.10	1.59	1.27	1.09	1.51
	Q1(cm−1)	0.66	0.67	1.01	1.06	0.77	1.18
	Q3(cm−1)	1.09	1.39	2.22	1.67	1.53	2.00
	CQV	24.4%	34.7%	37.5%	22.4%	33.0%	25.8%
SDC	M(cm−1)	0.23	0.29	0.37	0.36	0.27	0.38
	Q1(cm−1)	0.13	0.20	0.26	0.27	0.21	0.32
	Q3(cm−1)	0.33	0.38	0.52	0.43	0.42	0.51
	CQV	43.0%	30.8%	34.1%	23.1%	34.5%	21.9%
MeT	M(cm−1)	3.31	3.36	3.82	2.46	2.03	2.91
	Q1(cm−1)	2.50	3.07	3.30	1.95	1.66	2.31
	Q3(cm−1)	4.37	5.21	4.41	3.40	3.25	3.69
	CQV	27.2%	25.9%	14.3%	27.2%	32.5%	23.1%
MaT	M(cm−1)	10.44	11.23	26.41	10.26	7.27	15.25
	Q1(cm−1)	6.42	7.84	14.42	5.68	5.51	9.87
	Q3(cm−1)	16.91	29.40	40.88	15.97	11.88	28.72
	CQV	45.0%	57.9%	47.8%	47.5%	36.6%	48.8%
SDT	M(cm−1)	3.70	3.47	5.11	2.77	2.18	3.57
	Q1(cm−1)	2.05	2.51	3.31	1.63	1.65	2.35
	Q3(cm−1)	5.86	6.56	7.07	4.46	3.48	6.15
	CQV	48.2%	44.7%	36.2%	46.5%	35.6%	44.7%
TTS	M	0.06	0.05	0.15	0.16	0.06	0.17
	Q1	0.03	0.03	0.10	0.09	0.03	0.08
	Q3	0.08	0.08	0.18	0.19	0.11	0.25
	CQV	45.1%	46.9%	30.5%	34.0%	59.7%	50.1%

Table 3.

Pairwise Comparisons of Geometric Parameters among the Three Major Segments of the LADs and RCAs^*

	LAD (P-value)			RCA (P-value)
Geometric	Proximal	Proximal	Middle	Proximal	Proximal	Middle
parameter	vs.	Vs.	vs.	vs.	vs.	vs.
	Middle	Distal	Distal	Middle	Distal	Distal
MeC	0.59	0.16	0.01	0.04	0.30	0.20
MaC	0.02	<0.0001	<0.0005	0.16	1.00	0.07
SDC	0.11	<0.0005	0.005	0.16	0.74	0.04
MeT	0.26	0.65	0.29	0.39	0.15	0.05
MaT	0.05	<0.005	0.62	0.65	<0.005	0.005
SDT	0.10	0.07	0.46	0.94	0.01	0.03
TTS	0.52	<0.0001	<0.0001	<0.0001	0.64	<0.0001

^*Two tail t-test. Significant differences (P ≤ 0.05) are denoted in bold face.

3.1.1. Curvature

In the LADs, the variation of MeC among the three segments is small, with the median values ranging from 0.50 cm⁻¹ for the middle segment to 0.57 cm⁻¹ for the distal segment; only the difference between the middle and distal segments is statistically significant (P= 0.01). MaC, however, exhibits large variations among the three segments, with the median value increasing from 0.87 cm⁻¹ for the proximal segment to 1.59 cm⁻¹ for the distal segment; pairwise differences among the three segments are all statistically significant. The variation in MaC is accompanied by a similar trend in SDC, whose median value increases from 0.23 cm⁻¹ for the proximal segment to 0.37 cm⁻¹ for the distal segment; however, the increment in this parameter between the proximal and middle segments does not reflect a statistically significant differnce between the two populations. The finding that MaC and SDC tend to increase distally probably reflects the increasing sinuosity of the more distal portions of the artery.

In the RCAs, the median values of MeC of the proximal (0.66 cm⁻¹) and distal (0.62 cm⁻¹) segments are higher than that of the middle segment (0.58 cm⁻¹), and there is a significant difference between the proximal and middle segments (P = 0.04). The median values of MaC of the proximal (1.27 cm⁻¹) and distal segments (1.51 cm⁻¹) are also higher than that of the middle segment (1.09 cm⁻¹), although none of the pairwise differences is significant. Similarly, the median values of SDC of both the proximal (0.36 cm⁻¹) and distal (0.38 cm⁻¹) segments is higher than that of the middle segment (0.27 cm⁻¹), and the P-value for the difference between the middle and distal segments is significant (P = 0.04). Overall, the middle segment has the lowest curvature measures among the three segments.

3.1.2. Torsion

The torsion measures share some similarities with the curvature measures in the LADs. The median values of MeT are comparable among the three segments, with values of 3.31, 3.36 and 3.82 cm⁻¹ for the proximal, middle and distal segments, respectively. Similarly to MaC, the median of MaT increases distally, from 10.4 cm⁻¹ for the proximal segment to 26.4 cm⁻¹ for the distal segment, but the difference between the middle and distal segments is not significant. The median SDT of the distal segment is higher than that of the proximal and middle segments, although the differences between the corresponding populations are not statistically significant at the P=0.05 level.

In the RCAs, the torsion measures follow the pattern of the curvature measures, but with more significant differences; the distal segment exhibits the highest values. The median value of MeT of the middle segment (2.03 cm⁻¹) is lower than that of the proximal segment (2.46 cm⁻¹) and distal segment (2.91 cm⁻¹), and there is a marginally significant difference (P = 0.05) between the middle and distal segments. The median value of MaT of the distal segment (15.25 cm⁻¹) is considerably higher than that of the proximal (10.3 cm⁻¹) and middle segments (7.27 cm⁻¹), and this is reflected in the pairwise tests. The same is true for SDT, though the differences among the medians are not so large.

3.1.3. Tortuosity

In the LADs, the median value of TTS varies from 0.05 for the middle segment to 0.15 for the distal segment; the pairwise t-tests show that TTS is significantly higher in the distal segment than in the proximal or middle segments. The variation of TTS is lowest in the distal segment, suggesting that the high tortuosity of this segment has a low variability among individuals.

In the RCAs, the median value of TTS of the proximal segment (0.16) is similar to that of the distal segment (0.17), and both are considerably higher than that of the middle segment (0.06). This is paralleled by the results of the pairwise tests, which show significant differences in both cases. This result, and the curvature and torsion measures summarized above, consistently indicate that the course of the RCA is least tortuous in the middle segment. The CQV of TTS, however, is higher in the middle segment (59.7%) than in the proximal (34.0%) or distal (50.1%) segments.

3.1.4. Distribution of parameter extrema

The occurrences of extreme (highest or lowest) values of the geometric parameters among the major segments of the LAD and RCA are summarized in Table 4, which gives for each major segment the number of cases in which that segment exhibited the highest maximum curvature (MaC_H), highest and lowest mean curvature (MeC_H and MeC_L), highest maximum torsion (MaT_H), highest and lowest mean torsion (MeT_H and MeT_L), and highest and lowest tortuosity (TTS_H and TTS_L). Of particular interest are those variables whose extremes are found in a particular segment in most of the cases; these are denoted in bold face in the table. In the LAD, the variables for which this is the case are MaC_H, MaT_H and TTS_H, all of which are found predominantly in the distal segment, and TTS_L, which is seen most often in the proximal segment. This means that, for instance, in more than half of the LADs, MaC of the distal segment is higher than that of either the proximal or middle segments, and the TTS of the proximal segment is less than that of the middle or distal segments. In the RCAs, MaC_H, MaT_H, and MeT_H are found predominantly in the distal segment, and TTS_L is most frequent in the middle segment.

Table 4.

Distribution of Extreme Values of Geometric Parameters^*

Segment		Geometric parameter
		MaCH	MeCH	MeCL	MaTH	MeTH	MeTL	TTSH	TTSL
	Proximal	6	10	12	5	9	13	4	17
LAD	Middle	4	6	14	7	11	12	5	12
	Distal	22	16	6	20	12	7	23	3
	Proximal	10	14	10	8	9	13	16	6
RCA	Middle	5	8	17	6	7	17	2	22
	Distal	20	13	8	21	19	5	17	7

^*Subscript H/L to the geometric parameters denotes the highest/lowest value. Bold face denotes that the number of occurrences is over half of the total number.

3.1.5. Comparisons of geometric parameters between the LAD and RCA

Region-by-region analysis in the preceding sections demonstrates that the LAD generally has higher values of curvature, torsion and tortuosity at the distal portion, whereas the RCA consistently has lower values of these measures in the middle segment. To compare the overall geometries of the LAD and RCA, the seven geometric parameters were calculated for the entire length of the vessels. The comparison of these parameters is shown in Table 5. It can be seen that there are no significant differences in curvature measures between the LAD and the RCA; the LAD exhibits significantly higher torsion measures, but lower tortuosity, than the RCA. These findings are in keeping with our earlier report [34].

Table 5.

Comparison of the Geometric Parameters [Median(Q₁, Q₃)] of the LAD (N=32) and RCA (N=35)

Geometric Parameter	LAD	RCA	P-value*
MeC(cm−1)	0.59(0.45, 0.73)	0.63(0.50, 0.86)	0.14
MaC(cm−1)	1.80(1.16, 2.22)	1.73(1.48, 2.23)	0.60
SDC(cm−1)	0.37(0.28, 0.48)	0.38(0.33, 0.46)	0.29
MeT(cm−1)	3.73(3.38, 4.60)	2.84(2.39, 3.49)	<0.0001
MaT(cm−1)	31.16(21.42, 49.14)	20.44(14.50,29.73)	<0.005
SDT(cm−1)	5.52(3.88, 7.76)	3.76(2.97, 5.16)	<0.005
TTS	0.79(0.77, 0.85)	0.53(0.48, 0.62)	<0.0001

^*Wilcoxon rank-sum test. Significant differences are denoted in bold face.

3.2. Factor analysis

Seven geometric parameters were studied individually in the above analysis. The results show that there are quite large variations in LAD and RCA geometry among both individuals and vascular segments. Correlation analyses of these parameters revealed that they were not independent of one another. Therefore, FA was applied to derive a smaller number of independent factors that account for most of the variation of the seven parameters.

The transformed parameters LMeC, LMaC, LSDC, LMeT, LMaT, LSDT, and RTTS, which are summarized in Table 6, were used in the PCA, which strictly applies to normally distributed variables. Three segments in two LAD's and two segments in two RCA's were excluded from the analysis as outliers.

Table 6.

Summary of the Transformed Parameters [Mean(SD)]

Parameter	LAD			RCA
	Proximal	Middle	Distal	Proximal	Middle	Distal
LMeC	0.181(0.061)	0.182(0.050)	0.208(0.064)	0.225(0.060)	0.203(0.061)	0.213(0.061)
LMaC	0.261(0.070)	0.308(0.086)	0.415(0.134)	0.372(0.090)	0.329(0.098)	0.402(0.080)
LSDC	0.085(0.042)	0.105(0.037)	0.142(0.052)	0.133(0.043)	0.112(0.049)	0.144(0.036)
LMeT	0.648(0.182)	0.689(0.197)	0.685(0.087)	0.556(0.126)	0.529(0.146)	0.609(0.140)
LMaT	1.042(0.293)	1.213(0.402)	1.430(0.303)	1.019(0.240)	0.962(0.270)	1.243(0.277)
LSDT	0.663(0.258)	0.748(0.346)	0.799(0.212)	0.569(0.180)	0.546(0.214)	0.707(0.219)
RTTS	0.240(0.089)	0.228(0.088)	0.363(0.094)	0.390(0.123)	0.257(0.112)	0.375(0.135)

Table 7 gives the results of FA of the seven geometric parameters of the LAD and RCA segments. As shown in the table, for all six vessel segments, only two factors are needed to account for 82% to 89% of the total variance in each segment. It is interesting to notice that the two independent factors for each vessel segment of both the LAD and RCA are very similar, one (denoted as F_C) with dominant factor loadings from the three curvature measures (mean, maximum and SD) and tortuosity, and the other one (denoted as F_T) associated with the variation in the three torsion parameters. The score coefficients for calculating the factor scores of each case are listed in Table 8. In the Appendix, we will demonstrate how to use the results from the FA.

Table 7.

Factor Analysis of the Geometric Parameters

Parameter		Proximal			Middle			Distal
		F1	F2	h2*	F1	F2	h2	F1	F2	h2
	LMeCs	−0.567	0.708	0.824	0.938	−0.145	0.902	0.952	−0.034	0.908
	LMaCs	−0.160	0.952	0.931	0.958	0.074	0.924	0.953	0.101	0.919
	LSDCs	0.535	0.765	0.872	0.889	0.193	0.828	0.965	0.031	0.933
	LMeTs	0.899	−0.166	0.836	−0.070	0.947	0.902	−0.134	0.875	0.784
LAD	LMaTs	0.966	0.093	0.943	0.029	0.981	0.964	0.248	0.931	0.928
	LSDTs	0.980	−0.047	0.962	0.007	0.992	0.984	0.186	0.955	0.947
	RTTSs	−0.002	0.844	0.713	0.781	−0.143	0.630	0.829	0.313	0.785
	Proportion of variance	47.6%	39.2%	86.9%	45.8%	41.8%	87.6%	50.7%	37.9%	88.6%
	LMeCs	0.858	−0.255	0.801	0.845	−0.385	0.862	−0.326	0.857	0.840
	LMaCs	0.964	−0.063	0.933	0.965	0.024	0.932	0.094	0.892	0.805
	LSDCs	0.898	0.031	0.808	0.893	0.211	0.843	0.125	0.897	0.820
	LMeTs	−0.335	0.806	0.762	−0.146	0.931	0.888	0.932	−0.181	0.902
RCA	LMaTs	0.029	0.969	0.940	−0.007	0.978	0.957	0.955	0.018	0.912
	LSDTs	−0.040	0.980	0.962	−0.059	0.984	0.972	0.984	−0.047	0.971
	RTTSs	0.895	−0.121	0.816	0.796	−0.237	0.689	−0.216	0.674	0.501
	Proportion of variance	48.4%	37.6%	86.0%	44.3%	43.5%	87.8%	41.8%	40.3%	82.2%

^*h² – communality, which is the sum of squared loadings for a parameter across factors. Dominant factors are marked in bold face. Subscript s denotes the parameter after standardization.

Table 8.

Score Coefficients for Factor Scores

Parameter		Proximal		Middle		Distal
		FC	FT	FC	FT	FC	FT
	LMeCs	0.244	−0.152	0.292	−0.046	0.283	−0.082
	LMaCs	0.345	−0.022	0.299	0.029	0.274	−0.028
	LSDCs	0.296	0.183	0.278	0.069	0.282	−0.057
LAD	LMeTs	−0.036	0.267	−0.018	0.323	−0.102	0.355
	LMaTs	0.061	0.294	0.013	0.335	0.007	0.349
	LSDTs	0.010	0.294	0.006	0.339	−0.013	0.363
	RTTSs	0.310	0.023	0.243	−0.046	0.222	0.064
	LMeCs	0.246	−0.037	0.259	−0.084	0.293	−0.069
	LMaCs	0.294	0.048	0.321	0.061	0.328	0.080
	LSDCs	0.280	0.080	0.307	0.120	0.331	0.091
RCA	LMeTs	−0.043	0.296	0.002	0.306	−0.017	0.316
	LMaTs	0.082	0.388	0.051	0.330	0.057	0.334
	LSDTs	0.061	0.387	0.034	0.329	0.035	0.341
	RTTSs	0.268	0.019	0.251	−0.036	0.233	−0.040

4. Discussion

The geometry of the human vasculature and its implications for atherogenesis have been addressed in many studies [21–25,35–43]. Most previous characterizations of vascular geometry were focused on a number of geometric features in disease prone regions, and provided valuable insights into the role of vessel geometry in atherogenesis. Earlier studies of the entire coronary vasculature were focused on anatomical aspects such as the locations and dimensions of coronary artery segments [44–46]. The present study catalogues the axial geometry of 67 coronary arteries in a region-specific manner, defines a set of parameters that characterize the end diastolic axial geometry of the LAD and RCA, and describes their variations among individuals and vascular regions. This represents a first comprehensive documentation of this kind. It complements the former studies, and has the potential of adding new insights and providing useful tools for studying coronary disease by exploring the causal relationships among vascular geometry, biomechanics and atherogenesis. Further study will incorporate the coronary geometry at systolic phase so that dynamic nature of the heart can be reflected. The geometric features characterized in this study include curvature, torsion and tortuosity, with which the tortuous nature of the coronary artery can be described. This tortuous nature is, in fact, closely tied with unusual fluid dynamic and wall mechanical forces, particularly in the presence of the phasic cardiac motion that is imposed on these vessels. Presumably, the unusual biomechanics is among the primary factors that may put the vessel at a greater risk for atherosclerosis.

A key premise of the concept of geometric risk factors is that, for a particular geometric feature to mediate atherosclerotic risk, it must exhibit large variability among individuals or vascular regions, sufficient to cause a significant variability in mechanical stresses. In this study, characterization of 32 LADs and 35 RCAs indeed confirmed the presence of considerable geometric variability in the human coronary vasculature. For instance, in the LAD, there is nearly a two-fold difference between segments in maximum curvature and a 2.5-fold difference in maximum torsion. The CQV of mean curvature is 25% or more in all segments, and that of maximum torsion is nearly 60% in the middle segment, demonstrating that some geometric variables vary considerably among individuals. A geometric parameter that exhibits a large variability in the population may induce a corresponding variability in the mechanical environment of the vessel, and therefore would be more likely to be responsible for individual differences in disease susceptibility and localization.

Factor analysis reveals that, in every segment examined, much of the geometric variation of the coronary arteries is attributable to two factors, to which curvature-tortuosity and torsion measures are the dominant contributors. As can be seen in Table 7, the two factors explain more than 80% of the total variance in the transformed geometric parameters. The contributions of the two are similar; differing by no more than 13% in the LAD distal segment. Therefore, these two factors can form a basis for characterizing normal coronary artery geometry. The results in Table 6 and Table 8 provide a good starting point for this kind of study. The table entries can be updated as more cases are examined. Furthermore, when a certain number of cases has been analyzed, the effects of gender, age, and race et al. on coronary geometry can be examined. When norms have been established, it should be possible to identify individuals whose geometry is abnormal and whose risk of atherosclerotic disease may be more or less than expected on the basis of traditional risk factors.

Comparisons of geometric parameters between the LAD and RCA show that, overall, the curvature measures in the two vessels are comparable, although their distributions along the vessel are different. The torsion measures, however, are more than 30% higher in the LAD than in the RCA. Further investigation is needed to determine whether the difference in torsion measures is responsible for the greater disease susceptibility of the LAD [47], and if so, how torsion interacts with hemodynamic and wall mechanical parameters. For example, torsion may play a more important role than curvature in generating helical flow patterns in the vessel; helical flow has been found to relate to coronary disease [48].

The goal of this study is to catalogue the normal values and variabilities of coronary artery geometric parameters to guide future exploration and identification of geometric risk factors. The identification of vessel geometric risk factors will not only illuminate the mechanical mechanisms of atherogenesis, but potentially can be valuable to clinical practice as well. For instance, measurements of coronary geometry may be used prognostically in a patient-specific manner, as noted above. Knowledge of adverse geometric features can support surgical planning to achieve a satisfactory post-surgical geometry. Technically, measuring the geometry of coronary arteries is quite convenient at clinic, given the availability of biplane cineangiography and the increasing applicability of less invasive procedures such as x-ray computed tomography and magnetic resonance angiography.

It is worth noting that the axial geometry of the coronary arteries, the main focus of this study, is not the sole determinant of the mechanical environment of the vessel. Other geometric parameters, most notably those describing the vessel cross-sectional geometry, such as the vessel diameter and wall thickness, are also important determinants. A combination of axial and cross-sectional geometric parameters may be most useful for studying geometric risk factors. The inclusion of wall thickness would require another catheter based intervention, presumably intravascular ultrasound; however, lumen diameter data can be obtained from the angiograms. A mechanically appropriate way to introduce lumen diameter is to use it to multiplicatively nondimensionalize curvature and torsion. The nondimensional product of tube radius and axial curvature (or torsion) is the natural variable for parameterizing flow in a bend (or helix), and these variables will also be included in future work.

Finally, it should be pointed out that, in this study, the geometry of the coronary arteries was characterized at the end diastolic phase of the cardiac cycle, similar to that in [45,46]. Indeed, with the techniques used here, it is possible to characterize the coronary arterial geometry throughout the cardiac cycle. Measurements at specific times during the cycle, such as end diastole and end systole, will allow the dynamics of coronary geometry to be characterized. This effort is under way, with the hope that it will add a dynamic dimension to the definition of geometric risk factors.

Appendix

Application of the coronary geometry catalogue

We can use the data from the FA to evaluate the coronary geometry of a new case. For example, after 3-D reconstruction of the axis, the proximal segment of an LAD had the original geometric measures MeC, MaC, SDC, MeT, MaT, SDT, and TTS as 0.41cm⁻¹, 0.76 cm⁻¹, 0.24 cm⁻¹, 4.02 cm⁻¹, 23.52 cm⁻¹, 7.21 cm⁻¹, and 0.046. After the logarithmic transformation for the first six parameters and square root transformation of the last one, the mean and SD values of LAD proximal segment in Table 6 were used to standardize the data, resulted in −0.521, −0.221, 0.201, 0.290, 1.186, 0.974, and −0.287. By the product of these values and the factor score coefficients in Table 8, the scores on F_C and F_T of this case were obtained as −0.16 and 0.83, which means they are within about 0.2 and 0.8 standard deviation of the two factors’ population distributions respectively. So the geometry of this case is in a very normal range of population.