Abstract
Irinotecan, a chemotherapeutic agent for various solid tumors, is a prodrug requiring activation to SN-38. Irinotecan’s complex pharmacokinetics allows for potentially many genetic sources of variability. We explored relationships between pharmacokinetic pathways and polymorphisms in genes associated with irinotecan’s metabolism and transport. We fit a seven-compartment pharmacokinetic model with enterohepatic recirculation to concentrations of irinotecan and metabolites SN-38, SN-38G (glucuronide), and APC. Principal component analysis (PCA) of patient-specific parameter estimates produced measures interpretable along pathways. Nine principal components characterized overall variation well. Polymorphisms in genes UGT1A1, UGT1A7, and UGT1A9 had strong associations with a component corresponding to the irinotecan-to-SN-38 pathway and SN-38 recirculation and to a component relating to SN-38-to-SN-38G conversion and SN-38G’s elimination. The component characterizing irinotecan’s compartments was associated with HNF1α and ABCC2 polymorphisms. The exploratory analysis with PCA in this pharmacogenetic analysis identified known associations and may have allowed identification of previously uncharacterized functional polymorphisms.
Keywords: Pharmacogenetics, Pharmacokinetics, Cancer chemotherapeutics, Statistics, Modeling, Irinotecan, Polymorphisms, Principal component analysis
INTRODUCTION
Irinotecan has international regulatory approval for the treatment of colorectal cancer and is active against a wide variety of solid tumors.(1–5) Much is known about the drug’s metabolism and pharmacokinetics. Irinotecan’s hydrolysis by the high affinity carboxylesterase-2 (CES-2) is responsible for activation of irinotecan to SN-38 (7-ethyl-10-hydroxycamptothecin), a potent topoisomerase I inhibitor.(6) SN-38 formation within the tumor may be an important determinant of antitumor activity. Irinotecan inactivation pathways involve oxidation of irinotecan and glucuronidation of SN-38. CYP3A4 and CYP3A5 (itself polymorphic and expressed in only a subset of patients) produce a large number of irinotecan oxidative metabolites, the main one being APC (aminopentanoic acid metabolite formed via CYP3A4-mediated oxidative metabolism).(7) The final step of irinotecan metabolism is the inactivation of SN-38 by glucuronidation to SN-38 glucuronide (SN-38G) by UDP-glucuronosyltransferase 1A1 (UGT1A1).(8) In addition to UGT1A1, other human UGT isoforms (e.g., UGT1A7 and UGT1A9) appear to catalyze SN-38G formation.(9, 10)
In addition to metabolism, another important route of irinotecan elimination is through biliary excretion. Among the several ABC transporters, ABCB1 and ABCC2 are the two main transporters involved in the biliary elimination of irinotecan and SN-38 species.(11) Efflux of the parent compound and metabolites out of cells by several other transporters (e.g., ABCG2, ABCC1) also occurs.(12, 13) Liver uptake transporters might also be involved in the disposition of irinotecan and its metabolites.(14)
Investigators have uncovered some genetic sources of variation in the drug’s pharmacokinetics. The UGT1A1*28 polymorphism (7 tandem repeats of a sequence of TA nucleotides in the 6 TA repeat promoter region of the UGT1A1 gene) has been associated with altered SN-38 pharmacokinetics, increasing a patient’s risk of toxicity.(15) Several groups have also reported an association between the UGT1A1*6 polymorphism and clinical outcome among Asian populations.(16, 17) In addition to UGT1A1, variation in other genes related with irinotecan pharmacokinetics might play a role in interpatient variability in irinotecan disposition that is not explained by UGT1A1*28. The literature includes other pharmacogenetic studies of irinotecan pharmacokinetics and genes relating to transporters and drug metabolizing enzymes.(18, 19)
There are several statistical methods for inferring associations between polymorphisms and a drug’s pharmacokinetics. Models for drugs with complex pharmacokinetics, like irinotecan, will include many different parameters. Each parameter relates to some aspect of the metabolism. One may carry out separate analyses relating each parameter in the model to a list of genotypes. Inference from separate analyses may prove problematic, however. Aside from the issue of multiple comparisons, one may find it difficult to synthesize and summarize the results. Just by chance, associations may not consistently appear as significant across parameters in a common metabolic pathway captured by the pharmacokinetic model.
Alternatively, one can reduce the number of analyses by combining related pharmacokinetic parameters. One can then infer genetic sources of variation affecting these constructed meta-parameters. Associations revealed through such analyses may reflect genetic sources of variation linked to the corresponding pathway.
We wanted to reduce the number of pharmacogenetic analyses in a way that made sense with respect to a drug’s pharmacokinetics. Specifically, we sought a method to combine the pharmacokinetic model parameters into fewer patient-specific outcomes than arose from a complex multi-compartment model. The method should combine the fitted parameters such that the resulting combinations relate to different aspects or pathways in the drug’s pharmacokinetics. We chose to examine irinotecan, since considerable information already existed about its pharmacokinetics (20, 21) and pharmacogenetics.(22) We expected the analysis to highlight certain known pharmacogenetics relationships, while also providing some leads or insights into other as yet unknown relationships.
We present a principal component analysis (PCA) to determine pathway-related outcome measures. We analyzed genetic associations with respect to the PCA-based measures that relate to a pharmacokinetics model of irinotecan. We interpreted these associations in terms of the known metabolic pathways captured by our pharmacokinetic model. Our exploratory pharmacogenetic analysis sought polymorphisms that are associated with the metabolic pathways that correspond to the derived principal component.
RESULTS
Pharmacokinetic modeling
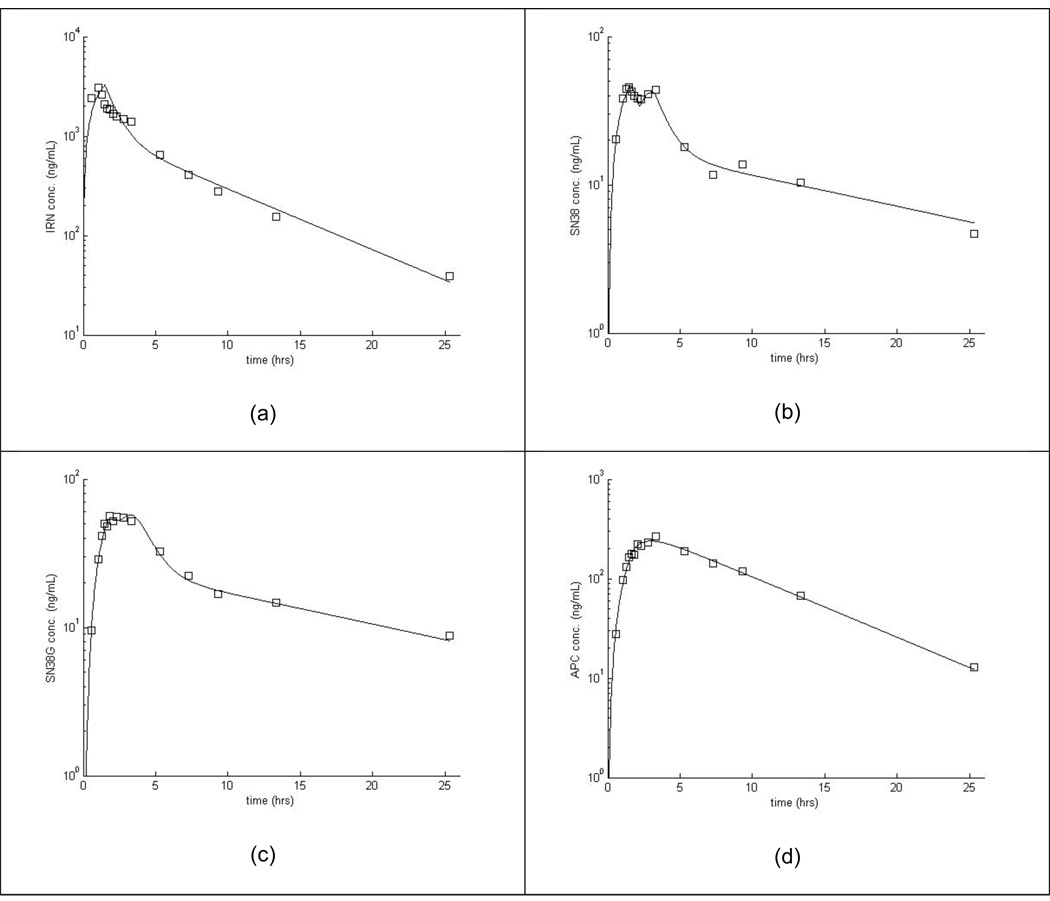
We first tried a model without considering EHR (i.e., fixing k3B=0). This initial model failed to describe the SN-38 disposition in a majority of the individuals. Specifically, this model completely missed the second “hump” in the SN-38 concentration versus time curve (seen at ~2.5 hr for the individual in Figure 2b). We chose to model recirculation of SN-38 rather than SN-38G, because recirculation of SN-38 described our data better. In particular, the second peak in the SN-38 curve is more distinct than on the SN-38G curve in our data. Next, the model allowed estimation of k3B but fixed kBG1=0, thereby only allowing SN-38 to pass from the bile to the gut during the period of gall bladder release. This model did not adequately describe the SN-38 concentration versus time data. Finally, we estimated all of the parameters describing EHR in our model and could adequately fit the SN-38 data (see for example Figure 2). Table 3 lists summary statistics for the fitted pharmacokinetics parameters.
Figure 2.
Example fit of model to one patient’s concentration-time data for irinotecan (a), SN-38 (b), SN-38G (c), and APC (d).
Table 3.
Distribution of patient-specific pharmacokinetic parameters (sample size=86)
| Stand. | |||||||
|---|---|---|---|---|---|---|---|
| Mean | Dev. | Min. | 25 %* | Median | 75th %* | Max. | |
| Irinotecan clearance | 14.97 | 5.11 | 4.75 | 12.09 | 14.13 | 16.92 | 36.62 |
| ke | 0.257 | 0.724 | 0.000 | 0.009 | 0.084 | 0.202 | 5.881 |
| V** | 40.73 | 18.72 | 2.10 | 28.82 | 41.23 | 52.44 | 93.96 |
| kcp | 2.69 | 5.84 | 0.10 | 0.35 | 0.73 | 2.11 | 42.98 |
| kpc | 0.660 | 0.472 | 0.069 | 0.275 | 0.529 | 0.948 | 2.560 |
| kSN | 0.233 | 0.269 | 0.026 | 0.137 | 0.198 | 0.265 | 2.477 |
| k30 | 0.054 | 0.112 | 0.000 | 0.003 | 0.012 | 0.053 | 0.670 |
| k35 | 7.95 | 6.96 | 1.34 | 3.85 | 6.40 | 9.93 | 43.08 |
| k50 | 1.95 | 2.48 | 0.45 | 1.11 | 1.45 | 2.06 | 22.50 |
| kAPC | 0.065 | 0.040 | 0.015 | 0.039 | 0.058 | 0.078 | 0.244 |
| k70 | 0.325 | 0.128 | 0.156 | 0.245 | 0.292 | 0.381 | 1.045 |
| k3B | 18.34 | 22.15 | 0.00 | 7.76 | 11.69 | 20.86 | 152.92 |
| EHRT** | 4.23 | 17.06 | 0.00 | 1.67 | 2.09 | 2.41 | 159.52 |
| kBG | 0.46 | 1.85 | 0.02 | 0.07 | 0.13 | 0.23 | 15.95 |
| kBG1** | 27.65 | 109.97 | 0.00 | 0.41 | 1.17 | 4.04 | 918.31 |
| kG3 | 7.64 | 19.54 | 0.02 | 0.30 | 0.71 | 3.08 | 104.62 |
| kBG1/kBG | 295.3 | 2192.5 | 0.0 | 3.5 | 9.5 | 24.0 | 20342.8 |
Percentile
Parameter not included when forming PCs
Statistical Model
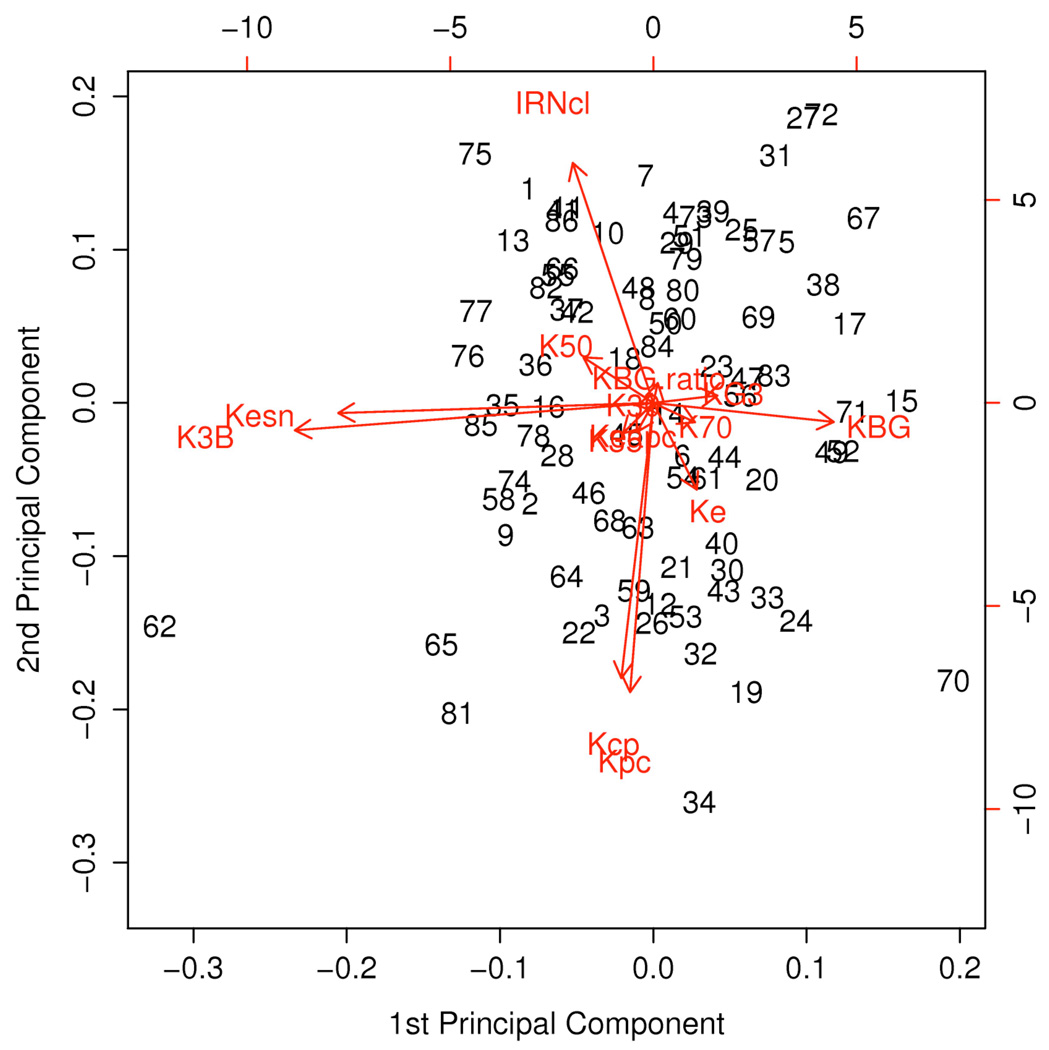
Because of functional relationships among several pharmacokinetic parameters, we removed 3 of the 17 pharmacokinetic parameters from consideration before computing the PCs (Table 3). After finding the PCs for the 14 pharmacokinetic parameters, we considered keeping between 6 and 9 of them. We chose to retain 9 PCs because of interpretability after rotation. These nine PCs accounted for 92% of the total variation in the standardized data (Table 4). Figure 3 is a biplot, showing each patient’s values for first and second PCs after rotation. The length of each arrow reflects the weight of the corresponding model parameter. The Figure shows how the parameters kBG, k3B, and kSN dominate the first PC, while irinotecan clearance and the inter-compartmental rate parameters, kcp and kpc, dominate the second.
Table 4.
PCs associated with each pharmacokinetic parameter. The table shows only PC coefficients greater than 0.10. Coefficients for parameters used in the interpretation of the PCs are shown in boldface type.
| Pc1 | Pc2 | Pc3 | Pc4 | Pc5 | Pc6 | Pc7 | Pc8 | Pc9 | |
|---|---|---|---|---|---|---|---|---|---|
| Irinotecan clearance | −0.151 | 0.500 | 0.262 | 0.134 | 0.489 | ||||
| ke | −0.181 | 0.817 | |||||||
| kcp | −0.573 | 0.237 | |||||||
| kpc | −0.603 | ||||||||
| kSN | −0.593 | 0.103 | |||||||
| k30 | −0.962 | ||||||||
| k35 | 0.609 | 0.111 | 0.140 | −0.120 | |||||
| k50 | −0.131 | 0.611 | −0.235 | 0.173 | 0.123 | ||||
| kAPC | 0.896 | ||||||||
| k70 | −0.927 | ||||||||
| k3B | −0.674 | 0.153 | 0.137 | −0.115 | |||||
| kBG | 0.340 | 0.454 | 0.156 | 0.284 | 0.147 | −0.482 | −0.126 | ||
| kG3 | 0.121 | 0.171 | 0.111 | 0.845 | |||||
| kBG1/kBG | −0.953 | ||||||||
| Proportion of Variance | 22.2% | 18.1% | 11.1% | 10.1% | 9.0% | 7.1% | 6.1% | 5.1% | 3.6% |
| Cumulative Proportion | 22.2% | 40.3% | 51.4% | 61.5% | 70.5% | 77.6% | 83.7% | 88.8% | 92.4% |
| IRN to SN-38 & SN-38 recirculation | IRN Compartments | SN-38 to SN-38G & SN-38G elimination | IRN to APC | APC elimination | EHR | SN-38 recirculation without EHR | SN-38 elimination | IRN elimination | |
Figure 3.
Biplot showing the first two PCs after rotation. The numbers in the graph refer to patients (numbered consecutively). The scales of the axes refer to the PC scores (see text) for each patient. Each arrow is labeled with the corresponding parameter from the pharmacokinetic model (Figure 1).
The bottom of Table 4 shows our interpretation of the PCs in terms of pathways in the pharmacokinetic model (Figure 1), based on the model parameters loading most heavily (PC coefficient > 0.1) on the PC. For example, the following parameters loaded most heavily on the first PC after rotation (Table 4): the rate parameter for the path from the central irinotecan compartment to SN-38 and the rate parameters governing the pathway of SN-38 through the bile, the gut, and then back to the SN-38 compartment. Thus, we considered the first PC as capturing the conversion of irinotecan to SN-38 and the recirculation of SN-38 through the bile and the gut (Figures 4 and 5). The second PC was most associated with the two compartments relating to the parent compound (Figures 4 and 5). The third PC was related to glucuronidation of SN-38 to SN-38G and the elimination of SN-38G, as well as the passage of SN-38 from the bile to the gut.
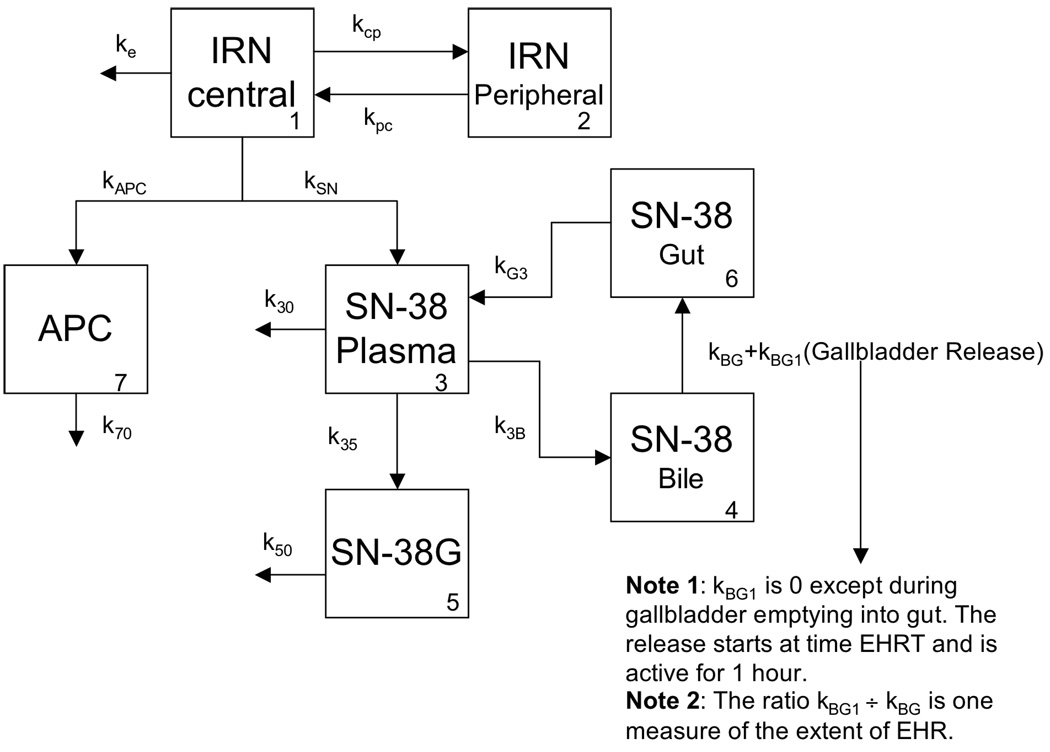
Figure 1.
Pharmacokinetic model with enterohepatic recirculation (EHRT). The numbers in the lower right corner of the compartments identify each compartment.
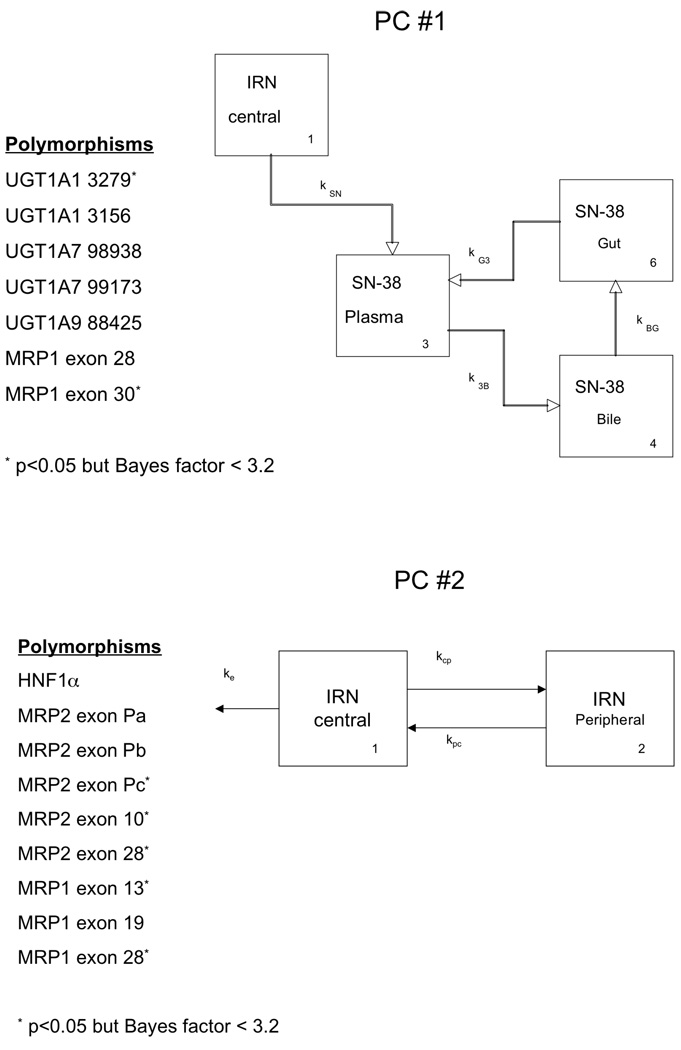
Figure 4.
The first two PCs as pharmacokinetic pathways with associated polymorphisms.
Table 5 lists the smallest p values and largest Bayes factors for each pair of polymorphisms and the PCs. We found seven polymorphisms with significant associations with the first PC (see Figure 4); five of these seven showed strong evidence of association according to the Bayes factors. These polymorphisms are in the UGT1A1 (n=2), UGT1A7 (n=2), UGT1A9 (n=1), and ABCC1 (n=2) genes. The second PC (Figure 4) was associated with polymorphisms in HNF1α (n=1), CYP3A5 (n=1), ABCC2 (n=5), and ABCC1 (n=3) genes (9 with p < 0.05 and 4 with Bayes factor > 3.2). The third PC was significantly associated with polymorphisms in UGT1A1 (n=3), UGT1A7 (n=2), UGT1A9 (n=1), SLCO1 (n=1), and CES2 (n=1) (p<0.05 for each association). The Bayes factors indicate strong evidence of an association only between this PC and the UGT polymorphisms.
Table 5.
Associations between the principal components and polymorphisms. The table shows the p values and Bayes factors, respectively, separated by a “/.” P values < 5% and Bayes factors > 3.2 are shown in boldface.
| Polymorphism | PC1 | PC2 | PC3 | PC4 | PC5 | PC6 | PC7 | PC8 | PC9 |
|---|---|---|---|---|---|---|---|---|---|
| UGT1A1, −53A(TA)6>7TAA, PROMOTER | 0.086 / 0.5 | 0.301 / 0.2 | 0.007 / 4.9 | 0.019 / 1.8 | 0.216 / 0.2 | 0.009 / 3.4 | 0.314 / 0.2 | 0.204 / 0.2 | 0.123 / 0.4 |
| UGT1A1, −3279G>T (UGT1A1*60), PBREM | 0.021 / 1.7 | 0.056 / 0.7 | 0.043 / 0.9 | 0.027 / 1.3 | 0.588 / 0.1 | 0.001 / 24.8 | 0.482 / 0.1 | 0.527 / 0.1 | 0.046 / 0.8 |
| UGT1A1, −3156G>A, PBREM | 0.008 / 4.2 | 0.136 / 0.3 | 0.014 / 2.6 | 0.017 / 2.0 | 0.322 / 0.2 | 0.005 / 6.7 | 0.031 / 1.1 | 0.268 / 0.2 | 0.083 / 0.5 |
| UGT1A7, 387G>T (N129K), EXON 1 | 0.007 / 4.6 | 0.139 / 0.3 | 0.001 / 26.7 | 0.050 / 0.8 | 0.050 / 0.8 | 0.103 / 0.4 | 0.116 / 0.4 | 0.186 / 0.3 | 0.114 / 0.4 |
| UGT1A7, 622T>C (W208R), EXON 1 | 0.000 / 77.5 | 0.392 / 0.2 | 0.002 / 17.3 | 0.019 / 1.8 | 0.332 / 0.2 | 0.003 / 11.2 | 0.289 / 0.2 | 0.055 / 0.7 | 0.270 / 0.2 |
| UGT1A9, −118(T)9>10, UGT1A9*1b, PROMOTER | 0.003 / 12.3 | 0.258 / 0.2 | 0.001 / 36.4 | 0.017 / 2.0 | 0.054 / 0.7 | 0.025 / 1.4 | 0.067 / 0.6 | 0.279 / 0.2 | 0.066 / 0.6 |
| UGT1A9, −2152C>T, PROMOTER | 0.809 / 0.1 | 0.453 / 0.1 | 0.293 / 0.2 | 0.703 / 0.1 | 0.328 / 0.2 | 0.473 / 0.1 | 0.615 / 0.1 | 0.238 / 0.2 | 0.784 / 0.1 |
| UGT1A9, −275T>A, PROMOTER | 0.632 / 0.1 | 0.217 / 0.2 | 0.297 / 0.2 | 0.764 / 0.1 | 0.148 / 0.3 | 0.583 / 0.1 | 0.527 / 0.1 | 0.245 / 0.2 | 0.944 / 0.1 |
| HNF-1α, 79A>C (I27L), EXON 1 | 0.625 / 0.1 | 0.001 / 37.3 | 0.154 / 0.3 | 0.434 / 0.1 | 0.527 / 0.1 | 0.423 / 0.2 | 0.517 / 0.1 | 0.366 / 0.2 | 0.213 / 0.2 |
| CYP3A4, −392A>G, CYP3A4*1B, 5’-UTR | 0.414 / 0.2 | 0.556 / 0.1 | 0.337 / 1.2 | 0.967 / 0.4 | 0.721 / 0.1 | 0.323 / 0.2 | 0.772 / 0.2 | 0.487 / 0.3 | 0.923 / 0.1 |
| CYP3A5, 6986A>G, CYP3A5*3, INTRON 3 | 0.861 / 0.4 | 0.179 / 0.9 | 0.255 / 0.5 | 0.489 / 0.1 | 0.124 / 0.4 | 0.704 / 0.1 | 0.536 / 0.1 | 0.822 / 0.1 | 0.443 / 0.1 |
| SLCO1B1, 388A>G (N130D), SLCO1B1*1b, EXON 4 | 0.079 / 0.5 | 0.106 / 0.4 | 0.023 / 1.6 | 0.097 / 0.4 | 0.580 / 0.1 | 0.379 / 0.2 | 0.317 / 0.2 | 0.038 / 1.0 | 0.269 / 0.2 |
| SLCO1B1, 521T>C (V174A), SLCO1B1*15, EXON 5 | 0.878 / 0.1 | 0.614 / 0.6 | 0.600 / 0.1 | 0.433 / 0.2 | 0.751 / 0.2 | 0.159 / 0.5 | 0.942 / 0.1 | 0.145 / 0.3 | 0.066 / 0.6 |
| ABCC2, −1549A>G, 5’-Flanking region | 0.383 / 0.2 | 0.001 / 47.4 | 0.301 / 0.2 | 0.308 / 0.2 | 0.171 / 0.3 | 0.749 / 0.1 | 0.705 / 0.1 | 0.253 / 0.2 | 0.643 / 0.1 |
| ABCC2, −1019A>G, 5’-Flanking region | 0.583 / 0.1 | 0.002 / 15.4 | 0.254 / 0.2 | 0.249 / 0.2 | 0.398 / 0.2 | 0.732 / 0.1 | 0.681 / 0.1 | 0.226 / 0.2 | 0.809 / 0.1 |
| ABCC2, −24C>T, 5’-UTR | 0.985 / 0.1 | 0.013 / 2.7 | 0.575 / 0.2 | 0.950 / 1.1 | 0.054 / 0.9 | 0.221 / 0.7 | 0.402 / 0.2 | 0.641 / 0.1 | 0.366 / 0.6 |
| ABCC2, 1249G>A (V417I), EXON 10 | 0.443 / 0.1 | 0.045 / 0.9 | 0.934 / 0.1 | 0.358 / 0.2 | 0.521 / 0.1 | 0.329 / 0.2 | 0.495 / 0.1 | 0.002 / 14.9 | 0.706 / 0.1 |
| ABCC2, −34T>C, INTRON 26 | 0.469 / 0.1 | 0.258 / 0.2 | 0.963 / 0.1 | 0.167 / 0.3 | 0.639 / 0.1 | 0.829 / 0.1 | 0.049 / 0.8 | 0.734 / 0.1 | 0.345 / 0.2 |
| ABCC2, 3972C>T (I1324I), EXON 28 | 0.250 / 0.2 | 0.011 / 3.1 | 0.224 / 0.2 | 0.103 / 0.4 | 0.013 / 2.5 | 0.144 / 0.3 | 0.175 / 0.3 | 0.200 / 0.3 | 0.149 / 0.3 |
| ABCC1, 1062T>C (N354N), EXON 9 | 0.136 / 0.3 | 0.179 / 0.3 | 0.221 / 0.2 | 0.120 / 0.4 | 0.139 / 0.3 | 0.684 / 0.1 | 0.013 / 2.3 | 0.228 / 0.2 | 0.082 / 0.5 |
| ABCC1, −48C>T, INTRON 11 | 0.302 / 0.2 | 0.187 / 0.3 | 0.840 / 0.2 | 0.175 / 0.3 | 0.105 / 0.4 | 0.748 / 0.5 | 0.577 / 0.2 | 0.642 / 0.1 | 0.084 / 0.6 |
| ABCC1, 1684T>C (L562L), EXON 13 | 0.405 / 0.2 | 0.018 / 2.0 | 0.414 / 0.2 | 0.098 / 0.4 | 0.579 / 0.1 | 0.436 / 0.1 | 0.805 / 0.1 | 0.037 / 1.0 | 0.233 / 0.2 |
| ABCC1, −30C>G, INTRON 18 | 0.188 / 0.3 | 0.004 / 8.0 | 0.362 / 0.2 | 0.155 / 0.3 | 0.879 / 0.1 | 0.620 / 0.1 | 0.526 / 0.1 | 0.061 / 0.6 | 0.177 / 0.3 |
| ABCC1, 4002G>A (S1334S), EXON 28 | 0.001 / 29.4 | 0.022 / 1.7 | 0.300 / 0.2 | 0.195 / 0.3 | 0.416 / 0.2 | 0.096 / 0.4 | 0.184 / 0.3 | 0.064 / 0.6 | 0.072 / 0.6 |
| ABCC1, +18A>G, INTRON 30 | 0.023 / 1.6 | 0.198 / 0.3 | 0.424 / 0.2 | 0.825 / 0.1 | 0.365 / 0.2 | 0.296 / 0.2 | 0.217 / 0.2 | 0.403 / 0.2 | 0.236 / 0.2 |
| ABCB1, −129T>C, 5’-UTR | 0.559 / 0.5 | 0.811 / 0.1 | 0.610 / 0.3 | 0.977 / 0.2 | 0.725 / 0.9 | 0.807 / 0.4 | 0.163 / 0.3 | 0.177 / 0.3 | 0.009 / 3.5 |
| ABCB1, −25G>T, INTRON 4 | 0.229 / 0.3 | 0.774 / 0.1 | 0.832 / 0.5 | 0.826 / 1.1 | 0.635 / 0.1 | 0.877 / 0.2 | 0.368 / 0.2 | 0.661 / 0.1 | 0.832 / 0.1 |
| ABCB1, −44A>G, INTRON 9 | 0.147 / 0.3 | 0.605 / 0.1 | 0.618 / 0.1 | 0.570 / 0.1 | 0.109 / 0.4 | 0.156 / 0.3 | 0.096 / 0.4 | 0.338 / 0.2 | 0.051 / 0.8 |
| ABCB1, 1236C>T (G412G), EXON 12 | 0.182 / 0.3 | 0.437 / 0.1 | 0.382 / 0.2 | 0.482 / 0.1 | 0.090 / 0.5 | 0.280 / 0.2 | 0.106 / 0.4 | 0.376 / 0.2 | 0.153 / 0.3 |
| ABCB1, +24C>T, INTRON 13 | 0.725 / 0.1 | 0.439 / 0.1 | 0.491 / 0.1 | 0.540 / 0.1 | 0.532 / 0.1 | 0.076 / 0.5 | 0.100 / 0.4 | 0.306 / 0.2 | 0.016 / 2.1 |
| ABCB1, +38A>G, INTRON 14 | 0.627 / 0.1 | 0.538 / 0.1 | 0.669 / 0.1 | 0.540 / 0.1 | 0.532 / 0.1 | 0.054 / 0.7 | 0.100 / 0.4 | 0.306 / 0.2 | 0.033 / 1.1 |
| ABCB1, 2677G>A/T (A893T/S), EXON 21 | 0.302 / 0.2 | 0.543 / 0.1 | 0.491 / 0.1 | 0.962 / 0.1 | 0.943 / 0.1 | 0.309 / 0.2 | 0.210 / 0.2 | 0.890 / 0.1 | 0.004 / 6.9 |
| ABCB1, 3435C>T (I1145I), EXON 26 | 0.319 / 0.2 | 0.441 / 0.1 | 0.531 / 0.1 | 0.631 / 0.1 | 0.664 / 0.1 | 0.644 / 0.1 | 0.402 / 0.2 | 0.226 / 0.2 | 0.013 / 2.5 |
| ABCG2, 34G>A (V12M), EXON 2 | 0.479 / 0.1 | 0.828 / 0.1 | 0.139 / 0.3 | 0.348 / 0.2 | 0.588 / 0.2 | 0.673 / 0.1 | 0.087 / 0.5 | 0.219 / 0.2 | 0.780 / 0.1 |
| ABCG2, 421C>A (Q141K), EXON 5 | 0.565 / 0.1 | 0.397 / 0.2 | 0.421 / 0.2 | 0.435 / 0.1 | 0.628 / 0.1 | 0.256 / 0.2 | 0.708 / 0.1 | 0.533 / 0.1 | 0.787 / 0.1 |
| CES2, −363C>G, 5’-UTR | 0.999 / 2.3 | 0.546 / 0.2 | 0.028 / 1.9 | 0.899 / 0.1 | 0.379 / 0.6 | 0.922 / 0.1 | 0.586 / 0.1 | ||
| CES2, +1361A>G, INTRON 1 | 0.381 / 1.0 | 0.549 / 0.2 | 0.616 / 0.8 | 0.629 / 0.1 | 0.275 / 0.3 | 0.260 / 0.2 | 0.352 / 0.2 | ||
| Split to SN-38 & SN-38 to Bile to Gut to SN-38 | IRN Compartments | SN-38 to SN-38G & SN-38G Elimination | Split to APC from IRN Central Compartment | APC Elimination | EHR | SN-38 recirculation w/o EHR | SN-38 Elimination | IRN Elimination |
The more conservative Bayes factors do not indicate strong evidence of associations between SNPs and the APC part of the pharmacokinetic model (the fourth or fifth PCs). If one uses p values, however, one can identify statistically significant associations (p < 0.05) between several UGT1A1, UGT1A7, and UGT1A9 polymorphisms and the fourth PC and a significant association between the fifth PC and a SNP in the ABCC2 gene (Table 5). These p-value-based associations may be false signals, since the pharmacology does not suggest an association between the UGTs and the metabolite APC.
The sixth PC is almost entirely related to the extent of EHR. We found evidence of associations between polymorphisms in the UGT1A1 and UGT1A7 genes and this PC. The associations may be indirect, since these genes are not transporter genes. Alternatively, the association may reflect EHR dependence on the extent of glucuronidation and SN-38-SN-38G recycling in the gut. The seventh PC characterized recirculation of SN-38 without EHR. Although several SNPs had a significant association (p < 0.05) with this PC, Bayes factors did not indicate strong evidence of association. SN-38 elimination (PC 8, k30 in Figure 1) was associated with a SNP in the ABCC2 gene. A SNP in the SLCO1 gene and one in the ABCC1 gene had a significant association with this PC (p<0.05). The last PC reflected the irinotecan clearance and elimination (ke in Figure 1). We found strong evidence of associations between the ABCB1 gene and this PC.
Discussion
We have shown how statistical methods for dimension reduction can allow inference in complex biomedical applications. Specifically, we applied PC analysis to pharmacokinetic model parameter estimates to produce measures we could interpret in terms of pathways in the compartmental model of irinotecan’s pharmacokinetics. Additionally, regression analysis of PC scores on polymorphisms allowed us to assess relationships between polymorphisms and pathways. We found strong evidence for some associations, but we view the analysis as exploratory. This is the first application of this methodology to pharmacogenetic analysis as far as we know.
One of the unique aspects of irinotecan pharmacokinetics is the enterohepatic recirculation of SN-38. Specifically, SN-38 can be formed in the liver from irinotecan, or in the intestine from SN-38 glucuronide through the action of bacterial glucuronidases.(23–25) The gall bladder periodically releases its contents into the gut (usually after a meal), leading to a bolus infusion of SN-38 and/or SN-38 glucuronide into the intestine, which is then reabsorbed, via portal circulation, into the plasma. This reabsorption leads to a transient increase in plasma SN-38 and SN-38G concentrations when one expects them to be decreasing. While this pharmacokinetic process has been modeled for several other drugs (e.g. morphine),(26, 27) it has only been described noncompartmentally in irinotecan disposition.(28)
In our data, we found strong evidence of associations we expected to see. For example, we expected and the analysis found an association between the UGT1A1*28 polymorphism and glucuronidation of SN-38 to SN-38G. On the other hand, the ABCB1 1236 C>T polymorphism, for which a report found significant associations with total irinotecan AUC and SN-38 AUC,(18) did not appear to have a strong relationship with any of our derived phenotypes. Most of the polymorphisms in the candidate genes did not show strong associations. Possibly, many of these polymorphisms are not functional. In some cases, however, the lack of association may have been a result of the small number of individuals who possessed the rare allele. For example, the two polymorphisms in the ABCG2 transporter gene had either two individuals homozygous for the rare allele (ABCG2 BCRP G34A) or none (ABCG2 BCRP C421A). Thus, the sample size was too small in some key instances.
We recognize some limitations to the analyses. First of all, we analyzed individual pharmacokinetic parameter estimates from separate analyses, rather than fitting a population model. An advantage of a population model is that the estimates would borrow strength across patients and exhibit some shrinkage. One is therefore less likely to find extreme observations that might dominate the inference. We did check the data for outliers and examined influence of patient estimates on the principal components. By analyzing the logarithms of the estimates, we reduced skewness. In the end, we are confident that one or two patients did not heavily influence our PCs.
We carried out our analysis in several stages, instead of building one large encompassing model. Although there are reasons to criticize two-stage (or multi-stage) analyses, we feel that our approach was more straightforward, less difficult to implement, and easier to explain. While our PCs, based on estimates from pharmacokinetic models, ignore uncertainty in the estimates, they reflect the between-patient variation. We feel that between-patient variation exceeds the uncertainty in the parameter estimates. We are working on a larger population model that will allow us to learn about the different components of variation.
We had to impose some constraints to ensure identifiability of the model parameters. For a compartmental model such as ours, one can either uniquely estimate the volumes or the elimination rate constants in peripheral compartments.(29) We chose to estimate the elimination rates and fix the volumes of the compartments. Had we fixed the rate constants, the PCs for the new parameter estimates would have had different loadings but likely still split the same way with respect to the pathways. It does not seem likely that different genes would associate with the PCs.
We also somewhat arbitrarily fixed the duration of gall bladder emptying in our model to be one hour, which we thought to be reasonable. Varying this time slightly would have little effect on the parameter estimates. If we made the duration a continuous parameter to estimate, we would in effect have set the model parameter kBG1 to be zero and would not have gotten a reasonable fit to the second SN-38 peak in most cases.
There are admittedly unaccounted sources of variation, because of the limitations of the data. For example, we have no measurements of eliminated metabolites. Also, we did not fix the timing of the patients’ meals, which would affect gall bladder release and, subsequently, enterohepatic recirculation. GI tract surgery might affect pharmacokinetics, although we are not aware of any data supporting this hypothesis.
Whenever one carries out a large number of hypothesis tests, one worries about false discoveries. We view this study as exploratory and report associations that were significant at the 0.05 level without adjusting for multiple comparisons. Additionally, we computed Bayes factors to evaluate the strength of evidence in the data against the null hypothesis of no association. Bayes factors actually provide a more direct measure of the strength of evidence than do p values.(30) The polymorphisms that exhibited strong evidence of association by Bayes factors in our data were a subset of the same ones that had significant (p < 0.05) associations.
In any genetic analysis, one has to make a decision about how best to deal with polymorphisms with very low minor allele frequencies. Several polymorphisms in our data had only 1 or 2 patients who were homozygous for the rare allele. In some cases, we combined them with the heterozygotes to avoid noise influencing the inference. Combining may have masked some functional polymorphisms if the trait is recessive and the allele frequencies low. Also, since our population was predominantly Caucasian and African-American, we might not have found some polymorphisms that are important in other populations, especially Asian.
In summary, principal component analysis (PCA) provides a statistically valid way to reduce the dimensionality of a problem. We showed how to use PCA to construct phenotypes from parameter estimates in a large and complex pharmacokinetic model. After selecting the PCs that account for the majority of the total variation in the data and applying a rotation, we could interpret the retained PCs as representing pathways in the pharmacokinetic model. PCA thus allows exploration and evaluation of associations between pharmacokinetic pathways and patient characteristics.
METHODS
The patient population consisted of 86 patients with advanced solid tumors who enrolled in a prospective phase I study at the University of Chicago evaluating the relationship between the UGT1A1*28 polymorphism and irinotecan toxicity. All patients provided written consent for this study, which was approved by the University of Chicago Institutional Review Board. The patients received single-agent irinotecan at doses of 300 mg/m2 (20 patients) or 350 mg/m2 (66 patients) infused over 90 minutes every three weeks, as described elsewhere.(31, 32) We had pharmacokinetic data for 86 patients. Table 2 contains patient demographics. Genotype information was missing for one patient at the 350 mg/m2 dose, so analyses relating genotype to pharmacokinetics include 85 patients.
Table 2.
Characteristics of the 86 patients
| No. of patients | |
|---|---|
| Dose | |
| 300 mg/m2 | 66 (77%) |
| 350 mg/m2 | 20 (23%) |
| Sex | |
| Male | 49 (57%) |
| Female | 37 (43%) |
| Age, median (range) | 59 (34–85) |
| Ethnicity | |
| White | 68 |
| African-American | 11 |
| Hispanic | 4 |
| Asian | 2 |
| Pacific Islander | 1 |
| BSA (m2), median (range) | 1.82 (1.41 – 2.55) |
| Prior chemotherapy regimens, median (range) | 2 (0–6) |
| Tumor type | |
| Lung | 26 |
| Gastroesophageal | 16 |
| Colorectal | 14 |
| Others | 30 |
Sampling of venous blood (7 ml) into sodium heparinized evacuated tubes for pharmacokinetic analysis occurred after the first irinotecan administration (at cycle 1). Sampling times were day 1 of cycle 1 (prior to irinotecan infusion) and at 0.5, 1.0, 1.5, 1.67, 1.83, 2.0, 2.25, 2.5, 3.0, 3.5, 5.5, 7.5, 13.5, 25.5 hours after the start of the infusion.
Chromatography analysis, as previously described (32), yielded concentrations of irinotecan and metabolites SN-38, SN-38G, and APC.
Pharmacokinetics
The pharmacokinetic model describing the disposition of irinotecan and its metabolites included enterohepatic recirculation (EHR) (33) and contained 7 compartments (Figure 1). The model characterized the disposition of irinotecan with two compartments (a central and a peripheral compartment). The parameters for these two compartments were ke_total=(kSN+kAPC+ke), the total elimination of irinotecan (i.e., the sum of the irinotecan converted to SN-38 and APC, along with other elimination pathways) (1/hr); V (L/m2), the volume of the irinotecan central compartment; and kcp and kpc, the inter-compartmental parameters (1/hr). In addition, we computed irinotecan clearance as CL=ke*V (L/hr/m2). Finally, to allow for the identifiability of the parameters, we set the volumes of the SN-38, SN-38G, and APC compartments equal to the volume of the irinotecan compartment (V).
Three compartments described SN-38 concentrations over time. One compartment corresponded to plasma, and two compartments (bile and gut) characterized EHR. Specifically, kSN (1/hr) described the formation of SN-38 from irinotecan, and k30 (1/hr) described the elimination of SN-38. The transition of SN-38 from plasma to bile is described by k3B (1/hr), and kBG+kBG1 (1/hr) characterizes the transition of SN-38 from the bile to the gut. Specifically kBG is a constant parameter describing the baseline effect; kBG1 is a step function that is zero, except when the gall bladder is emptying into the gut. This emptying occurs from time EHRT to EHRT+1 (hr). The ratio of kBG1 to kBG provides a measure of the extent of enterohepatic recirculation. Finally, kG3 (1/hr) describes the reabsorption of the SN-38 into the plasma from the gut. SN-38G and APC are formed from SN-38 (k35) and irinotecan (kAPC), respectively, and eliminated with first-order kinetics (k50 for SN-38G and k70 for APC). We fit the model to each individual’s concentration-versus-time data using the maximum likelihood estimation algorithm as implemented in the ADAPT II software.(34)
Genetic variants
Table 1 lists the polymorphisms we considered, along with available references to genotyping methods. An appendix contains detailed genotyping methodology for several variants. Candidate genes reflected the role of enzymes and biliary transporters in the systemic disposition of irinotecan and its metabolites, as described in the Introduction. The vast majority of the candidate gene variants listed in Table 1 had expected frequencies of at least 10% in Caucasian and/or African-American populations. Some polymorphisms had three or fewer individuals homozygous for the rare allele; we combined them with the heterozygotes.
Table 1.
Polymorphisms considered in the analysis, with expected allele frequencies (allele in parentheses) from publicly available sources.
| Polymorphism | Expected allele frequencies in Caucasians | Expected allele frequencies in African-Americans | Genotyping |
|---|---|---|---|
| UGT1A1, −53A(TA)6>7TAA, PROMOTER | 0.709(6) | 0.62(6) | (15, 24) |
| :0.286(7) | :0.38(7) | ||
| UGT1A1, −3279G>T (UGT1A1*60), PBREM# | 0.47(G) | 0.85(G) | |
| :0.53(T) | :0.15(T) | ||
| UGT1A1, −3156G>A, PBREM | 0.69(G) | 0.715(G) | |
| :0.31(A) | :0.285(A) | ||
| UGT1A1, 211G>A (G71R), UGT1A1*6, EXON 1 | 0(A) | 0(A) | |
| :1(G) | :1(G) | ||
| UGT1A1, 686C>A (P229Q), UGT1A1*27, EXON 1 | 0(A) | 0(A) | |
| :1(C) | :1(C) | ||
| UGT1A7, 387G>T (N129K), EXON 1 | 0.646(G) | 0.522(G) | (Appendix2) |
| :0.354(T) | :0.478(T) | ||
| UGT1A7, 391C>A (R131K), EXON 1 | 0.646(G) | 0.522(G) | |
| :0.354(T) | :0.478(T) | ||
| UGT1A7, 622T>C (W208R), EXON 1 | 0.521(T) | 0.729(T) | |
| :0.479(C) | :0.271(C) | ||
| UGT1A9, −118(T)9>10, UGT1A9*1b, PROMOTER | 0.59(9) | 0.56(9) | (42) |
| :0.41(10) | :0.44(10) | ||
| UGT1A9, −2152C>T, PROMOTER | 0.91(C) | ||
| :0.09(T) | Unknown3 | ||
| UGT1A9, −275T>A, PROMOTER | 0.91(T) | ||
| :0.09(A) | Unknown3 | ||
| HNF-1α, 79A>C (I27L), EXON 1 | 0.75(A) | (Appendix2) | |
| :0.25(C) | Unknown3 | ||
| CYP3A4, −392A>G, CYP3A4*1B, 5’-UTR | 0.977(A) | 0.321(A) | (43) |
| :0.023(G) | :0.679(G) | ||
| CYP3A5, 6986A>G, CYP3A5*3, INTRON 3 | 0.023(A) | 0.633(A) | |
| :0.977(G) | :0.367(G) | ||
| SLCO1B1, 388A>G (N130D), SLCO1B1*1b, EXON 4 | 0.396(C) | 0.717(C) | (Appendix2) |
| :0.604(T) | :0.283(T) | ||
| SLCO1B1, 521T>C (V174A), SLCO1B1*15, EXON 5 | 0.083(C) | 0.022(C) | |
| :0.917(T) | :0.978(T) | ||
| ABCC1, 1062T>C (N354N), EXON 9 | 0.458(C) | 0.643(C) | (44) |
| :0.542(T) | :0.357(T) | ||
| ABCC1, +8A>G, INTRON 9 | 0.643(A) | 0.433(A) | |
| :0.357(G) | :0.567(G) | ||
| ABCC1, −48C>T, INTRON 11 | 0.146(T) | 0(T) | |
| :0.854(C) | :1.0(C) | ||
| ABCC1, 1684T>C (L562L), EXON 13 | 0.917(C) | 0.848(C) | |
| :0.083(T) | :0.152(T) | ||
| ABCC1, −30C>G, INTRON 18 | 0.042(C) | 0.217(C) | |
| :0.958(G) | :0.783(G) | ||
| ABCC1, 4002G>A (S1334S), EXON 28 | 0.688(C) | 0.955(C) | |
| :0.312(T) | :0.045(T) | ||
| ABCC1, +18A>G, INTRON 30 | 0.213(T) | 0.042(T) | |
| :0.787(C) | :0.958(C) | ||
| ABCC2, −1549A>G, 5’-Flanking region | 0.43(A) | 0.485(A) | (44) |
| :0.57(G) | 0.515(G) | ||
| ABCC2, −1019A>G, 5’-Flanking region | 0.43(G) | 0.365(G) | |
| :0.57(A) | :0.635(A) | ||
| ABCC2, −24C>T, 5’-UTR | 0.230(A) | 0.06(A) | |
| :0.770(G) | :0.940(G) | ||
| ABCC2, 1249G>A (V417I), EXON 10 | 0.146(A) | 0.239(A) | |
| :0.854(G) | :0.761(G) | ||
| ABCC2, −34T>C, INTRON 26 | 0.17(C) | 0.25(C) | |
| :0.83(T) | :0.75(T) | ||
| ABCC2, 3972C>T (I1324I), EXON 28 | 0.380(A) | 0.280(A) | |
| :0.620(G) | :0.720(G) | ||
| ABCB1, −129T>C, 5’-UTR | 0.620(C) | 0.043(C) | (44) |
| :0.938(T) | :0.957(T) | ||
| ABCB1, −25G>T, INTRON 4 | 0.273(T) | 0.385(T) | |
| :0.737(G) | :0.615(G) | ||
| ABCB1, −44A>G, INTRON 9 | 0.409(C) | 0.20(C) | |
| :0.591(T) | :0.80(T) | ||
| ABCB1, 1236C>T (G412G), EXON 12 | 0.523(C) | 0.864(C) | |
| :0.477(T) | :0.136(T) | ||
| ABCB1, +24C>T, INTRON 13 | 0.50(T) | 0.467(T) | |
| :0.50(C) | :0.533(C) | ||
| ABCB1, +38A>G, INTRON 14 | 0.429(A) | 0.389(A) | |
| :0.571(G) | :0.611(G) | ||
| ABCB1, 2677G>A/T (A893T/S), EXON 21 | 0.614(G) | 0.923(G) | |
| :0.386(T) | :0.077(T) | ||
| ABCB1, 3435C>T (I1145I), EXON 26 | 0.375(C) | 0.848(C) | |
| :0.625(T) | :0.152(T) | ||
| ABCG2, 34G>A (V12M), EXON 2 | 0.017(A) | 0.071(A) | (Appendix2) |
| :0.983(G) | :0.929(G) | ||
| ABCG2, 421C>A (Q141K), EXON 5 | 0.045(A) | 0.023(A) | |
| :0.955(C) | :0.977(C) | ||
| CES2, −363C>G, 5’-UTR | 0.810(C) | 0.733(C) | (Appendix2) |
| :0.190(G) | :0.267(G) | ||
| CES2, +1361A>G, INTRON 1 | 0.143(G) | 0.438(G) | |
| :0.857(A) | :0.562(A) | ||
| CES2, 108C>G, 3’-UTR | 0.004(G) | 0(G) | |
| :0.996(C) | :1.0(C) | ||
PBREM, phenobarbital-responsive enhancer module
Appendix with genotyping information is available as supplementary material at http://www.nature.com/cpt
Data are not publicly available
Statistical Methods
We applied the statistical method PCA (35) to reduce the dimensionality of the multivariate phenotype characterized by the parameters in the pharmacokinetic model. Briefly, PCA yields linear combinations of the variables such that these new measures explain most of the variation in the data. These linear combinations are mutually orthogonal. The principal components (PCs) are, in fact, the eigenvectors of the data space.(35) The percent of total variation explained by each principal component is related to the PC’s associated eigenvalue.
Once one has computed and put all of the PCs in descending eigenvalue order, one generally finds that the last few PCs account for negligible amounts of variation. Thus, one can drop these last PCs and still have a set of components that accounts for almost all of the total variation in the data set. In this way, PCA reduces the dimension of the problem.
Each of the PCs may be difficult to interpret, being combinations of model parameters. We applied varimax rotation (35, 36) to aid interpretation. This method reorients the set of retained PCs in a way that often improves interpretability while leaving alone the total variation explained by the set. The reorientation maximizes the association of each PC with at least one of the data variables while minimizing the association with other variables. Additionally, each variable will associate with at least one PC.
With fewer PCs than variables, the end result will be PCs that each align with one or several pharmacokinetic parameters. If the model parameters having the greatest association with a PC also relate to a particular section of the compartmental pharmacokinetic model (Figure 1), then we can use this single PC to represent that part of the model. In this way, rotation could allow us to interpret the PCs in terms of the drug’s metabolic pathways. We then have a single measure for a pharmacokinetic pathway and avoid carrying out separate analyses for each model parameter.
We computed PC-specific scores for each patient as patient-specific measures that related to pathways in the model. Each patient’s score for a particular PC is the product of the PC’s coefficients (after rotation) times the patient’s corresponding parameter estimates. The PC coefficients (also called loadings) reflect the weight of each pharmacokinetic parameter in the composition of the PC. Variation in the scores across patients reflected variation in the corresponding pharmacokinetic pathways.
We explored relationships between pharmacokinetics (i.e., the PCs) and genetic polymorphisms by regressing the PC scores on the genetic information (analysis of variance or ANOVA). That is, the patient-specific PC scores served as phenotypes corresponding to particular pathways in the pharmacokinetics of irinotecan. Any polymorphism that explained some of the variation in the PC scores in the data set would appear to be associated with the pathway.
We computed the PCs using the logarithms of the pharmacokinetic parameter estimates, because of skewness in the data. Since the magnitudes for the parameters varied widely, we standardized the data by subtracting the sample mean and dividing by the sample standard deviation. Standardizing the variables before applying PC analysis keeps the first PC from picking up large variation arising because of measurement units (e.g., volumes versus rate parameters). In essence, we analyzed the correlation matrix rather than the covariance matrix. We computed the PCs with the function “prcomp” in the statistical analysis environment R.(37)
For each PC-polymorphisms analysis, we considered each of the possible models that might characterize the influence of a polymorphism on the PC-based phenotype. We considered the null model (no difference between the genotype groups), a dominant model for the rare allele, and a recessive model for the rare allele. We also considered an additive model, in which the phenotype changed linearly across genotype levels, from homozygous for the common allele to heterozygote to homozygous for the rare allele. We did not fit a full ANOVA model for all three genotype groups, since we did not consider the possibility of overdominance, i.e., the two homozygote groups are the same but differ from the heterozygotes.
We used a 5% cutoff for two-sided p values to declare associations significant, and we did not adjust for multiple comparisons in this exploratory analysis. We also evaluated the strength of evidence of the associations using Bayes factors. They have the advantage that, unlike p values, they are not influenced by sample size and arise naturally from a Bayesian view of inference.(38, 39) A Bayes factor ≥3.2 (= √10), as suggested by Jeffreys (40), indicated strong evidence of association (i.e., large Bayes factors). We computed the Bayes factors using an objective prior based on Zellner’s gprior corresponding to unit information.(41) When carrying out the regression analysis, we first centered the independent categorical variables (genotypes). The prior distribution for the residual variance was inverse-gamma with shape and scale parameters equal to 4. This prior is proper but still allows the data to dominate inference.
Supplementary Material
Supplementary information is available at http:// www.nature.com/cpt
Acknowledgements
This research was partially supported by NIH grants GM61393 and CA075981. We thank Jackie Ramirez for her help with the allele frequencies and two reviewers for their helpful comments.
References
- 1.Rivera F, Vega-Villegas ME, Lopez-Brea MF. Chemotherapy of advanced gastric cancer. Cancer Treat Rev. 2007;33:315–324. doi: 10.1016/j.ctrv.2007.01.004. [DOI] [PubMed] [Google Scholar]
- 2.Markman M. New, expanded, and modified use of approved antineoplastic agents in ovarian cancer. Oncologist. 2007;12:186–190. doi: 10.1634/theoncologist.12-2-186. [DOI] [PubMed] [Google Scholar]
- 3.MacCallum C, Gillenwater HH. Second-line treatment of small-cell lung cancer. Curr Oncol Rep. 2006;8:258–264. doi: 10.1007/s11912-006-0030-8. [DOI] [PubMed] [Google Scholar]
- 4.Kumar A, Wakelee H. Second-and third-line treatments in non-small cell lung cancer. Curr Treat Options Oncol. 2006;7:37–49. doi: 10.1007/s11864-006-0030-9. [DOI] [PubMed] [Google Scholar]
- 5.Garcia-Carbonero R, Supko JG. Current perspectives on the clinical experience, pharmacology, and continued development of the camptothecins. Clin Cancer Res. 2002;8:641–661. [PubMed] [Google Scholar]
- 6.Humerickhouse R, Lohrbach K, Li L, Bosron WF, Dolan ME. Characterization of CPT-11 hydrolysis by human liver carboxylesterase isoforms hCE-1 and hCE-2. Cancer Res. 2000;60:1189–1192. [PubMed] [Google Scholar]
- 7.Santos A, Zanetta S, Cresteil T, Deroussent A, Pein F, Raymond E, et al. Metabolism of irinotecan (CPT-11) by CYP3A4 and CYP3A5 in humans. Clin Cancer Res. 2000;6:2012–2020. [PubMed] [Google Scholar]
- 8.Iyer L, Ratain MJ. Clinical pharmacology of camptothecins. Cancer Chemother Pharmacol. 1998;42 Suppl:S31–S43. doi: 10.1007/s002800051077. [DOI] [PubMed] [Google Scholar]
- 9.Gagne JF, Montminy V, Belanger P, Journault K, Gaucher G, Guillemette C. Common human UGT1A polymorphisms and the altered metabolism of irinotecan active metabolite 7-ethyl-10-hydroxycamptothecin (SN-38) Mol Pharmacol. 2002;62:608–617. doi: 10.1124/mol.62.3.608. [DOI] [PubMed] [Google Scholar]
- 10.Ciotti M, Basu N, Brangi M, Owens IS. Glucuronidation of 7-ethyl-10-hydroxycamptothecin (SN-38) by the human UDP-glucuronosyltransferases encoded at the UGT1 locus. Biochem Biophys Res Commun. 1999;260:199–202. doi: 10.1006/bbrc.1999.0453. [DOI] [PubMed] [Google Scholar]
- 11.Mathijssen RH, van Alphen RJ, Verweij J, Loos WJ, Nooter K, Stoter G, et al. Clinical pharmacokinetics and metabolism of irinotecan (CPT-11) Clin Cancer Res. 2001;7:2182–2194. [PubMed] [Google Scholar]
- 12.Luo FR, Paranjpe PV, Guo A, Rubin E, Sinko P. Intestinal transport of irinotecan in Caco-2 cells and MDCK II cells overexpressing efflux transporters Pgp, cMOAT, and MRP1. Drug Metab Dispos. 2002;30:763–770. doi: 10.1124/dmd.30.7.763. [DOI] [PubMed] [Google Scholar]
- 13.Ma MK, McLeod HL. Lessons learned from the irinotecan metabolic pathway. Curr Med Chem. 2003;10:41–49. doi: 10.2174/0929867033368619. [DOI] [PubMed] [Google Scholar]
- 14.Nozawa T, Minami H, Sugiura S, Tsuji A, Tamai I. Role of organic anion transporter OATP1B1 (OATP-C) in hepatic uptake of irinotecan and its active metabolite, 7-ethyl-10-hydroxycamptothecin: in vitro evidence and effect of single nucleotide polymorphisms. Drug Metab Dispos. 2005;33:434–439. doi: 10.1124/dmd.104.001909. [DOI] [PubMed] [Google Scholar]
- 15.Innocenti F, Undevia SD, Iyer L, Chen PX, Das S, Kocherginsky M, et al. Genetic variants in the UDP-glucuronosyltransferase 1A1 gene predict the risk of severe neutropenia of irinotecan. J Clin Oncol. 2004;22:1382–1388. doi: 10.1200/JCO.2004.07.173. [DOI] [PubMed] [Google Scholar]
- 16.Minami H, Sai K, Saeki M, Saito Y, Ozawa S, Suzuki K, et al. Irinotecan pharmacokinetics/pharmacodynamics and UGT1A genetic polymorphisms in Japanese: roles of UGT1A1*6 and *28. Pharmacogenet Genomics. 2007;17:497–504. doi: 10.1097/FPC.0b013e328014341f. [DOI] [PubMed] [Google Scholar]
- 17.Han JY, Lim HS, Shin ES, Yoo YK, Park YH, Lee JE, et al. Comprehensive analysis of UGT1A polymorphisms predictive for pharmacokinetics and treatment outcome in patients with non-small-cell lung cancer treated with irinotecan and cisplatin. J Clin Oncol. 2006;24:2237–2244. doi: 10.1200/JCO.2005.03.0239. [DOI] [PubMed] [Google Scholar]
- 18.Mathijssen RH, Marsh S, Karlsson MO, Xie R, Baker SD, Verweij J, et al. Irinotecan pathway genotype analysis to predict pharmacokinetics. Clin Cancer Res. 2003;9:3246–3453. [PubMed] [Google Scholar]
- 19.Zhou Q, Sparreboom A, Tan EH, Cheung YB, Lee A, Poon D, et al. Pharmacogenetic profiling across the irinotecan pathway in Asian patients with cancer. Br J Clin Pharmacol. 2005;59:415–424. doi: 10.1111/j.1365-2125.2004.02330.x. [DOI] [PMC free article] [PubMed] [Google Scholar]
- 20.Klein CE, Gupta E, Reid JM, Atherton PJ, Sloan JA, Pitot HC, et al. Population pharmacokinetic model for irinotecan and two of its metabolites, SN-38 and SN-38 glucuronide. Clin Pharmacol Ther. 2002;72:638–647. doi: 10.1067/mcp.2002.129502. [DOI] [PubMed] [Google Scholar]
- 21.Xie R, Mathijssen RH, Sparreboom A, Verweij J, Karlsson MO. Clinical pharmacokinetics of irinotecan and its metabolites: a population analysis. J Clin Oncol. 2002;20:3293–3301. doi: 10.1200/JCO.2002.11.073. [DOI] [PubMed] [Google Scholar]
- 22.Kim TW, Innocenti F. Insights, challenges, and future directions in irinogenetics. Ther Drug Monit. 2007;29:265–270. doi: 10.1097/FTD.0b013e318068623b. [DOI] [PubMed] [Google Scholar]
- 23.Takasuna K, Hagiwara T, Hirohashi M, Kato M, Nomura M, Nagai E, et al. Involvement of {beta}-Glucuronidase in Intestinal Microflora in the Intestinal Toxicity of the Antitumor Camptothecin Derivative Irinotecan Hydrochloride (CPT-11) in Rats. Cancer Res. 1996;56:3752–3757. [PubMed] [Google Scholar]
- 24.Iyer L, King CD, Whitington PF, Green MD, Roy SK, Tephly TR, et al. Genetic predisposition to the metabolism of irinotecan (CPT-11). Role of uridine diphosphate glucuronosyltransferase isoform 1A1 in the glucuronidation of its active metabolite (SN-38) in human liver microsomes. J Clin Invest. 1998;101:847–854. doi: 10.1172/JCI915. [DOI] [PMC free article] [PubMed] [Google Scholar]
- 25.Kehrer DFS, Sparreboom A, Verweij J, de Bruijn P, Nierop CA, van de Schraaf J, et al. Modulation of Irinotecan-induced Diarrhea by Cotreatment with Neomycin in Cancer Patients. Clin Cancer Res. 2001;7:1136–1141. [PubMed] [Google Scholar]
- 26.Hoglund P, Ohlin M. Effect modelling for drugs undergoing enterohepatic circulation. Eur J Drug Metab Pharmacokinet. 1993;18:333–338. doi: 10.1007/BF03190182. [DOI] [PubMed] [Google Scholar]
- 27.Westerling D, Frigren L, Hoglund P. Morphine pharmacokinetics and effects on salivation and continuous reaction times in healthy volunteers. Ther Drug Monit. 1993;15:364–374. doi: 10.1097/00007691-199310000-00003. [DOI] [PubMed] [Google Scholar]
- 28.de Jong FA, Kitzen JJ, de Bruijn P, Verweij J, Loos WJ. Hepatic transport, metabolism and biliary excretion of irinotecan in a cancer patient with an external bile drain. Cancer Biol Ther. 2006;5:1105–1110. doi: 10.4161/cbt.5.9.3294. [DOI] [PubMed] [Google Scholar]
- 29.Godfrey K. Compartment Models and Their Application. New York: Academic Press; 1983. [Google Scholar]
- 30.Delampady M, Berger JO. Lower Bounds on Bayes Factors for Multinomial Distributions, with Application to Chi-Squared Tests of Fit. Ann Statist. 1990;18:1295–1316. [Google Scholar]
- 31.Innocenti F, Undevia SD, Ramirez J, Mani S, Schilsky RL, Vogelzang NJ, et al. A phase I trial of pharmacologic modulation of irinotecan with cyclosporine and phenobarbital. Clin Pharmacol Ther. 2004;76:490–502. doi: 10.1016/j.clpt.2004.07.016. [DOI] [PubMed] [Google Scholar]
- 32.Iyer L, Das S, Janisch L, Wen M, Ramirez J, Karrison T, et al. UGT1A1*28 polymorphism as a determinant of irinotecan disposition and toxicity. Pharmacogenomics J. 2002;2:43–47. doi: 10.1038/sj.tpj.6500072. [DOI] [PubMed] [Google Scholar]
- 33.Shou M, Lu W, Kari PH, Xiang C, Liang Y, Lu P, et al. Population pharmacokinetic modeling for enterohepatic recirculation in Rhesus monkey. Eur J Pharm Sci. 2005;26:151–161. doi: 10.1016/j.ejps.2005.05.010. [DOI] [PubMed] [Google Scholar]
- 34.D'Argenio DZ, Schumitzky A. ADAPT II User's Guide: Pharmacokinetic / Pharmacodynamic Systems Analysis Software. Los Angeles: Biomedical Simulations Resource; 1997. [Google Scholar]
- 35.Jolliffe IT. Principal Component Analysis. 2nd edn. New York: Springer; 2002. [Google Scholar]
- 36.Kaiser HF. The Varimax Criterion for Analytic Rotation in Factor Analysis. Psychometrika. 1958;23:187–200. [Google Scholar]
- 37.Team" RDCR. A Language and Environment for Statistical Computing. Manual. Vienna, Austria: R Foundation for Statistical Computing; 2007. [Google Scholar]
- 38.Kass RE, Raftery AE. Bayes Factors. J Am Stat Assoc. 1995;90:773–795. [Google Scholar]
- 39.Goodman SN. Toward evidence-based medical statistics. 2: The Bayes factor. Annals of Internal Medicine. 1999;130:1005–1013. doi: 10.7326/0003-4819-130-12-199906150-00019. [DOI] [PubMed] [Google Scholar]
- 40.Jeffreys H. Theory of Probability. 3 edn. Oxford, U.K.: Oxford University Press; 1961. [Google Scholar]
- 41.Zellner A. On Assessing Prior Distributions and Bayesian Regression Analysis with g-Prior Distributions. In: Goel PK, Zellner A, editors. Basic Bayesian Inference and Decision Techniques: Essays in Honor of Bruno de Finetti. Amsterdam: North-Holland; 1986. pp. 233–243. [Google Scholar]
- 42.Innocenti F, Liu W, Chen P, Desai AA, Das S, Ratain MJ. Haplotypes of variants in the UDP-glucuronosyltransferase1A9 and 1A1 genes. Pharmacogenet Genomics. 2005;15:295–301. doi: 10.1097/01213011-200505000-00004. [DOI] [PubMed] [Google Scholar]
- 43.Blanco JG, Edick MJ, Hancock ML, Winick NJ, Dervieux T, Amylon MD, et al. Genetic polymorphisms in CYP3A5, CYP3A4 and NQO1 in children who developed therapy-related myeloid malignancies. Pharmacogenetics. 2002;12:605–611. doi: 10.1097/00008571-200211000-00004. [DOI] [PubMed] [Google Scholar]
- 44.Leabman MK, Huang CC, DeYoung J, Carlson EJ, Taylor TR, de la Cruz M, et al. Natural variation in human membrane transporter genes reveals evolutionary and functional constraints. Proc Natl Acad Sci U S A. 2003;100:5896–5901. doi: 10.1073/pnas.0730857100. [DOI] [PMC free article] [PubMed] [Google Scholar]
Associated Data
This section collects any data citations, data availability statements, or supplementary materials included in this article.
Supplementary Materials
Supplementary information is available at http:// www.nature.com/cpt