Skip to main content
PMC home page
Bioinformatics logoLink to Bioinformatics
. 2009 Jul 20;25(20):2677–2684. doi: 10.1093/bioinformatics/btp442

Multi-dimensional correlations for gene coexpression and application to the large-scale data of Arabidopsis

Kengo Kinoshita 1,2,*, Takeshi Obayashi 1
PMCID: PMC2759550  PMID: 19620096

Abstract

Background: Recent improvements in DNA microarray techniques have made a large variety of gene expression data available in public databases. This data can be used to evaluate the strength of gene coexpression by calculating the correlation of expression patterns among different genes between many experiments. However, gene expression levels differ significantly across various tissues in higher organisms, as well as in different cellular location in eukaryotes in different cell state. Thus the usual correlation measure can only evaluate the difference of tissues or cellular localizations, and cannot adequately elucidate the functional relationship from the coexpression of genes.

Method: We propose a new measure of coexpression by expanding the generally used correlation into a multidimensional one. We used principal component analyses to identify the major factors of gene expression correlation, and then re-calculate the correlation by subtracting the major components in order to remove biases cased by a few experiments. The repeated subtractions of the major components yielded a set of correlation values for each pair of genes. We observed the correlation changes when the first ten principal components were subtracted step-by-step in large-scale Arabidopsis expression data.

Results: We found two extreme patterns of correlation changes, corresponding to stable and fragile coexpression. Our new indexes provided a good means to determine the functional relationships of the genes, by examining a few examples, and higher performance of Gene Ontology term prediction by using the support vector machine and the multidimensional correlation.

Availability: The results are available from the expression detail pages in ATTED-II (http://atted.jp).

Contact: kinosita@hgc.jp

Supplementary information: Supplementary data are available at Bioinformatics online.

1 INTRODUCTION

Biological functions of genes are usually determined by the interactions of gene products or proteins, and thus genes in related biological processes are often expressed cooperatively. Therefore, gene coexpression can provide key information to understand complex biological systems (Eisen et al., 1998; Lee, et al., 2004a, b). Gene coexpression data has been used in the design of a wide variety of experiments, such as gene targeting, regulatory investigations and identification of potential partners in protein–protein interactions (Aoki et al., 2007; Shoemaker and Panchenko, 2007).

In principle, coexpressed gene sets can be determined by using two or more samples. When a small number of samples are used, the biological meaning of coexpression is straightforward and thus it is very useful for target-specific studies (Bulow et al., 2007; Hughes et al., 2000; Shapira et al., 2004; Spellman, et al., 1998). On the other hand, although the biological meaning may be obscure, coexpression with a large number of samples may provide more reliable and general co-regulatory relationships among genes. As a result, many coexpression databases with large-scale data have been constructed and are widely used (Manfield et al., 2006; Obayashi et al., 2007, 2008, 2009; Steinhauser et al., 2004; Toufighi et al., 2005; Zimmermann et al., 2005).

As a consequence of the vast accumulation of high quality expression data in public databases (Barrett et al., 2007; Craigon et al., 2004; Ikeo et al., 2003; Parkinson et al., 2007; Shi et al., 2006; Swarbreck et al., 2008), coexpression databases with large-scale data are gaining increasing importance, as they have the potential power to unravel complicated biological systems. In addition, coexpression data are very useful to reveal integrated networks in combination with protein–protein interaction data (Lee et al., 2004a, b, 2008), to predict protein–protein interactions (Cui et al., 2008), or the functions of gene products (Aoki et al., 2007). However, a major drawback of using large-scale coexpression data is that some frequently contributed data can determine almost all of the strength of coexpression. For example, a pair of genes encoding proteins in the same tissue, such as a subunit of light harvesting complex (LHCB) and a subunit of cytochrome b6f complex (PETC), can have high correlation values, even though they only have weak functional relations, but are located in the same organelle, such as the chloroplast thylakoid membrane.

In this study, we describe a new approach to reduce the unbalanced effects of the small number of experiments, by using principal component analyses (PCA) in samples space. Among the other available techniques, we tried to use biclustering algorithms, where the clusters with correlated genes and supported subsets of samples were found (Prelic et al., 2006), but the algorithm could not be applied for the large number of genes and samples used in this study, mainly due to the large calculation costs. The other problems of biclustering algorithm for the large dataset is described in Hibbs et al. (2007). Progressive iterative signature algorithm (PISA) is another interesting approach, where larger functional modules are iteratively identified and removed to find more subtle functional modules (Kloster et al., 2005). But, as in the case of biclusters, PISA algorithm is focused on the finding of the functional modules rather than the refinements of the pair relations. These techniques are designed to obtain the good functional groups, but we would like to focus on the improvement of the gene-to-gene relationship to construct better networks. When the number of ‘primary variables’ that affect the expression level is limited, surrogate variable analysis (SVA) will give fruitful information (Leek and Storey, 2007), but it may be difficult to apply SVA to the dataset including many possible sources for expression variations. PCA is a popular technique used to find the major component of multivariate data, in DNA microarray analyses, it is used to find the gene groups that cooperatively change expressions over several experiments (Brunet et al., 2004), where PCA is done in gene space. We used a similar technique to identify the groups of similar samples in this study, to reveal the samples with large contributions. We applied the method to analyze the large-scale expression data in Arabidopsis thaliana taken from TAIR (Swarbreck et al., 2008), where 1388 samples and 22 746 probes were available for the analyses. Our results revealed two extreme patterns of coexpression changes, when we subtracted the effects of samples with large contributions one-by-one. We also show that the change of expression patterns is a good indicator of the functional relationships between genes.

2 MATERIALS AND METHODS

2.1 Expression Data

Raw data were obtained from AtGenExpress at TAIR as of the end of 2007. We selected the data from the Affy 22k GeneChip, which is one of the most frequently used platforms in Arabidopsis. All of the expression levels were treated in logarithmic scale with the base of 2, and were normalized by subtracting the average expression levels for each gene after MAS5 summarization by R/BioConductor. The numbers of samples and probes of the GeneChip were 1388 and 22 746, respectively.

2.2 PCA

PCA was performed in the sample space. The expression level of each probe was treated as a 1 388 dimensional vector Ep, and PCA was performed in the 1388 dimensional spaces by using R. As a result, the number of principal components (PCs) with the orthogonal basis vector rjPC (j = 1… n, n = 1388) was obtained. Pearson's correlations in the PC space without the first i PCs between probe p and q was calculated for the projected expression values epj by

graphic file with name btp442m1.jpg (1)

where μpi and σpi are the mean and standard deviation of epj without the first i elements, i.e. j = i + 1,…, n. The epj was obtained by

graphic file with name btp442m2.jpg (2)

The calculation of cor0 is done in the PCA space, thus it corresponds to the signal balancing approach used in Hibbs et al. (2007).

2.3 Gene Ontology (GO) term assignment to each gene

Due to the hierarchical topology of the GO terms and the different importance of the terms, we had to select appropriate GO terms to represent the gene functions. The selection was conducted based on the information content of the GO terms. All annotations were first mapped to all upper GO terms, up to the root terms. Since the terms associated with too many genes are less informative, they cannot be used to design new experiments. We fixed the lower limit to 5 and checked the upper limits of 10, 20, 50, 100 and 500, and observed the true positive rate, or the ratio of the gene pairs sharing the same GO term. As a result, the ratios were not much different in 20-all upper limits, but increased for the upper limit 10. Although we would like to use specific term as possible, we should avoid the artifact caused by this upper limit, and thus we used GO terms associated with from 5 to 20 genes. As a result, 376 Biological Process (BP) terms, 79 Cellular Component (CC) terms and 268 Molecular Function (MF) terms were selected, which resulted in 2280, 648 and 2035 genes in each category with the GO terms. Although we chose this gene number range based on the characteristics of the randomized coexpressed gene lists, our results are not affected by selection of other ranges.

2.4 GO prediction by SVM with multidimensional correlation

GO predictions by support vector machine (SVM) were performed for each GO category with libsvm version 2.86, with the radial basis function kernel (Fan et al., 2005). For each GO category, 20 000 pairs of probe sets were selected randomly and 5000 pairs of them were used for training of a SVM and the remaining pairs were used to evaluate the performance by using the trained SVM. For each pair of the probe set, we have 11 correlations as described, and the first n correlations were used as the input vectors of the SVM. For example, in the case of n = 3, the 3D vector (cor0, cor1, cor2) was an input. Note that one-dimensional vector was used for the prediction based on the Pearson's correlation (PCC) and Spearman's correlation (SCC). We judged a probe pair to be functionally related, if the GO terms of the corresponding genes of the probe sets share one or more common GO terms.

Optimum value of kernel parameter gamma and cost parameter C for object functions were searched by considering all the combination of 2L for gamma and 2M for C(L = −15… 3, M = −5… 15) according to the recommended protocol of libsvm (Fan et al., 2005). For each combination, we repeated the training and test for 100 times and calculated the mean and standard deviation of the area under the receiver operating characteristic (ROC) curve, and the gamma and C-values for the best mean value were selected. SVM is a binary classifier, and thus to obtain the ROC curves, we calculated the distance from the decision plane and used it as the prediction score (Ishida and Kinoshita, 2007). The numbers of correlations used to obtain the best performance are shown in parentheses of Table 2 in the Results and Discussion section. The gamma and C values for the best performance were (215, 2−15) for CC with six correlations, (2−4, 2−9) for BP with six correlations, (2−1, 2−14) for MF with three correlations, respectively.

Table 2.

GO prediction performance by AUC

CC BP MF
PCC 0.694±0.0086 0.609±0.015 0.603±0.018
SCC 0.688±0.0009 0.628±0.0001 0.607±0.0002
SVMmcor 0.733±0.014 (6) 0.645±0.029 (6) 0.641±0.024 (3)
Open in a new tab

Prediction performance based on PCC, SCC and SVMmcol. The number in the parenthesis is the number of used correlations for multidimensional correlations. See section ‘Materials and methods’ for details.

3 RESULTS AND DISCUSSION

3.1 Dataset

All of the microarray data were obtained from TAIR (Swarbreck et al., 2008) as of the end of 2007, and we selected the Affymetrix GeneChip 25 k ATH1 data with raw values, so that we could perform the normalization ourselves. All of the expression levels were normalized by the MAS5 algorithm with R. After the normalization, the average expression value for each probe set for all sample groups was calculated, and then subtracted from each expression value to remove the difference of the basal expression level of each probe set. On the Affymetrix GeneChip 25 k, we used the entire probe set (22 746 probe sets) for the calculation of PCA, and finally, we used 20 628 probe sets that can be mapped onto single genes.

3.2 PCA in sample space

By applying PCA in sample space, we obtained 1388 PCs, which correspond to the number of samples. As shown in Supplementary Figure S1, 23.8% (330) of the PCs are necessary to describe 80% of the variation of the 1388 samples, and the contribution of the first 10 PCs is 28.9% (Figure S1). We observed the correlation changes on subtracting the contribution from the first 10 PCs, which is comparable to the number of informative experiments proposed by Fukushima et al. (2008). They argued that a small number of samples (∼20) is enough to reproduce the Pearson's correlation values by all experiments, and they tried to find the core experiments. However, we would like to remove the unbalancing effects from the core experiments in order to observe more weak correlations and to understand the gene functions. In short, we consider 11 correlations for a pair of probe sets; the correlation with all expression data, the correlation without the first PC, that without the first two PCs, and that without the first 10 PCs, respectively. See Section 2.2 for the calculation details.

3.3 Correlation change overview and measurement of stability

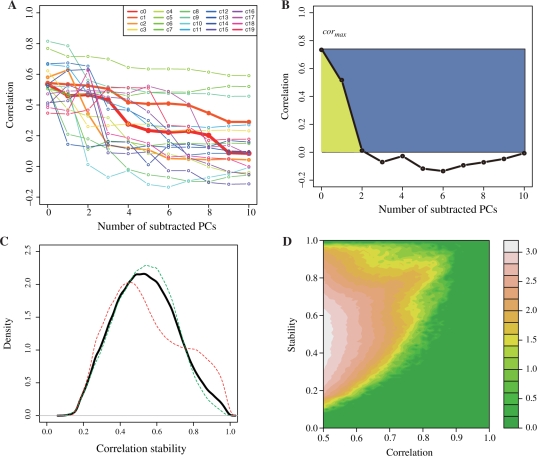
A correlation change for each pair of probe sets was visualized by using a line plot with 11 data points, as in Figure 1, where the 11 data points correspond to the number of correlations considered in this study. Thus, we obtained 22746C2 lines (22 746 = the number of probe sets). To focus on the modestly coexpressed gene pairs, we chose the pairs of probe sets with a correlation value of 0.5 in at least one of the 11 correlations, yielding 563 585 pairs, which corresponded to 0.22 % of all possible pairs of probe sets. Since the number is still too large to grasp the general tendency, we carried out single linkage clustering by using root mean square deviations (rmsd) between two pairs of lines as a distance of correlation changes, and found 167 clusters with <0.1 rmsd threshold and 3470 clusters with <0.05 rmsd threshold. The latter clusters were used for the following analyses, and some of the former clusters are displayed in Figure 1A to show the general trends of correlation changes. The number of pairs in the cluster, or the cluster size, has approximate power law distribution as shown in Supplementary Figure S2. In other words, there are very few popular clusters, while there are many rare clusters. The first 20 clusters actually contain 551 851 pairs, corresponding to 97.9% of all gene pairs. The top 20 clusters for the 3470 clusters are also shown in the Supplementary Figure S3. Please note that denote the cluster number starting with c for the cluster with <0.1 rmsd threshold and c′ for that with <0.05.

Fig. 1.

Fig. 1.

Open in a new tab

(A) Frequently observed patterns of correlation changes revealed by rough clustering (rmsd <0.1), (B) schematic explanation of stability values, S, for the correlation change, (C) the distribution of stability values for all pairs we consider (black), the pairs with decrease cases (green) and those with increase cases (red), where the number of probe pairs, the mean of the S values and its standard deviation for the decrease cases are 430 866 (76.5%), 0.533 and 0.159, respectively, while those for the increase cases are 132 719 (23.5%), 0.547 and 0.199, and (D) frequency plot to show the relationship between correlation and stability. Frequency is shown in 10 base logarithmic scales. The stability tends to be high for the gene pairs with >0.7 correlations, but for the pairs with <0.7 correlations their correlations are usually fragile as indicated by low stability.

Figure 1A shows the 20 most frequently observed clusters among the above 167 clusters. Each line corresponds to one cluster, and the correlation values for each cluster were taken from an arbitrary probe pairs in the cluster. The thicknesses of the lines indicate the number of pairs in each cluster, where a thicker line means a larger cluster. As shown in the figure, the most frequently observed patterns (red and orange lines) were just what we expected, where the correlation values gradually decreased with the increase in the number of PCs to be subtracted. However, there are also two extreme patterns, such as the three lines at the upper right (slow decrease) and the four cases at the lower left (rapid decrease).

To evaluate these changes more quantitatively, we defined a measure of stability of correlation change (S) by

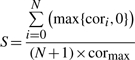graphic file with name btp442m3.jpg (3)

where cori is the correlation without the first i PCs, cormax is their maximum value (i =0… N), and N = 10 was used in this study. The numerator and denominator correspond to the area under the curve and that between cormax and 0.0, which is the ratio of the yellow area to the total of the blue and yellow areas in Figure 1B. Therefore, the S-values will change from 0.0 to 1.0, and the larger S-values indicate stable correlations or small changes of correlations, while smaller S-values mean fragile coexpression, or imply that the cor0 was determined from a small number of experiments.

The distribution of the S-values for all modestly coexpressed gene pairs (black line) is shown in Figure 1C. The mean and standard deviation of S are 0.536 and 1.169, respectively. It may be noteworthy that only 6.89% (38 708) pairs of probe sets have stability values of 0.8 or more. The relationship between stability and cor0 is shown in Figure 1D, where we can see that the gene pairs with < 0.7 are often fragile. The stability of every gene pair is now available from the ATTED-II database (http://atted.jp) (Obayashi et al., 2009).

In addition, when we defined the correlation change as a ‘decrease pattern’ if cormax =cor0, and an ‘increase case’ for others, 76.5% (430 866) of the patterns are decrease ones and 23.5% (132 719) of the patterns are increase ones. For both cases, high stability indicate a small change in the correlation upon the subtraction of the main PCs, and thus the difference between the increase and decrease patterns is not significant, while their differences become meaningful when the S-value is small. In any case, a pair of probe sets with high cormax but small S-values indicates that their correlation comes only from a few major experiments, and is fragile. Thus, the S-values are a good measure to evaluate the importance of the coexpression along with the cor0 value. We use some examples to describe this later. The distributions of the S-values for the increase and decrease cases are also shown in Figure 1C.

To obtain the biological meaning of the correlation changes, we observed the coexpression changes of the Arabidopsis genes involved in photosystem II (PS-II) and in glycerolipid metabolism. The former genes were selected as the genes with the GO term of GO:0009523 as of April 11, 2008 (Ashburner et al., 2000) and the latter ones were chosen from their KEGG annotations (Kanehisa et al., 2008).

3.4 Correlation change for a specific case: Photosystem II

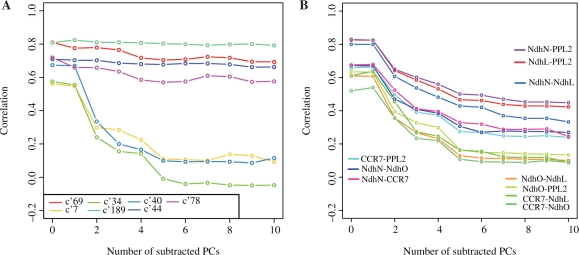
In our dataset, 19 genes and 135 pairs of corresponding probe sets were found to be related with the GO term of PS-II (GO:0009523) and have correlation values of 0.5 in at least one of the 11 correlations. Figure 2A shows the correlation changes of the clusters with more than five pairs of the probe sets from PS-II, where the clusters obtained by rmsd <0.05 were used. As seen in the figure, all of the genes involved in PS-II have relatively high correlation values when no PC contributions are subtracted. This is probably because all of the genes in PS-II are expressed in chloroplast thylakoid membranes. When the genes in the chloroplast are not expressed simultaneously under a few specific conditions, such as in root cells, all of the genes in the chloroplast can be seen as acting cooperatively or they are regarded as being coexpressed to some extent, even though their functional relationship is not very tight. If the genes are tightly coupled, then their coexpression will be very robust, but if not, then their coexpressions will be fragile. This actually happens for the genes in PS-II (Fig. 2A). As seen in the figure, two extreme patterns are observed in PS-II. According to the above discussions, the stable gene pairs (the gene pairs in clusters c′ 189, c′ 69, c′ 44 and c′ 78 and involved in PS-II in Fig. 2A) have strong functional relations, and the others do not. It should be noted that rapid decrease such as c′ 7 is one of the most frequently observed patterns, since the c′ 7 is one of the largest clusters. In other words, the usual correlation values should be carefully used for function speculation, as pointed out by Yanai et al. (2006), since they are too sensitive to the tissues differences.

Fig. 2.

Fig. 2.

Open in a new tab

Correlation changes (A) in the genes in Photosystem II and (B) in NDH-related genes. Each line corresponds to the cluster with rmsd <0.05, and the names of gene pairs in each cluster are shown in Table 1 for (A) and specified in the figure for (B).

Table 1 shows all of the genes in PS-II involved in each cluster, where the first four clusters are stable ones, and the latter three are fragile ones. By checking this table, we noticed that there were five genes that were only involved in the fragile clusters, and these are underlined in Table 1, that is, HFC136 (At5g23120), PPL1 (At3g55330), PPL2 (At2g39470), PsbQ3.1 (At1g14150), PsbQ3.2 (At3g01440), where the code in parentheses is the Arabidopsis Genome Initiative (AGI) code for each gene. HCF136 is known as an assembly factor of PS-II (Plucken et al., 2002), which is required for the maturation of the PS-II complex, but the mature PS-II does not contain any HCF136. In other words, the interactions between HCF136 and the other components in PS-II are transient. PPL1 and PPL2 are known as PsbP1-like proteins, and have about 25% sequence identities. According to the mutant analyses (Ishihara et al., 2007), PPL1 is an efficient photo-damage repair factor of PS-II, and thus the interaction between PPL1 and PS-II is probably transient. PPL2 is an accumulation factor of the NAD(P)H dehydrogenase (Ndh), complex as discussed later, and thus it will not interact with PS-II directly. PsbQ3.1 and PsbQ3.2 are PsbQ paralogs, and they show weak sequence similarity to PsbQ1 and PsbQ2 with 25–28% identities. The functions of PsbQ1 and PsbQ2 were inferred as oxygen evolving enhancers, from double knock-out experiments by RNAi (Yi et al., 2006). The functions of PsbQ3.1 and PsbQ3.2 were also inferred to be related to PS-II only from their sequence similarities to PsbQ, but there is no experimental support for their functions. According to the fragile coexpression of PsbQ3.1 and PsbQ3.2 and their weak homologies, we think that their functional relationships to PS-II will be subtle. In summary, the functional relatedness of all of the genes in the fragile clusters is either weak or transient.

Table 1.

Gene list of each cluster involved in Photosystem II

Cluster number List of coexpressed genes
c′ 189 PsbO1–PsbR, PsbP1–PsbX, PsbY–PsbP1, PsbY–PsbX, PsbP1–PsbR, PsbY–PsbO1, PsbQ1–PsbTn
c′ 69 PsbY–PsbW, PsbQ-2–PsbTn, PsbQ1–PsbW, PsbY–PsbQ1, PsbTn–PsbX, PsbQ-2–PsbP1, PsbY–PsbTn, PsbO1–PsbO2, PsbP1–PsbW, PsbO1–PsbX, PsbQ1–PsbX, PsbO1–PsbQ2, PsbY–PsbQ2, PsbTn–PsbW
c′ 44 PsbR–PsbX, PsbX–PsbW, PsbQ2–PsbR, PsbO2–PsbR, PsbQ2–PsbX, PsbY–PsbR
c′ 78 PsbO-2–PsbX, PsbTn–PsbR, PsbR–PsbW, PsbO-1–PsbQ-1, PsbQ-1–PsbR, PsbO-1–PsbTn
c′ 7 PsbO2–PsbQ3.1, PPL1–PsbQ2, HCF136–PsbP1, PPL1–PsbW, PPL1–PsbP1, HCF136–PsbTn, PsbO1–PPL1, HCF136–PsbX, PPL1–PsbX, PsbP3–PsbQ3.2
c′ 40 PsbY–PPL2, HCF136–PPL2, PsbQ1–PsbQ3.1, PsbQ1–PPL2, PsbP3–PPL1, PsbTn–PPL2
c′ 34 PsbQ3.1–PsbX, PsbQ2–PPL2, PsbP1–PPL2, PsbX–PPL2, PsbO2–PPL2, PsbY–PsbQ3.1, PsbTn–PsbQ3.1, PsbQ-2–PsbQ3.1, PPL2–PsbW
Open in a new tab

Upper four and lower three clusters exhibit stable and fragile coexpressions, respectively. Underlined genes indicate those with fragile coexpression. c′ indicates clusters obtained by rmsd <0.05.

As described above, PPL2 was recently identified as an accumulation factor of Ndh (Ishihara et al., 2007). Thus, we checked the coexpression changes of PPL2 and the genes in the Ndh complex. In higher organisms, all of the components of Ndh have not been fully elucidated, and they are known to be very diverse among species (Rumeau et al., 2005). But we could identify the following four Ndh-related genes in our dataset according to the annotations in TAIR, NdhL (At1g70760), NdhO (At1g74880), CRR7 (At5g39210) and NdhN (At5g58260). According to the annotations and the references in TAIR, NdhL is thought to be a subunit of the Ndh complex and its mutant exhibited weak Ndh activity (Shimizu et al., 2008), CRR7 is considered as an essential factor of Ndh formation, NdhN is a required element for Ndh complex formation, and NdhO appeared to be a factor involved in Ndh complex assembly (Rumeau et al., 2005). In our analyses (Fig. 2B), three pairs (NdhL–PPL2, NdhN–PPL2 and NdhN–NdhL) have relatively high stability (S =0.62–0.69), while four pairs (NdhO–NdhL, NdhO–PPL2, CCR7–NdhL and CCR7–NdhO) have low stabilities (S =0.41 –0.45). In the former three pairs, PPL2 is always involved, and in the latter four pairs, NdhO and CCR7 are involved. Therefore, these results suggested that PPL2 is very likely to be involved in the Ndh complex, but NdhO and CCR7 are unlikely to be or only transiently related with the Ndh complex.

3.5 Correlation change of a specific case: metabolic pathway

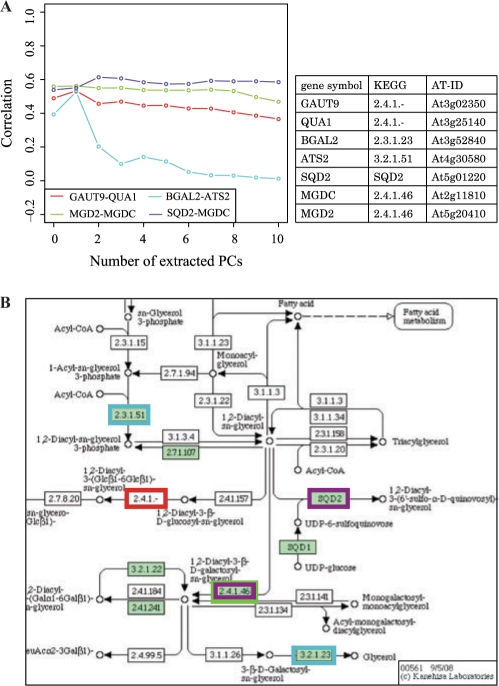
In the glycerolipid metabolism pathway (ath00561), seven genes were included in the four modestly co-expressed gene pairs, MGDC (At2g11810), MGD2 (At5g20410), SQD2 (At5g01220), GAUT9 (At3g02350), QUA1 (At3g25140), BGAL2, (At3g52840) and ATS2 (At4g30580).

As shown in Figure 3A, the coexpression levels with all PCs were relatively lower than those of the gene pairs in PS-II. There may be a general trend that the coexpression caused by a metabolic pathway is weaker than that due to the same cellular localization, and two extreme patterns were observed again. The three pairs with stable coexpression are GAUT9–QUA1 (S = 0.887), SQD2–MGDC (S = 0.953) and MGD2–MGDC (S = 0.981), and the fragile pair is BGAL2–ATS2 (S = 0.354). The location of the pairs of genes in the KEGG pathway is shown in Figure 3B by the boxes with the same color as the coexpression change lines. The stable pairs clearly show a functional relationship: the MGD2–MGDC pair and the GAUT–QUA1 pair are the subunits of an enzyme complex, which is stable, and SQD2–MGDC catalyzed the successive reactions. On the other hand, the genes in the fragile pair are very far apart from each other, and it is hard to imagine their functional relationships.

Fig. 3.

Fig. 3.

Open in a new tab

(A) Correlation change for genes in Glycerolipid metabolism (ath00561) and (B) their location in KEGG pathways.

3.6 GO prediction using multidimensional correlations and SVM

To evaluate the average effectiveness of the multidimensional correlations or 11 correlations, we carried out GO term predictions based on the multidimensional correlations. We assigned GO terms for each gene, as described in the ‘Materials and methods’ section, and then we tested whether the pair of genes has common GO terms or not. If the pair has at least one common term, we regarded the pair as having a functional relationship. The performance of the prediction result was estimated by the area under the ROC curve (Zweig and Campbell, 1993), which is a plot of sensitivity against specificity and can evaluate the trade-off between sensitivity and specificity of the prediction. An area under the ROC curve (AUC) = 1.0 indicates a perfect prediction, while an AUC = 0.5 means a random prediction. We evaluated the performance for each GO category, that is, cellular component (CC), biological process (BP), and molecular function (MF), respectively.

Table 2 shows the AUC values of the predictions using a SVM for a single Pearson's correlation coefficient (PCC), for a multidimensional correlation (SVMmcol) and for Spearman correlation coefficient (SCC), in each GO category. For PCC and SCC, their values were used as inputs for SVM, and for multidimensional correlations, the first n correlations (n = 2..11) were used as input vectors. The genes sharing the same GO term was judged to have a functional relationship, and the best AUC values for the prediction results were shown (see the ‘Materials and methods’ section for details.). The performance with other number of correlations was also shown in Supplementary Figure S4. As in the figure, the significant performance improvements were observed for a few specific numbers of correlations. In other words, more correlations did not always raise the prediction performance, and the best numbers of correlation were different in each GO category. It may be noteworthy that good performance was obtained both in BP and CC when we used the first six correlations out of the eleven correlations, but the six correlations resulted in bad performance in MF.

In general, SVMmcol outperformed the PCC-based predictions, and the improvements in the MF categories were especially impressive, because we thought that our multidimensional correlations might be suitable to describe the hierarchy of tissues. The performance in the CC category is better than the others, which could imply that common cellar components are the best target for prediction by coexpression. But it should be noted that the higher true positive rate of CC (1.85%) than those of BP (0.63%) and MF (0.51%) can also contribute to the higher performance in CC.

SCC did not improve the performance in CC and MF categories compared with PCC, but in BP category it showed large improvement.

3.7 Interpretation of the major PCs

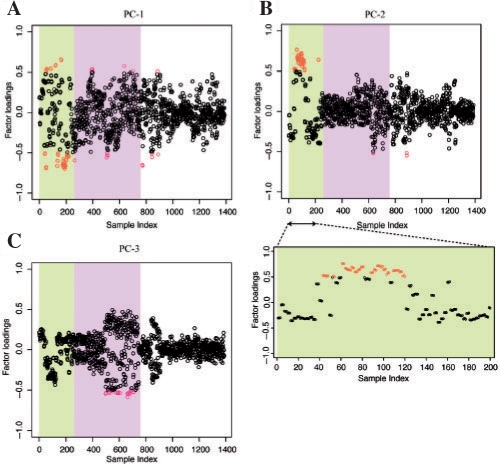
We carried out a PCA to observe the main contributors to each PC by calculating the factor loading of each sample, which can be obtained as a correlation coefficient between each PC and a sample. Figure 4 shows the distribution of the factor loadings of the first three major PCs against the sample index, where the red dots indicate those that exceeded 0.5. The details of the samples with the sample index are provided in Supplementary Table 1, and here we focused on the mainly contributed samples. The 1388 samples can roughly be divided into three categories, that is, developmental stage (1–237), time course samples (238–771) and others (772–1388). As shown in Figure 4, the first two PCs mainly consist of the developmental stages, while the third PC is composed of the time course samples. Furthermore, the main contributors to the first PC are samples 40–42, 52–57, 85–87, 121–123, 133–141, 163–265 and 175–202, which are related to the shoot or flower stages. On the other hand, the main samples that contributed to the second PC are 43–48, 52–54, 61–81, 88–105, 109–120, which are young rosetta leaves (see Supplementary Table 1 for sample descriptions by sample index). In other words, the second PC is mainly derived from the early developmental stages before flowering, and the first PC consists of the later developmental stages after flowering. For the first PC, since there are some samples with large contributions (Fig. 4A and Supplementary Table 1), we also checked the possibility that other factors such as the bias of experimental series (Alter et al., 2000) and of different strains, but in this dataset we could not observe the relation between these factors and the first PC. As seen in Figure 4C, the main contributor to the third PC is distributed in the middle region of samples, which corresponds to the time course samples with various stresses. We could not get clear interpretations of the PCs after the fourth components (data not shown).

Fig. 4.

Fig. 4.

Open in a new tab

Factor loading of each sample in (A) first PC, (B) second PC, with the plot expanded for sample 1–200, and (C) third PC. The red dots indicate the largely contributing samples, or those with factor loadings >0.5. The background colors in the plots correspond to the rough classifications: developmental stage (1–237), time course samples (238–771) and others (772–1388).

4 CONCLUSION

In this study, we observed the correlation change by removing the effects of large contribution bias to the variety of gene expression, and found that the large fraction of gene pairs with high correlation can have the weak functional relationship, or fragile coexpression. Our interpretation about the fragility of coexpression may be biased by the data used in this study, but, in general, gene pairs coexpressed in the specific condition such as the protein–protein interaction in signal cascade will be fragile due to their limited interactions. As described in the examples shown in this article, a correlation by using expression values from all experiments is too sensitive to the cellular components, and the improvement in the GO prediction in MF suggests that our approach successfully reduced the unbalanced effect of the tissue difference to provide more information from large-scale expression data.

Supplementary Material

[Supplementary Data]
btp442_index.html (942B, html)

ACKNOWLEDGEMENTS

The authors would like to thank Dr Ashwini Patil for her careful reading of the manuscript and constructive comments.

Funding: Grant-in-Aid for Scientific Research on Priority Areas Transportsome from the Ministry of Education, Culture, Sports, Science and Technology of Japan (to K.K.); the Global COE Program (Center of Education and Research for Advanced Genome-Based Medicine), MEXT, Japan (to T.O.).

Conflict of Interest: none declared.

REFERENCES

  1. Alter O, et al. Singular value decomposition for genome-wide expression data processing and modeling. Proc. Natl Acad. Sci. USA. 2000;97:10101–10106. doi: 10.1073/pnas.97.18.10101. [DOI] [PMC free article] [PubMed] [Google Scholar]
  2. Aoki K, et al. Approaches for extracting practical information from gene co-expression networks in plant biology. Plant Cell Physiol. 2007;48:381–390. doi: 10.1093/pcp/pcm013. [DOI] [PubMed] [Google Scholar]
  3. Ashburner M, et al. Gene ontology: tool for the unification of biology. The Gene Ontology Consortium. Nat. Genet. 2000;25:25–29. doi: 10.1038/75556. [DOI] [PMC free article] [PubMed] [Google Scholar]
  4. Barrett T, et al. NCBI GEO: mining tens of millions of expression profiles—database and tools update. Nucleic Acids Res. 2007;35:D760–D765. doi: 10.1093/nar/gkl887. [DOI] [PMC free article] [PubMed] [Google Scholar]
  5. Brunet JP, et al. Metagenes and molecular pattern discovery using matrix factorization. Proc. Natl Acad. Sci. USA. 2004;101:4164–4169. doi: 10.1073/pnas.0308531101. [DOI] [PMC free article] [PubMed] [Google Scholar]
  6. Bulow L, et al. PathoPlant: a platform for microarray expression data to analyze co-regulated genes involved in plant defense responses. Nucleic Acids Res. 2007;35:D841–D845. doi: 10.1093/nar/gkl835. [DOI] [PMC free article] [PubMed] [Google Scholar]
  7. Craigon DJ, et al. NASCArrays: a repository for microarray data generated by NASC's transcriptomics service. Nucleic Acids Res. 2004;32:D575–D577. doi: 10.1093/nar/gkh133. [DOI] [PMC free article] [PubMed] [Google Scholar]
  8. Cui J, et al. AtPID: Arabidopsis thaliana protein interactome database—an integrative platform for plant systems biology. Nucleic Acids Res. 2008;36:D999–D1008. doi: 10.1093/nar/gkm844. [DOI] [PMC free article] [PubMed] [Google Scholar]
  9. Eisen MB, et al. Cluster analysis and display of genome-wide expression patterns. Proc. Natl Acad. Sci. USA. 1998;95:14863–14868. doi: 10.1073/pnas.95.25.14863. [DOI] [PMC free article] [PubMed] [Google Scholar]
  10. Fan RE, et al. Working set selection using second order information for training SVM. J. Machine Learn. Res. 2005;6:1889–1918. [Google Scholar]
  11. Fukushima A, et al. SVD-based anatomy of gene expressions for correlation analysis in Arabidopsis thaliana. DNA Res. 2008;15:367–374. doi: 10.1093/dnares/dsn025. [DOI] [PMC free article] [PubMed] [Google Scholar]
  12. Hibbs MA, et al. Exploring the functional landscape of gene expression: directed search of large microarray compendia. Bioinformatics. 2007;23:2692–2699. doi: 10.1093/bioinformatics/btm403. [DOI] [PubMed] [Google Scholar]
  13. Hughes TR, et al. Functional discovery via a compendium of expression profiles. Cell. 2000;102:109–126. doi: 10.1016/s0092-8674(00)00015-5. [DOI] [PubMed] [Google Scholar]
  14. Ikeo K, et al. CIBEX: center for information biology gene expression database. C R Biol. 2003;326:1079–1082. doi: 10.1016/j.crvi.2003.09.034. [DOI] [PubMed] [Google Scholar]
  15. Ishida T, Kinoshita K. PrDOS: prediction of disordered protein regions from amino acid sequence. Nucleic Acids Res. 2007;35:W460–W464. doi: 10.1093/nar/gkm363. [DOI] [PMC free article] [PubMed] [Google Scholar]
  16. Ishihara S, et al. Distinct functions for the two PsbP-like proteins PPL1 and PPL2 in the chloroplast thylakoid lumen of Arabidopsis. Plant Physiol. 2007;145:668–679. doi: 10.1104/pp.107.105866. [DOI] [PMC free article] [PubMed] [Google Scholar]
  17. Kanehisa M, et al. KEGG for linking genomes to life and the environment. Nucleic Acids Res. 2008;36:D480–D484. doi: 10.1093/nar/gkm882. [DOI] [PMC free article] [PubMed] [Google Scholar]
  18. Kloster M, et al. Finding regulatory modules through large-scale gene-expression data analysis. Bioinformatics. 2005;21:1172–1179. doi: 10.1093/bioinformatics/bti096. [DOI] [PubMed] [Google Scholar]
  19. Lee HK, et al. Coexpression analysis of human genes across many microarray data sets. Genome Res. 2004a;14:1085–1094. doi: 10.1101/gr.1910904. [DOI] [PMC free article] [PubMed] [Google Scholar]
  20. Lee I, et al. A probabilistic functional network of yeast genes. Science. 2004b;306:1555–1558. doi: 10.1126/science.1099511. [DOI] [PubMed] [Google Scholar]
  21. Lee I, et al. A single gene network accurately predicts phenotypic effects of gene perturbation in Caenorhabditis elegans. Nat. Genet. 2008;40:181–188. doi: 10.1038/ng.2007.70. [DOI] [PubMed] [Google Scholar]
  22. Leek JT, Storey JD. Capturing heterogeneity in gene expression studies by surrogate variable analysis. PLoS Genet. 2007;3:1724–1735. doi: 10.1371/journal.pgen.0030161. [DOI] [PMC free article] [PubMed] [Google Scholar]
  23. Manfield IW, et al. Arabidopsis Co-expression Tool (ACT): web server tools for microarray-based gene expression analysis. Nucleic Acids Res. 2006;34:W504–W509. doi: 10.1093/nar/gkl204. [DOI] [PMC free article] [PubMed] [Google Scholar]
  24. Obayashi T, et al. ATTED-II: a database of co-expressed genes and cis elements for identifying co-regulated gene groups in Arabidopsis. Nucleic Acids Res. 2007;35:D863–D869. doi: 10.1093/nar/gkl783. [DOI] [PMC free article] [PubMed] [Google Scholar]
  25. Obayashi T, et al. COXPRESdb: a database of coexpressed gene networks in mammals. Nucleic Acids Res. 2008;36:D77–D82. doi: 10.1093/nar/gkm840. [DOI] [PMC free article] [PubMed] [Google Scholar]
  26. Obayashi T, et al. ATTED-II provides coexpressed gene networks for Arabidopsis. Nucleic Acids Res. 2009;37:D987–D991. doi: 10.1093/nar/gkn807. [DOI] [PMC free article] [PubMed] [Google Scholar]
  27. Parkinson H, et al. ArrayExpress—a public database of microarray experiments and gene expression profiles. Nucleic Acids Res. 2007;35:D747–D750. doi: 10.1093/nar/gkl995. [DOI] [PMC free article] [PubMed] [Google Scholar]
  28. Plucken H, et al. The HCF136 protein is essential for assembly of the photosystem II reaction center in Arabidopsis thaliana. FEBS Lett. 2002;532:85–90. doi: 10.1016/s0014-5793(02)03634-7. [DOI] [PubMed] [Google Scholar]
  29. Prelic A, et al. A systematic comparison and evaluation of biclustering methods for gene expression data. Bioinformatics. 2006;22:1122–1129. doi: 10.1093/bioinformatics/btl060. [DOI] [PubMed] [Google Scholar]
  30. Rumeau D, et al. New subunits NDH-M, -N, and -O, encoded by nuclear genes, are essential for plastid Ndh complex functioning in higher plants. Plant Cell. 2005;17:219–232. doi: 10.1105/tpc.104.028282. [DOI] [PMC free article] [PubMed] [Google Scholar]
  31. Shapira M, et al. Disruption of yeast forkhead-associated cell cycle transcription by oxidative stress. Mol. Biol. Cell. 2004;15:5659–5669. doi: 10.1091/mbc.E04-04-0340. [DOI] [PMC free article] [PubMed] [Google Scholar]
  32. Shi L, et al. The MicroArray Quality Control (MAQC) project shows inter- and intraplatform reproducibility of gene expression measurements. Nat. Biotechnol. 2006;24:1151–1161. doi: 10.1038/nbt1239. [DOI] [PMC free article] [PubMed] [Google Scholar]
  33. Shimizu H, et al. CRR23/NdhL is a subunit of the chloroplast NAD(P)H dehydrogenase complex in Arabidopsis. Plant Cell Physiol. 2008;49:835–842. doi: 10.1093/pcp/pcn058. [DOI] [PubMed] [Google Scholar]
  34. Shoemaker BA, Panchenko AR. Deciphering protein-protein interactions. Part I. Experimental techniques and databases. PLoS Comput. Biol. 2007;3:e42. doi: 10.1371/journal.pcbi.0030042. [DOI] [PMC free article] [PubMed] [Google Scholar]
  35. Spellman PT, et al. Comprehensive identification of cell cycle-regulated genes of the yeast Saccharomyces cerevisiae by microarray hybridization. Mol. Biol. Cell. 1998;9:3273–3297. doi: 10.1091/mbc.9.12.3273. [DOI] [PMC free article] [PubMed] [Google Scholar]
  36. Steinhauser D, et al. CSB.DB: a comprehensive systems-biology database. Bioinformatics. 2004;20:3647–3651. doi: 10.1093/bioinformatics/bth398. [DOI] [PubMed] [Google Scholar]
  37. Swarbreck D, et al. The Arabidopsis Information Resource (TAIR): gene structure and function annotation. Nucleic Acids Res. 2008;36:D1009–D1014. doi: 10.1093/nar/gkm965. [DOI] [PMC free article] [PubMed] [Google Scholar]
  38. Toufighi K, et al. The botany array resource: e-Northerns, expression angling, and promoter analyses. Plant J. 2005;43:153–163. doi: 10.1111/j.1365-313X.2005.02437.x. [DOI] [PubMed] [Google Scholar]
  39. Yanai I, et al. Similar gene expression profiles do not imply similar tissue functions. Trends Genet. 2006;22:132–138. doi: 10.1016/j.tig.2006.01.006. [DOI] [PubMed] [Google Scholar]
  40. Yi X, et al. The PsbQ protein is required in Arabidopsis for photosystem II assembly/stability and photoautotrophy under low light conditions. J. Biol. Chem. 2006;281:26260–26267. doi: 10.1074/jbc.M603582200. [DOI] [PubMed] [Google Scholar]
  41. Zimmermann P, et al. Gene-expression analysis and network discovery using Genevestigator. Trends Plant Sci. 2005;10:407–409. doi: 10.1016/j.tplants.2005.07.003. [DOI] [PubMed] [Google Scholar]
  42. Zweig MH, Campbell G. Receiver-operating characteristic (ROC) plots: a fundamental evaluation tool in clinical medicine. Clin. Chem. 1993;39:561–577. [PubMed] [Google Scholar]

Associated Data

This section collects any data citations, data availability statements, or supplementary materials included in this article.

Supplementary Materials

[Supplementary Data]
btp442_index.html (942B, html)
btp442_1.pdf (152.3KB, pdf)
btp442_bioinf-2009-0303-File002.doc (278.5KB, doc)
btp442_bioinf-2009-0303-File003.csv (248KB, csv)

Articles from Bioinformatics are provided here courtesy of Oxford University Press

RESOURCES