Functional Energetic Landscape in the Allosteric Regulation of Muscle Pyruvate Kinase I. Calorimetric Study

Abstract

Rabbit muscle pyruvate kinase (RMPK) is an important allosteric enzyme of the glycolytic pathway catalyzing a transfer of the phosphate from phosphoenolpyruvate (PEP) to ADP. The energetic landscape of the allosteric regulatory mechanism of RMPK was characterized by isothermal titration calorimetry (ITC) in the temperature range from 4°C to 45°C. ITC data for RMPK binding to substrates PEP and ADP, for the allosteric inhibitor Phe, as well as for combination of ADP and Phe were globally analyzed. The thermodynamic parameters characterizing the linked-multiple- equilibria system were extracted. Four novel insights were uncovered 1. The binding preference of ADP for either the T- or R-state is temperature dependent; namely, more favorably to the T- and R-state at high and low temperature, respectively. This cross over of affinity towards R and T-state implies that ADP plays a complex role in modulating the allosteric behavior of RMPK. Depending on the temperature, binding of ADP can regulate RMPK activity by favoring the enzyme to either the R- or T-state. 2. The binding of Phe is negatively coupled to that of ADP i.e. Phe and ADP prefer not to bind to the same subunit of RMPK. 3. The release or absorption of protons linked to the various equilibria is specific to the particular reaction. As a consequence, pH will exert a complex effect on these linked equilibria resulting in proton being an allosteric regulatory ligand of RMPK. 4. The R↔T equilibrium is accompanied by a significant ΔC_p rendering RMPK most sensitive to temperature under physiological conditions. During muscle activity, both pH and temperature fluctuations are known to happen; thus, results of this study are physiologically relevant.

A serious challenge of the post-genomic era is to establish the correlation between protein structural folds and functions. Knowing the protein sequence through the genomic data, a popular practice is to employ various types of algorithms to model the structural fold as defined by the protein sequence. However, it is soon recognized that diverse functions are carried out by proteins with essentially identical folds but different sequences. Many protein structural folds have been identified e.g. the various folds involved in signal transduction (1–3). The chemical principles that govern the relation between function and sequence differences within a fold are still unclear.

We have chosen the biological phenomenon of allosteric regulation as the focus to tackle the issue of sequence-function correlation. The rationale for the choice is that allostery is a predominant regulatory mechanism and an allosteric system consists of a variety of functions that can be modulated by a change in sequence.

Rabbit muscle pyruvate kinase (RMPK) is an ideal system that has an outstanding chance for revealing the chemical principles of allostery. The unique feature that makeS RMPK an ideal system is that PK exists in four isozymic forms (4, 5). Between two of these isozymes only 22 amino acid changes out of 530 residues per subunit are required to convert an enzyme with a classical Michealis-Menten activity profile to one with distinct sigmoidal activity profiles. Thus, imbedded in these two isoforms of PK is information to relate change in protein sequence to functional changes. Furthermore, no significant structural changes in RMPK are associated with these changes in residues (4, 5).

RMPK is an important allosteric enzyme of the glycolytic pathway catalyzing a transfer of the phosphate from phosphoenolpyruvate (PEP) to ADP (6–10):

$$\mathit{\text{PEP}}+\mathit{\text{ADP}}\stackrel{\mathit{\text{PK}}}{\iff }\mathit{\text{Pyruvate}}+\mathit{\text{ATP}}$$

Production of ATP is essential in the cell energetics and therefore it is not surprising that RMPK activity is subjected to an intriguing pattern of regulation. RMPK consists of four identical subunits (11). Its activity is regulated by metabolites. Besides the two substrates, PEP and ADP, the enzyme requires also Mg²⁺ and K⁺ for its activity (12). RMPK was found to be allosterically inhibited by L-phenylalanine (Phe) (13). Although the in vivo significance of this allosteric inhibitor is not fully understood yet, its effect on enzyme kinetics and related conformational changes were well documented by both structural data (14–17) and steady state enzyme kinetics (8, 10, 14–21). It was shown that steady-state kinetic data follow a simple hyperbolic Michaelis–Menten equation in the absence of Phe. However, the steady-state kinetic behavior exhibits increasing sigmoidicity in the presence of increasing Phe concentration. Phe binding was found to induce a highly cooperative conformation change as monitored by sedimentation techniques (18), analytical gel-filtration chromatography (22), and small angle neutron scattering (21). In particular, binding of Phe to one of the four equivalent subunits causes all subunits to change conformation in a concerted manner.

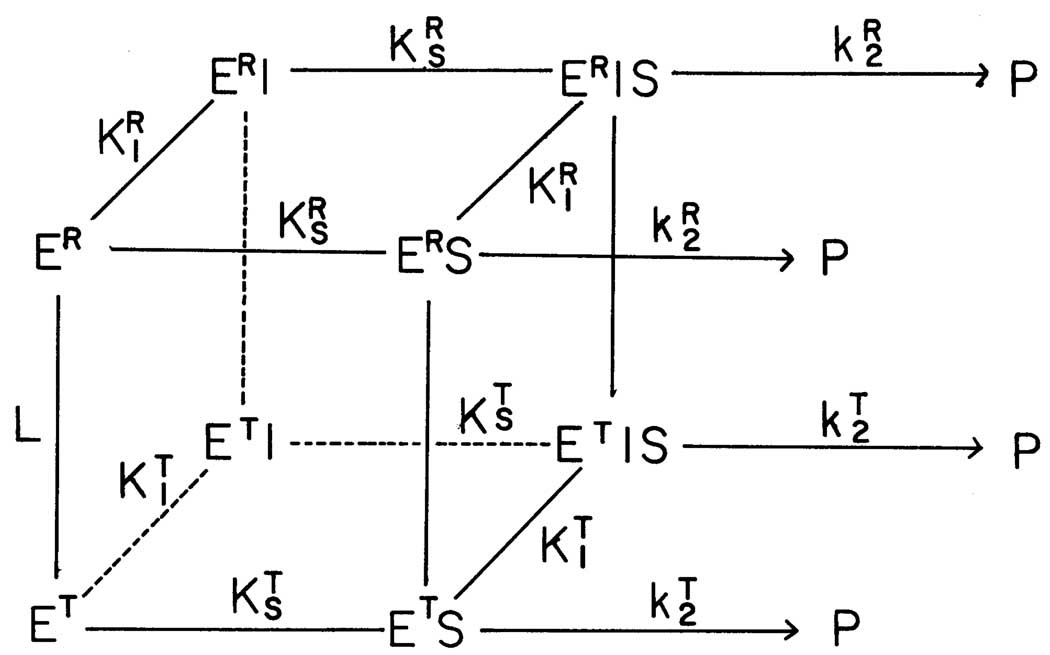
Thorough analysis of the experimental evidence (8, 10, 18, 19) suggested that all data can be consistently described by a concerted allosteric model (23) where protein assumes an active (R) and an inactive (T) form with differential affinities for ligands, as shown in Fig.1. Without significant interconversion of the secondary structure during the R↔T transition, the two forms of the enzyme differ in hydrodynamic properties as well as in their flexibility and internal dynamics (24). In particular, The R-state is characterized by a compact symmetric conformation of the enzyme and the T-state assumes an expanded form with a significantly loosen structure. Therefore it is not surprising that ligands may exhibit different affinities to the R and T-state and consequently they perturb the equilibrium between these states by shifting it to one or the other form. Fourier-transformed infra-red (FT-IR) experiments probing the RMPK protein dynamics by H↔D exchange suggested that the allosteric regulation of the enzyme is a consequence of perturbation of the distribution of states in which the R and T-states represent the two extreme end states (24). Based on the results of steady-state kinetic and other spectroscopic or hydrodynamic measurements the substrate PEP and the allosteric inhibitor Phe were reported to bind preferentially to the R and T-state, respectively (8, 10, 21, 22, 24). The second substrate ADP was found to bind to both states with about the same affinity at 23°C (19).

Fig. 1.

The proposed two-state model for the allosteric behavior of RMPK (8). L = [T]/[R] ; K^T and K^R are equilibrium constants for substrates, S, and inhibitor, I, binding to the T and R-state, respectively. The model assumes that the affinities of RMPK for both S and I are dependent only on the conformational state of the enzyme i.e. the constant for the binding of S to E^T is the same as that of S to E^T•I. Similarly, the affinity of S for E^R and E^R•I is assumed to be the same.

Despite an apparent simplicity of the two-state model, full quantitative thermodynamic characterization of PK regulatory properties has yet to be attempted. A closer examination of the reactions involved in modulating RMPK activity shows that the minimum number of metabolites interact with RMPK is four; namely, two substrates (PEP and ADP), one inhibitor (Phe) and one activator (FBP). The number of reactions linking all these metabolites interacting with the two conformation states of RMPK increases exponentially. Obviously, in the presence of multiple ligands, such as in an in vivo cellular environment, the simple two state R↔T equilibrium model explodes into a highly intricate model involving simultaneous, multiple equilibria that are rather difficult to quantitatively characterize without an in-depth dissection. Though very useful, steady state enzyme kinetics suffer by an inherent limitation that two substrates, PEP and ADP, have to be always present simultaneously in the reaction mix in order to induce RMPK activity. Moreover, thermodynamic coupling between ligands cannot be avoided. Since information extractable from the data is always limited, published kinetic data offer only a partial characterization of the RMPK behavior.

A major assumption of our two-state model is that the binding of ligands is state-dependent e.g. the binding constant of Phe to either the R or T-state is defined by the state only, namely $K_{\mathit{\text{Phe}}}^R=K_{\mathit{\text{ADP}},\mathit{\text{Phe}}}^R$ even if ADP is bound as long as PK is in the R-state. In this study, we wish to test the validity of this assumption for the Phe/ADP pair.

In the present paper we focused on a thermodynamic characterization of the allosteric regulatory behavior of RMPK by isothermal titration calorimetry (ITC). ITC experiments allow a direct access of fundamental thermodynamic parameters associated with ligand binding and RMPK conformational transitions. Since ITC experiments are not based on an enzymatic activity, binding of single ligands can be measured and interaction between ligands investigated. Detailed description of the regulatory behavior of the wild type RMPK is essential for modeling its regulation under physiological conditions. It also creates an essential baseline for understanding perturbations induced by targeted genetic modifications of the recombinant enzyme.

MATERIALS AND METHODS

Materials

RMPK, phosphoenolpyruvate (PEP) and ADP were purchased from Boeringer-Manheim. Trizma-base, Bis-Tris, Phe and KCl were bought from Sigma and MgSO₄ from Fisher. Purity of protein was monitored by the SDS gel electrophoresis.

Methods

TKM or BTKM buffers at pH 7.5 contained 50 mM Trizma-base or Bis-Tris, respectively, 72 mM KCL, and 7.2 mM MgSO₄. A correction for temperature coefficients of the buffers was applied at every experimental temperature.

Ammonium sulphate precipitates of RMPK were centrifuged; the pellet was resuspended in a desired buffer and exhaustively dialyzed. Concentration of RMPK was adjusted using absorptivity of 0.54 mg ml⁻¹ cm⁻¹ at 280 nm (12) and molecular weight of 220 kDa (8). A single batch of protein was used for all experiments.

Isothermal titration calorimetry (ITC)

Calorimetric titrations were performed on the Omega microcalorimeter (MicroCal, Inc.). Concentrations of RMPK ranged from 15 µM to 70 µM. Stock solutions of 40 mM PEP, 100 mM of Phe and 100 mM of ADP were used for injections. The titrants were prepared by dilution of the ligands in the dialyzate in order to avoid thermal effects caused by a buffer mismatch. The pH of the titrants was checked and adjusted, if necessary. When RMPK was titrated by Phe in the presence of a fixed concentration of ADP, the same concentration of ADP was present in the injectant. Typically 15–25 aliquots of ligand were injected into a 1.4 ml sample. To correct data for heats of dilution of an injectant a control experiment was performed at the same conditions except a buffer was substituted for the sample. The overall reaction heats were calculated by integration of the corrected ITC curves.

The extent of irreversible processes caused by mixing of the protein at high temperatures in the calorimeter was also evaluated. Only insignificant decrease of 3% ± 3% activity was observed after a 1-hour calorimetric experiment at 40 °C.

Global fitting

Multiple data sets were simultaneously analyzed by a global fitting routine described in detail by Knutson et al. (25, 26). The global analysis is an extension of an ordinary non-linear least square fitting (27) for simultaneous analysis of multiple experimental data sets using a single model that encompasses them all. Experiments performed under a variety of conditions. The most important feature of the approach is that some parameters are inherently common for the different but related curves. Then the global fitting exploits relationships between these curves and over-determines these parameters. Such over-determination helps both in distinguishing between competing models and in the recovery of these parameters. During the global fitting the overall sum of weighted squared deviations of calculated values from the measured data (χ²) is minimized in order to obtain model parameters that are consistent with all data curves simultaneously. This approach was proven to be highly robust and was shown to maximize information retrievable from the analyzed data (28–34). A home-coded program utilizing the Marquardt-Levenberg minimization procedure (35) was used for the global analysis of the calorimetry data.

RESULTS

Description of the model

Based on the published thermodynamic and steady-state kinetic results from this laboratory, a model is developed. It is based on a simple, yet very versatile, model for the cooperative binding of ligands by macromolecules described by Monod et al. (23) and elaborated for the tertameric RMPK by Oberfelder et al. (8), as shown in Fig.1 For any single ligand the two-state Monod-Wyman-Changeux (MWC) model can be described by the following scheme:

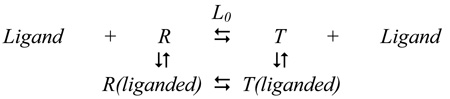According to this model an overall reaction heat Q_tot accompanying saturation of the enzyme by a ligand can be treated as a composite heat of three major reactions: heats $Q_{\mathit{\text{lig}}}^R\text{and}{Q}_{\mathit{\text{lig}}}^T$ of ligand binding to the R and T state, respectively, and a heat Q_R↔T accompanying the R↔T:

$$Q_{\mathit{\text{tot}}}{=}^{\mathit{\text{sat}}}{f}_{\mathit{\text{lig}}}^R·Q_{\mathit{\text{lig}}}^R{+}^{\mathit{\text{sat}}}{f}_{\mathit{\text{lig}}}^T·Q_{\mathit{\text{lig}}}^T+{(}^{\mathit{\text{sat}}}{f}_{\mathit{\text{lig}}}^T-f_0^T)Q_{R\leftrightarrow T}$$ (1)

Terms ${}^{\mathit{\text{sat}}}{f}_{\mathit{\text{lig}}}^R\text{and}{}^{\mathit{\text{sat}}}{f}_{\mathit{\text{lig}}}^T$ are fractions of RMPK in the R and T state, respectively, at the end of the titration when the enzyme is fully saturated by the ligand. The term $f_0^T$ is a fraction of the unliganded T-state at the beginning of the experiment.

The R↔T transition can be accompanied by protonation or deprotonation of the enzyme. Heat contributions from such linked proton absorptions may be expressed as follows:

$$Q_{\mathit{\text{lig}}}^{\mathit{\text{state}}}=4M_0{V}_0·(\mathrm{\Delta }{H}_{\mathit{\text{lig}}}^{\mathit{\text{state}}}+\mathrm{\Delta }{n}_{\mathit{\text{lig}}}^{\mathit{\text{state}}}·\mathrm{\Delta }{H}_{\mathit{\text{ion}}})$$ (2)

$$Q_{R\leftrightarrow T}=M_0{V}_0·(\mathrm{\Delta }{H}_{R\leftrightarrow T}+\mathrm{\Delta }{n}_{R\leftrightarrow T}·\mathrm{\Delta }{H}_{\mathit{\text{ion}}})$$ (3)

The term M₀ stands for molar concentration of RMPK, V₀ is a sample volume, ΔH_ion is the ionization enthalpy of the buffer, and $\mathrm{\Delta }{n}_{\mathit{\text{lig}}}^{\mathit{\text{state}}}$ and Δn_R↔T are changes in molar amount of protons as ligand binds to state R or T and as RMPK undergoes R↔T transition, respectively. A positive or negative value for Δn indicates an absorption or release of proton, respectively. The enthalpies $\mathrm{\Delta }{H}_{\mathit{\text{lig}}}^{\mathit{\text{state}}}$ and ΔH_R↔T are calculated per mol of binding sites and per mol of tetrameric RMPK, respectively.

In the two-state model the equilibrium constant L₀ between the unliganded R and T states is characterized by the ratio:

$$L_0=\frac{[T_0]}{[R_0]}$$ (4)

where [T₀] and [R₀] are equilibrium concentrations of the unliganded T and R state, respectively. Then, the fraction $f_0^T$ of the unliganded RMPK in the T-state can be expressed as:

$$f_0^T=L_0/(1+L_0)$$ (5)

and

$$f_0^T+f_0^R=1$$ (6)

Results of the steady-state kinetic measurements (10) as well as the recent fluorescence data (36) indicate that within the temperature range from 5 °C to 40 °C a saturating concentration of PEP and Phe shifts the RMPK population completely to the R and T-state, respectively. As a consequence, eq. (1) is substantially simplified because ${}^{\mathit{\text{sat}}}{f}_{\mathit{\text{Phe}}}^R={}^{\mathit{\text{sat}}}{f}_{\mathit{\text{PEP}}}^T=0\text{and}{}^{\mathit{\text{sat}}}{f}_{\mathit{\text{PEP}}}^R={}^{\mathit{\text{sat}}}{f}_{\mathit{\text{Phe}}}^T=1$ . Under these conditions it can be seen from Eq.(1–3) that experiments at saturation of a ligand yield information about the binding enthalpies only and the information on entropy towards the equilibrium binding constant is lost because there is no change of state.

It was shown by steady-state enzyme kinetics that at room temperature ADP exhibits only negligible differential affinity to the R and T-states (19). When RMPK is titrated by ADP, the full eq. (1) should be used for the analysis of the ITC data because only minor shifts of the R ↔ T equilibrium are expected. When RMPK is titrated by Phe in the presence of a fixed concentration of ADP, the apparent R↔T equilibrium constants ${}^{\mathit{\text{nonsat}}}{L}_{0,\mathit{\text{ADP}}}=[T_{\mathit{\text{ADP}}}]/[R_{\mathit{\text{ADP}}}]\text{and}{}^{\mathit{\text{nonsat}},\mathit{\text{sat}}}{L}_{0,\mathit{\text{ADP}},\mathit{\text{Phe}}}=[T_{\mathit{\text{ADP}},\mathit{\text{Phe}}}]/[R_{\mathit{\text{ADP}},\mathit{\text{Phe}}}]$ at the beginning and at the end of the Phe titration, respectively, could differ from the ones in the absence of ADP and these new constants should be used for calculation of the corresponding fractions ${}^{\mathit{\text{nonsat}}}{f}_{\mathit{\text{ADP}}}^T\text{and}{}^{\mathit{\text{nonsat}},\mathit{\text{sat}}}{f}_{\mathit{\text{ADP}},\mathit{\text{Phe}}}^T$ in eq.(1). Based on the WMC model adopted for the tetrameric enzyme (8) the new equilibrium constants between the R and T state in the presence of an arbitrary concentration of ADP can be expressed for tetrameric RMPK as:

$$\begin{array}{ccc}{}^{\mathit{\text{nonsat}}}{L}_{0,\mathit{\text{ADP}}}=L_0{\left(\frac{1+[\mathit{\text{ADP}}]/K_{\mathit{\text{ADP}}}^T}{1+[\mathit{\text{ADP}}]/K_{\mathit{\text{ADP}}}^R}\right)}^4,& & {}^{\mathit{\text{nonsat}},\mathit{\text{sat}}}{L}_{0,\mathit{\text{ADP}},\mathit{\text{Phe}}}{=}^{\mathit{\text{nonsat}}}{L}_{0,\mathit{\text{ADP}}}{\left(\frac{K_{\mathit{\text{Phe}}}^R}{K_{\mathit{\text{Phe}}}^T}\right)}^4\end{array}$$ (7)

where $K_{\mathit{\text{ligand}}}^{\mathit{\text{state}}}$ is a microscopic dissociation constant. Moreover, an additional differential heat ΔQ_eq resulting from the reequilibration of ADP between R and T-states after an addition of Phe should be added to eq. (1):

$$\mathrm{\Delta }{Q}_{\mathit{\text{eq}}}=4M_0{V}_0{(}^{\mathit{\text{nonsat}},\mathit{\text{sat}}}{f}_{\mathit{\text{ADP}},\mathit{\text{Phe}}}^T{-}^{\mathit{\text{nonsat}}}{f}_{\mathit{\text{ADP}},0}^T)[Y_{\mathit{\text{ADP}}}^T·(\mathrm{\Delta }{H}_{\mathit{\text{ADP}}}^T+\mathrm{\Delta }{n}_{\mathit{\text{ADP}}}^T\mathrm{\Delta }{H}_{\mathit{\text{ion}}})-Y_{\mathit{\text{ADP}}}^R·(\mathrm{\Delta }{H}_{\mathit{\text{ADP}}}^R+\mathrm{\Delta }{n}_{\mathit{\text{ADP}}}^R\mathrm{\Delta }{H}_{\mathit{\text{ion}}})$$ (8)

$Y_{\mathit{\text{ADP}}}^R$ is fractional saturation of the ADP binding site in the RMPK monomer:

$$Y_{\mathit{\text{ADP}}}^{\mathit{\text{state}}}=\frac{[\mathit{\text{ADP}}]/K_{\mathit{\text{ADP}}}^{\mathit{\text{state}}}}{1+[\mathit{\text{ADP}}]/K_{\mathit{\text{ADP}}}^{\mathit{\text{state}}}}$$ (9)

For the global analysis, experiments performed at different temperatures can be linked together by a temperature dependence of the involved equilibrium constants:

$$-\mathit{\text{RT}}·\text{ln}(L_0)=\mathrm{\Delta }{H}_{R\leftrightarrow T}-T·\mathrm{\Delta }{S}_{R\leftrightarrow T}$$ (10)

$$\mathit{\text{RT}}·\text{ln}(K_{\mathit{\text{lig}}}^{\mathit{\text{state}}})=\mathrm{\Delta }{H}_{\mathit{\text{lig}}}^{\mathit{\text{state}}}-T·\mathrm{\Delta }{S}_{\mathit{\text{lig}}}^{\mathit{\text{state}}}$$ (11)

Isothermal titration calorimetry (ITC)

In order to establish the energetic landscape of the regulatory behavior of RMPK in the presence of its ligands, we performed a series of ITC experiments at temperatures between 4 and 45 °C. In order to separate contribution of the buffer ionization heat ΔH_ion from the overall reaction heat, all titrations were performed in two buffers with different ΔH_ion. Typically two experiments were performed in each buffer system and the data were averaged.

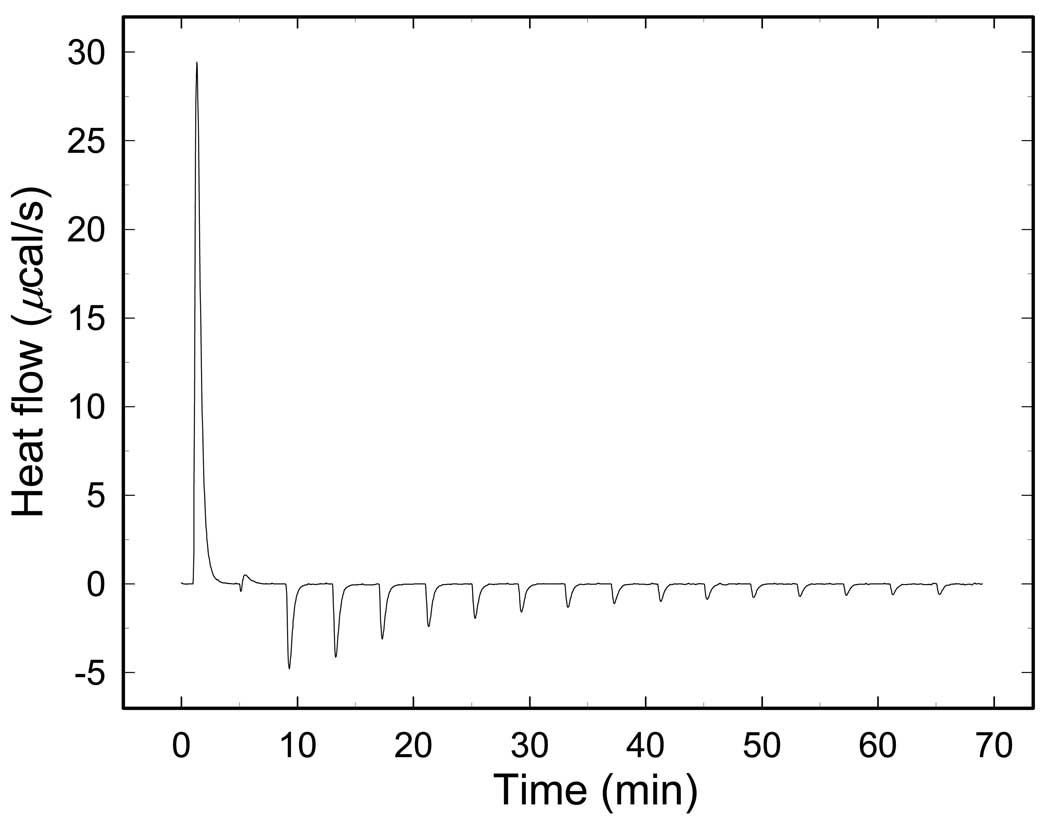
Fig.2 presents one example of the ITC titration curve - titration by Phe at 38°C. The sign of heat exchange for the reaction changes from positive to negative during the titration. This is a clear indication that the reaction is complex and consists of at least two heat-generating processes with opposite signs. Actually many reactions may contribute to the shape of ITC curves. The observation is consistent with the general mechanism of the WMC model which includes binding to both enzyme states, a ligand-induced shift of the R↔T equilibrium accompanied by the change of the RMPK conformation and linked proton reactions as described in our model. Heats resulting from re-equilibration of ligands between the R and T-state upon perturbation of the R↔T equilibrium contribute to the detailed shape of the titration curves as well.

Fig. 2.

ITC curve of the RM PK titrated by Phe at 38°C.

Since the patterns of the ITC data are quite complex, the consequence of linked multiple equilibria, a detailed interpretation of such curves is rather difficult. Therefore we decided not to make conclusions based only on the shape of the ITC curves. Instead, at different temperatures we titrated RMPK to saturation and the data expressed as overall reaction heats. Each data point in Fig. 3–6 therefore represents at least one ITC experiment.

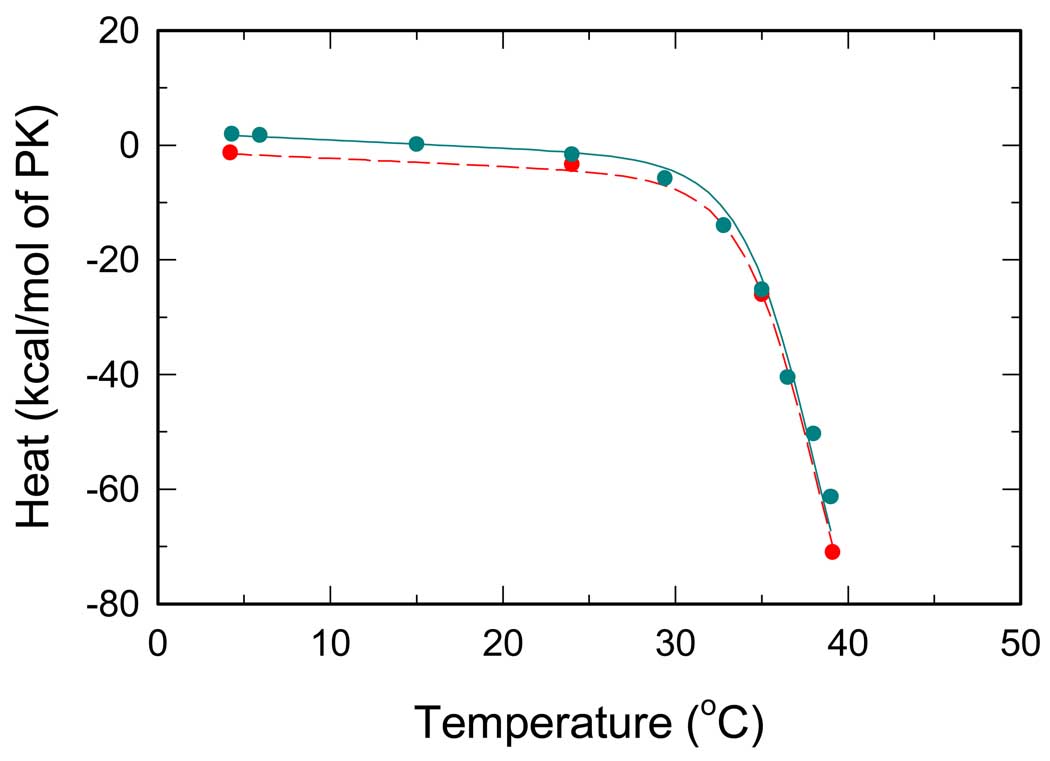
Fig. 3.

Temperature dependence of overall reaction heats for RMPK titrated by PEP. Cyan and red symbols represent ITC titrations in the TKM and the BTKM buffer, respectively. Lines represent the best global fit all ITC data, i.e. all data from Fig.2 – Fig. 5.

Fig. 6.

Overall reaction heats of RMPK titrated by Phe in the presence of 2 mM ADP. Cyan and red symbols represent ITC titrations in the TKM and the BTKM buffer, respectively. Lines represent the best global fit all ITC data, i.e. all data from Fig.2 – Fig. 5. To avoid dilution artifacts the same 2 mM concentration of ADP was present in the injectant during the ITC experiments.

PEP binding

ITC titrations by PEP are shown in Fig. 3 which shows that the measured reaction heats exhibit pronounced dependence on temperature. In this titration, there are only two linked reactions, namely, PEP binding and RMPK conformation change. At low temperatures below 30°C, the magnitude of heat of reaction is a linear function of temperature with a small negative slope. Such a behavior reflects an essentially temperature independent heat of reaction for PEP binding. In contrast, there is an abrupt decrease of the ${\mathrm{\Delta }H}_{\mathit{\text{PEP}}}^{\mathit{\text{tot}}}$ above 30°C. This significant change most likely reflects the contribution of heat due to the linked reaction of RMPK conformation change. Since earlier work indicated that RMPK is present predominantly in the R-state under these experimental conditions (8, 10, 19), a possible cause for the significant change in ${\mathrm{\Delta }H}_{\mathit{\text{PEP}}}^{\mathit{\text{tot}}}$ is the conversion to the T-state at these high temperatures and binding of PEP shifts RMPK back to the R-state i.e. the observed change could be assigned mainly to the R↔T transition. As temperature increases, the fraction of the T-state increases. Binding of PEP with a higher affinity to the R-state shifts the R↔T equilibrium back toward the R-state. Therefore a heat of the R↔T transition is expected to be detected in addition to ligand binding heats, Eq. (1). The observed temperature dependence of ${\mathrm{\Delta }H}_{\mathit{\text{PEP}}}^{\mathit{\text{tot}}}$ in Fig.3 is qualitatively in agreement with the behavior predicted by the two-state model.

The values of ${\mathrm{\Delta }H}_{\mathit{\text{PEP}}}^{\mathit{\text{tot}}}$ are quite similar in two buffers of significantly different heats of ionization. This trend implies that PEP binding does not involve change in proton release or absorption. Another possibility is that the changes in proton in PEP binding and R↔T transition are similar in magnitude but opposite in sign, thus, canceling the contribution of each other.

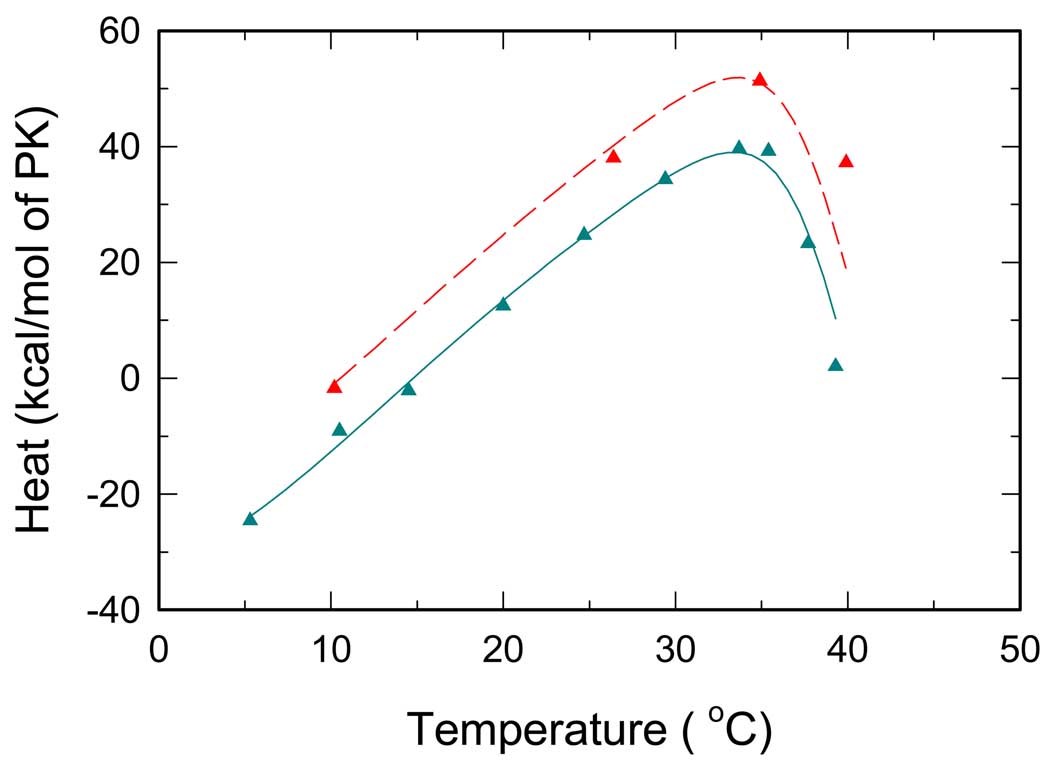
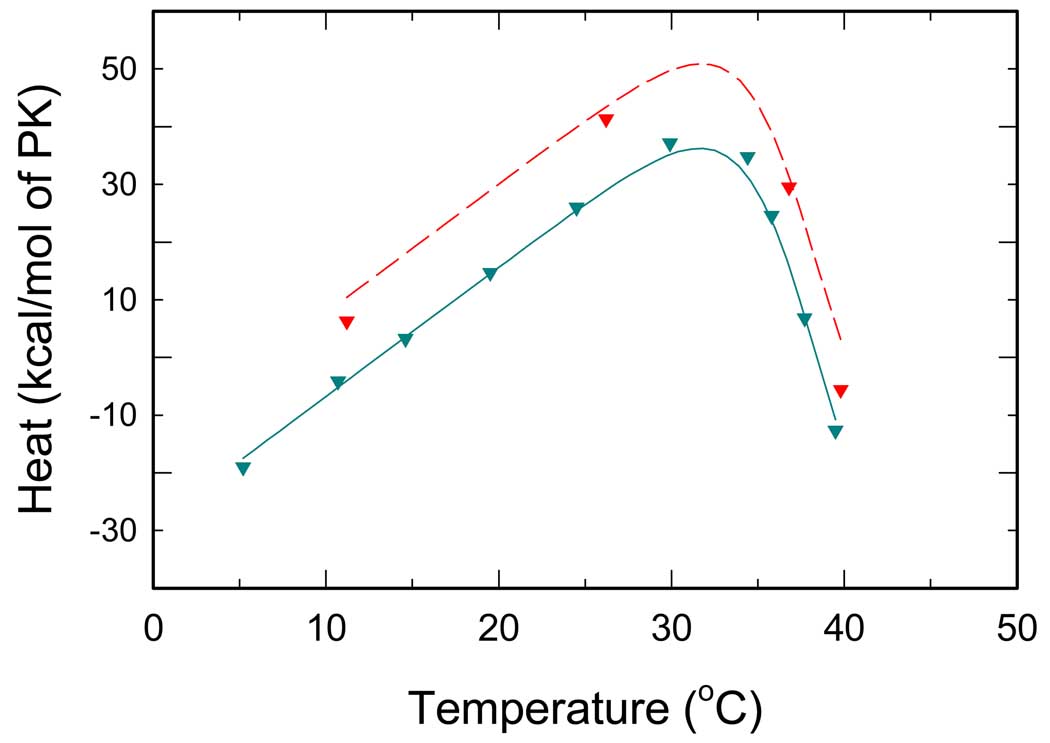
Phe binding

ITC titration curves for Phe are depicted in Fig. 4. In this case, the values of heat of reaction increase with increasing temperature. However, at 30°C the values decrease significantly with further increase in temperature. Again, in this titration only three linked reactions are involved, namely, R↔T conversion and binding of Phe to either of these states. The interaction with Phe is apparently analogous to the PEP-PK interaction. Similar thermal effects can be expected for binding of Phe that exhibits preferential binding to the T-state (8, 10, 19). As the fraction of the T-state decreases with decreasing temperature, binding of Phe shifts the R↔T equilibrium back toward the T-state. Because at a given temperature both PEP and Phe titrations start from the same distribution of states dictated by the R↔T equilibrium, similar (or complementary) curves are expected to be observed for the two ligands. Contrary to expectations, a plateau was not observed at low temperatures for the Phe titration. Instead, a positive slope of ${\mathrm{\Delta }H}_{\mathit{\text{Phe}}}^{\mathit{\text{tot}}}$ is detected. Such data are not consistent with the model described by Eqs.(1–11); thus, and some assumptions of the model have to be modified.

Fig. 4.

Temperature dependence of overall reaction heats for RMPK titrated by Phe. Cyan and red symbols represent ITC titrations in the TKM and the BTKM buffer, respectively. Lines represent the best global fit all ITC data, i.e. all data from Fig.2 – Fig. 5.

There are three possible causes for the observed effect. First, at low temperatures the differential affinity of Phe to the R and T states is not high enough to shift the R↔T equilibrium completely to the T-state. Second, there is an isobaric heat capacity change ΔC_p involved in the binding of Phe or, third, in the R↔T transition.

In order to test for the first possibility, the model was modified and an incomplete R↔T transition was assumed to take place when RMPK was titrated by Phe. In particular, we assumed that ${}^{\mathit{\text{sat}}}{f}_{\mathit{\text{Phe}}}^T<1$ in Eq.(1). However, the global analysis of the ITC data for PEP and Phe data from Fig. 3 and Fig. 4 resulted in an unacceptably poor fit. This model is also in contradiction with published steady-state kinetic data (10) and therefore it was rejected. The second case was ruled out when a global fit of the data sets from Fig. 3 and Fig. 4 completely failed (the program did not reach convergence) assuming a nonzero heat capacity change associated with the Phe binding, $\mathrm{\Delta }{H}_{\mathit{\text{Phe}}}^T=\mathrm{\Delta }{H}_{0,\mathit{\text{Phe}}}^T+\mathrm{\Delta }{C}_{p,\mathit{\text{Phe}}}^T·(T-T_0)$ .

To test for the third case, we incorporated to the model an isobaric heat capacity change ΔC_P,R↔T associated with the R↔T transition. In particular, we used ΔH_R↔T = ΔH_{0, R↔T} + ΔC_P,R↔T · (T − T₀) and ΔS_R↔T = ΔS_0,R↔T + ΔC_P,R↔T · ln(T / T₀) for evaluation of L₀ in Eq. (10). With this model we obtained a successful global fit of all curves from Fig. 3 and 4.

The values of ${\mathrm{\Delta }H}_{\mathit{\text{Phe}}}^{\mathit{\text{tot}}}$ are quite different in two buffers of significantly different heats of ionization. This trend implies that Phe binding involves change in proton release or absorption.

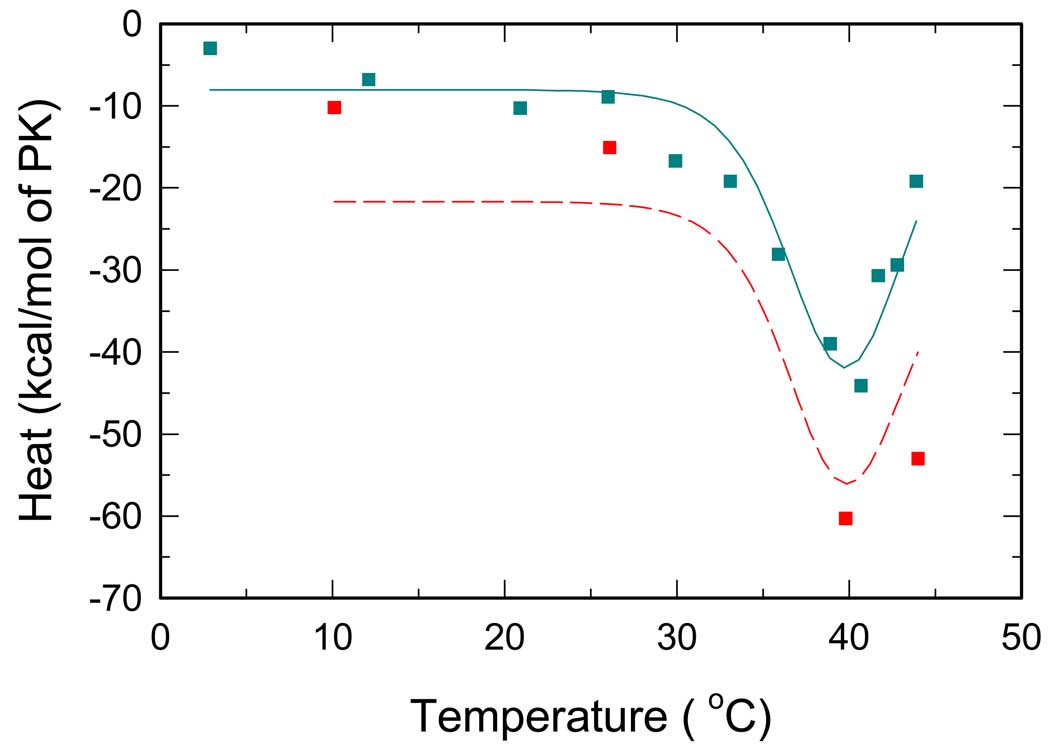
ADP binding

Fig. 5 demonstrates temperature dependence of thermal effects upon saturation of RMPK by ADP. A visual inspection of the figure reveals a pronounced minimum of the ${\mathrm{\Delta }H}_{\mathit{\text{ADP}}}^{\mathit{\text{tot}}}$ curve at temperatures above 35 °C. Interestingly, the sign of the dip agrees with the sign of ${\mathrm{\Delta }H}_{\mathit{\text{PEP}}}^{\mathit{\text{tot}}}$ at high temperatures in Fig. 3, where the R↔T transition is responsible for the major heat effects accompanying the PEP titration. Based on this observation we suggest that at temperatures above 30 °C the presence of ADP perturbs the R↔T equilibrium as a consequence of a differential affinity to the R and T-state. Specifically, the presence of ADP seems to shift the R↔T equilibrium toward the R-state. Consistent with published data (8, 10, 19), a flat region of ${\mathrm{\Delta }H}_{\mathit{\text{ADP}}}^{\mathit{\text{tot}}}$ around room temperature indicates only minor shifts of the R↔T equilibrium induced by ADP binding. When curves from Fig. 5 were included to the global data set, an excellent global fit of all six curves from Fig. 3–5 was achieved with negligible changes of the parameters associated with the R↔T transition. This strongly supports our conclusion about ΔC_P,R↔T since all data sets are linked by the same R↔T equilibrium.

Fig. 5.

Temperature dependence of overall reaction heats for RMPK titrated by ADP. Cyan and red symbols represent ITC titrations in the TKM and the BTKM buffer, respectively. Lines represent the best global fit all ITC data, i.e. all data from Fig.2 – Fig. 5.

Coupling between ADP and Phe bindings

Having characterized RMPK behavior in the presence of single ligands, the Phe titrations were repeated in the presence of 2mM ADP in order to evaluate possible interaction between ADP and Phe. The measured temperature dependence of ${\mathrm{\Delta }H}_{\mathit{\text{ADP}},\mathit{\text{Phe}}}^{\mathit{\text{tot}}}$ is shown in Fig. 6. We found that ${\mathrm{\Delta }H}_{\mathit{\text{ADP}},\mathit{\text{Phe}}}^{\mathit{\text{tot}}}$ in the presence of ADP is significantly different from ${\mathrm{\Delta }H}_{\mathit{\text{Phe}}}^{\mathit{\text{tot}}}$ shown in Fig. 4. Although the shape of the curves seems to be similar, absolute values of the reaction heats differ and a maximum of ${\mathrm{\Delta }H}_{\mathit{\text{ADP}},\mathit{\text{Phe}}}^{\mathit{\text{tot}}}$ is located at higher temperature compared to that of ${\mathrm{\Delta }H}_{\mathit{\text{Phe}}}^{\mathit{\text{tot}}}$ . When curves from Fig. 6 were included to the global data set assuming that there is no interaction between the binding sites for ADP and Phe, the quality of the global fit significantly degraded that invalidated our assumption of the non-interacting sites for these ligands. Based on the fitting results, as well as an independent evidence of the ADP-Phe interaction gleened from florescence data (36), we introduced an interaction enthalpy term, ${\mathrm{\Delta }\mathrm{\Delta }H}_{\mathit{\text{ADP}},\mathit{\text{Phe}}}^T$ and an interaction entropy term, ${\mathrm{\Delta }\mathrm{\Delta }S}_{\mathit{\text{ADP}},\mathit{\text{Phe}}}^T$ , for binding of Phe to the T-state in the presence of ADP:

$$\mathrm{\Delta }{H}_{\mathit{\text{ADP}},\mathit{\text{Phe}}}^T=\mathrm{\Delta }{H}_{\mathit{\text{Phe}}}^T+\mathrm{\Delta }\mathrm{\Delta }{H}_{\mathit{\text{ADP}},\mathit{\text{Phe}}}^T$$ (12)

$$\mathrm{\Delta }{S}_{\mathit{\text{ADP}},\mathit{\text{Phe}}}^T=\mathrm{\Delta }{S}_{\mathit{\text{Phe}}}^T+\mathrm{\Delta }\mathrm{\Delta }{S}_{\mathit{\text{ADP}},\mathit{\text{Phe}}}^T$$ (13)

The described modification renders dissociation constant $K_{\mathit{\text{ADP}},\mathit{\text{Phe}}}^T$ independent of. $K_{\mathit{\text{Phe}}}^T$ . However, due to the interaction we can no longer assume that PK saturated with Phe is always in the T-state, irrespective of temperature and ADP concentration. The full eq.(1) was used for calculation of the reaction heats. After the model modification the global fit of all 8 curves from Fig. 3–Fig. 6 dramatically improved.

RMPK conformation change

The best global fit is shown in Fig. 3–Fig. 6 by solid and dashed lines. Fitted parameters are summarized in Table 1. The R↔T concerted conformational transition is strongly entropy driven with a significant entropy term of 152 cal/K/mol of enzyme. The transition involves also a fairly large enthalpy change of 48 kcal/mol of PK. Such large values indicate strong temperature dependence of the equilibrium between the active and the inactive state. Moreover, the heat capacity change of 2.2 kcal/K/mol of enzyme associated with the transition causes L₀ to deviate from a monotonic dependence on temperature. The minimum of L₀, where RMPK is mostly in the active R-state, was found to be located near −3 °C.

Table I.

Parameters obtained by global fitting of the ITC data.

Reaction	Parameter	Value	Unit a
R↔T	ΔS0,R→T	152 (6) c, e	cal·mol−1·K−1 b
	ΔH0,R→T	48 (10) c	kcal·mol−1 b
	ΔCp,R→T	2.2 (0.2) c	kcal·mol−1·K−1 b
	ΔnR→T	0.5 (0.3) d, f	mol−1 b
Phe binding	${\mathrm{\Delta }S}_{\mathit{\text{Phe}}}^R$	7 (5)	cal·mol−1·K−1
	${\mathrm{\Delta }H}_{\mathit{\text{Phe}}}^R$	0.9 (2.0)	kcal·mol−1
	${\mathrm{\Delta }S}_{\mathit{\text{Phe}}}^T$	13 (7) g	cal·mol−1·K−1
	${\mathrm{\Delta }H}_{\mathit{\text{Phe}}}^T$	0.8 (1.0)	kcal·mol−1
	${\mathrm{\Delta }n}_{\mathit{\text{Phe}}}^T$	−0.9 (0.1) f	mol−1 b
PEP binding	${\mathrm{\Delta }H}_{\mathit{\text{PEP}}}^R$	−2.1 (0.8)	kcal·mol−1
	${\mathrm{\Delta }n}_{\mathit{\text{PEP}}}^R$	0.18 (0.03) f	mol−1 b
ADP binding	${\mathrm{\Delta }S}_{\mathit{\text{ADP}}}^R$	−20 (2)	cal·mol−1·K−1
	${\mathrm{\Delta }H}_{\mathit{\text{ADP}}}^R$	−10.3 (1.0)	kcal·mol−1
	${\mathrm{\Delta }n}_{\mathit{\text{ADP}}}^R$	0.74 (0.06)
	${\mathrm{\Delta }S}_{\mathit{\text{ADP}}}^T$	−29 (3)	cal·mol−1·K−1
	${\mathrm{\Delta }H}_{\mathit{\text{ADP}}}^T$	−13 (2)	kcal·mol−1
	${\mathrm{\Delta }n}_{\mathit{\text{ADP}}}^T$	1.00 (0.02) f	mol−1 b
ADP-Phe coupling	$\mathrm{\Delta }\mathrm{\Delta }{S}_{\mathit{\text{ADP}},\mathit{\text{Phe}}}^T$	−2.5 (2.0)	cal·mol−1·K−1
	$\mathrm{\Delta }\mathrm{\Delta }{H}_{\mathit{\text{ADP}},\mathit{\text{Phe}}}^T$	−0.46 (0.30)	kcal·mol−1
	$\mathrm{\Delta }{n}_{\mathit{\text{ADP}},\mathit{\text{Phe}}}^R$	−1.7 (1.0) f	mol−1 b

^aper mol of a ligand

^bper mol of tetramer

^cFor T₀=20°C. T₀ was a fixed parameter.

^dBuffer ionization heats are 11.3 kcal/mol and 6.8 kcal/mol for TKM and BTKM, respectively (40)

^eEstimated deviations from multiple fitting

^fNumber of protons absorbed

^gThis value was taken from the limited global fitting of the ITC and the fluorescence data

DISCUSSION

We were cognizant that the multidimensional χ² surface could contain local minima. To avoid being trapped in such minimum, the global fitting procedure was initiated with data from a subset of curves only. Then data from additional curves were individually added. This was followed by a subsequent optimization of parameters until all data sets were included. This procedure was repeated by initiating the analysis process with several different sets of data and expanding the data base by adding different data sets in different orders. Identical final values were derived for the same parameter regardless of the specific order of data was included in the analysis procedure; thus, we are confident that the reported values for these parameters represent the global minima. The global fitting was also initiated from different starting estimated values for these parameters to ensure that the fitting converges to the same global χ² minimum.

The results of this in-depth dissection of the thermodynamic signatures of RMPK interacting with metabolites provide novel insights on the mechanism of allosteric regulation of RMPK:

1. The state of RMPK that ADP preferentially binds is temperature dependent. ADP binds more favorably to the T- and R-state at high and low temperature, respectively. This cross over of affinity towards R and T-state implies that ADP does not only serve as a substrate but also plays an important and intricate role in regulating RMPK activity.

2. The binding of Phe is negatively coupled to that of ADP in addition to the shifting of the R↔T equilibrium due to the relative affinities of Phe or ADP to these two states i.e. the assumption that ligand binding to RMPK is state dependent is only correct for PEP but not Phe/ADP.

3. The release or absorption of protons linked to the various equilibria is specific to the particular reaction. As a consequence, pH will exert a complex effect on these linked equilibria with the net effect being manifested in the regulatory behavior of RMPK.

4. The R↔T equilibrium is accompanied by a significant ΔC_p.

Binding of ADP to both states of RMPK was found to be strongly enthalpy driven with binding enthalpies to the R and T-state about −10 kcal/mol and −13 kcal/mol. This is consistent with a binding mechanism that involves electrostatic interaction with the highly charged ADP substrate. Both entropy and enthalpy changes for binding of ADP were found to be the largest among all investigated ligands. ADP binding and the differential affinity towards the R and T-states exhibit pronounced temperature dependence. The affinity to the T-state is larger at elevated temperatures. As a consequence, at high temperature ADP binds more favorably to the T-state resulting in shifting the R↔T equilibrium towards the inactive T-state; thus, in this particular regard, ADP behaves like an inhibitor at high temperature. However, by virtue of its chemical structure, ADP is still a substrate of RMPK. In earlier studies, it was concluded that ADP behaves strictly as a substrate which plays a minor role in the allosteric regulation of RMPK because it does not show any differential affinity towards the two states of RMPK. However, as a consequence of extending the temperature range in this study, it is revealed that ADP actually plays a major role in the allosteric mechanism in RMPK under physiological relevant temperatures.

Phenylalanine binding in the presence of ADP revealed that an antagonism exists between the two ligands, i.e. Phe was found to bind more weakly in the presence of ADP. Table I indicates that due to the interaction enthalpy, ${\mathrm{\Delta }\mathrm{\Delta }H}_{\mathit{\text{ADP}},\mathit{\text{Phe}}}^T$ , of about −0.5 kcal/mol, the enthalpy term $\mathrm{\Delta }{H}_{\mathit{\text{ADP}},\mathit{\text{Phe}}}^T=\mathrm{\Delta }{H}_{\mathit{\text{Phe}}}^T+\mathrm{\Delta }\mathrm{\Delta }{H}_{\mathit{\text{ADP}},\mathit{\text{Phe}}}^T$ is reduced almost to zero. Concomitantly, the entropy change, $\mathrm{\Delta }{S}_{\mathit{\text{ADP}},\mathit{\text{Phe}}}^T=\mathrm{\Delta }{S}_{\mathit{\text{Phe}}}^T+\mathrm{\Delta }\mathrm{\Delta }{S}_{\mathit{\text{ADP}},\mathit{\text{Phe}}}^T$ , becomes smaller by 2.5 cal·mol⁻¹·K⁻¹. The net consequence of the coupling between ADP and Phe bindings is a reduction of the enthalpy term for Phe binding to essentially zero and a less favorable entropy term i.e. the presence of a bound ADP exerts a negative effect on Phe binding to the T-state. Thus, at high but physiologically relevant temperatures, the bound ADP modulates the inhibitory efficiency of Phe by reducing its affinity to the T-state.

Information related to linked proton reactions associated with the ligand binding and the state transition is also available from Table I. The following reactions summarize these results: Reactions with proton absorption -

$$\begin{array}{l}0.2{\mathrm{H}}^{+}+\text{PEP}+\mathrm{R}\leftrightarrows \text{PEP}•\mathrm{R};0.5{\mathrm{H}}^{+}+\mathrm{R}\leftrightarrows \mathrm{T}\\ 0.7{\mathrm{H}}^{+}+\text{ADP}+\mathrm{R}\leftrightarrows \text{ADP}•\mathrm{R};1.0{\mathrm{H}}^{+}+\text{ADP}+\mathrm{T}\leftrightarrows \text{ADP}•\mathrm{T}\end{array}$$

Reactions with proton release -

$$\text{Phe}+\mathrm{T}\leftrightarrows \text{Phe}•\mathrm{T}+0.9{\mathrm{H}}^{+};\text{\hspace{1em}ADP}+\text{Phe}+\mathrm{T}\leftrightarrows \text{ADP}•\text{Phe}•\mathrm{T}+1.7{\mathrm{H}}^{+}$$

Binding of substrates apparently always absorb protons, although the binding of ADP involves a larger amount of protons absorbed. Consequently the binding of ADP would be more sensitive to pH perturbations. The R →T transition would also absorb protons. For the reactions which involve in proton absorption, lower pH would shift the equilibria to the right, as defined by the Le Chatelier’s principle. Thus, lower pH would favor the bindings of ADP, PEP and the T-state. The net result would be an expected change in cooperativity in substrate binding, the extent of which is pH dependent.

In contrast, binding of Phe to the T-state, in the presence or absence of ADP, leads to release of protons. Another significant observation is that the amount of proton released almost doubles in the presence of ADP. If the bindings of Phe and ADP were simply a summation of the two reactions (absorption of 0.7 and release of 0.9 H⁺ for ADP and Phe binding, respectively), then the net amount of proton release is expected to be about zero; however, instead the observation is a doubling of H⁺ release to 1.7. This is a clear indication of the coupling of the two binding events. Binding of Phe and ADP to the T-state seems to be more pH dependent.

These results clearly indicate that the effect of pH on the basic allosteric behavior of RMPK is a composite of the nature and magnitude of proton release or absorption linked to the various reactions. According to the Wyman's linked-function theory (38) there should be dependence of dissociation constants on a concentration of protons and shift of the R↔T equilibrium. For example, at low pH the T-state is favored but the binding of Phe would be weakened. Thus, a binding isotherm of Phe is pH dependent as a function of the relative values of equilibrium constants which define the distribution of the R and T-state and the relative affinities of Phe to these states. Simultaneously, the affinity of substrates would be affected. Thus, one should expect that the allosteric behavior of RMPK is a complex phenomenon defined by the specific experimental conditions. It is most gratifying to note that such an expectation was reported in 1990 by Consler et. al.(19). Based on steady-state kinetic studies, these authors reported the synergistic effects of proton and Phe on the regulation of RMPK.

The kinetic results (10) are consistent with the present study that binding of Phe was found to be entropy driven with the entropy term, ${\mathrm{\Delta }S}_{\mathit{\text{Phe}}}^T$ , for binding to the T-state being about twice as large as the entropy change for binding to the R-state, ${\mathrm{\Delta }S}_{\mathit{\text{Phe}}}^R$ . These results imply that the binding of Phe is driven mainly by hydrophobic interactions that generally strengthen with increasing temperature and Phe binds more favorably to the T-state. Relatively small and similar values of the enthalpy changes $\mathrm{\Delta }{H}_{\mathit{\text{Phe}}}^R=0.9\text{kcal}/\text{mol}\text{and}\mathrm{\Delta }{H}_{\mathit{\text{Phe}}}^R=0.8\text{kca}/\text{mol}$ for binding of Phe to the R and the T-state, respectively, indicate only weak dependence of the binding constants on temperature. Calorimetric data revealed that binding of the PEP substrate to the active R conformation of the enzyme involves the enthalpy change of $\mathrm{\Delta }{H}_{\mathit{\text{PEP}}}^R=-2.1\text{kcal}/\text{mol}$ . The entropy change, ${\mathrm{\Delta }S}_{\mathit{\text{PEP}}}^R$ , as well as parameters characterizing PEP binding to the T-state were not accessible from our data primarily because in the absence of ligands the equilibrium for the conformation state of RMPK is heavily in favor of the R-state. Since PEP binds much favorably to the R state and the binding to the T-state most likely is not enthaly driven. As a consequence, no parameters associated with PEP binding to the T-state can be defined with confidence.

The significant ΔC_p detected in the R↔T transition is consistent with the report of dynamic movement of the B domain with respect to the rest of the molecule as detected by small angle neutron scattering in conjunction with molecular modeling (21). This domain movement can be modulated by mutation as detected by X-ray crystallography in S402P RMPK (39).

Our conclusions derived from calorimetric data are in full agreement with those based on our published steady-state kinetic studies. These conclusions are further strengthened by our fluorescence data and model simulations described in two following papers of this issue (36, 37).