Semiparametric Inference for a General Class of Models for Recurrent Events

Abstract

Procedures for estimating the parameters of the general class of semiparametric models for recurrent events proposed by Peña and Hollander (2004) are developed. This class of models incorporates an effective age function encoding the effect of changes after each event occurrence such as the impact of an intervention, it models the impact of accumulating event occurrences on the unit, it admits a link function in which the effect of possibly time-dependent covariates are incorporated, and it allows the incorporation of unobservable frailty components which induce dependencies among the inter-event times for each unit. The estimation procedures are semiparametric in that a baseline hazard function is nonparametrically specified. The sampling distribution properties of the estimators are examined through a simulation study, and the consequences of mis-specifying the model are analyzed. The results indicate that the flexibility of this general class of models provides a safeguard for analyzing recurrent event data, even data possibly arising from a frailtyless mechanism. The estimation procedures are applied to real data sets arising in the biomedical and public health settings, as well as from reliability and engineering situations. In particular, the procedures are applied to a data set pertaining to times to recurrence of bladder cancer and the results of the analysis are compared to those obtained using three methods of analyzing recurrent event data.

1 Introduction

Recurrent events occur in many settings such as in biomedicine, public health, clinical trials, engineering and reliability studies, politics, economics, sociology, actuarial science, among others. Examples of recurrent events in the biomedical and public health settings are the re-occurrence of a tumor after surgical removal in cancer studies, epileptic seizures, drug or alcohol abuse of adolescents, outbreak of a disease such as encephalitis, recurring migraines, hospitalization, movement in the small bowel during fasting state, onset of depression, nauseous feeling when taking drugs for the dissolution of cholesterol gallstones, recurrence of caries, ulcers or inflammation in an oral health study, and angina pectoris for patients with coronary disease. Some other specific biomedical examples of recurrent events are described in Cook and Lawless (2002). In the engineering and reliability settings, recurrent events could be the breakdown or failure of a mechanical or electronic system, the discovery of a bug in an operating system software, the occurrence of a crack in concrete structures, the breakdown of a fiber in fibrous composites, among others. Non-life insurance claims, traffic accidents, terrorist attacks, the Dow Jones Industrial Average decreasing by more than 200 points on a trading day, change of employment, among many others, are but a few examples of recurrent phenomena in other settings.

There are several models and methods of analysis used for recurrent event data. See for example Hougaard (2000), Therneau and Hamilton (1997), and Therneau and Grambsch (2000) for some current approaches to analyzing recurrent event data. However, as pointed out in Peña and Hollander (2004), there is still a need for a general and flexible class of models that simultaneously incorporates the effects of covariates or concomitant variables, the impact on the unit of accumulating event occurrences, the effect of performed interventions after each event occurrence, as well as the effect of latent or unobserved variables which, for each unit, endow correlation among the inter-event times. In recognition of this need, Peña and Hollander (2004) proposed a general class of models for recurrent events which satisfies the above requirements. This class of models will be described in Section 2. The current paper deals with inference issues, specifically the estimation of parameters, for this new class of models. However, we limit the scope of this paper to examining the finite-sample properties through simulation studies of the resulting estimators and defer the analytical and asymptotic analysis of their properties to a forthcoming paper.

We consider an observational unit (e.g., a patient in a biomedical setting, an electronic system in a reliability setting) that is being monitored for the occurrence of a recurrent event over a study period $[0,\tau ]$, where $\tau$ may represent an administrative time, time of study termination, or some other right-censoring variable. The time $\tau$ could be a random time governed by an unknown probability distribution function $G\left(t\right)=\mathbf{P}(\tau \le t)$. Let $S_0\equiv 0<S_1<S_2<S_3<\dots$ be the successive calendar times of event occurrences, and let $T_1,T_2,T_3,\dots$ be the times between successive event occurrences. Thus, for $i=1,2,3,\dots ,T_i=S_i-S_{i-1}$ and $S_i=T_1+T_2+\dots +T_i$. Over the observation period $[0,\tau ]$, the number of event occurrences is $K=max\{k\in \{0,1,2,\dots \}:S_k\le \tau \}$, which is a random variable whose distribution depends on the distributional properties of the inter-occurrence times $T_{i}s$ and the distribution $G$ of $\tau$. As such, $K$ is informative with regards to the distributional properties of event occurrences.

Assume for this unit a, possibly time-varying, $q$-dimensional vector of covariates such as gender, age, race, disease status, white blood cell counts (WBC), prostate specific antigen (PSA) level, weight, blood pressure, treatment regimen, etc. We suppose that over the period $[0,\tau ]$, the realization of this covariate process is observable. We denote this covariate process by $\left\{\mathbf{X}\right(s)=(X_1\left(s\right),X_2\left(s\right),\dots ,X_q\left(s\right){)}^{\text{t}}:0\le s\le \tau \}$, with “ ${}^t$” representing vector/matrix transpose. For this subject, the observable entities over the study period $[0,\tau ]$ are therefore

$$D(\tau )\equiv \{(X(s):0\le s\le \tau ),K,\tau ,T_1,T_2,\dots ,T_K,\tau -S_K\}.$$ (1)

Notice that since $S_K={\sum }_{j=1}^K{T}_j$, specifying $\tau -S_K$ renders $\tau$ redundant; however, we still include $\tau$ to indicate that $\tau -S_K$ is the right-censoring variable for the inter-occurrence time $T_{K+1}$. Furthermore, since $K$ is random, then the distributional properties of both $\tau -S_K$ and $T_{K+1}$ may be of a complicated form. When considering the data structure in this recurrent event situation, there is a need to recognize that $K$ is informative and that the censoring mechanism for $T_{K+1}$ is informative (cf., Wang and Chang, 1999; Lin et al., 1999; Peña et al., 2001). These aspects are borne out of the sum-quota data accrual scheme since the number of observed events is tied-in to the distributions governing the event occurrences themselves.

The observable entities may also be represented more succinctly and beneficially through the use of stochastic processes. Still considering one unit, with $I\{·\}$ denoting indicator function, define for calendar time $s$, $N^{†}\left(s\right)={\sum }_{j=1}^{\infty }I\{S_j\le s,S_j\le \tau \}$, which is the process counting the number of events observed on or before calendar time $s$ during the study period $[0,\tau ]$. Furthermore, define for calendar time $Y^{†}\left(s\right)=I\{\tau \ge s\}$, the “at-risk” process which indicates whether the subject is still under observation at calendar time $s$ or not. The data $\mathbf{D}\left(\tau \right)$ in (1) could be represented by

$$D(s^{*})=\{(X(s),N^{†}(s),Y^{†}(s)):0\le s\le s^{*}<\infty \},$$ (2)

where $s^{*}(\ge \tau )$ is an upper limit of observation time. Note that even though $\mathbf{X}\left(s\right)$ is not observed for $s>\tau$ this does not pose a problem since for $s>\tau ,Y^{†}\left(s\right)=0$, and so for such a subject, there will be no information obtainable beyond $\tau$. If in the study there are $n$ subjects, the observables will be $\mathbf{D}(s*)=\left({\mathbf{D}}_1\right(s*),{\mathbf{D}}_2(s*),\dots ,{\mathbf{D}}_n(s*\left)\right)$, where $s^{*}\ge {max}_{1\le i\le n}{\tau }_i$ and for $i=1,2,\dots ,n$,

$$D_i(s^{*})=\{(X_i(s):s\le {\tau }_i),K_i,{\tau }_i,T_{i1},T_{i2},\dots ,T_{i{K}_i},{\tau }_i-S_{i{K}_i}\}.$$ (3)

Equivalently,

$$D_i(s^{*})=\{(X_i(s),N_i^{†}(s),Y_i^{†}(s)):0\le s\le s^{*}<\infty \},\hspace{0.17em}\text{where}$$

$$N_i^{†}(s)=\sum _{j=1}^{\infty }I\{S_{ij}\le s,\hspace{0.17em}{S}_{ij}\le {\tau }_i\}\hspace{0.17em}\text{and}\hspace{0.17em}{Y}_i^{†}(s)=I\{{\tau }_i\ge s\},$$

and $S_{i1}<S_{i2}<\dots$ are the calendar times of successive event occurrences for the $i$th subject, $T_{ij}=S_{ij-1},j=1,2,\dots$ and ${\tau }_i$ is the censoring time of the $i$th subject.

We provide an outline of the contents of this paper. Section 2 will present a description of the class of models for recurrent events that is under investigation. Section 3 will examine the problem of estimating the parameters of the model when there are no frailty components. The results here are needed for the estimation procedure in the presence of frailties described in Section 4. Section 5 will summarize results of the simulation studies pertaining to the properties of the estimators. We demonstrate the estimation procedures discussed in Sections 3 and 4 on real data sets in Section 6. Section 7 will provide some concluding thoughts.

2 A General Class of Models

In this section we describe the general class of models for recurrent events in Peña and Hollander (2004). Let $\mathbf{Z}=(Z_1,Z_2,\dots Z_n)$ be a vector of independent and identically distributed (i.i.d.) positive-valued random variables from a parametric distribution $H(z,\xi )=\mathbf{P}(Z\le z|\xi )$ where $\xi$ is a finite-dimensional parameter taking values in $\Xi \subseteq {\Re }^r$. These variables are unobservable random factors affecting the event occurrences for the subjects. Also, let $\mathbf{F}=\{{ℱ}_s:0\le s\le s*\}$ be a filtration or history on some probability space $(\Omega ,ℱ,\mathbf{P})$ such that the ${\mathbf{X}}_i$ and $Y_i^{†}$ are predictable and such that the $N_i^{†}$ are counting processes with respect to $\mathbf{F}$. The general class of models requires the specification, possibly done dynamically, of predictable observable processes $\left\{{ℰ}_i\right(s):0\le s\le s*\},i=1,2,\dots ,n$, satisfying the following conditions: (I) ${ℰ}_i\left(0\right)=e_{i0}$, almost surely (a.s.), where $e_{i0},i=1,2,\dots ,n$, are nonnegative real numbers; (II) ${ℰ}_i\left(s\right)\ge 0,i=1,2,\dots ,n$; and (III) On $(S_{ik-1},S_{ik}],{ℰ}_i\left(s\right)$ is monotone and almost surely differentiable with a positive derivative ${ℰ}_i^{\prime }\left(s\right)$. The class of models is obtained by postulating that, conditionally on $\mathbf{Z}$, the $\mathbf{F}$-compensator of $N_i^{†}$ is $\left\{A_i^{†}\right(s|\mathbf{Z},{\mathbf{X}}_i):0\le s\le s*\}$ with

$$A_i^{†}(s|Z,X_i)=\underset{0}{\overset{s}{\int }}{Y}_i^{†}(v){\lambda }_i(v|Z,X_i)\text{d}v;$$ (4)

$${\lambda }_i(s\left|Z,X_i\right|=Z_i{\lambda }_0[{ℰ}_i(s)]\rho [N_i^{†}(s-);\alpha ]\psi [{\beta }^t{X}_i(s)].$$ (5)

This means that the process $M_i^{†}\left(s\right|\mathbf{Z},{\mathbf{X}}_i)=N_i^{†}(s)-A_i^{†}(s|\mathbf{Z},{\mathbf{X}}_i)$ is a square-integrable $\mathbf{F}$-martingale. In (5), ${\lambda }_0(·)$ is an unknown baseline hazard rate function; $\rho (·;\alpha ):{\mathbf{Z}}_{+}\equiv \{0,1,2,\dots \}\to {\Re }_{+}$ is of known functional form with $\rho (0;\alpha )=1$ and with $\alpha \in A\subseteq {\Re }^p$; and $\psi (·)$ is a nonnegative link function of known functional form with $\beta \in B\subseteq {\Re }^q$. The unknown model parameters are $\left({\lambda }_0\right(·),\alpha ,\beta ,ℰ)$, where ${\lambda }_0(·)$ is non-prarametrically specified, and $\alpha ,\beta$, and $\epsilon$ are finite-dimensional parameters. The main impetus in introducing this general class of models for recurrent events is that it incorporates simultaneously the effects of covariates through the link function $\psi (·)$, the associations among the event inter-occurrence times through the unobservable frailty variables $Z_i,$ the effects attributable to the accumulating event occurrences for a subject through the component $\rho (·;\alpha )$, and the effects of performed interventions after each event occurrence through the effective age processes $\left\{{ℰ}_i\right(·\left)\right\}$ which act on the baseline hazard rate function ${\lambda }_0(·)$, and which may even have nonlinear forms. There is a potential interplay between the effective age process $ℰ(·)$ and the $\rho (·;·)$ function. This issue will be discussed in Section 5 dealing with the simulation studies and in the Section 6 dealing with the applications.

With no frailty, the generality of this class of models was discussed in Peña and Hollander (2004). With the added feature of frailty, this class of models subsumes many models in the literature, as described below. Indeed, one may view this class of models as a general synthesis of several recurrent event models in survival analysis and reliability, such as the modulated renewal process of Cox (1972b) and those by Self and Prentice (1982), Prentice and Self (1983), Kessing et al. (1999), and in the examples that follow where the model is described for only one unit, i.e., with $n=1$.

Example 2.1

Beginning with no frailty $(Z=1)$, taking $\rho (k;\alpha )=1,\psi \left(w\right)=1$, and $ℰ\left(s\right)=s-S_{N^{†}(s-)}$, we obtain i.i.d. inter-occurrence times, one of the models examined in Gill (1981) and Peña et al. (2001). With frailty, one obtains associations among the inter-occurrence times, a model also considered in Peña et al. (2001) and Wang and Chang (1999). Still with no frailty but taking $\psi \left(w\right)=exp\left(w\right)$ gives the extended Cox proportional hazards model considered by Prentice et al. (1981), Lawless (1987), and Aalen and Husebye (1991). Further changing to $ℰ\left(s\right)=s$ gives a model examined by Prentice et al. (1981), Brown and Proschan (1983), and Lawless (1987) referred to in the reliability literature as an imperfect repair model, since it arises by `restoring a system to the state just before it failed (minimally repaired)' whenever the system fails.

Example 2.2

Let $I_1,I_2,I_3,\dots$ be a sequence of i.i.d. Bernoulli random variables with success probability $p$. Define the process $\left\{\eta \right(s):s\in [0,\tau ]\}$ via $\eta \left(s\right)={\sum }_{i=1}^{N†\left(s\right)}{I}_i$. Also let $0\equiv {\Gamma }_0,{\Gamma }_1,{\Gamma }_2,<\dots$ be defined according to ${\Gamma }_k=min\{j>{\Gamma }_{k-1}:I_j=1\},$, $k=1,2,3,\dots$. By setting $Z=1,\rho (k;\alpha )=1$ and $ℰ(s)=s-S_{{\Gamma }_{\eta (s-)}}$, we obtain

$$\lambda (s|Z,X)={\lambda }_0(s-S_{{\mathrm{\Gamma }}_{\eta (s-)}})\psi ({\beta }^{t}X(s)).$$ (6)

This is the Brown and Proschan (1983) imperfect repair model, also studied by Whitaker and Samaniego (1989) who noted that the inter-failure times and the repair modes suffice for model identifiability. If the success probability $p$ depends on the time of event occurrence, the Block et al. (1985) model obtains (see Hollander et al., 1992; Presnell et al., 1994). Note in this example that the ${\Gamma }_k$s represent event occurrences in which intervention causes the unit to acquire an effective age of zero. Furthermore, $S_{{\Gamma }_{\eta (s-)}}$ is the last time prior to $s$ that the subject had an effective age of zero. More generally, the class of models also subsumes the general repair model of Last and Szekli (1998), which includes as special cases models of Dorado et al. (1997), Kijima (1989), Baxter et al. (1996), and Stadje and Zuckerman (1991).

Example 2.3

Lindqvist et al. (2003) proposed the trend-renewal process (TRP) model and the heterogeneous TRP (HTRP) model for repairable systems, which are models built on the idea behind the inhomogeneous gamma process model of Berman (1981). The TRP has two parameters: a distribution function $F$ and a cumulative hazard function $\Lambda$, and is such that if $S_1<S_2<\dots$ are the event times, then $\left\{\Lambda \right(S_1),\Lambda (S_2),\dots \}$ forms a renewal process from the distribution function $F$. The TRP becomes a special case of the general class of models with effective age process $ℰ(s)=({\Lambda }_0^1○{\Lambda }_F^{-1}○{\Lambda }_0)\left(s-S_{N^{†}(s-)}\right)$ where ${\Lambda }_F$ is the cumulative hazard function associated with $F$ and $○$ is function composition, $\rho (k;\alpha )\equiv 1$ and $\psi \left(v\right)\equiv 1$. However, for the inference setting we are considering in this paper, this is not covered because $ℰ(·)$ would not be observable since ${\Lambda }_F(·)$ would not be known. Meanwhile, the HTRP model is simply the version with a frailty component.

Example 2.4

A special case obtains via $\rho \left[N^{†}\right(s-);\alpha ]=max\{\alpha -g[N^{†}(s-)],0\}$, where $\alpha$ is some positive real number, and $g(·)$ is some nondecreasing function. One could interpret the parameter $\alpha$ as an initial measure of the unit’s susceptibility to events, and $g(·)$ specifies the rate at which this unit is becoming stronger as the event occurrences accumulate. If we take $ℰ\left(s\right)=s-S_{N^{†}(s-)}$, the resulting model possesses the interesting property that the unit's defects contribute to the event occurrence intensity multiplicatively through the baseline hazard rate function ${\lambda }_0(·)$. If $g\left[N^{†}\right(s-\left)\right]=N^{†}(s-)$ and ${\lambda }_0\left(s\right)={\lambda }_0$, where ${\lambda }_0$ is some positive constant, then the Gail et al. (1980) tumor occurrence model and the Jelinski and Moranda (1972)) software reliability model are obtained.

Example 2.5

A popular load-sharing model is the equal load-share model considered in Kvam and Peña (2005). One context is a $K$-component parallel system consisting of identical components, for which the event of interest is the occurrence of a component failure. Failed components are not replaced, and when a component fails, the load of the system is redistributed equally over the remaining functioning components. To model this, we let $\alpha =\left({\alpha }_0\equiv 1,{\alpha }_1,\dots ,{\alpha }_{K-1}\right)$ be an unknown vector of constants, and take the hazard rate of event occurrence at calendar time $s$ as $\lambda \left(s\right)={\lambda }_0\left(s\right)[K-N^{†}(s-\left)\right]{\alpha }_{N^{†}(s-)}$, where ${\lambda }_0(·)$ is the hazard rate of each component at time zero and $N^{†}\left(s\right)$ denotes the number of components that have failed up to time $s$. This model is then a special case of the general model with $\epsilon \left(s\right)=s,\rho (j;\alpha )=(K-j){\alpha }_j$, and one has the added flexibility of also incorporating a link function involving covariates if such are observed, as well as frailty components which could model unobserved operating environmental factors.

3 Estimation of Parameters: Model without Frailties

By virtue of the generality of the class of models, it is thus of importance to develop appropriate statistical inference methods. We address in this section the problem of estimating the model parameters ${\Lambda }_0(·)={\int }_0{\lambda }_0\left(w\right)dw,\alpha$, and $\beta$ for the model where it is assumed that $Z_i\equiv 1$, that is, the model without frailties. Thus, the model of interest has intensity process

$${\lambda }_i(s|X_i)={\lambda }_0[{ℰ}_i(s)]\rho [N_i^{†}(s-);\alpha ]\psi ({\beta }^t{X}_i(s)).$$ (7)

The observables for the $n$ subjects, which now include the observable effective age processes, are $\left\{\right({\mathbf{X}}_i\left(s\right),N_i^{†}\left(s\right),Y_i^{†}\left(s\right),{ℰ}_i\left(s\right)):0\le s\le s*\},i=1,2,\dots ,n$, where $N_i^{†}\left(s\right)={\sum }_{j=1}^{\infty }I\{S_{ij}\le s,S_{ij}\le {\tau }_i\}$ and $Y_i^{†}\left(s\right)=I\{{\tau }_i\ge s\}$. The statistical identifiability of this class of models without frailties has been established in Theorem 1 of Peña and Hollander (2004). The two basic conditions to achieve identifiability, aside from the non-triviality of $\psi (·)$ and sufficient variability of $\mathbf{X}$, are that for each value of the parameter set $\left({\lambda }_0\right(·),\alpha ,\beta )$, the support of $ℰ\left(S_1\right)$ should contain $[0,\tau ]$, and that $\rho (·,·)$ should satisfy the condition that $\rho (k;{\alpha }^{\left(1\right)})=\rho (k;{\alpha }^{\left(2\right)})$ for each $k\in \{0,1,2,\dots \}$ implies ${\alpha }^{\left(1\right)}={\alpha }^{\left(2\right)}$. These two conditions are henceforth assumed to hold.

For this model, letting $A_i^{†}\left(s\right)={\int }_0^s{Y}_i^{†}\left(v\right){\lambda }_0\left[{ℰ}_i\right(v\left)\right]\rho \left[N_i^{†}\right(v-);\alpha ]\psi \left({\beta }^{\text{t}}{\mathbf{X}}_i\right(v\left)\right)dv$, then with respect to the filtration $\mathbf{F}$, the vector of processes

$$M^{†}=(M_1^{†},\dots ,M_n^{†})=N^{†}-A^{†}=(N_1^{†}-A_1^{†},\dots ,N_n^{†}-A_n^{†})$$

consists of orthogonal square-integrable martingales with predictable quadratic covariation processes $\langle M_{i_1}^{†},M_{i_2}^{†}\rangle \left(s\right)=A_{i_1}^{†}\left(s\right)I\{i_1=i_2\}$. The usual martingale theory utilized by Aalen (1978), Gill (1980), Andersen and Gill (1982), and others (cf., Fleming and Harrington, 1991; Andersen et al., 1993) does not apply directly for the purpose of estimating ${\Lambda }_0(·)$. The reason is that the ${\lambda }_0(·)$ appearing in $A_i^{†}(·)$ is time-transformed by the observable predictable process ${ℰ}_i(·)$, while of interest is to estimate ${\Lambda }_0\left(t\right)$ for a given $t$. It is tempting and would seem natural to simply define new processes involving the gap times between the event occurrences. However, as pointed out in Peña et al. (2001), this approach does not work since the resulting processes no longer satisfy martingale properties owing to the effect of the sum-quota accrual scheme.

The technique utilized in Peña et al. (2001), extending an idea of Sellke (1988) and Gill (1981), is to define a doubly-indexed process $Z_i(s,t)=I\left\{{ℰ}_i\right(s)\le t\},i=1,2,\dots ,n$. (Note that there is a notational, but tolerable, conflict with the frailty variables.) The index s represents calendar time, which is the natural time of data accrual; while the index $t$ represents gap times. This process indicates whether at calendar time $s$, the effective age of the $i$th subject is no more than $t$. For $i=1,2,\dots ,n$, define also the doubly-indexed processes

$$\begin{array}{l}{N}_i(s,t)=\underset{0}{\overset{s}{\int }}{Z}_i(v,t)N_i^{†}(\text{d}v);\hspace{0.17em}\hspace{0.17em}\hspace{0.17em}{A}_i(s,t)=\underset{0}{\overset{s}{\int }}{Z}_i(v,t)A_i^{†}(\text{d}v);\\ M_i(s,t)=N_i(s,t)-A_i(s,t)=\underset{0}{\overset{s}{\int }}{Z}_i(v,t)M_i^{†}(\text{d}v).\end{array}$$

Note that $N_i(s,t)$ is the number of events for the $i$th unit that occurred over $[0,s]$ with effective ages at most $t$. For a given $t$, by utilizing the martingale property of $M_i^{†}$ and the predictability of $Z_i(·,t)$, the process $M_i(·,t)$ is a square-integrable zero-mean martingale; however, for fixed $s$, the process $M_i(s,·)$ is not a martingale, but nevertheless, it also has mean zero.

A critical result is an equivalent expression for $A_i(s,t)$ which involves ${\lambda }_0\left(t\right)$ directly, instead of its time-transformed version. To reveal this expression, define for $j=1,\dots ,K_i+1$ the processes

$${ℰ}_{ij-1}(v)={ℰ}_i(v)I\{S_{ij-1}<v\le S_{ij}\}\hspace{0.17em}\text{on\hspace{0.17em}}\{Y_i^{†}(v)>0\}.$$ (8)

Thus, ${ℰ}_{ij-1}(·)$ is the restriction of ${ℰ}_i(·)$ on the $j$th interval bounded by successive event occurrence times for the $i$th subject. Note that on $(S_{ij-1},S_{ij}]$, the paths of ${ℰ}_{ij-1}(·)$ are one-to-one, so its inverse exists; and furthermore, it is also differentiable. We now provide the alternative expression for $A_i(s,t)$ in Proposition 1. The proof of the result is analogous to that in Peña et al. (2000). To achieve a more concise notation, with ${ℰ}_{ij}^{\prime }(s)=\frac{d}{ds}{ℰ}_{ij}(s),$ we define

$${\varphi }_{ij}(s;\alpha ,\beta )\equiv \frac{\rho [N_i^{†}(s-);\alpha ]\psi [{\beta }^t{X}_i(s)]}{{ℰ}_{ij}^{\prime }(s)}.$$ (9)

Proposition 1 For each $i=1,2,\dots ,n,A_i(s,t)={\int }_0^t{Y}_i(s,w){\lambda }_0\left(w\right)dw$, where

$$\begin{array}{l}{Y}_i(s,w)\equiv Y_i(s,w|\alpha ,\beta )=\sum _{j=1}^{N_i^{†}(s-)}{I}_{({ℰ}_{ij-1}(S_{ij-1}+),{ℰ}_{ij-1}(S_{ij})]}(w){\varphi }_{ij-1}\left({ℰ}_{ij-1}^{-1}(w);\alpha ,\beta \right)+\\ I_{({ℰ}_{i{N}_i^{†}(s-)}(S_{i{N}_i^{†}(s-)}+),\hspace{0.17em}{ℰ}_{i{N}_i^{†}(s-)}(s\wedge {\tau }_i)]}(w){\varphi }_{i{N}_i^{†}(s-)}\left({ℰ}_{i{N}_i^{†}(s-)}^{-1}(w);\alpha ,\beta \right).\end{array}$$

The process $Y_i(s,w)$ is a generalized at-risk process and is an adjusted count of the number of events for the $i$th unit which occurred over $[0,s]$ whose effective ages during their occurrences are at least $w$. Using Proposition 1, we have the identity

$$M_i(s,t)=N_i(s,t)-\underset{0}{\overset{t}{\int }}{Y}_i(s,w){\mathrm{\Lambda }}_0(\text{d}w),\hspace{0.17em}i=1,2,\dots ,n,$$

So that ${\sum }_{i=1}^n{M}_i\left(s,dw\right)={\sum }_{i=1}^n{N}_i\left(s,dw\right)-S_0(s,w){\Lambda }_0\left(dw\right)$, where

$$S_0(s,t)\equiv S_0(s,t|\alpha ,\beta )=\sum _{i=1}^n{Y}_i(s,t|\alpha ,\beta ).$$ (10)

Because ${\sum }_{i=1}^n{M}_i\left(s,dw\right)$ has mean zero, a method-of-moments ‘estimator’ of ${\Lambda }_0\left(t\right)$, given $(\alpha ,\beta )$ is

$${\widehat{\mathrm{\Lambda }}}_0(s,t|\alpha ,\beta )=\underset{0}{\overset{t}{\int }}\left\{\frac{J(s,w|\alpha ,\beta )}{S_0(s,w|\alpha ,\beta )}\right\}\left\{\sum _{i=1}^n{N}_i(s,\text{d}w)\right\},$$ (11)

with $J(s,w|\alpha ,\beta )=I\{S_0(s,w|\alpha ,\beta )>0\}$ and with the convention that $0/0=0$. Notice that this ‘estimator’ is of the same flavor as the Nelson-Aalen estimator or the Aalen-Breslow estimator in single-event settings, although it should be pointed out that the derivation as well as the structure of the processes are quite different.

Next we develop the profile likelihood for $(\alpha ,\beta )$ from which the estimator of $(\alpha ,\beta )$ will be obtained. Following Jacod (1975) (see also Andersen et al., 1993), if the distribution $G$ of $\tau$ does not involve the model parameters, then the full likelihood process associated with the observables for the general model without frailties is

$$\begin{array}{l}{L}_F^{†}(s|{\lambda }_0(\cdot ),\alpha ,\beta ,D(s*))=\left\{\prod _{i=1}^n{\prod _{v=0}^s\left[Y_i^{†}(v)\rho [N_i^{†}(v-);\alpha ]\psi ({\beta }^{\text{t}}{X}_i(v)){\lambda }_0[{ℰ}_i(v)]\right]}^{N_i^{†}(\mathrm{\Delta }v)}\right\}\times \\ \left\{exp\left[-\sum _{i=1}^n\underset{0}{\overset{s}{\int }}{Y}_i^{†}(v)\rho [N_i^{†}(v-);\alpha ]\psi ({\beta }^{\text{t}}{X}_i(v)){\lambda }_0[{ℰ}_i(v)]\text{d}v\right]\right\}.\end{array}$$ (12)

The argument of the exponential function could be re-expressed via

$$\sum _{i=1}^n\underset{0}{\overset{s}{\int }}{Y}_i^{†}(v)\rho [N_i^{†}(v-);\alpha ]\psi ({\beta }^{\text{t}}{X}_i(v))\hspace{0.17em}{\lambda }_0[{ℰ}_i(v)]\text{d}v=\underset{0}{\overset{\infty }{\int }}{S}_0(s,w|\alpha ,\beta ){\mathrm{\Lambda }}_0(\text{d}w).$$

Since from (11), we have ${\widehat{\mathrm{\Lambda }}}_0(s,\text{d}w|\alpha ,\beta )={\sum }_{i=1}^n{N}_i(s,\text{d}w)/S_0(s,w|\alpha ,\beta ),$ it therefore follows that ${\int }_0^{\infty }{S}_0(s,\hspace{0.17em}w|\alpha ,\beta )\hspace{0.17em}{\widehat{\mathrm{\Lambda }}}_0(s,\text{d}w|\alpha ,\beta )={\sum }_{i=1}^n{N}_i(s,\infty ),$ which is independent of $(\alpha ,\beta )$. Upon substituting the ‘estimator’ ${\widehat{\mathrm{\Lambda }}}_0(s,t|\alpha ,\beta )$ for ${\Lambda }_0\left(t\right)$ in the argument of the exponential function in (12), the resulting term will not contribute to the profile likelihood for $(\alpha ,\beta )$.

On the other hand, substituting ${\widehat{\mathrm{\Lambda }}}_0(s,w|\alpha ,\beta )$ for ${\Lambda }_0\left(w\right)$ in the first term of (12), we obtain the relevant portion of the profile likelihood of $(\alpha ,\beta )$ to be

$$L_P(s|\alpha ,\beta ,D(s*))=\prod _{i=1}^n\prod _{j=1}^{N_i^{†}(s)}{\left[\frac{\rho (j-1;\alpha )\psi [{\beta }^{\text{t}}{X}_i(S_{ij})]}{S_0[s,{ℰ}_i(S_{ij})|\alpha ,\beta ]}\right]}^{\mathrm{\Delta }{N}_i^{†}(S_{ij})}.$$ (13)

This process could also be viewed as the partial likelihood process for $(\alpha ,\beta )$, which is a generalization of the partial likelihood for the Cox model (cf., Cox, 1972a, 1975; Andersen and Gill, 1982). The logarithm of the profile likelihood could be conveniently expressed in integral form via

$$\begin{array}{l}{l}_P(s|\alpha ,\beta ,D(s*))=\sum _{i=1}^n\underset{0}{\overset{s}{\int }}[log\hspace{0.17em}\rho [N_i^{†}(v-);\alpha ]+log\hspace{0.17em}\psi ({\beta }^{\text{t}}{X}_i(v))-\\ log\hspace{0.17em}{S}_0(s,{ℰ}_i(v)|\alpha ,\beta )]N_i^{†}(\text{d}v).\end{array}$$ (14)

From this profile likelihood, the estimators of $\alpha$ and $\beta$ will be obtained. It is easy to see that the estimating equations for the profile maximum likelihood estimators are

$$\sum _{i=1}^n\underset{0}{\overset{s*}{\int }}\left[\frac{\frac{\partial }{\partial \alpha }\rho [N_i^{†}(v-);\alpha ]}{\rho [N_i^{†}(v-);\alpha ]}-\frac{\frac{\partial }{\partial \alpha }{S}_0(s,{ℰ}_i(v)|\alpha ,\beta )}{S_0(s,{ℰ}_i(v)|\alpha ,\beta )}\right]\hspace{0.17em}{N}_i^{†}(\text{d}v)=0;$$ (15)

$$\sum _{i=1}^n\underset{0}{\overset{s*}{\int }}\left[\frac{\frac{\partial }{\partial \beta }\psi ({\beta }^{\text{t}}{X}_i(v))}{\psi ({\beta }^{\text{t}}{X}_i(v))}-\frac{\frac{\partial }{\partial \beta }{S}_0(s,{ℰ}_i(v)|\alpha ,\beta )}{S_0(s,{ℰ}_i(v)|\alpha ,\beta )}\right]\hspace{0.17em}{N}_i^{†}(\text{d}v)=0.$$ (16)

Because $N_i^{†}(·)$ is a step process with a finite number of jumps, then both of these estimating equations are finite sums with respect to the calendar times $S_{ij}s$. Also, just like estimating equations in simpler models, such as for the Cox proportional hazards model, it is clear that numerical techniques will be needed to obtain the estimates $\widehat{\alpha }$ and $\widehat{\beta }$.

Upon obtaining the estimators $\widehat{\alpha }$ and $\widehat{\beta }$ from the estimating equations (15) and (16), the estimator of ${\Lambda }_0\left(t\right)$ based on the realizations of the observables over $[0,s*]$ is obtained by substituting ( $\widehat{\alpha },\hspace{0.17em}\widehat{\beta }$) for $(\alpha ,\beta )$ in the expression of ${\widehat{\mathrm{\Lambda }}}_0(s*,t|\alpha ,\beta )$ given in (11). Thus,

$${\widehat{\mathrm{\Lambda }}}_0(s*,t)=\underset{0}{\overset{t}{\int }}\left\{\frac{J(s*,\hspace{0.17em}w|\widehat{\alpha },\widehat{\beta })}{S_0(s*,\hspace{0.17em}w|\widehat{\alpha },\widehat{\beta })}\right\}\left\{\sum _{i=1}^n{N}_i(s*,\text{d}w)\right\}.$$ (17)

Finally, for an estimator of the baseline survivor function associated with ${\Lambda }_0(·)$ defined via ${\overline{F}}_0(t)=exp\{-{\mathrm{\Lambda }}_0(t)\},$ by the product-integral representation and the substitution principle, we obtain

$$\widehat{\overline{F}}(s^{*},t)=\prod _{w=0}^t[1-{\widehat{\mathrm{\Lambda }}}_0(s*,\text{d}w)]=\prod _{w=0}^t\left[1-\frac{{\sum }_{i=1}^n{N}_i(s*,\text{d}w)}{S_0(s*,w|\widehat{\alpha },\widehat{\beta })}\right].$$ (18)

This estimator is of a product-limit type analogous to those arising in the estimation of the baseline survivor function in the Cox proportional hazards model or the multiplicative intensity model (see Cox, 1972a; Andersen and Gill, 1982).

For the i.i.d. interoccurrence times model in Example $2.1$, which obtains when $\psi \left(w\right)=1$ (no covariate effects), $\rho \left(w\right)=1$ (no effects of accumulating event occurrences), and ${ℰ}_i\left(s\right)=s-S_{N_i^{†}(s-)}$ (upon each event occurrence, effective age is reset to zero, so this is just the backward recurrence time), the estimator of ${\overline{F}}_0(t)$ in (18) simplifies to that considered in Peña et al. (2001). Note, in particular, that for this special model, $ℰ{\prime }_i\left(s\right)=1$, and since ${ℰ}_{ij-1}\left(S_{ij}\right)=S_{ij}-S_{ij-1=}{T}_{ij}$, then the process $Y_i(s,w)$ simplifies to

$$Y_i(s,w)=\sum _{j=1}^{N_i^{†}(s-)}I\{T_{ij}\ge w\}+I\{min(s,{\tau }_i)-S_{i{N}_i^{†}(s-)}\ge w\},$$

which is the natural at-risk process for the gap times over the observation period $[0,s]$.

4 Estimation of Parameters: Model with Frailties

We now consider the estimation of the parameters when the class of models includes frailties. It will be assumed that the frailties $Z_1,Z_2,...,Z_n$ are i.i.d. from a distribution $H(·|\xi )$ where $\xi \in \Xi \subseteq {\Re }^r$. A common choice for this $H$, which we adopt here, is the gamma distribution with unit mean and variance 1/ $\xi ,H=Gamma(\xi ,\xi )$. Imposing the restriction that the gamma shape and scale parameters are identical, together with the identifiability conditions for the model without frailty stated in the beginning of Section 3, is needed to have model identifiability. We do not provide a rigorous proof of this identifiability result since it will lead us to excursions into product spaces and measures and ideas behind identifiability proofs for mixture models, but see, for example, Parner (1998) for such ideas. Recall at this stage that the $Z_i$ are not observed. For the model at hand, the conditional intensity function is as given in (5), which for convenience is again displayed below:

$${\lambda }_i(s|Z_i,X_i)=Z_i{\lambda }_0[{ℰ}_i(s)]\rho [N_i^{†}(s-);\alpha ]\psi ({\beta }^{\text{t}}{X}_i(s)).$$

To achieve brevity, we let $\theta \equiv \left({\Lambda }_0\right(·),\alpha ,\beta ,\xi )$. If the $\mathbf{Z}=\mathbf{z}=(z_1,z_{2,...,}{z}_n)$ are observed, the complete likelihood process for the model parameters $\theta$ is given by

$$\begin{array}{l}{L}_C^{†}(s*|\theta ,z,D(s*))=\prod _{i=1}^n[\frac{{\xi }^{\xi }}{\mathrm{\Gamma }(\xi )}{z}_i^{\xi -1}\hspace{0.17em}exp\{-\xi z_i\}\times \\ \left\{\prod _{v=0}^{s*}{\left[z_i{Y}_i^{†}(v){\lambda }_0[{ℰ}_i(v)]\rho [N_i^{†}(v-);\alpha ]\psi [{\beta }^{\text{t}}{X}_i(v)]\right]}^{N_i^{†}(\mathrm{\Delta }v)}\right\}\times \\ exp\hspace{0.17em}\left\{-\underset{0}{\overset{s*}{\int }}{z}_i{Y}_i^{†}(v){\lambda }_0[{ℰ}_i(v)]\rho [N_i^{†}(v-);\alpha ]\psi [{\beta }^{\text{t}}{X}_i(v)]\text{d}v\right\}].\end{array}$$ (19)

Since the $Z_i$ are unobserved, integrating them out in (19) yields the full likelihood process, which is

$$\begin{array}{l}{L}_F(s*|\theta ,D(s*))=\prod _{i=1}^n\{\left[\frac{\mathrm{\Gamma }(\xi +N_i^{†}(s*))}{\mathrm{\Gamma }(\xi )}\right]\times \\ {\left[\frac{\xi }{\xi +{\int }_0^{s*}{Y}_i^{†}(v)\rho [N_i^{†}(v-);\alpha ]\psi ({\beta }^{\text{t}}{X}_i(v)){\lambda }_0[{ℰ}_i(v)]\text{d}v}\right]}^{\xi +N_i^{†}(s*)}\times \\ \left(\prod _{v=0}^{s*}{\left[\frac{Y_i^{†}(v)\rho [N_i^{†}(v-);\alpha ]\psi ({\beta }^{\text{t}}{X}_i(v)){\lambda }_0[{ℰ}_i(v)]}{\xi }\right]}^{N_i^{†}(\mathrm{\Delta }v)}\right)\}.\end{array}$$ (20)

The maximum likelihood estimators of the model parameters are the maximizers of this full likelihood process, with the proviso that the maximizing ${\Lambda }_0(·)$ jumps only at observed values of ${ℰ}_i\left(S_{ij}\right)$. The expectation-maximization (EM) algorithm described in the sequel finds this set of maximizers.

In estimating the model parameters $\xi ,{\Lambda }_0(·),\alpha$, and $\beta$, we generalize and extend the approach implemented in Peña et al. (2001) which dealt with the frailty model without covariates, and without the $\rho (\alpha ,\alpha )$ term, and with ${ℰ}_i\left(s\right)=s-S_{i{N}_i^{†}(s-)}$. The computations of the estimates will be facilitated through the EM algorithm introduced by Dempster et al. (1977), and implemented in counting process frailty models by Nielsen et al. (1992). The main ingredients of this algorithm for the general class of recurrent event models are as follows. For the expectation-step, given $\theta$ and $\mathbf{D}(s*)$, the conditional expectations of $Z_i$ and log $\left(Z_i\right)$ are, respectively,

$$E\left\{Z_i\right|\theta ,D(s*)\}=\frac{\xi +N_i^{†}(s*)}{\xi +{\int }_0^{s*}{Y}_i^{†}(v)\rho [N_i^{†}(v-);\alpha ]\psi ({\beta }^{\text{t}}{X}_i(v)){\lambda }_0[{ℰ}_i(v)]\text{d}v};$$ (21)

$$E\{log\hspace{0.17em}{Z}_i|\theta ,D(s*)\}=\text{DG\hspace{0.17em}}[\xi +N_i^{†}(s*)]-log\hspace{0.17em}[\xi +N_i^{†}(s*)]+log\hspace{0.17em}[E\left\{Z_i\right|\theta ,D(s*)\}],$$ (22)

where $DG(·)$ is the di-gamma function, that is, $\text{DG}(\alpha )=\frac{d}{d\alpha }\hspace{0.17em}log\hspace{0.17em}\mathrm{\Gamma }(\alpha ).$ For the maximization-step, with $l_C^{†}$ denoting the logarithm of the complete likelihood function $L_C^{†}$ and with ${\mathbf{E}}_{\mathbf{Z}\left|\theta \right(0)}$ denoting expectation with respect to $\mathbf{Z}$ when the parameter vector equals ${\theta }^{\left(0\right)}$, define the function

$$\begin{array}{l}Q(\theta |{\theta }^{(0)},D(s*))=E_{Z|{\theta }^{(0)}}\left\{l_C^{†}(s*|\theta ,\hspace{0.17em}Z,\hspace{0.17em}D(s*))\right\}\\ =n\xi \hspace{0.17em}log\xi -nlog\mathrm{\Gamma }(\xi )+\sum _{i=1}^n(N_i^{†}(s*)+\xi -1){\widehat{logZ}}_i{}^{(1)}-\\ \sum _{i=1}^n\left(\xi +\underset{0}{\overset{s*}{\int }}{Y}_i^{†}(v)\rho [N_i^{†}(v-);\alpha ]\psi ({\beta }^{\text{t}}{X}_i(v))\hspace{0.17em}{\lambda }_0[{ℰ}_i(v)]\text{d}v\right){\widehat{Z}}_i{}^{(1)}+\\ \sum _{i=1}^n\underset{0}{\overset{s*}{\int }}log\hspace{0.17em}(Y_i^{†}(v)\rho [N_i^{†}(v-);\alpha ]\psi ({\beta }^{\text{t}}{X}_i(v))\hspace{0.17em}{\lambda }_0[{ℰ}_i(v)])\hspace{0.17em}{N}_i^{†}(\text{d}v),\end{array}$$

where

$${\widehat{logZ}}_i{}^{(1)}\equiv E\{log\hspace{0.17em}{Z}_i|{\theta }^{(0)},\hspace{0.17em}D(s*)\}\hspace{0.17em}\text{and}\hspace{0.17em}{\widehat{Z}}_i{}^{(1)}\equiv E\{Z_i|{\theta }^{(0)},\hspace{0.17em}D(s*)\}.$$

In this maximization step, the function $\mathbf{Q}\left(\theta \right|{\theta }^{\left(0\right)},\mathbf{D}\left(s^{*}\right))$ is maximized with respect to $\theta$. This is achieved by separate maximization of the mappings given by

$$\begin{array}{l}({\mathrm{\Lambda }}_0(\cdot ),\hspace{0.17em}\alpha ,\beta )\mapsto \sum _{i=1}^n\{\underset{0}{\overset{s*}{\int }}log\left[{\widehat{Z}}_i{}^{(1)}{Y}_i^{†}(v)\rho [N_i^{†}(v-);\alpha ]\psi ({\beta }^{\text{t}}{X}_i(v))\hspace{0.17em}{\lambda }_0[{ℰ}_i(v)]\right]N_i^{†}(\text{d}v)-\\ \underset{0}{\overset{s*}{\int }}{\widehat{Z}}_i{}^{(1)}{Y}_i^{†}(v)\rho [N_i^{†}(v-);\alpha ]\psi ({\beta }^{\text{t}}{X}_i(v))\hspace{0.17em}{\lambda }_0[{ℰ}_i(v)\text{d}v\};\end{array}$$ (23)

$$\xi \mapsto n\xi log\xi -n\hspace{0.17em}log\hspace{0.17em}\mathrm{\Gamma }(\xi )+\xi \sum _{i=1}^n{\widehat{logZ}}_i{}^{(1)}-\xi \sum _{i=1}^n{\widehat{Z}}_i{}^{{}^{(1)}}.$$ (24)

For the maximization of the mapping in (23), we basically adopt the procedures developed in the case without frailties. Examining the mapping, we note that the only difference with the case without frailties is that $Y_i^{†}\left(v\right)$ gets replaced by $Z_i{Y}_i\left(v\right)$. Consequently, given $\mathbf{Z}=\left(Z_{1,....,}{Z}_n\right),\alpha ,\beta$, and the data $\mathbf{D}(s*)$, the ‘estimator’ of ${\Lambda }_0(·)$ is given by

$${\widehat{\mathrm{\Lambda }}}_0(s*,t|Z,\alpha ,\beta )=\underset{0}{\overset{t}{\int }}\left\{\frac{J(s*,\hspace{0.17em}w|Z,\alpha ,\beta )}{S_0(s*,\hspace{0.17em}w|Z,\alpha ,\beta )}\right\}\left\{\sum _{i=1}^n{N}_i(s*,\text{d}w)\right\},$$ (25)

where $J(s,w|\mathbf{Z},\alpha ,\beta )=I\{S_0(s,w|\mathbf{Z};\alpha ,\beta )>0\}$ with $S_0(s,w|\mathbf{Z},\alpha ,\beta )={\sum }_{i=1}^n{Z}_i{Y}_i(s,w|\alpha ,\beta )$. Analogously to the estimating equations for $\alpha$ and $\beta$ in the model without frailties in (15) and (16), given $\mathbf{Z}$ and ${\widehat{\mathrm{\Lambda }}}_0(s*,\cdot |Z,\alpha ,\beta )$, we may estimate $\alpha$ and $\beta$ by solving the estimating equations

$$\sum _{i=1}^n\underset{0}{\overset{s*}{\int }}\left[\frac{\frac{\partial }{\partial \alpha }\rho [N_i^{†}(v-);\alpha ]}{\rho [N_i^{†}(v-);\alpha ]}-\frac{\frac{\partial }{\partial \alpha }{S}_0(s,{ℰ}_i(v)|Z,\hspace{0.17em}\alpha ,\beta )}{S_0(s,{ℰ}_i(v)|Z\hspace{0.17em},\alpha ,\beta )}\right]N_i^{†}(\text{d}v)=0;$$ (26)

$$\sum _{i=1}^n\underset{0}{\overset{s*}{\int }}\left[\frac{\frac{\partial }{\partial \beta }\psi ({\beta }^{\text{t}}{X}_i(v))}{\psi ({\beta }^{\text{t}}{X}_i(v))}-\frac{\frac{\partial }{\partial \beta }{S}_0(s,{ℰ}_i(v)|Z,\hspace{0.17em}\alpha ,\beta )}{S_0(s,{ℰ}_i(v)|Z,\hspace{0.17em}\alpha ,\beta )}\right]N_i^{†}(\text{d}v)=0,$$ (27)

which we implemented through a Newton-Raphson procedure. For the maximization of mapping (24), we also implemented the Newton-Raphson procedure, though clearly there are other options for maximizing this mapping.

With these ingredients at hand, the EM recipe for obtaining the estimates of the model parameters in this general model with frailties is described by the following steps:

Step 0 (Initialization)

Specify initial estimates ${\widehat{\xi }}^{(0)},\hspace{0.17em}{\widehat{\alpha }}^{(0)}$and ${\widehat{\beta }}^{(0)}$ of $\xi ,\alpha$, and $\beta$, respectively. By setting ${\widehat{Z}}_i^{(0)}=1,i=1,2,...,n$, obtain the initial estimate of ${\Lambda }_0(·)$ via

$${\widehat{\mathrm{\Lambda }}}_0^{(0)}(s*,\hspace{0.17em}t|{\widehat{Z}}^{(0)},{\widehat{\alpha }}^{(0)},\hspace{0.17em}{\widehat{\beta }}^{(0)})=\underset{0}{\overset{t}{\int }}\left\{\frac{J(s*,\hspace{0.17em}w|{\widehat{Z}}^{(0)},{\widehat{\alpha }}^{(0)},\hspace{0.17em}{\widehat{\beta }}^{(0)})}{S_0(s*,\hspace{0.17em}w|{\widehat{Z}}^{(0)},{\widehat{\alpha }}^{(0)},\hspace{0.17em}{\widehat{\beta }}^{(0)})}\right\}\left\{\sum _{i=1}^n{N}_i(s*,\text{d}w)\right\}$$

which is just the ‘estimator’ in (11) under the model without frailties.

Step 1 (E-step)

Given $({\widehat{\xi }}^{(0)},{\widehat{\alpha }}^{(0)},{\widehat{\beta }}^{(0)}),$ and ${\widehat{\mathrm{\Lambda }}}_0^{(0)}(s*,\cdot |{\widehat{Z}}^{(0)},{\widehat{\alpha }}^{(0)},{\widehat{\beta }}^{(0)}),$ obtain ${\widehat{Z}}_i{}^{(1)}$ and ${\widehat{logZ}}_i{}^{(1)}$ via formulas (21) and (22). Denote by ${\widehat{Z}}^{(1)}=({\widehat{Z}}_1{}^{(1)},\dots ,{\widehat{Z}}_n{}^{(1)}).$ By exploiting the property that the estimator ${\widehat{\mathrm{\Lambda }}}_0(\cdot )$ is a step function, these quantities could be obtained according to the following expressions: For $i=1,2,...,n$,

$${\widehat{Z}}_i{}^{(1)}=\frac{{\widehat{\xi }}^{(0)}+N_i^{†}(s*)}{{\widehat{\xi }}^{(0)}+{\widehat{A}}_i(s*;{\widehat{\mathrm{\Lambda }}}_0^{(0)},{\widehat{\alpha }}^{(0)},{\widehat{\beta }}^{(0)})};$$ (28)

$${\widehat{logZ}}_i{}^{(1)}=\text{DG}({\widehat{\xi }}^{(0)}+N_i^{†}(s*))-log({\widehat{\xi }}^{(0)}+N_i^{†}(s*))+log\hspace{0.17em}{\widehat{Z}}_i^{(1)},$$ (29)

where with $t_{\left(1\right)}<t_{\left(2\right)}<\dots <t_{\left(D\right)}$ being the $D$ distinct jump times of ${\widehat{\mathrm{\Lambda }}}_0^{(0)}(s*,\cdot )$ and ${\widehat{\lambda }}_0^{(0)}(s*,t_{(l)})={\widehat{\mathrm{\Lambda }}}_0^{(0)}(s*,t_{(l)})-{\widehat{\mathrm{\Lambda }}}_0^{(0)}(s*,t_{(l)}-)$ is the jump of ${\widehat{\mathrm{\Lambda }}}_0^{(0)}(s*,\cdot )$ at $t=t_{\left(l\right)}$, we have

$${\widehat{A}}_i^{(0)}\equiv \widehat{A_i}(s*;{\widehat{\mathrm{\Lambda }}}_0^{(0)},{\widehat{\alpha }}^{(0)},{\widehat{\beta }}^{(0)})=\sum _{l=1}^D{Y}_i(s*,t_{(l)}|{\widehat{\alpha }}^{(0)},{\widehat{\beta }}^{(0)}){\widehat{\lambda }}_0^{(0)}(s*,t_{(l)}).$$ (30)

Step 2 (M-step #1)

Applying formula (25), obtain ${\widehat{\mathrm{\Lambda }}}_0^{(1)}(s*,\hspace{0.17em}t|{\widehat{Z}}^{(1)},{\widehat{\alpha }}^{(0)},{\widehat{\beta }}^{(0)}).$

Step 3 (M-step #2)

After substituting ${\widehat{Z}}^{(1)}$ for $\mathbf{Z}$ in the estimating equations (26) and (27), obtain the solutions of these equations and denote them by ${\widehat{\alpha }}^{(1)}$and ${\widehat{\beta }}^{(1)}$.

Step 4 (M-step #3)

Obtain ${\widehat{\xi }}^{(1)}$ by maximizing the mapping in (24) in $\xi$. Alternatively, for this step, we may obtain ${\widehat{\xi }}^{(1)}$ by maximizing the full likelihood in (20) with respect to $\xi$ given the current values $({\widehat{\mathrm{\Lambda }}}_0^{(1)}(\cdot ),{\alpha }^{(1)},{\beta }^{(1)}).$ Through our numerical investigations, and via a mathematical proof (see appendix), using this alternative step also leads to the maximizing values of the full likelihood. In the simulation studies, the code using this alternative implementation was utilized.

Step 5 (Convergence)

Compare the values $({\mathbf{Z}}^{\left(1\right)},{\theta }^{\left(1\right)})$ with the values $({\mathbf{Z}}^{\left(0\right)},{\theta }^{\left(0\right)})$, according to some distance function, e.g., Euclidean distance. If the distance between the old and the new values satisfies a tolerance criterion, the algorithm terminates and the estimates are the final values in the iteration. If the distance criterion is not satisfied, then replace $({\xi }^{\left(0\right)},{\theta }^{\left(0\right)})$ by $({\xi }^{\left(1\right)},{\theta }^{\left(1\right)})$, and proceed to Step 1 of the algorithm. Because of the possibility of very large, possibly infinite, estimates of $\xi$, corresponding to the situation of approximate ‘uncorrelatedness,’ when comparing old and new iterates for $\xi$, we compare instead the associated values for $\eta =\xi =(1+\xi )$ since this ratio takes values in $(0,1]$.

Having obtained an estimator of the baseline hazard function ${\Lambda }_0(·)$ given by ${\widehat{\mathrm{\Lambda }}}_0(s*,\hspace{0.17em}\cdot )$, through the product integral representation, the semiparametric estimator of the baseline survivor function ${\overline{F}}_0(\cdot )$ for this model with frailty is ${\widehat{\overline{F}}}_0(s*,t)={\prod }_{\{w:\hspace{0.17em}w\le t\}}[1-{\widehat{\mathrm{\Lambda }}}_0(s*-,dw)]$. A computational implementation of the procedures and algorithms described in Sections 3 and 4 have been implemented in an R package (Ihaka and Gentleman, 1996) called gcmrec in González et al. (2003).

5 Properties of Estimators

5.1 Simulation Design

We performed computer simulation studies to examine numerically the properties of the parameter estimators developed in Sections 3 and 4. The specific goals of these studies are: (i) to examine the effect of sample size $\left(n\right)$ on the distributional properties of the estimators; (ii) to examine the bias, variance, and root-mean-square error (rmse) of the estimators; (iii) to examine the performance of the semiparametric estimator of the baseline survivor function ${\overline{F}}_0$ in terms of its bias function, variance function, and root-mean-squared error function at specified time points. The latter function is based on the loss function $L(\widehat{\overline{F}}(t),\overline{F}(t))={(\widehat{\overline{F}}(t)-\overline{F}(t))}^2$; (iv) to examine the consequences when data that have been generated with frailty components are analyzed using the model without frailties, an under-specified model; and (v) to examine the consequences, such as the loss in efficiency, when data that were generated using the model without frailties are analyzed with methods developed under the model with frailties, an over-specified model. For the first three items, simulation runs were performed for both the frailty-less model and for the model with frailty. We describe the settings for the different simulation parameters.

Sample Size

To examine the impact of sample size, we choose two values of $n:n\in \{30,50\}$. Though we do not report results here, we also performed simulation runs with $n=10$, which may not be realistic in biomedical and public health studies since they will usually have many subjects. However, small sample sizes may arise in the reliability and engineering settings, as in the hydraulic data set example. The simulation runs with $n=10$ did provide us some insights of the limitations of the numerical procedures for obtaining the estimates, such as non-convergence or convergence to a minimizing, instead of a maximizing, value of the likelihood.

Censoring Mechanism

The censoring variables ${\tau }_i$, $i=1,2,...,n$, are generated according to a uniform distribution over $[0,B]$ where $B$ is chosen in order that under perfect repair (i.e., $ℰ\left(s\right)=s-S_{N^{†}(s-)}$) and with $\alpha =1$, there are, on average, approximately 10 events per unit. Moreover, to place an upper limit to the number of events that could occur for a unit, when the number of events for a unit reaches 50 then we cease observing this unit and set ${\tau }_i=S_{i,50}$. This has the potential consequence of introducing some bias because this amounts to doing a combination of Type II and random censoring. Nevertheless, because the value of 50 is large enough, we conjecture that the bias introduced is negligible.

ρ Function

The $\rho$ function which handles the impact of accumulating event occurrences is assumed to be of form $\rho (k,\alpha )={\alpha }^k$ with $\alpha \in \{0.9,1.0,1.05\}$, which models the situations where an increasing number of event occurrences has a beneficial effect, has no effect, or has an adverse effect, respectively.

Effective Age Function

For the simulation studies we considered an effective age process corresponding to the general imperfect repair model (see Example 2.2) with perfect repair probability of $0.6$. Recall that the upper bound for the uniform censoring was determined under the perfect repair model and with $\alpha =1$ to have an average of approximately 10 events per unit. Because this did not take into consideration the exact form of $ℰ(·)$ and $\alpha$, the effective average number of events per unit in the simulations may either be smaller or larger than 10. This is a consequence of the interplay among the baseline hazard rate function (if it is increasing failure rate (IFR) or decreasing failure rate (DFR)), the minimal repairs performed, and the effect of increasing number of event occurrence quantified by $\alpha$.

Baseline Survivor Function

For the baseline hazard function ${\lambda }_0(·)$ we choose the flexible and commonly-used Weibull hazard function, with a unit scale parameter and shape parameter $(°)$ taking values in $\{.9,2\}$, the former leading to a DFR distribution, and the latter giving rise to an IFR distribution. Note that the estimation procedure proposed is semiparametric, hence the scale and shape parameters of this Weibull baseline distribution are not estimated.

Covariates

We consider a two-dimensional covariate vector $(X_1,X_2)$ with $X_1$ having a Bernoulli distribution with success probability of $0.5$, $X_2$ having a standard normal distribution, and with $X_1$ and $X_2$ stochastically independent. The regression coefficient vector $({\beta }_1,{\beta }_2)$ is set to be $(1,-1)$. The fact that the grouping induced by the first covariate is done using a symmetric Bernoulli mechanism leads sometimes to highly asymmetric allocations for some simulation replicates, which was the cause of some convergence problems in the iterative procedure when $n=10$.

Frailty Component

The parameter $\xi$ of the gamma distribution governing the frailty variable was set to $\{2,6,\infty \}$, with $\infty$ corresponding to the absence of frailties. With respect to the parametrization $\xi \mapsto \eta =\xi /(1+\xi )$, these frailty values convert to having $\eta \in \{\frac{2}{3},\frac{6}{7},1\}$.

For each combination of these simulation parameters, $1000$ replications were performed. In the analysis, we set $s*=10$. Also, to create the bias, variance, and root-mean-squared-error curves for the estimator of the baseline survivor function, we choose time values corresponding to the $\{0,1,2,...,99\}$ th percentiles of the true baseline distribution function.

5.2 Discussions of Simulation Results

In the discussion of the simulation results that follows, we will focus on the effects of changing $n$, changing $\xi$ or $\eta$, changing $\alpha$, and changing $\gamma$, on the distributional properties of the estimators of $\alpha ,\beta$, and $\eta$, as well as the estimator of the baseline survivor function ${\overline{F}}_0$. In addition, we address the consequences of analyzing data that follows the general model with frailties using procedures developed for the general model without frailties, an under-specification; and also consider the impact of over-specification, which is the situation where procedures developed under the model with frailties are utilized to analyze data from a model without frailties. Such analyses will provide information on which type of mis-specification is of a more serious type.

Results of the simulation studies are presented in Tables 1–3. Table 1 summarizes the mean values and standard deviations (i.e., standard errors of the estimates) of the sampling distributions of the estimators of $\alpha ,{\beta }_1,{\beta }_2$, and $\eta$ for $\alpha$ values of $0.9,1.0$, and $1.05$ as $n$ varies in the set $\{30,50\}$. We do not show the cases with $n=10$ to conserve space. Table 2 contains means and standard deviations summaries of the simulation runs pertaining to the under- and over-specified analysis. Table 3 contains plots of the bias and rmse curves for the estimator of ${\overline{F}}_0$ under the case where $\alpha =.9$ for $\xi \in \{2,6,\infty \}$ with the plots for different values of $n$ superimposed on each plot frame for a Weibull shape parameter of $\gamma =2.0$.

Table 1.

Summary of simulated means and standard deviations of the estimators of $\alpha ,\beta$, and $\eta =\xi /(1+\xi )$. The true value of $\beta$ is $(1;-1)$, and 1000 replications were run for each parameter combination. The other columns of this table are: $\gamma$ denotes the Weibull shape parameter; $n$ is the sample size; NC is the number of replicates in which there was no convergence; ${\widehat{\mu }}_{Ev}$ is the observed mean number of events per unit in all the simulation replications.

	$\alpha$	$\gamma$	$\xi$	$\eta$	$n$	NC	${\widehat{\mu }}_{Ev}$	$\widehat{\alpha }$	${\widehat{\sigma }}_{\widehat{\alpha }}$	${\widehat{\beta }}_1$	${\widehat{\sigma }}_{{\widehat{\beta }}_1}$	${\widehat{\beta }}_2$	${\widehat{\sigma }}_{{\widehat{\beta }}_2}$	$\widehat{\eta }$
A2	$0.9$	$0.9$	$2$	$0.67$	$30$	$0$	$4.1$	$0.898$	$0.031$	$1.012$	$0.379$	$-1.008$	$0.240$	$0.734$
A3	$0.9$	$0.9$	$2$	$0.67$	$50$	$0$	$5.2$	$0.899$	$0.021$	$1.017$	$0.287$	$-1.004$	$0.165$	$0.705$
A5	$0.9$	$0.9$	$6$	$0.86$	$30$	$0$	$4.3$	$0.900$	$0.030$	$0.988$	$0.300$	$-1.015$	$0.175$	$0.904$
A6	$0.9$	$0.9$	$6$	$0.86$	$50$	$0$	$5.3$	$0.899$	$0.021$	$0.998$	$0.221$	$-1.000$	$0.136$	$0.884$
A8	$0.9$	$0.9$	$\infty$	$1.00$	$30$	$0$	$4.8$	$0.893$	$0.025$	$1.031$	$0.222$	$-1.030$	$0.135$
A9	$0.9$	$0.9$	$\infty$	$1.00$	$50$	$0$	$4.4$	$0.895$	$0.018$	$1.024$	$0.158$	$-1.023$	$0.104$
A11	$0.9$	$2.0$	$2$	$0.67$	$30$	$0$	$7.8$	$0.902$	$0.016$	$1.010$	$0.348$	$-1.018$	$0.202$	$0.721$
A12	$0.9$	$2.0$	$2$	$0.67$	$50$	$0$	$6.7$	$0.902$	$0.012$	$0.994$	$0.271$	$-1.012$	$0.144$	$0.710$
A14	$0.9$	$2.0$	$6$	$0.86$	$30$	$0$	$8.9$	$0.900$	$0.016$	$1.009$	$0.236$	$-1.008$	$0.135$	$0.895$
A15	$0.9$	$2.0$	$6$	$0.86$	$50$	$0$	$7.2$	$0.900$	$0.012$	$0.998$	$0.173$	$-1.004$	$0.101$	$0.882$
A17	$0.9$	$2.0$	$\infty$	$1.00$	$30$	$0$	$8.4$	$0.898$	$0.015$	$1.017$	$0.155$	$-1.014$	$0.095$
A18	$0.9$	$2.0$	$\infty$	$1.00$	$50$	$0$	$7.4$	$0.899$	$0.011$	$1.003$	$0.112$	$-1.007$	$0.072$
B2	$1$	$0.9$	$2$	$0.67$	$30$	$2$	$9.5$	$1.000$	$0.011$	$1.010$	$0.374$	$-1.000$	$0.227$	$0.735$
B3	$1$	$0.9$	$2$	$0.67$	$50$	$0$	$8.7$	$1.000$	$0.007$	$0.989$	$0.280$	$-1.002$	$0.165$	$0.704$
B5	$1$	$0.9$	$6$	$0.86$	$30$	$0$	$7.7$	$1.000$	$0.012$	$1.014$	$0.286$	$-0.993$	$0.164$	$0.901$
B6	$1$	$0.9$	$6$	$0.86$	$50$	$0$	$7.3$	$1.000$	$0.007$	$1.013$	$0.201$	$-0.999$	$0.118$	$0.880$
B8	$1$	$0.9$	$\infty$	$1.00$	$30$	$0$	$8.1$	$0.998$	$0.008$	$1.029$	$0.185$	$-1.024$	$0.114$
B9	$1$	$0.9$	$\infty$	$1.00$	$50$	$0$	$9.1$	$0.999$	$0.006$	$1.010$	$0.130$	$-1.012$	$0.084$
B11	$1$	$2.0$	$2$	$0.67$	$30$	$0$	$9.5$	$1.000$	$0.008$	$1.016$	$0.336$	$-1.028$	$0.194$	$0.725$
B12	$1$	$2.0$	$2$	$0.67$	$50$	$0$	$13.0$	$1.000$	$0.006$	$1.004$	$0.258$	$-1.012$	$0.146$	$0.705$
B14	$1$	$2.0$	$6$	$0.86$	$30$	$0$	$13.8$	$1.000$	$0.008$	$1.006$	$0.228$	$-1.002$	$0.132$	$0.889$
B15	$1$	$2.0$	$6$	$0.86$	$50$	$0$	$10.8$	$1.000$	$0.006$	$1.003$	$0.168$	$-1.001$	$0.097$	$0.876$
B17	$1$	$2.0$	$\infty$	$1.00$	$30$	$0$	$14.0$	$0.999$	$0.007$	$1.017$	$0.133$	$-1.010$	$0.083$
B18	$1$	$2.0$	$\infty$	$1.00$	$50$	$0$	$11.2$	$1.000$	$0.005$	$1.010$	$0.099$	$-1.006$	$0.065$
C2	$1.05$	$0.9$	$2$	$0.67$	$30$	$3$	$11.8$	$1.051$	$0.007$	$0.994$	$0.366$	$-0.994$	$0.222$	$0.730$
C3	$1.05$	$0.9$	$2$	$0.67$	$50$	$0$	$9.7$	$1.050$	$0.004$	$1.009$	$0.284$	$-0.993$	$0.153$	$0.703$
C5	$1.05$	$0.9$	$6$	$0.86$	$30$	$1$	$12.9$	$1.051$	$0.007$	$1.002$	$0.271$	$-0.993$	$0.160$	$0.899$
C6	$1.05$	$0.9$	$6$	$0.86$	$50$	$0$	$13.9$	$1.050$	$0.005$	$1.006$	$0.196$	$-0.992$	$0.119$	$0.880$
C8	$1.05$	$0.9$	$\infty$	$1.00$	$30$	$0$	$10.9$	$1.049$	$0.007$	$1.020$	$0.154$	$-1.012$	$0.101$
C9	$1.05$	$0.9$	$\infty$	$1.00$	$50$	$0$	$13.8$	$1.050$	$0.004$	$1.009$	$0.121$	$-1.006$	$0.072$
C11	$1.05$	$2.0$	$2$	$0.67$	$30$	$0$	$12.3$	$1.050$	$0.006$	$1.026$	$0.336$	$-1.018$	$0.184$	$0.726$
C12	$1.05$	$2.0$	$2$	$0.67$	$50$	$0$	$13.4$	$1.050$	$0.005$	$1.008$	$0.248$	$-1.012$	$0.136$	$0.705$
C14	$1.05$	$2.0$	$6$	$0.86$	$30$	$0$	$10.9$	$1.050$	$0.006$	$1.019$	$0.225$	$-1.000$	$0.124$	$0.890$
C15	$1.05$	$2.0$	$6$	$0.86$	$50$	$0$	$14.3$	$1.050$	$0.004$	$0.997$	$0.166$	$-1.000$	$0.096$	$0.876$
C17	$1.05$	$2.0$	$\infty$	$1.00$	$30$	$0$	$18.5$	$1.050$	$0.005$	$1.004$	$0.123$	$-1.010$	$0.076$
C18	$1.05$	$2.0$	$\infty$	$1.00$	$50$	$0$	$13.5$	$1.050$	$0.004$	$1.004$	$0.090$	$-1.003$	$0.054$

Table 3.

Bias and root mean squared error curves for the estimator of the baseline survivor function as the sample size $\left(n\right)$ varies [ $n=10$ is red; $n=30$ is blue; $n=50$ is green]. This is for the case where $\alpha$ = $.90$ and a Weibull shape parameter of $\gamma$ = $2.0$.

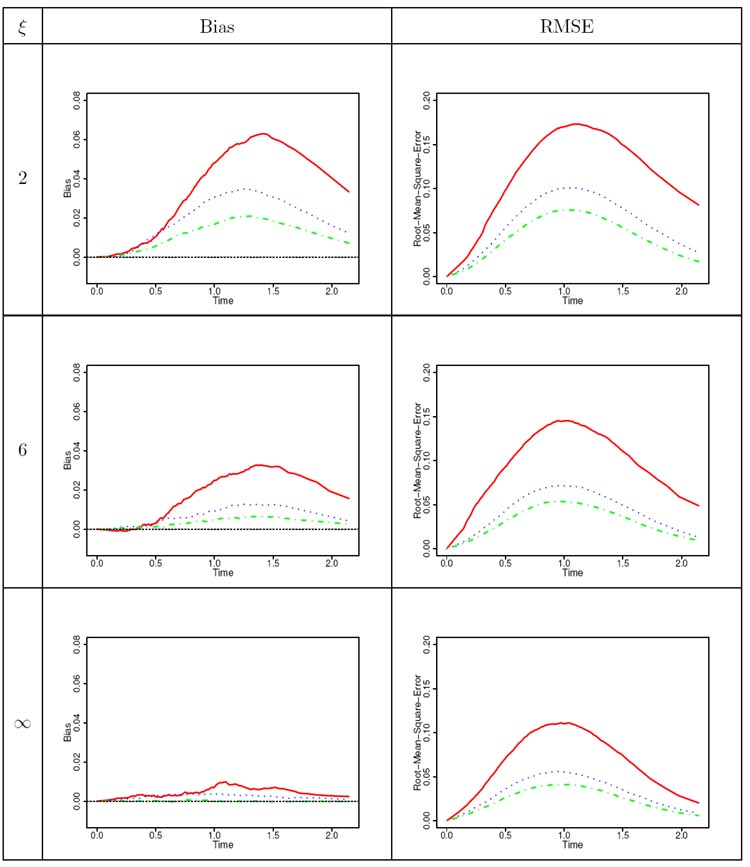
Table 2.

Summary of simulated means and standard deviations for the estimators of $\alpha ,{\beta }_1$, and ${\beta }_2$ for the situation of under-specification (label UVW) and over-specification (label XYZ). The true regression coefficients are $\beta =(1;-1)$ and 1000 replications were run for each parameter combination.

	$\alpha$	$\gamma$	$\xi$	$n$	NC	${\widehat{\mu }}_{\widehat{\alpha }}$	${\widehat{\sigma }}_{\widehat{\alpha }}$	${\widehat{\mu }}_{{\widehat{\beta }}_1}$	${\widehat{\sigma }}_{{\widehat{\beta }}_1}$	${\widehat{\mu }}_{{\widehat{\beta }}_2}$	${\widehat{\sigma }}_{{\widehat{\beta }}_2}$
U2.	$0.90$	$0.9$	$2$	$30$	$0$	$0.954$	$0.031$	$0.779$	$0.322$	$-0.770$	$0.210$
U3	$0.90$	$0.9$	$2$	$50$	$0$	$0.959$	$0.023$	$0.747$	$0.239$	$-0.740$	$0.154$
U5	$0.90$	$0.9$	$6$	$30$	$0$	$0.921$	$0.028$	$0.898$	$0.285$	$-0.919$	$0.168$
U6	$0.90$	$0.9$	$6$	$50$	$0$	$0.923$	$0.020$	$0.883$	$0.212$	$-0.888$	$0.131$
U8	$0.90$	$2.0$	$2$	$30$	$0$	$0.952$	$0.022$	$0.719$	$0.297$	$-0.728$	$0.187$
U9	$0.90$	$2.0$	$2$	$50$	$0$	$0.956$	$0.017$	$0.700$	$0.223$	$-0.707$	$0.139$
U11	$0.90$	$2.0$	$6$	$30$	$0$	$0.920$	$0.018$	$0.909$	$0.220$	$-0.901$	$0.138$
U12	$0.90$	$2.0$	$6$	$50$	$0$	$0.922$	$0.013$	$0.879$	$0.167$	$-0.879$	$0.101$
V2	$1.00$	$0.9$	$2$	$30$	$0$	$1.019$	$0.014$	$0.771$	$0.324$	$-0.751$	$0.215$
V3	$1.00$	$0.9$	$2$	$50$	$0$	$1.020$	$0.009$	$0.726$	$0.251$	$-0.715$	$0.157$
V5	$1.00$	$0.9$	$6$	$30$	$0$	$1.008$	$0.011$	$0.913$	$0.271$	$-0.888$	$0.172$
V6	$1.00$	$0.9$	$6$	$50$	$0$	$1.009$	$0.008$	$0.886$	$0.198$	$-0.868$	$0.129$
V8	$1.00$	$2.0$	$2$	$30$	$0$	$1.024$	$0.012$	$0.711$	$0.291$	$-0.723$	$0.191$
V9	$1.00$	$2.0$	$2$	$50$	$0$	$1.024$	$0.009$	$0.685$	$0.221$	$-0.695$	$0.136$
V11	$1.00$	$2.0$	$6$	$30$	$0$	$1.009$	$0.009$	$0.885$	$0.224$	$-0.879$	$0.137$
V12	$1.00$	$2.0$	$6$	$50$	$0$	$1.009$	$0.008$	$0.871$	$0.173$	$-0.867$	$0.104$
W2	$1.05$	$0.9$	$2$	$30$	$0$	$1.059$	$0.010$	$0.725$	$0.342$	$-0.720$	$0.226$
W3	$1.05$	$0.9$	$2$	$50$	$0$	$1.058$	$0.006$	$0.696$	$0.261$	$-0.691$	$0.158$
W5	$1.05$	$0.9$	$6$	$30$	$0$	$1.054$	$0.007$	$0.873$	$0.273$	$-0.869$	$0.179$
W6	$1.05$	$0.9$	$6$	$50$	$0$	$1.053$	$0.005$	$0.851$	$0.198$	$-0.842$	$0.128$
W8	$1.05$	$2.0$	$2$	$30$	$0$	$1.061$	$0.009$	$0.704$	$0.296$	$-0.704$	$0.179$
W9	$1.05$	$2.0$	$2$	$50$	$0$	$1.062$	$0.007$	$0.686$	$0.224$	$-0.684$	$0.138$
W11	$1.05$	$2.0$	$6$	$30$	$0$	$1.054$	$0.007$	$0.877$	$0.227$	$-0.880$	$0.132$
W12	$1.05$	$2.0$	$6$	$50$	$0$	$1.054$	$0.005$	$0.870$	$0.162$	$-0.870$	$0.104$
X2	$0.90$	$0.9$	$\infty$	$30$	$0$	$0.893$	$0.026$	$1.030$	$0.224$	$-1.031$	$0.144$
X3	$0.90$	$0.9$	$\infty$	$50$	$2$	$0.895$	$0.018$	$1.030$	$0.173$	$-1.022$	$0.105$
X5	$0.90$	$2.0$	$\infty$	$30$	$0$	$0.897$	$0.015$	$1.016$	$0.163$	$-1.015$	$0.099$
X6	$0.90$	$2.0$	$\infty$	$50$	$2$	$0.898$	$0.011$	$1.014$	$0.115$	$-1.015$	$0.076$
Y2	$1.00$	$0.9$	$\infty$	$30$	$6$	$0.998$	$0.010$	$1.023$	$0.186$	$-1.022$	$0.116$
Y3	$1.00$	$0.9$	$\infty$	$50$	$1$	$0.999$	$0.006$	$1.019$	$0.136$	$-1.019$	$0.086$
Y5	$1.00$	$2.0$	$\infty$	$30$	$2$	$0.999$	$0.007$	$1.013$	$0.138$	$-1.011$	$0.084$
Y6	$1.00$	$2.0$	$\infty$	$50$	$0$	$0.999$	$0.006$	$1.010$	$0.100$	$-1.007$	$0.066$
Z2	$1.05$	$0.9$	$\infty$	$30$	$6$	$1.050$	$0.005$	$1.015$	$0.162$	$-1.011$	$0.099$
Z3	$1.05$	$0.9$	$\infty$	$50$	$6$	$1.050$	$0.004$	$1.017$	$0.112$	$-1.013$	$0.073$
Z5	$1.05$	$2.0$	$\infty$	$30$	$2$	$1.050$	$0.005$	$1.014$	$0.126$	$-1.008$	$0.078$
Z6	$1.05$	$2.0$	$\infty$	$50$	$2$	$1.050$	$0.004$	$1.005$	$0.094$	$-1.005$	$0.055$

As is to be expected, for the simulation runs where there was no mis-specification, when the sample size increases, the performance of the estimators of the finite-dimensional parameters, as well as for the baseline survivor function, improved, with the biases decreasing and the standard errors also decreasing. This is also true for the over-specification runs. When the sample size is small, there is considerable over-estimation of $\eta =\xi =(1+\xi )$, though this bias decreases with increasing sample size. When there is under-specification however, all the estimators are extremely biased (see UVW-runs in Table 2), demonstrating the undesirable consequences of committing this under-specification. Regarding the effect of the frailty parameter $\xi$, for estimating the finite-dimensional parameters, the amount of bias for $n=30$ and $n=50$ are negligible. The impact of the $\xi$ is on the standard errors of the estimators, with larger values of $\xi$ translating into less correlation, leading to smaller standard errors for the same sample size. When considering on the other hand the estimator ${\widehat{\overline{F}}}_0$ of the baseline survivor function, by examining the curves in Table 3, as well as other curves from the simulations that are not shown here, we observe that the bias and rmse curves of this estimator decrease as $n$ increases, and the same could also be said as $\xi$ increases. Generally, the bias function is positive, and as is to be expected there is more bias and rmse in the middle portion of the survivor function.

Some care, however, must be observed when considering the effects of changing $\alpha$ and changing Weibull shape parameter $\gamma$ in the context of the precision of the estimators because the interplay between these two parameters leads to differing observed number of events. To see this, examine the column ${\widehat{\mu }}_{Ev}$ in Table 1, which represents the mean number of events observed per unit. In this table, we notice that when $\alpha <1$ and $\gamma <1$, the latter leading to a DFR Weibull baseline distribution, there tends to be a smaller number of observed events; whereas when $\alpha >1$ and $\gamma >1$, the latter making the Weibull baseline IFR, then there tends to be more events observed. These differences in the observed number of events can be explained by taking into account the minimal repair model considered in the simulation. In the first situation for instance, an $\alpha$ value less than unity makes the unit less likely to have events as calendar time increases since more event occurrences become beneficial to the unit and, in addition, when a minimal repair is performed, then the DFR nature (because $\gamma <1$) of the baseline distribution diminishes the rate of event occurrences thereby lengthening the inter-event times. Because the upper bound $B$ for the uniformly distributed follow-up time $\tau$ was determined under $\alpha =1$ and with a backward recurrence time effective age corresponding to a perfect repair mechanism, the impact of $\alpha <1$ and $\gamma <1$ is a smaller number of events compared to the target of approximately 10 events used in deriving $B$. An analogous argument, but in the opposite direction, holds true when dealing with $\alpha >1$ and $\gamma >1$. The impact of the minimal repair effective age and its interplay with a DFR or IFR baseline distribution can be further seen from Table 1 with $\alpha =1$, where we see that when the baseline distribution is DFR (IFR), the observed number of events per unit is less (more) than the target of approximately 10 events per unit used in deriving $B$. A fascinating situation is when $\alpha <1$ and $\gamma >1$, or when $\alpha >1$ and $\gamma <1$, for the effects of $\alpha$ and $\gamma$ are in opposite directions in the context of event occurrences. Examining the bottom portion of the A-runs in Table 1 and the upper half of the C-runs in Table 1, and with reference to the B-runs in this same table, we observe that for the chosen $\alpha$ and $\gamma$ values in the simulation, there was a more pronounced effect of the $\alpha$ values compared to the $\gamma$ values since when $\alpha =.9$ and $\gamma =2$, the observed number of events is slightly below 10, whereas when $\alpha =1.05$ and $\gamma =.9$, the observed number of events is more than 10. The greater effect of $\alpha$ than $\gamma$ on the mean number of events is not surprising, because $\gamma$ was partially accommodated in the determination of the upper bound $B$ for the censoring distribution. Apart from the impact on the precision of the estimates arising from the varying number of events due to the combination of values of $\alpha$ and $\gamma$ discussed above, the associate editor also perceptively pointed out that this interplay among whether ${\lambda }_0(·)$ is IFR or DFR, whether $\rho (·)$ is increasing or decreasing, and the form of the effective age $ℰ(·)$, will intrinsically impact the precision of the estimators. For instance, if $\alpha <1$ and $\gamma <1$ with $ℰ\left(s\right)=s$ in the simulation model, when both the $\alpha$ and $\gamma$ parameters are inducing a decrease in the number of events, the precision of their estimators will diminish since there is added uncertainty about their contributions to event occurrences. This decrease in the precision of estimators is a natural consequence of using a richer class of models which has the potential of better delineating the varied factors affecting event occurrences.

In the presence of model mis-specification, we find that under-specification leads to a non-negligible systematic bias that increases with $n$ and also with $\alpha$. In fact, for this type of mis-specification, we have observed that the mean of the process $W_n(s*,t)=\sqrt{n}[{\widehat{\overline{F}}}_0(s*,t)-{\overline{F}}_0(t)]$ in $t$ does not converge to the zero function as $n$ increases, implying that with this mis-specification, the estimator ${\widehat{\overline{F}}}_0$ may be inconsistent. In contrast, with over-specification, we find that there is no recognizable loss in efficiency compared to the correct analysis, though we observe some very slight increase in the standard errors of the finite-dimensional parameter estimators (see XYZ-runs in Table 2 and compare the standard deviations in the A9 row of Table 1 and the X3 row, B9 row of Table 1 with the Y3 row, and the C9 row of Table 1 and the Z3 row). This indicates that there is much to be gained in the context of robustness by simply fitting the frailty-based model since, if the data did come from the frailty model, then the analysis is correct, while if the data came from the frailty-less model, there is no significant efficiency loss incurred; whereas, if there is under-specification of the model, then the consequences are unacceptable if the data actually came from the model with frailty. This lends strong support that this new class of models provides a general and flexible class for fitting recurrent event data and provides an avenue for a robust method of analysis for real data sets.

In addition, we also examined the impact of mis-specifying the effective age process, which also has bearing in regards to the interplay between the $\rho (·,·)$ and $ℰ(·)$ components of the class of models. We considered the same simulation model with a perfect repair probability of $0.6$, and examined the impact of two types of effective age process mis-specification: that the interventions following event occurrences are all minimal repair, or that they are all perfect repair. The results (not shown) indicate an interesting interplay between the nature of the baseline survivor function (DFR/IFR) and the behavior of ${\widehat{\overline{F}}}_0$ and $\widehat{\alpha }$. We observed that under the minimal repair mis-specification, when ${\overline{F}}_0$ is DFR, ${\widehat{\overline{F}}}_0$ exhibits negative bias and $\widehat{\alpha }$ is positively biased. Additionally for this mis-specification, when ${\overline{F}}_0$ is IFR, ${\widehat{\overline{F}}}_0$ exhibits positive bias and $\widehat{\alpha }$ is positively biased. Alternately, when the mis-specification is perfect repair, an underlying baseline DFR (IFR) is associated with positive (negative) bias in ${\widehat{\overline{F}}}_0$ and negative (positive) bias in $\widehat{\alpha }$. We explain these findings as follows: When the model mistakenly assumes minimal repair at each event occurrence, it tends to overestimate the effective age of units. Hence, in the case of DFR, the model anticipates longer interevent times than are realized in the data, creating the negative bias, especially for larger interevent times, in the estimates of the baseline survivor function in this situation. In the case of IFR, the minimal repair mis-specification leads to longer interevent times in the data than are anticipated by the model, creating a positive bias in the estimated baseline survivor function. When a perfect repair is incorrectly assumed at each event occurrence, the model tends to underestimate the effective age of units. Hence, using reasoning analogous to that for the minimal repair mis-specification, there is positive (negative) bias in the estimated baseline survivor function in the case of DFR (IFR). Especially interesting is that this behavior induces biases also in the finite-dimensional parameter estimates, with $\widehat{\alpha }$, in particular, evidently compensating such that $\widehat{\alpha }$ is positively biased when the baseline distribution is DFR, and negatively biased when this distribution is IFR. These results indicate the importance of monitoring the effective age process.

6 Applications to Real Data

The first application is to the bladder cancer data used in Wei et al. (1989), which can be obtained from the survival package (Lumley and Therneau, 2003) in the R Library. These data provide the times to recurrence of bladder cancer for $n=85$ subjects. The covariates are $X_1$, the treatment indicator ( $1=$ placebo, $2=$ thiotepa); $X_2$, the size (in cm) of the largest initial tumor; and $X_3$, the number of initial tumors. We first fitted the general model using the backward recurrence time $ℰ\left(s\right)=s-S_{N^{†}(s-)}$ as effective age. With $s*=64$, the maximum observation period, we fitted the general model without frailties, and obtained $\widehat{\alpha }=0.9826$ and $({\widehat{\beta }}_1,{\widehat{\beta }}_2,{\widehat{\beta }}_3)=(-0.3188,-0.0154,0.1353)$. These are also the estimates obtained when the general model with frailty is fitted since in that case $\widehat{\xi }=5432999\hspace{0.17em}(\widehat{\eta }\approx 1)$, a very large value indicating that there is no need for the frailty component when the effective age is the backward recurrence time. Thus, using the approximate inverse of the partial likelihood information matrix from fitting the model without frailties, the associated estimated standard errors are $.0736$ for $\widehat{\alpha }$ and $(0.2051,0.0695,0.0511)$ for $\widehat{\beta }$. It remains to establish formally that these are indeed valid standard error estimates, an issue to be addressed in a future paper addressing asymptotic properties of model estimators. Since a formal theory for estimating standard errors under the general model with frailties is under development, we utilize jacknife estimates of the standard errors, which are the standard deviations of the $n$ estimates computed after deleting a unit. For the model without frailties for instance, the jacknife estimates of the standard errors $\left(jse\right)$ for the bladder cancer data are $.056$ for $\widehat{\alpha }$ and $(.226,.068,.052)$ for $({\widehat{\beta }}_1,{\widehat{\beta }}_2,{\widehat{\beta }}_3)$, which are close to the estimates obtained from the observed partial likelihood information matrix.

For lack of information about the effective age, we also fitted the general model with frailties assuming a ‘minimal repair’ after each event, $ℰ\left(s\right)=s$. In this situation, the estimates are $\widehat{\alpha }=.789 (jse=.13)$, $({\widehat{\beta }}_1,{\widehat{\beta }}_2,{\widehat{\beta }}_3)=(-.5743,-.0315,-.2220) [jse=(.36,.10,.10\left)\right]$, and $\widehat{\xi }=.974$, indicating the importance of the frailty component in this case. When the general model without frailties is fitted to this ‘always minimal repair’ data set, the resulting estimates are $\widehat{\alpha }=1.24 (jse=.08)$ and $({\widehat{\beta }}_1,{\widehat{\beta }}_2,{\widehat{\beta }}_3)=(-.32,-.03,-.14) [jse=(.25,.07,.06\left)\right]$. The estimates of the survivor functions for the two effective age specifications are presented in Figure 1. The lower curves (red), corresponding to the placebo group, are obtained by setting $X_1=1$ in the expression given by ${\{{\widehat{\overline{F}}}_0(t)\}}^{exp\{{\widehat{\beta }}_1{X}_1+{\widehat{\beta }}_2{\overline{X}}_2+{\widehat{\beta }}_3{\overline{X}}_3\}}$, while the upper curves (blue) are for the thiotepa group obtained by setting $X_1=2$. The observed means were ${\overline{X}}_2=2.01$ and ${\overline{X}}_3=2.11$. The solid curves are for the backward recurrence time effective age, while the dashed curves are for $ℰ\left(s\right)=s$. These plots seem to indicate that the thiotepa group has a higher survival rate than the placebo group, although the statistical significance of this difference depends on which effective age process was used. A question that we will address in future work is the assessment of which effective age process leads to a better fit. This issue is related to model validation and goodness-of-fit aspects of the model.

Fig. 1.

This plot contains estimates of the survivor function for the baldder cancer data set when the model with frailties is fitted. The red curve (lower curve in each line type) is for the placebo group $({\text{X}}_1=1)$, while the blue curve is for the thiotepa group $({\text{X}}_1=2)$, both evaluated at the mean values of ${\text{X}}_2$ and ${\text{X}}_3$. The solid curves are for effective age E $\left(s\right)=s–{\text{S}}_N$† $(s–)$ (perfect repair), while the dashed curves are when E $\left(s\right)=s$ (minimal repair).

It is of interest to compare the estimates of the regression coefficients from the general model with those obtained using the three existing methods of analysis described in Therneau and Hamilton (1997) and Therneau and Grambsch (2000). Table 4 summarizes the estimates from Andersen-Gill’s (AG) method, Wei, Lin and Weissfeld’s (WLW) marginal method, and Prentice, Williams and Peterson’s (PWP) conditional method as reported in Therneau and Grambsch (2000), together with the estimates obtained from the general model with frailty under these two specifications of the effective age process, $ℰ\left(s\right)=s-S_{N^{†}(s-)}$ and $ℰ\left(s\right)=s$. From this table we note the crucial role that the effective age process and the $\rho (k,\alpha )={\alpha }^k$ component play in this analysis and how they provide some reconciliation of the varied estimates from these different methods. When the effective age process corresponds to perfect repair (in which case $\widehat{\xi }\approx \infty$ so that estimates arising from the frailty and no-frailty models coincide) or when the effective age corresponds to minimal repair and the model without frailties is fitted, then the $\beta$-estimates from the general model are quite close to those obtained from PWP’s conditional method. On the other hand, when the effective age process corresponds to minimal repair and the model with frailties is fitted, the resulting estimates are close to those obtained from the WLW marginal method. The values from the AG method lie between these two cases. In the situation therefore where the model without frailties is fitted for both types of effective age specifications, it appears that the term $\lambda [ℰ(s\left)\right]{\alpha }^{N^{†}(s-)}$ in the general model induces a robustness property in the context of estimating the $\beta$ coefficients. Note that when we assume ‘always perfect repair' the $\alpha$ estimate is less than unity; whereas when we assume ‘always minimal repair' the $\alpha$ estimate is greater than unity (see the discussions in the preceding section pertaining to misspecified effective age process and the impact on the estimation of the baseline hazard and the $\alpha$ parameter). Interestingly, when the general model with frailties is fitted to the ‘always minimal repair' data, the $\alpha$ estimate now becomes less than unity, and the estimate of the frailty parameter $\xi$ is quite close to unity, indicating a strong association among the inter-event times for each subject. The ability of the general model to seemingly explain these varied estimates from these different methods indicates its flexibility and the crucial role of the effective age. Thus, there is a need to monitor this information since in its absence, different methods of analysis may produce varied estimates, which could lead to contradictory conclusions.

Table 4.

Summary of estimates for the bladder data set from the Andersen-Gill (AG), Wei, Lin and Weissfeld (WLW), and Prentice, Williams and Peterson (PWP) methods as reported in Therneau and Grambsch (2000), together with the estimates obtained from the general model using two effective ages corresponding to ‘perfect repairs’ and ‘minimal repairs.’

					General Model
					Perfect a	Minimal b	Minimal
Term	Param	AG	WLW Marginal	PWP Cond*nal	Both c	Frailty d	No Frailty e
log $N(s-)$	$\alpha$	-	-	-	$.98\left(.07\right)$	$.79\left(.13\right)$	$1.24\left(.08\right)$
Frailty	$\xi$	-	-	-	$\infty$	$.97$	-
rx	${\beta }_1$	$-.47\left(.20\right)$	$-.58\left(.20\right)$	$-.33\left(.21\right)$	$-.32\left(.21\right)$	$-.57\left(.36\right)$	$-.32\left(.25\right)$
Size	${\beta }_2$	$-.04\left(.07\right)$	$-.05\left(.07\right)$	$-.01\left(.07\right)$	$-.02\left(.07\right)$	$-.03\left(.10\right)$	$-.03\left(.07\right)$
Number	${\beta }_3$	$.18\left(.05\right)$	$.21\left(.05\right)$	$.12\left(.05\right)$	$.14\left(.05\right)$	$.22\left(.10\right)$	$.14\left(.06\right)$

^aEffective Age is backward recurrence time $(ℰ(s)=s-S_{\text{N}†(s-)})$.

^bEffective Age is calendar time $(ℰ(s)=s)$.

^cSame results are obtained for either the model with or without frailties.

^dReported standard errors are jacknifed estimates.

^eReported standard errors are jacknifed estimates.

Another biomedical example pertains to the rehospitalization of patients diagnosed with colorectal cancer. The data, which can be obtained from the gcmrec package in the R Library, provide the calendar times (in days) of the successive hospitalizations after the date of surgery. The first readmission time was considered as the time between the date of the surgical procedure and the first rehospitalization after discharge related to colorectal cancer. Each subsequent readmission time was defined as the difference between the current hospitalization date and the previous discharge date. There were a total of 861 rehospitalization events recorded for the 403 patients included in the analysis. This data set was analyzed in Gonzalez et al. (2005) using a gamma frailty model, which corresponds to the general model with $\alpha =1$. Their goal being to determine whether there were differences regarding the time of the recurrent hospitalization due to social-demographic or clinical outcomes. We reanalyze this data set using the full general model where we consider the following variables: tumor stage (Dukes classification: A-B, C or D); whether the patient received chemotherapy; and the distance between the hospital and the patient's residence. We have coded these covariates using dummy variables such that the regression coefficients can be interpreted as follows: ${\beta }_1$ pertains to patients diagnosed with Dukes C stage, and ${\beta }_2$ for patients with Dukes D stage; ${\beta }_3$ for patients who did not receive chemotherapy, and ${\beta }_4$ for patients whose residence is more than 30 kilometers from the hospital. Since in this case we have no information about the effective age, we assumed the backward recurrence time, $ℰ\left(s\right)=s-S_{N†(s-)}$ We fitted the general model without frailties, taking $s*=2060$, the maximum follow-up time. The resulting estimates of the parameters, together with the information-based (se) and jacknife (jse) estimates of their standard errors, are $\widehat{\alpha }=1.12 (se=0.01;jse=.13)$, ${\widehat{\beta }}_1=0.31 (se=0.12;jse=.16)$, ${\widehat{\beta }}_2=0.93 (se=0.14;jse=.19)$, ${\widehat{\beta }}_3=-0.12 (se=0.11;jse=.13)$, and ${\widehat{\beta }}_4=-0.01 (se=0.15;jse=.18)$. Observe that the information-based and jacknife estimates of the standard errors are somewhat discrepant for this data set. We also fitted the general model with frailties. After 35 iterations the EM algorithm converged. The estimate of the frailty parameter $\xi$ was quite small $[\widehat{\xi }=2.39 (jse=3.19)]$ so we conclude that the frailty component of the model is important for these data. The fitted frailty-based model provided the estimates: $\widehat{\alpha }=1.08 (jse=.14)$, ${\widehat{\beta }}_1=1.31 (jse=.17)$, ${\widehat{\beta }}_2=1.05 (jse=.20)$, ${\widehat{\beta }}_3=-.14 (jse=.14)$, and ${\widehat{\beta }}_4=0.03 (jse=.23)$, Based on these results, we conclude that among these covariates, only the advanced tumor stages (C or D) are associated with an elevated risk of rehospitalization. Furthermore, since the estimate of $\alpha$ is larger than unity, there is an indication that each hospitalization increases the risk of further hospitalization.

The next data set, given in Blischke and Murthy (2000) and which was analyzed in Kumar and Klefsjo (1992), concerns hydraulic load-haul-dump (LHD) subsystems used in moving ore and rock in underground mines in Sweden. The data set provides the calendar times (in hours), excluding repair or down times, of the successive failures of $n=6$ such systems during the two-year development phase. Because the censoring times were not provided, we set ${\tau }_i=S_{i{K}_i}$. The first two machines are the oldest, the second two machines are of medium age, and the last two are relatively new machines. The covariate is the categorized age of the machines, coded as $\mathbf{X}=(0,0)$ denoting old age, $\mathbf{X}=(1,0)$ denoting medium age, and $\mathbf{X}=(0,1)$ denoting young age. For our analysis, we assume that the effective age is the backward recurrence time $ℰ\left(s\right)=s-S_{N^{†}(s-)}$ The number of failure events for the six machines are $\mathbf{K}=(24,26,28,29,27,24)$. When the general model without frailty is fitted, the resulting parameter estimates are $\widehat{\alpha }=1.0265$ and $({\widehat{\beta }}_1,\hspace{0.17em}{\widehat{\beta }}_2)=(-0.0764,-0.0537)$. The corresponding standard errors, obtained from the estimate of the inverse of the partial likelihood information matrix, are ${\widehat{\sigma }}_{\widehat{\alpha }}=0.0106$ and ${\widehat{\sigma }}_{\widehat{\beta }}=(0.2014,0.2056)$ These estimates were obtained by setting $s*$ to any value larger than ${max}_{1\le i\le 6}{\tau }_i=4743$ hours. For the general model with gamma frailties, we find $\widehat{\xi }=2.53\times {10}^{28}$ or $\widehat{\eta }\approx 1$, which indicates the absence of unobserved frailties which would have induced additional heterogeneity among the machines. As a consequence, the estimates of $\alpha$ and ( ${\beta }_1,{\beta }_2$) were identical to those obtained when the model without frailties was fitted. A very large estimate of $ℰ$ is also obtained if we analyze the data under the assumption of ‘always minimal repair,’ that is, $ℰ\left(s\right)=s$. In this situation, $\widehat{\alpha }=1.014$ ( ${\widehat{\sigma }}_{\widehat{\alpha }}=.0244$ and $\widehat{\beta }=(-.1468,-.0520)[{\widehat{\sigma }}_{\widehat{\beta }}=(.2097,.2053)]$, so the main difference with the previous analysis is in the estimates of the parameter ${\beta }_1$.

7 Concluding Remarks

In this paper procedures for estimating the parameters of a general and flexible class of models for recurrent events were developed and their properties examined through computer simulation studies. The class of models, which includes as special cases many well-known models in survival analysis and reliability, possesses the appealing properties that it takes into account the effect of interventions which are administered after each event occurrence through the notion of an effective age, the possible weakening (or strengthening) effect of accumulating event occurrences, the possible presence of unobserved frailties that could be inducing correlations among the inter-event times per unit, and the effect of observable covariates. Some data sets in the biomedical and reliability/engineering settings were reanalyzed using this new class of models. It was found in the simulation studies that an under-specification of the model, in the sense of analyzing a data set generated from the model with frailties using procedures developed from the model without frailties, could have unacceptable consequences in that the resulting estimators will have non-negligible systematic biases. On the other hand, it was found that over-specification of the model may provide a robust method of analysis with an acceptable loss in efficiency. The application of the procedures to the bladder cancer data set also provided a reconciliation of seemingly varied estimates obtained from currently available methods of analyzing recurrent event data, and highlights the importance of monitoring the effective age process.

There are still many interesting and important questions that need to be examined with regards to this general model. The first is the ascertainment of asymptotic properties of the estimators, such as their asymptotic normality or the weak convergence to a Gaussian process of a properly normed estimator of the baseline survivor function. This will be the topic of another paper, and the resolution of this asymptotic problem may require empirical process methods utilized in Murphy (1994, 1995) and Parner (1998); see also the recent paper of Kosorok et al. (2004). Some asymptotic results for specific models subsumed by the general class of models could be found in Peña et al. (2001) and Kvam and Peña (2005). Through such asymptotic analysis we will be able to obtain expressions for approximating analytically the standard errors of the estimators which will reflect the effects of an informative right-censoring mechanism as well as the impact of the sum-quota accrual scheme (see Peña et al. (2001) for the special case of a renewal model).

The problem of validating the class of models after it has been fitted to a specific data set is open, and calls for suitable goodness-of-fit and model validation procedures. For example, in the illustration using the LHD data set, the survivor curve estimate for the medium age group is a little higher than for the new age group, and when one examines the data, there is a long gap in the third machine which might have led to this ordering. A question of interest is whether this particular inter-event time is an outlier. We anticipate that model validation and diagnostics procedures to be developed for this class of models will answer this question. Another issue of interest is in the absence of effective age data, might it have been better to fit a minimal repair effective age function, instead of the perfect repair effective age for this LHD data? This question leads to the recognition that an existing limitation of this class of models is that currently available data sets do not possess information regarding the effective age process. Thus, in applying this model to currently available data sets, we are forced to assume simple forms of the effective age process, such as the imperfect repair or perfect repair models discussed here. This problem of not knowing the effective age was first highlighted in Whitaker and Samaniego (1989), where they pointed out that if the repair modes, hence the effective ages, are not known in the minimal repair model, then the model is nonidentifiable. For the purpose of demonstrating their inference methods using Proschan (1963)'s air-conditioning data, which did not include the mode-of-repairs, they therefore augmented the inter-failure times data with assumed mode-of-repair data to illustrate the estimation of the reliability function. As demonstrated by our simulation studies to assess the impact of mis-specifying the effective age process in relation to the bladder cancer data application, a mis-specification on this effective age could lead to systematic biases on the estimators. It is therefore our hope that researchers will make an effort in assessing the effective age during the data gathering stage of studies. Though it may be potentially difficult to achieve in biomedical settings, such information, if acquired, will prove useful and informative in the modeling and analysis. This somehow calls for a paradigm shift in the data gathering of recurrent event data.

8 Appendix: Partial EM Algorithm

Consider the problem of finding the maximizing values $\left(\xi \theta \right)$ of a full likelihood function $L_F(\xi ,\theta |D)$ where $D$ is the observed data. We assume that when given $\theta$, maximizing $L_F(\xi ,\theta |D)$ in $\xi$ is practically feasible, but a joint maximization in $(\xi ,\theta )$ is difficult. We suppose that, when given a value $\left(\xi {,}^{\left(0\right)}{\theta }^{\left(0\right)}\right)$, we could implement the EM-step to get the next iterate $\left({\xi }_{EM}^{\left(1\right)}{\theta }_{EM}^{\left(1\right)}\right)$ and in such a way that in the M-step of the EM algorithm, ${\xi }_{EM}^{\left(1\right)}$ and ${\theta }_{EM}^{\left(1\right)}$ are obtained via maximization of two separate mappings, one depending only on $\xi$ and the other depending only on $\theta$, such as in our case. In the partial EM algorithm we implemented, ${\xi }_{EM}^{\left(1\right)}$ is replaced by ${\xi }_{PEM,}^{\left(1\right)}$ which is ${\xi }_{PEM}^{\left(1\right)}={\text{arg max}}_{\xi }{L}_F(\xi ,{\theta }_{EM}^{\left(1\right)}|D)$, so the next iterate is obtained by setting $\left(\xi {,}^{\left(0\right)}{\theta }^{\left(0\right)}\right)=\left(\xi {,}_{PEM}^{\left(0\right)}{\theta }_{EM}^{\left(0\right)}\right)$, and proceeding as described above. That this algorithm will also lead to a maximizing value if the iteration converges follows by observing that the inequalities $L_F({\xi }^{\left(0\right)},{\theta }^{\left(0\right)}|D)\le L_F({\xi }_{EM}^{\left(1\right)},{\theta }_{EM}^{\left(1\right)}\left|D\right)\le L_F({\xi }_{PEM}^{\left(1\right)},{\theta }_{EM}^{\left(1\right)}|D)$ hold. The first inequality is true because the EM-step guarantees an improved value in the likelihood, whereas the second inequality is immediate from the definition of ${\xi }_{PEM}^{\left(1\right)}$ In our specific implementation, in the notation above, $\theta$ will be associated with $\left({\Lambda }_0\right(·),\alpha ,\beta )$, while $\xi$ above will be associated with the frailty parameter in our model.