Learning Vector Quantization Neural Networks Improve Accuracy of Transcranial Color-coded Duplex Sonography in Detection of Middle Cerebral Artery Spasm—Preliminary Report

Abstract

To determine the performance of an artificial neural network in transcranial color-coded duplex sonography (TCCS) diagnosis of middle cerebral artery (MCA) spasm. TCCS was prospectively acquired within 2 h prior to routine cerebral angiography in 100 consecutive patients (54M:46F, median age 50 years). Angiographic MCA vasospasm was classified as mild (<25% of vessel caliber reduction), moderate (25–50%), or severe (>50%). A Learning Vector Quantization neural network classified MCA spasm based on TCCS peak-systolic, mean, and end-diastolic velocity data. During a four-class discrimination task, accurate classification by the network ranged from 64.9% to 72.3%, depending on the number of neurons in the Kohonen layer. Accurate classification of vasospasm ranged from 79.6% to 87.6%, with an accuracy of 84.7% to 92.1% for the detection of moderate-to-severe vasospasm. An artificial neural network may increase the accuracy of TCCS in diagnosis of MCA spasm.

Introduction

Transcranial Doppler sonography evaluation of blood flow velocities in the cerebral arteries allows for the rapid detection and serial assessment of cerebral vasospasm, because flow velocity increases with narrowing of the vessel (Aaslid et al. 1984; Babikian et al. 2000). Transcranial color-coded duplex sonography (TCCS) has recently facilitated more accurate determination of intracranial blood flow velocities (Bogdahn et al. 1990; Krejza et al. 2000). Considerable efforts have been devoted to discerning critical velocity thresholds that reliably differentiate cerebral vasospasm from hyperemia or physiologic blood flow (Lysakowski et al. 2001; Mariak et al. 2002; Krejza and Baumgartner 2004). As numerous physiologic factors influence blood flow velocities in a particular vascular segment, isolated velocity thresholds may be limited in their diagnostic accuracy. The shape of the pulsatile Doppler waveform provides further information and waveform analysis may yield several useful numerical parameters (so-called Doppler parameters) (Krejza et al. 1999; Babikian et al. 2002). The complex nature of velocity waveform analysis precludes rapid visual assessment for the detection of vasospasm, yet intelligent support system may be ideally suited for this task.

We applied artificial neural networks (ANNs) methodology to detect middle cerebral artery (MCA) spasm based on multi-parametric analysis of TCCS velocity data using digital subtraction angiography as a reference standard. The primary features of ANNs are the capacity of learning and the ability of approximation any nonlinear relationships that may defy simple mathematical relationships between input and output variables. Typical applications of ANNs include signal processing or forecasting, pattern recognition, and discrimination (Bishop 1997; Haykin 1999). Biomedical applications of ANNs have extended the scope of traditional statistical methods for data analysis. ANNs applications in clinical medicine have rapidly evolved in the last few years (Bishop 1997; Smith et al. 2003; Lisboa and Taktak 2006). Examples of successful clinical applications of ANNs include the detection of myocardial infarction with ECG signal analysis, diagnosis of tumor histology based on microscopic smears, forecasting and pattern recognition of the intracranial pressure signal (Koss et al. 1997; Swiercz et al. 2000), or data classification for computer-aided diagnostics in many other clinical problems (Siermala et al. 2007). These recent clinical applications suggested that ANNs may also be used to diagnose and classify cerebral vasospasm based on TCCS measurements. We evaluated the performance of Learning Vector Quantization (LVQ), a neural network architecture particularly adept in classification problems, and used angiographic data to determine a priori the desired outputs of the neural network. The results obtained with LVQ networks were compared with classification performed by the Support Vector Machines (SVM) algorithm, which is the method closely related to neural networks and in many application gives comparably high accuracy.

Methods and Results

The research protocol and informed consent were approved by the local ethics committee. Informed consent was obtained from either the patient or responsible family member. One hundred consecutive patients (54 men and 46 women; median age 50 years, range 18 to 74 years) were studied prospectively. TCCS was performed within 2 h prior to digital subtraction angiography of the cerebral circulation. Clinical indications for cerebral angiography included non-traumatic subarachnoid hemorrhage (n=46), intracerebral hemorrhage (n=31), post-operative evaluation of aneurysm clipping (n=12), intractable headache (n=6), brain tumor (n=2), ischemic stroke (n=2), and traumatic subarachnoid hemorrhage (n=1).

Transcranial Color-coded Doppler Sonography (TCCS)

Following a 15-min rest period in supine position, TCCS was performed on a sonographic scanner (Toshiba Applio, Toshiba Medical System, Tokyo, Japan) equipped with a 2.5 MHz 90° phased-array probe with B-mode and Doppler imaging. Proximal segments of the basal cerebral arteries were insonated via a transtemporal and were identified on grayscale and color imaging in relation to intracranial structures (Krejza et al. 2000). A 3-mm wide sample volume was placed on the color image of the proximal MCA (M1) about 10 mm distal to the terminal carotid or at the site of the highest flow velocity acceleration indicated by aliasing phenomenon. A linear marker was placed under visual guidance on the color image of the insonated vascular segment along the long axis of the vessel to determine the angle of insonation. The angle between this linear marker and the ultrasound beam, displayed automatically on the screen of the scanner, was considered a two-dimensional approximation of the angle of insonation. A typical TCCS image of MCA spasm is shown on Fig. 1. Angle-corrected peak systolic (V_PS), mean (V_MEAN), and end diastolic (V_ED) blood flow velocities were subsequently obtained. Automated blood flow velocity determinations were used, although manual tracing of the maximum frequency envelope of the Doppler waveform was used to obtain these values when a weak Doppler signal was noted. An expert radiologist reviewed the TCCS data for quality purposes and rejected 42 waveforms due to inferior quality. Further analyses were based on the remaining 158 data sets, including waveforms of the left and right MCA.

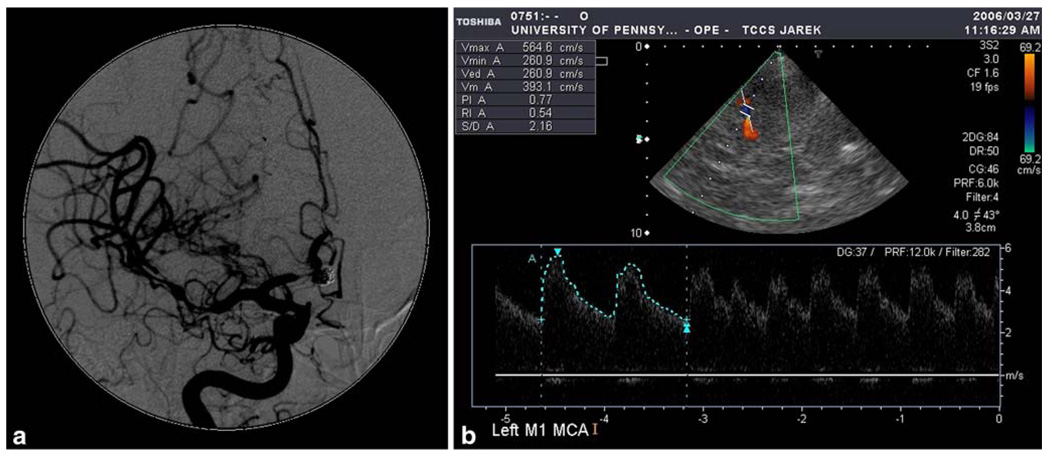
Fig. 1.

56-years old woman 6 days after subarachnoid hemorrhage due to rupture of aneurysm of the posterior cerebral communicating artery. a Digital subtraction angiography shows severe vasospasm of distal M1 segment of the middle cerebral and A1 segment of the anterior cerebral artery. b Transcranial color coded duplex sonography shows the spastic M1 segment in blue (aliasing artifact), which enables for the operator to place the sample volume precisely at the place of the highest velocity acceleration and correct for the angle of insonation, which is substantial—43°. Mean flow velocity is 393 cm/s after correction for the angle. The finding corresponds to patient’s hemiplegia

Digital Subtraction Angiography (DSA)

Selective DSA of bilateral internal carotid arteries and at least one vertebral artery was performed via the femoral artery using the Seldinger approach. Standard angiographic views, including antero-posterior, lateral, and oblique projections (30 cm field of view), were obtained routinely at injection rates of 6 ml/s and filming rates of three frames per second. Two experts blinded to the TCCS results reviewed the DSA studies to determine the presence and degree of cerebral vasospasm. Views illustrating the most severe degree of MCA narrowing were used for comparison with TCCS. All measurements were performed using calipers on the digital display. The spatial resolution of this technique is 0.1 mm. To quantify the degree of narrowing, site of maximal reduction of the horizontal segment of the MCA was compared with the “normal” section of the artery on both sides of the narrowed segment. The choice of a “normal” diameter was made according to a standard algorithm of selection of a non-affected denominator: choice 1: pre-narrowing segment; choice 2: post-narrowing segment; choice 3: terminal portion of the parent artery (Suarez et al. 2002). Vasospasm was classified as absent, mild (<25% of vessel caliber reduction), moderate (25–50%), or severe (>50%) (Lindegaard et al. 1989; Mariak et al. 2002). Vessel diameter was also compared with the contralateral vascular segment to facilitate classification of vasospasm.

Discordant angiographic readings were resolved by consensus with assistance of a third expert. Probability of a vessel’s membership in each subclass based on ratings of three angiographic raters was determined based on a model described by Uebersax (1992) and Bayes’ rule. A vessel was then assigned to the subclass to which it had the highest probability of membership.

Descriptions of Classifications Tools and Experimental Results

The basic descriptive statistics of data used in the study are presented in Table 1—both for the entire data set and for the each of four classes of vasospasm. As it can be noticed from data statistics, the mean values of peak systolic (V_PS), mean (V_MEAN), and end diastolic (V_ED) blood flow velocities increase with the increase of the vessel caliber reduction due to the development of vasospasm. For example, the mean values of all the blood velocities for patients with severe vasospasm are more than twice higher than for patients without reduction of the MCA diameter. Nevertheless, taking into account standard deviations of the blood velocities and comparing the inter-class data distribution (clearly visible in Fig. 4 and Fig. 5), one can say that data belonging to different classes of spasm occupy overlapping regions in the (V_PS– V_MEAN–V_ED) input space. The above observation justifies the efforts to find the classifiers, which are able to learn from data, how to generate optimal nonlinear boundaries between different classes of vasospasm.

Table 1.

Statistics of the data used in the study

Property name	Entire data set	VA1	VA2	VA3	VA4
Number of cases	158	117	15	17	9
VPS min	35.0	35.0	51.0	109.0	162.0
VPS mean	141.0	122.0	139.2	208.5	256.8
VPS max	352.0	227.0	205.0	277.0	352.0
VPS std. dev.	58.8	43.4	36.1	41.2	63.6
VPS 95% CI	9.2	8.1	18.6	19.9	48.9
VMEAN min	15.0	15.0	22.0	39.0	108.0
VMEAN mean	90.6	76.0	87.1	138.9	178.0
VMEAN max	255.0	153.0	136.0	173.0	255.0
VMEAN std. dev.	42.5	29.3	6.1	32.6	51.3
VMEAN 95% CI	6.7	5.5	12.9	15.7	39.4
VED min	7.0	7.0	10.0	16.0	76.0
VED mean	60.9	50.2	56.6	97.6	125.6
VED max	195.0	102.0	92.0	125.0	195.0
VED std. dev.	31.2	20.4	18.5	25.5	39.3
VED 95% CI	4.9	3.9	9.5	12.3	30.2

Vasospasm is categorized as class 1—normal (VA1), class 2—mild (VA2), class 3—moderate (VA3), and class 4—severe (VA4).

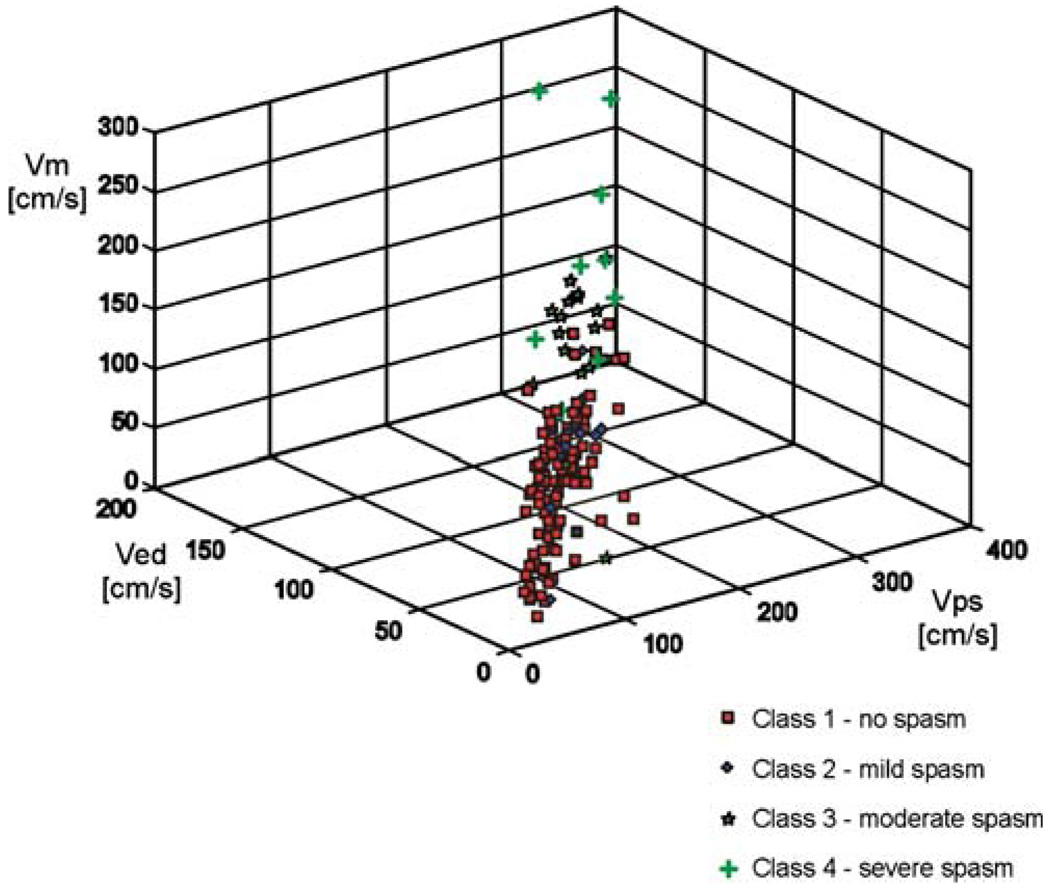
Fig. 4.

3-D plot of TCCS derived peak-systolic (V_PS), end-diastolic (V_ED) and mean (V_MEAN) blood flow velocities based on four angiographic classes of MCA spasm

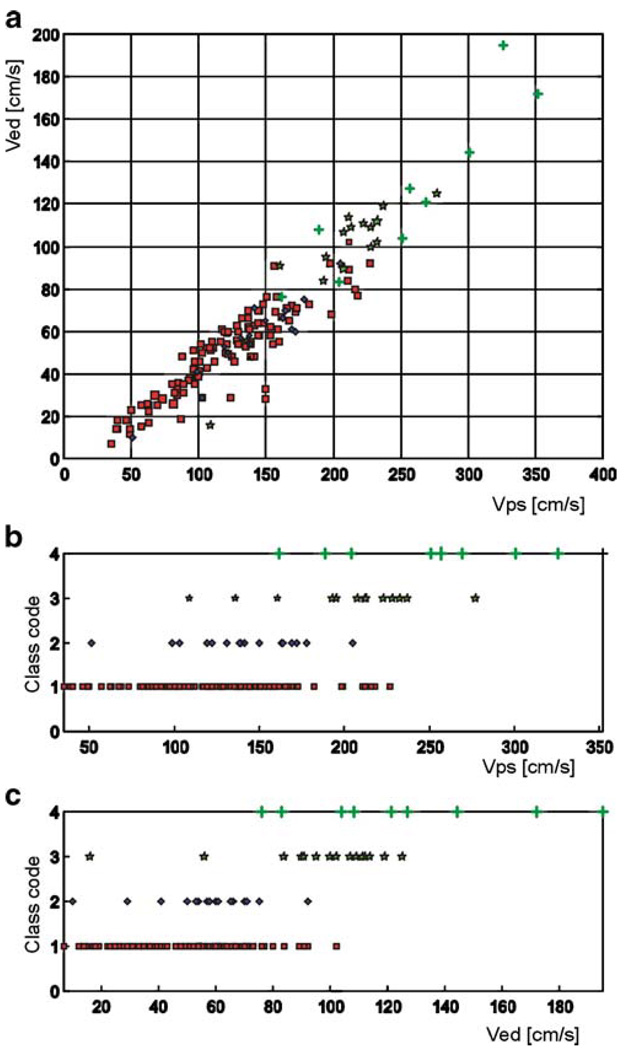
Fig. 5.

a 2-D projection of the velocity data presented in Fig. 4 onto the V_PS–V_ED plane. The markers symbolize the same classes of vasospasm as in Fig. 4. b Distribution of the V_PS for four classes of vasospasm. Class codes correspond to the same classes of vasospasm as denoted in Fig. 4. c Distribution of the V_ED for originally defined four classes of vasospasm. Class codes correspond to the same classes of vasospasm as denoted in Fig. 4

Learning Vector Quantization (LVQ) Neural Networks

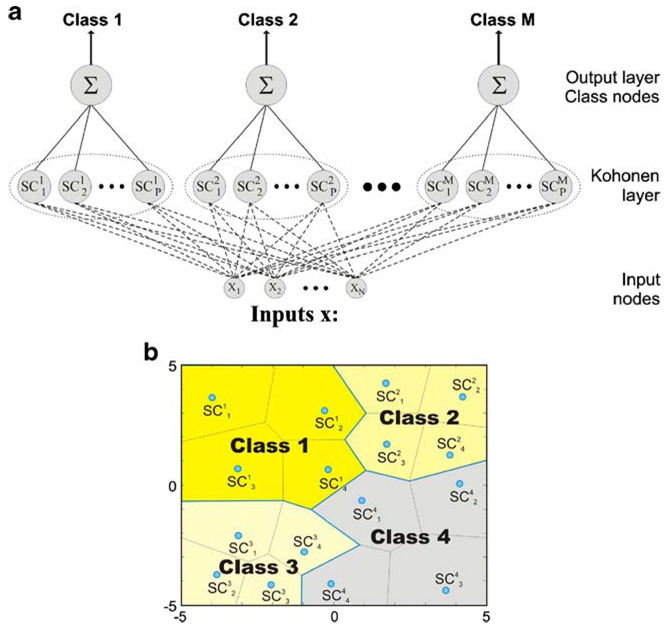
Learning Vector Quantization is a classification neural network (Kohonen et al. 1988), which assigns a vector representing multi-dimensional experimental data to one of several classes. The classes are defined by the user, so training of the LVQ network is performed in a supervised manner. An LVQ network consists of two computational layers: a competitive layer (Kohonen layer), which learns to detect regularities and correlations in the input vectors presented to the network and assigns them to as many subclasses as the number of neurons that the layer contains; an output or linear layer, which transforms the competitive layer’s output subclasses into target classes, defined by the user. The general architecture of the LVQ neural network, which assigns the input vector x (of the length N) to one of M classes, is presented in Fig. 2a.

Fig. 2.

a General architecture of the LVQ neural network, which assigns the input vector x (of the length N) to one of M classes. The neurons in the competitive layer, which create the centers of the subclasses are marked as ${\text{SC}}_j^i$. b The final split of the input space into classes by grouping the Voronoi polytopes by the output (summation) layer of the LVQ network

The basic version of the algorithm, used to train the Kohonen layer of an LVQ network, may be presented as follows (Fine 1999).

The distance of a training vector from each neuron (Processing Element, PE) is computed and the nearest PE is declared to be the winner. The Euclidean distance between a training vector, x, and each PE’s weight vector, w_i, is computed according to the standard formula:

$$d_i=\Vert w_i-x\Vert ={\left\{{\displaystyle \sum _{j=1}^N{(w_{ij}-x_j)}^2}\right\}}^{\raisebox{1ex}{$1$}\!\left/ \!\raisebox{-1ex}{$2$}\right.}$$ (1)

where N is the number of elements in the input vector, x (a dimension of the input space).

If the winning neuron is in the same class as the training vector (this class is known a priori in the supervised training mode), it is moved towards the training vector according to

$$w\prime =w-\alpha (x-w)$$ (2)

where 0<α<1 is the attraction coefficient.

If the winning neuron is not in the same class as the training vector, it is moved away (repulsed) from the training vector, according to:

$$w\prime =w-\gamma (x-w)$$ (3)

where 0<γ<1 is the repulsion coefficient.

During the training process, neurons assigned to a class migrate to the region associated with their class. As a result of the training process, the input space is divided into so-called Voronoi polytopes; the number of the polytopes is equal to the number of neurons (processing elements) in the Kohonen layer. The competitive neurons create the centers of the polytopes (marked as ${\text{SC}}_j^i$ in Fig. 2b); each input vector presented to the network is identified with the nearest subclass center, according to Euclidean distance (sometimes other distance measures are chosen for training and classification). The boundaries, found by the competitive layer, depend only on the distance between the input vectors. In the classification mode, the competitive layer computes the distance between an input vector and each neuron, and again, the nearest processing element is declared to be the winner. The output of this neuron is set to “1”, while the outputs of all the other neurons are set to “0”. The competitive layer splits the input space into S1 subclasses (S1 is the number of neurons in the Kohonen layer), which in turn are combined by the linear layer to form S2 target classes, specified by the user (S2 should never be greater than S1).

Unlike the widespread binary classifiers—the perceptrons, LVQ networks can classify any set of input vectors, not just linearly separable sets of input vectors. The decision boundaries (i.e. the borders, separating different classes) may form shapes in multidimensional space, which are more complex than ordinary hyperplanes, as it is shown in Fig. 2b, where the regions assigned to different classes are non-convex. The only requirement is that the competitive layer must contain enough neurons and each class must be assigned enough competitive neurons.

Learning Vector Quantization (LVQ) is commonly regarded as a flexible and robust non-parametric statistical classifier. LVQ is a method for training competitive networks in a supervised manner, which means that (in opposition to the ‘standard’ competitive neural networks) the available information about assignment of input vectors into target classes may be fully utilized. Classification problems may be, of course, solved also with the use of networks with continuous outputs, e.g. the multilayer perceptrons (MLP) or radial basis function (RBF) networks. In the LVQ network, as with the RBF network, each hidden unit can be thought of as representing a point in N-dimensional space. In both network types outputs of the hidden units are based on the proximity of the input vector; however the difference between the two is that in an RBF network, several Gaussian hidden units can have significant outputs, while in the LVQ network the output of all but one competitive unit is zero. The final output of both network types is determined by the weights of the linear output unit, so in the case of RBF networks additional post-processing stage is required to determine the final (1 of M) class, the input vector belongs to. For example, it is necessary to establish thresholds for the RBF outputs, on which it can be decided if the output should be accepted or neglected—such threshold values will be always subjective.

Moreover, in the LVQ network the structure of neuronal activity related to the performance of the network can be visualized directly by examining the coefficients (weights) for the competitive neurons that are related to each recorded neuron. It allows to control the number of neurons in Kohonen layer (changing the ‘granulation’ of Voronoi polytopes) and, in that way, to influence the shapes of class boundaries relatively easily.

The above features of the LVQ networks looked promising enough to choose this type of a neural classifier to solve the classification problem of the degree of MCA narrowing based on TCCS and DSA examination.

Support Vector Machines (SVM)

A Support Vector Machine (SVM) performs classification by constructing an N-dimensional hyperplane that optimally separates clusters of vector into two non-overlapping groups (Cristianini and Shawe-Taylor 2000). The cases with one category of the target variable are on one side of the plane and cases with the other category are on the other side of the plane. The vectors near the hyperplane, which determine the maximal margin for separation, are called the support vectors.

Unfortunately, this is not generally the case, so SVM must typically deal with separating the points with nonlinear curves (not a linear hyperplane), handling the cases where clusters simply cannot be completely separated and handling classifications with more than two categories.

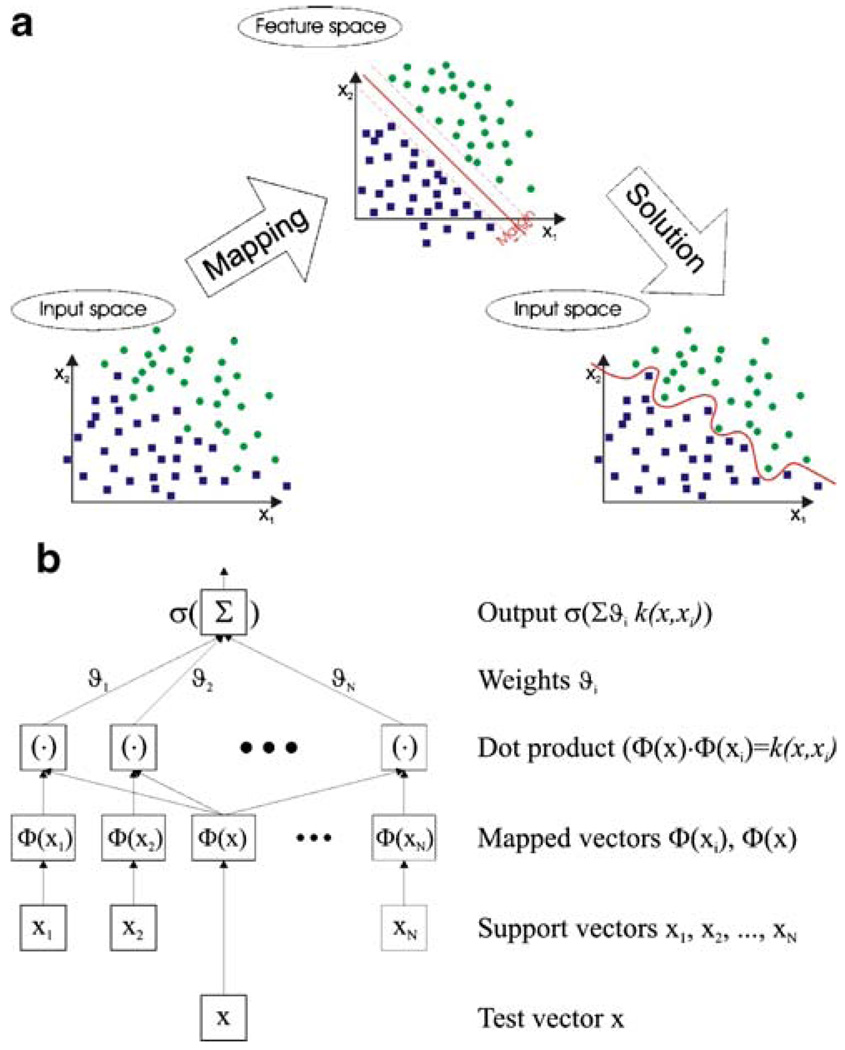
In some cases the optimal linear separation can be performed after data transformation from original input space to the feature space. The transformation is usually nonlinear and increases the dimensionality of the original data vectors, as it is shown in Fig. 3a. Nevertheless, when the optimal hyperplane is found in the feature space, after re-mapping data vectors to the original input space, the decision boundary may be highly nonlinear.

Fig. 3.

a General principle of the solution of the two-class separation by the Support Vector Machine (SVM). The transformation from the original input space into the feature space allows to find the optimal hyperplane, which perfectly separates the classes. Re-mapping to the original input space results in the nonlinear decision boundary. b The architecture of the SVM model, which uses kernel functions to perform data classification

So-called kernel functions allow to find the optimal separating hyperplane without mapping the input data to the feature space. Many kernel mapping functions can be used—probably an infinite number. But a few kernel functions have been found to work well in a wide variety of applications, i.e.:

$$\text{polynomial kernel}:k(x_i,x)={(x_i^{T}x+1)}^p$$ (4)

$$\text{Gaussian}(\text{radial})\text{kernel}:k(x_i,x)=\exp \left(-\frac{1}{2{\sigma }^2}{\Vert x_i-x\Vert }^2\right)$$ (5)

$$\text{sigmoid kernel}:k(x_i,x)=\tanh ({\beta }_0{x}_i^{T}x+{\beta }_1)$$ (6)

where x is the input vector and x_i is the i-th support vector.

SVM models are closely related to neural networks; e.g. a SVM model using a sigmoid kernel function is equivalent to a two-layer, feed-forward neural network. Using a kernel function, SVM’s are an alternative training method for polynomial, radial basis function and multilayer perceptron classifiers in which the weights of the network are found from available data, by solving an optimization problem.

The default and recommended kernel function is Gaussian (Radial Basis Function—RBF). Furthermore, the linear kernel is a special case of the RBF. A sigmoid kernel behaves the same as a RBF kernel for certain parameters. The RBF function has fewer parameters to tune than a polynomial kernel, and the RBF kernel has less numerical difficulties.

It should be however noticed, that even with the use of sophisticated kernel functions, perfect separation may not be possible, or it may result in a model with so many feature vector dimensions that the model does not generalize well to other data; this is known as over fitting. The architecture of the SVM classifier with kernel functions is shown in Fig. 3b.

Classification Results

An LVQ neural network and an SVM classifier were constructed based on TCCS velocity data and angiographic classifications of cerebral vasospasm. Four categorical descriptions of MCA vasospasm (normal, mild, moderate, and severe) on DSA defined the outputs of the constructed classifiers. TCCS determinations of blood flow velocities (V_PS, V_MEAN, and V_ED) were used as input variables for the LVQ network and the SVM model. The LVQ neural network and the SVM classifier were expected to automatically assign the set of three MCA blood flow velocities to a particular class of vasospasm.

In the group of 158 arteries included in analysis, mild vasospasm was angiographically diagnosed in 15, moderate in 17, and severe in nine. The kappa coefficient for interobserver agreement in angiographic diagnosis of the MCA spasm resulted in a kappa value of 0.80. The agreement between two radiologists, who classified the MCA spasm, appeared to be somewhat lower, at κ = 0.63.

Input vectors to the LVQ network were preprocessed using the MinMax Table transformation for all numerical experiments and the ‘In-Class Winner Always Learns’ algorithm was employed in LVQ training (Bishop 1997). Table 2 illustrates the diagnostic performance of two LVQ architectures in the four-class discrimination task. The overall classification rate (the ratio of the sum of correctly recognized cases in each class to the total number of cases classified) increased with the number of neurons in the Kohonen layer. The classification rate varied from 64.94% for eight competitive neurons to 72.34% for 16 competitive neurons. Table 2 also contains classification results for individual classes of vasospasm in the form of a confusion matrix. For ideal classification, the matrix should contain ones on the diagonal and zeros everywhere outside the diagonal. Each column of the matrix summarizes the classification of cases, which truly belong to a specific class; the numbers in this column represent the percentage of cases from this class, which were classified by the network as belonging to consecutive classes.

Table 2.

The diagnostic accuracy of LVQ networks for discrimination of four categories of vasospasm increases with the number of competitive neurons

	VA1-des	VA2-des	VA3-des	VA4-des
Number of neurons in Kohonen layer: 8
VA1-act	0.7168	0.3529	0.1053	0.2222
VA2-act	0.2478	0.5882	0.0526	0.0000
VA3-act	0.0354	0.0588	0.7368	0.2222
VA4-act	0.0000	0.0000	0.1053	0.5556
Overall classification rate=0.6494
Number of neurons in Kohonen layer: 16
VA1-act	0.8496	0.3529	0.2105	0.1111
VA2-act	0.0442	0.5294	0.0000	0.0000
VA3-act	0.0256	0.1176	0.7368	0.1111
VA4-act	0.0796	0.0000	0.0526	0.7778
Overall classification rate=0.7234

Vasospasm is categorized as class 1—normal (VA1), class 2—mild (VA2), class 3—moderate (VA3), and class 4—severe (VA4). All LVQ networks contained three input variables (TCCS velocity data) and four output variables (categories of vasospasm). Confusion matrices detail code of actual (act) class (rows) versus code of desired (des) class (columns)

The results of the four-class separation task, performed by the SVM classifiers with two kernel functions—RBF and sigmoid, are presented in Table 3. The overall classification rate is noticeably higher than for the LVQ networks (77.85% for both kernel functions), but the more careful analysis of the confusion matrices shows the drawbacks of the classification. The higher accuracy was obtained due to almost perfect classification of the normal category (patients without MCA narrowing), while the other categories of vasospasm were diagnosed much worse than by the LVQ networks. As the number of patients not suffering from vasospasm reaches 74% of the entire population used in the study, increasing the classification rate for this group highly influences the overall classification accuracy. It can be also noticed that almost all the patients with mild vasospasm were assigned by the SVM to the ‘no spasm’ category.

Table 3.

The confusion matrices, showing the diagnostic accuracy of SVM classifiers for discrimination of four categories of vasospasm

	VA1-des	VA2-des	VA3-des	VA4-des
RBF kernel
VA1-act	0.9646	0.9412	0.3158	0.2222
VA2-act	0.0000	0.0000	0.0000	0.0000
VA3-act	0.0354	0.0588	0.6842	0.6667
VA4-act	0.0000	0.0000	0.0000	0.1111
Overall classification rate=0.7785
Sigmoid kernel
VA1-act	0.9823	1.0000	0.4211	0.2222
VA2-act	0.0000	0.0000	0.0000	0.0000
VA3-act	0.0177	0.0000	0.5789	0.6667
VA4-act	0.0000	0.0000	0.0000	0.1111
Overall classification rate=0.7785

Vasospasm is categorized in the same way as for the LVQ networks (see Table 1); the inputs of the SVM classifiers were also the same

In a series of successive numerical experiments, groupings of the classes of vasospasm were used to define broader classifications of cerebral vasospasm. Table 4 details the classification results for the LVQ network trained to recognize any degree of vasospasm, thus the decision boundary in the training process was created between the normal artery state and any degree of vasospasm. In this case, the overall classification rate varied from 79.57% for eight competitive neurons to 87.57% for 16 neurons in the Kohonen layer. The performance of the SVM model in the same classification task is presented in Table 5. The overall classification rate varied from 81.65% for the sigmoidal kernel function to 82.91% for the RBF kernel.

Table 4.

The diagnostic accuracy of LVQ networks for discrimination of two categories of vasospasm

Number of neurons in Kohonen layer: 8			Number of neurons in Kohonen layer: 16
(a) Vasospasm is categorized as class 1—normal (VA1), and class 2—mild, moderate, or severe [VA(2–3–4)]
	VA1-des	VA(2–3–4)-des		VA1-des	VA(2–3–4)-des
VA1-act	0.9469	0.3556	VA1-act	0.9292	0.1778
VA(2–3–4)-act	0.0531	0.6444	VA(2–3–4)-act	0.0708	0.8222
Overall classification rate=0.7957			Overall classification rate=0.8757
(b) Vasospasm is categorized as class 1—normal or mild [VA(1–2)], and class 2—moderate or severe [VA(3–4)]
	VA(1–2)-des	VA(3–4)-des		VA(1–2)-des	VA(3–4)-des
VA(1–2)-act	0.9077	0.2143	VA(1–2)-act	0.9846	0.1429
VA(3–4)-act	0.0923	0.7857	VA(3–4)-act	0.0154	0.8571
Overall classification rate=0.8467			Overall classification rate=0.9209
(c) Vasospasm is categorized as class 1—normal, mild, or moderate [VA(1–2–3)], and class 2—severe (V4)
	VA(1–2–3)-des	VA4-des		VA(1–2–3)-des	VA4-des
VA(1–2–3)-act	0.9866	0.6667	VA(1–2–3)-act	0.9866	0.2222
VA4-act	0.0134	0.3333	VA4-act	0.0134	0.7778
Overall classification rate=0.6600			Overall classification rate=0.8822

Confusion matrices detail code of actual (act) class (rows) versus code of desired (des) class (columns). All LVQ networks contained three input variables (TCCS velocity data) and two output variables (categories of vasospasm)

Table 5.

The confusion matrices, showing the diagnostic accuracy of SVM classifiers for discrimination of two categories of vasospasm

RBF kernel			Sigmoid kernel
(a) Vasospasm is categorized as class 1—n ormal (VA1), and class 2 —mild, moderate, or severe [VA(2–3–4)]
	VA1-des	VA(2–3–4)-des		A1-des	VA(2–3–4)-des
VA1-act	0.9381	0.4444	VA1-act	0.9115	0.4222
VA(2–3–4)-act	0.0619	0.5556	VA(2–3–4)-act	0.0885	0.5778
Overall classification rate=0.8291			Overall classification rate=0.8165
(b) Vasospasm is categorized as class 1—normal or mild [VA(1–2)], and class 2—moderate or severe [VA(3–4)]
	VA(1–2)-des	VA(3–4)-des		VA(1–2)-des	VA(3–4)-des
VA(1–2)-act	0.9846	0.2857	VA(1–2)-act	0.9923	0.3571
VA(3–4)-act	0.0154	0.7143	VA(3–4)-act	0.0077	0.6429
Overall classification rate=0.9367			Overall classification rate=0.9304
(c) Vasospasm is categorized as class 1—normal, mild, or moderate [VA(1–2–3)], and class 2—severe (V4)
	VA(1–2–3)-des	VA4-des		VA(1–2–3)-des	VA4-des
VA(1–2–3)-act	1.0000	0.8889	VA(1–2–3)-act	1.0000	0.8889
VA4-act	0.0000	0.1111	VA4-act	0.0000	0.1111
Overall classification rate=0.9494			Overall classification rate=0.9494

Vasospasm is categorized in the same way as for the LVQ networks (see Table 3); the inputs of the SVM classifiers were also the same

Table 4 shows the classification results for the LVQ network trained to detect moderate to severe vasospasm (i.e. the decision boundary corresponds to 25% of vessel caliber reduction). In this case, the overall classification rate varied from 84.67% for eight competitive neurons to 92.09% for 16 neurons in the Kohonen layer. The corresponding results for the SVM classifier, presented in Table 5, varied from 93.04% for the sigmoidal kernel function to 93.67% for the RBF kernel. It should be noticed that the classification accuracy for the SVM model was slightly better than for the LVQ networks, even with higher number of competitive neurons.

Table 4 shows the classification results for the LVQ network trained to recognize severe vasospasm (i.e. to detect at least 50% of vessel caliber reduction). In this case, the overall classification rate varied from 66.00% for eight competitive neurons to 88.22% for 16 neurons in the Kohonen layer. Table 5 shows the performance of the SVM model in the same classification task. The overall classification rate is equal to 94.94% for both kernel functions used in experiments, however the analysis of the confusion matrix discloses serious drawback of the SVM performance. Almost all the data points were assigned to the class with no spasm or mild and moderate spasm; only one vector of nine allover classified was correctly assigned to the class of severe spasm. So, in the sense of proper location of the decision boundary, the LVQ networks behaved much better in diagnosis of severe spasm.

The lowest classification accuracy was obtained when four classes of vasospasm were detected at the same time, ranging from 65% for a smaller LVQ network architecture to over 72% for a more complex LVQ network. The diagnostic performance of the test is low, however, simple visual examination of the data distribution can explain this performance for the neural classifiers. Figure 4 illustrates the 3-D view (in V_PS–V_ED–V_MEAN coordinate system) of the desired four-class assignment, determined from angiographic data. The projections of the same data set onto the (V_PS–V_ED) plane are shown in Fig. 5.

In the next series of experiments, the data set was divided into three classes of vasospasm. Table 6 shows the classification results for the LVQ network with nine neurons in the Kohonen layer trained to recognize three classes of vasospasm. When two different groupings of classes of vasospasm were employed, the overall classification rate of the LVQ network remained similar (76.49% versus 77.27%). Even when the LVQ architecture was more complex (employing 15 neurons in the Kohonen layer), no significant differences were noted in the classification of vasospasm. The accuracies of the SVM classifiers for the same divisions of the data set into three classes are shown in Table 7. The results are better than for the LVQ networks (82.91% and 79.75% for the RBF kernel), however the class boundaries have not been established properly. Most of data, which in fact belong to the class of mild (or mild and moderate) spasm was assigned by the SVM model to the class of no spasm.

Table 6.

The diagnostic accuracy of LVQ networks for discrimination of three categories of vasospasm with 9 and 15 neurons in the Kohonen layer

Number of neurons in Kohonen layer: 9				Number of neurons in Kohonen layer: 15
(a) Vasospasm is categorized as class 1—normal (VA1), class 2—mild (VA2), and class 3—moderate or severe [VA(3–4)]
	VA1-des	VA2-des	VA(3–4)-des		VA1-des	VA2-des	VA(3–4)-des
VA1-act	0.8850	0.2941	0.0357	VA1-act	0.8766	0.4118	0.0764
VA2-act	0.0885	0.5882	0.1429	VA2-act	0.0669	0.5294	0.0764
VA(3–4)-act	0.0265	0.1176	0.8214	VA(3–4)-act	0.0669	0.0588	0.8576
Overall classification rate=0.7649				Overall classification rate=0.7542
(b) Vasospasm is categorized as class 1—normal (VA1), class 2—mild or moderate [VA(2–3)], and class 3—severe (VA4)
	VA1-des	VA(2–3)-des	VA4-des		VA1-des	VA(2–3)-des	VA4-des
VA1-act	0.9292	0.3333	0.1111	VA1-act	0.8850	0.3333	0.1111
VA(2–3)-act	0.0708	0.6111	0.1111	VA(2–3)-act	0.1150	0.6111	0.1111
VA4-act	0.0000	0.0556	0.7778	VA4-act	0.0000	0.0556	0.7778
Overall classification rate=0.7727				Overall classification rate=0.7579

Confusion matrices detail code of actual (act) class (rows) versus code of desired (des) class (columns). All LVQ networks contained three input

Table 7.

The confusion matrices, showing the diagnostic accuracy of SVM classifiers for discrimination of three categories of vasospasm

RBF kernel				Sigmoid kernel
(a) Vasospasm is categorized as class 1—normal (VA1), class 2—mild (VA2), and class 3—moderate or severe [VA(3–4)]
	VA1-des	VA2-des	VA(3–4)-des		VA1-des	VA2-des	VA(3–4)-des
VA1-act	0.9735	0.9412	0.2500	VA1-act	0.9735	0.9412	0.2500
VA2-act	0.0000	0.0000	0.0000	VA2-act	0.0000	0.0000	0.0000
VA(3–4)-act	0.0265	0.0588	0.7500	VA(3–4)-act	0.0265	0.0588	0.7500
Overall classification rate=0.8291				Overall classification rate=0.8291
(b) Vasospasm is categorized as class 1—normal (VA1), class 2—mild or moderate [VA(2–3)], and class 3—severe (VA4)
	VA1-des	VA(2–3)-des	VA4-des		VA1-des	VA(2–3)-des	VA4-des
VA1-act	0.9558	0.5833	0.1111	VA1-act	0.9558	0.6111	0.1111
VA(2–3)-act	0.0000	0.4167	0.5556	VA(2–3)-act	0.0000	0.3611	0.5556
VA4-act	0.0442	0.0000	0.3333	VA4-act	0.0442	0.0278	0.3333
Overall classification rate=0.7975				Overall classification rate=0.7848

Vasospasm is categorized in the same way as for the LVQ networks (see Table 5); the inputs of the SVM classifiers were also the same

Discussion

TCCS may provide consistent and reproducible measurements of blood flow velocities in the basal cerebral arteries (Krejza et al. 2000). A reliable diagnosis of vasospasm, however, requires appropriate definition of a critical velocity threshold or a set of TCCS parameters (Lysakowski et al. 2001; Mariak et al. 2002).

In our previous work, we used the receiver operating characteristics curve analysis to evaluate the overall diagnostic performance of TCCS in the detection of MCA spasm (Mariak et al. 2002; Krejza et al. 2003). In that study, we employed a single blood flow velocity as an indicator of vasospasm. We noted that TCCS may accurately classify vasospasm in up to 80% of cases. In the setting of moderate-to-severe vasospasm, the diagnostic accuracy of TCCS reached 93%. As a part of the study, we also established a V_PS threshold value of 182 cm/s as the optimal trade-off between sensitivity and specificity of the test. TCCS discrimination of any degree of vasospasm with respect to an absence of vasospasm met limited success and we therefore attempted to expand the set of parameters to successfully increase the accuracy of this method (Krejza et al. 2003). Integration of the expanded data set may be impractical, however, for routine clinical application. The development of an ANN and classification of data in multi-dimensional space for this purpose may facilitate this endeavor.

We constructed a LVQ network to solve a pattern recognition task, discerning patterns of blood flow velocity measurements that corresponded to angiographic classifications of cerebral vasospasm. The pattern presented to the network inputs consisted of a set of blood velocities: V_PS, V_ED and V_MEAN. The tasks performed by the LVQ network resemble the more conventional problem of discriminate analysis, which may be understood as partitioning multidimensional space into subspaces corresponding to the required classes of discrimination, where the number of dimensions in this hyper-space is equal to the number of analyzed parameters (Johnson and Wichern 1992). During training, the LVQ network created the boundaries of a selected number of sub-spaces corresponding to classes of vasospasm defined on angiography.

Several aspects of the constructed LVQ network were arbitrarily selected. The categorization scheme for cerebral vasospasm and subsequent groupings were user defined. This method of data classification enabled us to split the dataset into two classes (i.e. perform binary classification) and also study the performance of LVQ networks in the diagnosis of all primarily selected vasospasm classes. In the binary classification problem, we could differentiate normal angiographic findings from any class of vasospasm and distinguish severe vasospasm from any other status of the MCA. Several variations in LVQ architecture, employing different numbers of neurons in the Kohonen layer, were examined in various classification tasks. The number of LVQ outputs varied and was equal to the number of user-selected classes of vasospasm, while the number of inputs was always three: the values of V_PS, V_ED and V_MEAN.

The diagnostic accuracy or classification rate of the LVQ networks varied depending on the number of vasospasm classes delineated and the number of competitive neurons in the network architecture. The overall classification accuracy decreased with the number of vasospasm classes to be detected and increased with the number of neurons in the Kohonen layer. Diagnostic accuracy could probably be further augmented by using LVQ networks with a greater number of competitive neurons by splitting the input space into a greater number of small sub-regions and it would be possible to obtain more complex shapes for the decision boundaries. As each additional neuron is added to the Kohonen layer, the number of synaptic weights in the network increases. Assuming that the LVQ network has three inputs and four outputs, the number of synaptic weights assigned to each competitive neuron is equal to seven. As the number of data sets used for training is constant (at least limited by the number of patients examined), increasing the network complexity violates the condition known as the Vapnik– Chervonenkis dimension (Haykin 1999). This states that there should be an adequate number of training vectors compared to the number of network weights, and some researchers claim that this proportion should even be about 10:1. Otherwise, the network learns to memorize the training patterns and loses generalization abilities. In our experiments the number of competitive neurons never exceeded 16, including four outputs in the LVQ network and yielding 112 synaptic weights.

One can readily see that the data assigned to specific vasospasm classes occupy overlapping regions in the input space, spanned across the set of blood flow velocities. As the V_PS, V_ED, and V_MEAN for a patient are correlated, the data are also placed around the diagonal of each plot. A general trend of increasing velocities with vessel narrowing is clearly visible from the Fig. 4 and Fig. 5, yet no specific velocity set exists which may separate the regions associated with specific classes of vasospasm. The boundaries of these regions, corresponding to different classes of vasospasm, would be very complicated and are more likely created by the biological variability of cerebral vessels, than by the physical relationships between the class of vessel narrowing and the increase in flow velocities. Nevertheless, with the software used in numerical experiments it is possible to determine the contribution of individual network inputs to the classification results. The ANN methodology confirmed our previous finding that the best TCCS parameter for detection of MCA spasm is the peak systolic velocity (Mariak et al. 2002; Krejza et al. 2003).

The highest accuracy rate (85% for a smaller LVQ network architecture and 92% for more complex LVQ structure) was obtained for binary classification, i.e. discrimination between moderate-to-severe vasospasm from normal arterial states plus mild vasospasm. Such diagnostic performance may be regarded as very high, matching the results obtained with a conventional diagnostic approach, in which evaluation of TCCS data was performed by a human examiner. The relatively high accuracy of the conventional approach leaves minimal room for further improvement and the performance of ANN may therefore be regarded as close to perfect.

The accuracy for the binary classification of “no vasospasm” and “vasospasm of any severity” was significantly lower and amounted to 80% for the smaller LVQ network architecture and 87% for the complex LVQ structure. As the accuracy obtained by a human investigator (and estimated with ROC analysis) amounted to only 80%, our results suggest that an ANN may be a useful method for future integration of such diagnostic data (Mariak et al. 2002; Krejza et al. 2003).

The similar conclusions can be made from the analysis of the performance of the second powerful classification tool used in our experiments—the Support Vector Machine models. Due to the location of the data in overlapping regions in the input space, the classification done by SVM was also far from being perfect. For all the classification tasks, applied to specific groups of spasm data, the SVM models seemed to outperform the LVQ networks. Nevertheless, the class boundaries were not established properly by the SVM classifiers; it could be observed that the spasm classes with the small number of data vectors were “absorbed” by the classes with large number of members. It could be also noticed that for the SVM models the general trend of improvement the classification accuracy for simpler divisions of the data set was similar to these, observed for LVQ networks.

An important methodological consideration is that measures of performance for all methods of diagnosing cerebral vasospasm are always calculated against cerebral angiography—the “gold standard” in this particular clinical scenario. The angiography is not necessarily perfect but is the best available method today. The kappa coefficient for inter-observer agreement in angiographic detection of moderate-to-severe MCA spasm amounted to 0.80, whereas the agreement between two radiologists in the detection of mild MCA spasm was even lower, with a value of 0.63 (Krejza et al. 2003). As even expert classification of angiographic vasospasm is only modest the accuracy of any diagnostic method will be limited when compared to this gold standard. As a result of these limitations, the results generated by the ANN will always be biased with this uncertainty and the best attainable accuracy can never reach 100%.

Conclusions

The LVQ network show superior performance in the two-class separation problem. For the detection of moderate-to-severe MCA spasm, the classification accuracy reached 92% and 87% for identification of other classes of MCA vasospasm. Such diagnostic accuracy is better than the results obtained by a human investigator and the classification may be simultaneously determined for more than two classes of vasospasm.

Further improvements in diagnostic accuracy may be attained through increasing the number of input variables by adding other clinical data and extracranial carotid blood flow parameters (Lindegaard et al. 1989). In the numerical experiments, not documented in this study, also the impedance index of pulsatility (PI), calculated as PI=(V_PS-V_ED)/ V_MEAN was used as the fourth network input or in the combination with the selected pair of blood flow velocities. We also used the vessel resistivity index (RI), which could be computed from original Doppler recordings. The preliminary numerical experiments did not show significant improvement of classification, when the additional variables have been added to the input vector. However, in the case of the extended inputs in the three- or four-class classification problem, the number of competitive neurons in the LVQ networks could not be high enough, because the number of the synaptic weights is limited by the number of training samples available.

Alternative strategies may employ a more complex network structure. Such refinements, as well as increasing the number of network inputs, require a much larger sample of TCCS data.