Abstract
This brief review analyzes the evolution of motor control theories along two lines that emphasize active (motor programs) and reactive (reflexes) features of voluntary movements. It suggests that the only contemporary hypothesis that integrates both approaches in a fruitful way is the equilibrium-point hypothesis. Physical, physiological, and behavioral foundations of the EP-hypothesis are considered as well as relations between the EP-hypothesis and the recent developments of the notion of motor synergies. The paper ends with a brief review of the criticisms of the EP-hypothesis and challenges that the hypothesis faces at this time.
An Introduction: The History of the Active-Reactive Argument
The origins of voluntary movement and of the relations between human movements and their controller, the central nervous system (CNS), have been fascinating scientists at least since the times of the great Greek philosophers of the past. At that time, the problem of movement-CNS relation was more commonly formulated as that of the relation between the moving body and the controlling soul. For example, Plato viewed self-motion as a sign of immortal soul, which was apparently inherent to all animals capable of voluntary movements. Plato did not give a definition of “self-motion”, but likely he implied all movements of a living being that could not be expected from an inanimate object with the same mechanical properties given the forces acting on the body from the environment. As we will see later, this view is similar to stating that the soul contained what a contemporary researcher would call motor programs.
Aristotle was arguably the first to pay attention to a distinguishing feature of biological movement, that is its coordination. According to him, coordination came from the harmony of the world, as an interaction between the controlling soul and the environment – a step towards dynamic models of movements.
So, are movements produced in an active way (by a will, intention, or soul) or in a reactive way (as responses to signals from the environment)? This question has been debated hotly since the times of Plato and Aristotle, and the story of motor control is the story of discoveries that swung the pendulum back and forth, between the active and reactive theories.
In the beginning of the twentieth century, two great scientists contributed greatly to the development of the active theory based on reflexes. They were both Nobel Prize winners, and their works had shaped the field for decades to come. A great Russian physiologist, Ivan Pavlov, developed a theory of inborn and conditioned reflexes, according to which all movements represented combinations of those two groups of reflexes. New movements emerged as a result of new pathways through the CNS networks created by repetitive excitation of the involved neurons. Sir Charles Sherrington, the founder of contemporary neurophysiology (for a detailed review see Stuart et al. 2001), did not claim that movements represented combinations of reflexes; rather, according to his theory, movements were produced by modulation of parameters of reflexes. As we will see further in this article, this view is already rather close in spirit to the equilibrium-point hypothesis of motor control.
Despite the scientific prestige of Sherrington and Pavlov, their theories met with opposition from two younger and much less decorated opponents, Graham Brown and Bernstein. Graham Brown observed locomotion in animals without reflexes and started a line of research leading eventually to the notion of central pattern generators (CPGs). Bernstein argued in favor of motor programs (he called them “engrams”) stored in memory and recalled when a coordinated movement was required. The very first book by Bernstein was written in the middle 1930th and contained an argument with Pavlov and his school. Unfortunately, the book was published only about 70 years later (Bernstein 2003).
For the sake of brevity, let me jump over the development of these groundbreaking ideas by such outstanding scientists as von Holst and the Moscow school of Gelfand (CPGs and motor programs), and the schools of Eccles and Lundberg (reflexes).
In the 1970th the Bernstein idea of engrams was developed in the shape of a generalized motor program (schema theory, Schmidt 1975). Note that Bernstein did not view engrams as direct precursors of torque patterns, rather as time functions of abstract variables encoding salient features of movements such as their topology (Bernstein 1935, 1967). He realized that exact peripheral patterns of movements could not be encoded by neural signals, they emerged with equal participation of signals from peripheral receptors and the direct mechanical effects from the environment. In contrast, the theory of generalized motor programs assumed that patterns of mechanical variables such as muscle forces and joint torques were encoded in the CNS. They could be retrieved with different gains and time scales leading to stronger/weaker and faster/slower movement execution. According to this view, for example, a cyclic motor pattern has to be associated with a cyclic motor program.
The reactive (reflex) part of the story also developed in the form of the dynamic systems approach to movements. This development was inspired by two major sources. First, the development of dynamic systems theory in mathematics and its applications to physics showed that complex patterns could emerge in a complex system under simple control that had no obvious similarity to the patterns. For example, a pendulum swings in a cyclic fashion without any cyclic control, simply because of the laws of physics and the action of gravity. Similarly, a limb may swing at its natural frequency without a cyclic input from the CNS in an apparent contradiction to the ideas of generalized motor program.
The second source was the idea of direct perception introduced by Gibson (1979). The importance of sensory feedback has been accepted in all theories of movements. However, for a theory that views movements as built on reflexes (or other feedback-based mechanisms), feedback is vital for meaningful movements. In contrast, the theory of motor programs is expected to be able to produce desired motor patterns in the absence of feedback and, sometimes, even by overcoming the effects of the feedback (Gottlieb et al. 1990). Within this view, feedback signals can be used for starting, stopping, correcting, and parametrizing motor programs. In contrast, the idea of direct perception implies that movements always reflect feedback signals even if those are not consciously perceived by the actor. Certainly, this view remains incomplete unless activity within the system is allowed to emerge independently of the ongoing sensory feedback along the ideas of the physiology of activity that Bernstein started to develop in his final years of life (Bernstein 1967).
Recently, the motor programming ideas have been further developed based on the progress in control theory and engineering. According to these developments, memory is assumed to contain not generalized motor programs but sets of internal models (Kawato 1999; Wolpert et al. 1998; Shadmehr and Wise 2005), both direct and inverse, that is neural structures modeling or emulating physical processes involved in transformations leading from neural signals to peripheral mechanics (direct) and those involved in predicting neural signals that would produce desired mechanics (inverse).
In the turmoil of the discussions of the past half-century, one hypothesis has stood alone and withstood the abundant criticisms, the equilibrium-point (EP) hypothesis. Its fate is unique: Over all this time, it has been neither disproved nor accepted by a majority of researchers.
The Origins of the EP-hypothesis
As most non-trivial hypotheses, the EP-hypothesis has several layers with their own assumptions and mechanisms. These assumptions and mechanisms can be traced back to the general principles of physics and classical findings in neurophysiogy and motor behavior.
One of the main sources of the EP-hypothesis is physics. This is not unexpected given that its founder, Anatol Feldman, was trained as a physicist. According to the principle of relativity of Galileo, forces may emerge and disappear if you switch reference frames. For example, in the reference frame of a falling elevator (please, do not perform this experiment), the net force acting on a person within the elevator may be zero. In the external reference frame, the person moves at a constant acceleration under the influence of the force of gravity. This example shows that changing a reference frame may lead to the emergence or disappearance of forces. That is why, the recent development of the EP-hypothesis in its application to whole-body movements has been termed the reference configuration hypothesis (Feldman and Levin 1995; Feldman et al. 1998, 2007).
The EP-hypothesis combines principles from the “reflex” and “motor program” theories. In particular, it is based on the ideas of Sir Charles Sherrington who viewed muscle reflexes not as hardwired stereotypical responses to stimuli but rather as tunable mechanisms that formed the basis of motor behavior. Control of movements, according to Sherrington, was performed by changing parameters of reflexes, in particular of the tonic stretch reflex, an idea very close in spirit to the EP-hypothesis. On the other hand, the EP-hypothesis accepted the idea of Bernstein's engrams assuming that patterns of control variables (related to changes in the reference body configuration and expressed as parameters of reflexes – see the next section) were stored in memory and formed the basis for voluntary movements.
One of the very influential behavioral experiments related to the EP-hypothesis was performed by a famous German team of neurophysiologists (Wachholder and Altenburger 1927). They asked a seemingly naïve question: How can a person relax muscles acting at a joint at different joint positions? Indeed, muscle spring-like properties had been known at that time. Two springs acting against each other can only be in an equilibrium at one position; a change in that position would stretch one spring, shorten the other, and destroy the equilibrium. In their experiments, the researchers recorded muscle activation levels and confirmed that humans could indeed relax at different joint positions. They ended up with a revolutionary conclusion (ignored for decades!) that the CNS modified muscle spring properties during voluntary movements.
A similar question was posed by von Holst and Mittelstaedt (1950) a few decades later: How does the system produce voluntary changes in joint angle without inducing a posture-stabilizing resistance? Indeed, a host of posture-stabilizing mechanisms had been discovered by that time. They all contributed to resistance of human joints to external perturbations. Why is voluntary movement not triggering those mechanisms? Von Holst and Mittelstaedt introduced a reafference principle hypothesizing that voluntary movements changed a reference point with respect to which afferent signals were assessed in their posture-stabilizing action.
Approximately at the same time, arguably the first motor control hypothesis was introduced by Merton (1953). This hypothesis, termed the servo-hypothesis, postulated a particular physiological signal as the control variable in the production of voluntary movements. According to Merton's servo-hypothesis, signals to the system of gamma-motoneurons established a desired muscle length, and the tonic stretch reflex acted to make sure that the encoded length was achieved independently of the external load and its possible changes. In other words, the servo-hypothesis assumed that the tonic stretch reflex was a perfect length-controlling servo mechanism. Unfortunately for the hypothesis, further experiments failed to support its main assumptions such as the very high gain of the tonic stretch reflex loop (Matthews 1970; Vallbo 1970) and earlier activation of the gamma motoneurons as compared to the alpha motoneurons at movement initiation (Vallbo 1971).
At the end of the first half of the XXth century, Peter Matthews (1959) published a classical paper exploring the tonic stretch reflex in the decerebrate cat. In particular, Matthews showed that a fixed descending input into the spinal cord (a fixed level of stimulation of the descending pathways) was associated not with a fixed length, or a fixed force, or a fixed level of activation, but with a stable relation between muscle force and length, while muscle activation changed in parallel with the force. Changes in the stimulation level resulted in shifts of the force-length characteristics along the length axis. In other words, muscles behaved like non-linear springs with zero length dependent on the descending signals. These studies were direct precursors of experiments by Feldman that led to the formulation of the EP-hypothesis (Feldman 1966). In those experiments, Feldman did not decerebrate human subjects but asked them “not to interfere” assuming that this instruction leads to an unchanged descending command. He observed sets of joint-angle characteristics for the elbow joint that were similar to the force-length characteristics in the study of Matthews. In particular, a change in the initial state (that required a different descending command) was associated with a shift of the joint-angle characteristic along the angle axis.
The EP-hypothesis in the Nutshell
The equilibrium-point hypothesis is based on several major principles. Some of them such as the Galileo principle of relativity have been already mentioned. Another one is related to the design of the neuromuscular system, namely its threshold nature. As shown by Matthews (1959), changes in descending signals to the spinal segmental apparatus may be described as setting threshold values of muscle length for the tonic stretch reflex. If the length of a muscle is below this threshold, the muscle is silent. If it is over the threshold, the muscle is activated, and the level of activation grows with the difference between the actual muscle length and the threshold value. This activation tends to produce muscle contraction (shortening) thus bringing its length closer to the threshold value.
In other words, the difference between the threshold position defined mainly by descending signals and the actual position (sensed by proprioceptors) leads to activation of motoneurons and muscle fibers they innervate. These neural and muscular elements interact with each other and with the environment through both mechanics and neural loops. These interactions tend to reduce the activity of motoneurons and minimize the difference between the actual position and the threshold position. So, all muscles are trying to achieve minimal activation compatible with the external forces including those produced by other muscles. This may be viewed as a principle of minimal end-state action (a cousin of the principle of minimal interaction; Gelfand and Tsetlin, 1966). In real world, muscle length changes are constrained by the body anatomy and its interaction with the environment. As a result, at an equilibrium, some muscles typically show non-zero activation levels.
Let us start with a single muscle. Its steady-state may be described with two variables, length and force (Figure 1A). A control signal (λ) sets the threshold of the tonic stretch reflex, that is a dependence between active muscle force and length similar to the dependences observed by Matthews. The actual muscle force and length depend on both λ and the external load (L is Figure 1A). If a muscle is at an equilibrium point (EP1) acting against the load L, its force magnitude equals L. Any deviation of the muscle from that point would result in a change in its activation such that the active muscle force will be higher than L (if the muscle is stretch) or lower than L (if the muscle is shortened). If after such an imposed length change, the muscle is released, it will go back to EP1 because no other equilibrium state exists. The mechanisms that tend to bring the muscle back to EP1 are the posture-stabilizing mechanisms considered by von Holst and Mittelstaedt (see earlier).
Figure 1.
An illustration of single-muscle control within the EP-hypothesis. A: A central command (λ) defines a force-length characteristic. Given an external load (L), only one equilibrium point is possible (EP1). Any deviations (filled points) from EP1 will result in motion back to EP1. B: To perform an active movement, a change in λ is required (λ1 to λ2). As a result, a new equilibrium point (EP2) is established, and a motion to EP2 happens. C: Movements can occur passively, as a result of a change in the load (L1 to L2).
Imaging now that the force-length curve is shifted (from λ 1 to λ2 in Figure 1B). The previous equilibrium point, EP1 is no longer an equilibrium point. It is a deviation from the newly established equilibrium point, EP2. The same posture-stabilizing mechanisms that used to bring the muscle back to EP1 now tend to move it to EP2. So, posture stabilization and movement production are two peripheral consequences of the same central mechanism very much in compliance with the reafference principle.
Imagine now that the central command remains unchanged (λ1) but the load changed from L1 to L2 (as in Figure 1C). The previous equilibrium point becomes non-equilibrium, and a movement occurs to a new equilibrium point (EP2) where the active force of the muscle equilibrates the external load.
Panels B and C Figure 1 illustrate that within the EP-hypothesis, movements may result from two causes. A movement may be a consequence of a change in the external load while the person does not change the voluntary command to the muscle. A change in the load while keeping the command constant results in a new combination of muscle force and length along the same force-length curve, a movement that may be addressed as “involuntary”. A movement may also be produced by a change in the threshold of the tonic stretch reflex (a change in λ). Since λ is under control of the CNS, such movements may be called “voluntary”.
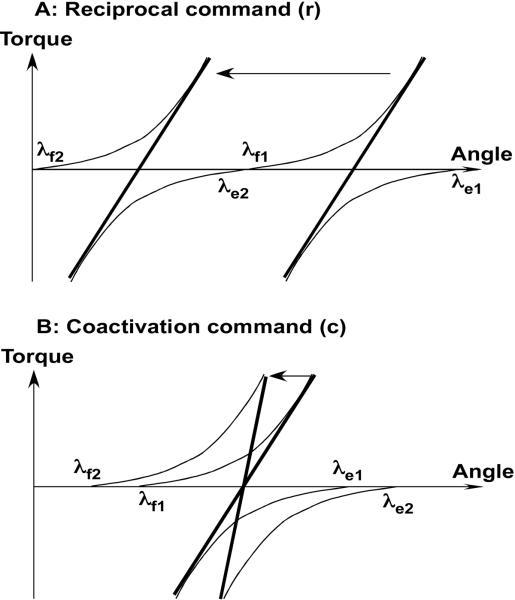
It is rather easy to generalize this scheme to a joint controlled by two muscles that produce joint torques in opposite directions, for example a flexor and an extensor muscle. Figure 2 illustrates the tonic stretch reflex curves for a pair of muscles with opposing actions using another pair of mechanical variables, torque and angle, that are more appropriate to describe rotational actions. Each muscle is controlled with its own command variable, λf for the flexor and λe for the extensor. The {λf; λe} pair defines an overall joint characteristic shown by the bold line in Figure 2. Equilibrium state of the joint and its mechanical behavior will also depend on the external torque. For example, if there is a constant external torque (Tq in Figure 2) acting on the joint, the system will be at an equilibrium at a combination of torque and angle values {T0, α0}.
Figure 2.
Control of a joint may be described with two variables, λf and λe on the torque-angle plane. The joint torque-angle haracteristic (thick lines) will represent the algebraic sum of the corresponding muscle characteristics. A: Shifts of both λf and λe in the same direction result in a shift of the joint characteristic parallel to the angle axis and may be associated with a reciprocal command (r). Shifts of λf and λe in opposite directions lead to a change in the slope of the joint characteristic and may be associated with a coactivation command (c).
Voluntary joint motion and/or torque production result from shifts of the two ls. It is easy to notice that, if both λf and λe shift in the same direction along the angle axis, the mechanical characteristic of the whole joint, which is the algebraic sum of the two muscle characteristics, shifts parallel to itself along the angle axis without a change in its shape (Figure 2A). This mode of control may be viewed as trying to activate one muscle and relax its antagonist. On the other hand, if λf and λe shift in opposite directions, there is little change in the location of the joint characteristic but a major change in its slope (Figure 2B). This will not move the joint by much but will “stiffen” it. To reflect these two modes of joint control explicitly, another pair of variables has been used that is equivalent to the {λf; λe} pair. These variables have been referred to as reciprocal command, r, and coactivation command, c (Feldman 1980, 1986). They can be defined as r = (λf + λe)/2; c = (λf − λe)/2.
To make a step to multi-joint and whole-body movements, the notion of a reference configuration has to be introduced. This notion was introduced by the group of Anatol Feldman as a control variable at a high level of a control hierarchy involved in the production of natural, multi-joint movements (Feldman and Levin 1995; Feldman et al. 2007). Reference configuration defines, in the external space, a configuration, at which all the muscles would attain a minimal level of activity – a set of threshold values for muscle activation. External forces may not allow the body to reach a current reference configuration; then, the difference between the reference configuration and an actual configuration will result in the non-zero muscle activations leading to force production against the external forces.
For now, let us assume that a hypothetical central controller can set values of ls for each muscle, and correspondingly, values of {r,c} for each joint independently of other factors. Under this assumption, control of a muscle can be adequately described with a time function λ(t). This time function may be viewed as a control variable supplied to the segmental apparatus controlling the muscle, its control trajectory.
If at any moment of time, t0, the current value of λ is frozen at λ(t0), and the system is allowed to reach an equilibrium, it will come to rest at an equilibrium point corresponding to a combination of muscle length and force (lEP,FEP) defined by λ(t0) and the external load. So, a control trajectory λ(t) may be associated with a time sequence of equilibrium points EP(t) or an equilibrium trajectory. Note that, by definition, the equilibrium trajectory incorporates both length and force changes.
While the control trajectory is assumed to be specified centrally, the equilibrium trajectory emerges with an equally important role played by the external force field. For example, if a movement is practiced against a constant external load, repeating the same control pattern (same control trajectory) can be expected to lead to the same equilibrium trajectory but only if the load does not change. Generating the same control trajectory against a changing load would result in a different equilibrium trajectory. This feature was used in a series of studies with the reconstruction of time patterns r(t) and c(t) using external loads that could change smoothly and unexpectedly (Latash and Gottlieb 1991; Latash 1992).
For a given equilibrium trajectory, actual trajectory, l(t) of the system will depend on many factors that may be united under a not-very-precise notion of dynamics. These factors include, in particular, the external force field, the mechanical properties of the moving segments, the time delays in the reflex arcs that bring about changes in muscle activation via the tonic stretch reflex loop, the properties of the transformation from muscle activation to force generation, etc.
Unfortunately, at the current level of experimental sophistication, analysis of time patterns of control variables (for example, λs) has been elusive. This is due to the fact that observed variables such as forces and displacements are indirect reflections of equilibrium trajectories, which are in turn indirect reflections of the λ(t) functions. Even in experiments with isometric force production in predictable conditions, regularities seen at the level of mechanical elemental variables cannot be viewed as adequate reflections of some hypothetical regularities at the level of control variables: Even if no overt motion happens during an isometric force production action, muscle activation leads to shortening of the muscle fibers and lengthening of the tendon such that the total length of the muscle+tendon complex remains unchanged while muscle length actually changes. Besides, muscle activation is accompanied by activation of the gamma-system that changes the sensitivity of the spindle sensory endings to both muscle length and velocity. Since spindle endings are a major source of reflex effects, the reflex contribution to muscle activation is expected to change even under isometric conditions.
There have been several attempts to reconstruct the time changes of λs (or of the {r,c} pairs) during natural actions (Latash and Gottlieb 1991; Latash 1992, 1994; Gomi and Kawato 1996). All these studies, however, used simplified mechanical models of the moving segments and, therefore, produced questionable results (see Gribble et al. 1998).
Another approach to identifying λ(t) or reference configurations has been based on an analysis of electromyographic patterns of large groups of muscles (Feldman et al. 1998; Lestienne et al. 2000). This approach is based on the following idea. Because of the gravity field, which provides a non-zero external load during most actions, actual joint configurations during natural movements rarely coincide with reference configurations thus leading to non-zero activation of certain muscle groups. However, during a quick movement with a reversal, one may expect that, at some point in time, the moving actual configuration will coincide with the moving reference configuration. If this happens, all the muscles participating in the action may be expected to show a minimum of their activation level at the same time. Such global minima of muscle activity were indeed observed in the cited studies. However, even this method offers only an indirect method of identifying a reference configuration at only one (or few) point during a movement.
The EP-hypothesis and Motor Synergies
Recently, a new view on synergies has been developed based on the principle of abundance (Gelfand and Latash 1998). According to this principle, when a neural controller faces a task that involves a large set of elements, it does not look for single solutions but organizes interactions among the elements in such a way that families of solutions emerge that are all capable of performing the task (reviewed in Latash et al. 2002, 2007). The freedom of selecting solutions from a large set allows the controller to deal with possible perturbations or perform other tasks at the same time using the same set of elements (e.g., Zhang et al. 2008).
With respect to single muscle control, the EP-hypothesis may be viewed as a particular example of a multi-element synergy with motor units playing the role of elements, and the overall muscle behavior (for example, the level of activation, or the active muscle force, or the joint position) playing the role of task variables. The tonic stretch reflex mechanism is an example of a feedback system that adjusts the rates of the action potential generation by individual motor units stabilizing the total level of muscle activation. For example, if one motor unit stops firing, the level of muscle activation drops, the balance of forces is violated such that the muscle is stretched by the external load, muscle spindles show an increase in their activity, the tonic stretch reflex produced more excitation of the motoneuronal pool, and all motoneurons increase their firing rate (and/or new motoneurons are recruited) thus compensating for the effects of the original problem (one motor unit stopped working).
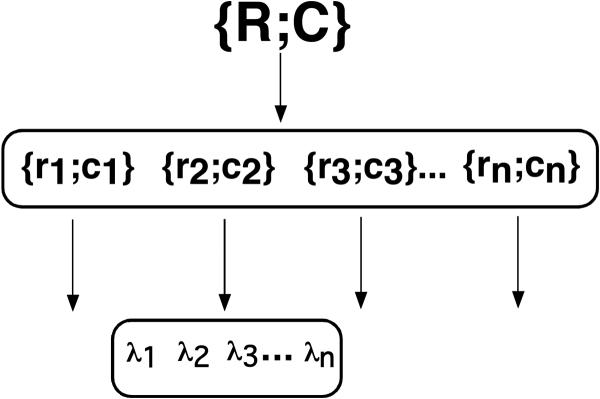
Can this approach be generalized to the control of multi-effector systems. To do this, we have to use the notion of reference configuration introduced ealier. If one understands the notion of reference configuration not as a detailed configuration of all the segments of the body (all its kinematic degrees-of-freedom) but as a combination of threshold positions of only important points (Pilon et al. 2007), this notion offers a very attractive framework to look at motor synergies at a control level. Assume a hierarchical control system where, at each level of the hierarchy, the system is redundant, that is it produces more output variables than the number of constraints specified by input variables (Figure 3). If the controller cares only about certain characteristics of a motor action, other characteristics may be allowed to vary based on some secondary considerations, possibly reflecting optimization of certain features of performance.
Figure 3.
An illustration of a hypothetical hierarchy for a multi-joint movement. A command for a desired motion of a particular point on the body (for example, the endpoint of a multi-joint limb) may be associated with a command {R,C}. It forms an input into a synergy using {r,c} commands to individual joints as elemental variables. Each {r,c} pair is the input into a multi-muscle synergy with λs as elemental variables.
For example, during a multi-joint movement, frequently trajectory of the endpoint is viewed as an important performance variable. In particular, this assumption was used by Gribble and Ostry (2000) in an elegant model of movement adaptation to velocity-dependent external force fields based on the EP-hypothesis. Assume that the CNS organizes feedback on the endpoint position and uses this feedback to produce a time profile of an output variable, which will be used as the input into the next, hierarchically lower control level, for example the level of individual joints. At each point in time, the CNS specifies threshold values of the endpoint location, and the discrepancy between the reference endpoint location and its actual location drives the output of that highest level of the hierarchy. These signals serve as the input into the next level of control, which will drive reference trajectories at a joint level.
Because the system is redundant, a reference trajectory at a higher hierarchical level does not specify unambiguously all the reference trajectories at a lower level. Emergence of particular lower-level reference trajectories may be based on a feedback mechanism (e.g., Todorov and Jordan 2002; Latash et al. 2005) or on a feedforward mechanism (e.g., Goodman and Latash 2006). Hence, a hierarchy of control levels, where each level functions based on the EP control principle, seems like a plausible control structure leading to motor synergies.
The problem gets a little bit more complicated if one want to incorporate a possibility of muscle co-contraction without changing limb configuration. Co-contraction is an important mechanism of motor control, reflected at the single-joint level by a special command, c-command. Humans can easily co-contract muscles without changing joint position. Assume that state of the endpoint of a multi-joint limb may be described with two commands, one defining its equilibrium position (R) and the other defining its stability about the equilibrium position (C) – equivalent to the {r,c} pair of commands introduced within the EP-hypothesis. An {R, C} pair maps on commands sent to individual joints; the control of a relatively simple joint with one kinematic degree-of-freedom can be described with a pair {r,c}. If a large number of joints define state of the endpoint, a multi-{r,c} synergy may be expected to stabilize required values of R and C. Most human joints, including relatively simple ones (such as the elbow joint), are crossed by more than two muscles. Hence, to define an {r,c} pair, the controller has to arrange a set of λ values for all the muscles. This is another typical problem of redundancy, and it makes sense to assume that the controller arranges a multi-λ synergy that stabilizes required values of the {r,c} pair.
Criticisms of the EP-hypothesis
The EP-hypothesis was introduced in the middle 1960th, at the time of active research and major discoveries in the filed of neurophysiology, in particular of the spinal cord. Those studies formed the foundation for the dominant view that the CNS was very complex and could not be understood without a meticulous analysis of all its constituent neural pathways. In contrast, the EP-hypothesis suggested that the neural control of a muscle could be described with just one variable, λ. Many decorated researchers brushed it away as something not worth arguing about, something too simplistic and formal to describe neural processes within the very-very complex human body. Very few papers were published by Anatol Feldman and his colleagues over the first 10 years of the EP-hypothesis, partly because journals in the USSR controlled by the establishment did not accept manuscripts presenting such a non-traditional view on the control of movements.
After the EP-hypothesis seeped through the Iron Curtain to the West, it attracted attention of several prominent researchers including Emilio Bizzi, Peter Greene, Scott Kelso, Richard Schmidt, and Michael Turvey (Kelso and Holt 1980; Kelso et al. 1980; Schmidt and McGown 1980; Bizzi et al. 1982; Greene 1982;). However, many others viewed this hypothesis with suspicion. Its original formulation created an impression of a mass-spring model that seemed to have limited applicability, maybe only to postural tasks, very slow movements, and only to mechanical variables. At that time, the common pattern of criticisms was as follows: The EP-hypothesis cannot explain a, b, and c based on the fact that no publications addressed a, b, or c using the framework of the EP-hypothesis (a, b, and c could be EMG patterns, fast movements, motor variability, multi-joint movements, movement disorders, differences in muscle activation in isotonic movements and isometric contractions, action of bi-articular muscles, etc.). The researchers who voiced these criticisms did not realize that the EP-hypothesis was developed by only one person, Anatol Feldman, with sporadic help with a handful of colleagues. Only in 1980th and 1990th, most of these questions have been answered showing that the EP-hypothesis can indeed handle those phenomena (reviewed in Latash 1993).
Additional confusion has been added by the formulation of the alpha-model based on a series of now classical experiments on deafferented monkeys demonstrating the existence of an equilibrium trajectory (Polit and Bizzi 1978, 1979; Bizzi et al. 1982). The deafferentation made sure that the monkeys could not sense perturbations and, therefore, they did not react to them – an important condition if one wants to reconstruct torque-angle joint characteristics. However, the deafferentation also eliminated the tonic stretch reflex, which is a crucial element within Feldman's EP-hypothesis. The monkeys learned how to move in the absence of the tonic stretch reflex; however, they were likely to use a different mode of control, adequate for the new state of their spinal cord. The only mechanism available to the deafferented monkeys was direct activation of alpha-motoneuronal pools leading to muscle activation patterns that were independent of muscle length (unlike the intact system). The limbs still behaved in an EP fashion due to the visco-elastic properties of the muscles given their activation levels, which allowed the estimation of equilibrium states and trajectories. Note, however, that the hypothetical control variable changed from λ (as in the original Feldman's formulation, sometimes addressed as the λ-model) to α (level of activation of the alpha-motoneuronal pool). This confusion is still present in some of the publications (e.g., Shadmehr and Wise 2005).
More recently, it has become fashionable to disprove the EP-hypothesis. Such claims have been abundant. A typical scheme is as follows: A simplified version of the hypothesis is accepted, predictions are made, they are falsified in experiments, and a conclusion is drawn that the hypothesis is wrong. In fact, only the simplified version is proven to be wrong. More precisely, the simplified version is shown to have a limited range of applicability, while the experiment went beyond that range. Claims of disproving of the EP-hypothesis have been based on such findings as violations of equifinality (Lackner and DiZio 1994; Hinder and Milner 2003), insufficient joint stiffness (Popescu et al. 2003), complex patterns of equilibrium trajectories (Gomi and Kawato 1996), and all of the above together (Gottlieb 1998). Indeed, most of these results are interpretable within the framework of the EP-hypothesis (Feldman and Latash 2005). For example, equifinality (getting to the same final position when a transient perturbation is applied) is expected from the EP control only under transient load changes, which are not accompanied by changes in the control variables and in any of the steps involved in the transformation of electrical signals to muscles into forces. Most studies of joint stiffness used questionable methods and models (for a detailed review see Latash and Zatsiorsky 1993).
A special species of criticisms is that the EP-hypothesis is not disprovable. As it has already been mentioned, the EP-hypothesis is complex; it is not a single statement. For example, the physical principle of control of mechanical systems with position dependent actuators (muscles) is indeed non-disprovable. The physiological implementation of this principle in the human body is very much disprovable. In fact, about 15 years ago, a group of researchers in the Laboratory of Gerry Gottlieb made predictions with respect to a particular experiment. These predictions were put on paper and signed by the participants. Then, one of the researchers went back to his native Yugoslavia (it still existed in those ancient times!) and performed the study. The EP-hypothesis made more accurate predictions than the dual-strategy hypothesis based on central control of the total presynaptic input into alpha-motoneurnal pools, the so-called “excitation pulse” (Jaric et al. 1994; also see Ilic et al. 1996).
So, are there alternatives to the EP-hypothesis? No and yes. No in a sense that the physical principle underlying the EP-hypothesis leaves no room for alternatives. Yes in a sense that the physiological mechanisms implementing this physical principle are unknown and the current views on those mechanisms may be wrong.
Challenges Facing the EP-hypothesis
Progress of scientific hypotheses depends crucially on development of new experimental approaches. Currently, the EP-hypothesis is in an urgent need of experimental tools that would allow to measure (reconstruct) the hypothetical control signals, λ(t) or {r(t),c(t)}. A number of earlier attempts to reconstruct equilibrium trajectories (Latash and Gottlieb 1991; Latash 1992; Gomi and Kawato 1996) have been rightfully criticized for using inadequately crude models of the peripheral neuromotor system (Gribble et al. 1998). However, no new methods have been developed over the recent years. As a result, the controversial N-shaped equilibrium trajectories do not have a reliably recorded alternative. Until we get good “lambda-meters”, the experimental foundation of the EP-hypothesis will remain limited to specific conditions (such as steady-states), for which having a reliable dynamic model of the moving system is not crucial.
As far as theoretical developments of the EP-hypothesis are concerned, it offers a uniquely attractive framework to unite issues of control and coordination for multi-element systems (as briefly described in the previous section). Studies of the multi-level hierarchies involved in the production of natural movements and analysis of across-levels interactions are new exciting directions of research offered by the cross fertilization of the EP-hypothesis and the recent developments of the notion of motor synergies. In particular, the framework of the uncontrolled manifold hypothesis (UCM hypothesis; Scholz and Schöner 1999; reviewed in Latash et al. 2007) has been until now used to analyze potential synergies in spaces of kinetic, kinematic, and electromyographic variables. Extending this method to control variables such as λs or {r,c} pairs would be a major step forward towards understanding the nature of synergies.
From its very conception, the EP-hypothesis has always been deeply grounded in neurophysiology. However, the number of neurophysiological studies testing the origins of the control signals and mechanisms of their transformation into mechanical variables has been limited. The idea of Feldman that λ may be associated with subthreshold depolarization of alpha-motoneuronal pools (e.g., Feldman 1986) is the only neurophysiological mechanism offered so far to mediate the principle of EP control, a mechanism that has only limited experimental support.
The EP hypothesis can also be applied to analysis of motor disorders and effects of motor rehabilitation. Such studies are few, however. They involve modeling of movements with dystonia within the EP-hypothesis framework (Latash and Gutman 1994) and a hypothesis on the origins of spasticity that views it as a disorder of control over shifts of the muscle force-length characteristics (Levin and Feldman 1994; Jobin and Levin 2000). As in other areas, the slow progress is to a large degree due to the lack of reliable methods of measuring the hypothetical control variables such as {r,c}.
I would like to end this review on an optimistic note. The EP-hypothesis is now viewed by most researchers in the area of motor control as a leading hypothesis in the field. Despite the relatively small number of researchers who have been actively developing the EP-hypothesis, its progress has been very impressive. It has been shown to offer a productive framework for analysis of a variety of phenomena (including motor variability, motor learning, and motor disorders) in a variety of spaces (kinetic, kinematic, and electromyographic). There are many unanswered exciting questions, and all are invited to join the quest for understanding the neural control of movements using the only hypothesis that makes intuitive sense and has deep foundations in both physics and physiology.
Acknowledgments
Supported in part by NIH grants NS-035032 and AG-018751. The author is very much grateful to Dr. Grzegorz Juras and his colleagues for the invitation to participate in the series of conference “Motor Control” in Poland, one of which resulted in this paper.
References
- Bernstein NA. The problem of interrelation between coordination and localization. Archives of Biological Science. 1935;38:1–35. in Russian. [Google Scholar]
- Bernstein NA. On the Construction of Movements. Medgiz; Moscow: 1947. in Russian. [Google Scholar]
- Bernstein NA. The Co-ordination and Regulation of Movements. Pergamon Press; Oxford: 1967. [Google Scholar]
- Bernstein NA. Contemporary Studies on the Physiology of the Neural Process. Smysl; Moscow, Russia: 2003. [Google Scholar]
- Bizzi E, Accornero N, Chapple W, Hogan N. Arm trajectory formation in monkeys. Experimental Brain Research. 1982;46:139–143. doi: 10.1007/BF00238107. [DOI] [PubMed] [Google Scholar]
- Feldman AG. Functional tuning of the nervous system with control of movement or maintenance of a steady posture. II. Controllable parameters of the muscle. Biophysics. 1966;11:565–578. [Google Scholar]
- Feldman AG. Superposition of motor programs. I. Rhythmic forearm movements in man. Neuroscience. 1980;5:81–90. doi: 10.1016/0306-4522(80)90073-1. [DOI] [PubMed] [Google Scholar]
- Feldman AG. Once more on the equilibrium-point hypothesis (λ-model) for motor control. Journal of Motor Behavior. 1986;18:17–54. doi: 10.1080/00222895.1986.10735369. [DOI] [PubMed] [Google Scholar]
- Feldman AG, Adamovich SV, Ostry Dl, Flanagan IR. The origin of electromyograms - explanations based on the equilibrium point hypothesis. In: Winters IM, Woo SL-Y, editors. Multiple Muscle Systems. Springer; Berlin, Heidelberg, New York: 1990. pp. 195–312. [Google Scholar]
- Feldman AG, Goussev V, Sangole A, Levin MF. Threshold position control and the principle of minimal interaction in motor actions. Progress in Brain Research. 2007;165:267–281. doi: 10.1016/S0079-6123(06)65017-6. [DOI] [PubMed] [Google Scholar]
- Feldman AG, Latash ML. Testing hypotheses and the advancement of science: Recent attempts to falsify the equilibrium-point hypothesis. Experimental Brain Research. 2005;161:91–103. doi: 10.1007/s00221-004-2049-0. [DOI] [PubMed] [Google Scholar]
- Feldman AG, Levin MF. Positional frames of reference in motor control: their origin and use. Behavioral and Brain Sciences. 1995;18:723–806. [Google Scholar]
- Feldman AG, Levin MF, Mitnitski AM, Archambault P. 1998 ISEK Congress Keynote Lecture: Multi-muscle control in human movements. Journal of Electromyography and Kinesiology. 1998;8:383–390. doi: 10.1016/s1050-6411(98)00019-4. [DOI] [PubMed] [Google Scholar]
- Gelfand IM, Latash ML. On the problem of adequate language in movement science. Motor Control. 1998;2:306–313. doi: 10.1123/mcj.2.4.306. [DOI] [PubMed] [Google Scholar]
- Gelfand IM, Tsetlin ML. On mathematical modeling of the mechanisms of the central nervous system. In: Gelfand IM, Gurfinkel VS, Fomin SV, Tsetlin ML, editors. Models of the structural-functional organization of certain biological systems. Nauka; Moscow: 1966. pp. 9–26. (1966) (in Russian, a translation is available in 1971 edition by MIT Press: Cambridge MA.) [Google Scholar]
- Gibson JJ. The Ecological Approach to Visual Perception. Houghton Mifflin; Boston, MA: 1979. [Google Scholar]
- Gomi H, Kawato M. Equilibrium-point hypothesis examined by measured arm stiffness during multijoint movement. Science. 1996;272:117–120. doi: 10.1126/science.272.5258.117. [DOI] [PubMed] [Google Scholar]
- Goodman SR, Latash ML. Feedforward control of a redundant motor system. Biological Cybernetics. 2006;95:271–280. doi: 10.1007/s00422-006-0086-4. [DOI] [PubMed] [Google Scholar]
- Gottlieb GL. Rejecting the equilibrium-point hypothesis. Motor Control. 1998;2:10–12. doi: 10.1123/mcj.2.1.10. [DOI] [PubMed] [Google Scholar]
- Gottlieb GL, Corcos DM, Agarwal GC, Latash ML. Principles underlying single-joint movement strategies. In: Winters JM, Woo SL-Y, editors. Multiple Muscle Systems: Biomechanics and Movement Organization. Springer-Verlag; New York e.a.: 1990. pp. 236–250. [Google Scholar]
- Greene PH. Why is it easy to control your arms? Journal of Motor Behavior. 1982;4:260–286. doi: 10.1080/00222895.1982.10735280. [DOI] [PubMed] [Google Scholar]
- Gribble PL, Ostry DJ. Compensation for loads during arm movements using equilibrium-point control. Experimental Brain Research. 2000;135:474–482. doi: 10.1007/s002210000547. [DOI] [PubMed] [Google Scholar]
- Gribble PL, Ostry DJ, Sanguineti V, Laboissiere R. Are complex control signals required for human arm movements? Journal of Neurophysiology. 1998;79:1409–1424. doi: 10.1152/jn.1998.79.3.1409. [DOI] [PubMed] [Google Scholar]
- Hinder MR, Milner TE. The case for an internal dynamics model versus equilibrium point control in human movement. Journal of Physiology. 2003;549:953–963. doi: 10.1113/jphysiol.2002.033845. [DOI] [PMC free article] [PubMed] [Google Scholar]
- Ilic DB, Corcos DM, Gottlieb GL, Latash ML, Jaric S. The effects of practice on movement reproduction: Implications for models of motor control. Human Movement Science. 1996;15:101–114. [Google Scholar]
- Jaric S, Corcos DM, Gottlieb GL, Ilic DB, Latash ML. The effects of practice on movement distance and final position reproduction: Implications for the equilibrium-point control of movements. Experimental Brain Research. 1994;100:353–359. doi: 10.1007/BF00227205. [DOI] [PubMed] [Google Scholar]
- Jobin A, Levin MF. Regulation of stretch reflex threshold in elbow flexors in children with cerebral palsy: a new measure of spasticity. Developmental Medicine and Child Neurology. 2000;42:531–540. doi: 10.1017/s0012162200001018. [DOI] [PubMed] [Google Scholar]
- Kawato M. Internal models for motor control and trajectory planning. Current Opinions in Neurobiology. 1999;9:718–727. doi: 10.1016/s0959-4388(99)00028-8. [DOI] [PubMed] [Google Scholar]
- Kelso JAS, Holt KG. Exploring a vibratory system analysis of human movement production. Journal of Neurophysiology. 1980;43:1183–1196. doi: 10.1152/jn.1980.43.5.1183. [DOI] [PubMed] [Google Scholar]
- Kelso JAS, Holt KG, Kugler PN, Turvey MT. On the concept of coordinative structures as dissipative structures. II. Empirical lines of convergence. In: Stelmach GE, Requin J, editors. Tutorials in Motor Behavior. N.-Holland Publ.Co; Amsterdam: 1980. pp. 49–70. [Google Scholar]
- Lackner JR, DiZio P. Rapid adaptation to Coriolis force perturbations of arm trajectory. Journal of Neurophysiology. 1994;72:1–15. doi: 10.1152/jn.1994.72.1.299. [DOI] [PubMed] [Google Scholar]
- Latash ML. Virtual trajectories, joint stiffness, and changes in natural frequency during single-joint oscillatory movements. Neuroscience. 1992;49:209–220. doi: 10.1016/0306-4522(92)90089-k. [DOI] [PubMed] [Google Scholar]
- Latash ML. Control of Human Movement. Human Kinetics; Urbana, IL: 1993. [Google Scholar]
- Latash ML. Reconstruction of equilibrium trajectories and joint stiffness patterns during single-joint voluntary movements under different instructions. Biological Cybernetics. 1994;71:441–450. doi: 10.1007/BF00198920. [DOI] [PubMed] [Google Scholar]
- Latash ML, Gottlieb GL. Reconstruction of elbow joint compliant characteristics during fast and slow voluntary movements. Neuroscience. 1991;43:697–712. doi: 10.1016/0306-4522(91)90328-l. [DOI] [PubMed] [Google Scholar]
- Latash ML, Gutman SR. Abnormal motor patterns in the framework of the equilibrium-point hypothesis: A cause for dystonic movements? Biological Cybernetics. 1994;71:87–94. doi: 10.1007/BF00198914. [DOI] [PubMed] [Google Scholar]
- Latash ML, Scholz JP, Schöner G. Motor control strategies revealed in the structure of motor variability. Exercise and Sport Science Reviews. 2002;30:26–31. doi: 10.1097/00003677-200201000-00006. [DOI] [PubMed] [Google Scholar]
- Latash ML, Scholz JP, Schöner G. Toward a new theory of motor synergies. Motor Control. 2007;11:275–307. doi: 10.1123/mcj.11.3.276. [DOI] [PubMed] [Google Scholar]
- Latash ML, Shim JK, Smilga AV, Zatsiorsky V. A central back-coupling hypothesis on the organization of motor synergies: a physical metaphor and a neural model. Biological Cybernetics. 2005;92:186–191. doi: 10.1007/s00422-005-0548-0. [DOI] [PMC free article] [PubMed] [Google Scholar]
- Latash ML, Zatsiorsky VM. Joint stiffness: Myth or reality? Human Movement Science. 1993;12:653–692. [Google Scholar]
- Lestienne FG, Thullier F, Archambault P, Feldman AG, Levin MF. Multi-muscle control of head movements in monkeys: the referent configuration hypothesis. Neuroscience Letters. 2000;283:65–68. doi: 10.1016/s0304-3940(00)00923-x. [DOI] [PubMed] [Google Scholar]
- Levin MF, Feldman AG. The role of stretch reflex threshold regulation in normal and impaired motor control. Brain Research. 1994;657:23–30. doi: 10.1016/0006-8993(94)90949-0. [DOI] [PubMed] [Google Scholar]
- Matthews PBC. The dependence of tension upon extension in the stretch reflex of the soleus of the decerebrate cat. Journal of Physiology. 1959;47:521–546. doi: 10.1113/jphysiol.1959.sp006260. [DOI] [PMC free article] [PubMed] [Google Scholar]
- Matthews PBC. The origin and functional significance of the stretch reflex. In: Andersen P, Jansen JKS, editors. Excitatory Synaptic Mechanisms. Universitets forlaget; Oslo, Norway: 1970. pp. 301–315. [Google Scholar]
- Merton PA. Speculations on the servo-control of movements. In: Malcolm JL, Gray JAB, Wolstenholm GEW, editors. The Spinal Cord. Little, Brown; Boston: 1953. pp. 183–198. [Google Scholar]
- Pilon J-F, De Serres SJ, Feldman AG. Threshold position control of arm movement with anticipatory increase in grip force. Experimental Brain Research. 2007;181:49–67. doi: 10.1007/s00221-007-0901-8. [DOI] [PubMed] [Google Scholar]
- Polit A, Bizzi E. Processes controlling arm movements in monkey. Science. 1978;201:1235–1237. doi: 10.1126/science.99813. [DOI] [PubMed] [Google Scholar]
- Polit A, Bizzi E. Characteristics of motor programs underlying arm movemnt in monkey. Journal of Neurophysiology. 1979;42:183–194. doi: 10.1152/jn.1979.42.1.183. [DOI] [PubMed] [Google Scholar]
- Popescu FC, Hidler JM, Rymer WZ. Elbow impedance during goal-directed movements. Experimental Brain Research. 2003;152:17–28. doi: 10.1007/s00221-003-1507-4. [DOI] [PubMed] [Google Scholar]
- Schmidt RA. A schema theory of discrete motor skill learning. Psychological Reviews. 1975;82:225–260. [Google Scholar]
- Schmidt RA, McGown C. Terminal accuracy of unexpected loaded rapid movements: Evidence for a mass-spring mechanism in programming. Journal of Motor Behavior. 1980;12:149–161. doi: 10.1080/00222895.1980.10735215. [DOI] [PubMed] [Google Scholar]
- Scholz JP, Schöner G. The uncontrolled manifold concept: Identifying control variables for a functional task. Experimental Brain Research. 1999;126:289–306. doi: 10.1007/s002210050738. [DOI] [PubMed] [Google Scholar]
- Shadmehr R, Wise SP. The computational neurobiology of reaching and pointing. The MIT Press; Cambridge, MA: 2005. [Google Scholar]
- Stuart DG, Pierce PA, Callister RJ, Brichta AM, McDonagh JC. Sir Charles S. Sherrington : Humanist, mentor, and movement neuroscientist. In: Latash ML, Zatsiorsky VM, editors. Classics in Movement Science. Human Kinetics; Urbana, IL: 2001. pp. 317–374. [Google Scholar]
- Todorov E, Jordan MI. Optimal feedback control as a theory of motor coordination. Nature Neuroscience. 2002;5:1226–1235. doi: 10.1038/nn963. [DOI] [PubMed] [Google Scholar]
- Vallbo A. Discharge patterns in human muscle spindle afferents during isometric voluntary contractions. Acta Physiologica Scandinavica. 1970;80:552–566. doi: 10.1111/j.1748-1716.1970.tb04823.x. [DOI] [PubMed] [Google Scholar]
- Vallbo AB. Muscle spindle response at the onset of isometric voluntary contractions. Time difference between fusimotor and skeletomotor effects. Journal of Physiology. 1971;218:405–431. doi: 10.1113/jphysiol.1971.sp009625. [DOI] [PMC free article] [PubMed] [Google Scholar]
- Von Holst E, Mittelstaedt H. Daz reafferezprincip. Wechselwirkungen zwischen Zentralnerven-system und Peripherie. Naturwiss. 19501973;37:467–476. 1950. [Google Scholar]; The reafference principle. In: Martin R, translator. The Behavioral Physiology of Animals and Man. The Collected Papers of Erich von Holst. Vol. 1. University of Miami Press; Coral Gables, Florida: pp. 139–173.
- Wachholder K, Altenburger H. Do our limbs have only one rest length? Simultaneously a contribution to the measurement of elastic forces in active and passive movements. Pflüg Arch ges Physiol. 1927;215:627–640. [PubMed] [Google Scholar]; Cited after: Sternad D. Foundational experiments for current hypotheses on equilibrium point control in voluntary movements. Motor Control. 2002;6:299–318. doi: 10.1123/mcj.6.4.299.
- Wolpert DM, Miall RC, Kawato M. Internal models in the cerebellum. Trends in Cognitive Science. 1998;2:338–347. doi: 10.1016/s1364-6613(98)01221-2. [DOI] [PubMed] [Google Scholar]
- Zhang W, Scholz JP, Zatsiorsky VM, Latash ML. What do synergies do? Effects of secondary constraints on multi-digit synergies in accurate force-production tasks. Journal of Neurophysiology. 2008;99:500–513. doi: 10.1152/jn.01029.2007. [DOI] [PMC free article] [PubMed] [Google Scholar]