A Reconstruction Algorithm for Breast Cancer Imaging With Electrical Impedance Tomography in Mammography Geometry

Abstract

The conductivity and permittivity of breast tumors are known to differ significantly from those of normal breast tissues, and electrical impedance tomography (EIT) is being studied as a modality for breast cancer imaging to exploit these differences. At present, X-ray mammography is the primary standard imaging modality used for breast cancer screening in clinical practice, so it is desirable to study EIT in the geometry of mammography. This paper presents a forward model of a simplified mammography geometry and a reconstruction algorithm for breast tumor imaging using EIT techniques. The mammography geometry is modeled as a rectangular box with electrode arrays on the top and bottom planes. A forward model for the electrical impedance imaging problem is derived for a homogeneous conductivity distribution and is validated by experiment using a phantom tank. A reconstruction algorithm for breast tumor imaging based on a linearization approach and the proposed forward model is presented. It is found that the proposed reconstruction algorithm performs well in the phantom experiment, and that the locations of a 5-mm-cube metal target and a 6-mm-cube agar target could be recovered at a target depth of 15 mm using a 32 electrode system.

I. INTRODUCTION

Electrical impedance tomography (EIT) is a technique for determining the electrical conductivity and permittivity distribution in the interior of a body from measurements made on its surface. Currents are applied through electrodes placed on the body’s surface and the resulting voltages are measured, or alternatively, voltages can be applied and the resulting currents are measured. The conductivity and permittivity distribution inside the body can be computed from the current and voltage data measured at the electrodes by employing suitable reconstruction algorithms. Examples of medical applications of EIT [1] include monitoring for lung function ([2]–[4]), and cardiac changes ([5], [6]). Two-dimensional and 3-D EIT systems can be found in [7]–[11], and a recent comprehensive review of EIT imaging can be found in [12].

X-ray mammography is the principal standard imaging modality presently used for breast tumor screening in clinical practice. However, there are aspects of mammography showing that improvements are desirable. For example, the sensitivity of mammography was reported to be 74% and the specificity 60% in [13]. About 70%–80% of women who undergo biopsy have benign lesions. Mammograms also require X-ray exposure and they are difficult to interpret with the dense breast tissue common in younger women. Many women avoid mammograms as the breast compression is uncomfortable and sometimes painful.

The conductivity and permittivity of breast tumors have been studied and found to differ significantly from normal breast tissues. Dielectric properties of breast tissues were studied in [14], the impedance of breast tissues was measured in [15]–[17], and impedance measurements were used to distinguish carcinomas from normal and benign tumors in [18]. These findings encourage the investigation of the application of EIT in breast cancer detection. Electrical impedance imaging has been used clinically to screen for breast cancer using a commercial imaging device called T-SCAN [19]. The T-SCAN is an FDA-approved device which uses a hand-held probe carrying a rectangular electrode array. A constant voltage is applied between the probe electrodes and a hand-held ground electrode and the 2-D images of the currents through the electrode array are displayed. A breast cancer imaging system using EIT technology was also reported in [20], where current and voltage measurements on hand held electrodes are used to compute 3-D impedance distributions in the breast. Clinical imaging results of women obtained using a multi-frequency electrical impedance spectroscopy system have been presented in [13], in which a ring-shaped electrode array is placed around the breast, and images of the conductivity and permittivity distribution of the breasts are computed. A review of EIT techniques for breast cancer detection is presented in [21].

These breast imaging algorithms reconstruct the 3-D conductivity of the breast either in half space geometry as in the case of a patient lying supine [19], [20], or in the geometry of the breast hanging freely through an opening in the bed as in the case of patient lying prone [13]. This paper describes an EIT reconstruction algorithm that computes the 3-D distribution of breast conductivity in the mammography geometry and can be used in conjunction with X-ray mammography. The presently accepted standard for breast cancer detection is X-ray mammography. For the purpose of comparing the results from EIT imaging with the X-ray mammograms, it would be highly desirable to use the geometry of X-ray mammography in EIT. If the two imaging modalities used the same geometry, not only would it be easier to analyze the EIT images, but also the EIT images could augment the 2-D X-ray mammograms by providing 3-D images of the tissue being imaged. For this mammography geometry, distinguishability has been studied experimentally in [22], where the performances of various input current/voltage schemes were compared.

The goal of this paper is to propose a forward model of the mammography geometry, and a reconstruction algorithm for breast cancer imaging using that forward model. In Section II, the mammography geometry is modeled as a rectangular box with electrode arrays on the top and bottom planes. A forward model of the electrical impedance imaging problem is derived for a homogeneous conductivity distribution. The proposed forward model is validated in Section III by experiment using a phantom tank. In Section IV, a reconstruction algorithm based on a linearization approach is presented. The imaging results obtained from experimental data collected using the phantom are illustrated in Section V, followed by conclusions.

II. FORWARD MODEL OF A SIMPLIFIED HOMOGENEOUS MAMMOGRAPHY GEOMETRY

In X-ray mammography, the breast is compressed between two radiolucent plates and X-ray images of the breast are taken [23]. A schematic diagram is shown in Fig. 1. In order to image the electrical impedance distribution of the breast, electrodes need to be placed in contact with upper and lower flattened surfaces of the breast. This geometry is modeled as a rectangular box with electrodes on its top and bottom planes. This model considers only the portion of the breast that is placed directly between the two rectangular planes of electrodes. The effects of the chest and the region of the breast outside the box and not in contact with the electrodes are not considered in this simplified model. Currents are applied to the electrodes on the top and bottom electrode planes, and it is assumed that no current can flow through the side walls of the rectangular box.

Fig. 1.

Mammography geometry and its simplified model. (a) In mammography, the breast is flattened by two plates and X-ray images are taken. Electrodes are placed on the top and bottom surfaces for EIT imaging. (b) The mammography geometry is modeled as a box with electrodes on the top and bottom planes.

The electromagnetic field induced by applying a current density to the surface of a body is governed by Maxwell’s equations. At low frequencies and small field strengths, these can be simplified to the generalized Laplace’s equation [24]

$$\begin{array}{l}\nabla ·(\sigma (p)\nabla U(p))=0\text{inside the body B}\hfill \\ B=\{p=(x,y,z)|0\le x\le h_1,0\le y\le h_2,,-h_3\le z\le 0\}.\hfill \end{array}$$ (1)

Here, σ denotes the conductivity distribution, U the voltage inside the body, and h₁, h₂, h₃ the dimensions of the box as illustrated in Fig. 1. The application of currents through the electrodes on the surface S of the body induces a current density distribution whose inward normal component we denote by j.

Mathematically, this can be written as (2), where ν is the outward normal vector at the surface S

$$\begin{array}{cc}\sigma (p)\frac{\partial U(p)}{\partial \nu (p)}=j\hfill & \text{on S}.\hfill \end{array}$$ (2)

When the body has a homogeneous conductivity distribution σ(p) = σ₀, the expression (1) is reduced to

$$\begin{array}{cc}{\nabla }^{2}U(x,y,z)=0,\hfill & 0\le x\le h_1,0\le y\le h_2,,-h_3\le z\le 0,\hfill \end{array}$$ (3)

Application of currents through the electrodes of the top plane, where z = 0, induces a current density distribution at the top plane, denoted by j^t and can be written as

$${\sigma }_0\frac{\mathit{\text{dU}}(x,y,0)}{\mathit{\text{dz}}}=j^t(x,y).$$ (4)

The superscript t implies the top plane, and b implies the bottom plane. The current density distribution at the bottom plane, j^b, where z = −h ₃, can be written as

$${\sigma }_0\frac{\mathit{\text{dU}}(x,y,-h_3)}{d(-z)}=j^b(x,y).$$ (5)

Since there is no current flowing through the side walls, we can write four other boundary conditions of the problem

$$\begin{array}{ccc}{\sigma }_0\frac{\mathit{\text{dU}}(0,y,z)}{\mathit{\text{dx}}}=0\hfill & \text{and}\hfill & {\sigma }_0\frac{\mathit{\text{dU}}(h_1,y,z)}{\mathit{\text{dx}}}=0\hfill \end{array}$$ (6)

$$\begin{array}{ccc}{\sigma }_0\frac{\mathit{\text{dU}}(x,0,z)}{\mathit{\text{dy}}}=0\hfill & \text{and}\hfill & {\sigma }_0\frac{\mathit{\text{dU}}(x,h_2,z)}{\mathit{\text{dy}}}=0.\hfill \end{array}$$ (7)

The forward problem in EIT is to predict the voltages on the surface of a body given any current density distribution on the surface and conductivity distribution inside the body. A variety of methods can be used to solve the Laplace’s equation in (3). The finite element method, for example, can be used when a complex geometry is involved ([25], [26]). In this paper, we show that the simple method of separation of variables can be used to solve this problem and the resulting solution is in good agreement with the experimental results. From (3), we can write

$$U_{\mathit{\text{xx}}}+U_{\mathit{\text{yy}}}+U_{\mathit{\text{zz}}}=0.$$ (8)

Here, U_xx denotes the second partial derivative of U with respect to x, U_yy the second partial derivative with respect to y, etc. We look for a solution of the form

$$U(x,y,z)=X(x)Y(y)Z(z).$$ (9)

Hence, from (8) and (9), we get

$$X_{\mathit{\text{xx}}}\mathit{\text{YZ}}+X{Y}_{\mathit{\text{yy}}}Z+\mathit{\text{XY}}{Z}_{\mathit{\text{zz}}}=0.$$ (10)

Dividing both sides of (10) by X(x)Y(y)Z(z), and rearranging the terms, we get an expression in the form of X_xx/X = constant. Using the boundary condition (6), we get

$$X_n(x)=\text{cos}(n\pi x/h_1),n=0,1,2,\cdots .$$ (11)

Similarly, the solution for Y(y) can be obtained using the boundary condition (7), and Z(z) is obtained by solving $Z_{\mathit{\text{zz}}}/Z={\gamma }_{n,m}^2$ where ${\gamma }_{n,m}=\sqrt{{(n\pi /h_1)}^2+{(m\pi /h_2)}^2}$

$$\begin{array}{cc}{Y}_m(y)=\text{cos}(m\pi y/h_2),\hfill & m=0,1,2,\cdots \hfill \end{array}$$ (12)

$$\{\begin{array}{cc}{Z}_{n,m}(z)=\hfill & A_{n,m}\text{cosh}{\gamma }_{n,m}z\hfill \\ \hfill & +B_{n,m}\text{sinh}{\gamma }_{n,m}z,n\ne 0,m\ne 0.\hfill \\ Z_{0,0}(z)=\hfill & A_{0,0}+B_{0,0}z\hfill \end{array}$$ (13)

Summarizing the above we get (14), shown at the bottom of the page. The constants A_n,m and B_n,m are to be determined. A general solution for the voltage is given by

$$\{\begin{array}{c}{U}_{n,m}(x,y,z)=(A_{n,m}\text{cosh}{\gamma }_{n,m}z+B_{n,m}\text{sinh}{\gamma }_{n,m}z)·\text{cos}(n\pi x/h_1)\text{cos}(m\pi y/h_2),n\ne 0,m\ne 0\hfill \\ U_{0,0}(x,y,z)=A_{0,0}+B_{0,0}z\hfill \end{array}$$ (14)

$$\begin{array}{cc}U(x,y,z)\hfill & ={\displaystyle \sum _{\begin{array}{l}n=0,m=0\hfill \\ n+m\ne 0\hfill \end{array}}^{\infty }{U}_{n,m}(x,y,z)}\hfill \\ \hfill & =A_{0,0}+B_{0,0}z\hfill \\ \hfill & +{\displaystyle \sum _{\begin{array}{l}n=0,m=0\hfill \\ n+m\ne 0\hfill \end{array}}^{\infty }[A_{n,m}\text{cosh}{\gamma }_{n,m}z+B_{n,m}\text{sinh}{\gamma }_{n,m}z]}\hfill \\ \hfill & \times \text{cos}\left(\frac{n\pi x}{h_1}\right)\text{cos}(\frac{m\pi y}{h_2}).\hfill \end{array}$$ (15)

From (4) and (15)

$$\begin{array}{l}{\sigma }_0\left[B_{0,0}+{\displaystyle \sum _{\begin{array}{l}n=0,m=0\hfill \\ n+m\ne 0\hfill \end{array}}^{\infty }{\gamma }_{n,m}{B}_{n,m}\text{cos}\left(\frac{n\pi x}{h_1}\right)\text{cos}\left(\frac{m\pi y}{h_2}\right)}\right]\hfill \\ \hfill =j^t(x,y).\end{array}$$ (16)

Multiplying cos(ñπx/h ₁) cos(m̃πy/h ₂) to both sides of (16) and taking the integral over 0 ≤ x ≤ h ₁, 0 ≤ y ≤ h ₂, we obtain B_n,m so that the current density at the top plane in (16) can be written in a Fourier series expansion form

$$j^t(x,y)={\displaystyle \sum _{n=0}^{\infty }{\displaystyle \sum _{m=0}^{\infty }{j}_{n,m}^t\text{cos}\left(\frac{n\pi x}{h_1}\right)\text{cos}\left(\frac{m\pi y}{h_2}\right)}}$$ (17)

where

$$\begin{array}{l}{j}_{n,m}^t=\frac{4}{h_1{h}_2}{\displaystyle \underset{0}{\overset{h_1}{\int }}}{\displaystyle \underset{0}{\overset{h_2}{\int }}}\text{cos}\frac{n\pi x}{h_1}\text{cos}\frac{m\pi y}{h_2}{j}^t(x,y)dxdy,\hfill \\ \mathrm{n},\mathrm{m}=1,2,3\dots \hfill \\ j_{0,0}^t=\frac{1}{h_1{h}_2}{\displaystyle \underset{0}{\overset{h_1}{\int }}}{\displaystyle \underset{0}{\overset{h_2}{\int }}}{j}^t(x,y)dxdy\hfill \\ j_{0,m}^t=\frac{2}{h_1{h}_2}{\displaystyle \underset{0}{\overset{h_1}{\int }}}{\displaystyle \underset{0}{\overset{h_2}{\int }}}\text{cos}\frac{m\pi y}{h_2}{j}^t(x,y)dxdy\hfill \\ j_{n,0}^t=\frac{2}{h_1{h}_2}{\displaystyle \underset{0}{\overset{h_1}{\int }}}{\displaystyle \underset{0}{\overset{h_2}{\int }}}\text{cos}\frac{n\pi x}{h_1}{j}^t(x,y)dxdy\hfill \end{array}.$$

Let the current density distribution at the bottom plane be written in the similar form

$$j^b(x,y)={\displaystyle \sum _{n=0}^{\infty }{\displaystyle \sum _{m=0}^{\infty }{j}_{n,m}^b\text{cos}\left(\frac{n\pi x}{h_1}\right)\text{cos}\left(\frac{m\pi y}{h_2}\right)}}.$$ (18)

From (5) and (15)

$$\begin{array}{c}{j}^b(x,y)\hfill \\ =-\{{\sigma }_0{B}_{0,0}+{\sigma }_0{\displaystyle \sum _{\begin{array}{l}n=0,m=0\hfill \\ n+m\ne 0\hfill \end{array}}^{\infty }[{\gamma }_{n,m}{A}_{n,m}\text{sinh}{\gamma }_{n,m}(-h_3)}\hfill \\ \hfill +{\gamma }_{n,m}{B}_{n,m}\text{cosh}{\gamma }_{n,m}(-h_3)]\\ ·\text{cos}\left(\frac{n\pi x}{h_1}\right)\text{cos}\left(\frac{m\pi y}{h_2}\right).\}\hfill \end{array}$$ (19)

Comparing (18) and (19), we obtain A_n,m when n + m ≠ 0, and the voltage can be expressed as

$$\begin{array}{cc}U(x,y,z)\hfill & =\frac{j_{0,0}^t}{{\sigma }_0}z+{\displaystyle \sum _{\begin{array}{l}n=0,m=0\hfill \\ n+m\ne 0\hfill \end{array}}^{\infty }\frac{1}{{\sigma }_0{\gamma }_{n,m}}}\hfill \\ \hfill & \times \left(j_{n,m}^t\frac{\text{cosh}{\gamma }_{n,m}(z+h_3)}{\text{sinh}{\gamma }_{n,m}{h}_3}+j_{n,m}^b\frac{\text{cosh}{\gamma }_{n,m}z}{\text{sinh}{\gamma }_{n,m}{h}_3}\right)\hfill \\ \hfill & ·\text{cos}\left(\frac{n\pi x}{h_1}\right)\text{cos}\left(\frac{m\pi y}{h_2}\right).\hfill \end{array}$$ (20)

In the above equation, A _0,0 was set to zero, since it is a ground voltage.

Computation of the current density from the applied electrode current requires an electrode model. In this study, the “ave-gap model” ([27]) is used, which approximates the current density j(x,y) by

$$j(x,y)=\{\begin{array}{cc}{I}_l/A_l,\hfill & \text{for}(x,y)\text{on}{e}_l\hfill \\ 0,\hfill & \text{otherwise}\hfill \end{array}$$ (21)

$$V_l=\frac{1}{A_l}{\displaystyle \underset{e_l}{\int }U(s)\mathit{\text{ds}}}$$ (22)

where I_l is the current applied to the Ith electrode e_l, A_l is the surface area of e_l, and V_l is the voltage of the Ith electrode. The mathematical model of the electrode used here does not include the shunting effect [27] of the electrode nor the contact impedance between the electrode and the electrolyte. A model that does include these effects can be found in [27] and [28].

The current density on the top and bottom planes, j^t(x, y) and j^b(x, y) in (17) and (18), can be computed using (21) as follows. The superscript * stands for either t or b

$$j^{*}(x,y)={\displaystyle \sum _{n=0}^{\infty }{\displaystyle \sum _{m=0}^{\infty }{j}_{n,m}^{*}\text{cos}\left(\frac{n\pi x}{h_1}\right)\text{cos}\left(\frac{m\pi y}{h_2}\right)}}$$ (23)

where

$$\begin{array}{c}\begin{array}{l}{j}_{n,m}^{*}=\frac{4}{h_1{h}_2}{\displaystyle \sum _{l={\alpha }^{*}}^{{\beta }^{*}}\frac{I_l}{A_l}{\displaystyle \int }{\displaystyle \underset{e_l}{\int }}\text{cos}\frac{n\pi x}{h_1}\text{cos}\frac{m\pi y}{h_2}\mathit{\text{dxdy}},}\hfill \\ n,m=1,2,3,\cdots \hfill \end{array}\hfill \\ j_{0,0}^{*}=\frac{1}{h_1{h}_2}{\displaystyle \sum _{l={\alpha }^{*}}^{{\beta }^{*}}{I}_l}\hfill \\ j_{0,m}^{*}=\frac{2}{h_1{h}_2}{\displaystyle \sum _{l={\alpha }^{*}}^{{\beta }^{*}}\frac{I_l}{A_l}{\displaystyle \int }{\displaystyle \underset{e_l}{\int }}\text{cos}\frac{m\pi y}{h_2}dxdy}\hfill \\ j_{n,0}^{*}=\frac{2}{h_1{h}_2}{\displaystyle \sum _{l={\alpha }^{*}}^{{\beta }^{*}}\frac{I_l}{A_l}{\displaystyle \int }{\displaystyle \underset{e_l}{\int }}\text{cos}\frac{n\pi y}{h_1}dxdy}\hfill \end{array}$$

where a^t = 1, b^t = N^t, a^b = N^t + 1, b^b = N^t + N^b, N^t denotes the number of electrodes on the top plane, and N^b the number of electrodes in the bottom plane. The integrals in (23) can be computed if the electrode geometry of e_l is given. Let the current densities j^t and j^b induced by the kth current vector I^k be denoted as j^tk and j^bk, respectively, the voltage inside the body induced by I^k as U^k. Let (x_lc, y_lc) denote the x – y coordinate of the center of the lth electrode, and Δx, Δy the dimensions of the electrode. The voltage of the lth electrode when the kth current vector I^k is applied to the homogeneous tank, $V_{l,0}^k$, is given from (22) as follows. If the electrode is on the top plane

$$\begin{array}{cc}{V}_{l,0}^k\hfill & =\frac{1}{A_l}{\displaystyle \int }{\displaystyle \underset{e_l}{\int }{U}^k(x,y,z=0)\mathit{\text{dxdy}}}\hfill \\ \hfill & =\frac{1}{A_l}{\displaystyle \sum _{\begin{array}{l}n=0,m=0\hfill \\ n+m\ne 0\hfill \end{array}}^{\infty }\frac{1}{{\sigma }_0{\gamma }_{n,m}}\left(\frac{j_{n,m}^{\mathit{\text{tk}}}}{\text{tanh}{\gamma }_{n,m}{h}_3}+\frac{j_{n,m}^{\mathit{\text{bk}}}}{\text{sinh}{\gamma }_{n,m}{h}_3}\right)}\hfill \\ \hfill & \times {\displaystyle \int }{\displaystyle \underset{e_l}{\int }}\text{cos}\left(\frac{n\pi x}{h_1}\right)\text{cos}\left(\frac{m\pi y}{h_2}\right)\mathit{\text{dxdy}}.\hfill \end{array}$$ (24)

If the electrode is on the bottom plane, the voltage of the lth electrode is given by

$$\begin{array}{cc}{V}_{l,0}^k\hfill & =\frac{1}{A_l}{\displaystyle \int }{\displaystyle \underset{e_l}{\int }}{U}^k(x,y,z=-h_3)\mathit{\text{dxdy}}\hfill \\ \hfill & =\frac{-j_{0,0}^{\mathit{\text{tk}}}{h}_3}{{\sigma }_0}+\frac{1}{A_l}{\displaystyle \sum _{\begin{array}{l}n=0,m=0\hfill \\ n+m\ne 0\hfill \end{array}}^{\infty }\frac{1}{{\sigma }_0{\gamma }_{nm}}}\hfill \\ \hfill & \times \left(\frac{j_{n,m}^{\mathit{\text{tk}}}}{\text{sinh}{\gamma }_{n,m}{h}_3}+\frac{j_{n,m}^{\mathit{\text{bk}}}}{\text{tanh}{\gamma }_{n,m}{h}_3}\right)\hfill \\ \hfill & ·{\displaystyle \int }{\displaystyle \underset{e_l}{\int }}\text{cos}\left(\frac{n\pi x}{h_1}\right)\text{cos}\left(\frac{m\pi y}{h_2}\right)\mathit{\text{dxdy}}\hfill \end{array}$$ (25)

where

$$\begin{array}{c}{\displaystyle \int }{\displaystyle \underset{e_l}{\int }}\text{cos}\frac{n\pi x}{h_1}\text{cos}\frac{m\pi y}{h_2}\mathit{\text{dxdy}}\hfill \\ ={\displaystyle \underset{y_{lc}-\mathrm{\Delta }y/2}{\overset{y_{lc}+\mathrm{\Delta }y/2}{\int }}}{\displaystyle \underset{x_{lc}-\mathrm{\Delta }x/2}{\overset{x_{lc}+\mathrm{\Delta }x/2}{\int }}}\text{cos}\frac{n\pi x}{h_1}\text{cos}\frac{m\pi y}{h_2}\mathit{\text{dxdy}}\hfill \\ =\frac{h_1{h}_2}{\mathit{\text{nm}}{\pi }^2}2\text{cos}\frac{m\pi y_{lc}}{h_2}\text{sin}\frac{m\pi \mathrm{\Delta }y}{2h_2}2\text{cos}\frac{n\pi x_{lc}}{h_1}\text{sin}\frac{n\pi \mathrm{\Delta }x}{2h_1}.\hfill \end{array}$$

III. VALIDATION OF THE FORWARD MODEL BY EXPERIMENT

A. Test Tank

The forward solution in (24) and (25) was validated by comparing the electrode voltages predicted by the model with experimental results obtained using a test tank. The test tank (Fig. 2) is filled with 0.350 S/m saline solution and simulates a homogenous body. It is made of plexiglass and has the inner dimensions 50 mm (W) × 50 mm (D) × 50 mm (H). The height is determined by the level of the saline solution. Planar electrode arrays are located on the left and right side walls in the figure, which correspond to the top and bottom electrode arrays in Fig. 1. Each electrode plane consists of a 4 × 4 array of copper electrodes fabricated on a printed circuit board. The total number of electrodes is 32; each electrode dimensions is 10 mm × 10 mm and the gap between them is 2 mm. The conductivity of the saline solution was chosen to approximate that of healthy breast tissue. No target was used in this model-validation experiment since the homogenous body is being studied. The dimensions of the test tank were chosen to be close to the depth of an ACR mammographic accreditation phantom which is 45 mm high.

Fig. 2.

Phantom used in the experiment. A target is suspended inside the tank.

B. Comparison of the Electrode Voltages

The ACT3 system ([6], [7]) was used in this experiment to apply the currents and measure the voltage data. ACT3 has been used extensively to image ventilation and perfusion of human subjects. This instrument can apply independent currents to 32 electrodes, and measure 32 electrode voltages. Since it is known that the current patterns that maximize the voltages correspond to the eigenfunctions of the current-to-voltage map [29] and [30], we compute the eigenfunctions for a homogenous medium and apply them as current patterns to the electrodes.

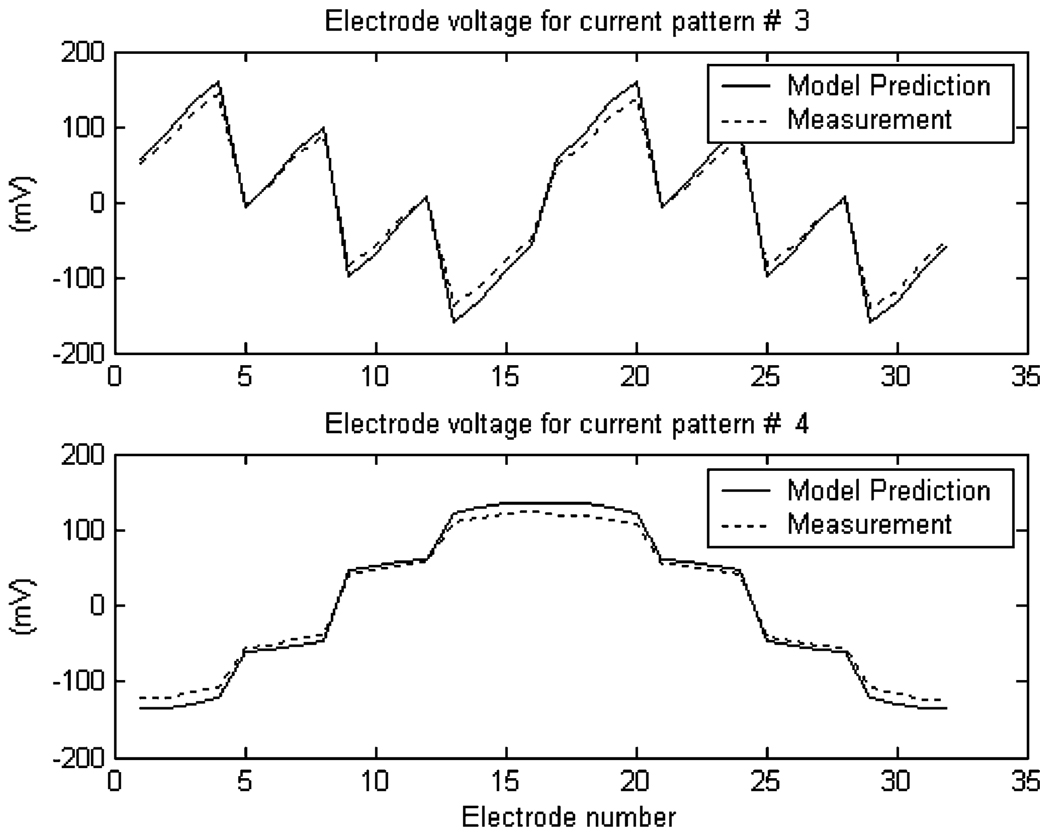
In the forward model of the mammography geometry given in (24) and (25), the infinite series ${\displaystyle {\sum }_{n=0,m=0,n+m\ne 0}^{\infty }(·)}$ must be approximated by a finite series ${\displaystyle {\sum }_{n=0,n+m\ne 0}^{N-1}{\displaystyle {\sum }_{m=0}^{M-1}(·)}}$ during the computation. In this section, N = M = 280 was used as it was the highest number that could be practically used in the computation using MATLAB. The electrode voltages predicted by the model are compared with the experimental data. For each current pattern, the forward model proposed in this paper was used to predict the electrode voltages. The same current pattern was applied to the experimental tank using ACT3, and the resulting electrode voltages were measured. From the voltage data sets that were measured, two sets of data are presented in Fig. 3.

Fig. 3.

Comparison of the electrode voltages predicted by the model with measurement data.

In order to provide a quantitative measure of the error in the forward model, the average error between the predicted and the measured voltages was computed. Let $V_j^i$ denote the predicted voltage of the j-th electrode, and ${\tilde{V}}_j^i$ denote the measured voltage. The average prediction error for the electrode voltages can be computed as an average of ${|({\tilde{V}}_j^i-V_j^i)/V_j^i|}_{V_j^i\ne 0}$ for i = 1, 2,…, 31, and j = 1, 2,…, 32, and was found to be 11.9%. The prediction error can be attributed to the inaccuracy of the ave-gap electrode model in (21), which omits the shunting effect of the electrodes and the contact impedance between electrode and electrolyte.

IV. RECONSTRUCTION ALGORITHM

In this section, the linearization approach used in [24] is applied to the mammography geometry presented in Section II. The k-th applied current vector and the k-th measured voltage vector for all the electrodes can be represented by $I^k={[I_1^k{I}_2^k{I}_3^k\cdots I_L^k]}^T$ and $V^k={[V_1^k{V}_2^k{V}_3^k\cdots V_L^k]}^T$, k = 1,2,…, K, where K is the number of applied current vectors and L is the number of electrodes. From (1) and (2), we can write

$$\nabla ·\sigma \nabla U^k=0\text{\hspace{1em} inside the body}B.$$ (26)

$$\sigma \frac{\partial U^k}{\partial \nu }=j^k\text{\hspace{1em} on}S$$ (27)

where U^k is the voltage inside the body and j^k is the current density on the surface induced by the k-th applied current I^k.

The reconstruction algorithm is based on the assumption that the spatially varying conductivity σ differs only slightly from a constant σ₀ by a perturbation η that is small in magnitude relative to σ₀, so that

$$\sigma (p)={\sigma }_0+\eta (p),p\in B,|\eta (p)|\ll {\sigma }_0.$$ (28)

Let U ₀(p) denote the voltage inside the body when the body is homogenous with the conductivity σ₀. It was shown in [24] that the perturbation η can be expressed as a linear combination of basis functions Φ_r, r = 1, 2, ⋯, N, and an approximate solution can be obtained under the assumption that the conductivity inside each voxel is constant

$$\eta (p)={\displaystyle \sum _{r=1}^N{\eta }_r{\mathrm{\Phi }}_r(p).}$$ (29)

In this paper, the body B was subdivided into a set of rectangular voxels ${\{B_r\}}_{r=1}^N$ as shown in Fig. 1(b), so that $B={\cup }_{r=1}^N{B}_r$. The basis function is

$${\mathrm{\Phi }}_r(p)=\{\begin{array}{cc}1,\hfill & \text{if}p\in B_r\hfill \\ 0,\hfill & \text{otherwise}\hfill \end{array}$$ (30)

and η_r is the voxel conductivity which is computed as follows. Details are described in [24]

$${\displaystyle \sum _{r=1}^N{A}_{x,k,r}{\eta }_r=D_{x,k},x,k=1,2,\cdots ,K}$$ (31)

where

$$A_{x,k,r}={\displaystyle \underset{B}{\int }{\mathrm{\Phi }}_r(p)\nabla U_0^x·\nabla U_0^k\mathit{\text{dp}}}$$ (32)

$$D_{x,k}={\displaystyle \sum _{l=1}^L{I}_l^k{V}_{l,0}^x-I_l^x{V}_l^k}.$$ (33)

Note that the right side of (33) consists of current and voltage data: $I_l^x$ is the lth electrode current for the xth current pattern, $V_{l,0}^x$ is the lth electrode voltage for the xth current pattern when the body is homogenous with the conductivity σ₀, and $V_l^k$ is the voltage measurement for an unknown conductivity σ = σ(p). The linear system in (31) can be rearranged in a matrix-vector multiplication form.

$$A\overrightarrow{\eta }=\overrightarrow{D}$$ (34)

where A is a K ² × N matrix, η⃗ is a N × 1 vector, and D⃗ is a K ² × 1 vector.

The voxel configuration consists of 8 layers with 8 × 8 voxels in each layer, hence the total number of voxels is N = 512. Let the rth voxel be defined by a rectangular box centered at (x_r, y_r, z_r) with dimensions δx, δy, and δz so that

$$\begin{array}{c}{B}_r=\{\left(x,y,z\right)|x_r-\frac{\delta x}{2}\le x\le x_r+\frac{\delta x}{2},\hfill \\ y_r-\frac{\delta y}{2}\le y\le y_r+\frac{\delta y}{2},z_r-\frac{\delta z}{2}\le z\le z_r+\frac{\delta z}{2}\}.\hfill \end{array}$$

From (20), (30) and, (32), we can compute A_{x, k, r}. Complete equations are described in the Appendix.

The conductivities of the voxels can be computed by solving the linear equation (34), once the matrix A and the data vector D⃗ are obtained. Since the matrix A is generally ill-conditioned, this linear system is solved by regularizing the matrix A. In this paper, the regularization scheme in the NOSER algorithm [31] and [32] is used, so that we solve the linear system

$$[A^{T}A+\epsilon \mathit{\text{Diag}}(A^{T}A)]\eta =A^{T}D$$ (35)

where ε is a small regularization parameter, and ε = 0.01 was used in this work. The conductivity of the saline in the phantom was used as the constant conductivity approximation σ₀. The number of current patterns applied to the electrodes is K = 31.

The reconstruction algorithm can be summarized as follows.

• Step 1)

  Compute the entries A_x,k,r using (37).

• Step 2)

  Apply currents ${\{I_l^k\}}_{k=1}^{L-1}$ and measure voltage data ${\{V_l^k\}}_{k=1}^{L-1}$ on electrodes e_l, l = 1, 2, · · ·, L, and k = 1, 2,…, K.

• Step 3)

  Compute the components of D_x,k using (33).

• Step 4)

  Solve the regularized linear equation in (35) for ${\{{\eta }_r\}}_{r=1}^N$

• Step 5)

  Compute the conductivity of the voxels σ_r = σ₀+η_r and display the result.

V. PHANTOM EXPERIMENT RESULTS

A. Voxel and Target Description

The reconstruction algorithm was tested using the phantom shown in Fig. 2. The phantom was filled with a 0.37 Siemens/meter saline solution. The voxel configuration used in the experiment consists of 8 layers with 8 × 8 voxels in each layer (Fig. 1), hence the dimensions of each voxel is 6.25 × 6.25 × 6.25 mm. Voxel layer 1 is adjacent to the top electrode array. Two targets were tested in the experiment: a 5-mm cube made of metal (solder) of conductivity 6.7 × 10⁶ S/m, and a 6-mm cube of agar target of conductivity 0.90 S/m. The conductivity of the agar was chosen to be about 2.5 times that of the saline, and was meant to represent the conductivity of cancer tissue. Each target was suspended in the phantom using a thin insulated rod as shown in Fig. 2. The electrode voltages ${\{V_{l,0}^k\}}_{k=1}^{L-1}$ were measured from the homogeneous tank without the target.

To study the spatial resolution of the reconstruction algorithm in the X-Y plane parallel to the electrode arrays, four locations A~D shown in Fig. 4(a) were tested while depth along the Z axis was fixed at the depth of position 1 shown in Fig. 4(b). Location A is directly beneath an electrode, location B is directly beneath the gap between two adjacent electrodes, location C is directly beneath the gap between four adjacent electrodes, and location D is beneath an electrode at the corner. To study the spatial resolution in the Z direction, the depths of positions 1 to 6 shown in Fig. 4(b) were tested at location A in the X-Y plane. The distances from the electrode to the upper surface of the target at position 1 to position 6 are 6, 9, 12, 15, 18, and 21 mm, respectively. The figure shows the layer that is occupied by the target at each position. For example, at position 2, 70% of the 5-mm agar target occupies layer 2 and 30% of the target occupies layer 3. For convenience, target location is represented by a letter-number pair. For example, A-3 implies a target location where its position in X-Y plane is A, and its position in Z axis is position 3. Note that since the phantom is symmetrical, it is sufficient to test the target locations in one quadrant of voxel layers and one half of the phantom depth, i.e., from layer 1 to layer 4.

Fig. 4.

Target locations. (a) Target positions in the X-Y plane. Four positions, A~D are tested. (b) Target positions in Z-axis.

B. Reconstructed Images of Metal Target

The 5-mm metal target was positioned at location A-1, and the reconstruction algorithm was used to compute the conductivities of the voxels. The true image of the voxels is computed and shown in Fig. 5. The four voxels occupied by the target in layer 2 have equivalent conductivity of 8 × 10⁵ S/m, while all other voxels have the conductivity close to that of the saline, since the 5-mm metal target is almost entirely inside layer 2 (see Fig. 4). The reconstructed images in Fig. 5 show the target at the correct location in layer 2. The ringing effect caused by the high conductivity of the target exists in other voxel layers. The reconstruction results of the target at location B-1 are also shown in the same figure. In the true conductivity image, the target shown in layer 2 corresponds to the position B in Fig. 4(a). The reconstructed image shows the target at the correct location. However, the image shows increased blurring and the voxel conductivity is lower compared to the results for the location A-1. This difference is attributed to the difference in the target locations. In the location A-1, the target is directly beneath an electrode, while in the location B-1, the target is beneath the gap between two adjacent electrodes. The recovered target image is sharper when the target is directly beneath an electrode.

Fig. 5.

Metal target (5 mm) reconstruction results. Target is located at A-1 and B-1. The conductivity of the voxels are shown. The number above each voxel layer is the layer number. The gray scale for the true image is 0 ~ 8×l0⁵S/m and the gray scale for the reconstructed image is 0.35~0.45 S/m.

The result shows that the locations of the targets are recovered well at the different target positions. Note that the numerical value of the reconstructed voxel conductivity is between 0.35 S/m and 0.45 S/m while the true value is much higher. This is the consequence of the assumption (28) that the spatially varying conductivity σ differs only slightly from a constant σ₀. Since the target conductivity is extremely high compared to that of the saline, assumption (28) is not satisfied, and there is a large discrepancy between the true and the reconstructed conductivity values.

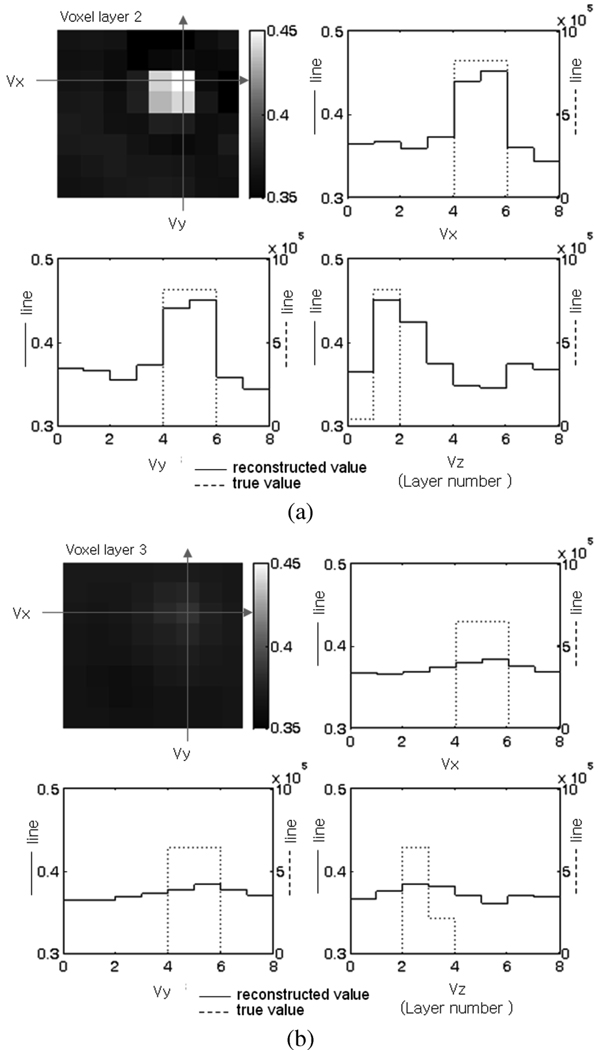
The reconstruction results of the 5-mm cube metal target at different depths in Z axis are shown in Fig. 6. The target is moved to locations A-1, A-2, A-3, and A-4, so that it occupies different voxel layers as shown in Fig. 4(b). For convenient comparison of the reconstructed conductivity with the true value, a cross sectional view of the voxel layers is used for illustration. The three axes passing through the voxel of the highest conductivity value in the reconstructed image are defined as V_x, V_y, and V_z, respectively, and the line plots of the true and reconstructed conductivities along the three axes are shown. The image of the layer which contains the voxel of the highest conductivity is shown in the upper left plot. Fig. 6(a) shows the result when the target is at location A-1. The voxel with the highest conductivity is in layer 2. The solid line is the reconstructed conductivity and is drawn on the left vertical scale. The dotted line is the true conductivity and is drawn on the right vertical scale. The horizontal axis represents the voxel number along V_x, V_y, or V_z axis, respectively and varies from 1 to 8. It can be seen that the target location is recovered well in V_x, V_y, and V_z directions. The result for the 5-mm metal target at A-4 in Fig. 6(b) shows that the reconstructed voxel conductivity decreases as the target moves away from the electrode plane, and it becomes increasingly difficult to distinguish the target location. The location of the target could still be recovered at location A-4, where the depth of target is 15 mm. When the target was further away from the electrodes as in location A-5 and A-6, it was difficult to determine its location with certainty.

Fig. 6.

Metal target reconstruction results. Cross sectional view of the voxel conductivity is shown. (a) Target location A-1. (b) Target location A-4. (Unit: S/m).

C. Reconstructed Images of Agar Target

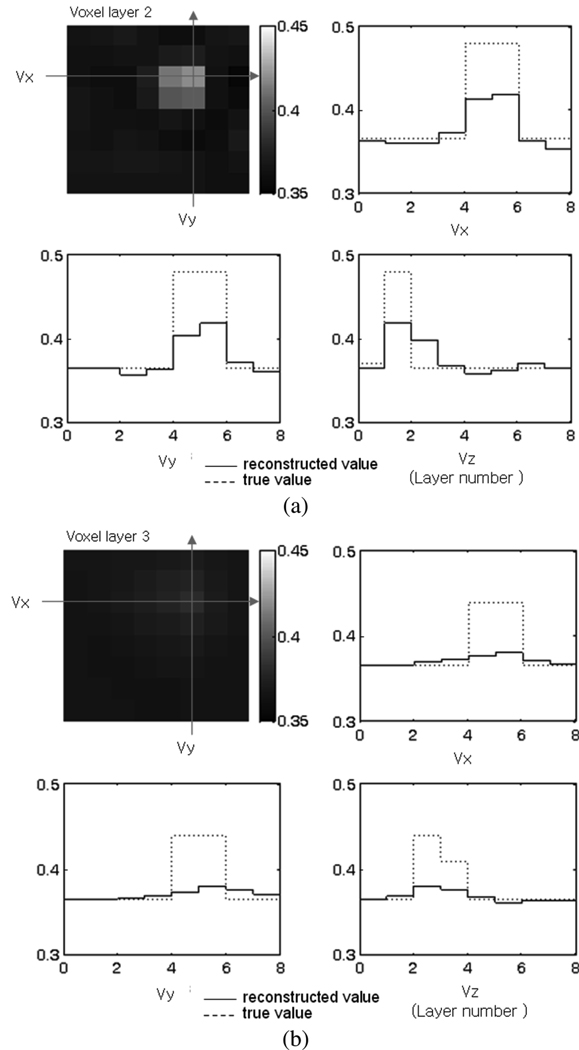
The reconstruction results of the 6-mm cube agar target at locations A-1 and A-4 are presented in Fig. 7. The figures show that the target locations are recovered well, up to the depth of 15 mm from the electrodes [Fig. 7(b)]. The magnitude of the reconstructed voxel conductivity is in better agreement with the true voxel conductivity compared to the results from the metal targets. The peak voxel conductivity in the reconstructed image in Fig. 7(a) is 0.420 S/m, while the true value is 0.485 S/m. This improvement is the consequence of the agar target conductivity (0.901 S/m) being closer to the background conductivity (0.370 S/m than the metal target (6.7 × 10⁶ S/m).

Fig. 7.

Agar target reconstruction results. Cross sectional view of the voxels is shown. (a) Target location A-1. (b) Target location A-4. (Unit: S/m).

D. Discussion

It is known that the distinguishability of the target by EIT imaging increases with the number of electrodes used to apply the currents and measure the voltages [22]. By increasing the number of electrodes and consequently reducing the area of each electrode, the shunting effect of the electrodes will be reduced and the accuracy of the forward model improved. Use of more accurate electrode models that include the unmodeled effects such as contact impedance will also contribute to the improvement of the EIT imaging. In this experiment, ACT3 was used, which can apply 32 electrode currents simultaneously. The next generation EIT machine, ACT4, is entering service and can apply 64 electrode currents simultaneously. We expect that using 64 electrodes will improve the spatial resolution of breast cancer detection and increase the maximum depth of the tumor detectable.

In the reconstruction results presented above, the electrode voltages ${\{V_{l,0}^k\}}_{k=1}^{L-1}$ were measured from the homogeneous tank and the saline conductivity was used as the background conductivity. In the clinical application, the background conductivity σ₀ and the electrode voltage measurement ${\{V_{l,0}^k\}}_{k=1}^{L-1}$ of the homogeneous body is not available. A possible solution is to compute the constant conductivity approximation of σ₀ that best represents the voltage measurements [24], and compute ${\{V_{l,0}^k\}}_{k=1}^{L-1}$ from the forward model presented in this paper. When the electrode voltages ${\{V_{l,0}^k\}}_{k=1}^{L-1}$ computed from the forward model were used, the reconstructed images could not distinguish the target from the background. This indicates that the forward model needs to be refined so that the model prediction error is less than 11.9% as shown in Section III. The present study is intended to show a proof of concept of the computation of the conductivity distribution in the mammography geometry with the ACT3 and preliminary electrode arrays which have effects that are not modeled accurately within the ave-gap model used in the paper.

In the application of the presented algorithm to breast imaging, the geometry of the breast under mammography examination will not be a rectangular shape. Some part of the breast will not be in contact with the electrodes, and the chest wall will act as a conducting body not included in the model. The mammography geometry model presented in this paper considers only the rectangular subregion of the breast that is surrounded by electrodes on top and bottom. The unmodeled factors are the effect of the region of the breast that are outside this rectangular volume and act as extra conducting bodies, and also the effect of the chest wall that act as another conducting body. The mammography geometry and the imaging algorithm presented in this work need to be modified to in order to deal with the above mentioned unmodeled factors.

The mammography geometry shows that the electrodes on the top and the bottom surface of the body are in the path of the X-ray and the mammograms will be adversely affected if the electrodes shade the X-rays. The electrodes need to be constructed of X-ray translucent material so that the effect of the electrode presence is minimized. We are presently applying ACT4 using a modified version of this algorithm and X-ray translucent electrodes to image breast cancer patients.

VI. CONCLUSION AND FUTURE WORK

A forward model of mammography geometry and a reconstruction algorithm for breast cancer imaging using the forward model were presented. The proposed algorithm was used to reconstruct the conductivity distribution in a phantom with experimental data collected using ACT3 with 32 electrodes. Two targets, a 5-mm metal cube and a 6-mm agar cube, were studied. The proposed algorithm was successful in recovering the location of the targets inside the phantom. As the targets move away from the electrodes, the reconstructed conductivity of the targets decreases, and it became increasingly difficult to locate the target. It was shown that the location of the two targets could be recovered at target depths up to 15 mm.

Further research effort needs to be focused on modifications that are expected to improve the reconstruction results. They include using ACT4 with more accurate and calibrated data; using a better-defined electrode array and accurate electrode models calibrated to the electrode arrays used; using data calibrated in a way that does not require homogeneous measurements to compensate for inaccurate electrode models; and changing boundary conditions of the mammography geometry to image part of the region under the electrodes without introducing artifact from not modeling the whole breast and chest wall.

$$A_{x,k,r}={\displaystyle \underset{B}{\int }}{\Phi }_r(p)\nabla U_0^x·\nabla U_0^{k}dp={\displaystyle \underset{B_r}{\int }\nabla U_0^x·\nabla U_0^{k}dp=A_{x,k,r(1)}+A_{x,k,r(2)}+A_{x,k,r(3)}+A_{x,k,r(4)}}{A}_{x,k,r(1)}=\frac{j_{0,0}^{tx}{j}_{0,0}^{tk}}{{\sigma }_0^2}V(B_r),V(B_r)=\text{volume of the}r\text{thvoxel}{A}_{x,k,r(2)}=\frac{j_{0,0}^{tx}}{{\sigma }_0}{\displaystyle \sum _{n=0}^{\infty }{\displaystyle \sum _{\begin{array}{l}\hfill m=0\\ \hfill n+m\ne 0\end{array}}^{\infty }{\lambda }_{n,m}{W}_{n,m}\text{sinh}{\gamma }_{n,m}\frac{\delta z_r}{2}\left(j_{n,m}^{tk}\text{sinh}\left({\gamma }_{n,m}\left(z_r+h_3\right)\right)+j_{n,m}^{bk}\text{sinh}\left({\gamma }_{n,m}{z}_r\right)\right)}}$$ (37)

$$W_{n,m}=\{\begin{array}{cc}\frac{8h_1{h}_2}{nm{\pi }^2}\text{cos}\frac{n\pi x_r}{h_1}\text{sin}\frac{n\pi }{h_1}\frac{\delta x_r}{2}\text{cos}\frac{m\pi y_r}{h_2}\text{sin}\frac{m\pi }{h_2}\frac{\delta y_r}{2},\hfill & \left(n\ne 0,m\ne 0\right)\hfill \\ \frac{4h_2}{m\pi }\delta x_r\text{cos}\frac{m\pi y_r}{h_2}\text{sin}\frac{m\pi }{h_2}\frac{\delta y_r}{2},\hfill & \left(n=0,m\ne 0\right)\hfill \\ \frac{4h_1}{n\pi }\delta y_r\text{cos}\frac{n\pi x_r}{h_1}\text{sin}\frac{n\pi }{h_1}\frac{\delta x_r}{2},\hfill & \left(n\ne 0,m=0\right)\hfill \end{array}{A}_{x,k,r(3)}=\frac{j_{0,0}^{tk}}{{\sigma }_0}{\displaystyle \sum _{n=0}^{\infty }{\displaystyle \sum _{\begin{array}{l}\hfill m=0\hfill \\ \hfill n+m\ne 0\hfill \end{array}}^{\infty }{\displaystyle \sum _{n^{\prime }=0}^{\infty }{\displaystyle \sum _{\begin{array}{l}\hfill m^{\prime }=0\hfill \\ \hfill n^{\prime }+m^{\prime }\ne 0\hfill \end{array}}^{\infty }{\lambda }_{n,m}{W}_{n,m}\text{sinh}{\gamma }_{n,m}\frac{\delta z_r}{2}(j_{n,m}^{tx}}}}}\text{sinh}\left({\gamma }_{n,m}\left(z_r+h_3\right)\right)+j_{n,m}^{bx}\text{sinh}\left({\gamma }_{n,m}{z}_r\right))$$

$$A_{x,k,r(4)}={\displaystyle \sum _{s=t,b}{\displaystyle \sum _{n=0}^{\infty }{\displaystyle \sum _{\begin{array}{l}\hfill m=0\hfill \\ \hfill n+m\ne 0\hfill \end{array}}^{\infty }{\displaystyle \sum _{s^{\prime }=t,b}{\displaystyle \sum _{n^{\prime }=0}^{\infty }{\displaystyle \sum _{\begin{array}{l}\hfill m^{\prime }=0\hfill \\ \hfill n^{\prime }+m^{\prime }\ne 0\hfill \end{array}}^{\infty }{\lambda }_{n,m}{\lambda }_{n^{\prime },m^{\prime }}{j}_{n,m}^{sx}{j}_{n^{\prime },m^{\prime }}^{s^{\prime }k}\left(G_1+G_2+G_3\right)}}}}}}{G}_1=n{n}^{\prime }{\left(\frac{\pi }{h_1}\right)}^2{g}_{11}\left(n,n^{\prime }\right)g_{12}\left(m,m^{\prime }\right)g_{13}\left(n,n^{\prime },m,m^{\prime },s,s^{\prime }\right)g_{11}(n,n^{\prime })=\{\begin{array}{cc}0,\hfill & \text{when n}=0\text{or}{n}^{\prime }=0\hfill \\ \left[\frac{1}{2}\delta x_r-\frac{h_1}{(n+n^{\prime })\pi }\text{cos}\frac{(n+n^{\prime })\pi x_r}{h_1}\text{sin}\frac{(n+n^{\prime })\pi }{h_1}\frac{\delta x_r}{2}\right],\hfill & n=n^{\prime }\ne 0\hfill \\ [\frac{h_1}{(n-n^{\prime })\pi }\text{cos}\frac{(n-n^{\prime })\pi x_r}{h_1}\text{sin}\frac{(n-n^{\prime })\pi }{h_1}\frac{\delta x_r}{2}\hfill & \hfill \\ -\frac{h_1}{(n+n^{\prime })\pi }\text{cos}\frac{(n+n^{\prime })\pi x_r}{h_1}\text{sin}\frac{\left(n+n^{\prime }\right)\pi }{h_1}\frac{\delta x_r}{2}],\hfill & n\ne n^{\prime }\hfill \end{array}{g}_{12}(m,m^{\prime })=\{\begin{array}{cc}\delta y_{r,}\hfill & m=m^{\prime }=0\hfill \\ \left[\frac{1}{2}\delta y_r+\frac{h_2}{(m+m^{\prime })\pi }\text{cos}\frac{(m+m^{\prime })\pi y_r}{h_2}\text{sin}\frac{(m+m^{\prime })\pi }{h_2}\frac{\delta y_r}{2}\right],\hfill & m=m^{\prime }\ne 0\hfill \\ [\frac{h_2}{(m-m^{\prime })\pi }\text{cos}\frac{(m-m^{\prime })\pi y_r}{h_2}\text{sin}\frac{(m-m^{\prime })\pi }{h_2}\frac{\delta y_r}{2}\hfill & \hfill \\ +\frac{h_2}{(m+m^{\prime })\pi }\text{cos}\frac{(m+m^{\prime })\pi y_r}{h_2}\text{sin}\frac{(m+m^{\prime })\pi }{h_2}\frac{\delta y_r}{2}],\hfill & m\ne m\hfill \end{array}$$

$$g_{13}(n,n^{\prime },m,m^{\prime },s,s^{\prime })=\{\begin{array}{c}\frac{1}{({\lambda }_{n,m}+{\gamma }_{n^{\prime },m^{\prime }})}\text{cosh}\left(\left({\gamma }_{n,m}+{\gamma }_{n^{\prime },m^{\prime }}\right)z_r+\left({\gamma }_{n,m}{h}_3^s+{\gamma }_{n^{\prime },m^{\prime }}{h}_3^{s^{\prime }}\right)\right)\hfill \\ \times \text{sinh}\left(\left({\gamma }_{n,m}+{\gamma }_{n^{\prime },m^{\prime }}\right)\frac{\delta z_r}{2}\right)+\frac{1}{2}\text{cosh}\left({\gamma }_{n,m}{h}_3^s-{\gamma }_{n^{\prime },m^{\prime }}{h}_3^{s^{\prime }}\right)\delta z_r,\hfill \\ \hfill \text{when}\left(n^2-{n^{\prime }}^2\right)=\frac{h_1^2}{h_2^2}(m{\prime }^2-m2)\\ \begin{array}{l}\frac{1}{({\lambda }_{n,m}+{\gamma }_{n^{\prime },m^{\prime }})}\text{cosh}\left(({\gamma }_{n,m}+{\gamma }_{n^{\prime },m^{\prime }})z_r+\left({\gamma }_{n,m}{h}_3^s+{\gamma }_{n^{\prime },m^{\prime }}{h}_3^{s^{\prime }}\right)\right)\text{sinh}\left(({\gamma }_{n,m}+{\gamma }_{n^{\prime },m^{\prime }})\frac{\delta z_r}{2}\right)\hfill \\ +\frac{1}{\left({\gamma }_{n,m}-{\gamma }_{n^{\prime },m^{\prime }}\right)}\text{cosh}\left(({\gamma }_{n,m}-{\gamma }_{n^{\prime },m^{\prime }})z_r+\left({\gamma }_{n,m}{h}_3^s-{\gamma }_{n^{\prime },m^{\prime }}{h}_3^{s^{\prime }}\right)\right)\hfill \\ \hfill \text{sinh}\left(({\gamma }_{n,m}-{\gamma }_{n^{\prime },m^{\prime }})\frac{\delta z_r}{2}\right),\text{\hspace{1em}otherwise}\end{array}\hfill \end{array}{G}_2=m{m}^{\prime }{\left(\frac{\pi }{h_2}\right)}^2{g}_{21}(n,n^{\prime })g_{22}(m,m^{\prime })g_{23}(n,n^{\prime },m,m^{\prime },s,s^{\prime })g_{21}(n,n^{\prime })=\{\begin{array}{cc}\delta x_r,\hfill & n=n^{\prime }=0\hfill \\ \frac{1}{2}\delta x_r+\frac{h_1}{(n+n^{\prime })\pi }\text{cos}\frac{(n+n^{\prime })\pi x_r}{h_1}\text{sin}\frac{(n+n^{\prime })\pi }{h_1}\frac{\delta x_r}{2},\hfill & n=n^{\prime }\ne 0\hfill \\ \frac{h_1}{(n-n^{\prime })\pi }\text{cos}\frac{(n-n^{\prime })\pi x_r}{h_1}\text{sin}\frac{(n-n^{\prime })\pi }{h_1}\frac{\delta x_r}{2}+\frac{h_1}{(n+n^{\prime })\pi }\text{cos}\frac{(n+n^{\prime })\pi x_r}{h_1}\text{sin}\frac{(n+n^{\prime })\pi }{h_1}\frac{\delta x_r}{2},\hfill & n\ne n^{\prime }\hfill \end{array}$$

$$g_{22}(m,m^{\prime })=\{\begin{array}{cc}0,\hfill & \text{when m}=0\text{or}{\mathrm{m}}^{\prime }=0\hfill \\ \frac{1}{2}\delta y_r-\frac{h_2}{(m+m^{\prime })\pi }\left[\text{cos}\frac{(m+m^{\prime })\pi y_r}{h_2}\text{sin}\frac{(m+m^{\prime })\pi }{h_2}\frac{\delta y_r}{2}\right]\hfill & m=m^{\prime }\hfill \\ \frac{h_2}{(m-m^{\prime })\pi }\left[\text{cos}\frac{(m-m^{\prime })\pi y_r}{h_2}\text{sin}\frac{(m-m^{\prime })\pi }{h_2}\frac{\delta y_r}{2}\right]\hfill & \hfill \\ -\frac{h_2}{(m+m^{\prime })\pi }\left[\text{cos}\frac{(m+m^{\prime })\pi y_r}{h_2}\text{sin}\frac{(m+m^{\prime })\pi }{h_2}\frac{\delta y_r}{2}\right],\hfill & m\ne m^{\prime }\hfill \end{array}{g}_{23}(n,n^{\prime },m,m^{\prime },s,s^{\prime })=g_{13}(n,n^{\prime },m,m^{\prime },s,s^{\prime })G_3={\gamma }_{n,m}{\gamma }_{n^{\prime },m^{\prime }}{g}_{31}(n,n^{\prime })g_{32}(m,m^{\prime })g_{33}(n,n^{\prime },m,m^{\prime },s,s^{\prime })g_{31}(n,n^{\prime })=g_{21}(n,n^{\prime })g_{32}(m,m^{\prime })=g_{12}(m,m^{\prime })$$

$$g_{33}(n,n^{\prime },m,m^{\prime },s,s^{\prime })=\{\begin{array}{l}\frac{1}{\left({\gamma }_{n,m}+{\gamma }_{n^{\prime },m^{\prime }}\right)}\text{cosh}\left(\left({\gamma }_{n,m}+{\gamma }_{n^{\prime },m^{\prime }}\right)z_r+{\gamma }_{n,m}{h}_3^s+{\gamma }_{n^{\prime },m^{\prime }}{h}_3^{s^{\prime }}\right)\hfill \\ \times \text{sinh}\left({\gamma }_{n,m}+{\gamma }_{n^{\prime },m^{\prime }}\right)\frac{\delta z_r}{2}-\frac{1}{2}\text{cosh}\left({\gamma }_{n,m}{h}_3^s-{\gamma }_{n^{\prime },m^{\prime }}{h}_3^{s^{\prime }}\right)\delta z_r\hfill \\ \hfill \text{\hspace{1em}\hspace{1em}\hspace{1em}when}(n^2-{n^{\prime }}^2)=\frac{h_1^2}{h_2^2}\left({m^{\prime }}^2-m^2\right)\\ \frac{1}{\left({\gamma }_{n,m}+{\gamma }_{n^{\prime },m^{\prime }}\right)}\text{cosh}\left(\left({\gamma }_{n,m}+{\gamma }_{n^{\prime },m^{\prime }}\right)z_r+{\gamma }_{n,m}{h}_3^s+{\gamma }_{n^{\prime },m^{\prime }}{h}_3^{s^{\prime }}\right)\text{sinh}\left({\gamma }_{n,m}+{\gamma }_{n^{\prime },m^{\prime }}\right)\frac{\delta z_r}{2}\hfill \\ -\frac{1}{\left({\gamma }_{n,m}-{\gamma }_{n^{\prime },m^{\prime }}\right)}\text{cosh}\left(\left({\gamma }_{n,m}-{\gamma }_{n^{\prime },m^{\prime }}\right)z_r+{\gamma }_{n,m}{h}_3^s-{\gamma }_{n^{\prime },m^{\prime }}{h}_3^{s^{\prime }}\right)\hfill \\ \hfill \text{\hspace{1em}sinh}\left({\gamma }_{n,m}-{\gamma }_{n^{\prime },m^{\prime }}\right)\frac{\delta z_r}{2},\text{\hspace{1em}\hspace{1em}otherwise}\end{array}.$$

Biographies

Myoung Hwan Choi received B.S., M.S., and Ph.D. degrees in electronic engineering from Seoul National University, Seoul, Korea, in 1982, 1986, and 1992, respectively.

He is a Professor in the Department of Electrical and Electronics Engineering, Kangwon National University, Chunchon, Korea. He was a Visiting Research Scholar in Oak Ridge National Laboratory, Oak Ridge, TN in 1995, and a Visiting Professor in the Department of Biomedical Engineering, Rensselaer Polytechnic Institute, Troy, NY, in 2003. His research interests include electrical impedance tomography and its application to breast cancer imaging, and ultrasonic diagnostic imaging.

Tzu-Jen Kao (M’06) was born in Taipei, Taiwan, on January 18, 1971. He received the B.Sc. degree in computer science and engineering in 1993 from Tatung Institute of Technology (now called Tatung University), Taipei, medical degree (bachelors of medicine) in 1998 from Beijing Medical University (now called Peking University Health Science Center) Beijing China, and the M.S. and Ph.D. degrees in biomedical engineering in 2005 from Rensselaer Polytechnic Institute, Troy, NY, in 2002 and 2005, respectively.

In 1998, he became a Medical Intern in the Department of Thoracic Surgery, Peking University, 3rd Hospital. After using various surgical equipment, he decided to study abroad to learn medical instrument design. From 2000 to 2006, he was a Research Assistant, Post-doctoral Research Associate, and Research Associate in the electrical impedance imaging group at Rensselaer Polytechnic Institute. His research interests have included body surface potential for cardiac detection, electrical impedance imaging for cancer detection and treatment, and combined EIT with other modalities such as X-ray and ultrasound.

David Isaacson (M’ 86) received the Ph.D. degree in mathematics from the Courant Institute of Mathematical Sciences, New York, in 1976.

He is a Professor of Mathematical Sciences at Rensselaer Polytechnic Institute (RPI), Troy, NY. In the early years of his career, he worked on developing numerical methods to approximately solve problems arising in statistical mechanics, quantum mechanics, and quantum field theory. Since 1986, he has devoted his career to applying mathematics to the solution of problems in medicine and biology. Along with his collaborators at RPI he has developed adaptive current tomography systems for monitoring heart and lung function. He is currently collaborating on the construction of an electrical impedance tomography system specifically designed to improve the diagnosis of breast cancer.

Gary J. Saulnier (S’80-M’84-SM’95) received the B.S., M.E., and Ph.D. degrees in electrical engineering from Rensselaer Polytechnic Institute (RPI), Troy, NY in 1980, 1982, and 1985, respectively.

Since 1986, he has been on the faculty of the Electrical, Computer, and Systems Engineering Department at RPI, where he is currently a Professor. His primary research interests are in the areas of modulation and coding, with an emphasis on spread spectrum, OFDM and MIMO systems, and the development of electronic instrumentation for biomedical applications.

Dr. Saulnier has been an Associate Editor for the IEEE Transactions on Vehicular Technology since 2002.

Jonathan C. Newell (S’64-M’69) received the B.S. and M.S. degrees in electrical engineering from Rensselaer Polytechnic Institute (RPI), Troy, NY, where he graduated in 1968, and the Ph.D. degree in physiology from Albany Medical College, Albany, NY, in 1974.

He is now a Research Professor of Biomedical Engineering at RPI. His research interests have included the regulation of the pulmonary circulation and pulmonary gas exchange in injured patients with acute respiratory failure. More recently, he has been developing a multifrequency adaptive system for electrical impedance imaging, and applying it to the diagnosis of breast cancer.

APPENDIX

The voltage inside the homogenous body induced by the kth current vector can be computed from (20) as expressed in (36) where λ_n,m = 1/(σ₀γ_n,m sinh γ_n,mh ₃), $h_3^t=h_3$, $h_3^b=0$, and ${\gamma }_{n,m}=\sqrt{{(n\pi /h_1)}^2+{(m\pi /h_2)}^2}$. From (32), (30) and (36), we can compute A_x,k,r. The detail of the derivation is omitted

$$\begin{array}{l}{U}_0^k(x,y,z)=\frac{j_{0,0}^{\mathit{\text{tk}}}}{{\sigma }_0}z+{\displaystyle \sum _{s=t,b}{\displaystyle \sum _{n=0}^{\infty }{\displaystyle \sum _{\begin{array}{l}\hfill m=0\hfill \\ \hfill n+m\ne 0\hfill \end{array}}^{\infty }{\lambda }_{n,m}{j}_{n,m}^{\mathit{\text{sk}}}}}}\hfill \\ \times \text{cos}\left(\frac{n\pi x}{h_1}\right)\text{cos}\left(\frac{m\pi y}{h_2}\right)\text{cosh}{\gamma }_{n,m}(z+h_3^s).\hfill \end{array}$$ (36)

See (37) beginning on the previous page.