Abstract
We recently discovered that human activity possesses a complex temporal organization characterized by scale-invariant/self-similar fluctuations from seconds to ~4 hour—statistical properties of fluctuations remain the same at different time scales. Here, we show that scale-invariant activity patterns are essentially identical in humans and rats, and exist for up to ~24 hour: six-times longer than previously documented. Theoretically, such scale-invariant patterns can be produced by a neural network of interacting control nodes—system components with feedback loops—operating at different time scales. However such control nodes have not yet been identified in any neurophysiological model of scale invariance/self-similarity in mammals. Here we demonstrate that the endogenous circadian pacemaker (suprachiasmastic nucleus; SCN), known to modulate locomotor activity with a periodicity of ~24 hour, also acts as a major neural control node responsible for the generation of scale-invariant locomotor patterns over a broad range of time scales from minutes to at least 24 hour (rather than solely at ~24 hour). Remarkably, we found that SCN lesion in rats completely abolished the scale-invariant locomotor pattern between 4 and 24 hour and significantly altered the patterns at time scales <4 hour. Identification of the control nodes of a neural network responsible for scale invariance is the critical first step in understanding the neurophysiological origin of scale invariance/self-similarity.
Keywords: Activity, Scale-invariance, Suprachiasmatic nucleus lesion, Human, Rat, Network
The suprachiasmastic nucleus (SCN) in mammals generates self-sustained oscillations that orchestrate a wide range of neurophysiologic functions—from cellular processes to overt behaviors—with a time period of ~24 hour (Weaver, 1998). One of the fundamental processes influenced by the SCN is motor activity, which displays clear ~24 hour rhythms even under constant dark conditions in many species (Stephan and Zucker, 1972;Schwartz et al., 1986;Ralph et al., 1990;Cohen and Albers, 1991). The robust rhythmicity in activity is abolished when the SCN is ablated (Stephan and Zucker, 1972;Moore and Eichler, 1972), and can be subsequently restored in recipients of SCN transplantation (Ralph et al., 1990;Silver et al., 1996). These findings provide solid evidence that the SCN serves as a pacemaker generating ~24 hour rhythms in motor activity.
In addition to the circadian rhythms in activity, we recently discovered that the fluctuations in human activity during wakefulness exhibit robust scale-invariant fractal patterns with nonlinear dynamic features, i.e., statistical properties of activity fluctuations such as correlations and nonlinear Fourier phase interactions remain the same over a broad range of time scales from seconds to hours (Hu et al., 2004). We found that these scale invariant features could not be perturbed by adjusting extrinsic factors including scheduled events and the light dark/cycle, and they were unaffected by differences in the mean level of activity across days of the week and between individuals strongly suggesting an endogenously regulated scale invariance (Hu et al., 2004). Moreover, we showed that these scale-invariant features cannot be caused by ultradian rhythms at time scales less than ~4 hours (Hu et al., 2004).
Fluctuations with scale-invariant patterns are also observed in many other neurophysiological signals such as heartbeat intervals, breathing patterns, and gait (Peng et al., 1993;Ivanov et al., 1996;Hausdorff et al., 1996;Ashkenazy et al., 2001;Larsen et al., 2004). Simulations indicated that these scale-invariant patterns are unlikely to be caused by simple superposition of independent controlling factors (Hausdorff and Peng, 1996), hence interactions among controlling factors are required to explain such scale invariant patterns. Indeed, mathematical models of physical systems reveal that such scale-invariant patterns can be explained by interactions between multiple control system components—control nodes—that affect the overall system at different time scales (Mandelbrot, 1982;Bak et al., 1987;Basu et al., 2004). Similar complexity may be operating in numerous neurophysiological systems via networks of control nodes coupled by feedback loops (Ivanov et al., 1998;Ashkenazy et al., 2002). However such control nodes have not yet been specifically identified in any neurophysiological model of scale invariance in mammals. Based on our prior observations and the above noted theory, we hypothesized that there exists an intrinsic activity control system that orchestrates the short and long term influences on activity to produce an overall scale-invariant pattern via interacting activity control nodes operating at different time scales (Hu et al., 2004;Ashkenazy et al., 2002). To test this hypothesis, we examined the role of the SCN on these scale-invariant patterns by lesioning the SCN. If the SCN is one of the major nodes of the neural network producing scale-invariant patterns of activity, our hypothesis would predict that due to coupling between control nodes operating at different time scales, SCN lesioning would influence the scale-invariant behaviors not only at 24 hour but also at time scales outside the 24 hour time period. Specifically, we tested whether or not the scale-invariant patterns in activity: (i) exist across a six-fold wider time scale than previously identified (Hu et al., 2004), i.e., up to 24 h - the period of the circadian pacemaker; (ii) also exist in a mammalian species that is nocturnally active, i.e., Wistar rats; (iii) are influenced by the a strong circadian Zeitgeber, namely the 24 hour light/dark cycle; and (iv) are affected by lesioning of the SCN (main hypothesis).
Experimental procedures
To test our hypotheses, we used existing data collected in previous studies (Hu et al., 2004;Scheer et al., 2005), including activity data recorded for 10 days in: (a) human subjects living in dim light conditions (i.e., excluding the circadian Zeitgeber of light/dark cycles on activity) and with scheduled behaviors balanced across all circadian phases (Hu et al., 2004); (b) control rats living under 24 hour light/dark cycles, and again under constant darkness; and (c) rats with SCN lesions living under 24 hour light/dark cycles, and again under constant darkness (Scheer et al., 2005;Scheer et al., 2001).
Human study
Subjects and Protocol
Activity recordings of seven young subjects (4 males and 3 females, 21–32 years old) were made in the laboratory throughout a 10-day forced desynchrony protocol (Hu et al., 2004). Following two baseline days and nights of acclimatization to the laboratory, the sleep/wake cycles were adjusted to 28 hour, with sleep opportunity periods delayed by 4 hour every ‘day’ to ensure that the sleep/wake rhythm and scheduled activities were evenly balanced across all phases of the circadian cycle. The sleep opportunity remained one third of the sleep/wake cycle (i.e., 9 h and 20 min of sleep opportunity and 18 hour and 40 minute of wakefulness). Subjects repeated the same schedule in all wake periods including the timing of meals, showers, and other scheduled activity. To ensure that the circadian pacemaker oscillated at its inherent rate, subjects remained in dim light (<8 lux), and subjects had no external cues regarding the time of day. Room temperature was maintained at 23°C. The study was approved by the relevant institutional human subjects Internal Review Board. All subjects provided written informed consent prior to participation.
Data acquisition
Subjects wore a wristwatch-sized Actiwatch recorder (Mini-Mitter Co., OR, USA) that unobtrusively measured changes in forearm acceleration in any plane (sensitive to 0:01g, where g is the acceleration due to gravity) (Jean-Louis et al., 2000). Each data point recorded in the device’s internal memory represents the value of changes in acceleration sampled at 32 Hz and integrated over an epoch length of 60 seconds.
Rat studies
Animals and Protocol
Activity recordings were analyzed in 7 intact and 7 SCN-lesioned (SCNx) Wistar rats throughout separate 10-day protocols in light/dark (12 hour Light, 100 lux; 12 hour dark, 0.1 lux; LD) and constant dark (0.1 lux; DD) to exclude influences on activity from a very strong external Zeitgeber (light/dark cycle) (Scheer et al., 2005;Scheer et al., 2001). During the DD protocol, the transmitter of one SCNx rat had technical difficulties and, thus, activity data was analyzed from 6 SCNx rats and 7 intact rats during this phase of the study. Each rat lived individually in a cage with dimensions 39 × 38 × 38 cm. The study was approved by the relevant institutional Animal Care Committee.
SCN lesioning
To ablate the SCN, rats were first anesthetized with Hypnorm (Duphar, The Netherlands; 0.8 ml/kg i.m.), and mounted in a stereotactic instrument (David Kopf Instruments, Tujunga, CA, USA). Two electrode tips (0.2 mm diameter) were then placed bilaterally in the SCN (tooth bar at +5.0 mm; angle of −6°; coordinates: −2 mm rostral to bregma; +2 mm to midline; 7.4 mm below brain surface) and heated at 80 °C for 1 min (Scheer et al., 2005;Scheer et al., 2001). Thirty rats underwent this initial surgery. To avoid the inclusion of rats with incomplete lesions, the day/night rhythms in drinking water were investigated at least one month after the surgery, as previously described (Buijs et al., 1993). Eight rats with arrhythmic drinking behavior (water intake during 8-hour daytime equal to or more than 33% of that during 24 hour) then underwent the same two protocols (10 days in DD and 10 days in LD) as the control rats (Scheer et al., 2005). Secondly, after data acquisition, the presence of any vasoactive intestinal polypeptide (VIP) positive cells and vasopressin (VP) positive cells within the SCN in perfusion fixed brains (4% paraformaldehyde) were checked before data analyses (Buijs et al., 1993;Kalsbeek et al., 1992). Rats with the presence of rhythms in drinking behavior, or with the presence of VIP or VP positive neurons were excluded from the study. Seven of 30 rats met both behavioral and anatomical verification of complete SCN lesion (Scheer et al., 2005). The low success rate of approximately 25% conformed to the historical success rates of SCN lesions in our laboratory (Buijs et al., 1993) and reflected our goal to achieve both a selective lesion of the SCN together with very little damage to areas surrounding the SCN (see (Scheer et al., 2005) for more details).
Data acquisition
Activity data was continuously recorded from two infrared sensors in the ceiling of the cage which counted the number of movements of the rat across the surface of the cage floor (i.e., locomotor activity), and sampled at 0.8 Hz and integrated over 4-minute epochs (Scheer et al., 2005;Scheer et al., 2001). Core body temperature and heart rate were also monitored using an implanted transmitter that was secured to the inner muscle wall of the abdomen, and two electrodes that were secured to the muscles (one rostral and one caudal) to the heart (Scheer et al., 2005). Every 4 minutes, temperature and heart rate were sampled at 500 Hz for 10 seconds and the average values were stored,
Data analysis
Assessment of rhythmicity
In the DD protocol, individual circadian period for control rats was estimated from rhythmicity in core body temperature to obtain average activity waveforms in a circadian period, whereas in SCNx rats, in which circadian rhythmicity in temperature was eliminated, the average circadian period of all control rats was used for comparison of SCNx and control groups in activity waveforms (i.e., 24.1 h) (Scheer et al., 2005). To assess the influence of SCN lesion on the daily rhythms of activity, we calculated the power spectrum of locomotor activity for each subject (3600 points, 240 hours) with a spectral resolution (15 hour−1). The group averages of power spectrum densities for control and SCNx groups were obtained from individual spectral densities that were first normalized to have a unit total power. For the visualization of circadian rhythmicities in control rats and their absences in SCNx rats, we also obtained circadian waveforms of activity fluctuations for each individual. Brief simultaneous peaks in locomotor activity and temperature, caused by sporadic handling and cage management, were identified (total 5 hours over the total 240 hours recording) and replaced by the individual’s mean data for the power spectral analysis (Scheer et al., 2005).
Assessment of scale invariance
To assess the scale-invariant patterns in the activity fluctuations, we investigated two complementary statistical properties at an array of time scales: (i) correlation, associated with Fourier amplitudes/power spectrum of activity signals, and (ii) nonlinearity, related to information embedded in Fourier phases. Our previous study showed that these two statistical properties of human activity display robust scale-invariant patterns over a wide range of time scales from minutes to ~4hour (Hu et al., 2004).
(i) Correlation analysis
To estimate correlations in the activity fluctuations, we used the detrended fluctuation analysis (DFA) (Peng et al., 1994). Compared with traditional correlation analyses such as power spectral analysis and Hurst analysis, the DFA can accurately quantify correlations in signals that may be masked by underlying nonstationarities or trends (Hu et al., 2001;Chen et al., 2002;Xu et al., 2005). We used DFA to quantify the detrended fluctuations F(n) of activity at different time scales n. For each chosen time scale n, the DFA method involves the following steps (Peng et al., 1994): i) integrating the time series; ii) dividing the integrated time series into non-overlapped bins of equal size n (the chosen time scale); iii) in each bin, fitting the integrated time series with a second order polynomial function, which defines ‘local’ trends assumed to be the result of external influences. Second order polynomial functions were used to better remove effects of linear trends in original data (Hu et al., 2001); iv) detrending the integrated time series by subtracting the local trend; and v) calculating the root mean square of the residuals in all bins to obtain the value of fluctuations at the time scale n. The above procedure is repeated for different time scales n to obtain the detrended fluctuation function F(n). A power-law functional form indicates self-similarity (scale-invariance). This power-law functional form is defined by a straight line on a log-log plot of F(n) vs. time scale (bin width), yielding F(n)~nα. The parameter α called the scaling exponent, quantifies the correlation properties in the signal: if α=0.5, there is no correlation in the fluctuations (random noise); if α<0.5, the signal is anticorrelated, where large activity values are more likely to be followed by small activity values; if α>0.5, there are positive correlations, where large activity values are more likely to be followed by large activity values (and vice versa for small activity values).
(ii) Nonlinearity/Magnitude analysis
To assess the nonlinear properties of activity signals (Fourier phase interactions), we used the magnitude analysis (Ashkenazy et al., 2001;Hu et al., 2004). This method analyzes the “magnitude series” formed by taking the absolute values of the increments between consecutive activity values. We used DFA to quantify the detrended fluctuations Fmag(n) of magnitude series at different time scales n. Similar to the correlation analysis described above, a power-law functional form (Fmag(n) ~nαmag) indicates scale-invariance of the magnitude series. The parameter αmag, ranging from 0.5 to 1, quantifies the nonlinear properties of the original activity signal: if αmag=0.5, Fourier phases are random and the signal is linear; if αmag>0.5, there are interactions in the Fourier phases between fluctuations at different frequency/time scales and the signal is nonlinear. The nonlinearity is stronger when αmag is closer to 1. Note that two signals with identical correlation properties can exhibit different nonlinear properties (Fig. 1) (Theiler et al., 1992;Ashkenazy et al., 2001;Hu et al., 2004). The nonlinear properties cannot be caused by a simple summation of influences from independent factors such as circadian and ultradian rhythms that affect activity at different time scales, instead, the existence of scale-invariant nonlinearities requires a network of feedback interactions between multiple contributing factors organized in a self-similar manner (Ivanov et al., 1999;Ashkenazy et al., 2002).
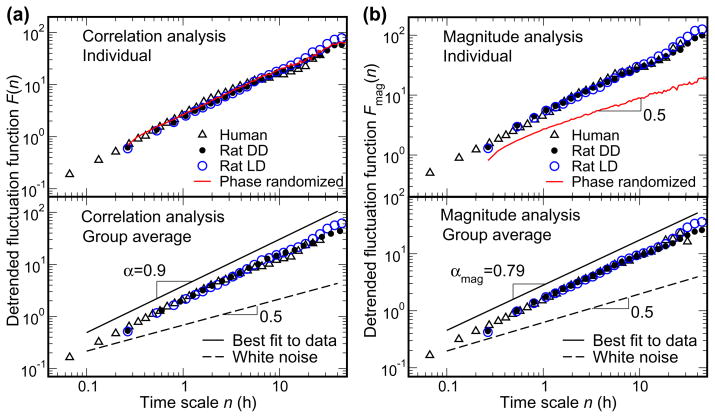
Fig. 1.
Similarity of scale-invariant patterns of activity fluctuations in humans and rats.
(A) Correlation analysis and (B) magnitude analysis (nonlinear properties) in the activity recordings throughout 10 day protocols in the laboratory in a representative individual human, a representative individual rat (upper plots), and in the group averages (lower plots). The phase randomized surrogate data (red line) was generated from the rat data during DD by performing a Fourier transform, preserving the amplitudes of the Fourier transform but randomizing the phases, and then performing an inverse Fourier transform. Such surrogate data has the same correlation properties as the original data, but contains no nonlinear information embedded in the Fourier phases. Data are shown on log-log plots. On the abscissa, n represents the time scale in hours. The detrended fluctuation functions F(n) and Fmag(n) are depicted on the ordinates in A and B respectively. Note, for both humans and rats, before averaging, the data of each subject were normalized to account for individual differences in the standard deviation of activity. The lines depicting the best fit to the data are vertically shifted for better visualisation, but the slope remains the same. The dashed line indicates the exponent 0.5 which occurs with a random signal (white noise). The power-law form of F(n) and Fmag(n) with α and αmag >0.5 indicate long-range correlations and nonlinearities in activity data. Virtually identical scaling exponents in humans and rats (α=0.90±0.04 [SD] and αmag=0.79±0.04 for human, α=0.89±0.04, and αmag=0.79±0.02 for rats during LD, and α=0.85±0.06 and αmag=0.75±0.04 during DD) indicate the same scale-invariant patterns in the two species. Scaling exponents are obtained by fitting data in the range from ~16 minute to 24 hour.
RESULTS
Human activity fluctuations exhibit scale-invariant patterns from minutes to 24 h
The results presented in Fig. 1 show that humans possess a scale-invariant pattern of activity across a very broad range of time scales: from minutes up to 24 h (result above 24h is not statistically reliable due to the restriction of data length as described by Hu et al., 2001). This scale-invariant pattern of activity is demonstrated as a group mean scaling exponent (α) of 0.90 (individuals’ α range = 0.84–0.97) on the correlation analysis log-log plot in Fig. 1A. This α exponent of 0.90 indicates positive correlations in activity fluctuations. In addition, we found a similar scale-invariant pattern of activity in the complementary magnitude analysis in the same time scale range from minutes to 24 h (Fig. 1B). The mean scaling exponent (αmag) of 0.79 (individuals’ αmag range = 0.76–0.87 indicates positive correlations in the magnitude series. To demonstrate that the observed positive correlations in the magnitude series indeed represent nonlinear features in the activity data, we performed a Fourier transform on the activity recording in a control rat during DD, preserving the amplitudes of the Fourier transform but randomizing the phases, and then performing an inverse Fourier transform (Theiler et al., 1992;Ashkenazy et al., 2001). This procedure of phase randomization generates a surrogate time series with the linear features of the original activity recording preserved but with the nonlinear features eliminated. The derived surrogate signal has the same rhythms in the power spectrum and the same correlation scaling behavior as the original activity recording (F(n); solid red line in Fig. 1A); but it exhibits uncorrelated behavior for the magnitude series (αmag=0.5, Fig. 1B). These results indicate that the original human activity data contains scale-invariant correlations and nonlinear Fourier phase interactions from minutes to ~24 hour.
Activity fluctuations in rats exhibit identical scale-invariant patterns to humans
We found that the fluctuations in activity of humans and rats possess remarkably similar scale-invariant dynamic patterns characterized by statistically identical slopes in the log-log plots of detrended fluctuation functions F(n) and Fmag(n) (Fig. 1). As seen in Fig. 1A, a power-law form of F(n) (straight line on the log-log plot with scaling exponent >0.5) exists in humans and rats with almost identical correlation properties at time scales spanning from ~16 minute to ~24 hour (α=0.90±0.04 [SD] for human, α=0.89±0.04 for rats during LD, and α=0.85±0.06 during DD). This indicates the existence of almost identical long-range correlations in activity fluctuations in both species. In the same time scale range (~16minute to ~24 hour), there also exists a power-law form of Fmag(n) (straight line on the log-log plot with scaling exponent >0.5) in both humans and rats with almost identical scaling behaviors (αmag=0.79±0.04 for human, αmag=0.79±0.02 for rats during LD, and αmag=0.75±0.04 during DD). This indicates the existence of almost identical nonlinear properties in activity fluctuations in both species. Moreover, there was no difference in these scale-invariant patterns when rats lived under LD and DD conditions, suggesting that this is an endogenous activity regulating mechanism, insensitive to a strong external influence.
Effect of SCN-lesion on 24 hour waveform of activity
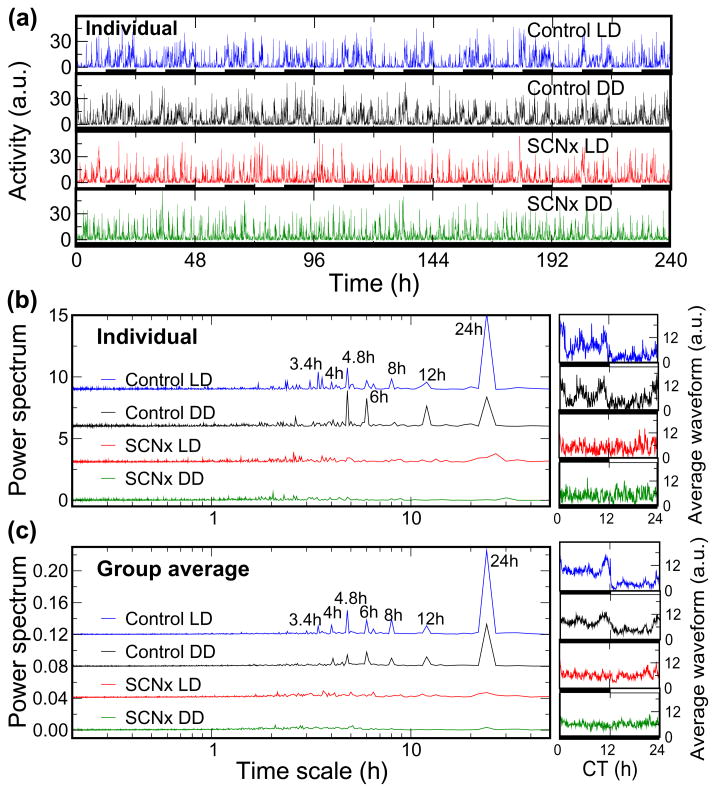
As expected, SCN lesion altered the 24 hour waveform of activity but did not significantly alter the 24 hour mean level of activity either during LD or DD when compared to control rats (mean 24 hour activity: Control LD = 101±29 [arbitrary units]; Control DD = 103±27; SCN-lesion LD = 93±14; SCN-lesion DD = 96±20; P>0.5; ANOVA). The ~24 hour waveform of mean activity level exhibited 3 or 4 specific peaks during the ‘biological’ nighttime (i.e., the active phase in nocturnal animals) in control rats in both LD and DD (Fig. 2). This non-sinusoidal waveform in control rats resulted in a power spectrum of activity with sharp peaks at precise harmonic frequencies of 24 h (i.e., 24/2 = 12 hour, 24/3 = 8 hour, 24/4 = 6 hour, 24/5 = 4.8 hour, 24/6 = 4 hour and 24/7 = 3.4 hour), with negligible spectral power between these harmonics (Fig. 2). These peaks in the power spectrum could be interpreted as independent ‘ultradian’ rhythms, or merely the result of a non-sinusoidal shape in the 24-h rhythm (these possibilities cannot be distinguished by this analysis). However, along with the 24-h periodicity in locomotor activity, the sharp peaks in the power spectrum at precise harmonic frequencies of 24-h essentially disappeared in SCNx rats in both LD and DD (Fig. 2). This strongly suggests that the apparent ultradian rhythms observed in activity are the result of SCN signaling with a 24-h waveform that is not purely sinusoidal. Indeed, an endogenous circadian waveform of locomotor activity with multiple peaks over 24 hour is consistent with the recent observations in rat of distinct neuronal populations in the circadian pacemaker all with ~24 h periodicities but with 4 to 5-h peaks in electrophysiological discharge rate occurring at different relative phases (Schaap et al., 2003). An alternative hypothesis is that ultradian rhythms in activity are generated from locations outside the SCN, but the fact that they occur at precise harmonics of the fundamental circadian oscillation and are abolished with lesioning of the SCN suggests that such ultradian rhythms must interact with and be coupled to the SCN pacemaker.
Fig. 2.
Circadian and ‘ultradian’ rhythms of activity in rats are virtually abolished by SCN lesion.
(A) 10-day continuous activity recordings of a representative control rat and a representative SCN-lesioned rat (SCNx) both throughout 12-hour light-dark cycles (LD) and under constant darkness (DD). In all plots, blue indicates control rats in LD; black, control rats in DD; red, SCNx rats in LD; and green, SCNx rats in DD. (B) The left panel shows power spectral densities of the individuals’ activity recordings from A, and the right panel shows the same individuals’ 10-day continuous activity recordings averaged over the estimated circadian period (i.e., ~24 h) after aligning the data according to the onset of darkness (circadian time, CT = 0 h). (C) The group average power spectral densities and average 24 hour activity waveforms of control rats and SCNx rats. The individual data and average waveform of activity is expressed in arbitrary units. For better clarity and to avoid overlap, power spectral curves are vertically offset. Note, the abscissa of the power spectrum is a log scale with time (thus higher frequencies appear to the left of lower frequencies). As seen in the power spectra in B and C, control rats exhibit a sharp peak in activity at ~24 hour with additional peaks at precise harmonics of 24 h, namely at 12, 8, 6, 4.8, 4, and 3.4 hour. The circadian rhythm and its harmonics were almost completely abolished by SCN-lesions.
The SCN imparts scale-invariant activity patterns across a broad range of time scales, from minutes to 24 h
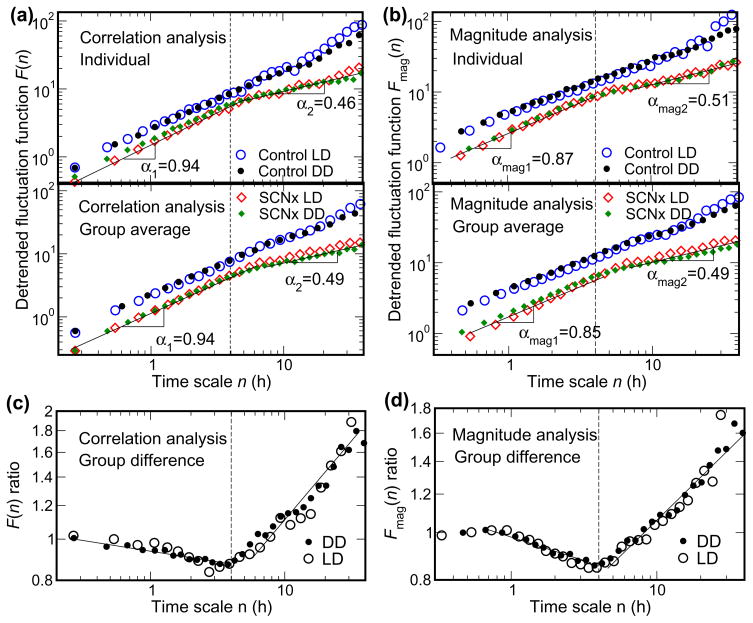
To test the hypothesis that the SCN operates as one of the major nodes of the control network regulating scale invariant activity, we next determined whether or not SCN lesion influences the DFA scaling exponents (α and αmag) at time scales other than the 24 hour time period. Indeed, we found that correlations and nonlinearities completely break down and that activity fluctuations of SCNx rats resemble white noise at time scales larger than 4 h. SCN lesion had strikingly different effects on the DFA scaling exponents at these longer time scales when compared to shorter time scales (Fig. 3). The precise time scale at which this distinction occurred is better demonstrated in the derived plots in Figs. 3C and 3D, which represent the ratio of control/SCNx rats. There is a clear turning point in these ratios at a time scale of 4 hour for both the correlation analysis (Fig. 3C, F(n)) and the magnitude analysis (Fig. 3D, Fmag(n)). Thus, we defined two time scale regions for analysis, Region 1 is 16 minute-4 hour (i.e., to the left of the dotted vertical line; indicated by exponents (α1 and αmag1) and region 2 is 4–24 hour (i.e., to the right of the dotted vertical line; indicated by exponents (α2 and αmag2). We found that the scale-invariant pattern of activity at time scales longer than 4 hour (Fig. 3; SCNx rats mean α2=0.51±0.06 during LD and α2=0.46±0.05 during DD; mean αmag2=0.45±0.03 during LD and αmag2=0.44 ±0.06 during DD) is dramatically different from those of control rats (and humans) who did not have 2 distinct regions (P<0.0001, ANOVA). We believe that the finding of scaling exponents α2≈0.5 and αmag2≈0.5 for SCNx rats at time scales larger than 4 h is the first experimental demonstration of the abolition of scale invariance in a mammalian neurophysiological system.
Fig. 3.
SCN lesion abolishes scale-invariant patterns of activity at time scales above 4 h. (A) Correlation analysis and (B) magnitude analysis (nonlinear properties) in the activity recordings throughout 10 day protocols in the laboratory in representative individual control and SCN lesioned rats (upper plots), and in the group averages (lower plots). Data are shown on log-log plots. On the abscissa, n represents the time scale in hours. The detrended fluctuation functions F(n) and Fmag(n) are vertically shifted for a better visualization of differences between control and SCN-lesioned rats (SCNx). (C) The F(n) ratio and (D) the Fmag(n) ratio of control/SCN-lesioned rats obtained from the group averages. Both ratios exhibit clearly a crossover point at a time scale of ~4 hour (see dotted vertical lines on each plot), which is caused by the different scaling behaviors of SCNx rats below and above 4 hour. At time scales larger than 4 h, the F(n) and Fmag(n) of SCNx rats, greatly differ from those of control rats, displaying a scaling behavior of white noise characterized by the scaling exponent α2≈0.5 and αmag2≈0.5. At time scales less than ~4 h, the SCN-lesioned rats still exhibit scale-invariant correlations and nonlinear patterns, although the scaling exponents are statistically larger than those of control rats.
Over the time range from minutes up to ~4 h, correlation and nonlinear properties of activity fluctuation are mostly conserved following SCN lesion, although there is still a small but consistent effect of SCN-lesion as indicated by slightly larger α1 and αmag1 (Fig 3; for SCNx rats, mean α1=0.98±0.05 during LD and α1=0.94±0.05 during DD; for control rats, mean α=0.89±0.04 during LD and 0.85±0.06 during DD; and for SCNx rats, mean αmag1=0.88±0.05 during LD and αmag1=0.85±0.06 during DD; for control rats, mean αmag=0.79±0.02 during LD and 0.75±0.04 during DD; P<0.0001 [ANOVA] for all comparisons between control and SCNx rats). Again, as with the control rats, in SCNx rats the light dark cycle did not affect the correlation and magnitude exponents. These findings that SCN lesion qualitatively changed the DFA exponents across a wide time scale provide clear evidence that the SCN is one of the key intrinsic factors contributing to scale-invariant patterns in activity fluctuations, and that this influence occurs over a very broad range of time scales spanning minutes to 24 hour (i.e., not only at a time scale close to 24 hour).
Discussion
Our prior work in humans demonstrated that scale-invariance in activity fluctuations during wakefulness was unrelated to extrinsic factors including scheduled events and the light dark/cycle, and unrelated to the average level of activity both within and between subjects (Hu et al., 2004). We now find that this scale-invariant pattern of activity: (i) spans a much wider time scale in humans; (ii) is unaffected by inclusion of activity recordings during sleep as well as during wakefulness; (iii) also occurs in rats with identical scaling exponents at the same time scales as occurs in humans; (iv) is unaffected by a very strong external Zeitgeber (light/dark cycle); and (v) cannot be explained by the simple summation of any underlying ultradian rhythms. Thus, there appears to exist a common underlying mechanism of scale-invariant activity regulation in humans and rats across the 24-hour cycle. In addition, our most striking finding was that in rats with SCN lesion, the scale-invariant patterns of activity completely break down at time scales >4 hour and display significant changes at time scale <4h. This influence of SCN lesioning across a broad range of time scales is consistent with our hypothesis that the SCN functions as a major node in a neuronal network that regulates motor control dynamics over a multitude of time scales. Circadian investigations over the past 34 years have mainly focused on understanding the generation and output of ~24-hour oscillations of the SCN. Our results suggest that the SCN does not act only as a generator of an oscillation with a fixed period, but also influences locomotor activity—over a very broad range of time scales from minutes to 24 h. Moreover, these influences of the SCN at a broad range of time scales are not simply the summation of any underlying ‘ultradian rhythms’ of activity, as discussed below.
Scale invariant organizations in activity beyond ultradian rhythms
Scale invariant correlations and nonlinearities in activity fluctuations reflects temporal organizations across different time scales, and suggest nonlinear interactions between influences on activity of underlying physiological processes at different time scales. In order to produce scale invariant correlations using multiple oscillations (ultradian rhythms), amplitudes of the oscillations at different time scales (peaks in power spectrum) must be arranged in a self-similar manner at different time scales, which is statistically unlikely if these oscillations are independent (Hausdorff and Peng, 1996). Moreover, nonlinearities, as revealed by the magnitude analysis, are independent of oscillatory components as described by power spectrum, i.e., two signals with the same power spectrum can have different nonlinearities (results not shown) (Theiler et al., 1992). Scale invariant nonlinearities reveal complex phase relationship among all oscillatory components in addition to overall organization of oscillatory amplitudes at different time scales. Thus, scale invariance in activity cannot be simple consequences of summation of multiple ultradian rhythms.
Physiological origin of scale invariance
The scale invariant correlations and nonlinearities in activity fluctuations that we observed indicate previously unrecognized intrinsic regulatory mechanisms. Scale-invariant patterns have been observed in physical systems far from equilibrium states and shown to be caused by nonlinear interactions between multiple control components affecting the overall system at different time scales (Mandelbrot, 1982;Bak et al., 1987;Basu et al., 2004). Similar complexity of multi-scale control may be operating in numerous neurophysiological systems via networks of coupled feedback loops (Ivanov et al., 1998;Ashkenazy et al., 2002). In order to build a physiological model of a neural network regulating activity with scale-invariant patterns, the crucial first step is to identify control nodes of such a network. This study has made the first important step in such a model by identifying a major neural node, the SCN, that is critical for scale-invariant patterns of activity at time scales >4 hour.
Contribution of the SCN to scale invariance above 4 hours
Our study cannot distinguish between the following two possible mechanisms causing multiscale regulation of activity over the time scale from 4 to 24 hour: (i) that the SCN contains all components of the multiscale activity regulator responsible for scale invariance above 4 hours (i.e., with varied coupled oscillators within the SCN affecting activity at varied frequencies); (ii) that the SCN interacts with other sites that together produce multiscale activity patterns (e.g., via released factors from the SCN and feedback regulation of behavioral activity itself upon SCN function).
Concerning the first proposed mechanism, previous investigators have found individual oscillators within the SCN have periods relatively close to 24 hour (range 20–28 hour) (Shirakawa et al., 2001). If each individual oscillation within the SCN has a similar sinusoidal waveform, generation of scale-invariant correlations and nonlinearities from 24 hour down to 4 hour would be mathematically unlikely within the SCN itself. However, it has been shown in rat that neuronal populations in the SCN display non-sinusoidal waveform with 4 to 5-hour peaks in electrophysiological discharge rate, and the positions of peaks are different for distinct neurons (Schaap et al., 2003). With nonlinear coupling between individual clock cells in the SCN network consisting of 20,000 coupled neurons (Yamaguchi et al., 2003), raises the possibility that the SCN could be a self-contained multioscillator system. Similar multiple activity regulating elements have been observed for the circadian pacemaker neurons in Drosophila melanogaster (Stoleru et al., 2004;Grima et al., 2004). A multioscillator control system could contribute to activity regulations at multiple time scales, possibly yielding scale invariance emanating from within the SCN itself [hypothesis i) above].
The second mechanism of the SCN interacting with other activity control nodes outside the SCN perhaps seems more likely because of the many known neural and humoral feedback interactions between the SCN and other neural nodes that could influence a wider range of time scales rather than only around 24 h. For instance, on the output side, the SCN releases multiple factors that can affect activity at varied time scales, including transforming growth factor-alpha (TGF-alpha), prokineticin 2 (PK2) and cardiotrophin-like cytokine (CLC) (Kramer et al., 2001;Cheng et al., 2002;Kraves and Weitz, 2006;Li et al., 2006). On the feedback side, it has been shown that activity can change the period of circadian rhythms in activity (Edgar et al., 1991), and that an animal’s activity also may influence the electrical activity of the SCN in vivo (Meijer et al., 1997). An important step to distinguish between these mechanisms will be the identification of the other relevant control nodes, and the characterization of their interactions with the SCN.
Control nodes responsible for scale invariance below 4 hours
The persistence of a scale-invariant pattern of activity in SCNx rats at time scales <4 hour indicates that another neuro-anatomical source(s) (other than the SCN) must be responsible for much of the scale-invariant organization of activity over this shorter time range. The fact that the DFA α and DFA αmag scaling exponents (quantifying correlations and nonlinearities, respectively) do not change over the time scale range from minutes to 4 hour as compared to the time scale range from 4 to 24 hour in intact animals implies that the SCN and the non-SCN mechanisms of activity regulation are coupled. These results are consistent with the hypothesis that a neural network of coupled multiple control nodes is responsible for scale-invariance.
To build a meaningful neurophysiological model of scale-invariant activity regulation, we need to identify the other nodes (besides the SCN) in the network regulating activity with scale-invariant patterns. There are numerous potential candidates for activity control nodes that can operate at different time scales and interact in an integrated and hierarchical fashion. For instance, to drive circadian rhythms in locomotor activity, the SCN sends direct projections and indirect projections with relay neurons in the subparaventircular nucleus (SPVN) to the dorsomedial hypothalamic nucleus (DMH), which conveys the SCN influences to locomotor activity through its output to lateral hypothalamic area (LHA) that contains orexin. Lesions of the DMH not only diminish the circadian rhythms of locomotor activity but also reduce the overall activity level (Chou et al., 2003). In addition, the DMH seems crucial for providing flexibility to adapt the behavioral and physiological cycles to 24-hour rhythm of food availability (Gooley et al., 2006) though it may not fully account for circadian rhythms in the food-anticipatory activity (Landry et al., 2006). Such anticipatory behavior may be caused in part by the peripheral clocks of different organs, the coupled cycles of energy and metabolic balance, and their feedback to the brain (Buijs and Kalsbeek, 2001). Both humoral and hormonal signals may play important roles in the communication between central nervous system and behaviors such as food intake and locomotor activity (Buijs and Kalsbeek, 2001), e.g., glucose, leptin, and ghrelin can send information regarding energy balance to the DMH via the ventromedial (VMH) and arcuate (ARC) nuclei in the hypothalamus (Saper et al., 2005). In addition to the DMH the spinal cord, for activity regulations at small time scales, may be also a major control node of the neural network responsible for the scale-invariant patterns.
Given the complexity of activity control, we are not yet at a stage to build a meaningful neurophysiological model of scale-invariant activity regulation. Nonetheless, despite this underlying complexity, it is all the more compelling that ablation of a single neural site (the SCN) can robustly influence activity fluctuations across so many time scales. Future experiments could be directed at determining the precise anatomical sites of other components of the multiscale activity regulator, and elucidating the nature of the interactions between the SCN and these components. For example, influences on locomotor activity of diffusible factors secreted by the SCN could be tested by measuring the effect upon scale-invariant activity patterns of activity in animals following SCN transplantation and where diffusible humoral signals are permitted but growth of direct neural connections is prevented (Silver et al., 1996).
Contribution of the SCN to scale invariance in different species
In the current study, the contributions of the SCN to the scaling behavior of activity were only detected from the results of rats. Since the SCN generates ~24 hour oscillations in activity of both rats and humans, and humans showed the same scaling patterns in activity fluctuations as control rats, it is tempting to speculate that the SCN has the same contribution to the scale-invariant patterns in human activity. However, there are clear differences between these species in the effect of the SCN on activity, possibly limiting the extrapolation of the data from SCN-lesioned rodents to human activity regulation. For instance, the SCN has opposite influences on activity levels in the two species, with rats being nocturnally active and humans diurnally active. Second, intact rats exhibit well pronounced ultradian rhythms in activity (Fig. 2), that are not as obvious or systematic in human (Hu et al., 2001). Thus, further studies are necessary to test whether the SCN influences on scale-invariant patterns of activity are the same in humans as in rats.
Quantification of scale invariance over different time scale ranges
In the present study, for statistical reasons, the largest time scale we could reliably test the scaling behavior of activity is ~24 hours—one tenth of the signal length (240 hours). Above 24 hour, the scaling behavior is not statistically stable according to the previous simulations of surrogate signals (Hu et al., 2001). In the DFA method, detrending with higher order polynomial functions (the second order polynomial function used in this study, DFA-2) can reduce the artifacts caused by the local trends associated with environmental influences, but it may also lead to an overestimation of the transitional time scale (Hu et al., 2001). Therefore, the actual transition time scale in the scaling behavior of SCNx rats (4h) might be up to a factor of two smaller than the estimation (~4h) based on the DFA-2 results. This result would not change the interpretation of the findings but must be considered if future studies utilize different analytical techniques.
Scale-invariant behavior exists in many neurophysiological systems. There may be some physiological benefit imparted by such scale-invariant patterns. Loss of the scale-invariance may indicate a simpler physiological control system that is less adaptive to perturbations and which is more vulnerable to catastrophic events (Huikuri et al., 2000;Perkiomaki et al., 2001). For instance, reduced scale-invariant correlations of heartbeat intervals occurs with cardiovascular disease and this is associated with reduced survival (Peng et al., 1995;Ashkenazy et al., 2001;Goldberger et al., 2002;Stein et al., 2005). However, until now such behavior has defied explanation in terms of neural mechanisms. Here, we report, for the first time a neural site (i.e., the SCN) that is completely responsible for scale-invariant regulation of a fundamental neurophysiological system over a range of specific time scales. Our results exemplify that experimental manipulations (such as SCN lesioning) can be used to understand the origin of scale-invariant behavior in a neurophysiological system.
Acknowledgments
The research is supported by grants from NIH/NHLBI K24 HL076446 to S.A.S., and Pickwick Fellowship to F.A.J.L.S.
Footnotes
Publisher's Disclaimer: This is a PDF file of an unedited manuscript that has been accepted for publication. As a service to our customers we are providing this early version of the manuscript. The manuscript will undergo copyediting, typesetting, and review of the resulting proof before it is published in its final citable form. Please note that during the production process errors may be discovered which could affect the content, and all legal disclaimers that apply to the journal pertain.
References
- Ashkenazy Y, Hausdorff JM, Ivanov PCh, Stanley HE. A stochastic model of human gait dynamics. Physica A-Statistical Mechanics and Its Applications. 2002;316:662–670. [Google Scholar]
- Ashkenazy Y, Ivanov PC, Havlin S, Peng CK, Goldberger AL, Stanley HE. Magnitude and sign correlations in heartbeat fluctuations. Phys Rev Lett. 2001;86:1900–1903. doi: 10.1103/PhysRevLett.86.1900. [DOI] [PubMed] [Google Scholar]
- Bak P, Tang C, Wiesenfeld K. Self-organized criticality: An explanation of the 1/f noise. Phys Rev Lett. 1987;59:381–384. doi: 10.1103/PhysRevLett.59.381. [DOI] [PubMed] [Google Scholar]
- Basu S, Foufoula-Georgiou E, Porte-Agel F. Synthetic turbulence, fractal interpolation, and large-eddy simulation. Phys Rev E Stat Nonlin Soft Matter Phys. 2004;70:026310. doi: 10.1103/PhysRevE.70.026310. [DOI] [PubMed] [Google Scholar]
- Buijs RM, Kalsbeek A. Hypothalamic integration of central and peripheral clocks. Nat Rev Neurosci. 2001;2:521–526. doi: 10.1038/35081582. [DOI] [PubMed] [Google Scholar]
- Buijs RM, Kalsbeek A, Van der Woude TP, Van Heerikhuize JJ, Shinn S. Suprachiasmatic nucleus lesion increases corticosterone secretion. Am J Physiol. 1993;264:R1186–R1192. doi: 10.1152/ajpregu.1993.264.6.R1186. [DOI] [PubMed] [Google Scholar]
- Chen Z, Ivanov PC, Hu K, Stanley HE. Effect of nonstationarities on detrended fluctuation analysis. Phys Rev E Stat Nonlin Soft Matter Phys. 2002;65:041107. doi: 10.1103/PhysRevE.65.041107. [DOI] [PubMed] [Google Scholar]
- Cheng MY, Bullock CM, Li C, Lee AG, Bermak JC, Belluzzi J, Weaver DR, Leslie FM, Zhou QY. Prokineticin 2 transmits the behavioural circadian rhythm of the suprachiasmatic nucleus. Nature. 2002;417:405–410. doi: 10.1038/417405a. [DOI] [PubMed] [Google Scholar]
- Chou TC, Scammell TE, Gooley JJ, Gaus SE, Saper CB, Lu J. Critical role of dorsomedial hypothalamic nucleus in a wide range of behavioral circadian rhythms. J Neurosci. 2003;23:10691–10702. doi: 10.1523/JNEUROSCI.23-33-10691.2003. [DOI] [PMC free article] [PubMed] [Google Scholar]
- Cohen RA, Albers HE. Disruption of human circadian and cognitive regulation following a discrete hypothalamic lesion: a case study. Neurology. 1991;41:726–729. doi: 10.1212/wnl.41.5.726. [DOI] [PubMed] [Google Scholar]
- Edgar DM, Martin CE, Dement WC. Activity feedback to the mammalian circadian pacemaker: influence on observed measures of rhythm period length. J Biol Rhythms. 1991;6:185–199. doi: 10.1177/074873049100600301. [DOI] [PubMed] [Google Scholar]
- Goldberger AL, Amaral L, Hausdorff JM, Ivanov PCh. Fractal dynamics in physiology: alterations with disease and aging. Proc Natl Acad Sci U S A. 2002;99:2466–2472. doi: 10.1073/pnas.012579499. [DOI] [PMC free article] [PubMed] [Google Scholar]
- Gooley JJ, Schomer A, Saper CB. The dorsomedial hypothalamic nucleus is critical for the expression of food-entrainable circadian rhythms. Nat Neurosci. 2006;9:398–407. doi: 10.1038/nn1651. [DOI] [PubMed] [Google Scholar]
- Grima B, Chelot E, Xia R, Rouyer F. Morning and evening peaks of activity rely on different clock neurons of the Drosophila brain. Nature. 2004;431:869–873. doi: 10.1038/nature02935. [DOI] [PubMed] [Google Scholar]
- Hausdorff JM, Peng C. Multiscaled randomness: A possible source of 1/f noise in biology. PHYSICAL REVIEW E STATISTICAL PHYSICS, PLASMAS, FLUIDS, AND RELATED INTERDISCIPLINARY TOPICS. 1996;54:2154–2157. doi: 10.1103/physreve.54.2154. [DOI] [PubMed] [Google Scholar]
- Hausdorff JM, Purdon P, Peng CK, Ladin Z, Wei JY, Goldberger AL. Fractal dynamics of human gait: stability of long-range correlations in stride interval fluctuations. J Appl Physiol. 1996;80:1448–1457. doi: 10.1152/jappl.1996.80.5.1448. [DOI] [PubMed] [Google Scholar]
- Hu K, Ivanov PC, Chen Z, Carpena P, Stanley HE. Effect of trends on detrended fluctuation analysis. Phys Rev E Stat Nonlin Soft Matter Phys. 2001;64:011114. doi: 10.1103/PhysRevE.64.011114. [DOI] [PubMed] [Google Scholar]
- Hu K, Ivanov PCh, Hilton FM, Chen Z, Shea SA. Non-random fluctuations and multi-scale dynamics regulation of human activity. Physica A. 2004;337:307–318. doi: 10.1016/j.physa.2004.01.042. [DOI] [PMC free article] [PubMed] [Google Scholar]
- Huikuri HV, Makikallio TH, Peng CK, Goldberger AL, Hintze U, Moller M. Fractal correlation properties of R-R interval dynamics and mortality in patients with depressed left ventricular function after an acute myocardial infarction. Circulation. 2000;101:47–53. doi: 10.1161/01.cir.101.1.47. [DOI] [PubMed] [Google Scholar]
- Ivanov PC, Amaral LA, Goldberger AL, Havlin S, Rosenblum MG, Struzik ZR, Stanley HE. Multifractality in human heartbeat dynamics. Nature. 1999;399:461–465. doi: 10.1038/20924. [DOI] [PubMed] [Google Scholar]
- Ivanov PC, Nunes Amaral LA, Goldberger AL, Stanley HE. Stochastic feedback and the regulation of biological rhythms. Europhys Lett. 1998;43:363–368. doi: 10.1209/epl/i1998-00366-3. [DOI] [PubMed] [Google Scholar]
- Ivanov PCh, Rosenblum MG, Peng C-K, Mietus J, Havlin S, Stanley HE, Goldberger AL. Behaviour of heartbeat intervals obtained by wavelet-based time-series analysis. Nature. 1996;383:323–327. doi: 10.1038/383323a0. [DOI] [PubMed] [Google Scholar]
- Jean-Louis G, Mendlowicz MV, Gillin JC, Rapaport MH, Kelsoe JR, Zizi F, Landolt H, von Gizycki H. Sleep estimation from wrist activity in patients with major depression. Physiol Behav. 2000;70:49–53. doi: 10.1016/s0031-9384(00)00228-6. [DOI] [PubMed] [Google Scholar]
- Kalsbeek A, Buijs RM, Van Heerikhuize JJ, Arts M, Van der Woude TP. Vasopressin-containing neurons of the suprachiasmatic nuclei inhibit corticosterone release. Brain Research. 1992;580:62–67. doi: 10.1016/0006-8993(92)90927-2. [DOI] [PubMed] [Google Scholar]
- Kramer A, Yang FC, Snodgrass P, Li X, Scammell TE, Davis FC, Weitz CJ. Regulation of daily locomotor activity and sleep by hypothalamic EGF receptor signaling. Science. 2001;294:2511–2515. doi: 10.1126/science.1067716. [DOI] [PubMed] [Google Scholar]
- Kraves S, Weitz CJ. A role for cardiotrophin-like cytokine in the circadian control of mammalian locomotor activity. Nat Neurosci. 2006;9:212–219. doi: 10.1038/nn1633. [DOI] [PubMed] [Google Scholar]
- Landry GJ, Simon MM, Webb IC, Mistlberger RE. Persistence of a behavioral food-anticipatory circadian rhythm following dorsomedial hypothalamic ablation in rats. Am J Physiol Regul Integr Comp Physiol. 2006;290:R1527–R1534. doi: 10.1152/ajpregu.00874.2005. [DOI] [PubMed] [Google Scholar]
- Larsen PD, elder DE, Tzeng YC, Campbell AJ, Galletly DC. Fractal characteristics of breath to breath timing in sleeping infants. Respir Physiol Neurobiol. 2004;139:263–270. doi: 10.1016/j.resp.2003.11.001. [DOI] [PubMed] [Google Scholar]
- Li JD, Hu WP, Boehmer L, Cheng MY, Lee AG, Jilek A, Siegel JM, Zhou QY. Attenuated Circadian Rhythms in Mice Lacking the Prokineticin 2 Gene. J Neurosci. 2006;26:11615–11623. doi: 10.1523/JNEUROSCI.3679-06.2006. [DOI] [PMC free article] [PubMed] [Google Scholar]
- Mandelbrot B. The Fractal Geometry of Nature. New York: W.H. Freeman and Company; 1982. [Google Scholar]
- Meijer JH, Schaap J, Watanabe K, Albus H. Multiunit activity recordings in the suprachiasmatic nuclei: in vivo versus in vitro models. Brain Res. 1997;753:322–327. doi: 10.1016/s0006-8993(97)00150-9. [DOI] [PubMed] [Google Scholar]
- Moore RY, Eichler VB. Loss of a circadian adrenal corticosterone rhythm following suprachiasmatic lesions in the rat. Brain Res. 1972;42:201–206. doi: 10.1016/0006-8993(72)90054-6. [DOI] [PubMed] [Google Scholar]
- Peng CK, Havlin S, Hausdorff JM, Mietus JE, Stanley HE, Goldberger AL. Fractal mechanisms and heart rate dynamics. Long-range correlations and their breakdown with disease. J Electrocardiol. 1995;28(Suppl):59–65. doi: 10.1016/s0022-0736(95)80017-4. [DOI] [PubMed] [Google Scholar]
- Peng CK, Mietus J, Hausdorff JM, Havlin S, Stanley HE, Goldberger AL. Long-range anticorrelations and non-Gaussian behavior of the heartbeat. Phys Rev Lett. 1993;70:1343–1346. doi: 10.1103/PhysRevLett.70.1343. [DOI] [PubMed] [Google Scholar]
- Peng C-K, Buldyrev SV, Havlin S, Simons M, Stanley HE, Goldberger AL. Mosaic organization of DNA nucleotides. 1685–1689 (1994) Phys Rev E Stat Phys Plasmas Fluids Relat Interdiscip Topics. 1994;49:1685–2689. doi: 10.1103/physreve.49.1685. [DOI] [PubMed] [Google Scholar]
- Perkiomaki JS, Zareba W, Daubert JP, Couderc JP, Corsello A, Kremer K. Fractal correlation properties of heart rate dynamics and adverse events in patients with implantable cardioverter-defibrillators. Am J Cardiol. 2001;88:17–22. doi: 10.1016/s0002-9149(01)01578-8. [DOI] [PubMed] [Google Scholar]
- Ralph MR, Foster RG, Davis FC, Menaker M. Transplanted suprachiasmatic nucleus determines circadian period. Science. 1990;247:975–978. doi: 10.1126/science.2305266. [DOI] [PubMed] [Google Scholar]
- Saper CB, Scammell TE, Lu J. Hypothalamic regulation of sleep and circadian rhythms. Nature. 2005;437:1257–1263. doi: 10.1038/nature04284. [DOI] [PubMed] [Google Scholar]
- Schaap J, Albus H, VanderLeest HT, Eilers PH, Detari L, Meijer JH. Heterogeneity of rhythmic suprachiasmatic nucleus neurons: Implications for circadian waveform and photoperiodic encoding. Proc Natl Acad Sci U S A. 2003;100:15994–15999. doi: 10.1073/pnas.2436298100. [DOI] [PMC free article] [PubMed] [Google Scholar]
- Scheer FAJL, Pirovano C, Van Someren EJW, Buijs RM. Environmental light and Suprachiasmatic nucleus interact in the regulation of body temperature. Neuroscience. 2005;132:465–477. doi: 10.1016/j.neuroscience.2004.12.012. [DOI] [PubMed] [Google Scholar]
- Scheer FAJL, Ter Horst GJ, Van der Vliet J, Buijs RM. Physiological and anatomic evidence for regulation of the heart by suprachiasmatic nucleus in rats. Am J Physiol Heart Circ Physiol. 2001;280:H1391–H1399. doi: 10.1152/ajpheart.2001.280.3.H1391. [DOI] [PubMed] [Google Scholar]
- Schwartz WJ, Busis NA, Hedley-Whyte ET. A discrete lesion of ventral hypothalamus and optic chiasm that disturbed the daily temperature rhythm. J Neurol. 1986;233:1–4. doi: 10.1007/BF00313981. [DOI] [PubMed] [Google Scholar]
- Shirakawa T, Honma S, Honma K. Multiple oscillators in the suprachiasmatic nucleus. Chronobiol Int. 2001;18:371–387. doi: 10.1081/cbi-100103962. [DOI] [PubMed] [Google Scholar]
- Silver R, LeSauter J, Tresco PA, Lehman MN. A diffusible coupling signal from the transplanted suprachiasmatic nucleus controlling circadian locomotor rhythms. Nature. 1996;382:810–813. doi: 10.1038/382810a0. [DOI] [PubMed] [Google Scholar]
- Stein PK, Domitrovich PP, Huikuri HV, Kleiger RE. Traditional and nonlinear heart rate variability are each independently associated with mortality after myocardial infarction. J Cardiovasc Electrophysiol. 2005;16:13–20. doi: 10.1046/j.1540-8167.2005.04358.x. [DOI] [PubMed] [Google Scholar]
- Stephan FK, Zucker I. Circadian rhythms in drinking behavior and locomotor activity of rats are eliminated by hypothalamic lesions. Proc Natl Acad Sci U S A. 1972;69:1583–1586. doi: 10.1073/pnas.69.6.1583. [DOI] [PMC free article] [PubMed] [Google Scholar]
- Stoleru D, Peng Y, Agosto J, Rosbash M. Coupled oscillators control morning and evening locomotor behaviour of Drosophila. Nature. 2004;431:862–868. doi: 10.1038/nature02926. [DOI] [PubMed] [Google Scholar]
- Theiler J, Eubank S, Longtin A, Galdrikian B, Farmer JD. Testing for nonlinearity in time- series - the method of surrogate data. Physica D. 1992;58:77–94. [Google Scholar]
- Weaver DR. The suprachiasmatic nucleus: a 25-year retrospective. J Biol Rhythms. 1998;13:100–112. doi: 10.1177/074873098128999952. [DOI] [PubMed] [Google Scholar]
- Xu L, Ivanov PCh, Hu K, Chen Z, Carbone A, Stanley HE. Quantifying signals with power-law correlations: A comparative study of detrended fluctuation analysis and detrended moving average techniques. Phys Rev E. 2005;71:851101. doi: 10.1103/PhysRevE.71.051101. [DOI] [PubMed] [Google Scholar]
- Yamaguchi S, Isejima H, Matsuo T, Okura R, Yagita K, Kobayashi M, Okamura H. Synchronization of cellular clocks in the suprachiasmatic nucleus. Science. 2003;302:1408–1412. doi: 10.1126/science.1089287. [DOI] [PubMed] [Google Scholar]