First-principles study of non-heme Fe(II) halogenase SyrB2 reactivity

Abstract

We present here a computational study of reactions at a model complex of the SyrB2 enzyme active site. SyrB2, which chlorinates L-threonine in the syringomycin biosynthetic pathway, belongs to a recently discovered class of α-ketoglutarate (αKG), non-heme Fe(II) dependent halogenases that shares many structural and chemical similarities with hydroxylases. Namely, halogenases and hydroxylases alike decarboxylate the αKG co-substrate, facilitating formation of a high-energy ferryl-oxo intermediate that abstracts a hydrogen from the reactant complex. The reaction mechanisms differ at this point, and mutation of active site residues (Asp for the hydroxylase to Ala or Ala to Asp/Glu for halogenase) fails to reproduce hydroxylating activity in SyrB2 or halogenating activity in similar hydroxylases. Using a density functional theory (DFT) approach with a recently implemented Hubbard U correction for accurate treatment of transition-metal chemistry, we explore probable reaction pathways and mechanisms via a model complex consisting only of the iron center and its direct ligands. We show that the first step, αKG decarboxylation, is barrierless and exothermic, while the subsequent hydrogen abstraction step has an energetic barrier consistent with that accessible under biological conditions. In the model complex we use, radical chlorination is barrierless and exothermic, while the analogous hydroxylation is found to have a small energetic barrier. The hydrogen abstraction and radical chlorination steps are strongly coupled: the barrier for the hydrogen abstraction step is reduced when carried out concomitantly with the exothermic chlorination step. Our work suggests that the lack of chlorination in mutant hydroxylases is most likely due to poor binding of chlorine in the active site, while mutant halogenases do not hydroxylate for energetic reasons. While secondary shell residues undoubtedly modulate the overall reactivity and binding of relevant substrates, we show that a small model compound consisting exclusively of the direct ligands to the metal can help explain reactivity heretofore not yet understood in the halogenase SyrB2.

Introduction

Density functional theory (DFT) is the method of choice for studying transition-metal complexes anywhere from a handful to a few hundred atoms in size, both because of its affordable scaling and its treatment of correlation. Self-interaction, wherein each electron resides in the total electric field of the system, greatly limits the accuracy and predictive nature of DFT; however, a recently introduced Hubbard U correction to standard DFT has been shown to provide systematic improvements^1,2. Estimates of barrier heights and spin state splittings, which may exhibit errors around 20 kcal/mol within standard DFT³ (here, GGA), are improved by an order of magnitude with the addition of a Hubbard U term^1,2 referred to as GGA+U. We apply the Hubbard U approach for the first time to biological systems, focusing in particular on SyrB2, a halogenase that is part of a recently discovered class of α-ketoglutarate (αKG), non-heme Fe(II) dependent enzymes⁴.

Many man-made and over 4500 natural halogenated molecules have been characterized, with chlorine being the predominant modifier⁵. Natural organic halogenated compounds with known therapeutic capabilities include vancomycin and chlortetracycline⁵. Halogenation is commonly employed in drug synthesis because therapeutics can exhibit 4–10 fold increase in efficacy upon chlorination of a single site, but chlorination of unactivated alkanes can be quite challenging^6,7,8. There are several types of chlorinating enzymes reliant upon cofactors or metal centers including the recently structurally characterized non-heme Fe(II) enzyme, SyrB2^4,9. The two-His, Fe center enzymes, including SyrB2, are particularly interesting because they are known to form C-Cl bonds at typically unreactive, aliphatic carbons^10,11. Mechanisms of this latter class of halogenases may be inferred from numerous closely related hydroxylases^12,13, but the differences that induce halogenation in lieu of hydroxylation are not well understood. While structures of halogenating active sites have recently been determined⁴, few electronic structure calculations have been carried out using these structures, despite the fact that such calculations can help to elucidate nuances of halogenase activity.

SyrB2 is found in a Pseudomonas syringae biosynthetic pathway and is part of a larger set of proteins that create an antifungal peptide called syringomycin E¹⁰. The ninth residue of the Syringomycin E lipo-nonapeptidolactone is a chlorinated threonine (4-Cl-L-Thr). The substrate for SyrB2 is L-Thr, which is attached to a 66 kDa protein SyrB1 via a phosphopantetheine arm¹⁰. When the L-Thr-S-SyrB1 complex is delivered into the center of the SyrB2 active site, the extent to which the residues near the SyrB2 active site reorient is unknown. SyrB2 reacts with L-Thr to produce 4-Cl-Thr-S-SyrB1, which is later used by the SyrE protein to complete the formation of syringomycin E¹⁴. SyrB2 has been shown to be capable of bromination in the absence of chlorine, although chlorine is preferred over bromine by a factor of 180; no other halogenation (with F⁻ or I⁻) nor hydroxylation has been observed^4,15.

Non-heme iron halogenases are homologous to a family of hydroxylases, which are comparatively well studied¹⁶. The hydroxylases have an iron center ligated by two histidine ligands; addition of a carboxylate, absent in the halogenases, completes the motif known as the “facial triad”¹⁷. Reactivity is also dependent upon decarboxylation of a metal ligating co-substrate such as α-ketoglutarate (αKG; Fig. 1). Most hydroxylases act on free amino acid or polypeptide chains, but very recent biochemical work has demonstrated that the hydroxylase SyrP acts on L-Asp to produce L-3-OH-Asp only when the substrate is loaded on a phosphopantetheine prosthetic group similar to the one that delivers substrate to SyrB2¹⁸. The best-characterized non-heme iron hydroxylase is Taurine/αKG dependent dioxygenase, known as TauD^19,20,21. Studies of TauD show that the His99 that is coplanar with αKG is a prerequisite for an active enzyme, while the distal His255 can be substituted with as much as 81% activity maintained²⁰. The carboxylate of the ligand Asp101 is thought to be important for retaining activity, but it may be substituted with Glu or, alternatively, Ala in the presence of formate. The latter amino acid substitution likely recovers hydroxylase activity by creating a space in which the formate may bind and mimic the carboxylate of Asp. Such an effect with formate was observed in a similar enzyme upon mutation of the Asp to Gly²², further suggesting that the carboxylate ligand to Fe(II) in these enzymes is not mandatory. Mutation of TauD’s Asp to Ala and addition of Cl⁻ did not reproduce halogenase activity²⁰. Stopped-flow absorption and Mössbauer experiments suggest a large kinetic isotope effect (KIE) associated with the C-H bond cleavage step, indicating both that high-spin Fe(IV)=O intermediate decay is strongly coupled to C-H bond cleavage²¹ and that tunneling is relevant²⁰.

Figure 1.

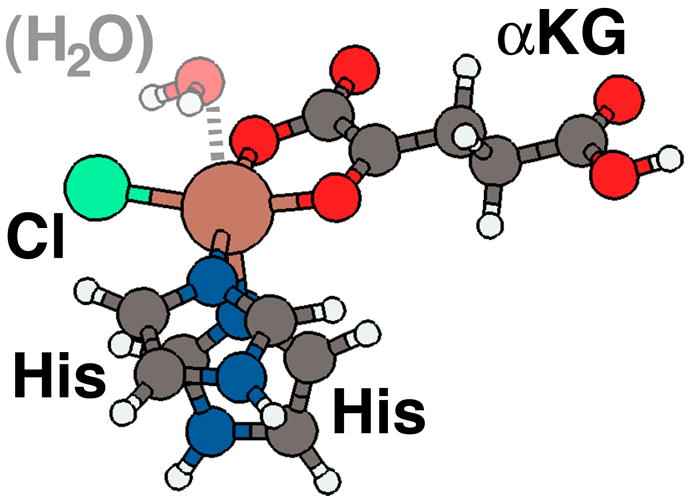
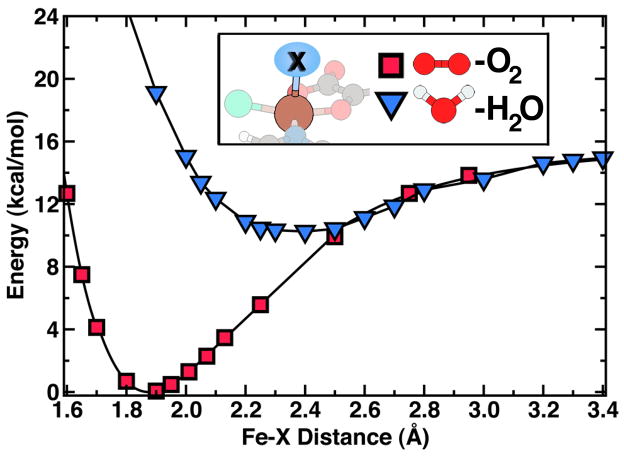
Model of SyrB2 active site employed in calculations. The four equatorial ligands to the iron metal center are chloride, oxygen atoms from bidentate αKG, and a truncated histidine residue. The proximal axial ligand, here H₂O, changes during the catalytic cycle; the distal ligand is another histidine.

The crystal structure of SyrB2 with Fe(II), αKG, and Cl⁻ bound but without the substrate has recently been solved at a resolution of 1.60 Å⁴. The structure is comprised of 2465 atoms, which includes the 310 protein residues, co-substrates and metal ions⁴. The catalytic cycle is known to be Fe(II), αKG, Cl⁻ and O₂ dependent, and the reaction also produces succinate, CO₂, and OH⁻ ion for charge balance (Eq. 1–3). While much of the active site motif, two histidines and bidentate αKG, is conserved with respect to the hydroxylases, SyrB2 is one of the first mononuclear iron proteins to coordinate Fe(II) with Cl⁻ instead of a carboxylate. A water molecule, which is likely displaced by the L-Thr-S-SyrB1 substrate, occupies the remaining axial site in the crystal structure. Based on spectroscopic studies, it is believed that a high-valent Fe(IV)=O center is generated via O₂ attack and decarboxylation of αKG as follows²³:

$$[{\text{Fe}}^{\text{II}}{-\text{OH}}_2]-\text{Cl}+{\text{O}}_2+\alpha \text{KG}\to [{\text{Fe}}^{\text{IV}}=\text{O}]-\text{Cl}+{\text{H}}_2\text{O}+{\text{CO}}_2+\text{succinate}.$$ (1)

The Fe(IV)=O intermediate can then abstract a hydrogen from the substrate, leaving behind a radical:

$$[{\text{Fe}}^{\text{IV}}=\text{O}]-\text{Cl}+\text{R}-{\text{CH}}_3\to [{\text{Fe}}^{\text{III}}-\text{OH}]-\text{Cl}+\text{R}-{\text{CH}}_2^{•}.$$ (2)

The methyl radical of the substrate then abstracts Cl:

$$[{\text{Fe}}^{\text{III}}-\text{OH}]-\text{Cl}+\text{R}-{\text{CH}}_2^{•}\to {\text{Fe}}^{\text{II}}-\text{OH}+\text{R}-{\text{CH}}_2\text{Cl}.$$ (3)

In hydroxylases, an OH radical is delivered instead of a Cl radical to the substrate via a radical rebound mechanism. Mutation of the alanine in SyrB2’s Cl⁻ binding pocket to an aspartic acid that is present in hydroxylases fails to induce hydroxylation⁴. Chlorination of the alkyl radical has been proposed to be very thermodynamically favorable as a possible explanation for why halogenation might predominate over hydroxylation²⁴. Here, using a first principles approach, we comprehensively study the steps of the catalytic cycle and, in particular, evaluate the relative energetics of alkyl radical chlorination versus hydroxylation.

The model system was chosen to include direct ligands that mimic the environment present around the Fe(II) center in the SyrB2 active site. This ligand set includes an equatorial, bidentate αKG molecule, both equatorial and distal histidines modeled as imidazole rings, an equatorial chloride, and an open axial site initially populated by a water molecule (Fig. 1). For SyrB2 reactivity, a minimal model size is expected to work particularly well because only two of the ligand interactions are derived from amino acid residues. Furthermore, the omitted second sphere residues, which may undergo some rearrangement upon SyrB1 binding, are believed to primarily position and bind the other co-substrate-based ligands (i.e. Cl⁻ and αKG). As long as the electronic structure of iron and the geometry of the direct ligand set are in agreement with experimentally measured values of the active site of the full protein, then this minimal model system should be sufficient. Spurious effects, which are derived from the lack of a more complete protein backbone, may arise from the absence of a histidine-iron-histidine angle constraint, a hydrophobic pocket that stabilizes chloride binding, and both hydrogen bonding and π-stacking interactions that constrain the placement of the αKG²⁵. While the absence of some of these secondary structural characteristics is likely to slightly modulate barrier heights, we show that a small model is sufficient for describing the reactivity of the full protein.

Methods

Calculations on the model system included as few as 34 atoms and as many as 51 atoms when the L-threonine substrate was present, including hydrogen capping to saturate bonds. Plane-wave calculations were carried out using the PBE-GGA exchange-correlation functional²⁶, as implemented in the Quantum-Espresso package²⁷. This semi-local GGA accurately describes hydrogen bonds but does not include van der Waal’s interactions, which, while not relevant for this model system, can contribute as much as 0.2 kcal/mol to total energies²⁸. Ultrasoft pseudopotentials were employed to model the core electrons (note: for Fe, the semi-core 3s and 3p states were treated in the valence); wavefunction and charge density plane-wave cutoffs were chosen to be 30 and 300 Ry, respectively. Standard GGA calculations were augmented with a self-consistent, Hubbard U term calculated from linear-response (referred to as GGA+U)^2,29 and averaged over several intermediates to be 5.6 eV (see sections S.1-2 of the Supporting Information). GGA+U is used here to improve the structure, energetics, transition-state barrier heights and spin state ordering of transition-metal complexes^1,2. The structures were placed in a large cubic cell, roughly 18 Å on each side to ensure there were no periodic image effects, and neutrality of the complete model system was always maintained. In most cases, energetic barriers were determined using the nudged-elastic band (NEB) method along with the improvements of climbing image and variable springs for better resolution around the transition-state^30,31. Forces on the path images in NEB calculations were minimized to less than 0.05 eV/Å to ensure convergence. Since quantum effects on the protons were neglected in the hydrogen abstraction step, the barrier heights calculated for this step should be viewed as an upper bound. For barrierless steps, binding curves or dissociations were determined via a constrained relaxation. In all constrained relaxations throughout this work, the interatomic distance between two atoms was fixed and all other degrees of freedom were permitted to relax. Oxidation states were obtained from the occupation matrix obtained from projection onto the localized 3d states of iron.

Results

Preliminary relaxations of the SyrB2 model complex were carried out to ensure that the geometry and electronic structure of the minimal model reasonably reflected that of the full enzyme. The weakly bound water molecule in the axial site (structure in Fig. 1; energetics in Fig. 2), is consistent with the observation that water is displaced upon substrate binding and with the experimental crystal structure finding that water interacts with the neighboring protein environment⁴. In our GGA calculations, we observe a shortened, 2.30 Å, Fe(II)-Cl bond, compared to the 2.44 Å value observed in the crystal structure⁴, and shortened Fe-O distances for both αKG coordinated oxygen atoms of nearly 0.10 Å. Using our GGA+U methodology, which has a tendency to elongate bonds with respect to standard GGA¹, we achieve an improved estimate of 2.41 Å for the Fe(II)-Cl bond, which is within 0.03 Å of the value observed in the crystal structure⁴, and the Fe-O_αKG distances are also in agreement with the experiment. Both GGA and GGA+U iron-histidine distances are consistent with crystal structure values, but the His-Fe-His angle in the minimal model, which fluctuates without any constraint from 80 to 86°, is larger than the 69° experimental value⁴ for the full protein. Underlying the errors for GGA in the geometric description of our model complex, we find that GGA overestimates charge transfer from the Fe center to surrounding ligands, essentially predicting an Fe(III) oxidation for the reactant complex. GGA+U on the other hand recovers the known Fe(II) character¹⁰ of the model system by tuning charge transfer between iron and its ligands. We therefore justify our use of this small model by its good agreement with experimentally known quantities and through larger-scale calculations (see section S.3 of the Supporting Information).

Figure 2.

Binding curves of H₂O and O₂ in the axial site of the starting SyrB2 model compound. The binding curves of water and dioxygen are aligned at their respective dissociation limits. The binding of H₂O (blue triangles) is weak compared to that of the displacing O₂ (red squares).

Decarboxylation and Fe(IV)=O formation

The first step for halogenation is the decarboxylation of α-ketoglutarate (αKG) via oxidative attack from an O₂ molecule bound to Fe in the proximal axial position²³ Binding of O₂ is favorable, with the lowest electronic state, a quintet, corresponding to a relatively short, 1.84 Å, equilibrium bond length between the iron center and O₂ and a dissociation energy of 16 kcal/mol (Fig. 2). The triplet state, which is 3 kcal/mol higher in energy than the quintet state, has a bond length of 1.88 Å and a higher dissociation energy of 26 kcal/mol (see Table 1). Population of this excited triplet state could lead to inactivation of the enzyme, which occurs experimentally after around 7 turnovers²³. The bond length of O-O, when bound in the quintet intermediate, is lengthened by over 0.1 Å with respect to gas phase O₂, indicating a decrease in bond order that should expedite the O-O bond cleavage step in αKG decarboxylation.

Table 1.

Summary of bond lengths (Å) and dissociation energies (kcal/mol) of axial (H₂O, O₂, O, and OH) and equatorial (Cl) ligands in the SyrB2 model complex intermediates.

Ligand	2S+1	Re (Å)	De (kcal)	State
H2O	5	2.40	6	Fe(II)
	3	2.10	7	Fe(II)
O2	5	1.84	16	Fe(III)
	3	1.88	26	Fe(III)
O	5	1.65	42	Fe(IV)
	3	1.74	23	Fe(IV)
OH	6	1.88	52	Fe(III)
	4	1.84	43	Fe(III)
Cleq	6	2.34	13	Fe(III)
	4	2.29	5	Fe(III)

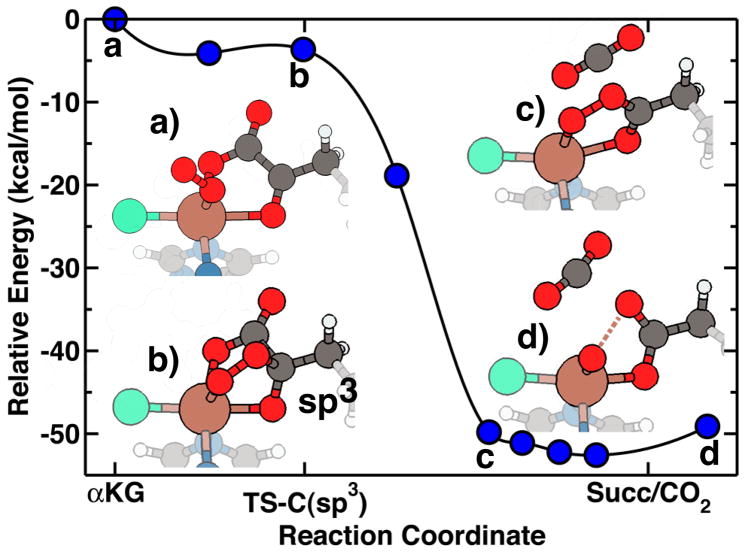
Upon addition of the oxygen to αKG, decarboxylation proceeds, leaving behind the Fe(IV)=O intermediate. Calculations of this decarboxylation step show that once the additive oxygen from O₂ is in the vicinity of the αKG carbon backbone, the electronic structure at the attacked carbon evolves. The carbon geometry becomes more tetrahedral, indicating the transformation in hybridization from sp² to sp³(from a to b in Fig. 3). This step is essentially barrierless and is followed by the exothermic release of CO₂ from the sp³ activated carbon that then returns to an sp²-like geometry (c in Fig. 3). Concomitantly, the O-O bond of the axial dioxygen breaks, and the newly formed succinate molecule returns to the plane of the other two iron ligands (d in Fig. 3). Succinate may bind in a bidentate fashion; however, our electronic structure calculations slightly favor a monodentate structure, in which there is one short, 2.1 Å and one long, 2.7 Å Fe-O_succinate bond. Overall, the GGA+U calculations predict the barrierless decarboxylation step to be exothermic by 50 kcal/mol (Fig. 3). Using a standard GGA approach, release of CO₂ and subsequent rotation of the succinate to the equatorial plane is prohibitive by nearly 12 kcal/mol, but this barrier is likely an artifact of self-interaction errors (see section S.5 of the Supporting Information). It was considered that CO₂ might bind to or interact with either the iron directly or other active site ligands, but GGA+U calculations showed that CO₂ would not preferentially bind anywhere on the minimal model.

Figure 3.

Reaction pathway energetics and structure for the exothermic decarboxylation of αKG in SyrB2 model compound. Relevant structures along the pathway are identified by a) reactants with bound axial O₂, b) O₂-induced sp3 hybridization in the αKG backbone, c) return to sp² hybridization following CO₂ elimination, and d) breaking of the O₂ bond and succinate in equatorial position.

The iron-oxo intermediate that is formed upon decarboxylation has been identified spectroscopically as a high spin, highly-oxidized Fe(IV)=O species^23,32. Our GGA+U calculations confirm the experimentally observed high spin state. The oxidation state is nominally Fe(IV), in which four majority-spin electrons doubly occupy the δ and π states. The Fe(IV)=O bond length is a very short 1.65 Å, in agreement with recent EXAFS measurements (1.66 Å)³². The short bond length reflects greater similarity with the tightly-bound diatomic X ⁶Σ⁺ FeO⁺ molecule² than with the Fe(II)-OH₂ intermediate, which has a bond length that is longer by nearly 0.8 Å (Table 1). We also observe in the Fe(IV)=O complex a shortened 2.30 Å Fe(IV)-Cl bond in agreement with EXAFS results (2.31 Å)³².

Calibrating hydrogen abstraction energetics

The formation of methyl radical via hydrogen abstraction from methane was studied alongside abstraction from L-threonine both because of the greatly reduced computational cost to studying methane and because comparison between the substrates ultimately permits identification of the degree of substrate selectivity of the model complex. The abstraction of hydrogen from the substrate is a key step in the overall halogenation reaction carried out by the full SyrB2 enzyme. However, this hydrogen abstraction step is actually quite common in a large number of αKG-dependent enzymes, several of which are involved in hydroxylation or other reactions⁶. We first ensure that theoretical treatments of the hydrogen abstraction step catalyzed by the SyrB2 model complex are calculated accurately by comparing calculations of uncatalyzed gas phase values with their experimental values.

Gas phase calculations on isolated methane and L-Thr were carried out through constrained relaxations in which a hydrogen, H_abs, was gradually abstracted from the relevant methyl group while the remainder of the molecule was permitted to relax freely. Both methane and L-Thr form stable methyl radicals as the hydrogen is abstracted, with the other bonds to the methyl carbon becoming co-planar with angles around 120^o. The calculated radical formation energy of 99 kcal/mol for methane (from extrapolation to the dissociation limit) is in good agreement with the 103 kcal/mol value from experiments³³. The L-Thr radical formation energy is 92 kcal/mol, and this smaller energetic cost with respect to methane is consistent with the experimentally observed trend of increasing radical stability with size³³.

Methane: separate hydrogen abstraction and chlorination steps

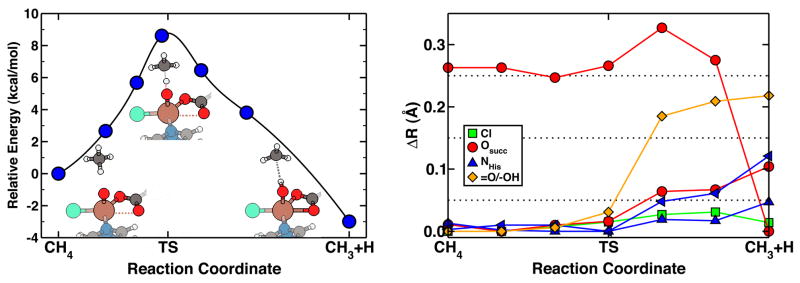
The energetic cost of hydrogen abstraction from methane by the SyrB2 model is reduced ten-fold from the uncatalyzed value to under 10 kcal/mol, and the reaction step is exothermic by 3 kcal/mol (Fig. 4).

Figure 4.

Reaction pathway energetics and structure of methane hydrogen abstraction via SyrB2 model compound. The hydrogen abstraction step (left, with structures) has a barrier of 9 kcal/mol but is weakly exothermic. Tracking of key structural parameters (right) show elongation of the Fe-O bond at the transition state, and a preference for two short Fe-O_succinate distances in the product complex.

The use of a NEB chain-of-states approach enables us to identify changes in structural properties along the minimum-energy path. The critical Fe-ligand bond lengths for the hydrogen abstraction are plotted in Fig. 4 in terms of their displacement from the shortest values, which typically correspond to the value in the reactant complex. The majority of the Fe-ligand bonds lengthen upon the formation of an O-H_abs bond in the transition state (Fig. 4). This feature is due to the increasing electron density at the iron center and decreasing electron density in iron-ligand bonds associated with a transition from Fe(IV) towards Fe(III). The Fe-Cl and Fe-N_His bond lengths increase slightly (0.02–0.08 Å). In contrast, a dramatic change occurs at the transition state for the axial oxygen- from 1.65 Å for Fe(IV)=O to 1.85 Å in Fe(III)-OH - with none of the path images corresponding to an intermediate distance between the short and long Fe-O bond regimes. Interestingly, one Fe-O_succinate bond length decreases from 2.7 Å to 2.4 Å, while the other Fe-O_succinate bond length increases slightly from 2.1 Å to 2.2 Å, corresponding to a move from monodentate to succinate binding also brought on by changes in the iron oxidation state.

While hydrogen abstraction is a common step for non-heme iron enzymes, the subsequent chlorination step at an aliphatic carbon, is specific to the halogenase subfamily²³. To determine the energetic cost of this step, we investigated methyl-radical chlorination by model SyrB2 complex through constrained relaxations with incrementally fixed methyl-Cl distances. We find that the chlorination of the free methyl radical is barrierless and exothermic by 14 kcal/mol (Table 2).

Table 2.

Summary of activation barriers, E_a, and reaction exothermicities, ΔE_r, in kcal/mol for the hydrogen abstraction, (H_abs), chlorination, (-Cl), and hydroxylation steps, (-OH), for both methane and L-threonine substrates with and without the SyrB2 model catalyst.

		CH4 (kcal/mol)			L-Thr (kcal/mol)
		Habs	-Cl	-OH	Habs	-Cl	-OH
No Catalyst	Ea	99	0	2	92	0	2
	ΔEr	99	−15	−41	92	−19	−40
SyrB2	Ea	9	0	4	7	0	4
	ΔEr	−3	−14	−29	−4	−20	−29
Coupled	Ea	-	-	-	3	0	-
	ΔEr	-	-	-	-	−24	-

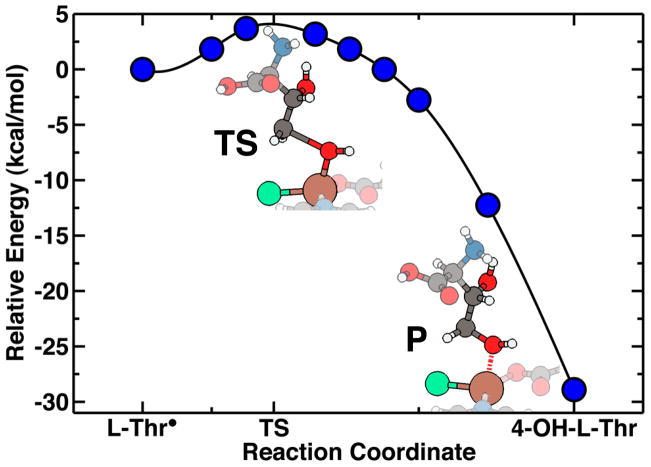
L-threonine: a coupled hydrogen abstraction and chlorination mechanism

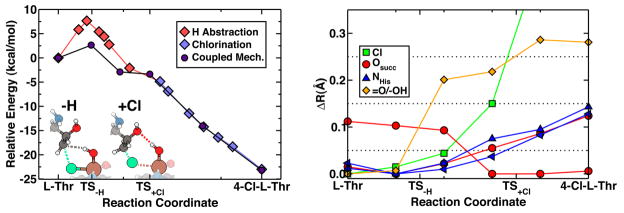
As with methane, abstraction of hydrogen from L-Thr is calculated to have a greatly reduced energetic barrier (~7 kcal/mol with respect to the uncatalyzed 92 kcal/mol value, in Table 2). The transition state in the hydrogen transfer step is found to be the point at which the hydrogen is shared equally between L-Thr and the iron-oxo species (Fig. 5). Upon abstraction of the hydrogen from L-Thr, the newly formed axial –OH_abs ligand stabilizes the radical via hydrogen bonding to the -OH group of L-Thr. The structural trends along the reaction coordinate in other iron-ligand bond lengths reflect those observed previously for the hydrogen abstraction on methane.

Figure 5.

Reaction pathway energetics and structure for coupled chlorination of L-Thr by SyrB2 model compound. Energetics (left) of coupled mechanism show a reduced barrier of 3 kcal/mol (purple circles) compared to that of 7 kcal/mol for separate hydrogen abstraction (red diamonds) and halogenation (blue diamonds) steps. Cartoon representations (left) and tracking of key structural parameters (right) show that in coupled hydrogen abstraction (TS_−H), equatorial Fe-Cl elongation stabilizes L-Thr, and in coupled chlorination (TS_+Cl), hydrogen bonding from Fe-OH stabilizes L-Thr.

We next considered wither hydrogen abstraction and chlorination are concerted, coupled, or uncoupled steps. Since the hydrogen abstraction step has a small barrier and the chlorination step was previously observed to be exothermic and barrierless, it follows that some barrier height reduction is likely when the two steps are coupled. Therefore, we carried out NEB calculations in which the chlorination and hydrogen abstraction steps were permitted to occur at the same time. These results show (Fig. 5) that the partial stabilization of the substrate by interactions between the methyl carbon and the chlorine slightly reduce the barrier height to 3 kcal/mol from the 7 kcal/mol value as determined only for hydrogen abstraction. The abstracted hydrogen forms a hydrogen bond with the –OH group of the L-Thr radical, further stabilizing the molecule to accept the chlorine atom, as part of a reaction mechanism. The overall exothermicity of the abstraction and chlorination is 24 kcal/mol in both the isolated and coupled mechanisms. Interaction of the model complex’s axial hydroxyl with the carbon backbone of the substrate is also possible and would stabilize the substrate, though to a lesser degree. However, the absence of hydroxyl-substrate interactions would not prevent the highly exothermic and barrierless chlorination step from occurring, as is apparent from recent work that characterizes chlorination of L-Val by SyrB2³².

We do not find a single transition state for both the hydrogen abstraction and chlorination steps, and therefore it cannot be said that these steps are strictly concerted. The structural trends along the reaction coordinate show that some Fe-Cl elongation occurs prior to completion of the hydrogen abstraction (Fig. 5) as a result of stabilizing interactions between chlorine and the forming L-Thr radical. As for the hydrogen abstraction step, we again observe a shortening of the equatorial Fe-O_succinate bonds, while the Fe-N_His bonds elongate slightly in the transition. Interestingly, we find a significant amount of Fe-OH_abs bond elongation is favorable during the chlorination, likely due to the –OH_abs participation in a hydrogen bond with the substrate in the model system. Overall, the chlorination from this structural arrangement is amenable to constraints that would be imposed by the substrate being loaded on the SyrB1 phosphopantetheine arm. While some translation of the substrate is preferred to induce chlorination, it is still far less than required for the rebound hydroxylation step described below.

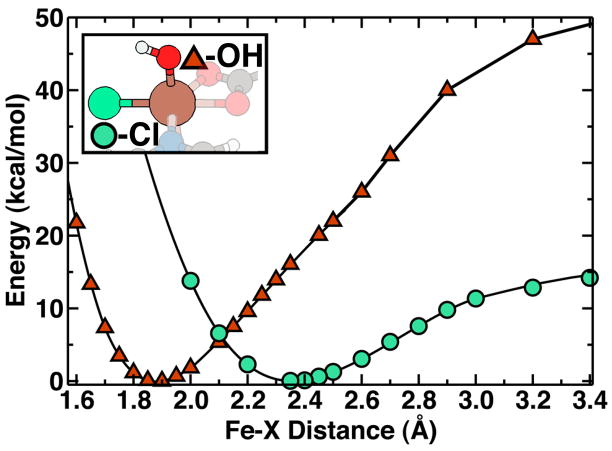
Hydroxylation vs. chlorination

The hydrogen bond, which forms between the L-threonine radical and the model complex, further implies that hydroxylation as the next step would be prohibitive. A rebound attack on the hydroxyl ligand by the L-threonine radical would first require rotation of the -OH_abs group and breaking of the hydrogen bond (Fig. 5). Additionally, the carbon and oxygen would have to move closer together in order for the chemical bond to form, thus requiring either unfavorable translation of L-Thr further into the active site or strain of Fe-OH out of the axial position and towards the substrate.

An understanding of the relative binding energies of the axial hydroxyl ligand compared to the equatorial chloride ligand interaction should give some further clues to why this enzyme prefers halogenation. Hydroxyl binding strength is also relevant because regeneration of SyrB2 to its resting state requires replacement of the hydroxyl with an easily displaced water molecule. As shown in Fig. 6, the binding energy, 52 kcal/mol, is large for the hydroxyl radical in the lowest sextet state. The bond length of the second-lowest state, a quartet, is around 1.84 Å, slightly shorter than the 1.88 Å value for the sextet ground state (Table 1). Both states exhibit binding energies over 40 kcal/mol, suggesting that the bare hydroxyl radical cannot be easily removed without a modifying step, such as protonation. Our results indicate that the energetic cost of breaking the Fe(III)-Cl bond is around 13 kcal/mol, which is much less than the 52 kcal/mol binding energy for the sextet Fe(III)-OH bond (Fig. 6). The shallow chlorine binding curve shows that fluctuations over 0.10 Å in the Fe(III)-Cl bond length, which occur along the reaction coordinate, have only small energetic effects on the order of 1 kcal/mol. This observation suggests that the apparent variations of iron-chloride bonds in the full SyrB2 enzyme from 2.4–2.44 Å in Fe(II)-Cl bonds^4,32, which are long with respect to 2.2–2.3 Å values observed for model compounds, and shorter 2.31 Å Fe(IV)-Cl³² are not likely to have a major role in reactivity. After the hydrogen abstraction step, chlorination of any substrate should be barrierless because the energetic gain of forming a C-Cl bond outweighs the relatively small cost for breaking the Fe-Cl bond. Further, the relative binding energies of -OH and -Cl to the iron center in a particular active site should modulate the relative rates of hydroxylation and chlorination³⁴.

Figure 6.

Potential energy curves of equatorial Cl and axial OH ligands in the SyrB2 model compound. The binding of chloride in an equatorial site (green circles) is weak compared to the axial hydroxyl (red triangles), as indicated by a lower dissociation energy and a longer bond length.

Study of the hydroxylation step reveals that the most probable minimum energy path has a small barrier of around 4 kcal/mol (Fig. 7). The greatest cost in undergoing hydroxylation appears to be the significant elongation of the Fe-OH bond from the equilibrium value of 1.85 Å to over 2.0 Å in the transition-state directly prior to forming 4-OH-L-Thr. The small barrier for the hydroxylation reaction is a direct result of the strong Fe(III)-OH bonding, yet hydroxylation is still quite exothermic at about 29 kcal/mol (Table 2).

Figure 7.

Reaction pathway energetics and key structures for the theoretical hydroxylation of L-Thr by SyrB2 model compound. The hydroxylation step has a small 4 kcal/mol barrier as a result of strain of the axial Fe-OH bond in the transition state (TS) but forms products (P) exothermically.

Comparison of the catalyzed chlorination and hydroxylation steps against comparable reactions of a bare methyl or L-Thr radical with a reference source of chlorine or hydroxyl radicals, Cl₂ and H₂O₂ molecules, respectively, show similar reaction energetics (Table 2). That is, reaction of a methyl or L-threonine radical with free Cl· from Cl₂ is barrierless and exothermic to the same extent as the reaction with the equatorial chlorine ligand of SyrB2 model complex. Similarly, the reaction of OH· from H₂O₂ with methyl or L-threonine radical exhibits an energetic barrier comparable to that of the reaction of a radical with the axial hydroxyl ligand of the model complex.

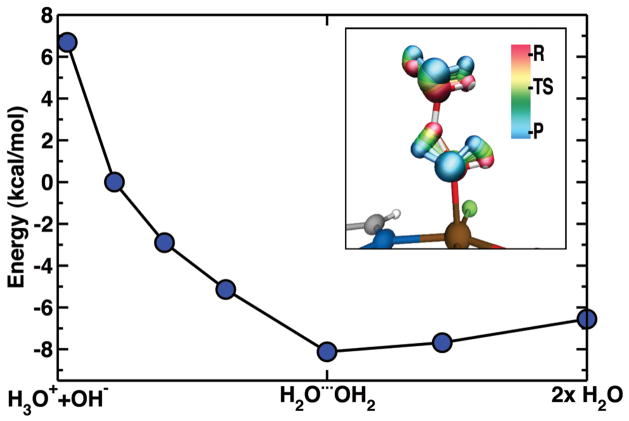
Catalyst regeneration

The removal of the axial hydroxyl ligand left behind following halogenation may occur via either charge transfer from the iron to produce a stable, dissociated OH⁻ or, more likely, via a protonation event, which leaves behind a more loosely bound water molecule. Using a hydronium ion source, calculations were carried out on the protonation step, which was found to be barrierless and exothermic. Once the proton is donated from hydronium to the hydroxyl, forming water, a hydrogen bond persists between the two water molecules and breaking this bond costs a small amount of energy, about 1.4 kcal/mol. Overall, the donation of the proton to the hydroxyl is exothermic by nearly 14 kcal/mol. Structurally, the transfer is marked by a decrease of the O-H bond lengths in the hydronium concomitant with the donation of a proton and elongation of the newly-formed Fe-OH₂ bond in SyrB2 (Fig. 8). Protonation by a neutral water molecule would be less exothermic but also feasible.

Figure 8.

Energetics and trajectory of hydroxyl protonation step via proton transfer from a hydronium ion. Following this exothermic and barrierless step, the water molecules hydrogen bond to each other.

Discussion

The halogenation reaction of L-Thr to 4-Cl-L-Thr by a model complex of SyrB2 has been studied here in detail using a recently introduced Hubbard U correction to standard density functional theory. Using only the ligands directly bound to iron in the enzyme active site, we were able to study and understand many of the key catalytic steps that have been postulated to be relevant in the full biological system. The inclusion of the Hubbard U correction has been previously shown^1,2 to improve energetic estimates of barrier heights, spin state ordering, and dissociation energies, all of which are key in determining likely reaction mechanisms. In this work, the GGA+U approach improves both qualitative and quantitative descriptions of probable reaction mechanisms by correcting GGA descriptions of oxidation states, eliminating self-interaction-related artifacts in reaction pathways, and improving binding energy and distances (see section S.4 of the Supporting Information). EXAFS results, which were published after the initial preparation of this manuscript³², predict bond lengths for Fe(IV)-Cl and Fe(IV)=O as 2.31 Å and 1.65 Å, or within 0.01 Å of our calculated values for the ferryl intermediate (see Fig. 4). Furthermore, the inclusion of this self-consistent Hubbard U correction adds minimal overhead to standard exchange-correlation functionals, thereby allowing the same approach to be applied directly with uncompromised accuracy to larger models up to several hundreds of atoms in size.

Here, we used this computational model to understand the various steps along the reaction coordinate of SyrB2. We found that following barrierless decarboxylation of α-ketoglutarate to form succinate, a high-energy Fe(IV)=O intermediate is formed that has been previously characterized spectroscopically in the analogous halogenase CytC3²³ and recently in SyrB2³². This reactive intermediate greatly reduces the energetic cost of hydrogen abstraction to form radicals from the uncatalyzed theoretical values for both L-threonine and methane, 92 and 99 kcal/mol, respectively, to under 7 and 9 kcal/mol. As hydrogen abstraction barriers are greatly reduced in both methane and L-threonine by the presence of the Fe(IV)=O intermediate, hydrogen abstraction by the iron-oxo of any substrate’s methyl group should be energetically favorable. The subsequent step, chlorination, should occur spontaneously following the formation of a substrate radical in the active site because it was shown to be barrierless and exothermic for both radical substrates by around 15 kcal/mol. The two key components of SyrB2 reactivity, hydrogen abstraction and chlorination, are likely to be favorable for any number of substrates with methyl groups that are chemically comparable to that in L-Thr. Our results suggest that the apparent selectivity of the full enzyme is determined primarily by the relative efficiency with which various substrates are delivered to the active site by SyrB1 and secondarily by whether the substrates are sterically compatible with the active site geometry. Indeed, recently published experimental work of Matthews, et al.³² has demonstrated that halogenation of alternative substrates by SyrB2 is possible.

Considering only the energetics of the reaction steps, hydroxylases with a source of chlorine radical in the active site should be able to halogenate as well. That is, study of a model SyrB2 complex has demonstrated exothermic and barrierless chlorination in the presence of radical substrate intermediates. Hydroxylases that have undergone site-directed mutagenesis to make the first shell active site residues highly homologous to SyrB2 should also be able to release a chlorine atom to the radical if the binding energy of the chlorine to the metal center is comparable to that in SyrB2. However, it was previously noted that these mutated hydroxylation enzymes, in which the aspartic acid is replaced with an alanine, do not halogenate at any experimentally observable level²⁰. These results on the model complex suggest that the lack of halogenation in hydroxylases even following site-directed mutagenesis is not for energetic reasons. Rather, the absence of bound chloride at the active site in a location proximal to the substrate is the most likely reason hydroxylases do not halogenate. Such a hypothesis has been strengthened by recently published crystal structures of an open conformation of the halogenase CytC3 in which Cl⁻ is not bound because the surrounding residues that form interactions with both αKG and Cl⁻ are at incompatible distances²⁵.

It is more challenging to understand why halogenases do not measurably hydroxylate, even after site directed mutagenesis of the first shell alanine residue to aspartic acid. Firstly, in the unmodified SyrB2 model complex, calculations presented here support the idea that halogenation is preferred as a result of differences in binding strength between the more weakly bound equatorial chlorine and the four times more strongly bound axial hydroxyl. We further discovered that the formation of 4-Cl-L-Thr is even more energetically favorable when the abstraction and chlorination are coupled and occur in rapid succession. The interaction of the L-threonine’s methyl carbon with chlorine stabilizes the forming methyl radical during the removal of a hydrogen via the iron-oxo ligand. Upon abstraction of hydrogen, the chlorination step in the model complex is further ensured by the presence of a hydrogen bond between the -OH ligand of the iron catalyst and an -OH group on L-Thr, though the chlorination step exothermicity is unchanged by this interaction. In contrast, an analogous coupled hydrogen abstraction and hydroxylation mechanism does not exist, as the hydroxylation step requires first the breaking of a hydrogen bond with the substrate and the subsequent straining of the Fe-OH bond, supporting the idea that no hydroxylation would occur in the presence of bound chlorine. We note that the axial hydroxyl interactions with the substrate’s carbon or, alternatively, second shell residue interactions with the substrate could instead stabilize the substrate for chlorination in reactions with other amino acids³².

The proposal that the enzyme might increase the reactivity of Cl⁻ through the lengthening of the Fe-Cl bond⁴ is not consistent with our Fe-Cl binding curve. Variations in the Fe-Cl bond length (2.3–2.4 Å) along the reaction coordinate, reflecting values obtained in calculations and experiments alike⁴, have a very small energetic contribution because the binding curve is quite shallow (see Fig. 6), indicating that reactivity is not strongly dependent on bond length. The second sphere residues that are absent in this work are potentially instrumental in reducing the iron-hydroxyl bond strength in active hydroxylases, while the already weak iron-chlorine bond in halogenases requires no further modulation by interactions with the protein scaffold. Direct ligand modulation of Fe-OH bond strength is also possible, particularly if distal ligand interactions with Fe(III) weaken the proximal bond or if a carboxylate, such as Asp in several hydroxylases, formed interactions with the axial hydroxyl. However, preliminary substitution of Cl⁻ with Asp in our model system has not led to a weaker Fe(III)-OH bond in the presence of Asp. Screening via systematic ab initio calculations, which focus on modeling small changes to the local electronic structure of the Fe-OH ligand, may help to identify conditions under which this Fe-OH bond may be made weaker or stronger. Utilizing this knowledge to construct analogous model systems could permit a route to compounds capable of switching between hydroxylation and halogenation.

The positioning of the substrate in an active site may also influence reactivity toward hydroxylation versus chlorination. In all model complex reaction mechanisms considered, most of the substrate was at least 2 Å from the catalytically active moiety in the axial position of the complex. In order for radical hydroxylation to occur, the substrate must move closer to the axial hydroxyl ligand, and differences in the mobility of the substrate within the active site could dictate the extent to which the hydroxylation step is favored.

Regeneration of the catalyst and associated removal of the tightly bound hydroxyl moiety was considered and found to be most likely achieved through protonation via an energetically compatible source to form a weakly bound water molecule. The Fe(II)-OH₂ bond length of about 2.4 Å for the ground state quintet SyrB2 model complex is nearly 0.6 Å longer than that for the Fe(III)-OH bond and over 0.85 Å longer than the strong Fe(IV)=O bond (see Fig. 2). Similarly, dissociation energies are reduced from around 50 kcal/mol for the oxo and hydroxyl ligands to about 5 kcal/mol, a ten-fold reduction in the energetic cost of dissociation. A survey of the main residues in the active site shows that there are no acidic amino acids within 8.0 Å available for proton donation. Instead, a free source from solution, most likely hydronium ions, has been shown to be capable of protonating the hydroxyl ligand.

Undoubtedly, second shell residues help to modulate the binding of substrates and co-substrates as well as affecting the relative barrier heights of the various mechanistic steps. However, using only a model complex between 34 and 51 atoms in size, we are able to describe a plausible mechanism for halogenation that has implications for the full enzyme. Use of a small model is supported by the fact that second-sphere residue interactions serve to mostly stabilize the co-substrate ligands, Cl⁻ and αKG, which are found to be well-bound in gas phase calculations. The results presented here suggest that the distinctive halogenase activity of SyrB2 is achieved by the overall promotion of chlorine uptake and binding near the active site, which is not achieved in mutant hydroxylases.