Extracting Tractosemas from a Displacement Probability Field for Tractography in DW-MRI

Abstract

In this paper we present a novel method for estimating a field of asymmetric spherical functions, dubbed tractosemas, given the intra-voxel displacement probability information. The peaks of tractosemas correspond to directions of distinct fibers, which can have either symmetric or asymmetric local fiber structure. This is in contrast to the existing methods that estimate fiber orientation distributions which are naturally symmetric and therefore cannot model asymmetries such as splaying fibers. We propose a method for extracting tractosemas from a given field of displacement probability iso-surfaces via a diffusion process. The diffusion is performed by minimizing a kernel convolution integral, which leads to an update formula expressed in the convenient form of a discrete kernel convolution. The kernel expresses the probability of diffusion between two neighboring spherical functions and we model it by the product of Gaussian and von Mises distributions. The model is validated via experiments on synthetic and real diffusion-weighted magnetic resonance (DW-MRI) datasets from a rat hippocampus and spinal cord.

1 Introduction

The estimation of neuronal fiber orientations from diffusion-weighted MR images (DW-MRI) and the reconstruction of complex structures such as splaying and decussating fibers are problems whose solutions contribute toward achieving tractography in regions of the brain such as the optic chiasm, the hippocampus, the brain stem and others.

The local orientation of a single fiber bundle can be estimated easily from diffusion tensor images (DTI). In DTI datasets, a 2^nd-order tensor has been commonly employed to approximate the local diffusivity [1]. However, it is known that 2^nd-order tensors fail to approximate more complex fiber structures such as crossings, splaying and kissing structures [2].

More than one distinct fiber tract structure within a voxel can be estimated by employing more sophisticated models for reconstruction of the diffusion-weighted MR signal. Some of the models that have been proposed in literature include discrete [3] and continuous [4] mixture of Gaussians, higher-order tensors [5], and the spherical harmonic transformation [6]. After reconstruction of the signal, one has to compute its Fourier transform in order to obtain the displacement probability whose peaks correspond to distinct fiber orientations. The displacement probability profiles can also be computed by transforming the diffusivity profiles using the diffusion orientation transform (DOT) [7]. Multiple fiber orientations can also be estimated by reconstructing the orientation distribution function (ODF) [8] using the so called Q-ball imaging [9]. Most of the above techniques ([1,3,8,4]) can be expressed as a special case of a more generalized method in which the DW-MR signal can be expressed as the convolution over the sphere of a fiber bundle response function with the ODF [10,11]. In this spherical deconvolution approach there is no limitation regarding the number of the distinct fiber populations in the estimated ODF.

The result produced by all the above models is in the form of a spherical function representing either an ODF or an iso-surface of the displacement probability profile. In both cases the estimated spherical function characterizes the intra-voxel fiber structure without taking into consideration any inter-voxel information. As a result, the computed function is always anti-podally symmetric and therefore it can only model either single fiber tracts or symmetric crossings of multiple fiber tracts. However, it is well known that neural fiber tracts can also form asymmetric local structures such as in sprouting fibers [2]. To date there are no existing methods in literature for estimating locally asymmetric fiber orientation functions and one has to resort to an existing fiber tracking procedure that can accommodate for multiple fibers at a voxel [12,13,2], in order to infer the presence of a sprouting or anti-symmetric crossing structures.

In this paper we present a novel method for estimating an intra-voxel asymmetric spherical function that can model complex local fiber structures using inter-voxel information. The peaks of the estimated spherical function correspond to directions that point to distinct local fiber tracts and are appropriately dubbed tractosemas. Tractosema is a pointer/sign used here for neural tracts and has its roots in the Greek word sēma (sign). In our work here, we extract a field of tractosemas from a given field of ODFs or displacement probabilities by following asymmetric and orientation depended diffusion of spherical functions. The kernel that controls the diffusion process between two elements (in our case spherical functions) is defined as a function over the spatial location (ℜ³) and the domain (S² unit sphere) of the two elements, which leads us to the space (ℜ³ × S²) × (ℜ³ × S²). We construct the diffusion kernel as a tensor product of the von Mises and Gaussian probability distributions and by using it we derive an update formula for the field of tractosemas which is expressed in the form of a discrete kernel convolution.

The main contribution of this paper is that the tractosemas can depict complex asymmetric fiber structures without the need for fiber tracking. To the best of our knowledge, it is the first method that estimates a field of asymmetric spherical functions for modeling splaying fibers and other asymmetric as well as symmetric structures. Furthermore, the estimated field of tractosemas can be used as input by any existing fiber tracking algorithm for finding fiber junctions and branches without the need for multiple seeds (a common requirement in many existing methods [12,14,15,2]). Finally, the experimental results demonstrate the robustness and accuracy of our model in estimating fiber orientations in the presence of varying amount of noise as demonstrated via simulation experiments with realistic MR data synthesis [16].

2 Estimation of Tractosemas from DW-MRI

In this section we present our method on extracting tractosemas from a given field of displacement probability iso-surfaces.

2.1 Displacement Probability Estimation

The water molecule displacement probability is given by the Fourier integral

$$P(r_0\mathbf{r})=\int \frac{S(\mathbf{q})}{S_0}{e}^{-2\pi i{\mathbf{q}}^T\mathbf{r}{r}_0}d\mathbf{q}$$ (1)

where q is the reciprocal space vector, S(q) is the DW-MRI signal value associated with vector q, S₀ the zero gradient signal and r and r₀ is the direction and magnitude respectively of the displacement vector [17]. There are several existing methods for computing P(r₀r) in which we either first reconstruct the signal S(q) and then evaluate Eq. 1 [4], or we directly estimate the displacement probability from given diffusion-weighted MR data [7,18]. Also, one may obtain an alternative representation called the fiber orientation distribution (from the Q-Ball images) from which one can find the optimal fiber orientations [13,19].

In order to estimate the orientations of the underlying distinct fiber bundles a spherical function p(r) is extracted from the volume of P(r₀r) by either fixing r₀ [7] or by integrating over r₀ [3]. Then the orientations that correspond to the maxima of p(r) are estimated and are used either for neural fiber tracking or further analysis [20,13,21].

S(q) is naturally modeled by an anti-podally symmetric function and therefore its Fourier transform exhibits antipodal symmetry as well. As a result the estimated probability iso-surface p(r) in a single voxel can not model asymmetric local neural structures such as splaying fibers. Using inter-voxel information it is possible to estimate tractosemas – which are spherical functions that are not necessarily symmetric – by diffusing a field of probability iso-surfaces. The peaks of tractosemas point to directions of distinct fiber tracts and we can extract them by employing the method presented in the following section.

2.2 Extracting Tractosemas by Diffusing Probability ISO-Surfaces

After having estimated the displacement probability p_x(r) ∀x ∈ ℜ³, where x is the lattice index, we use the obtained spherical function field in the following diffusion process. In this process the spherical functions are updated iteratively by diffusing the displacement probability field. In general, diffusion can be seen as a smoothing process which can be performed by minimizing a smoothness measure. In our case, we minimize the following function with respect to p_x(r).

$$E(p_{\mathbf{x}}(\mathbf{r}))={\int }_{{\mathfrak{R}}^3}{\int }_{S^2}K(\mathbf{x},\mathbf{y},\mathbf{r},\mathbf{v})\mathit{dist}(p_{\mathbf{x}}(\mathbf{r}),p_{\mathbf{y}}(\mathbf{v}))d\mathbf{v}d\mathbf{y}$$ (2)

Eq. 2 is expressed in the form of a kernel integration, where dist(.) can be any norm or “edge-stopping ”function [22], the kernel K(.) is a function of x, y, r, v, and the integration is over all vectors y and unit vectors v. In our particular application, the kernel is a probability function expressing the probability of diffusion between the elements p_x(r) and p_y(v). The kernel we seek should exhibit the following properties: a) the probability of diffusion between locations x and y decreases with their distance, b) the probability of diffusion between orientations r and v decreases with the angle between them, and c) the probability of diffusion is larger at the locations along the maxima of p_x(r). These properties are satisfied by single peaked distributions. One such function used here is,

$$K(\mathbf{x},\mathbf{y},\mathbf{r},\mathbf{v})=K_{\mathit{dist}}(||\mathbf{y}-\mathbf{x}||)K_{\mathit{orient}}(\mathbf{r}·\mathbf{v})K_{\mathit{fiber}}(\mathbf{r}·(\mathbf{y}-\mathbf{x})/||\mathbf{y}-\mathbf{x}||)).$$ (3)

The first property mentioned above is imposed by defining K_dist using a multivariate Gaussian distribution.

$$K_{\mathit{dist}}(||\mathbf{y}-\mathbf{x}||)=\frac{1}{{(2\pi \sigma )}^{3/2}}{e}^{-\frac{{\left|\right|\mathbf{y}-\mathbf{x}\left|\right|}^2}{2{\sigma }^3}}$$ (4)

The most natural way to impose the last two properties is to employ the single peaked von Mises distribution for both K_orient and K_fiber, given by,

$$K_{\mathit{orient}}(\mathit{cos}(\phi ))=K_{\mathit{fiber}}(\mathit{cos}(\phi ))=\frac{\kappa e^{\kappa \mathit{cos}(\phi )}}{4\pi \mathit{sinh}(\kappa )}$$ (5)

where φ is the angle between r and v, and the angle between r and (y − x) in K_orient and K_fiber respectively. The distribution parameters σ and κ in Eq. 4 and 5 respectively control the sharpness of the kernel.

Having a discrete lattice of probabilities p_x(r) the integral over ℜ³ in Eq. 2 becomes summation over the lattice. Furthermore, since the Gaussian part of the kernel takes its largest values in the region around its center (at location x), we can define a set N (x) that contains the lattice indices in the neighborhood of x. Furthermore, we discretize the space of unit vectors by using a 4^th order subdivision of the icosahedral tessellation of the unit sphere. By using the above discretization, Eq. 2 can be written in the following form

$$E(p_{\mathbf{x}}(\mathbf{r}))={\sum }_{\mathbf{y}\in N(\mathbf{x})}{\sum }_{\mathbf{v}\in S}K(\mathbf{x},\mathbf{y},\mathbf{r},\mathbf{v})\mathit{dist}(p_{\mathbf{x}}(\mathbf{r}),p_{\mathbf{y}}(\mathbf{v}))$$ (6)

By setting for simplicity dist(a, b) = (a − b)² and taking the derivative of Eq. 6 with respect to p_x(r) and setting it equal to zero, we derive the following update formula for the field of spherical functions (tractosemas)

$$p_{\mathbf{x}}^{\prime }(\mathbf{r})={\sum }_{\mathbf{y}\in N(\mathbf{x})}{\sum }_{\mathbf{v}\in S}K(\mathbf{x},\mathbf{y},\mathbf{r},\mathbf{v})p_{\mathbf{y}}(\mathbf{v})$$ (7)

Eq. 7 is expressed in the form of a discrete kernel convolution and it is applied iteratively to all indices x and vectors r on the discretized S². This method produces very efficient implementations since only kernel multiplications are involved in the evaluation of Eq. 7, which is a fully parallelizable process. Furthermore, only few iterations (2 to 3) are required to observe visually the diffused asymmetric tractosemas. Finally, choosing a different dist (e.g. L1 norm), would lead to more anisotropic solutions, something we are currently investigating.

3 Experimental Results

In the experiments presented in this section, we tested the performance of our method using simulated diffusion-weighted MR signal and real HARDI data sets from an isolated rat hippocampus and an excised rat spinal cord.

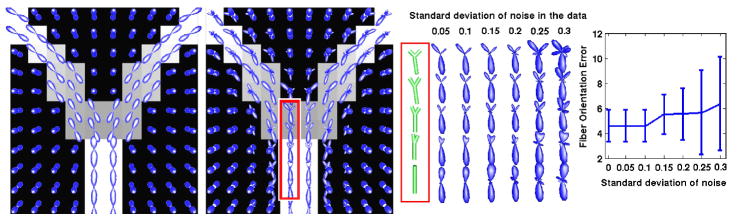
For the validation of tractosemas we synthesized a dataset representing splaying fiber bundles, whose orientations were taken to be tangent to two ellipsoids centered at the two lower corners of the image. The data set was of size 16×16×16 and was generated by simulating the diffusion-weighted MR signal using the realistic simulation model in [16] (b-value=1250s/mm², 81 gradient directions). After that, we estimated the displacement probability field (Fig. 1a) from the simulated signal by using the method in [18] (one can also use any other method).

Fig. 1.

Synthetic data example: a) Simulated data, b) The field of computed tractosemas, c) Tractosemas in ROI under varying noise, d) Plot of fiber orientation errors

The above obtained field of probability functions was then input to our proposed method for extracting tractosemas (σ = 1, κ = 10, 3 iterations). Fig. 1b shows the field of tractosemas computed by our technique. By observing the figure, we can see that our method estimated correctly single fiber distributions in the lower part of the image and splaying fibers in the central region of the field, which demonstrates the effectiveness of our technique. Note the smooth transition from single fiber to splaying structure in the ROI, and the expected anti-aliasing effect observed in the voxels close to the splaying fibers.

Furthermore, to quantitatively test the performance of our method in estimating fiber orientations we added varying amounts of Riccian noise (SNR between 20:1 and 3.3:1) to the data. We applied our method to these noise corrupted data sets and then computed the estimated fiber orientation errors. Figure 1d depicts a plot of the mean and the standard deviation of the angle error between computed and ground truth orientations (in degrees). These results validate the accuracy of our model and demonstrate its robustness to noise.

The proposed method was also applied to a real DW-MRI from an isolated rat hippocampus (Fig. 2 left). The dataset consists of 22 images acquired using a pulsed gradient spin echo pulse sequence with TR=1.5 s, TE= 28.3 ms, G= 415 mT/m, δ = 2.4 ms, Δ = 17.8 ms, T_δ = 17 ms and b ≃ 1250s/mm².

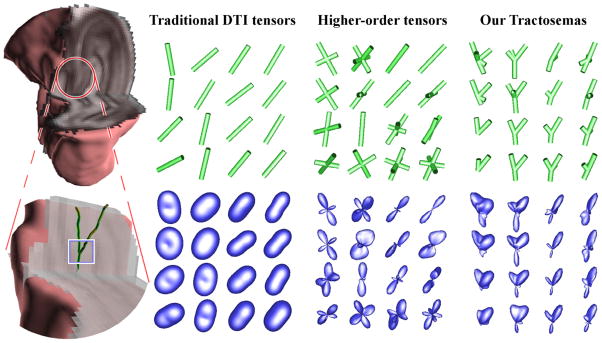
Fig. 2.

Real hippocampal data. Left: The data set shown in 3D (top) and the region of interest shown enlarged (bottom). The rest of the plates depict the displacement probability profiles (bottom) and the orientations corresponding to their maxima shown as tubes (top) obtained by using: a) DTI, b) fourth order tensors, and c) Tractosemas.

Figure 2 shows a region of interest (ROI) in the hippocampus containing mixture of CA3 stratum pyramidale, stratum lucidum and part of the hilus. The rest of the images in this figure show a comparison of the estimated local fiber structures using a) Diffusion tensors (order-2 DTs), b) fourth order tensors, and c) tractosemas. In the DT field we can observe two dominant orientations one pointing to the upper left and the other to the upper right corner of the ROI, however, the structure at the junction is lost. The junction was recovered using the fourth order tensors however, they depict the two aforementioned fiber orientations as symmetric structures. The complicated junction structure is correctly captured in the estimated field of tractosemas with asymmetric structures that depict splaying fibers. Fig. 3 depicts fiber tracks estimated from the hippocampal data set by following the peaks of tractosemas. The capability of tractosemas in capturing various structures is demonstrated on the left of this figure.

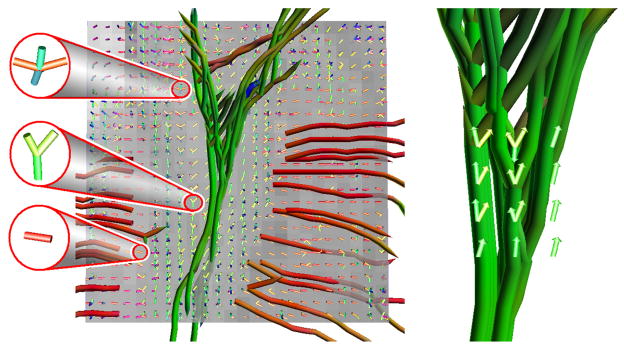
Fig. 3.

The field of tractosemas estimated from the hippocampal data set. Left: Three zoomed voxels depicting the variability in the estimated structures. Right: The fiber sprouting with the estimated tractosemas superimposed.

Finally, we extracted tractosemas from 2 control and 3 injured rat’s spinal cord datasets (21 diffusion-weighted images, b ≃ 1125s/mm²). Fig. 4 shows the Cornu Posterius region in one of the control (left) and one of the injured (center) spinal cords. A variety of different fiber structures are shown (single bundles, crossings, branchings). In order to compare the estimated structures we plotted the average percentage of tractosemas with 1,2,3… peaks found in all control and injured sets. As it was expected, we observe a decrease in the number of peaks in the injured cords due to loss in connectivity as a result of the injury.

Fig. 4.

Tractosemas extracted from a control (left) and an injured (center) rat’s spinal cord dataset. Right: comparison of the number of peaks in the estimated tractosemas.

4 Discussion

The key difference between the proposed tractosemas and the fiber orientation distributions is that the first one is asymmetric, while the latter is symmetric. The peaks of tractosema correspond to directions that if we follow we will find the body of a distinct fiber bundle. This capability of tractosemas is due to the intervoxel information taken into consideration during the spherical function diffusion process. Finally, tractosemas are less sensitive to noise in the DW-MRI data than the displacement probability or the fiber orientation distribution. This property is evident since large amount of noise is removed by minimizing the proposed regularization term.