Ultrasound Transducer and System for Real-Time Simultaneous Therapy and Diagnosis for Noninvasive Surgery of Prostate Tissue

Abstract

For noninvasive treatment of prostate tissue using high intensity focused ultrasound (HIFU), this paper proposes a design of an integrated multi-functional confocal phased array (IMCPA) and a strategy to perform both imaging and therapy simultaneously with this array. IMCPA is composed of triple-row phased arrays: a 6 MHz array in the center row for imaging and two 4 MHz arrays in the outer rows for therapy. Different types of piezoelectric materials and stack configurations may be employed to maximize their respective functionalities, i.e., therapy and imaging. Fabrication complexity of IMCPA may be reduced by assembling already constructed arrays. In IMCPA, reflected therapeutic signals may corrupt the quality of imaging signals received by the center row array. This problem can be overcome by implementing a coded excitation approach and/or a notch filter when B-mode images are formed during therapy. The 13-bit Barker code, which is a binary code with unique autocorrelation properties, is preferred for implementing coded excitation, although other codes may also be used. From both Field II simulation and experimental results, whether these remedial approaches would make it feasible to simultaneously carry out imaging and therapy by IMCPA was verifeid. The results showed that the 13-bit Barker code with 3 cycles per bit provided acceptable performances. The measured −6 dB and −20 dB range mainlobe widths were 0.52 mm and 0.91 mm, respectively, and a range sidelobe level was measured to be −48 dB regardless of whether a notch filter was used. The 13-bit Barker code with 2 cycles per bit yielded −6dB and −20dB range mainlobe widths of 0.39 mm and 0.67 mm. Its range sidelobe level was found to be −40 dB after notch filtering. These results indicate the feasibility of the proposed transducer design and system for real-time imaging during therapy.

I. INTRODUCTION

In recent years, high intensity focused ultrasound (HIFU) has become increasingly important in the noninvasive treatment of malignant tissues [1]. Several clinical studies have been conducted to investigate the feasibility of HIFU treatment for breast, liver, and prostate cancer [2]–[6]. HIFU therapy is usually performed in cooperation with medical imaging modalities such as magnetic resonance imaging (MRI), ultrasound imaging, and computed tomography (CT) in order to select and monitor a treatment region. MRI provides a high-resolution image and an efficacious temperature map, but it is expensive and requires a large space. Ultrasound is another common tool for image guidance. It offers advantages in real-time imaging, cost-effectiveness, excellent portability, and potential integration with other devices[7].

The major challenges in a HIFU treatment process are precise localization of lesions and quantification of the dose in a targeted region based on thermal and mechanical mechanisms. It is also necessary to track undesired tissue movement and monitor feedback induced by a treated target during treatment [8]. The most frequently cited and useful solution to these difficulties is to carry out noninvasive visualization during treatment [7]–[9]. There have been several attempts to develop a real-time simultaneous ultrasound imaging guided HIFU (US-guided HIFU) system. Several investigators have proposed a system equipped with two spatially separated transducers for treatment and imaging [9], [10]. Yet another paper reported integration of therapeutic and diagnostic functions into a single transducer array based on dual-mode operation, switching between treatment and diagnosis [7], [11]. However, these techniques have achieved limited success in real-time therapeutic and imaging capability. Spatially separated transducers may miss a target due to misalignment between two transducers [12]. Implementation of switching mode using a single transducer array may degrade the performance of both treatment and diagnosis because the piezoelectric material and configuration of HIFU transducers are generally different from these of diagnostic transducers [13], [14]. Recently, an interleaving method, i.e., inserting imaging signals into therapeutic signals alternatively has been utilized by a number of researchers. In this method, a pulsed wave (PW) was used for treatment [15], [16].

In a similar effort to realize simultaneous therapy and imaging, this paper describes the feasibility of real-time imaging during therapy using not only PW but also continuous wave (CW). For this purpose, we propose a design of a HIFU transducer called integrated multi-functional confocal phased array (IMCPA). The transducer consists of triple-row phased arrays: a 6 MHz array in the center row for imaging and two 4 MHz arrays in the outer rows for therapy. Since one of the most common applications of commercial US-guided HIFU systems currently is the treatment of prostate tissue, all design specifications such as dimension, frequency, and focal depth of the proposed transducer targeted this application..

The most critical issue to achieve our goal with IMCPA is how to suppress reflected therapeutic signals received by the center-row array which is used for imaging. When PW or CW signal for treatment and a pulsed signal for imaging are transmitted to a target at the same time, the imaging signal may hardly be detected due to the high amplitude of reflected therapeutic signals. One simple way to solve this problem may be either to decrease the intensity of transmitted therapeutic signals or to increase the intensity of transmitted imaging signals. However, these are not practical solutions because the intensity of therapeutic signal should be large enough to produce thermal necrosis, and the intensity of diagnostic ultrasound must be below that mandated by the Food and Drug Administration (FDA) [17], [18]. As a practical solution to these limitations, this paper proposes a coded excitation technique with a notch filter to form a B-mode image during therapy. Through Field II simulation studies and experimental results, it was demonstrated that the proposed method might be used to effectively suppress the interference signals during B-mode imaging while therapy was being carried out.

II. METHODS

A. Transducer Design

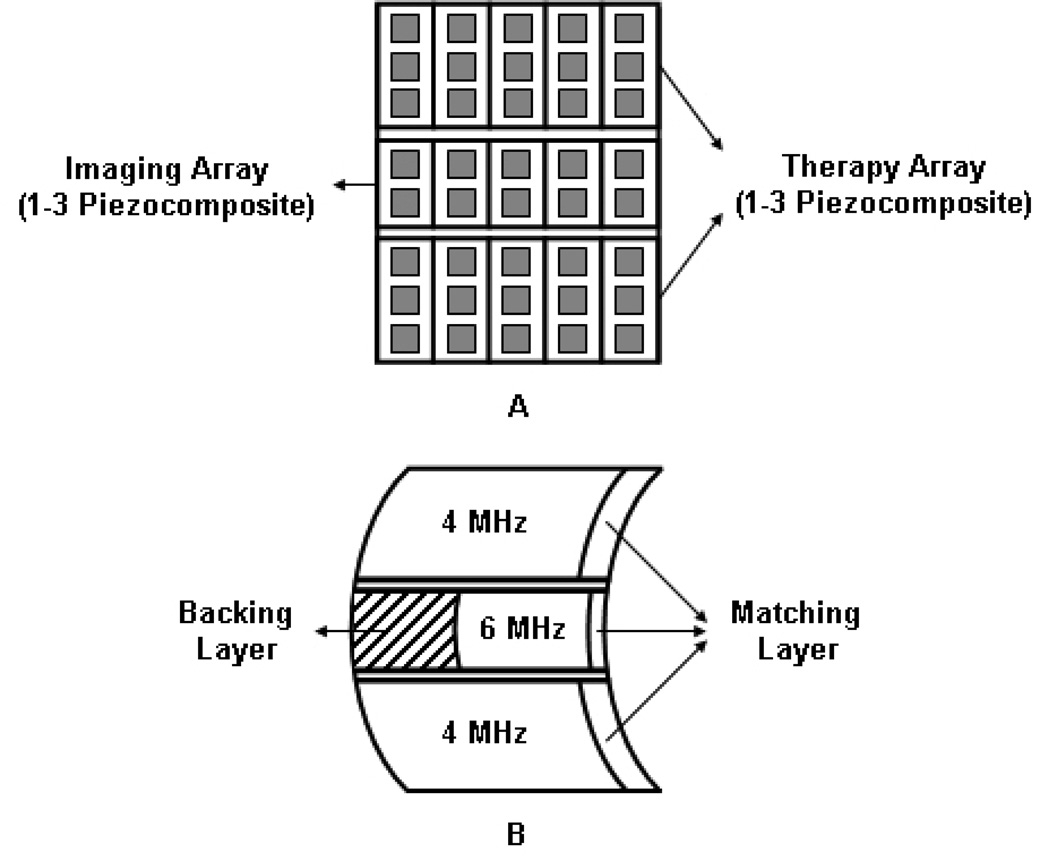
In general, a HIFU array transducer should provide highly flexible control to change a focal spot along either lateral or axial direction without moving the transducer [19], [20]. There have been several types of multi-row array transducers for US-guided HIFU system reported in the literature [16], [21]. IMCPA proposed in the paper was also a multi-row array transducer composed of triple-row phased arrays: a 6 MHz array in the center row for imaging and two 4 MHz arrays in the outer rows for therapy as shown in Fig. 1. For HIFU therapy, a frequency range from 1 MHz to 4 MHz was preferred to increase thermal treatment effect [22]. The frequencies in the range from 3 MHz to 4 MHz have been widely used for treatment of prostate cancer given the depth of penetration [4]–[6]. Considering the requirements on efficient thermal necrosis and the depth of penetration (i.e., 4 cm ~ 5 cm for prostate), 4 MHz and 6 MHz frequencies were respectively chosen for treatment and imaging for IMCPA. Since the second harmonic component of 4 MHz therapeutic signal would be generated at approximately 8 MHz, the imaging transducer should have an effective bandwidth of between 4 MHz and 8 MHz. Therefore, a 6 MHz transducer with a −6 dB fractional bandwidth of 50% is required for imaging.

Fig 1.

Simplified schematic diagram of IMCPA transducer with 5 × 3 elements. (a) The front view of IMCPA without a matching layer. (b) The side view of IMCPA with a matching layer. All arrays had 1–3 piezocomposite structures and their surfaces had a common focal point in elevational direction. The center imaging array had a backing layer to increase the bandwidth and the outer therapy arrays had air backings to maximize transmission of ultrasound. A matching layer would also increase the transmission efficiency of IMCPA.

For the purpose of efficient therapy and imaging with IMCPA, the 6 MHz imaging array had 128 elements with 0.73λ = 188 µm pitch, 25 µm kerf, and 8 mm height, while each 4 MHz therapy array had 128 elements with 0.5λ = 188 µm pitch, 25 µm kerf, and 14 mm height. The total dimension of IMCPA was 24 mm × 36 mm. These dimensions should be acceptable as an endocavity transducer. The dimension of the therapy array was 24 mm × 28 mm, which could generate an intensity of about 2000 W/cm² at a focal spot [23]. The therapy array with half wavelength spacing between elements should be able to protect normal tissues from the grating lobes of HIFU beam. The f-numbers of lateral and elevational directions were 1.7 and 1.1 at a focal depth of 40 mm. The novel aspect of IMCPA was that all arrays were focused on the same region by a geometrically curved surface in the elevational direction eliminating the need for orienting transducers [16]. Also, a press-focused array was more efficacious than a lens-focused array because of acoustic energy absorption by a lens itself [24]. Fig. 1 describes a schematic diagram of IMCPA with 5 × 3 elements as a simple example.

In IMCPA design, all arrays should be fabricated with a piezoelectric 1–3 composite for surface conformation and for its low acoustic impedance. However, the materials constituting 1–3 piezocomposite used for therapy transducers are typically different from those for imaging transducers. The piezoelectric materials with a high Curie temperature and a low dielectric/mechanical loss such as PZT4 and PZT8 are more desirable for therapy transducers [25]–[27]. PZT-5H with a high dielectric constant and electromechanical coupling has been widely used for imaging array transducers [28]. A high thermal resistance epoxy with a high glass transition temperature may be used for a composite therapy transducer resulting in improved temperature durability. A volume fraction ratio between piezoelectric material and epoxy of IMCPA of 75% was selected, given the specifications, which should be enough to generate the required acoustic intensity [27]. A matching layer would reduce the acoustic impedance mismatch between the transducer and the body resulting in a high transmission efficiency. It is also advisable to construct a HIFU transducer without a backing layer to allow maximal energy transmission in the forward direction and to alleviate fabrication difficulties [19], [25].

A strategy for fabricating IMCPA is to assemble together individual arrays after they are designed and fabricated separately. A press-focused method may be used before or after combining these transducers. Another advantage of this configuration is that the amplitude of reflected therapeutic signals received by the imaging transducer might be reduced due to an elevational angle difference between the therapy and the imaging arrays, causing most reflected therapeutic signals be directed toward the therapy arrays rather than the imaging array.

B. Proposed Signal Processing

For therapy, the spatial-peak temporal-average intensity (I_spta) at a focal point should be higher than 1000 W/cm² to accomplish thermal necrosis [17]. The PW with a high duty cycle might be used if it can satisfy the requirement. Although the proposed method can employs PW as well as CW for therapy, we used 4 MHz CW signal with a 100% duty factor so as to yield an intensity of 2000 W/cm² for simulations and experiments presented in this paper. A 6 MHz 1-cycle short pulse was chosen for imaging. Its duty factor was 0.042% under the condition of a typical 2.5 kHz pulse repetition frequency (PRF) so that I_spta could be 18.8 mW/cm² as a diagnostic intensity in accordance with the FDA guideline [29]. With these parameters, the peak pressures of the CW signal and the 1-cycle short pulse at a focal point were computed and found to be 7.75 MPa and 1.16 MPa, respectively, from the formula [30]:

$$P=\sqrt{\frac{2Z{I}_{\mathit{\text{spta}}}}{t_{\mathit{\text{df}}}},}$$ (1)

where Z is the acoustic impedance of water (1.5 MRayl) and t_df represents the duty factor. Given the two computed peak pressure values, transmit ultrasound pressures for both therapy and imaging were adjusted in all simulations and experiments. It was assumed that the amplitude of the second harmonic signal at 8 MHz was −10 dB less than that at its fundamental frequency [31].

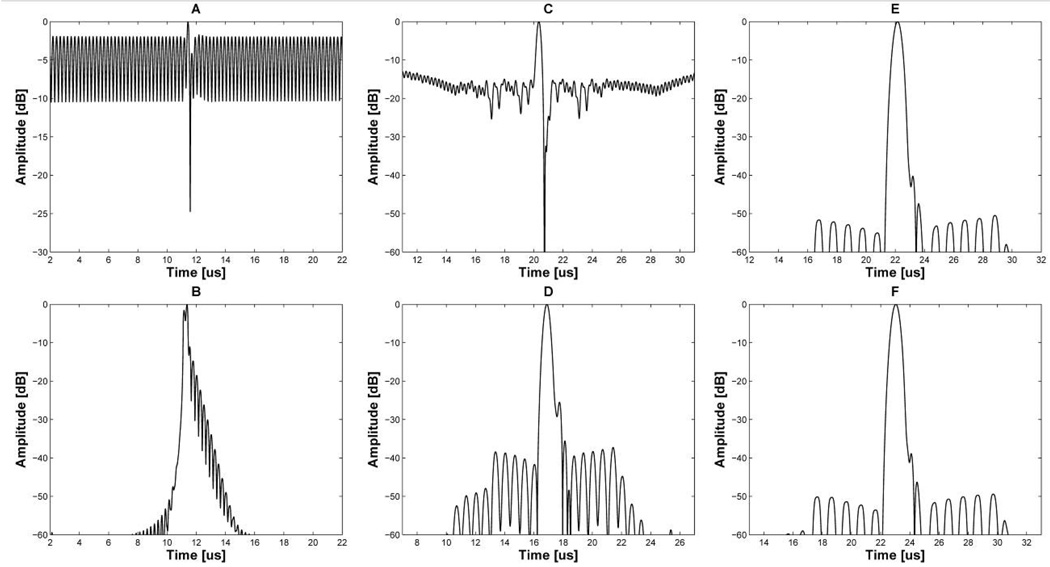
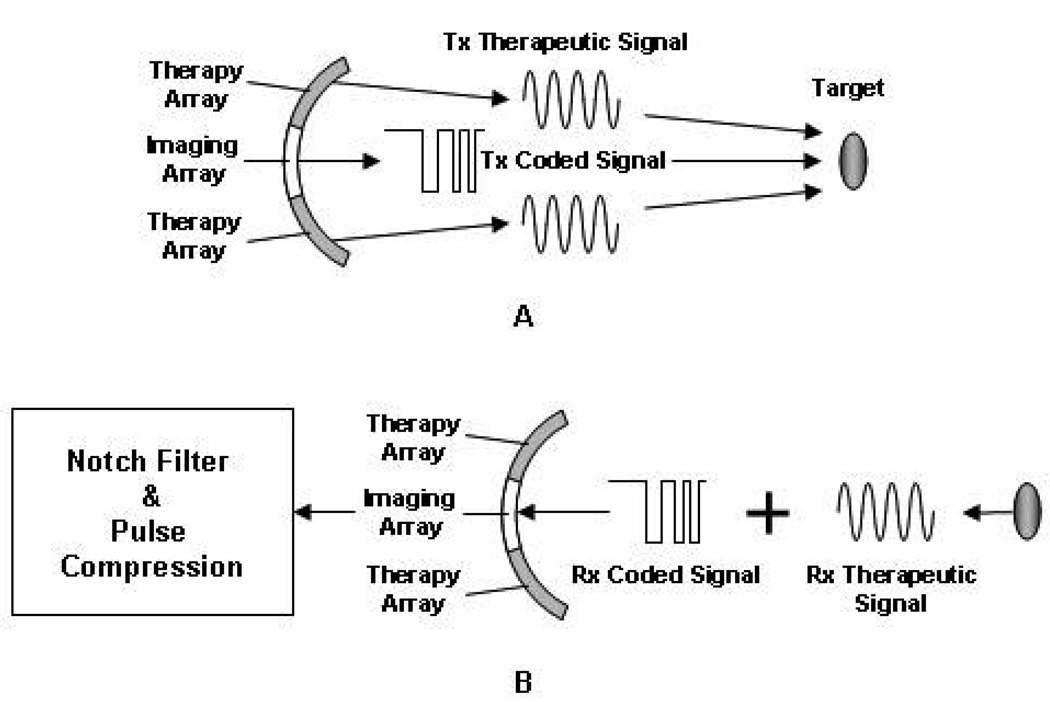
When IMCPA fires 2-cycle short pulses for imaging and CW signals for therapy, the imaging array would receive echoes containing the high amplitude of 4 MHz and 8 MHz interference signals. This interference decreases the signal-to-noise ratio (SNR) of the imaging signals. The range sidelobe level of the envelope signal extracted from the echoes (Fig. 2(a)) was found to be approximately −2 dB, thus resulting in poor image quality. The easiest way to improve the SNR for imaging is to increase input power of the imaging array, but it may violate the FDA guideline. As a practical solution for this limitation, a coded excitation technique may be used for imaging with IMCPA because this technique may improve the SNR by increasing the average power without changing the peak power [32]. In addition, the correlation between coded imaging signals and CW interference signals is significantly lower than that when a short pulse signal is used for imaging. Fig. 3 depicts the proposed method using IMCPA in which two outer therapy arrays transmit 4 MHz CW signals to the target. At the same time, its inner imaging array emits 6 MHz coded signals similar to conventional sector scanning. The imaging array receives the reflected coded signals along with reflected therapeutic signals. After pulse compression, the SNR may be improved and it should be less than −40 dB for B-mode imaging.

Fig 2.

Envelopes of imaging signals with CW interference: 2-cycle short pulses, (A) before and (B) after notch filtering; the 13-bit Barker code with 2 cycles per bit, (C) before and (D) after notch filtering; the 13-bit Barker code with 3 cycles per bit, (E) before and (F) after notch filtering.

Fig 3.

Signal processing for real-time imaging during therapy by using IMCPA. (A) The therapeutic and coded imaging signals are emitted to the target at the same time. (B) The reflected therapeutic signal received by imaging array can be removed by means of notch filtering and pulse compression.

Conventional coded excitation employs chirps, Barker codes, and Golay codes [32]–[35]. Among them, the Barker code was chosen for imaging due to its relatively simple hardware implementation and excellent robustness in noise suppression. The Barker code consists of N-bit biphase codes, and the optimal peak and range sidelobe level can be obtained from an autocorrelation function. Its range mainlobe width and sidelobe level depend on the number of bits and the number of sub-cycles per bit. By using a conventional sidelobe suppression filter, an acceptable sidelobe level, which is less than −40 dB for B-mode imaging, can be obtained [35]. Currently, a 13-bit biphase code sequence (+1 +1 +1 −1 +1 −1 −1 +1 +1 −1 +1 −1 +1) is the largest length realized for the Barker code.

The mainlobe in the spectrum of the 13-bit Barker code with 1 cycle per bit goes beyond the frequency range from 4 MHz to 8 MHz. This broad frequency response results in a serious distortion of the mainlobe due to 4 MHz and 8 MHz reflected therapeutic signals. Since more than the 4-cycle-per-bit Barker code might generate poor axial resolution, 2- and 3-cycle-per-bit Barker codes were considered in this study.

When the 13-bit Barker code with 2 cycles per bit is used, the 4 MHz and 8 MHz CW interference signals corrupt the received signal quality for imaging. The frequency distortion around 4 MHz and 8 MHz arising from the interference signals leads to a relatively high range sidelobe level, i.e., around −18 dB as shown in Fig. 2(c). Although being 16 dB lower than the short pulse signal in Fig. 2(a), this level is still not enough to obtain an acceptable image quality. The 13-bit Barker code with 3 cycles per bit has about −50 dB range sidelobe level in spite of the interference signals as shown in Fig. 2(e). These two different results are due to the null point locations in their spectrums. The null points of the 3-cycle-per-bit Barker code are located around 4 MHz and 8 MHz, thus resulting in minimized mainlobe distortion. The −50 dB range sidelobe level of the 3-cycle-per-bit Barker code is acceptable for B-mode imaging. However, its axial resolution is poorer than that of the 2-cycle-per-bit Barker code. The −6 dB axial beamwidths of the 2- and 3-cycle-per-bit Barker code in Fig. 2(c) and (e) are 0.27 mm and 0.49 mm, respectively. Therefore, the focus of this study was on how the range sidelobe level of the 13-bit Barker code with 2 cycles per bit could be decreased to at least −40 dB in order to achieve a high axial resolution.

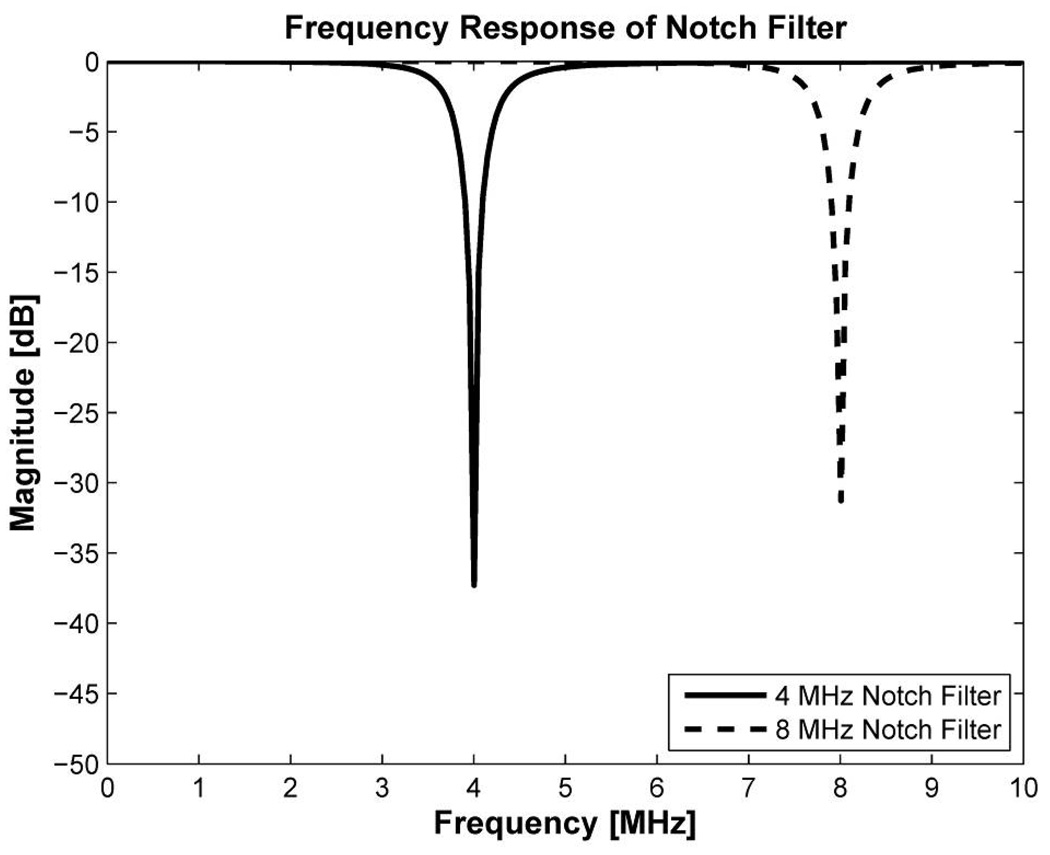
Fortunately, a reflected CW has a fixed frequency component, so that the known interference signal may be successfully minimized with a notch filter capable of rejecting a narrow band of frequency. A notch filter is widely used in radar or speech processing to attenuate CW signals at specific frequencies while nearby frequencies are relatively unaffected. [36]–[38]. A notch filter was designed using Matlab (The MathWorks Inc., Natick, MA) and notch attenuations were found to be around −37 dB and −31 dB at 4 MHz and 8 MHz, respectively, as shown in Fig. 4. Note that the sharpness of the notch filter depends on a quality factor defined as the ratio of notch frequency over bandwidth of the notch filter [38]. The quality factor should be properly determined by considering over shoot or under shoot in a pass band. In this design, the quality factors for 4 MHz and 8 MHz were 7 and 14, respectively. The difference of 6 dB notch attenuation between two frequencies of the notch filter may be compensated by a 10 dB amplitude difference between fundamental and harmonic components of the interference signals.

Fig 4.

Frequency response of 4 MHz and 8 MHz notch filters. The notch attenuation is −37 dB and −31 dB at 4 MHz and 8 MHz, respectively.

This notch filter was applied to conventional 2-cycle short pulse signal, the 13-bit Barker code with 2-and 3 cycles per bit. The amplitude of interference signals was successfully suppressed after notch filtering in all cases. However, a serious frequency distortion of the short pulse around 4 MHz and 8 MHz generated undesired ripples in its envelope as shown in Fig. 2(b). In the case of the Barker code with 2 cycles per bit, frequency distortions at around 4 MHz and 8 MHz were less than the short pulse signal since the locations of null points were close to 4 MHz and 8 MHz. The Barker code with 2 cycles per bit as in Fig. 2(d) had a −40 dB range sidelobe level which was 22 dB lower than the code without notch filtering, i.e., −18 dB shown in Fig. 2(c). As the locations of null points of the Barker code with 3 cycles per bit became closer to interference frequencies, its range sidelobe level in Fig. 2(f) approached −50 dB that was similar to the pulse compression result without notch filtering (Fig. 2(e)). This means that the null point played a pivotal role in efficaciously decreasing the effect of reflected therapeutic signals on image quality, and a notch filter helped to further decease the effect when the null points did not perfectly match the frequencies of the interference signals.

III. RESULTS

A. Simulation Results

A point target simulation was performed with using the Field II program [39]. The design parameters of IMCPA described in the Methods section were used in this simulation. The two outer row arrays transmitted 4 MHz or 8 MHz CW signals and the center row array received the reflected interference signals. The center row array was only used to obtain echo signals for imaging by a transmission/reception process and then the interference signals were added to the echo signals. Note that the 8 MHz CW signal was regarded as the second harmonic component of the 4 MHz CW signal. In this simulation, a steering angle for CW transmission was fixed assuming the follwoing treatment protocol: The CW beam was focused on a target for a duration of a few seconds. The −6 dB fractional bandwidths of the imaging and therapy arrays were 50% and 30%, respectively. The bandwidth of the therapy array was lower than the imaging array due to the lack of backing of the therapy array. A 4th order Butterworth filter was used to model transfer functions of these transducers in order to carry out more realistic simulation [34]. The band stop attenuation of the notch filter was −37 dB and −31 dB at 4 MHz and 8 MHz, respectively, as shown in Fig. 4.

Fig. 5 shows point target images when therapeutic interference signals were added to a reflected short pulse signal. All figures were logarithmically compressed with a dynamic range of 40 dB. The interference signals mixed with a short pulse signal seriously degraded image quality as presented in Fig. 5(b). The Barker code with 3 cycles per bit produced a high SNR image (Fig. 5(f)) because the interference was greatly suppressed. The 2-cycle-per-bit Barker code generated a high range sidelobe level that primarily appeared around the center scan line (Fig. 5(d)).

Fig 5.

Point target simulation with imaging signals in which CW interference was superimposed. All figures were logarithmically compressed with a dynamic range of 40 dB: 2-cycle short pulses, (A) without and (B) with interference; the 13-bit Barker code with 2 cycles per bit, (C) without and (D) with interference; the 13-bit Barker code with 3 cycles per bit, (E) without and (F) with interference.

Fig. 6 indicates the performance of the notch filter when the interference was superimposed on the imaging signals. The Barker code with 3 cycles per bit provided a low noise image shown in Fig. 6(c) which was similar to the image quality without the notch filter (Fig. 5(f)). The image produced by the short pulse signal shows not only an enhanced range sidelobe level in Fig. 6(a) due to the notch filter, but also undesired ripples in the axial direction. Fig. 6(b) illustrates an improved range sidelobe level of the 2-cycle-per-bit Barker code compared to that without notch filtering (Fig. 5(d)). This point target simulation indicates that a short pulse signal with a notch filter could be used for B-mode imaging, although there are ripples. In reality, it might be difficult to completely remove the continuous sinusoidal waves as demonstrated by the simulation even using a notch filter. This is because other frequency components around 4 MHz and 8 MHz would be also mixed with the imaging signals. These undesired interference signals increased the range sidelobe level of the envelope signal of the short pulse signal, and this phenomenon was experimentally verified.

Fig 6.

Point target images of interference-mixed imaging signals after notch filtering. All figures were logarithmically compressed with a dynamic range of 40 dB: (A) 2-cycle short pulses, (B) the 13-bit Barker code with 2 cycles per bit, and (C) the 13-bit Barker code with 3 cycles per bit.

B. Experimental Results

Usually, echo signals contain several types of noises that are different from white noise but can be neglected due to their small amplitude. These noises are associated with the transducer itself, acoustic loads, and electronic components [40]–[41]. In the case of HIFU, these interference signals might become significant because of high voltage applied to a HIFU transducer for a rather long duration compared to the case of imaging. Under this situation, the performances of the proposed method, evaluated with computer simulation described above, would be degraded. Therefore, the main purpose of this experiment is to verify whether a coded excitation method with a notch filter can successfully remove the noises as well as reflected therapeutic signals. Because experimental instruments to evaluate the performances of the proposed method under these conditions were not yet available, we had no choice but to use commercial single element transducers and equipments for this experiment. A polished quartz plate was used to generate strong reflected CW signals including the noises which were termed spurious signals in this paper.

Experiments were conducted to obtain imaging and CW signals as described in Fig. 7. First, 6 MHz imaging signals were collected by a 5.5 MHz single element transducer (V308, Olympus, Waltham, MA) with a −6 dB fractional bandwidth of 60% (Fig. 7(a)). To acquire 4 MHz CW signal, a 4.5 MHz single element transducer (IBK5-2, Olympus, Waltham, MA) with a −6 dB fractional bandwidth of 50% was used as a transmitter and the 5.5 MHz transducer as a receiver (Fig. 7(b)). To mimic the second harmonic component of 4 MHz CW signal, 8 MHz CW signal was excited by firing a 10 MHz single element transducer (A327R, Olympus, Waltham, MA) with a −6 dB fractional bandwidth of 50% and received by the 5.5 MHz transducer. The transmit transducer was tilted to the receive transducer as much as the angle difference of IMCPA allowed. Note that the difference between center frequencies of the commercial transducers and needed frequency components could be negligible because the amplitude of all collected data was modified based on equation (1).

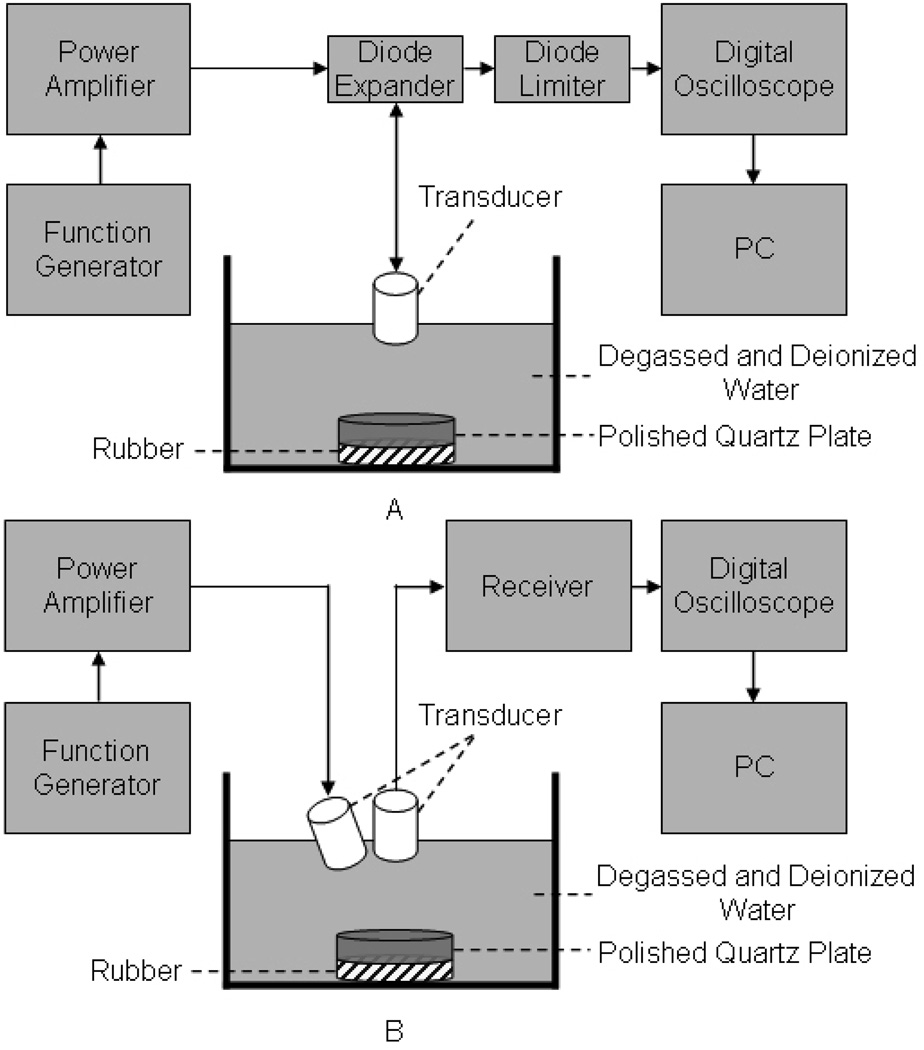
Fig 7.

Experimental arrangement to collect echo data of (A) imaging signals and (B) CW signals as interference signals.

A function generator (33250A, Agilent, Santa Clara, CA) was utilized to produce both CW and imaging signals such as 2-cycle short pulses and the 13-bit Barker code with 2 and 3 cycles per bit. The transmit signals from the function generator were sent to a RF power amplifier (325LA, ENI Co., Santa Clara, CA) to boost their amplitude and subsequently used to excite the transducers. With a receiver (5900PR, Panametrics Inc., Waltham, MA) and a digital oscilloscope (LC534, LeCroy, Chestnut Ridge, NY), echo signals were amplified and recorded to perform the proposed signal processing with a Matlab program. As a protection circuit, a diode expander (DEX-3, Matec, Northborough, MA) and a diode limiter (DL-1, Matec, Northborough, MA) were used. As a target, a polished quartz plate was immersed into a degassed/deionized water tank and a thin rubber was placed beneath the quartz plate to minimize reflected signals coming back from the bottom of the water tank.

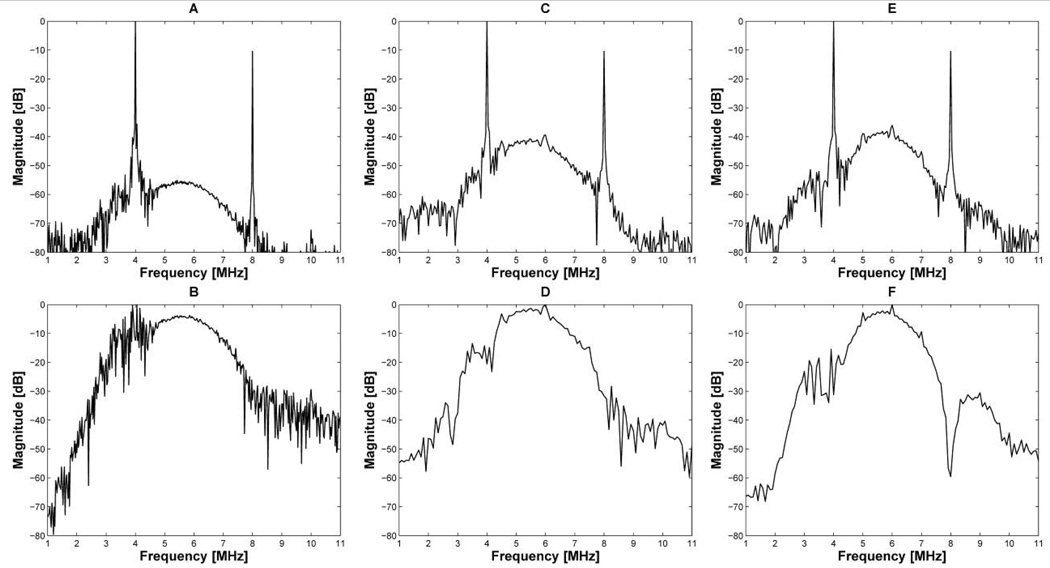
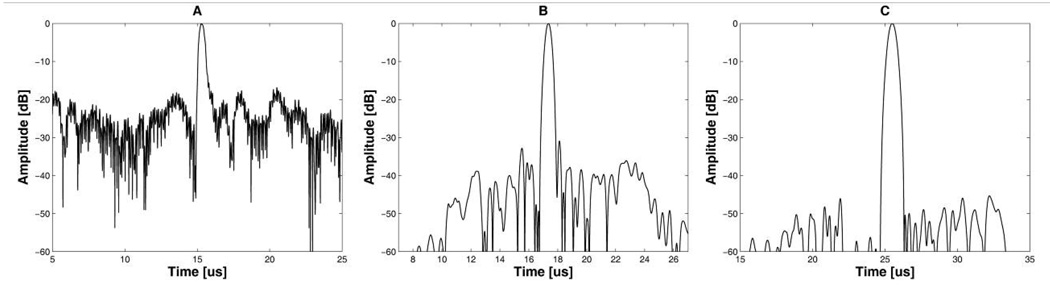
Fig. 8 shows the frequency responses of received echo signals (Fig. 8(a), (c), (e)) and the effect of notch filtering on each spectrum (Fig. 8(b), (d), (f)). The specifications of the notch filter (Fig. 4) described in the Methods section were used in this experiment. As expected, high amplitude interference signals appeared at around 4 MHz and 8 MHz frequencies. Although the notch filter dramatically reduced the amplitude of 4 MHz and 8 MHz CW signals mixed with 2-cycle short pulses, spurious signals around 4 MHz and 8 MHz frequencies still remained as shown in Fig. 8(b). These undesired interference signals could not be removed by a notch filter. As a result, the envelope of 2-cycle short pulses in Fig. 9(a) had a range sidelobe level of −18 dB due to the remaining interference. It is clear from Fig. 8(d) and (f) that the 13-bit Barker code with 2 and 3 cycles per bit have high robustness in suppressing the noise, thus providing the SNR improvement after pulse compression. The 2- and 3-cycle-per-bit Barker code offered a range sidelobe level of −40 dB and −48 dB after pulse compression as shown in Fig 9(b) and (c), respectively. Note that the 13-bit Barker code with 3 cycles per bit can also provided the best range sidelobe level without the notch filtering, which was about −47 dB.

Fig 8.

Frequency responses of 2-cycle short pulses (A), the 13-bit Barker code with 2 cycles per bit (C), and the 13-bit Barker code with 3 cycles per bit (E). After notch filtering, the interference signals appearing on the frequency responses were suppressed such as (B) of 2-cycle short pulses, (D) of the 13-bit Barker code with 2 cycles per bit, and (F) of the 13-bit Barker code with 3 cycles per bit.

Fig. 9.

Envelope signals: (A) 2-cycle short pulses, (B) the 13-bit Barker code with 2 cycles per bit after pulse compression, and (C) the 13-bit Barker code with 3 cycles per bit after pulse compression.

To compare the axial resolution, −6 dB and −20 dB axial beamwidths were measured and the results were summarized in Table I. The 2-cycle-per-bit Barker code had a −6 dB axial beamwidth of 0.39 mm which was 0.02 mm wider than that of the 2-cycle short pulses, but 0.13 mm narrower than that of the 3-cycle-per-bit Barker code. The −20 dB axial beamwidth of the 2-cycle-per-bit Barker code was 0.24 mm narrower than that of the 3-cycle-per-bit Barker code. However, the −20 dB axial beamwidth of 2-cycle short pulses could not be measured because its range sidelobe level was around −18 dB, so that it could not be used for imaging in spite of notch filtering.

Table I.

Experimental −6 dB axial beamwidths, −20 dB axial beamwidths, and range sidelobe levels of three different imaging signals.

	Pulse (2 cycles)	13-bit Barker code (2 cycles per bit)	13-bit Barker code (3 cycles per bit)
−6 dB axial beamwidth (mm)	0.37	0.39	0.52
−20 dB axial beamwidth (mm)	—	0.67	0.91
Range sidelobe level (dB)	−18	−40	−48

IV. SUMMARY AND CONCLUSION

In this paper, a novel ultrasound transducer design and a scheme to achieve real-time imaging during treatment were described and the feasibility was demonstrated through simulation and experimental results. By combining two therapy arrays and one imaging array, the fabrication complexity of IMCPA may be decreased, and each array may maintain its own optimal performance. The confocal structure of IMCPA in the elevational direction may improve the detection capability. Field II simulation and experimental results indicate that coded excitation and/or a notch filter may be able to improve the range sidelobe level of the B-mode image during therapy. In IMCPA, if high amplitude CW signals generated by therapy arrays are mixed with a short pulse signal, it would be difficult to extract the imaging signal from the mixed signal with current signal processing approaches. The coded excitation technique may overcome this limitation by reducing its range sidelobe level through pulse compression. When the 13-bit Barker code was used as an imaging signal mixed with CW signals, the Barker code with 3 cycles per bit provided a range sidelobe level of −50 dB after pulse compression. On the other hand, the 2-cycle-per-bit Barker code offered a range sidelobe level of −18 dB which was 16 dB lower than that of a short pulse signal. However, it still could not be used for imaging. It was demonstrated that this was related to the locations of null points in the frequency response of the Barker code. The null points of the 3-cycle-per-bit Barker code were located much closer to 4 MHz and 8 MHz frequencies than those of the 2-cycle-per-bit Barker code, thus reducing the effect of CW interference. However, the −6 dB axial beamwidth of the 3-cycle-per-bit Barker code was 0.15 mm wider than that of the short pulse signal and 0.13 mm broader than the Barker code with 2 cycles per bit as summarized in Table I. As a remedy, a notch filter technique was proposed to decrease a range sidelobe level of the 2-cycle-per-bit Barker code. With the notch filtering, we could achieve a −40 dB range sidelobe level of the 2-cycle-per-bit Barker code. In the case of the 3-cycle-per-bit Barker code, its range sidelobe was maintained at about −48 dB level regardless of whether notch filtering was implemented. Although Field II simulation in Fig. 6(a) shows the feasibility of using a short pulse signal with a notch filter, the experimental results indicated that the remnant CW components around 4 MHz or 8 MHz after notch filtering resulted in a −18 dB range sidelobe level. This undesired interference signal may be reduced by pulse compression of coded excitation successfully as shown in Fig. 9(b), (c). In the future, the design and fabrication of an IMCPA and the development of a system to implement a coded excitation technique with a notch filter will be pursued.