Detection of Small Bowel Slow Wave Frequencies from Noninvasive Biomagnetic Measurements

Abstract

We report a novel method for identifying the small intestine electrical activity slow wave frequencies from noninvasive biomagnetic measurements. Superconducting QUantum Interference Device (SQUID) magnetometer measurements are pre-processed to remove baseline drift and high frequency noise. Subsequently, the underlying source signals are separated using the well-known SOBI algorithm. A simple classification scheme identifies and assigns some of the SOBI components to a section of small bowel. Slow wave frequencies were clearly identified in 10 out of 12 test subjects to within 0.09–0.25 cycles per minute. The method is sensitive at the 40.3–55.9% level, while false positive rates were 0–8.6%. This technique could potentially be used to help diagnose gastrointestinal ailments and obviate some exploratory surgeries.

I. INTRODUCTION

In healthy small bowel, periodic depolarizations of the interstitial cells of Cajal (ICC) and the longitudinal muscle cells generate potentials which constitute the omnipresent slow wave of the small intestine [1]. The small bowel slow wave is known to exhibit a piece-wise aboral frequency gradient in virtually all primates. For instance, in humans the slow wave frequency (SWF) is typically about 12 cycles per minute (cpm) in the duodenum; about 9–11 cpm in the jejunum; and 8–10 cpm in the ileum [2]. Like the heart, diseases of the small bowel cause changes in the electrical activity that may indicate underlying pathology. Previous studies suggest that there are changes in the intestinal SWF and uncoupling that occur shortly after the onset of ischemia [3], [4], [5]. Thus, intestinal SWF content provides valuable information regarding the health of the small bowel. Often the surgeon must perform an exploratory laparotomy to confirm the suspicion of mesenteric ischemia or strangulated obstruction. Therefore, a noninvasive system for monitoring gastrointestinal (GI) electrical activity, and detecting the early signs of ischemia, is highly desirable in a clinical setting.

Previously, Chen et al. [6] and Martinez-de-Juan et al. [7] reported measuring the SWF using cutaneous electrode measurements. However, the success of their method relies on the subject having a low body-mass-index (BMI) as the low-conductivity of abdominal fat layers significantly attenuates and distorts cutaneous measurements of electrical potentials generated by GI electrical activity [8]. It is unlikely, therefore, that this method could be generally applied in a clinical setting.

Because the trans-abdominal GI magnetic field is not attenuated by these volume conduction effects [8], we previously proposed utilizing a SQUID magnetometer for noninvasive detection and assessment of both gastric and intestinal (GI) electrical activity and viability [9], [10]. Studies in our lab have demonstrated the ability of SQUIDs to detect changes in the SWF after the onset of ischemia in an animal model [11]. However, this experiment was performed under ideal conditions (suspension of respiration, no motion artifacts, etc.) which are unrealistic expectations for a clinical scenario. We have also previously reported [12] that the well-known SOBI algorithm developed by Belouchrani et al. [13] is capable of detecting small bowel electrical activity even when the SQUID signals are contaminated with environmental noise and large artifacts of biological and non-biological origin.

Herein, we describe a more powerful signal processing method for simultaneous detection of multiple small bowel slow wave frequencies. It contains two additional preprocessing steps—slowly varying drift (“baseline”) removal and low-pass filtering—which enhance the capability to detect SWF. Additionally, we have implemented an automated procedure to aid the clear identification of the SWF. The method is shown to be accurate, sensitive, and specific. In addition, it is able to localize multiple slow wave frequencies in accord with the known physiology of the animal model.

II. Physiological Measurements

A. Experiment Overview

All procedures were performed in accordance with the policies of the Institutional Animal Care and Use Committee at Vanderbilt University. Electrical potential and magnetic measurements were made simultaneously in adult pigs with body mass ≈ 40 kg. We used a porcine model because its GI system and abdominal wall architecture closely resembles that of a human. Serosal electrode recordings (SERs) are the standard against which we validate the noninvasive SQUID measurement and signal processing technique. After a baseline recording session lasting 30–60 minutes, the small intestine was surgically excised. Subsequently, electrical and magnetic measurements are taken for another 30–60 minutes. For some experiments (N=4) the entire organ was removed. For others (N=8), the duodenum was not removed because ligating the large amount of vasculature interconnected to the pancreas rendered timely removal impractical. Results obtained before and after the enterectomy were compared to unambiguously identify the origin of the magnetic source signals. Figure 1 illustrates the experimental set-up for simultaneous electrical and magnetic recordings in a porcine model.

Fig. 1.

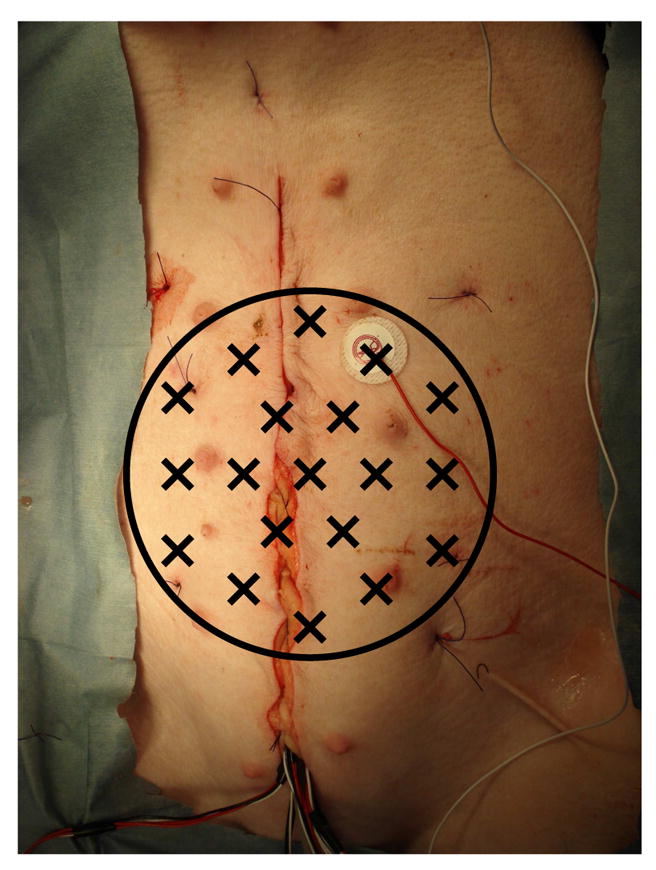
Simultaneous serosal electrode (SER) and magnetic (MENG) recordings of small bowel electrical activity were made in a porcine model. The black circle indicates the extent of the abdominal area covered by the SQUID magnetometer; X’s mark the positions of the detection coils. The sutured incision giving access to the GI organs is evident running vertically. The bundle of wires emerging from the bottom of the incision are connected to the serosal electrodes. The cutaneous electrode affixed to the right of the incision is the common-mode reference electrode.

Throughout the duration of the experiment, the respiration rate was held constant at about 26 cpm using a mechanical ventilator (Hallowell EMC Model 2000, Pittsfield, MA). The heart rate was maintained at about 92 beats per minute. The motivation for setting this high respiration rate was to aid the unambiguous identification of small bowel slow wave (see Discussion).

B. Serosal Electrode Recordings

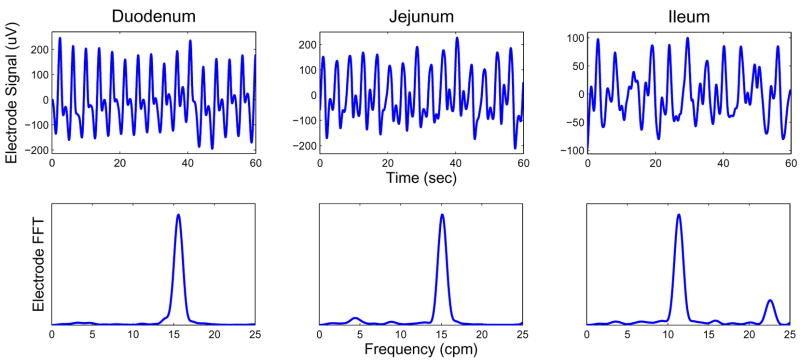
The test subjects were anesthetized and a laparotomy was performed to gain access to the GI organs. Direct (invasive) measurements of electrical activity in the small bowel were obtained by suturing silver-chloride electrodes onto the serosal surface of the duodenum, jejunum, and ileum [14]. Serosal electrode platforms were placed at the following sites (the number in parentheses indicates the number of individual electrodes on each platform): proximal duodenum, 10 cm distal to gastro-duodenal junction (4); jejunum, 20 cm distal to Ligament of Treitz (LT) (4); jejunum, 30 cm distal to LT (16); and distal ileum, 20 cm proximal to ileo-cecal junction (4). SERs were acquired at 256 Hz with the Biosemi Active II recording system (Amsterdam, Netherlands), and subsequently resampled to 30 Hz. Figure 2 shows typical serosal electrode recordings (SERs) and corresponding frequency spectra obtained from each bowel section. (All frequency spectra reported in this manuscript were computed with the Fast-Fourier transform (FFT).)

Fig. 2.

Top row: Serosal electrode recordings from the duodenum (left); jejunum (middle); and ileum (right). Signals are 2nd order Butterworth filtered in the band 2–60 cpm. Bottom row: corresponding frequency spectra. The dominant frequencies noted for the duodenum, jejunum, and ileum were 15.6, 15.1, and 11.4 cpm, respectively.

C. SQUID Magnetometer Measurements

A multichannel SQUID magnetometer (637i, Tristan Inc., San Diego CA) was used to make measurements of enteric electrical activity—we refer to these as the ”magnetoenterogram” (MENG). In essence, the SQUID converts magnetic flux incident on detection coils into voltage signals. A set of 19 detection coils arranged in gradiometer format are spaced in a hexagonal close-packed array in the x-y plane over an area with a 10 cm radius. (However, note that for all experiments described herein, data were acquired from 16 sensors only; 3 sensors were not in service due to data acquisition hardware issues for which a timely remedy was impractical.) These coils are used to measure the magnetic flux in the ẑ direction, B_z, approximately normal to the frontal surface of the test subject. The SQUID was placed over the mid-abdomen during the experiment. SQUID signals were passed into a pre-amplifier stage (QuantumDesign, Model 5000) with a gain of 5 and a low-pass filter set to 1 kHz. Data were acquired at 3 kHz and subsequently down-sampled to f_s = 30 Hz. Figure 3 shows a typical 60 second-long MENG recording.

Fig. 3.

Sample MENG recordings from 16 sensors. Vertical scale bar: 7.1 pT. Horizontal scale bar: 60 sec. Although we analyzed 120-second segments of data, a 60-second recording is shown here for clarity. The large oscillation (26 cpm, ≈ 2–7 pT) that dominates on most sensors is due to respiration of the test subject. Slow drift is also noticeable in many of the sensors. The large spike at t = 24 sec is probably due to a transient external signal, such as a metal door opening outside the laboratory.

MENG recordings contain a mixture of signals, a linear superposition of flux incident from any magnetic source. Magnetic sources other than the small bowel slow wave are considered to be interfering sources. They are generated by both non-biological sources (computers, power lines, other laboratory equipment) and biological sources (cardiac, respiration, muscular contraction/motion). Contamination by the former is limited, in part, by performing studies inside of a mumetal shielded room (Amuneal; Philadelphia, PA); the latter cannot be avoided. We are, of course, interested in identifying the enteric sources in this noisy environment.

It is important to note that magnetic sources sum linearly and (approximately) instantaneously at the SQUID coils, hence the MENG measurements, x, are well-described by the mixture model:

$$\mathbf{x}(t)=\mathbf{As}(t)+\mathbf{n}(t)$$ (1)

To be explicit, in eq. (1), SQUID data are sampled at times t = nΔt_s (Δt_s = 1/f_s), and each sensor’s data is arranged in rows: x(t) = [x₁(t), x₂(t),…, x_m(t)]^T, where x_i(t) is the recording on SQUID channel i. Similarly, s(t) = [s₁(t), s₂(t),…, s_m(t)]^T, where s_i(t) is the ith underlying component, of GI or non-GI origin. A is termed the mixing-matrix, as it describes how much each source signal is projected onto each SQUID sensor. n(t) represents the noise present in each channel, assumed to be white and not spatially correlated.

III. SQUID SIGNAL PROCESSING

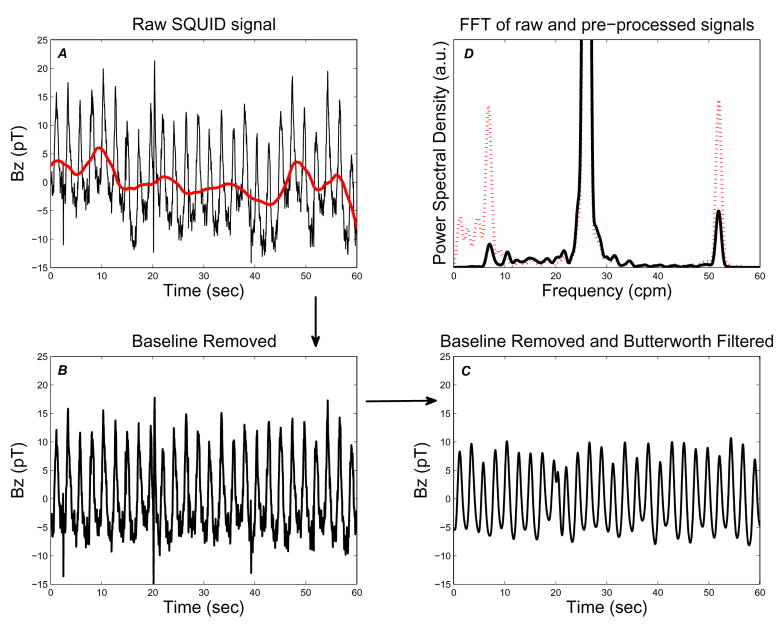
Signal processing proceeds in several stages: removal of slowly varying drift; low-pass filtering; application of the Second-Order Blind Identification (SOBI) algorithm; and classification and identification or the resulting source components. Each stage is described in more detail below. We processed 120 second-long data segments in steps of 60 seconds (e.g., 0–120 seconds, 60–180 seconds, etc.). Figure 4 illustrates the sequence and effect of the pre-processing steps which are described in detail below.

Fig. 4.

Pre-processing of SQUID signals. Raw SQUID signal (thin, black trace) with baseline drift signal (thick, red trace) overlaid (A); signal after baseline removal (B) and low-pass filtering (C). SQUID signal power spectrum before (dotted, red) and after (solid, black) pre-processing (D). The large signal that goes off scale centered at 26 cpm is due to the large respiration artifact, as is the first harmonic at 52 cpm. Note that removal of the slow drift baseline greatly reduces the low-frequency (f ≤ 5 cpm) energy content, while leaving the energy contained in the SWF range (≈ 10–18 cpm) essentially unaltered.

A. Baseline Drift Removal

The raw MENG signals are contaminated by slowly varying (“baseline”) drift with power concentrated in the low-frequency range (f ≤ 5 cpm). The slow drift is generated, in part, by biological sources (e.g., the colon). These components can dominate the SOBI separation process making the underlying enteric signals “invisible.” To remove them, in essence, we approximate the baseline signal by using a wavelet projection method, retaining coefficients only at large-scales. Our approach is inspired by previous reports of removing slowly varying drift from fMRI signals using a general linear model with a projection onto a subspace of large-scale wavelets [15], [16]. However, rather than employing an information criterion to estimate the appropriate scale of the wavelet projection, we use the a priori knowledge that the frequency range of the small bowel slow wave should be in the range of about 10–20 cpm.

Specifically, the baseline signal of x_i(t) consisting of T samples is subtracted according to:

$$\begin{array}{c}{b}_i(t)=\sum _{m=m_o}^{\lceil {log}_{2}T\rceil }\sum _n{c}_{m,n}^{(i)}{\psi }_{m,n}\\ x_i(t)\leftarrow x_i(t)-b_i(t)\end{array}$$ (2)

The discrete wavelet transform (DWT) coefficients $c_{m,n}^{(i)}$ (for level m, at time point n) are obtained through the inner product of the ith MENG signal with the mother wavelet: $c_{m,n}^{(i)}=\langle x_i(t),{\psi }_{m,n}\rangle$. We used a ‘db4’ mother wavelet, and chose m_o = 8. This choice of m_o correlates to subtracting a baseline signal from MENG signal with (equivalent Fourier) frequencies up to 5.02 cpm. Figure 4 (A and B) illustrates the result of baseline drift removal from a SQUID signal. The resulting decrease in power at low frequencies (f ≤ 5 cpm) is made evident by comparing the FFT of the signal before and after baseline removal (Figure 4 D).

B. Low-Pass Filtering

Subsequently, the signals are low-pass filtered to remove high frequency noise to render the SOBI separation process more sensitive to frequencies in the enteric range. We used a 2nd order Butterworth filter with a cutoff frequency tuned to f_c = 50 cpm. The low-pass filter essentially constrains (almost) all resulting SOBI components to have a dominant frequency f_d ≤ f_c. The effect of the low-pass filter pre-processing step is depicted in Figure 4 C).

C. Application of SOBI

As discussed in section II-C, the MENG recordings are well-described by an instantaneous mixture model: x(t) = As(t) + n(t). To separate the unknown underlying (non-) physiological sources we use the well-known SOBI algorithm [13]. Briefly, SOBI is a blind-source separation (BSS) technique which exploits the second-order statistics of the measurements to compute an estimate of the mixing matrix (full details can be found in [13]). The key step in the algorithm is to rotate a set of time-lagged cross-correlation matrices of (whitened observations, denoted by underlined quantity) SQUID data, R_xx(τ_k) = E[x(t + τ_k)x*(t)] so that they are jointly approximately diagonalized. In other words, SOBI attempts to identify underlying sources which are as uncorrelated as possible through a given set of time-lags. The output of the algorithm is an estimate of the mixing matrix, Â. The underlying sources are then estimated as: ŝ = Â⁻¹x. (For the remainder of this manuscript, we drop the hat notation for clarity.)

We always chose to separate the maximum possible number of sources (equal to the number of sensors in the MENG recording) because the small bowel contains multiple (≥ 3) distinct dominant frequencies [17], and some sources would be “used up” on respiration, motion, and other artifacts. The performance of the SOBI algorithm depends on a judicious choice of a set of p time lags, τ_k (k = 1, 2,…, p) [18]. We empirically chose a set of p = 200 time-lags corresponding to the range of 1/30 – 13.3 seconds, in intervals of 1/15 second (see Section V). The choice to use an interval of 1/15 sec was simply to speed up the procedure—no difference in performance was noted compared to using the minimum possible time-lag of 1/30 second. Note that for signals in the 10–15 cpm range, 13.3 seconds corresponds to about 2–3 full cycles.

D. Classification of primarily sinusoidal components

Because the passive volume conductor effects of the abdomen act as a low-pass spatial filter on the magnetic fields measured distant from the underlying current sources [8], [19], the slow wave signals recorded by the MENG are expected to a smoothed representations of the corresponding electrical activity (e.g. signal in top row of figure 2). Therefore, we expect the slow-wave, as recorded by the MENG, to be primarily sinusoidal—i.e., well-described as a regular periodic signal. We wanted to distinguish SOBI components which steadily oscillate from those that do not. For this classification task we implemented a support-vector machine (SVM) with a quadratic kernel. Classification was based on two features: 1) the sparseness of the FFT and 2) a measure of goodness-of-fit between a SOBI component and its best-matched sinusoid of the same dominant frequency. Choosing components with a high degree of sparseness essentially selects for those which have (at most) a few dominant peaks in the FFT power spectrum. The second criterion further refines the selection to include only components which are primarily comprised of one dominant sinusoid. The sparseness measure we used (originally introduced by Hoyer [20]) is given by:

$$\mathit{sparseness}(\mathbf{y})=\frac{\sqrt{n}-(\sum \mid y_i\mid )/\sqrt{\sum y_i^2}}{\sqrt{n}-1}$$ (3)

where n is the dimensionality of y. The expression evaluates to 1 if there exists only one non-zero entry if y, and 0 if all values in y are equal.

The goodness-of-fit measure between a SOBI component s_i(t) and its best-fit sinusoid, V_i(t), is computed as:

$$g_i=1-\frac{\mid V_i(t)-s_i(t)\mid }{\mid V_i(t)\mid }$$ (4)

where V_i(t) is constructed to have frequency f_si, the dominant frequency of s_i. (The dominant frequency is defined as: f_d = arg max_f FFT {s_i}.)

$$V_i(t)=C_1\mathit{cos}(2\pi f_{s_i}t)+C_2\mathit{sin}(2\pi f_{s_i}t).$$ (5)

In eq. 5, C₁ and C₂ are chosen to minimize the the difference between V_i(t) and s_i(t) in the least-squares sense. A value of g_i = 1 indicates that V_i(t) perfectly describes s_i(t) whereas a value of 0 indicates that V_i(t) very poorly describes s_i(t).

The training set for the SVM consisted of 45 randomly-selected SOBI sources generated from 3 different studies. Training set waveforms were judged by visual-inspection of multiple observers to label each as primarily sinusoidal, or not. The trained SVM was then used to classify all SOBI components evaluated over twelve studies (about 10,000 total).

E. Assigning Components to a bowel section

The final step is to assign a subset the primarily-sinusoidal SOBI components to a bowel section: duodenum, jejunum, or ileum. These bowel sections are denoted hereafter as classes {D, J, I}, respectively. Our approach essentially is to look for components with dominant frequencies “close to” those observed in the serosal electrode recordings which regularly appear during the pre-surgery period, but not during the postenterectomy period.

Whereas electrical measurements are made from four specific points along the small bowel, magnetic measurements are made from the entire organ. Therefore, legitimate small bowel frequencies may be observed in the MENG which are not observed in the serosal electrode recordings. Electrodes placed at nearly the most proximal and distal regions of the small bowel provide information regarding the minimum and maximum bounds on slow wave frequencies. For the purposes of assigning SOBI components to a section of small bowel, we consider the enteric frequency range to be

$$f_{\mathit{enteric}}\in \left[\underset{j}{min}(f_{e_j})-0.25,\underset{j}{max}(f_{e_j})+0.25\right]$$

(in units of cpm) where f_ej is the dominant frequency observed with the jth electrode (j = 1, 2,…, N_electrodes). The factor of 0.25 cpm derives from the magnitude of the slow wave’s aboral frequency gradient, typically about 0.5 cpm/30 cm.

For each 120-second data segment in the pre-enterectomy period, we consider each s_i previously labeled as primarily-sinusoidal. If the dominant frequency of s_i fell within the enteric range, f_s ∈ f_enteric, then we computed the difference Δf_i,j = |f_si − f_ej| ∀ j. Component s_i was assigned to the bowel section {D, J, I} corresponding to electrode j such that Δf_i,j is the minimum value.

During the post-enterectomy period, electrical measurements from excised bowel sections were no longer available to define their frequency ranges. (Serosal electrode measurements were still made on the duodenum during the experiments for which we did not remove it.) We defined the lower and upper bounds of the frequency ranges of excised bowel section to be the minimum and maximum SOBI component frequencies, f_si in each class {D, J, I} observed over the entire pre-surgery period.

When the duodenum was not excised, we first assigned all component frequencies, f_si, differing from the duodenal SWF (in the SER) by ≤ 0.25 cpm to the duodenum. Then we declared all remaining components in the enteric frequency range to be false-positives and assigned them accordingly to either of {J, I}. When the duodenum was excised we declared all components with frequencies in the enteric frequency range to be false positives and assigned them accordingly to the appropriate class {D, J, I}.

For each class we computed the sensitivity as the fraction of time points for which (at least) one SOBI component was assigned to that bowel section. Similarly, the false-positive rate was defined as the fraction of time points for which (at least) one false-hit was identified. Finally, we computed a signal-to-noise ratio for each class as:

$$\mathit{SNR}=\frac{\mathit{sensitivity}}{\mathit{false}-\mathit{positive}\mathit{rate}}$$

If the SNR ≥ 5, then this section of the bowel to declared to be clearly identified. A value of 5 corresponds to the threshold for which a blinded observer can clearly detect the presence of small bowel frequencies during the pre-surgery period, and the absence of them during the post-surgery period, by visual means (see Figure 7, for example).

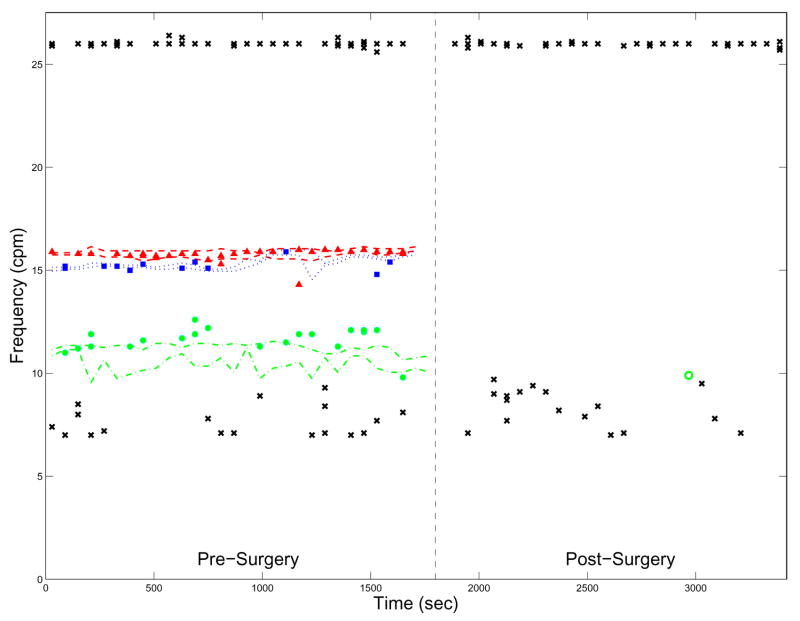
Fig. 7.

The dominant frequencies observed with SERs over time with frequencies of MENG-SOBI components overlaid. The minimum and maximum frequency measured in a bowel section (varying over time) is plotted for each bowel section as follows—Red, dashed: duodenum. Blue, dotted: jejunum. Green, dash-dotted: ileum. MENG-SOBI components assigned to a section of the bowel are represented as red triangles (duodenum); blue squares (jejunum); or green circles (ileum). An unfilled marker of the same shape and color denotes a false-positive observed during the post-surgery period. A black ‘x’ marks the frequency of a SOBI component of non-enteric origin. The components persisting at 26 cpm correspond to respiration. The vertical dashed line demarcates the end of the pre-surgery data acquisition period.

Lastly, as a measure of how well a blinded observer can discriminate between enteric and non-enteric frequencies, for each clearly-identified bowel section we computed the average minimum distance between f_si and the frequency of the nearest non-enteric source. We term this quantity the frequency band gap:

$$\delta f=\underset{\eta }{min}\mid f_{s_i}-f_{s_{\eta }}\mid$$ (6)

where f_sηdenotes the frequency of any primarily sinusoidal SOBI component, s_η, not assigned to any bowel section.

IV. RESULTS

A. Enteric Source Frequency Identification

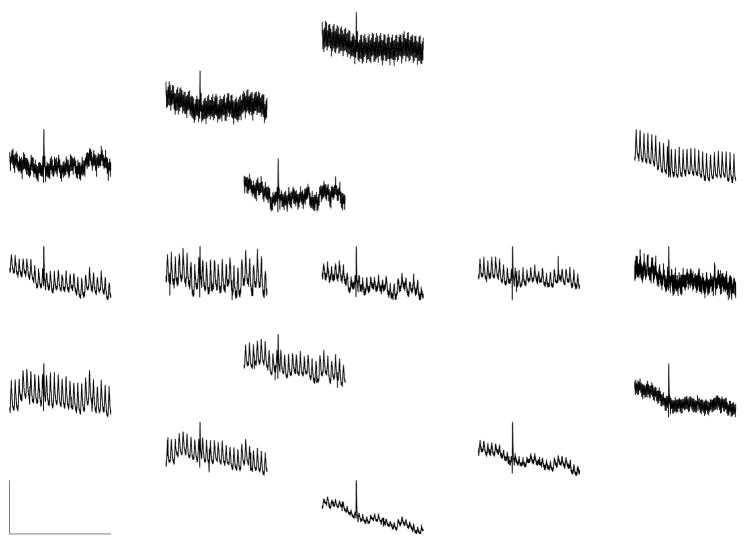
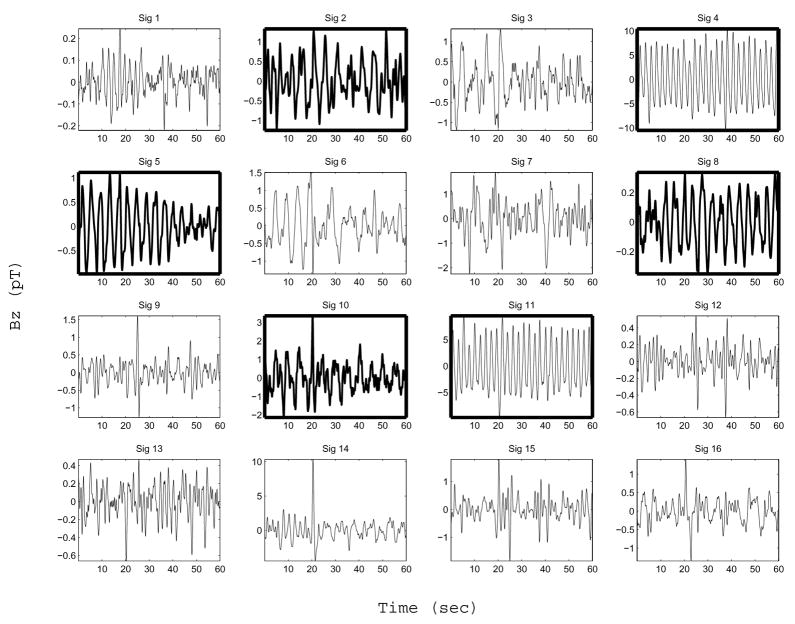
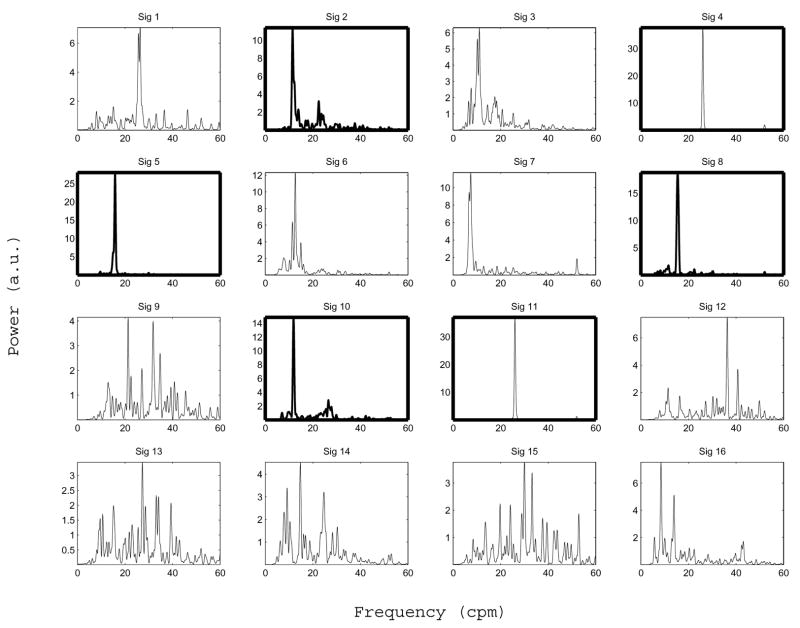
Figure 5 shows typical SOBI sources obtained with our signal processing method. These SOBI components were obtained by processing the MENG signals shown in Figure 3 according to the procedure described above. Figure 6 shows the corresponding FFT spectrum for each source. In this case six out of sixteen sources separated by SOBI were found to be primarily sinusoidal (component numbers 2, 4, 5, 8, 10 and 11). Two of these (components 4 and 11) are clearly attributed to respiration, as the dominant frequency of both is 26 cpm, exactly matching the known respiration rate of the test subject. Component 1 is also accounted for by the respiration artifact, though it is not primarily sinusoidal. Components 2 and 10 (dominant frequencies of 11.5 and 11.9 cpm) are attributed to the ileum. Component 5 (15.4 cpm) is attributed to the jejunum, and component 8 (15.8 cpm) to the duodenum. Components 9 appears to capture the spike-like artifact that occurs in the raw MENG at about t = 24 sec, as do components 14 and 16, to a lesser extent. Although components 3, 6, and 7 are possibly enteric in origin as the dominant frequency lies within the known enteric range, they are not considered in further analysis because they were not classified as being primarily sinusoidal. The origin of the other three noisy components (12, 13, and 15) is unidentified.

Fig. 5.

SOBI components. Although we analyzed 120 second-long data segments, only 60-second segments are shown for clarity. Boxes in bold mark components which are well-described as a sinusoid containing a single dominant frequency (according to the criterion described in section III-D). The subset of bold boxes that contain a waveform also drawn in bold are components identified as being enteric in origin (Sig 2, 5, 8, and 10). The two non-bold waveforms in bold boxes are attributed to respiration (Sig 4 and 11). See text regarding the origin of the other SOBI components. Each component shown has been scaled by the maximum value contained within the corresponding column vector of the mixing matrix—i.e. max_i |a⃗_ij |·s_j.

Fig. 6.

SOBI component frequency spectra corresponding to the sources shown in 5. The boxes in bold mark components which are classified as primarily sinusoidal (according to the criterion described in section III-D). The subset of bold boxes which contain a frequency spectrum also drawn in bold mark components identified as being enteric in origin (Sig 2, 5, 8, and 10). The two non-bold waveforms in bold boxes (Sig 4 and 11) are attributed to respiration. See text regarding the origin of the other SOBI components.

Figure 5 also indicates the oscillation amplitudes of the components. Each source shown has been scaled according to the maximum absolute value of the entries in the column vector corresponding to the source—i.e. max_i |a⃗_ij | · s_j The amplitudes of the enteric components were typically in the range of few-tenths of a pT – 1 pT. It is important to ask whether these amplitudes are reasonable. Indeed, the measured amplitudes are in reasonable accord with the values predicted by a dipole-based slow wave model described in detail in [21].

Figure 7 illustrates a typical result from one entire study. The dominant frequencies of all SOBI components classified as primarily-sinusoidal are plotted versus time. The frequencies bounds of the duodenum, jejunum, and ileum are also indicated on the graph as dashed, dotted, and dash-dotted lines, respectively. Importantly, dominant frequencies determined with the MENG and SOBI-based signal processing scheme were regularly identified in the enteric frequency range during the pre-surgery period, but not at all during the post-surgery period, with exception of one false-positive for the ileum at t ≈ 2900 sec. Furthermore, the SWF determined by the MENG and SERs are in excellent agreement for the duodenum and jejunum. The ileal SWF determined with the MENG is also in good agreement and shifted up relative to the SER-determined value. This result is consistent with the idea that the duodenum and jejunum were positioned directly beneath the SQUID sensor array, while the ileum was situated caudal to it.

The almost omnipresent 26 cpm component is due to respiration. The few time points at which it was not identified correspond to data acquisition segments during which the test-subject’s respiration was temporarily suspended. The results show that our method for detecting SWF is impervious to the presence of respiration—components were identified equally well even when a large respiration artifact was present. The absence of any component within the frequency band 17–26 cpm makes identification of the jejunal and duodenal SWF unambiguous. It also suggests that, in a clinical setting, a patient could be asked to comfortably hyperventilate for a short period of time to aid discerning the SWF. Some primarily-sinusoidal, non-enteric components irregularly cluttered lower frequencies (6–8 cpm). This was also typical of most studies. In a few more severe cases, the low-frequency clutter precluded unambiguous identification of the ileal SWF.

B. Frequency Detection Results Summary

Table 1 summarizes the results from ten of twelve experiments for which at least one small bowel section was clearly identified. One bowel section was clearly identified in two experiments; two bowel sections in six experiments; and all three bowel sections in two experiments. The duodenum was clearly identified in six studies, the jejunum in ten, and the ileum in four. In the case that two sections were identified they were contiguous (duodenum and jejunum, or jejunum and ileum), suggesting that the position of the magnetometer significantly influences the detectability of SWF in a particular bowel section.

TABLE I.

Summary Results for 10 enterectomy experiments. “D”: Duodenum. “J”: Jejunum. “I”: Ileum. Values quoted in each of the first ten rows are the mean ± st.dev for individual experiments. A dash indicates no value applicable (bowel section not clearly identified). The bottom two rows are the mean and standard-deviation of the mean values across all experiments, respectively. The average sensitivity is calculated over all experiments for which the bowel section was clearly identified. See text for description of each characteristic quantity.

	Frequencies Detected (cpm)			ΔF (cpm)			Sensitivity (%)			False Positive Rate (%)			Frequency Band Gap (cpm)
	D	J	I	D	J	I	D	J	I	D	J	I	D	J	I
	15.6±0.1	14.4±0.0	-	0.12±0.11	0.00±0.00	-	8.33	1.67	0	0.0	0.0	-	6.3±1.4	5.2±0.0	-
	15.0±0.5	13.9±0.4	-	0.10±0.10	0.05±0.08	-	41.7	60.0	0	-	6.8	-	5.0±1.1	3.9±1.4	-
	-	13.8±0.1	-	-	0.02±0.04	-	0	52.5	0	-	0	-	-	3.5±0.8	-
	16.7±0.4	16.4±0.2	10.7±0.2	0.07±0.06	0.06±0.08	0.07±0.07	4.6	18.5	21.5	-	0	4.9	8.5±0.35	7.5±1.3	2.8±3.7
	-	15.9±0.3	11.3±0.3	-	0.09±0.11	0.19±0.23	0	11.1	69.8	-	1.75	14.0	-	6.3±1.0	1.8±0.77
	15.6±0.7	15.2±0.5	-	0.10±0.10	0.06±0.01	-	72.2	72.2	0	-	9.7	-	4.8±2.1	4.6±1.9	-
	14.5±0.9	13.4±0.4	-	0.13±0.17	0.10±0.11	-	78.3	50.0	0	-	6.8	-	4.2±1.2	3.1±1.1	-
	15.8±0.1	15.2±0.3	11.5±0.6	0.04±0.05	0.15±0.23	0.23±0.43	89.3	39.3	60.7	0	0	3.7	9.1±1.2	9.5±1.6	7.8±5.3
	-	14.7±1.1	12.6±0.7	-	0.09±0.07	0.21±0.19	0	10.7	71.4	-	0	11.5	-	7.5±1.1	3.7±2.5
	-	14.1±0.8	-	-	1.33±0.76	-	0	22.2	0	-	0	-	-	3.7±1.8	-
Mean	15.5	14.8	11.1	0.09	0.07	0.25	49.1	40.3	55.9	0.0	3.9	8.6	6.3	5.6	5.3
SDM	0.7	1.1	0.6	0.03	0.05	0.25	36.6	26.4	23.4	0.0	4.4	5.0	2.1	2.4	3.5

The MENG-SOBI determined SWF were close to those determined with SERs. The difference between them (ΔF in Table 1) was typically ≤ 0.1 cpm for the duodenum and jejunum, and ≈ 0.25 cpm for the ileum. The less frequent identification of, and the larger ΔF value observed for, the ileum is consistent with the idea that the SQUID was positioned towards the upper abdomen, cephalad to the ileum.

The sensitivity of the method varied between experiments and among bowel sections. Typically, when sensitivity for one bowel section was relatively low, another section had a higher value. For example, the results listed in the fifth row of Table 1 indicate that, although the sensitivity for the jejunum was 11.1 %, the sensitivity for the ileum was 69.8 %.

The false positive rate was low for all three bowel sections. The ileum had, on average, the highest false positive rate. This result is due to the “clutter” of primarily sinusoidal components that exist typically in the ≈ 5–10 cpm range which sometimes overlap into the ileal frequency range.

The average frequency band gap was typically ≈ 4–6 cpm for the duodenum; about 3–5 cpm for the jejunum; and 1–3 cpm for the ileum. (The average value quoted for the ileum in Table 1 is skewed by one experiment (out of four) for which the discrimination distance was unusually large.) Non-enteric, primarily sinusoidal components typically do not confound determination of the SWF via visual inspection of a frequency vs time plot (e.g., Figure 7) for the duodenum or jejunum. The ileal SWF is sometimes more difficult (or impossible) to clearly identify due to low frequency clutter.

C. Enteric Source Localization

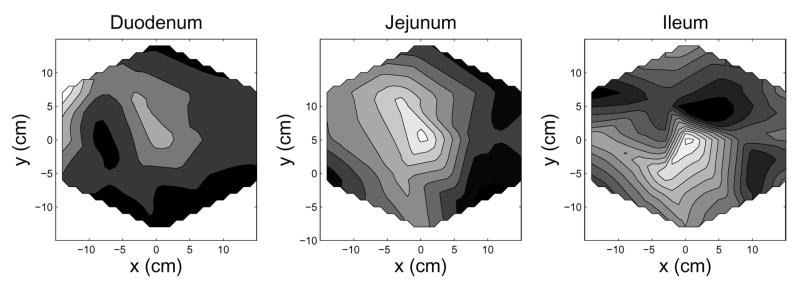
For potential use in a clinical setting, it is important to be able to spatially localize the origin of an identified enteric frequency. Source localization can be accomplished by projecting a MENG-SOBI source back onto the SQUID sensor array. Figure 8 shows spatial intensity maps for each of three enteric components corresponding to the duodenum, jejunum, and ileum) projected back onto the SQUID array. A source is spatially localized according to a region of high intensity (white on the spatial intensity maps.) This figure indicates that the duodenal, jejunal, and ileal sources can be crudely localized to the top-left (duodenum); upper-middle (jejunum); and lower-middle (ileum) of the SQUID sensor array. This finding is consistent with the known anatomy of the test-subject’s GI system. Note that, in a clinical diagnostic setting, if the spatial origin of the source is concentrated in an abnormal location, then the corresponding frequency may be strongly indicative of an unhealthy (ischemic) section of bowel.

Fig. 8.

Spatial Intensity contour maps show the relative location (focus) of the each bowel section. These spatial intensity maps were created for each bowel section by projecting an averaged column vector back onto the SQUID sensor array: a⃗_avg = Σ_k a⃗_γk (t_k) where a⃗γ_k is the column vector from A_k (the SOBI mixing matrix computed at time point t_k), and γ_k indexes the column number corresponding to the SOBI component of enteric origin. In the gray scale contour maps white is higher-intensity; black is less-intensity. The positions noted for each bowel section are consistent with the known physiology and aboral frequency gradient of the small bowel.

V. DISCUSSION

We have reported a robust method for noninvasive detection of small-bowel electrical activity. Importantly, the method is accurate, sensitive, specific, and able to generally localize the origin of the small bowel slow wave sources. The reason for failing to detect any small bowel frequencies in two experiments may be attributed, in part, to the fact that these data sets have a very high rate of occurrence of large spike-like artifacts. These tend to dominate the SOBI separation process at the expense of potentially separating enteric components. This problem might be remedied by adding an additional spike-identification and removal pre-processing step. For these cases, it would be also wise to re-evaluate the identifiability criterion detailed in section III-D.

The respiration frequency was maintained for most studies at 26 cpm to preclude potential overlap of respiration and small bowel frequencies. We have found that a setting the respiration rate as low as 21 cpm does not complicate separation and identification of enteric frequencies from the MENG. If, in a clinical setting, it is believed that a patient’s natural respiration rate would preclude clear identification of the SWF, the patient could be asked to comfortably hypo- or hyper-ventilate to shift his respiration rate away from the suspected SWF. The patient can also be asked to wear a respiration monitor so that any subsequent SOBI component that is well-matched to the known respiration waveform can be properly assigned as such.

It is important to further comment on the results obtained for the experiments during which the duodenum was not excised. When the duodenum SWF was clearly identified preenterectomy, it was also identified post-enterectomy in all cases. However, in some cases, when the duodenum was not clearly identified pre-enterectomy, it was identified during the post-enterectomy period. During the pre-enterectomy period the SOBI separation process was more sensitive to the jejunum SWF by virtue of it lying anterior to the duodenum and closer to the SQUID sensors. During the post-enterectomy period, however, the separation process was able to separate the duodenum SWF, as it was no longer “in competition” with the jejunum SWF. Importantly, these experiments crucially served as a control experiment verifying that there was nothing in the surgery process that accounted for the disappearance of enteric frequency components during the post-surgery data acquisition period.

The choice of parameters used in the signal processing stages of our method merits further comment. We found the wavelet projection baseline removal method to be more effective than applying a standard digital high-pass filter with a cutoff of 5 cpm. Note that this method has the unfortunate side effect of discarding any gastric slow wave components (typically at 3 cpm) that may be present in the MENG. Regarding the choice of low-pass cutoff frequency, we observed that using a narrower-band filter (f_c = 30 or 40 cpm) often resulted in a significant number of false-positives in the enteric range, confounding clear identification of enteric components.

Our choice of SOBI time-lags was empirically tuned. We investigated tag-lag sets consisting of p = 50, 100, 200, 300, and 450 time-lags corresponding to maximum tag-lag values of τ_max = 3.3, 6.7, 13.3, 20.0, and 30.0 seconds, respectively. A set of p = 50 lags was insufficient to separate putative small bowel sources; a set of p = 100 inconsistently separated them (relatively low sensitivity). Using the longest set of lags (p = 450, τ_max = 30 sec) tended to separate low-frequency components (f_si ≤ 7 cpm) at the expense of components that were enteric in origin. A small, but appreciable, difference in performance was noted between sets consisting of p = 200 and p = 300 time-lags.

Regarding the choice of BSS algorithm: We have found SOBI to be superior to other signal processing algorithms for this task. The success of SOBI for our application derives from the fact that the algorithm explicitly exploits the underlying time-structure of the MENG recordings. This feature is desirable because the source signals we are trying to detect are steadily oscillating sinusoids. We evaluated several other well-known BSS algorithms for the task of separating enteric components. None was satisfactory. The fastICA [22] and JADE [23] algorithms tend to output spike-like components characteristic of over-fitting. We observed this result despite attempts to tune the parameters (learning rate, contrast function) of the fastICA algorithm.

The minimum required length of data segments needed to clearly identify enteric components is 120 seconds. Using 120 second segments allowed for simultaneous detection of multiple slow wave frequencies which differed by as little as 0.3 cpm, whereas 60 second-long segments usually did not. Processing 60 second-long segments also yielded a much higher false-positive rate for all three bowel sections because many SOBI components were classified as primarily sinusoidal. Processing a longer data segment improves the accuracy of correlation matrices utilized by SOBI, which likely explains the benefits of using the 120 second-long MENG recordings. However, processing even longer data segments (e.g. 180 sec) does not necessarily lead to even better results. On the contrary, longer data segments are more likely to contain multiple large (spike-like) artifacts that can dominate the separation process at the expense of the small bowel components.

Regarding the SVM classification method: The results for a 2-D classification were very similar to those found with a 1-D linear discrimination based on the second criterion (goodness-of-fit measure) alone. About 3% of components that contained a small “spike-like” artifact, but were otherwise highly-sinusoidal, were classified as sinusoids with the SVM, but not with the threshold-linear discrimination. In this case, the spike tends to lower the value for g_i while the spareseness measure remains high. It may be worth exploring the possibility of integrating an amplitude criterion for this classification task, using the knowledge that enteric components are typically ≤ 1 pT peak-to-peak. Since we often identified some non-primarily sinusoidal components which had a dominant frequency within the enteric range, it is also worth exploring relaxing the classification scheme to accept these components as well.

Finally, we should mention an inherent limitation with our method: If two disparate sections of bowel share the same SWF (to within ≤ 0.2 cpm), it is unlikely both can be properly detected because separation of sources with the same frequency spectrum is unfavorable for SOBI [13]. In this case, the computed sensitivity for a particular section of bowel would potentially decrease by up to a factor of two. One possible remedy is to greatly increase the number of SQUID channels so that more sources can be separated, making it more likely that two sources can share the (nearly) the same frequency spectrum. Another possibility is to modify the set of matrices that SOBI diagonalizes by adding a term which allows the separation procedure to “focus” on the enteric frequency range, thereby aiding the separation and detection of multiple small bowel sections that share the same SWF.