Evaluating Existing Measures of Health Numeracy Using Item Response Theory

Abstract

Objective

To evaluate existing measures of health numeracy using Item Response Theory (IRT).

Methods

A cross-sectional study was conducted. Participants completed assessments of health numeracy measures including the Lipkus Expanded Health Numeracy Scale (Lipkus), and the Medical Data Interpretation Test (MDIT). The Lipkus and MDIT were scaled with IRT utilizing the 2-parameter logistic model.

Results

Three-hundred and fifty-nine (359) participants were surveyed. Classical test theory parameters and IRT scaling parameters of the numeracy measures found most items to be at least moderately discriminating. Modified versions of the Lipkus and MDIT were scaled after eliminating items with low discrimination, high difficulty parameters, and poor model fit. The modified versions demonstrated a good range of discrimination and difficulty as indicated by the Test Information Functions.

Conclusion

An IRT analysis of the Lipkus and MDIT indicate that both health numeracy scales discriminate well across a range of ability.

Practice Implications

Health numeracy skills are needed in order for patients to successfully participate in their medical care. The accurate assessment of health numeracy may help health care providers to tailor patient education interventions to the patient’s level of understanding and ability. Item response theory scaling methods can be used to evaluate the discrimination and difficulty of individual items as well as the overall assessment.

1. Introduction

The construct of health numeracy reflects one’s ability to use numeric information in the context of health care. Health numeracy is recognized as one of the key domains of the general construct of health literacy in a model put forth by the Institute of Medicine (1). The ability to understand and use numeric information is core to a number of tasks one must undertake in health care including the appropriate dosing of medications, understanding health risks, and balancing risks and benefits when considering a medical decision. Studies have reported an association between numeracy and knowledge of cancer risk (2), mammography risk (3), and comprehension of food labels (4). Numeracy has also been associated with better disease control indicators related to obesity, asthma, anticoagulation management, and diabetes (5–8). Given the central role of numeracy across a spectrum of health care activities and its association with clinical outcome measures, the assessment of health numeracy becomes an important issue with both clinical and research implications. Several measures have been developed to assess general health numeracy including the 3-item numeracy measure developed by Schwartz (3), the 11-item expanded numeracy scale developed by Lipkus (9), the numeracy component of the Test of Functional Health Literacy in Adults (TOFHLA) (10), the Medical Data Interpretation Test (MDIT) (11), and The Newest Vital Sign (4). In addition to these objective measures, a subjective assessment of Health Numeracy called the Subjective Numeracy Scale has been developed (12).

These numeracy measures have generally been developed using classical test theory to evaluate each item’s difficulty and the internal consistency of the entire measure. Construct validity has been evaluated through comparison with level of education, existing measures of health or overall literacy, mathematical achievement test scores, or the ability to interpret risk information or complete utility assessments (2–14). Another approach to evaluating these measures is to use Item Response Theory (IRT). Item response theory is a psychometric scaling procedure that allows one to evaluate the ability of each item to discriminate between those with different levels of a given trait (e.g. numeracy) at each level of difficulty. This approach also allows one to evaluate the ability of a test as a whole to discriminate between those with different levels of an underlying trait (15, 16). Using IRT to evaluate existing measures of health numeracy will result in a more accurate evaluation of the strength of specific items that are currently in use, as well as the test as a whole, in terms of the ability to discriminate between levels of numeracy. It will also provide a methodology for determining whether existing measures may be shortened without any loss to the psychometric properties of the instrument, such as the ability to discriminate between examinees. The primary objective of this study is to provide insight into the discriminatory ability of selected measures that exist to assess the construct of health numeracy. A secondary objective is to demonstrate how IRT can be applied in the evaluation of health numeracy measures.

2. Methods

A cross-sectional survey was conducted. Participants were recruited from one of three internal medicine primary care clinics associated with an academic medical center. The sample was stratified by race and clinic site in order to purposefully select participants that were diverse in race and education. To obtain participants, a recruitment letter was sent to a random sample of enrollees. Those who responded to the letter via a telephone call, email, or by returning a self-addressed, stamped post card were then contacted by telephone and those that met eligibility criteria and were interested in participating were enrolled in the study. Inclusion criteria were age 40 to 74 years of age. The age criteria were determined in order to identify participants that were eligible for cancer screening tests as the assessment of cancer screening adherence was an objective of the parent study. Exclusion criteria were poor vision, inability to speak English, or cognitive dysfunction as measured by a mini mental status exam score of 23 or less. Prior to taking the survey, participants completed a Folsteins Mini Mental Status Exam, a vision test, and the Rapid Estimation of Adult Literacy in Medicine (REALM) (17). Those who tested lower than a 9th grade reading level were given the option of having the survey read to them. Participants responded to the survey in a private room with a research associate available to answer questions and were paid $50.00 at the completion of the survey to compensate them for their time. Participants were evaluated with several numeracy measures including the Lipkus scale (9), the TOFHLA-numeracy component (10), and the MDIT (11). Mathematic grade level achievement was assessed with the Wide Range Achievement Test-Arithmetic (WRAT_A) (13). In addition, the survey included other measures of health attitudes and behaviors, none of which are the focus of the current analysis

2.1. Item Response Theory Assumptions and Interpretation

Item Response Theory (IRT) focuses on the item, as well as the interaction between each item and ability, as the unit of analysis by using a set of probability models to determine the likelihood of ‘success’ on a given item (15,16). This allows one to obtain sample-free estimates of item parameters (i.e. difficulty and discrimination estimates), as well as ability estimates for each examinee. The primary assumptions of the most common scaling techniques used in IRT are that 1) a single latent ability accounts for differences in performance on the measure, otherwise known as unidimensionality, 2) responses to different items on the measure are statistically independent, otherwise known as local independence, and 3) the relationship between ability and item performance can be described by a monotonic function.

In this study, data were analyzed using the two-parameter logistic (2-PL) model, which measures the probability of answering an item correctly, given one’s ability level, as a function of how difficult the item is and how well it can discriminate between various levels of the underlying trait (16). Specifically, the monotonic function that relates ability and the characteristics of a particular item (i.e. difficulty and discrimination) to the probability of successfully responding to that item can be expressed by the following equation:

$$P(X=1\mid \theta )=\frac{1}{1+e^{-1.7a(\theta -b)}}$$

Where θ = the ability of a particular examinee

a = the discrimination of a particular item, and

b = the difficulty of a particular item.

Estimates of item difficulty and discrimination can then be used to determine which items are functioning satisfactorily and which are not. Theoretically, item difficulty ranges from negative infinity to positive infinity. In practice item difficulty typically ranges between −4 and 4. A difficulty parameter of −4 reflects an extremely easy item while a difficulty level of 4 reflects an extremely difficult item. Deviations from this range are indicative of an item that is not functioning satisfactorily. Item discrimination can theoretically range from 0 to infinity, with lower values indicating a less discriminating item. Items with very low discrimination parameters cannot differentiate between examinees that possess different levels of the underlying trait.

2.2. Data Analysis

The distribution of the responses on each of the numeracy and literacy measures were summarized. The TOHFLA-N has a potential range of 0 to 17. The median number of correct responses on the TOHFLA-N was 15 among study participants with an interquartile range of 16–17. The Lipkus has a potential range of 0 to 11. The median number of correct responses on the Lipkus measure was 8 among study participants with an interquartile range of 6–10. The MDIT has a potential range of 0 to18. The median number of correct responses on the MDIT was among study participants with an interquartile range 7–12. The 2 health numeracy measures that demonstrated the most variability in scores (Lipkus and MDIT) were chosen for further analysis using IRT. The Lipkus numeracy scale consists of eleven items with two items (#8 and #9) having a shared stem and the remaining nine items having unique stems with scores ranging from 0–11 (Link to Lipkus article, reference #9). The MDIT consists of 20 items, including a number of testlets, where a scenario is presented and a series of questions follows. In the MDIT some items responses are combined to calculate a score leading to a range in scores from 0 to18 (www.vaoutcomes.org/downloads/medical_data_test.pdf).

The Lipkus and MDIT were scaled separately using classical test theory and item response theory utilizing the 2-PL model using Multilog version 7.0.2. (18). The classical test theory measures used were the percent correct to assess item difficulty, the item-subscale correlation to assess item discrimination, and Chronbach’s alpha to assess internal consistency and reliability (19). The IRT measures used were difficulty and discrimination parameters to assess item difficulty and discrimination, respectively. The IRT model fit of each item was assessed using information from a combination of sources. Each item’s corresponding difficulty and discrimination indices were reviewed in conjunction with a test for item fit. IRT item fit statistics are based on the chi-square distribution which is highly dependent upon sample size, therefore, some items which showed a lack of fit based on the chi-square statistics were still retained if their difficulty and discrimination indices were considered acceptable. Items that were flagged as poor, due to low discrimination or having estimated parameters that were outside the range of feasible values (implying problems with convergence of the model) were dropped and the modified versions of the Lipkus and MDIT were rescaled. Finally, the IRT test information functions, which provide an additive measure of the amount of information the test provides at each level of the ability continuum, were compared to determine if the modified versions of the measure differed from the original versions of the measure.

3. Results

3.1. Study Population

Recruitment letters were mailed to 1938 persons; 369 met inclusion criteria and presented for the study session (19%). Ten persons were excluded due to low scores on the MMSE. The final study cohort included 359 persons (18.5%). Participants were older than non-participants (58.8 years (SD 8.9) vs. 57.4 years (SD 9.0), p<0.01). Participation rates varied by race; Whites (23.2%), Asian (20%), Blacks (13.8%), and Hispanics (6.2%), p<0.001, and by gender; females (19.8%) and males (15.4%), p=0.021. Participants were diverse in race, income, level of education and had a high level of general health literacy as assessed by the REALM and the TOFHLA (Table 1). Participants demonstrated a broader range in mathematical achievement and numeracy (Table 1 and 2) in response to the Lipkus, MDIT, and WRAT-A than the TOFHLA-N (Table 2).

Table 1.

Participant Characteristics	n (359)	%
Age (years)
40–49	60	17
50–64	192	54
65–74	107	30
Gender
Male	90	25
Female	269	75
Race
White	251	70
Black	97	27
American Indian	5	1
Asian	6	2
Ethnicity
Non-Hispanic	345	97
Hispanic	10	3
Education
Up to 11 years	27	4
12 years (high school graduate or GED)	76	21
Some college experience	124	35
4 or more years of college	132	37
REALM reading levels
3’rd Grade and Below	1	0.3
4’th to 6’th Grade	7	2
7’th to 8’th Grade	36	12
High School	315	88
TOFLHA
Inadequate literacy	2	<1
Marginal	8	2
Adequate	349	97
WRAT-Arithmetic Grade Levels
1’st grade	1	<1
2’nd grade	1	<1
3’rd grade	5	1
4’th grade	13	4
5’th grade	30	8
6’th grade	51	14
7’th grade	49	14
8’th grade	35	10
High School	132	37
Post High School	42	12

Table 2.

Descriptive Statistics of Numeracy and Math Achievement Measures

Measure	Potential Range of Scores	Observed Scores Median (Range)	Observed Scores Mean (SD)	Cronbachs Alpha
Lipkus	0–11	8 (0–11)	7.53 (2.66)	0.79
Modified Lipkus	0–9	6 (0–9)	5.90 (2.20)	0.76
TOFHLA-Numeracy	10–17	16 (10–17)	15.36 (1.53)	0.48
MDIT	0–18	9(1–18)	9.50 (3.25)	0.73
Modified MDIT	0–16	9 (0–16)	9.03 (3.23)	0.73
WRAT_A	15 to 55	39 (15–55)	39.10 (5.66)	0.88

3.2. Item Analysis of Lipkus Scale

An item analysis was undertaken using both classical test theory and IRT scaling procedures for the Lipkus measure. Most items demonstrated a low level of difficulty using both the classical test theory and IRT indicators. The percent correct for individual items was generally high, varying from 68% to 89%, with the exception of items 2, 3 and 11. A low level of difficulty for items was also supported by the IRT analysis. The IRT difficulty parameters were less than 0 with the exception of items 3 and 11(Table 3A). Item 3 appears to be the most difficult item as indicated by a percent correct of only 18% and a high IRT difficulty parameter of 1.16. Item 11 is also a difficult item with a percent correct of only 41% and an IRT difficulty parameter of 0.35. Of particular interest are items 8 and 9 which have extremely large IRT discrimination parameters. Contextually, those items stated that the chance of getting a disease is 10%. Respondents were then asked how many people would be expected to get the disease out of 100 and out of 1,000, respectively. It could be argued that determining the number of people out of 1,000 that will get the disease partially depends on one’s ability to determine how many people out of 100 will get the disease. If the assumption of local independence is violated then fitting a standard IRT model, such as the 2-PL, would result in inflated estimates of item discrimination and item and test information, underestimates of standard errors, and overestimates of reliability, due to the traditional IRT model’s inability to handle the excess correlation between dependent items (20–22).

Table 3.

Classical and Item Response Theory Results for the Lipkus Expanded Numeracy Scale

	A. Full Lipkus							B. Modified Lipkus
Item	% Correct	Item-Subscale Correlation	IRT Discrimination	IRT Difficulty	Chi- Square	df	p	Item-Subscale Correlation	IRT Discrimination	IRT Difficulty
1	0.69	0.60	1.57	−0.68	24.70	7	< 0.01	.49	1.69	−0.70
2	0.54	0.57	1.48	−0.13	7.57	6	0.28	.49	1.58	−0.16
3	0.18	0.51	2.42	1.16	0.68	2	0.70	.43	3.59	1.03
4	0.88	0.45	1.44	−1.75	8.44	7	0.35	.35	1.31	−1.92
5	0.89	0.39	1.32	−1.94	14.50	7	< 0.05	.28	1.05	−2.35
6	0.84	0.55	1.69	−1.36	9.87	7	0.27	.43	2.58	−1.21
7	0.80	0.65	1.92	−1.06	6.30	6	0.40	.52	3.31	−0.95
8	0.84	0.55	12.92	−0.95	728.00	2	< 0.01	--	--	--
9	0.79	0.58	6.08	−0.80	240.00	3	< 0.01	--	--	--
10	0.68	0.58	1.68	−0.63	13.50	7	0.08	.48	1.53	−0.70
11	0.41	0.60	1.66	0.35	9.73	5	0.09	.47	1.56	0.33

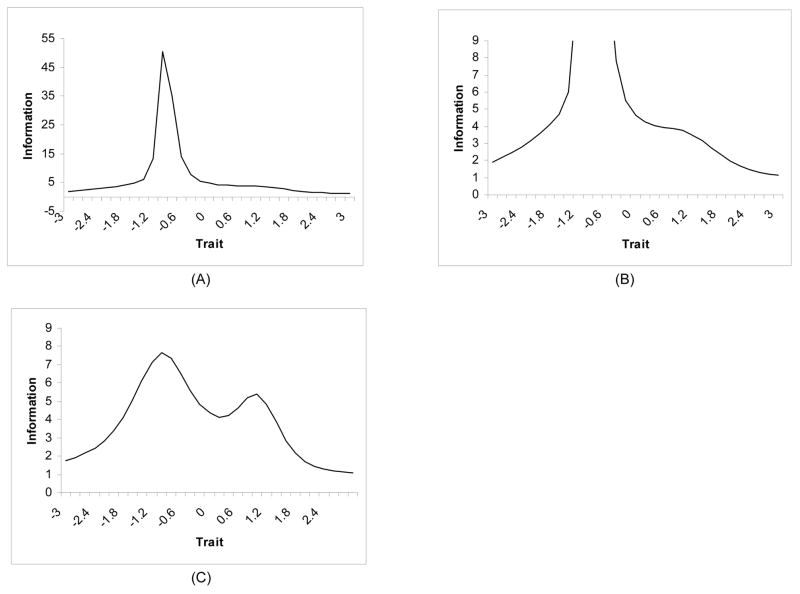
Further, an investigation of the item characteristic curves for Lipkus items 8 and 9 showed that item 8 was only providing information at a single ability level rather than across a range of abilities. Examinees with an ability level less than −1 had virtually no chance of obtaining the correct answer to this item while examinees with an ability level greater than −1 were almost certain of obtaining the correct answer. This was also the case for item 9. Moreover, as depicted in Figure 1, the extreme discrimination parameters for items 8 and 9 heavily influenced the amount of total test information provided for the ability range of approximately −1.2 to 0.06. The test information function for the original Lipkus was found to have an extremely high peak at these ability levels indicating a poor model fit for these items.

Figure 1.

Test Information Function Curves for the original (A and B) and modified (c) Lipkus Expanded Numeracy Scale. The high peak in the test information function at −1.2 to 0.6 in Figure 1A and 1B are caused by the high discrimination parameters of items 8 and 9. The high peak is indicative of a poor model fit for these items.

3.3. Item Analysis of the MDIT Scale

The results obtained using both classical and IRT scaling procedures for the MDIT are provided in Table 4A. Most items on the MDIT were found to be at least moderately discriminating with discrimination parameters ranging from 0.22 to 1.72. Items 3 and 13–14 (an inferred score based upon response to item 13 and item 14) were found to have discrimination parameters much lower than what is desired for a quality item (a = .19 and .01, respectively). These items were also found to have low item-scale correlations (r = .15), and very high IRT difficulty parameters (b = 11.63 and 57.01, respectively). Item 3 was a question that attempted to distinguish between the importance of all cause mortality and disease specific mortality. In this question, more than 80% of respondents incorrectly identified that disease specific verses overall mortality was the most important outcome. Item 13–14 was scored by comparing a response to two individual questions: an estimate of 10-year risk of dying from a heart attack and an estimate of 10-year risk of dying for any reason, a task called a class-inclusion judgment. In this item only 32% answered the question correctly. These two items were also found to be the most difficult items in the original validation study of the MDIT (11). Our analysis suggests that they are not only difficult items but items that do not discriminate well between more and less numerate persons.

Table 4.

Classical and Item Response Theory Results for the Medical Data Interpretation Test

	A. Full MDIT							B. Modified MDIT
Item	% Correct	Item-Subscale Correlation	IRT Discrimination	IRT Difficulty	Chi- Square	df	p	Item-Subscale Correlation	IRT Discrimination	IRT Difficulty
1	0.71	0.37	0.80	−1.26	6.11	10	0.80	0.25	0.80	−1.25
2	0.26	0.30	0.53	2.11	9.00	11	0.55	0.18	0.52	2.13
3	0.10	0.15	0.19	11.63	13.40	11	0.26	--	--	--
4	0.37	0.52	1.19	0.57	10.30	11	0.50	0.40	1.19	0.58
5	0.51	0.43	0.66	−0.09	11.40	11	0.45	0.28	0.66	−0.09
6	0.77	0.47	1.72	−1.07	19.20	9	< 0.05	0.40	1.74	−1.06
7–20	0.53	0.47	0.88	−0.19	9.36	10	0.50	0.32	0.87	−0.19
8	0.41	0.21	0.22	1.77	32.80	11	< 0.01	0.07	0.22	1.77
9	0.67	0.34	0.52	−1.46	7.84	11	0.77	0.19	0.52	−1.46
10	0.76	0.48	1.48	−1.06	10.90	10	0.40	0.38	1.49	−1.05
11	0.46	0.41	0.73	0.23	12.30	10	0.26	0.28	0.73	0.23
12	0.81	0.36	1.29	−1.46	7.66	9	0.55	0.32	1.30	−1.45
13–14	0.32	0.15	0.01	57.01	41.3	11	< 0.01	--	--	--
14–15	0.51	0.40	0.62	−0.09	5.94	11	0.85	0.25	0.62	−0.09
16	0.66	0.38	0.69	−1.05	23.30	11	< 0.01	0.25	0.69	−1.05
17	0.41	0.47	1.11	0.40	9.38	10	0.50	0.35	1.11	0.40
18	0.61	0.56	1.66	−0.41	17.90	11	0.08	0.43	1.65	−0.41
19	0.58	0.54	1.51	−0.30	21.60	10	< 0.05	0.43	1.50	−0.30

3.4. Analysis of Modified Versions of Lipkus and MDIT Scales

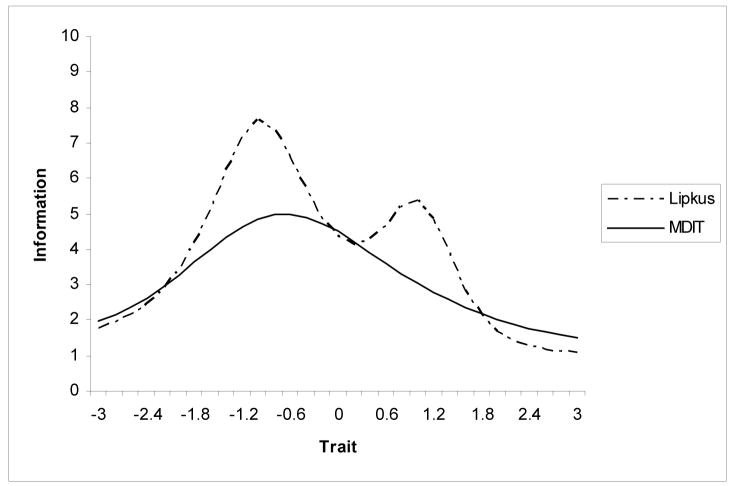
Given these findings, items 8 and 9 were removed from the Lipkus scale and this modified version of the Lipkus was reevaluated. The results revealed only a slight decrease in reliability with coefficient alpha dropping from α = .79 for the full version to α = .76 for the modified version. Moreover, a more realistic test information function was obtained for the modified version of the Lipkus. The original and modified test information functions are displayed in Figure 2. The test information function for the modified version of the Lipkus can be described as bimodal and provides a large amount of information for the range of ability levels from −0.18 to 1.8. Similarly, based upon the IRT analysis of MDIT, a modified MDIT that did not include items 3 and 13–14 was undertaken. The results of the modified MDIT using both classical and IRT analysis are presented in Table 4B. The test information functions for the full and modified MDIT were similar, providing evidence that removal of the two items that were performing poorly did not change the amount of information provided by the test. Furthermore, the removal of these items did not lead to a decrease in reliability, but rather the internal consistency remained the same (α = .73). Figure 2 depicts the overlaid test information curves for the modified versions of the Lipkus and the MDIT. As the figure illustrates, these two measures provide a comparable amount of information about the relative traits that they are measuring.

Figure 2.

Test Information Curves for the Modified Lipkus Expanded Numeracy Scale and the Medical Data Interpretation Test

4. Discussion and Conclusion

4.1. Discussion

Health numeracy is recognized as an important construct in the field of health care education, patient-physician communication, and medical decision making as demonstrated in a number of recent reviews (23, 24). Health numeracy is one domain within the overall framework of general health literacy as defined by the Institute of Medicine (1). The health numeracy construct itself includes various sub-domains. The types of numeric skills applicable in the medical context range from those requiring a basic understanding of numeric concepts and operations to increasingly abstract and interpretive skills such as those used in applying probability and statistical inference (25–28). Numeracy skills, across these domains, are required for a wide range of activities in health care. For example, taking one’s medications correctly requires the ability to count and measure, a numeric skill in the domain of number sense. Applying cancer risk information in decision making requires some understanding of probability. Interpreting and applying evidence from medical studies requires some conceptual understanding of statistical inference. In summary, numeracy is needed in order for patients to be active participants in disease management and informed decision-making.

The assessment of health numeracy has several implications clinical practice. Just as it is important to know whether a patient is able to read prior to giving them written instructions, a provider should know a patients level of numeracy prior to providing directions that require numeric skills. Use of literacy measures as a routine part of the health visit is controversial due in part to concerns about a labeling effect and the potential shame or embarrassment that patients with a lower level of education may feel when taking these tests (29). However, numeracy assessed by disease specific measures consistently demonstrates an association with improved clinical outcomes and use of self management behaviors (5–8). Identification of low numeracy may lead to modified patient education approaches that address this deficit. Further, the selection of items at an appropriate level of difficulty could decrease the burden and potential embarrassment of respondents. Given the potential benefit of accurate assessments, future studies are needed to evaluate the efficacy of screening interventions on clinical outcomes related to disease management and medical decision making.

The IRT analysis we conducted demonstrates that both the Lipkus and the MDIT discriminate well between more and less numerate persons across a range of ability. The analysis was able to identify two items in each measure that were less discriminating and suggests that a shorter test that deletes the items provides an equally strong measure of the numeracy trait. On the basis of this analysis we recommend that the shorter versions of the Lipkus or MDIT measures be used.

We report that the statistical characteristics of the Lipkus and the MDIT measures are comparable. However, this finding does not address differences that exist between the measures with respect to content validity and the definition of the health numeracy construct used to develop each measure. Validity can be defined as how well a measure fulfills the function for which it is being used or how accurate the inferences are that are made based on performance on the measure. It has been described as “scientific inquiry into test score meaning” (15). Whether to use the Lipkus, the MDIT, or another measure of health numeracy depends on the nature of skills one is interested in assessing. The items on the Lipkus primarily focus on the domains of number sense (i.e., understanding the relationship of different forms of numbers, the relative risk magnitude of different forms of numbers in the context of risk communication) and probability. In contrast, the items on the MDIT focus on the interpretation of numeric data from clinical studies, a numeracy domain that includes principles of scientific study design and statistical inference. Therefore, while both tests evaluate important skills for the use of numeric information in communication and medical decision making, they focus on different aspects of health numeracy.

Given the complexity of the construct of health numeracy (26), one problem faced by the use of these measure is how to choose a valid assessment that does not incur an excessive respondent burden. Item response theory offers one approach to do so. Through the use of IRT, a pool of psychometrically tested items can be developed. The choice of items administered can then be tailored based upon the response to initial items, thereby limiting the length of the assessment. The use of IRT methods may be used not only to modify existing tests but have the potential to combine strongly performing items across various numeracy measures to create a more discriminating and efficient assessment of health numeracy. This approach has the potential to be facilitated by computer administration (31).

This study has some limitations. First, we evaluated two measures of health numeracy but did not have data on other numeracy measures that may also have performed well if tested with IRT methods. Second, the numeracy assessments were given in a set order and were part of a larger survey study and fatigue could have played a factor in performance on the measures. Third, the study was conducted in a single institution and the psychometric properties determined may have differed in a sample with a different spectrum of educational achievement and general health literacy. Our study population was diverse in race, income, and level of education with 25% having no more than a high school level education. However, most participants demonstrated adequate reading literacy and only 4% with less than 12 years of formal education. The study population is most representative of a primary care clinical population located in a mid-western metropolitan area.

4.2 Conclusion

Health numeracy is recognized as a distinct construct in the general framework of health literacy. In this study we used IRT methods to evaluate the psychometric properties of two existing measures of health numeracy; the Lipkus expanded health numeracy scale and the Medical Data Interpretation Test. We report that both the Lipkus and MDIT scales discriminate well between more and less numerate persons across a range of ability. In addition, modified tests with fewer items were found to be equally strong measures of the health numeracy trait. We recommend use of these modified measures as an option in the assessment of health numeracy.

4.3 Practice Implications

Health numeracy skills are needed in order for patients to successfully complete a variety of task that we ask them to do in the context of health care. The assessment of health numeracy may help health care providers to tailor patient education interventions to the patient’s level of understanding and ability. Future work is needed to evaluate the efficacy of such interventions. Item Response Theory is a psychometric method that has increasingly been applied in the medical field (31, 32). The application of IRT methods to the selection, development, and assessment of health numeracy measures will lead to improved numeracy assessments with the potential for broader use in both clinical and research settings.