The Limitation of Species Range: A Consequence of Searching Along Resource Gradients

Abstract

Ecological modelers have long puzzled over the spatial distribution of species. The random walk or diffusive approach to dispersal has yielded important results for biology and mathematics, yet it has been inadequate in explaining all phenomenological features. Ranges can terminate non-smoothly absent a complementary shift in the characteristics of the environment. Also unexplained is the absence of a species from nearby areas of adequate, or even abundant, resources. In this paper, I show how local searching behavior - keyed to a density-dependent fitness - can limit the speed and extent of a species’ spread. In contrast to standard diffusive processes, pseudo-rational movement facilitates the clustering of populations. It also can be used to estimate the speed of an expanding population range, explain expansion stall, and provides a mechanism by which a population can colonize seemingly removed regions - biogeographic islands in a continental framework. Finally, I discuss the effect of resource degradation and different resource impact/utilization curves on the model.

1 Introduction

As questions of habitat fragmentation and degradation continue to arise, it is increasingly important to understand how populations of organisms establish their spatial ranges. Lima and Zollner (1996) pointed out the need to incorporate a behavioral ecology at the landscape level to better describe animal habitat choice and movement. Potential theories should account for an animal’s perceptual range, the ability to attract or repel conspecifics, and exhibit game-theoretic decisions and distributions on the landscape. Gaston (2003) similarly held that robust studies of movement would identify potential factors inhibiting and facilitating dispersal, dynamically incorporate those factors, and establish the genetics governing organismal response to the environment. The current paper addresses the impact that directed movement (specifically a form of taxis by which individuals climb density-dependent fit- ness gradients) has on the overall distribution of a population. The results and methodology of this paper fall under Lima and Zollner’s (1996) rubric and address the first two concerns of Gaston (2003).

Population distributions are characterized by the physical ranges which they occupy and their behavior in the interior and at the edge of those ranges. A species commonly occupies only a fraction of the available domain that external observers might deem “suitable”(Lawton et al., 1994; Brown and Lomolino, 1998; Holt and Keitt, 2005), and those segements that are occupied do not necessarily incorporate all of the “best” subsections present in the larger environment. Additionally, distributions that feather or smooth out at their limits have both mathematical and biological appeal - in the case of the latter, such a peripheral population distribution could be indicative of the formation and sustaining of population sinks in poor areas (Pulliam, 2000). Yet more abrupt limits to population density do appear. Myriad causations of rapid or sudden range termination are suspected (Caughley et al., 1988; Lawton et al., 1994; Brown et al., 1996; Brown and Lomolino, 1998), with the most commonly cited culprits including quick transitions between climatic zones and climatic change (Parmesan and Yohe, 2003; Root et al., 2003) or competitive pressures posed by an invasive or resident species (Peterson, 2003). External discontinuities or quasi-discontinuities in the environment do not account for all range restrictions, however, as they also occur in landscapes that possess continuous, smoothly varying properties (Holt and Keitt, 2005). Further, range limits may respond to the impact of drift and natural selection on traits that directly or indirectly affect habitat viability (Holt, 2003).

Different modeling traditions have been advanced to address the dispersal and distribution of species either in isolation or as part of a community as-semblage. Classic treatments include metapopulations (Levins, 1969, 1970; Hanski, 1999), with the landscape partitioned into site-quality classes, while ideal-free distributions (Fretwell and Lucas, 1970; Fretwell, 1972) evolved from a game-theoretic treatment of the problem of discrete habitat selection. Further, over the last quarter-century, reaction-diffusion models have been a particularly rich and well-studied field for population dynamics (e.g. Okubo, 1980; Blat and Brown, 1984; Cantrell and Cosner, 2001; Rowell, 2003).

In the last case above, standard diffusion (Okubo, 1980; etc.) is the product of unbiased random walk processes. External factors (e.g. convection or spatially-dependent diffusivity) can introduce directional bias to this motion, but bias can also be the result of a rational (or “pseudo-rational”) organism moving in accord with environmental information. Additional partial differential equations have also been developed to study motion to reduce over- crowding (porous medium equation, Arnoson, 1986) and the clustering effects of chemotactic attraction (cf. Lin and Segel, 1988), the latter perhaps being the most well-known example of directed motion in mathematical biology.

The current paper finds itself part of a burgeoning group within the literature that, despite their varied and independent origins, fundamentally converge in their study of the ecological impact of directed movement by organisms in pursuit of fitness optimization. The earliest model (Grindrod, 1988) was a system of partial differential equations whose density equation contained a flux term (i.e. that component which represents movement or flow through a location) that included both diffusion and a fitness gradient-climbing taxis. The primary test-case was the Allee effect generated by a simple bistable fitness function within a homogeneous resource environment. More recently, Cosner (2005) tied together gradient-climbing (Belgacem and Cosner, 1995) with the concept of a continuum ideal-free domain (Kshatriya and Cosner, 2002) in a partial differential equation where the logistic function was both the reaction term and the measure guiding directed movement.

In counterpoint to the continuous models above, Armsworth and Roughgarden’s (2005a) system was conceived as taking place within a linearly arranged compartment-model. The intrinsic fitness of each compartment-patch varied randomly but was spatially auto-correlated. In their model, directed motion restricted the population away from sink areas and, depending upon the het-erogeneity of the landscape and historical presence of the population, could prevent the spread of an organism into all quality locations. Finally, Cressman and Křivan (2006) combined traditional, continuous-time population dynamics with the ideal-free distribution on general patch networks (see also Cressman et al., 2004; Křivan et al., 2008). Their model featured a contrast between an absolute “ideal” concept of migration with a myopic, one-patch sampling rule, the latter representing a naturally limited evaluation of the environment, and they also considered the role of different operational time-scales for migration and population dynamics.

The model of the current paper assumes a continuous representation of space and time. Movement of a population’s density is an aggregate result of a tactical process designed to move an individual in the perceived direction of greatest improved individual fitness or per-capita resource availability. This fitness is nominally density-dependent (as a measure of competition pressures), and the principal fitness used in this paper is analogous to a special case of the Beddington-DeAngelis functional response of consumer interference (Beddington, 1975; DeAngelis et al., 1975). The time needed for an individual to collect the available resources at a location increases linearly with the presence of competitors. An additional underlying assumption is that individuals are myopic, i.e. only capable of evaluating local variations in habitat quality and competition.

After introducing and justifying the model, I examine some of its resulting properties. As an example, range limitation is a natural development as the current model is a dynamic analog to strategic patch selection (cf. Kshatriya and Cosner, 2002; Cosner, 2005), and this fact is compounded by globally worsening environments or sudden population depressions which produce a tighter clustering within the density distribution.

Furthermore, I discuss the importance of differing time scales for movement and reproduction-mortality processes. By utilizing a fast-time/slow-time approach (cf. Cressman et al., 2004; Cressman and Křivan, 2006; Křivan et al., 2008), wherein one process is held in abeyance while the other process is taken to its equilibrial state, this model can compute the expansion speed of a population from a central resource peak to the outer reaches of its environment. This method also demonstrates how satellite subpopulations can be generated and preserved at a distance from the parent population - precursing a possible para- or peripatric speciation event if genetics were folded into the model.

Finally, I conclude the paper by introducing both resource degradation and recovery and alternative resource utilization functions. The various combinations of dynamic components elicit distinct distributions in the population and resource. Where possible, analytic representations of these patterns are provided.

2 Ideal Free Movement with Handling Considerations

This paper draws upon two traditions: reaction-diffusion-advection models and ideal-free distributions. From the former, the model inherits the continuous representation of time and space and the mathematical machinery to address changes in population density resulting from (possibly non-uniform) movement. From the latter, the model incorporates a rules-driven expression of movement based upon local fitness gradients.

In organisms capable of evaluating their environment, there is reasonable argument for the minimization of randomness in movement in favor of a more tactical response (but see Cosner and Lou (2003) for an intriguing counter-example). The extent of an organism’s perceptual range is not a trivial question; however, to maintain a consistent mathematical focus within this paper, evaluation of the environment is assumed to occur on the local (gradient) scale (cf. Cressman and Křivan, 2006). Meso- and global-scale searching are touched upon in the concluding discussion.

Time is a real, non-negative variable, t ∈ [0,∞), and the physical space,Ω, is simply connected, finite, of arbitrary dimensionality, and taken to have a sufficiently smooth boundary, ∂Ω. Over this environment is placed a continuous, piecewise-smooth resource curve, R(x⃗), that is everywhere non-negative and zero at the boundary.

Let the population density be denoted u(x⃗, t). The flux, or directional movement of the density, is based upon a perceived fitness measure which is a function of both the local resource and population density, S(R, u). The function S defines a literal adaptive landscape of resource availability that is responsive to the current state of the population. The population flux is taken to be proportional to the gradient of S and to the number of individuals making use of the local information,

$$\overrightarrow{J}=\mathit{ku}\nabla S.$$ (1)

The constant of proportionality, k, represents organismal sensitivity to variations in fitness or resource availability. The change in population density as a consequence of movement is equal to the negative divergence of flux (−∇·J⃗).

Compare the implications of this flux with that of the traditional ideal-free domain. There is neither an incumbency advantage nor an energetic cost to movement, and movement effectively ceases once an optimal configuration is achieved wherein no individual may improve their lot by moving independently (i.e when local individual fitness is uniform over a contiguous, occupied region and equal to or less than that in the nearby unoccupied region). It differs from the traditional ideal-free domain, though, in that the range of information is restricted to only the most local sense. The connection between the two is important, because ideal-free distributions are known as the end result of populations’ evolutionary trajectories in many other treatments (Fryxell and Lundberg, 1998; Holt and Barfield, 2001; Kshatriya and Cosner, 2002; Holt, 2003; Cosner, 2005; Cressman and Křivan, 2006; Křivan et al., 2008).

To complete the model, let us assume that consumed resources are converted into reproductive growth with an efficiency r and that there is a continuous density-independent per capita mortality, μ. The general model describing the rate of change in the population density is

$$\begin{array}{c}\frac{\partial u}{\partial t}=-k\nabla ·(u\nabla S)+u(rS-\mu )\text{on}\mathrm{\Omega }\times (0,\infty ),\\ u(\overrightarrow{x},0)=\varphi (\overrightarrow{x})\ge 0\text{on}\overline{\mathrm{\Omega }},\\ u(\overrightarrow{x},t)=0\text{on}\partial \mathrm{\Omega }\times [0,\infty ),\\ R(\overrightarrow{x})\in C^0,\text{piecewise}{C}^2\text{on}\mathrm{\Omega },\\ |\nabla R|<\infty \text{on}\mathrm{\Omega },\\ R\ge 0\text{on}\mathrm{\Omega },\text{and}\\ R\equiv 0\text{on}\partial \mathrm{\Omega }.\end{array}$$ (2)

For ease of reference, (2) is here termed the Reaction-Searching Problem (a la the “reaction-diffusion problem”). Likewise, when the reproductive and mortality terms are neglected (i.e. movement only, r = μ = 0), then the model will be known simply as the Searching Problem.

The dynamic equation in (2) is very similar to the formulation by Grindrod (1988), and in most respects, (2) should be viewed as a special case of equation (1.8) from that paper. In translating that work to this discussion, assume diffusivity δ and velocity smoothing parameter ε are both 0. Further, assume that the sensitivity parameter, λ, was not scaled out but retained (here, k). Whereas Grindrod (1988) worked with the assumption that searching was predicated on net fitness (reproductive success - mortality, i.e. rS − μ), mortality, μ, has been intentionally omitted from the measure S in the current model. As it is, the model organism of this paper is blind to risk, the source-sink consequences of which are examined later.

Because S does not include all elements contributing to fitness, it is more correctly said to be a search measure rather than a fitness measure (cf. mate choice preferences in Rowell and Servedio, preprint). This leaves the terminology consistent for future pursuits concerning incomplete information, bias and preference choices, and predator avoidance. Where per capita mortality is uniform, as in this paper’s basic model, however, the search measure S coincides with the fitness measure of population growth, and so fitness measure is used hereafter to facilitate reader familiarity.

In general, the fitness function S(R, u) must satisfy the following conditions

$$\begin{array}{c}S(R,u)\text{piecewise}{C}^2\text{on}[0,\infty )\times [0,\infty ),\\ \frac{\partial S}{\partial R}>0\text{on}[0,\infty )\times [0,\infty ),\\ \frac{\partial S}{\partial u}<0\text{on}(0,\infty )\times [0,\infty ),\text{and}\\ S(0,u)=0\text{on}[0,\infty ).\end{array}$$ (3)

When specificity is required, this paper assumes that the fitness is based upon the per-consumer Beddington-DeAngelis functional response without per-item handling,

$$S=\frac{R}{u+h}.$$ (4)

The consumed resource has instant recovery (or equivalently, it is a continuous input resource without a standing crop). The dynamic inclusion of consumer impact on resources, along with other functional responses, is discussed in Section 3.5. The collection of resources, R, is mitigated by a site sweeping time, h, and conspecific competition for resource access, au. The total consumer impact saturates with increasing population density, and scaling will be chosen so that the interference coefficient a = 1. Without loss of generality, allow any additional constants of proportionality placed on S to be absorbed into the sensitivity coefficient, k and conversion factor r, as appropriate.

3 Results

This section describes several mathematical and biological consequences of (2). Both technical and heuristic arguments for these conclusions may be found in the Appendices at the end of the article.

3.1 The Searching Problem

For a resource landscape containing a single local maximum (or supremum), the Searching Problem (equation 2, r = μ = 0) has a unique, optimally con-figured distribution in which the population inhabits only a subset of the domain, fitness is uniform within the occupied region and no greater immediately elsewhere, and the population density at the range limits is generally non-differentiable. Additionally, this distribution is indexed by a unique positive number, C, that is determined by the overall size of the population. If the resource is multi-peaked, however, uniqueness is dependent upon the total population size.

C is a contour value in the sense that it denotes a unique curve or surface in (x⃗, u)-space, on which the measure, S, equals the contour value, C, wherever u > 0. Contours of different values cannot overlap except in the trivial sense where u = 0. Furthermore, the contour curves are nested within one another, the value C decreasing as a population increases.

Appendices A and B contain formal and informal arguments supporting this conclusion. The former examines the general compressive tendency to equalize fitness, while the latter covers the one-to-one correspondence between population size and contour value.

In the special case of the fitness function S = R/(u + h), it is possible to specify the conclusions above. For all initial distributions of a population of a given size, if R is unimodal, then there exists a unique, positive number C such that the steady state solution defined by C,

$$u=\mathbf{\{}\begin{array}{cc}\frac{R}{C}-h,& R\ge Ch;\\ 0,\hfill & \text{otherwise},\end{array}$$ (5)

is the attractor to the Searching Problem (2, r = μ = 0).

The uniformity of fitness over the inhabited regions makes this an ideal free distribution (Figure 1). In multi-peaked resource landscapes, smaller sub-populations can be isolated from one another to varying degrees, but larger populations form corridors that ensure that a common fitness is a shared globally.

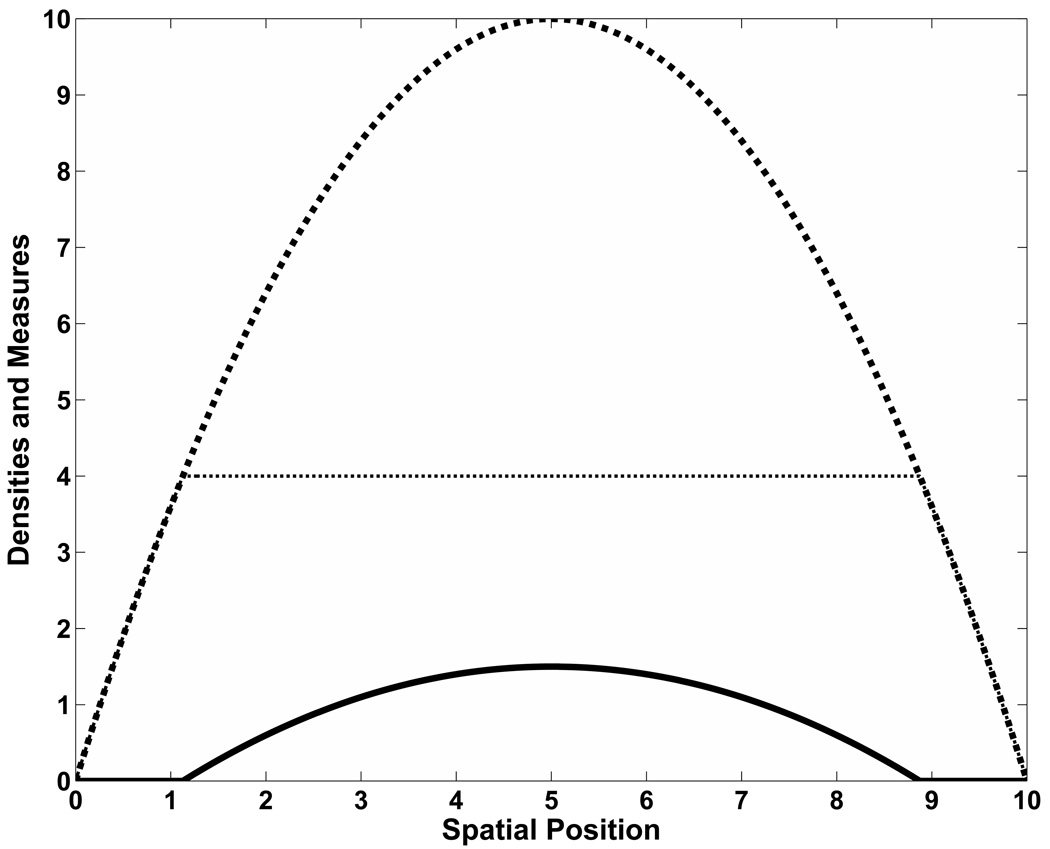
Fig. 1.

A comparison of resource and population densities and fitness measure at steady-state. The resource density, R(x) = 10 − .4(x − 5)², is represented by the diamond or large-block curve, while the population density, u(x), is shown by the solid line. The fitness measure, S = R/(u+h) with h = 1 and C = 4, is given by the dotted line. The measure is uniform over the interval where the population density is non-trivial; elsewhere, it is proportional to the resource.

Uniformity of fitness has two important consequences. First, in all steady-state solutions to the Searching Problem, there is a non-trivial sub-domain where the population density, u, is 0. The resources available in these absence regions are not negligible, nor are they necessarily of “sink” quality. Until population growth dictates otherwise, however, there is simply no incentive to expand into the “lesser” resource areas.

Second, if the resource gradient is 0 only at its peak or the boundary, the population terminus is abrupt; that is, the distribution is not differentiable at its range limit. This can be easily seen in the case of S = R/(u + h) by noting that the directional derivative of u is proportional to that of the resource curve R within the region supporting a positive population, Ω_C = {x⃗ : R(x⃗) ≥ Ch}, but 0 outside of it,Ω − Ω_C. Under the assumption that interior extrema are restricted to a single maximum (and there are no saddles), externally and internally evaluated directional derivatives of u at any point on ∂Ω_C will disagree save for those directions tangential to ∂Ω_C, when it will be 0. The population density is differentiable when the range limit coincides with a saddle in the resource distribution, but in general it is non-differentiable at the range limit.

This is true even in more general contexts and fitness functions. If the population is constrained to an ideal distribution established by a given contour value C, the implicit and chain rules of differentiation hold that the population gradient within the inhabited region is

$$\nabla u=-{\left(\frac{\partial S}{\partial u}\right)}^{-1}\left(\frac{\partial S}{\partial R}\right)\nabla R.$$ (6)

The multiplier (−S_R/S_u) is strictly positive. If additional resource peaks are admitted into the problem, as is illustrated in Figure 2 and Figure 3, the one-to-one relationship between contour level and total population size does not always hold in the searching problem. Consider the example of a resource environment dominated by two unequal high-resource areas. Let R₁ and R₂ represent the smaller and larger peak values, respectively, and let R_V denote the resource value in the trough between them (Fig. 2). If S = R/(u + h), there exists a unique steady-state distribution for all Ch < R_V because the overall population forms a contiguous distribution utilizing both resource peaks (also, diagonal line in Fig. 3A).

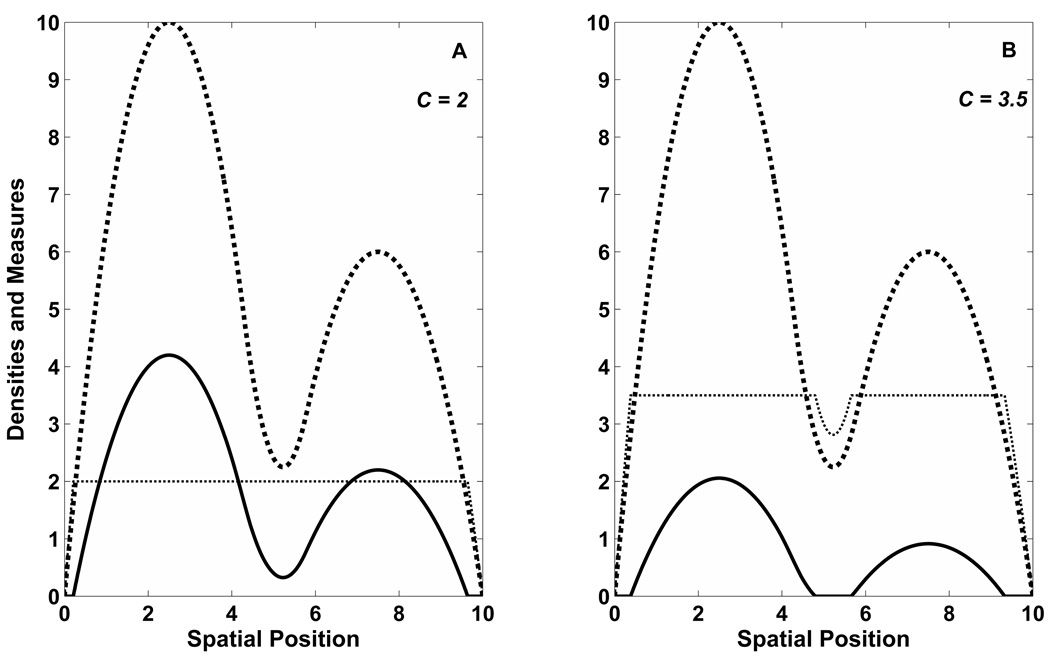
Fig. 2.

Divorcement of a multi-peaked population. This figure demonstrates the impact of either a sudden decimation event or a rising global mortality on a population. In both plots above, the resource curve is signified by the same double-peaked, diamond-marked curve which is piecewise C². As in Fig. 1, the population density and the fitness measure, S = R/(u + h), are illustrated by the solid and dotted lines, respectively. In 2A, h = .8 and C = 2. The population is large enough to occupy a contiguous region. In 2B, C = 3.5. Allopatry has been induced as a result of reduction in population, and the fitness measure exhibits a dip in the center corresponding to the unpopulated zone between the two sub-populations.

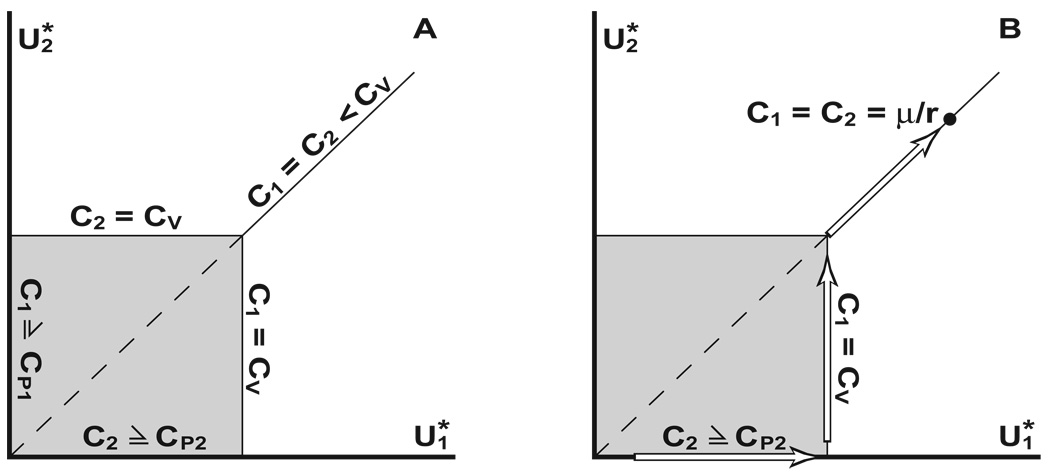
Fig. 3.

Multiple and unique population distributions. Fig. 3A diagrams a common bifurcation in the possible ways in which a given population can be ideally-distributed under a multi-peaked resource. $U_1^{*}\text{and}{U}_2^{*}$ represent the sub-populations under the first and second peak, respectively. The gray area represents multiple equilibrium distributions for a given population size (along the line $U_1^{*}+U_2^{*}=U_{\mathit{Total}}$). For large populations (corresponding to a common, small contour value C < C_V), there is a unique distribution (the solid line). The dashed segment represents non-contiguous distributions sharing a common contour value. Fig. 3B shows an example of colonial peripatry under fast-time/slow-time dynamics (Section 3.4). The population begins entirely under the first resource peak until it grows to reach the resource valley. All additional growth is directed to the sub-population under peak 2. Once the two populations are contiguous, they both grow together until C = μ/r.

In contrast, when Ch > R_V , the population is partitioned into two non-interacting groups (Fig. 2B). Looking at the population density under each peak in isolation, the sub-populations are bounded away from the trough by the same arguments that restricted the density to a proper subset of the available physical space. In fact once the contour value exceeds R_V/h, each subgroup can be governed by an independent contour value intermediate to the scaled resource values at the trough and the local peak value (Fig. 3A, gray area). The old one-to-one relationship between population size and contour value still exists within the sub-populations, but the different regions do not need to share a common contour value, and there are infinite arrangements that can maintain a common overall population level.

Such multi-peak landscapes easily support the occurrence of allopatry during the on-start of environmental calamities. Elevated mortality increases the contour value (C = μ/r, see the next section). A similar result is reached when there is a global decline in resource values (Holt, 2003) - e.g a heat wave or cold snap reducing vegetation. The commonality between the two is that the current contour level (as set by population level or birth-death processes) exceeds the resource value of some segment of the inter-peak region. Section 3.4 continues the discussion of multi-peak environments as it relates to parapatry.

3.2 Incorporating Reproduction and Mortality

In the previous section, it was assumed that the sole dynamic factor was population movement (the Searching Problem). Now, let us reinstate the birth-death processes of the original Reaction-Searching Problem (2), i.e. r, μ > 0.

The steady-state behavior of this system is similar to the Searching Problem, but there is only a single possible contour value, namely C = μ/r, whose corresponding steady-state distribution is an attractor for all reasonable initial distributions. We have already seen that contour solutions eliminate the flux, but the critical value C = μ/r, hereafter referred to as the effective mortality, also corresponds to where mortality is offset by reproductive fitness. The existence of isolated sub-populations under multiple peaks could be an arti-fact giving evidence to historic distributions, but they could also be recent developments of spatial divergence from an initial population located within a resource valley.

Figure 4A shows the evolution of a representative population distribution when movement, growth, and mortality all occur over the same or comparable time scales. Figure 4B presents the same distributions in cross-section at various, equally spaced points in time (the dotted lines). While it is possible to write down an explicit formula for the steady-state distribution, there is no method available to analytically describe the transient distributions of the population. The next section concerns a way in which we can circumvent this problem through a time-scale technique.

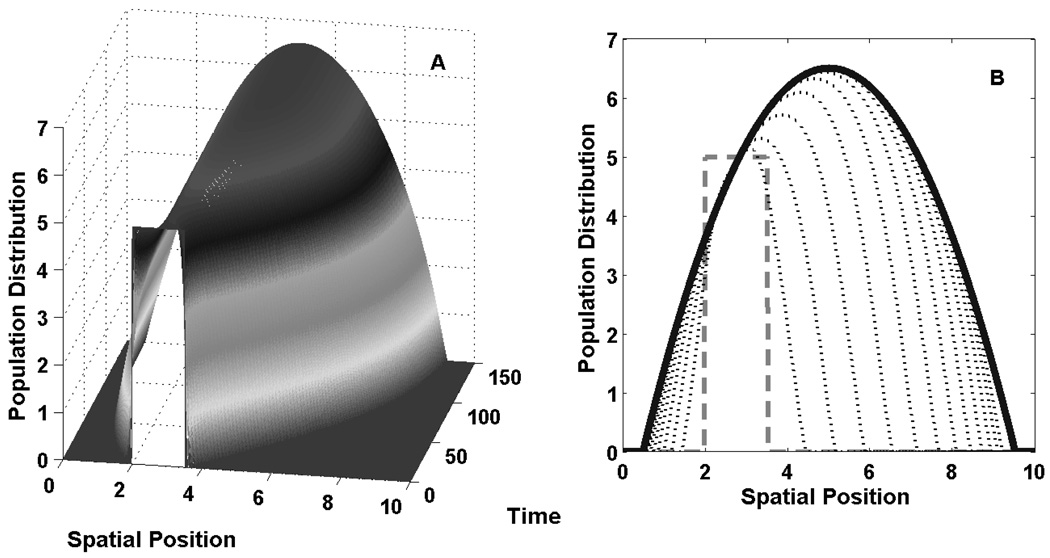
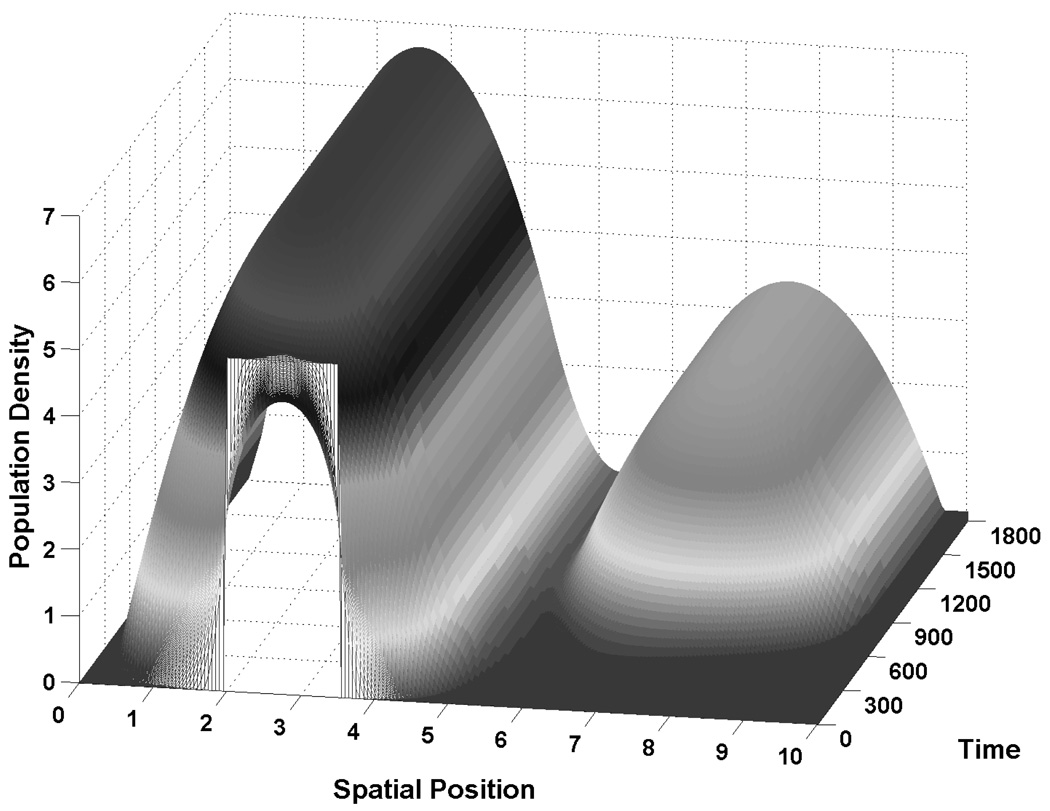
Fig. 4.

Expansion of the population. Figures 4A,B give a representative example of how the population distribution changes to occupy the available space when movement, mortality, and growth are on comparable time-scales. The initial distribution is u ≡ 5 on [2, 3.5] and 0 elsewhere (the rectangular aperture). h, R and S as in Figure 1. Fig. 4B presents a cross-sectional view of the distributions in 4A in regular increments of 14.5 time units, shown by the series of expanding, dotted curves. The parabolic solid curve represents the terminal steady-state distribution. During expansion, the leading edge of the distribution has a strong wave-front characteristic with the density rapidly falling away from the current peak or edge as it distribution moves rightward.

3.3 The Speed of Range Expansion

Population maneuvering need not occur on the same time scale as birth-death processes, and there is reason to suppose that the former occurs at a much faster scale than the latter in smaller regions. Movement may occur in a matter of seconds to days, while the reproductive and mortality rates are viewed from a seasonal or generational perspective. On the other hand, transitioning to larger, continental landscapes might reverse the ordering of time scales.

A fast-time/slow-time dichotomy presents an interesting opportunity to look at how ranges expand or contract without fretting over the internal non-linear dynamics. Assume that movement occurs on a fast time scale, one sufficient enough that the population reaches its ideal steady-state distribution as determined by the present population size. If fitness is measured by the function S = R/(u + h), the rate of change in the contour value C is

$$\frac{\mathit{dC}}{\mathit{dt}}=C(rC-\mu )\left(\frac{\mathit{Ch}}{\langle R\rangle }-1\right),$$ (7)

where 〈R〉 is the average resource level within the inhabited area. See Appendix C for the derivation of (7). By definition of the sub-domain, 〈R〉 is greater than or equal to Ch. Although it is ultimately a function of the contour value, we can treat the average resource as a constant and examine heuristically the implications of equation (7). The equilibria are at C = 0 (always unstable), μ/r, and 〈R〉/h. The larger of the last two values is unstable, and the smaller is stable - a feature echoing an underlying transcritical bifurcation when effective mortality equals the gathering-mediated resource peak value.

This comports with the idea that when mortality exceeds the fitness benefits of occupying the peak resource, the population is doomed to extinction. That is, for large μ/r, C increases to match the average sweep-adjusted resource value in Ω_C. The average resource 〈R〉 also increases as the subdomain shrinks, because it is restricted to ever choicer locales. If there is no subdomain where the average resource exceeds the effective mortality, the contour value goes to the adjusted resource peak value, R_peak/h, and the population collapses. Not incidentally, an equation like (7) also serves as a heuristic argument for the stable attraction of the steady-state solution in the Reaction-Searching Equation.

Now that it is possible to express the rate of change of contour values, we can address the important ecological question of how fast a population spreads out into its environment. If x⃗ represents a point on the edge of a population’s range, the outward speed of range expansion at that point, |v⃗| = |dx⃗/dt|, can be developed by examining changes in the resource value, R. From a spatial perspective, change in R can be explained by ΔR = ∇R · Δx⃗, but it is also governed by ΔR = hΔC

$$\nabla R·\frac{\mathrm{\Delta }\overrightarrow{x}}{\mathrm{\Delta }t}=h\frac{\mathrm{\Delta }C}{\mathrm{\Delta }t}$$

In the limit of Δt → 0 and in the direction of the outward normal, one can conclude

$$|\overrightarrow{v}|=h\frac{|\partial C/\partial t|}{|\nabla R|}.$$ (8)

In shallow resource gradients (where the resource is close to uniform), the expansion edge has a high velocity. Similarly, environments displaying rapid changes in resources (steeper gradients) retard the expansion of species’ ranges. As the system evolves over time, the outward velocity can both accelerate and decelerate, but it ultimately stalls as the contour value approaches effective mortality.

This result stands in marked contrast with measures of spread via purely diffusive mechanisms (Andow et al., 1990), where the speed V is given by the formula

$$V={\left[4\alpha D+(4D/t)\ln (N_0/\sqrt{4\pi Dt}{N}_T)\right]}^{1/2}.$$

Here D is diffusivity, α is a constant per-capita exponential growth rate, and N₀ and N_T are the original and detection-threshold population levels, respectively. Instead of eventually stalling, as with the model in this paper, the diffusive edge speed asymptotically approaches a constant value, $V=\sqrt{4\alpha D}$.

Finally, I note that for a general fitness function S(R, u), (7–8) can be generalized. The rate of change in contour value is

$$\frac{\mathit{dC}}{\mathit{dt}}=\frac{(rC-\mu ){\displaystyle {\int }_{{\mathrm{\Omega }}_C}u(R,C)dV}}{{\displaystyle {\int }_{{\mathrm{\Omega }}_C}\frac{\partial u}{\partial C}dV}},$$ (9)

and the outer expansion speed is

$$|\overrightarrow{v}|={\left(\frac{\partial S}{\partial R}\right)}^{-1}\frac{|\partial C/\partial t|}{|\nabla R|},$$ (10)

evaluated at the current threshold resource, R_L(C) (i.e. S(R_L, 0) = C).

3.4 Continental Islands And Source-Sink Dynamics

Section 3.1 showed that a multi-peak landscape could induce allopatric sub-populations given a sufficient effective mortality, resource loss or other contour changing event. When combined with the range expansion view of fast and slow time-scales, however, this type of landscape also facilitates movement leading to para- or peripatry.

Consider the fitness function S = R/(u + h) over a double-peaked resource landscape, such as the one discussed in 3.1, over the interval [0, L] with peak values R₁ ≥ R₂ and trough value R_V at x = x^*. Assume that the initial population is entirely to the left of the trough (i.e. the area pertaining to the first peak). Again assuming that movement occurs on a faster time-scale than birth-death processes, the population density evolves initially in accord with a changing contour value restricted to that region.

Once the population reaches the trough (hC = R_V), a change occurs in the dynamics. The left population “stabilizes” - all reproduction in excess of replacement is shunted away from the parent population toward a colonial population centered around the second resource peak (the diagonal in Fig. 3B). Under fast-slow dynamics, this secondary population is peripatric (non-contiguous); however if the time scales are more comparable, then it is connected to the original population by a lightly populated corridor (parapatry). In either scenario, the parent population continues to add to the satellite population as the latter grows.

The spatial implications of this arrangement are important for gene flow. In addition to being asymmetric - specifically one-way - the satellite community receives a contribution from only the nearby peripheral segment of the parent population. Mutations arising in removed portions of the parent group are unlikely to reach the satellite population (contrast this with the well-mixed treatment of standard island or metapopulation models).

Figure 5 illustrates an population that establishes itself and then supports a parapatric population. It is assumed that (hμ/r)+ ε= R_V for some positive ε, else the satellite region is never colonized save by a random occurrence. Eventually, the two populations fully reconnect, corresponding to hC₁ = hC₂ = R_V. From that point forward, the joint population evolves as a whole until it reaches equilibrium, C = μ/r (Fig. 3B,Fig 5).

Fig. 5.

Support of a peripheral population. The resource is identical to the double–peaked resource in Fig. 2 S = R/(u + h). The initial population, u ≡ 5 on [2, 3.5], is limited to the area under the left resource hump. The satellite population is not begun until the parent population achieves a rough optimal distribution that reaches the trough.

Is there any way in which this population merger fails? Yes, if one allows the incidence of mortality to vary spatially. For the sake of simplicity, assume that mortality is a piecewise constant variable

$$\mu (x)=\mathbf{\{}\begin{array}{cc}{\mu }_1,& x\le x^{*}\\ {\mu }_2,& x>x^{*}\end{array}$$

with μ₁ < rR_V /h < μ₂.

As was stated earlier, the model organism is blind to risk. In this scenario, the density distribution of the original population stabilizes with limits at the trough. The satellite population also stabilizes but at a contour value C^* ∈ (R_V /h, μ₂/r). It thus appears distinct from the parent population despite constant population support and gene flow. Because the satellite population is maintained at a level where mortality exceeds reproduction, the region has been rendered an artificial sink. (It would be a true sink if μ₂/r > R₂/h.)

This fact can be generalized by stating that source-sink dynamics can only arise when organisms suffer one of two forms of strategic mistake: strategic action based upon incomplete or inaccurate environmental information (such as the model organism here ignoring spatial variation in the risk of mortality), or errors in the execution of decision processes. The latter provides another interpretation for diffusion’s random-walk basis.

3.5 Resource Degredation and Other Utilization Functions

In this final section, I relax the time-independence condition on R and introduce a second equation to govern resource degradation in the presence of a consumer that moves according to a rational search. The Beddington-DeAngelis functional response without per-item handling is again assumed initially, but additional forms of fitness - which relax one or more of the basic conditions on S - are also examined.

Resources change over time according to

$$\frac{\mathit{dR}}{\mathit{dt}}=gR(R_m-R)-m\frac{\mathit{Ru}}{u+h}\text{on}\overline{\mathrm{\Omega }}\times (0,\infty ).$$ (11)

The coefficient m is the sensitivity of the resource to consumer activity, g is a measure of recovery speed, and R_m(x⃗) is both the undisturbed and initial resource distribution. This equation contains no mechanism by which to spatially “smooth” out the resource, and discontinuities theoretically could be formed by a slow, heavy consumer.

When the consumer is absent (u ≡ 0) the resource is either locally trivial (unstable) or equal to the undisturbed resource value R_m(x⃗) (stable). Assuming that the resource peak is unimodal, there is a single steady-state solution to this problem. The consumer distribution is in line with previous results:

$$u^{*}=\mathbf{\{}\begin{array}{cc}\frac{R^{*}}{C}-h,& R_m>\mathit{Ch},\\ 0,\hfill & \text{otherwise},\end{array}$$ (12)

but R^*is the equilibrium resource value. Over the sub-domain where R_m > Ch, the consumed resource approaches

$$R^{*}=\frac{1}{2}\left(R_m-m/g+\sqrt{{(R_m-m/g)}^2+4\mathit{Chm}/g}\right).$$ (13)

In this scenario, the total population is

$$\begin{array}{cc}{U}^{*}& =\frac{1}{2C}{\displaystyle {\int }_{{\mathrm{\Omega }}_C}{R}_{m}dV-\frac{m/g+2\mathit{Ch}}{2C}|{\mathrm{\Omega }}_C|}\hfill \\ & +\frac{1}{2C}{\displaystyle {\int }_{\mathrm{\Omega }}\sqrt{{(R_m-m/g)}^2+4\mathit{Chm}/g}\mathit{dV}.}\hfill \end{array}$$ (14)

As the grazing effect diminishes (m → 0), the resource and total population levels converge to the values determined in previous sections. The ultimate attracting contour value for the population distribution u remains C = μ/r. Conversely, for large m (m → ∞), the population over-exploits the resource, leading to its extinction, and the resource slowly recovers only after the population has been cleared from the system.

Let us also consider the ramifications of using different functions to describe consumption or fitness. We begin with the traditional mass-action process (Holling type 1 functional), Ru/h, with corresponding per capita fitness

$$S=\frac{1}{h}R.$$ (15)

There are no crowding or competition effects that directly diminish the resource value of a location (∂S/∂u = 0). This functional form is ill-suited to models lacking consumer impact on the resource (m = 0), as any peaks in the resource lead to the formation of population singularities (a problem for chemotaxis, too, cf. Lin and Segel, 1988). For m > 0, the steady-state solution to the problem is

$$R^{*}=\mathbf{\{}\begin{array}{cc}\frac{h\mu }{r},& R_m>h\mu /r\\ R_m,& \text{otherwise}.\end{array}$$ (16)

The population density is

$$u^{*}=\mathbf{\{}\begin{array}{cc}\frac{\mathit{gh}}{m}\left(R_m-\frac{h\mu }{r}\right),& R_m>h\mu /r\\ 0,\hfill & \text{otherwise}.\end{array}$$ (17)

Mass-action consumption produces a tale-tell signature in the flattened, “table-top” appearance of resource abundance. This version of the model is closest in spirit with Parker’s Matching Principle (Parker, 1978) as the population is set by a site’s resource input rate (growth rate) rather than the standing crop size; however, under Lessells’ (1995) interpretation, Parker’s Matching Principle holds in each case where the resource is dynamically responsive to consumption.

In a similar vein, consider the Holling type-2 functional response that includes resource item handling (~ 1/h) without consumer interference

$$S=\frac{R}{R+h}.$$ (18)

Again, ∂S/∂u = 0. Assuming that r > μ, the resource distribution is slightly modified, becoming

$$R^{*}=\mathbf{\{}\begin{array}{cc}\frac{h\mu }{r-\mu },& R_m>h\mu /(r-\mu )\\ R_m,\hfill & \text{otherwise}.\end{array}$$ (19)

The population density is

$$u^{*}=\mathbf{\{}\begin{array}{cc}\frac{g}{m}\left(\frac{\mathit{rh}}{r-\mu }\right)\left(R_m-\frac{h\mu }{r-\mu }\right),& R_m>h\mu /(r-\mu )\\ 0,\hfill & \text{otherwise}.\hfill \end{array}$$ (20)

Lastly, suppose that the response incorporates an Allee effect that represents the effect of consumer cooperation at low densities (∂S/∂u > 0 for small u. The total consumer impact is

$$R\frac{u^2}{u^2+{\alpha }^2},$$ (21)

with the population flux equal to k∇[Ru/(u²+α²)]. Locally there are two basic non-trivial steady-state densities, although alternations between the normative, threshold and trivial densities are possible. The threshold density is unstable to local perturbations (as a bistable problem) but also to nearby spatial variations. The latter can even promote sub-threshold populations to a persistent level because of the clustering phenomenon caused by directed movement. The normative (upper) solution is

$$u=\frac{1}{2\mu }\left(rR+\sqrt{r^2{R}^2-4{\alpha }^2{\mu }^2}\right).$$ (22)

In the limit as t → ∞, the population exists only where R > 2αμ/r (compare to the condition R > hμ/r in the previous cases); however, it need not exist everywhere in this region. Organisms moving in accord with this kind of fitness are unlikely to expand their region by purely deterministic drives, so discontinuities in the distribution can arise. Grindrod’s (1988) inclusion of diffusion overcame this tendency (q.v. movement errors at end of the preceding subsection). Even if the suitable region were fully occupied, there would be a discontinuity in the population density at the range limit, for u would be non-zero at the range boundary.

No explicit formula is given for the steady-state resource under grazing, as the solution involves a quartic equation.

4 Discussion and Conclusions

The formation and evolution of range limits are a macroscopic expression of individual movement processes. This paper has presented a model where individual movement is a non-random exercise designed to improve individual fitness and then examined the ramifications that such directed motion has on the larger distribution of a species in a continuous environment. Populations whose members search for improved personal fitness generally evolve to a distribution that is a continuum analog to the ideal-free distribution. Consequently, the inhabited range forms only a subset of the available habitat, and there is a potentially non-smooth termination of the population at the range limits. Furthermore, by concentrating on how range limits change over time, this model can express the speed of expansion of a population and explain how a parent population can support seemingly removed satellite communities.

The language of this paper has framed the discussion from a rational, strategic standpoint; however motion could also be a pseudo-rational phenotypic response to variations within the environment (Armsworth and Roughgarden 2005a,b). Furthermore, the model “resource” value could represent, in part or in whole, additional biotic and abiotic enivironmental factors such as the presence of other species or temperature that affect individual fitness.

The derivation of the equation for the rate of change in population density parallels those produced by Grindrod (1988) and Cosner (2005) in that flux - at least in part - is intended to move individuals up a fitness gradient. Associating the flux of population density to the fitness gradient is not an arbitrary choice. Fitness-gradient climbing reveals an important link between dynamic modeling approaches and traditional, static games of allocation (Armsworth and Roughgarden, 2005a,b; Lima and Zollner, 1996). It induces a movement governed by rules very similar to those operating in ideal-free domains (Fretwell, 1972) and the attracting equilibrium is a continuum analog of the ideal-free distribution (Kshatriya and Cosner, 2002; Cosner, 2005; Cressman and Křivan, 2006). Finally, local ideal-free distributions are experimentally found with a variety of animals in various contexts (see Stephens and Stevens (2001) for experimental references, as well as Ramp and Coulston’s (2004) study of kangaroos Macropus giganteus and citations therein, and interference studies by Johnson et al. (2005) of house sparrows Passer domesticus), though under-matching is also found (e.g. Johnson et al. 2005).

If organismal positioning is an error-free, strategic process, individuals will always avoid entry into sub-standard areas, and those located in such regions will quickly vacate if a path of egress is available to them. Over time, the inhabited region becomes a finite subsection of the available landscape, and the peripheral population’s density is often non-differential at the boundary and perhaps even discontinuous (q.v. Section 3.5). The computation of equilibrium distributions is straightforward for most fitness functions, and in unimodal resource landscapes there is a single steady-state distribution characterized by a unique index set by the population’s intrinsic mortality and metabolic resource conversion rate.

Range limitation carries with it an important implication for territorial spread. Outward expansion will necessarily stall in the long run as the limits of the species’ range encounter increasingly poorer areas which erode any perceived advantage from escaping conspecific competition. By comparison, the speed of the leading edge for a diffusing population asymptotes to a constant, non-zero value (Andow et al., 1990).

One of the clear conceptual problems that movement models must address is how populations in a locally “good” region can be induced to cross “poor” terrain to reach another “good” region. This problem has been similarly asked in regards to evolution in a fitness landscape (traditionally understood) or in numerical optimization routines. In the most strict sense, any entry into poorer regions must be considered either a procedural or a perceptual error.

Procedural errors account for random walks, incorrect strategic choices or execution of such choices, and mutations - all of which may be commonly rep-resented by diffusion. Perceptual errors, in contrast, are strategically correct but rely on an incomplete or inaccurate information set. Aspects of overall fitness are either ignored (e.g. being blind to risk), misinterpreted (e.g. mimic signaling), or suffer a valuation imbalance relative to the actual interplay of fitness factors. Both procedural and perceptual errors facilitate the advent of source-sink dynamics as population movement is consistently sub-optimal by external measures. These errors could be beneficial in the long-run, however, as poorer regions are traversed and become corridors between distant quality habitats.

This paper provides an alternative, mechanistic explanation of valley passage stemming from the existence of temporally varying environmental properties at the local, regional, or global scale (proxied by shifts in the resource curve, region-wide mortality or shifts in population levels). When threshold conditions are met (e.g. via growth of the population or decline in mortality) flow across local troughs occurs. This flow continues until either the entire population is contiguous over the larger region or the release of individuals results in a constriction of range in the original population. A return to the original environmental conditions cements the isolation of the two groups. The corridors that connected the populations are no longer tenable, and any residents vacate.

A critical feature of the model is the implicit, local information constraint imposed on individuals. This may be an adequate condition for some animals, but others such as birds (Hanski, 1982) have perceptual abilities or searching behaviors that strengthen the ability to locate suitable habitats in remote locations (see Cressman and Křivan (2006) for myopic versus global sensing in patch networks). Additionally, local resource peaks are vacated for superior sites despite poor intervening regions.

The flux description must be adjusted to account for wider detection capabilities. A meso-scale searcher, such as Hanski’s birds sampling the larger neighborhood, examines the surrounding neighborhood and compares its average fitness with that obtained by shifting the search zone. In mathematical terms, the flux would then be proportional to the gradient of a fixed-sized volume integral of fitness about the current position. In addition to simply granting the individual a larger view of the landscape, the meso-scale might be more appropriate for some species because of neighborhood crowding (see Sasaki (1997) for a diffusive model) or resource consumption which samples the territory surrounding the organism. This alteration also presents an intriguing possibility as it can simultaneously retard outward expansion and provide a mechanism for jumping resource valleys, but the final disposition of these hypotheses requires further study.

At the extreme end of the knowledge spectrum, organisms can possess information about the entire region under consideration. Flux would be a measure of the difference between the peak fitness currently available and the organisms’ current fitness. Globally searching organisms will situate on the greatest resource peaks firsts (cf. Kshatriya and Cosner, 2002), however harrowing the intervening passage might prove. A slight modification to this set up would be to discount the value of a site by its distance from the particular organism.

Finally, the methodology of this paper can be extended to community assemblages (cf. Cressman et al., 2004; Křivan et al., 2008). In a minimalist sense, communities arise from overlapping species ranges (Holt and Keitt, 2005), and inter-specific interactions within an assemblage can be the primary influence on the range limits (Gaston, 2003; Case et al., 2005). One important contrast between direct competitors is the ratio of error/diffusion to fitness gradient climbing (Cosner and Lou, 2003). Searching afar diffusively carries with it high risks and rewards for the individual. Other points of comparison are inter-specific competition for access to resources, site coverage and resource handling times, mortality and resource conversion, and sensitivity to local variations in fitness. These are the subject of a follow-up paper in progress. Furthermore, one could apply directed movement to predator-prey models, with prey-taxis and predator avoidance working at cross-purposes. Lastly, the principle of directed movement also operates on the level of social dynamics, and this framework holds promise in exploring problems of group identification, mate choice, speciation, and hybridization. Recently in the case of mate choice, male preferences for female traits was shown to facilitate as-sortative mating on a “reproductive landscape” of available females (Rowell and Servedio, 2009).

Appendix

A Towards a Uniform Fitness in a Constant Population

This appendix discusses two formal results and subsequent heuristic reasons for concluding that the search measure evolves to a uniform state over the inhabited region. Throughout the appendix, it is assumed that the total population is held constant, i.e. r = μ = 0, and that S, R, and u are sufficiently piecewise smooth.

Lemma 1

Interior fitness maxima never increase and generally decrease, and interior fitness minima never decrease and generally increase.

Proof

By application of the chain rule, the rate of change of fitness is given by the equation

$$\frac{\partial S}{\partial t}=-k\frac{\partial S}{\partial u}[\nabla ·(u\nabla S)]=\left(-k\frac{\partial S}{\partial u}\right)(\nabla u·\nabla S)+\left(-ku\frac{\partial S}{\partial u}\right){\nabla }^{2}S$$ (A.1)

Without loss of generality, let x⃗^* ∈ Ω be the location at time τ of an interior local maximum in S. |∇S(x⃗^*)| = 0, and ∇²S(x⃗^*) ≤ 0. If u(x^*) = 0, then S_t = 0. If u(x^*) > 0, then −k∂S/∂u > 0 everywhere except ∂Ω, so S_t(x⃗^*) has the same sign as ∇²S(x⃗^*). Therefore, no interior maximum may increase, but it may decrease given sufficient curvature in the fitness landscape. In like manner, no interior minimum may decrease, but it can increase.

As a technical note, the initial colonization of a resource peak or saddle is a momentary rarefaction and shock event traversing a discontinuity in one of the variables or their spatial derivatives.

There are two consequences to the lemma above. First, novel isolated extrema cannot appear in the fitness landscape, for in their creation a local maximum must grow and/or a local minimum must decrease to produce the qualifying contrast. This does not preclude the creation of additional extrema formed in contact with existing ones - indeed, the ultimate distribution typically consists of a large, connected set of equally maximal points of fitness. Further, points within such extremal sets may become isolated as set boundaries constrict in response to nearby population movement. The second consequence is that maxima and minima cannot pass through each other. When they are brought together, they merge and mutually annihilate - at best, surviving as a saddle.

Lemma 2

Let R and u be continuous, piecewise C² functions over Ω = [a, b]. If x^* is a populated local fitness extremum, then there exists a range about x^* such that the fitness at all non-extremal points are decreasing if x^* is a maximum (and increasing if it is a minimum).

Proof

Without loss of generality, let x^* be a local maximum at time τ of the fitness function S(R, u), re-expressed here as a spatio-temporal function S(x, t). Define the current set of equally fit and populated points as Y_c = {x : S(x, τ) = S(x^*, τ) ^ u(x, τ) > 0}, with closure Y̅ _c. Let X_c ⊆ Y_c be a closed, connected subset containing the point x^*. In the case of an isolated maximum, this set is the singleton X_c = {x^*}. Finally, define M_c = sup_x∈Xc |u_x/u|, and let the ε-neighborhood of X_c be B(X_c,ε) = {x : min_x′∈Xc |x − x′| ≤ ε}.

There are four crucial neighborhoods of X_c that satisfy central properties:

1. By definition of a locally C² fitness maximum, Ǝε₁ > 0 such that ∀x ∈ B(X_c,ε₁) − Y̅_c the second derivative is negative, S_xx < 0.

2. By continuity of population density, Ǝε₂ > 0 such that ∀x ∈ B(X_c, ε₂) the population is non-trivial, u(x, τ) > 0.

3. By locally continuous differentiability of u, ∀M > M_c, Ǝε₃ > 0 such that ∀x ∈ B(X_c,ε₃), |u_x/u| ≤ M.

4. By l’Hopitale’s Rule, if S_xx(X_c) = 0, then as one approaches X_c, the first derivative, S_x, goes to 0 faster than does the second, S_xx. Thus ∀M > 0, Ǝε₄ > 0 such that ∀x ∈ B(X_c,ε₄) − Y̅_c, M|S_x| < |S_xx|.

Therefore, ∀M > M_c, Ǝε ≤ min{ε₁, ε₂, ε₃, ε₄} such that ∀x ∈ B(X_c,ε) − Y̅_c

$$\begin{array}{cc}\frac{\partial S}{\partial t}(x,\tau )\hfill & =\left(-\mathit{ku}\frac{\partial S}{\partial u}\right)\left(\frac{u_x}{u}\frac{\partial S}{\partial x}+\frac{{\partial }^{2}S}{\partial x^2}\right)\hfill \\ \hfill & \le \left(-\mathit{ku}\frac{\partial S}{\partial u}\right)\left(\left|\frac{u_x}{u}\right|\left|\frac{\partial S}{\partial x}\right|+\frac{{\partial }^{2}S}{\partial x^2}\right)\hfill \\ \hfill & \le \left(-k\frac{\partial S}{\partial u}\right)\left(M\left|\frac{\partial S}{\partial x}\right|+\frac{{\partial }^{2}S}{\partial x^2}\right)<0\hfill \end{array}$$ (A.2)

Stated in a non-technical fashion, one can conclude that for any given tolerance for the relative rate of change in the population about X_c, there is a neighborhood about X_c such that all populated, non-maximal points are strictly decreasing in fitness. [The proof for minima follows likewise.]

The change in fitness in the region surrounding X_c (whether increasing or decreasing) only ceases if for all tolerances on the relative change in u, and for all ∊ satisfying (i − iv), B(X_c,ε) − Y̅ _c = ∅; i.e. there is locally uniform fitness across a populated area. The lemma also is not applicable to cases where S_xx is not defined on the boundary ∂X_c.

This lemma extends to higher dimensions, but with an important caveat. The conclusion that S_t(x⃗, τ) < 0 in the vicinity of a maximal set X_c (or the reverse) is only permitted if the fitness level curve or surface on which x⃗ lies, ∑ = {y⃗ : S(y⃗, τ) = S(x⃗, τ)}, is a locally convex covering about X_c at x⃗. That is, at time τ, x⃗ is a local fitness maximum on the tangent plane to ∑ (or a minimum in the reverse case). This variant of the lemma follows from the decomposition of the Laplacian into normal and tangential components, ${\nabla }^{2}S-{\nabla }_n^{2}S+{\nabla }_T^{2}S$. By requiring the point to be a maximum (or minimum) on the tangent, ${\nabla }_T^{2}S$ is either 0 or the same sign as ${\nabla }_n^{2}S$.

Lemmas 1 and 2 do not formally establish the convergence of fitness to uniformity across a populated region, but they do form the basis for a strong heuristic argument in support of that conclusion. Fitness peaks and valleys undergo a generally compressive or flattening evolution that is irreversible except where the extremum is lost as such. Even when the extrema themselves are arrested, the fitness in the surrounding populated region is compressing as a result of the nearby areas constituting population sinks and sources. This nearby compression, in turn, tightens the curvature leading up to the extremum until eventually the Laplacian is again non-zero or fitness becomes insufficiently smooth at the boundary of X_c. As this process continues, the fitness landscape flattens out where the population inhabits, and the population flees sub-optimal regions along the border of the domain.

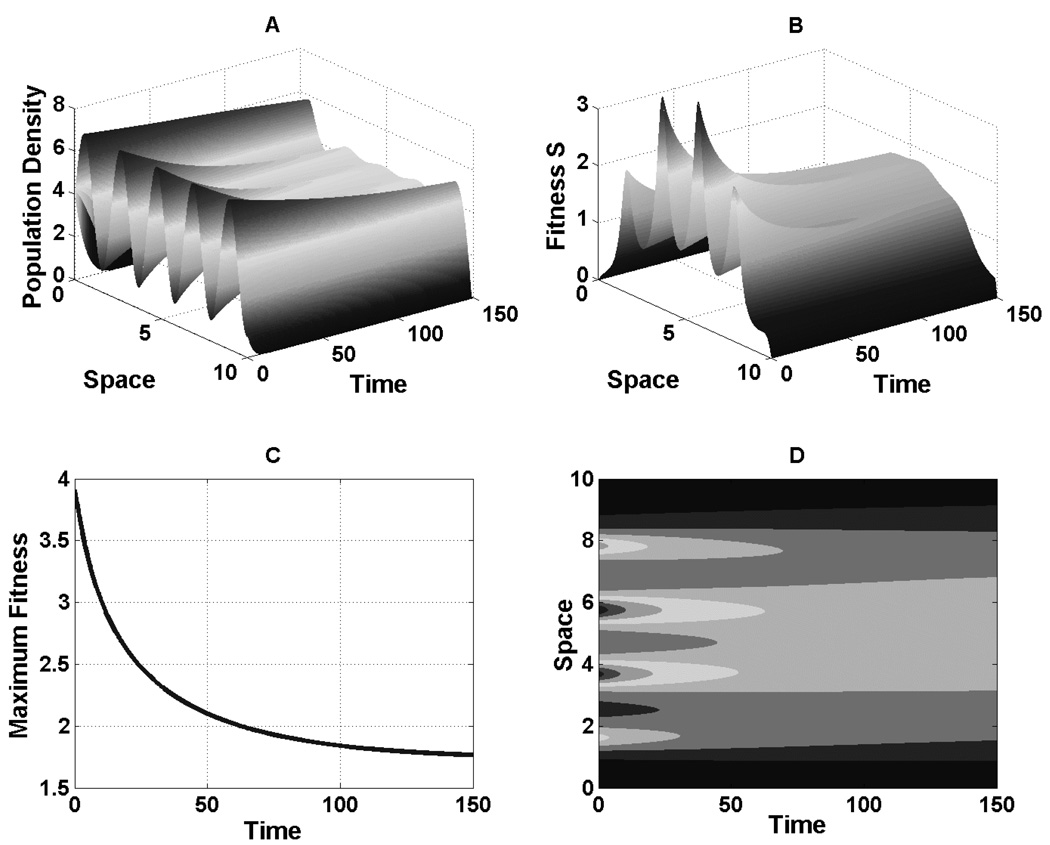
Figure A.1 illustrates the compressive evolution of fitness even as the population exhibits a wildly varying distribution that produces multiple peals and valleys in the fitness landscape. As the system evolves, even while the population maintains a wavy profile, the fitness landscape eliminates this feature en route to flattening out.

Fig. A.1.

Compression effect. The population is intitially distributed sinusoidally, u(x, 0) = 4+3 sin(3x), over a parabolic resource, R = 10 −.4(x−5)². the population distribution changes only through movement (r = μ = 0). A.1A: The distribution maintains a wavy pattern for much of its history, with densities near the range boundary particularly resistant to change. A.1B: The fitness landscape is much more responsive, with compression of extrema clearly evident. This same information is shown as a space-time contour plot of fitness in A.1D. A.1C: As an additional measure of compression, the global maximum fitness in Ω monotonically decreases over time.

B Characterizing the Steady-State for the Searching Problem

Because of the boundary conditions on u and R in (2) (u = R = 0 on ∂Ω), there is neither immigration into nor emigration from the region Ω. Therefore, when there are no dynamics occurring within the population aside from movement (r = μ = 0), the total population remains constant.

Lemma 3

Assume u is ideally distributed across a unimodal resource R(x⃗), then there is a 1–1 correspondence between total population size, U, and the distribution’s contour value, C.

Proof

Assume u is ideally distributed as described above so that in all occupied areas S(R, u) = C. Define R_L as the minimum threshold for supporting an ideally distributed population with contour C (i.e. S(R_L, 0) = C)

$$S(R,u)=\mathbf{\{}\begin{array}{cc}C,\hfill & R\ge R_L;\text{and}\hfill \\ S(R,0)\le C,\hfill & R<R_L.\hfill \end{array}$$ (B.1)

Holding the resource constant against changing contour values, we can use inverse and implicit derivatives to show that on the constraint S(R, u) = C, the rate at which population density changes with respect to the contour value (for u > 0) is

$$\frac{\partial u}{\partial C}={\left(\frac{\partial S}{\partial u}\right)}^{-1}<0.$$ (B.2)

Likewise, under the constraint S(R_L, 0) = C, we can establish the rate of change in the resource threshold

$$\frac{\partial R_L}{\partial C}={\left(\frac{\partial S}{\partial R_L}\right)}^{-1}>0.$$ (B.3)

Let Ω_C be the subregion in which u > 0 with volume |Ω_C|. By (B.3), as C increases, the minimum required resource increases, and |Ω_C| decreases as fewer areas of Ω sport sufficiently high resources. Now the total population in the domain equals

$$U={\displaystyle {\int }_{\mathrm{\Omega }}u}\mathit{dV}={\displaystyle {\int }_{{\mathrm{\Omega }}_C}u}\mathit{dV}.$$ (B.4)

In assessing ∂U/∂C, note that both the volume of integration and the positive integrand decrease with respect to C. Therefore U is a strictly decreasing function of C, and there must exist a one-to-one correspondence for all U ∈ (0,∞) and C ∈ (0, S(R_max, 0)).

Therefore there exists a unique value C defining an ideal distribution for a population of any given size.

Lemma 3 generalizes for arbitrary resource surfaces, even ones that are non-differentiable or possess only piecewise continuity. If there are multiple peaks in the resource (differentiable or not, including local suprema), the one-to-one relationship persists only under the formal restriction that C is constant over the entire domain Ω (see section 3.4 for an example of when this restriction is waved).

In conjunction with the results of Appendix A, which argues that populations push towards ideal distributions, the ideal distribution determined from the initial population size is the suggested attractor for the general Searching Problem.

C Derivation of the Rate of Change of the Contour Value (Eq. 7)

This appendix calculates the rate of change in the contour values of ideally distributed populations under the local fitness function S(R, u) = R/(u + h) when growth and mortality transpire on a slower time-scale than that on which movement occurs. This rate of change (7) can then be used to calculate the speed of expansion or contraction of a population’s range (Section 3.3).

Let the density u be ideally-distributed with contour value C under a unimodal resource curve R(x⃗),

$$u=\mathbf{\{}\begin{array}{cc}\frac{R}{C}-h,& R\ge \mathit{Ch}\hfill \\ 0,\hfill & \text{otherwise}.\hfill \end{array}$$ (C.1)

The notation [R] and 〈R〉 will be used, respectively, for the integration and average value of R, over the sub-domain Ω_C. For a given contour value C, the rate of change in the total population based on the slow-time processes is computed as

$$\begin{array}{cc}\frac{\partial U}{\partial t}\hfill & ={\displaystyle \int \frac{\partial u}{\partial t}}\mathit{dV}={\displaystyle {\int }_{{\mathrm{\Omega }}_C}\frac{\partial u}{\partial t}\mathit{dV}}\hfill \\ \hfill & ={\displaystyle {\int }_{{\mathrm{\Omega }}_C}\left[-k\nabla ·\left[u\nabla S\right]+u\left(rC-\mu \right)\right]\mathit{dV}}\hfill \\ \hfill & =0+\left(rC-\mu \right){\displaystyle {\int }_{{\mathrm{\Omega }}_C}u}\mathit{dV}\hfill \\ \hfill & =\frac{(rC-\mu )}{C}[R]-h(rC-\mu )|{\mathrm{\Omega }}_C|\hfill \end{array}$$ (C.2)

The Divergence Theorem holds that the first part of the integration is zero because u = 0 on ∂Ω_C. This is true even as the range expands or contracts. Alternatively, the rate of change can be taken directly from the definition of total population,

$$U={\displaystyle {\int }_{{\mathrm{\Omega }}_C}\frac{R}{C}-h\mathit{dV},}$$

whose time derivative is

$$\frac{\partial U}{\partial t}={\displaystyle {\int }_{{\mathrm{\Omega }}_C}\frac{-R{C}_t}{C^2}}\mathit{dV}\mathrm{+}{\displaystyle {\iint }_{\partial {\mathrm{\Omega }}_C}(\overrightarrow{v}\cdot \overrightarrow{n})\left(\frac{R}{C}-h\right)\mathit{dA}.}$$

The vector v⃗ is the local velocity for the boundary as it expands or contracts. The surface integral is trivial because of the constraint that R = Ch on ∂Ω_C. This simplifies the equation to

$$\frac{\partial U}{\partial t}=-\frac{C_t}{C^2}[R].$$ (C.3)

Equating (C.2) and (C.3) yields an equation for the rate of change in contour value.

$$\frac{-[R]}{C^2}\frac{\partial C}{\partial t}=\frac{(rC-\mu )}{C}[R]-h(rC-\mu )|{\mathrm{\Omega }}_C|$$ (C.4)

Noting that 〈R〉 = [R]/|Ω_C|, the final step is to isolate dC/dt as in (7).