Sampling bottlenecks in de novo protein structure prediction

Summary

The primary obstacle to de novo protein structure prediction is conformational sampling: the native state generally has lower free energy than non-native structures but is exceedingly difficult to locate. Structure predictions with atomic level accuracy have been made for small proteins using the Rosetta structure prediction methodology, but for larger and more complex proteins, the native state is virtually never sampled and it has been unclear how much of an increase in computing power would be required to successfully predict the structures of such proteins. In this paper we develop an approach to determining how much computer power is required to accurately predict the structure of a protein, based on a reformulation of the conformational search problem as a combinatorial sampling problem in a discrete feature space. We find that conformational sampling for many proteins is limited by critical “linchpin” features, often the backbone torsion angles of individual residues, which are sampled very rarely in unbiased trajectories and when constrained dramatically increase the sampling of the native state. These critical features frequently occur in less regular and likely strained regions of proteins that contribute to protein function. In a number of proteins, the linchpin features are in regions found experimentally to form late in folding, suggesting a correspondence between folding in silico and in reality.

Introduction

A central challenge in computational biology and chemistry is to accurately predict the three-dimensional structures of proteins given just their amino acid sequences. This is a formidable problem given the very large number of degrees of freedom and hence very large conformational space of a polypeptide chain. Since proteins generally fold to their lowest free energy states, the problem can be stated very simply: identify the lowest free energy state of the protein chain. A protein structure prediction method need not compute energies with extremely high accuracy to be successful: in order for proteins to fold to single unique states, the energy gap between the native structure and typical non-native conformation, the driving force for folding, must be quite large to overcome the very large entropic barrier to folding (here and throughout the text we use “energy” to refer to the enthalpy plus the entropy associated with the hydrophobic effect; this is the free energy minus the configuration entropy).

The Rosetta de novo structure prediction methodology can predict the structure of some small proteins with high-resolution accuracy as confirmed in numerous blind structure prediction tests^{1; 2; 3}. The primary obstacle to predicting the structures of proteins more generally with this approach appears to be conformational sampling: even with the imperfections in the Rosetta energy function, the native state almost always has lower energy than Rosetta-generated non-native models, but particularly for larger and more complex proteins, the native state is almost never sampled by Rosetta trajectories starting from the extended chain.

Since native structures appear to have consistently lower computed energies than non-native models, the protein structure prediction problem is in principle solved modulo sufficient computing power to adequately sample the native state. It is straightforward to determine empirically how much computation is required if the native structure can be sampled in readily available amounts of computer time. But for proteins for which the native state is sampled very rarely or not at all, it is very difficult to determine how much additional computing power is necessary. The question of how much more computing power is necessary is critical: if the answer is ten-fold more the problem may be solved by increasing computing resources, but this is not a feasible solution if the answer is a million-fold more. Estimation of the magnitude of the sampling problem is thus quite important, as is the identification of the primary bottlenecks to conformational sampling, which could lead to improved approaches to the problem.

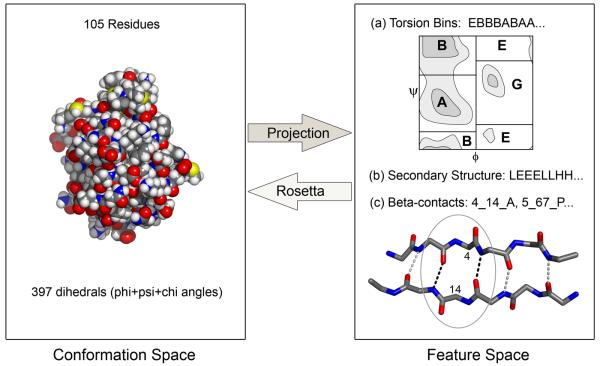
Here we characterize the conformational sampling problem in Rosetta using a discrete feature space representation of protein structures that enables the estimation of the amount of conformational searching (and computer time) required to predict the structure of proteins quite generally. The discrete features we employ are secondary structure, torsion angle bins, and beta-contacts (Figure 1). We first show that the native feature values provide sufficient information for Rosetta trajectories to consistently sample the native structure for a wide variety of proteins. Next, we show that the general conformational sampling problem can be formulated as a discrete sampling problem in feature space, and that this allows the estimation of the amount of sampling required for predicting the structure of proteins that are out of reach of current computing power. We find proteins that require very large amounts of sampling contain “linchpin” features whose native values are sampled at extremely low rates, and enforcing the native values of these features drastically increases the rate of native state sampling. The linchpin features frequently occur in functional regions that are likely under local conformational strain, and comparison to experimental studies of protein folding suggests that these obstacles to folding in silico may also be obstacles to folding in reality.

Figure 1. Mapping between three-dimensional structures and a lower dimensional discrete feature space.

The transformation from conformation space to feature space can be achieved by reading off the (a) torsion angle bins, (b) secondary structure and (c) beta-contacts from the three-dimensional structure. The transformation from feature space to conformation space can be achieved by carrying out Rosetta trajectories in which the feature values in a particular feature string are enforced.

Results

Previous successes in high-resolution de novo structure prediction using Rosetta have relied on generating low-resolution models on a large number of sequence homologs along with the target sequence in order to successfully sample the near-native region of the energy landscape. With the large amount of CPU time available through Rosetta@home, which consists of over 150,000 computers roughly half of which are available for use at any given time, large-scale sampling runs without using information from sequence homologs can be successful. To determine how well structures can be predicted using single sequence information and to set a baseline for subsequent experiments, we investigated the performance of Rosetta on a test set of 32 small alpha-helical and alpha-beta protein domains by generating many independent models using different random number seeds starting from an extended chain. Models were generated using the standard Rosetta Monte Carlo and gradient-based energy-minimization strategy, which consists of a low-resolution conformational search followed by full-atom refinement. Trajectories were also started from the native structure using the full-atom refinement protocol to obtain an estimate of the energy in the native region⁴.

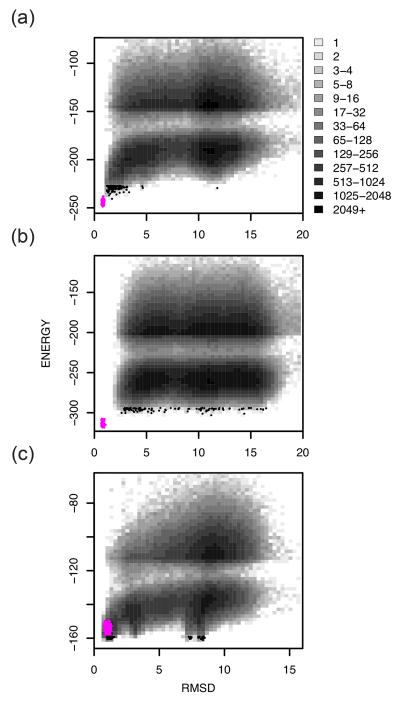
The results of these calculations are grouped into three different categories in Table 1. The first category includes proteins for which Rosetta, with this level of conformational sampling, is successful in producing an accurate (root mean square deviation (RMSD) of α-carbons to the native structure less than 2 Å) lowest-energy model. 9 of the 32 proteins in our test set were in this category (1aiu, 1b72, 1di2, 1dtj, 1elw, 1pgx, 1r69, 256b, and 2reb). The second category includes proteins for which the native state was not sampled but there was an energy gap between the models and refined native structures. The majority of proteins are in this category (1acf, 1a19, 1a68, 1bm8, 1bq9, 1cc8, 1ctf, 1dcj, 1iib, 1mky, 1n0u, 1opd, 1tif, 1ubi, 2chf, 2ci2 and 4ubp). A number of proteins within this category had lowest-energy models that were less than 3.5 Å RMSD from the native and two had core RMSDs of less than 2.0 Å (1bq9, 1.85 Å, and 1dcj, 1.15 Å, Table 1). The last category includes proteins that had incorrect lowest-energy models that were lower in energy than the refined natives (1a32, 1hz6, 1ig5, 1tig, 1scj and 5cro). These proteins likely reflect inaccuracies in the current Rosetta energy function, the influence of crystal packing interactions on the experimentally determined structure, or missing interactions with a bound ligand. Energy versus RMSD plots of one example from each category are shown in Figure 2.

Table 1.

Structure prediction performance and sampling

	RMSD lowest energy model			# of runs for lowest energy RMSD < 2 (3) Å
Protein	Native SS + Torsiona	Controlb	Control Corec	Native SS + Torsion	Control
Category 1: Successful high-resolution predictions
1aiu	1.29	1.69	1.21	15	59000
1b72	1.14	1.54	0.78	300	1462000
1di2	1.10	1.96	1.83	8	2960000
1dtj	1.97	1.43	0.77	125000	327000
1elw	0.93	1.23	0.73	18	14
1pgx	0.89	0.87	0.48	5	100000
1r69	0.83	1.40	1.31	2	12000
256b	2.04	1.96	1.36	(6)	48000
2reb	1.19	0.90	0.69	1	44
Category 2: More sampling may lead to successful predictions
1a19	0.94	2.67	2.33	28000
1a68	4.47	12.40	11.41	-
1acf	2.83	5.12	4.26	(16000)
1bm8	2.27	13.44	11.75	(7)
1bq9	1.85	3.30	1.85	165000
1cc8	2.30	2.88	2.27	(40)
1ctf	1.39	5.52	5.73	8
1dcj	1.17	2.19	1.15	3
1iib	1.11	3.42	2.82	21000
1mky	3.01	13.82	11.09	-
1n0u	1.45	11.64	9.60	35000
1opd	0.96	3.24	2.99	6000
1tif	2.57	9.40	4.64	(23)
1ubi	2.25	3.14	2.73	(16000)
2chf	2.69	11.21	7.89	(26000)
2ci2	1.10	7.48	6.14	500
4ubp	3.29	10.15	8.48	-
Category 3: Non-native lowest energy models lower in energy than refined natives
1a32	1.19	8.35	5.03	8
1hz6	1.10	2.53	1.08	36
1ig5	2.33	2.91	1.82	(37000)
1scj	1.27	7.24	6.40	93
1tig	1.34	11.91	9.59	1000
5cro	1.36	9.87	6.78	9

^asampling runs where the native secondary structure and torsion bin features were enforced.

^bunconstrained sampling runs.

^cresidues with less than twenty percent solvent accessible surface area in the native structure were considered core residues.

Figure 2. Successes and failures in large scale de novo protein structure prediction calculations using Rosetta@home.

Representative 2-dimensional histograms of C_α-RMSD (x-axis) versus the Rosetta all-atom energy (y-axis) from unbiased Rosetta trajectories for a representative protein in category 1 (a; 1aiu), category 2 (b; 2chf), and category 3 (c; 1a32) (see text for description of categories). Refined native structures and 100 lowest energy models are shown in magenta and black points, respectively. The two distinct clouds of points in the 2-dimensional histograms are due to a score filter used during all-atom minimization for computational efficiency.

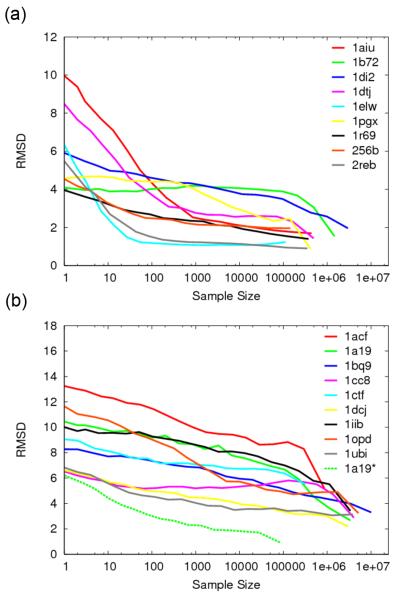
To quantify the dependence of structure prediction accuracy on the amount of sampling, we extracted random subsets of models from the control runs, and determined the average RMSD of the lowest-energy models as a function of subset size. The results for category 1 and 2 proteins are shown in Figure 3a and b, respectively. The majority of proteins in the category 1 group required a sample size of less than 100,000 for an average RMSD of the lowest-energy models of less than 2 Å. Two of these proteins, 1elw and 2reb, required a sample size of less than 100, and on the other extreme, 1b72 and 1di2 required a sample size of over 1 million. Among the category 2 group, the average RMSDs of 9 proteins generally decreased with increased sampling (Figure 3b).

Figure 3. Dependence of structure prediction accuracy on the number of independent trajectories.

The y-axis is the average C_α-RMSD of the lowest energy models in 500 random subsets of a given size (x-axis) taken from the unbiased Rosetta control runs. For example, an x-axis value of 10 indicates that the RMSDs of the lowest energy model in each of 500 randomly selected subsets of size 10 were averaged (y axis). (a) Category 1 proteins. (b) Category 2 proteins. Category 2 proteins whose average C_α-RMSDs did not improve with increased sample size have been omitted. The sampling curve from the native secondary structure and torsion bin enforced run of 1a19 is shown for comparison (dashed line).

Sampling in feature space

The category 2 proteins for which sampling is insufficient even with Rosetta@home are the major focus of this paper. How much sampling is required to successfully solve the structures of these proteins computationally? There is an obvious limit to how well this question can be answered by continued brute-force sampling, and instead we have developed an alternative approach. As shown in Figure 1, a protein conformation can be described in part by a string of features. The features used in this study include backbone torsion bins with five possible values for each residue position, ABEGO⁵, representing different regions in ramachandran space (and cis-peptide torsion angles (O)), secondary structure with three possible values, strand (E), helix (H) and loop (L), and beta-contacts represented by the pair of contacting residues, the orientation of the pairing (parallel or antiparallel), and the pleating.

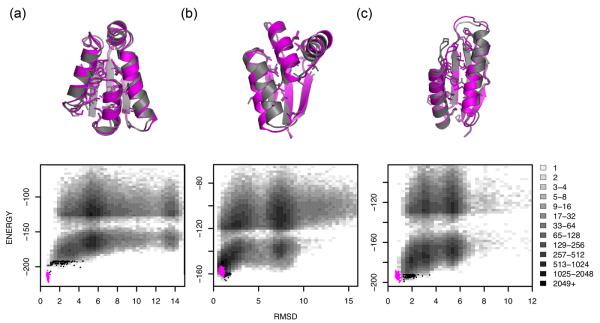
For this feature space representation to be useful, there must be a way to invert the projection from a three-dimensional structure onto a feature string, i.e. to go from the feature string back to a three-dimensional structure. In particular, the native feature string must provide sufficient information to determine the native three-dimensional structure. Rosetta structure prediction calculations in which torsion angles (or the other features) are constrained to lie within the discrete feature bins in principle can provide such a mapping from feature strings back to three-dimensional structures. To investigate the extent to which the native feature string encodes the native three-dimensional structure in this sense, we carried out a second set of structure generation calculations in which the native torsion bin and secondary structure features for every position were enforced. The results of this test are listed in Table 1 (columns 2 and 5). For 29 of the 32 proteins, the lowest energy models had RMSDs less than 3 Å; in 22 of these the RMSD was less than 2Å. Thus, once the overall region of conformational space is indicated by the native torsion bin and secondary structure feature strings, Rosetta conformational search can generally identify the native minimum. As shown in Figure 4, the low energy models superimpose well with the native structure.

Figure 4. Rosetta generates accurate high-resolution structures when native feature strings are constrained.

(top) Superpositions of the lowest-energy models (gray) with experimental structures (magenta) displaying core side chains for 1a19 (a), 1ctf (b), and 1tig (c). (bottom) Corresponding 2-dimensional histograms of C_α-RMSD (x-axis) against the Rosetta all-atom energy (y-axis) for models that were generated with constrained native torsion bin and secondary structure feature descriptions. The refined natives and 100 lowest energy models are highlighted as magenta and black points, respectively. Native secondary structure was assigned using DSSP.

Linchpin Features

Since the native feature string provides sufficient information to sample the native three-dimensional structure using Rosetta, we can now formulate the probability of sampling the native state in structure prediction calculations as the product of the probability of sampling the native feature string in unconstrained trajectories with the probability of sampling the native state given the native feature string, i.e. P(native state) = P(native feature string) * P(native state | native feature string). The second (conditional probability) term can be estimated by determining the frequency of sampling the native state in calculations such as those in Figure 4 in which the native feature string is enforced. An example of such a constrained sampling curve is shown in Figure 3b (dashed line).

The above formulation allows us to recast the sampling problem in feature space: the amount of sampling required to solve a given structure can be related to the frequency of sampling the native feature string. For almost all proteins, the native values of most features are sampled frequently in Rosetta trajectories. For example, unbiased trajectories for 1di2 frequently sample the native torsion bin features for all but one nonterminal residue (Figure 5). This is not surprising as one of the central ideas in the Rosetta approach is to model as accurately as possible the distribution of local conformations populated by each segment of the protein chain. However, for some proteins, particularly those that require large amounts of sampling to locate the native state, we find one to three features whose native values are almost never sampled in unconstrained runs (such as the torsion bin for residue 23 in Figure 5) yet are almost always present in low-energy near-native structures. A previously described example of such a feature is a rarely sampled kinked helix present in the native structure (residue F65 in 1pva) and enriched in low-energy low-RMSD models produced by Rosetta⁶.

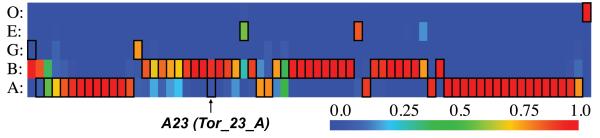
Figure 5. Native torsion bin features are frequently sampled with Rosetta.

The frequency of each torsion bin feature (rows labeled on the left) for each residue position (columns) from a random set of unbiased control run models of 1di2 is displayed according to the color scale on the bottom right. Native torsion bin values are boxed in black and the position of the linchpin feature in 1di2 is indicated with an arrow.

As described in the Materials and Methods, we systematically searched for rarely sampled features which when constrained yielded a much greater frequency of near-native structures. Such “linchpin” features were identified for 16 proteins in our test set and are listed in Table 2. Columns 5 and 6 compare the frequencies of these features in the overall sample population to the frequencies in low-energy low-RMSD models from the control runs. The frequencies in the overall control run population (column 5) ranged from 0.41 to 0.00046, while in contrast the frequencies in low-energy low-RMSD models (column 6) were greater than 0.80 for most of the proteins.

Table 2.

Linchpin features

	Cutoffs used for good models			Control Run			Forced Run	P(good)
Protein	RMSD	Energy	Feature	Feature freq overall	Feature freq goodb	P(good|feature)	P(good|feature)	Observed	Estimated
1a19	2.22	−186.68	Pair_4_52 Tor_55_G	0.006518	0.78	0.00177	0.000906	1.48E-05	5.91E-06
1bm8	3.50	−208.60	Pair_32_74 Tor_41_G	0.010018	-	-	0.000627	-	6.28E-06
1bq9	2.26	−87.99	Pair_5_48 Tor_41_A	0.002217	0.66	0.00148	0.000109	4.95E-06	2.41E-07
1ctf	2.00	−148.82	Pair_6_40 Tor_43_B SS_43_E	0.0000036a	-	-	0.000472	-	1.70E-09
1dcj	1.90	−139.93	Pair_4_33 Tor_8_G	0.013533	0.86	0.00108	0.000736	1.69E-05	9.96E-06
1di2	1.42	−144.45	Tor_23_A	0.023311	0.84	0.000609	0.000408	1.69E-05	9.52E-06
1dtj	1.58	−154.92	Tor_43_B	0.413734	0.98	0.000281	0.000293	1.18E-04	1.21E-04
1iib	1.74	−222.51	Pair_53_75	0.041423	1.00	0.000387	0.000130	1.60E-05	5.38E-06
1n0u	2.00	−135.64	Pair_4_41 Tor_29_A SS_29_L	0.000460	-	-	0.000252	-	1.16E-07
1opd	1.97	−172.79	Pair_5_62	0.006090	1.00	0.00166	0.000103	1.01E-05	6.29E-07
1pgx	0.95	−122.26	Tor_8_B Tor_39_B	0.043960	0.90	0.00309	0.00315	1.50E-04	1.38E-04
1tif	2.50	−119.48	Pair_5_44 Tor_25_E SS_25_E	0.0000080a	-	-	0.00230	-	1.84E-08
1ubi	2.32	−149.33	Pair_5_67 Tor_54_B	0.001092	0.41	0.00473	0.00198	1.26E-05	2.16E-06
2chf	2.59	−279.86	Tor_108_O	0.085884	0.90	0.000209	0.000195	1.99E-05	1.67E-05
2ci2	2.50	−127.62	Pair_28_46	0.003396	-	-	0.0000358	-	1.22E-07
2reb	0.84	−140.59	Tor_14_G	0.338975	1.00	0.000425	0.000968	1.81E-04	3.28E-04

^adue to small counts, the overall frequency was approximated using P(feature2,feature3|feature1)*P(feature1) where P(feature2,feature3|feature1) is the frequency of having both feature2 and feature3 in the feature 1 forced run, and P(feature1) is the frequency of feature1 in the control run.

^b“good” indicates low-energy low-RMSD models using the cutoffs in columns 2 and 3.

^-“good” models were not sampled in the control runs for 1bm8, 1ctf, 1n0u, 1tif, and 2ci2.

For each protein with identified linchpin features, the probability of generating a low-energy low-RMSD structure was estimated using P(native structure) = P(native linchpin features) * P(native structure | native linchpin features); P(native linchpin features) is the frequency of sampling the native values of the linchpin features in the unconstrained population and P(native structure | native linchpin features) is the frequency of sampling the native state when the linchpin features are constrained at their native values. The validity of this approximation can be assessed directly for the proteins for which the native structure was sampled in unbiased runs (category 1), since P(native structure) can be measured directly (it is simply the frequency of low-energy low-RMSD structures in the unbiased runs; Table 2 column 9). These directly observed values are compared to the values obtained using the above approximation in Table 2 (column 10 = column 5 * column 8). For the majority of proteins, the predicted value was reasonably consistent with the observed value--the observed probabilities of 8 out of 11 proteins were within a factor of 3 of the modeled values (as described in the Materials and Methods, discrepancies exist since P(native structure|feature) is somewhat underestimated in constrained runs due to artifacts introduced by the constraint).

As illustrated in Table 2, the increases in the frequency of sampling the native state when constraining a small number of linchpin features to their native values are often quite dramatic. For some cases, such as ribosomal protein l7/l12 (1ctf) and translation initiation factor IF3 (1tif), rare but critical native beta-contact, torsion, and secondary structure features were never simultaneously sampled in the control runs. The undetectably low frequency of sampling critical combinations of rare features was estimated in such cases by determining the frequency of one of the features and multiplying by the frequency of the other features in calculations where the first feature was constrained: P(feature 1 and feature 2) = P(feature 1) * P(feature 2 | feature 1). For 1ctf and 1tif the predicted frequencies of sampling the native linchpin features simultaneously were 0.0000036 and 0.0000080, respectively—in these cases the origin of the sampling bottleneck is clearly evident at the feature space level. For the two proteins, enforcing the linchpin features reduced the amount of sampling predicted to be necessary for a successful structure prediction by nearly 280,000 and 130,000 fold.

The P(native structure) estimates range widely for the different proteins in Table 2. At one extreme is recA (2reb), with an observed value of 0.000181, which corresponds to sampling the native state approximately 1 out of every 6000 unbiased runs. At the other extreme, for 1ctf and 1tif, the frequency of sampling the native state in unbiased runs is estimated to be 1.70×10⁻⁹ and 1.84×10⁻⁸, respectively. The corresponding estimates of the number of trajectories necessary for successful structure prediction for these two proteins are 588 million and 54 million, respectively. Clearly this result cannot be determined by brute force computation! The estimated P(native structure) provides an answer to the question of how much computer power is required to solve the structure of a given protein by de novo structure prediction, and in a sense provides a part of the solution to the prediction problem.

Structural Context of Linchpin Features

The estimated probabilities for successful predictions highlight the limitations of brute-force sampling using Rosetta—the amount of computing required may be considerably out of range of current capabilities. On the other hand, since linchpin features represent rare structural features that are important for sampling near-native conformations, understanding their structural context may help in the development of improved sampling methods. The structural context of the identified linchpin features for each protein is shown in Figure 6 (linchpin features are labeled with bold italicized text). Three general characteristics stand out and are described in detail below.

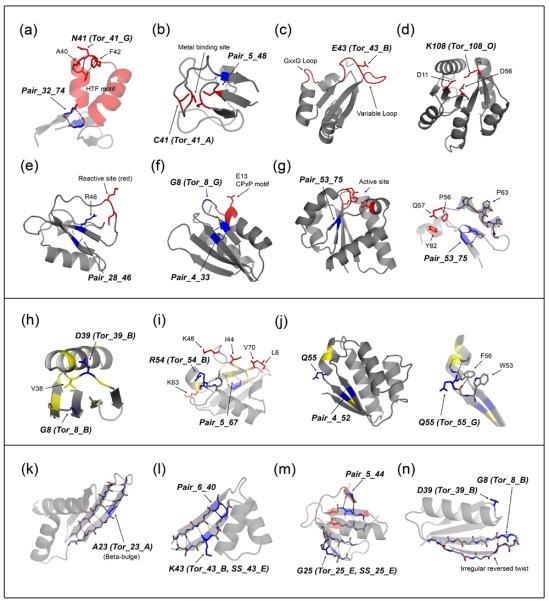
Figure 6. Structural context of linchpin features.

Functional regions (top panel): (a) residues 28-76 of 1bm8, (b) 1bq9, (c) 1dtj, (d) 2chf, (e) 2ci2, (f) 1dcj, and (g) 1iib (right: residues 50-85). Regions that form late in folding (middle panel): (h) 1pgx, (i) 1ubi, and (j) 1a19 (right: residues 2-7 and 50-62). Irregular beta-strands (bottom panel): (k) 1di2, (l) residues 1-47 of 1ctf, (m) 1tif, and (n) 1pgx. Linchpin positions are highlighted in blue and labeled in bold italicized text. Functional positions are highlighted in red, and positions with unambiguous low Φ-values (≤ 0.2) indicating regions that form late in folding are highlighted in yellow. Hydrogen bonds in linchpin regions are shown in black dotted lines and hydrogen bonds in irregular strands are shown in gray dotted lines. For a more detailed view, only the relevant part of the protein is shown in (a), (g; right), (j; right), and (l).

Functional regions (Figure 6, top panel)

Many linchpin features were found within or close to functional regions of the protein (highlighted in red in Figure 6). The proteins with linchpin features located within regions important for function include the DNA-binding domain of Mbp1 (1bm8), Rubredoxin (1bq9), the Nova-2 K-homology RNA-binding domain (1dtj), and CheY (2chf). In 1bm8, the positive phi torsion feature of N41 is located within the turn of a helix-turn-helix DNA binding motif⁷ (Figure 6a). N41 is involved in capping the first helix of the motif and makes the hydrophobic interaction between residues A40 and F42 possible. A beta-contact feature is also located at the termini of a conserved segment that contains the motif. In 1bq9, a torsion and beta-contact feature involve two of four cysteines that make up its metal-binding site (Figure 6b). The torsion feature of E43 in 1dtj is located within a variable loop that, along with a highly conserved GxxG loop motif, is part of a vise-like binding site for RNA⁸ (Figure 6c). The cis-peptide torsion feature of K108 in 2chf is located in a highly conserved position involved in the active site (Figure 6d). In chymotrypsin inhibitor 2 (2ci2; Figure 6e), YhhP (1dcj; Figure 6f), and IIBcellobiose (1iib; Figure 6g), functional residues are located in positions between paired parallel strands associated with short-range beta-contact linchpin features. A highly exposed loop that contains the reactive site⁹ in 2ci2 lies between the paired strands of the beta-contact feature, Pair_28_46, and the R46 side-chain of this feature interacts with the reactive site and may be functionally important (Figure 6e). In addition to the beta-contact feature in 1dcj, the positive phi torsion feature of G8 is also located near E13, which lies within a strictly conserved CPxP helix capping motif and is critical for function¹⁰ (Figure 6f). In 1iib, the paired strands of the beta-contact feature, Pair_53_75, bring together three strictly conserved residues suggested to be part of the active site, Q57, P56, and Y82¹¹ (Figure 6g, right). Functional residues were also located close to linchpin features in ubiquitin (1ubi; Figure 6i) and translation initiation factor IF3 (1tif; Figure 6m).

Regions that form late in folding (Figure 6, middle panel)

For proteins whose folding pathway and transition state have been experimentally characterized and whose transition state is structurally polarized with regions that are significantly formed and disrupted, linchpin features were found in regions of the protein that form late in folding: i.e. regions with low Φ-values. In protein G (1pgx), the lowest Φ-values are in the first beta turn and the loop connecting the helix with the second hairpin; these two regions are in contact in the three dimensional structure (Figure 1h yellow). The linchpin features G8 and D39 lie in the first beta turn and the connecting loop, respectively. The torsion angles of D39 position the adjacent residue V38 which packs on G8; taken together these data suggest the formation of the first beta hairpin and packing on the connecting loop occur late in protein G folding and are bottlenecks in Rosetta simulations. In ubiquitin (1ubi), the positions with the lowest Φ-values¹² (Figure 6i, highlighted in yellow) are located in the C-terminal region of the protein, which includes the linchpin residues R54 (Tor_54_B) and L67 (Pair_5_67). Both R54 and L67 are involved in important tertiary interactions; the backbone CO of R54 caps the N-terminal end of the major helix through non-local backbone hydrogen bonds, and the side-chain of L67 is part of the protein core. Positions with the lowest Φ-values in barstar¹³ (Figure 6j; 1a19, highlighted in yellow) flank two linchpin residues, Q55, which has a positive phi torsion feature and is involved in capping the third helix, and V4 from the beta-contact feature, Pair_4_52. The backbone conformation of Q55 is stabilized by a perpendicular aromatic interaction between residues W53 and F56, and backbone hydrogen bonds that are involved in adjacent secondary structure elements (Figure 6j, right). The tight transition between the strand and helix along with the positive phi torsion feature suggest that this part of the backbone may be under conformational strain. In CheY (2chf) the linchpin residue K108 is in the C-terminal portion of the protein that was found experimentally to form late in folding and where mobility may be important for function (Figure 6d, right half of protein)^{14; 15}.

Both in Rosetta trajectories and in reality, the regions described above likely do not form early in folding because they are energetically unfavorable in the absence of stabilizing non-local interactions. In Rosetta these interactions may not form later because they require a concerted “clicking in” which stochastic Monte Carlo moves may not hit upon; in this case the interactions would be missing in the final structures and would be detected as linchpin features by our analysis.

Irregular strands (Figure 6, bottom panel)

Linchpin features were identified within or adjacent to irregular strands in dsRNA binding domain (1di2), ribosomal protein l7/l12 (1ctf), translation initiation factor IF3 (1tif), and protein G (1pgx). In 1di2, there is a single beta-bulge in an otherwise regular beta-sheet and the torsion feature at the beta-bulge position was identified as a linchpin feature (Figure 6k). For 1ctf, a beta-contact feature (Pair_6_40) in combination with a torsion angle and secondary structure feature at K43 was identified as a linchpin feature. The three-stranded beta-sheet in 1ctf is highly irregular, particularly in the strands involved in Pair_6_40. Beta bulges exist in the first and second strands at K7 and L42, respectively, and hydrogen bonding is disrupted between the strands at the position following K43 (Figure 6l). For 1tif, a beta-contact feature (Pair_5_44) along with a torsion and secondary structure feature at G25 were identified as a linchpin feature (Figure 6m). A beta-bulge exists at the position adjacent to G25, and the corresponding edge strand contains a prominent bend. Pair_5_44 consists of a beta pairing between a very short edge strand that consists of only two backbone hydrogen bonds and an irregular strand that contains a beta-bulge. The edge strand in 1pgx has an irregular left-handed twist and convex curve near the torsion feature, Tor_8_B (Figure 6n). A common characteristic of the linchpin features described above is that the irregular local structures they lie in are primarily edge strands. Irregular edge strands are commonly found in proteins to avoid edge-to-edge aggregation¹⁶.

Discussion

Solving the de novo protein structure prediction problem requires repeated sampling of the native free energy basin in unbiased trajectories. In this paper we show that the number of trajectories required for such consistent sampling and hence the amount of computing time required for solving the structure prediction problem can be determined using a feature space representation of the sampling problem. In this feature space representation, the conformational search problem is transformed into a discrete combinatorial sampling problem. A difficult to predict protein may have several linchpin features which occur independently very rarely in unbiased trajectories, and occur simultaneously essentially never, but when simultaneously constrained reduce the sampling problem many orders of magnitude. If we assume independence between the features, we can estimate the probability of sampling them simultaneously (and hence succeeding in structure prediction) by simple multiplication of the individual probabilities. As shown in the 1ctf example in the text, we can improve on this approximation by directly determining the couplings between different features from constrained runs. The feature space approach provides a route to determining the amount of sampling required to compute the native structure and hence a specification of the solution of the protein structure prediction problem for a given protein; all that remains is to carry out the requisite number of independent trajectories. As shown for some proteins, the computing time required exceeds what is currently available, and therefore, their structures cannot currently be solved by de novo structure prediction using single sequence information.

It must be noted that our method for estimating the amount of computing necessary to accurately predict the structure of a protein requires knowledge of the native feature string and hence the native structure. To obtain estimates for a protein of unknown structure, the method can be used to determine the amount of computing necessary for proteins of known structure with similar length and predicted secondary structure content, and the results extrapolated to the protein of unknown structure. Indeed, the method developed in this paper can be applied to a wide range of proteins of known structure to determine how the compute time required for accurately predicting a structure depends on size and secondary structure class.

Our calculations show that enforcement of only a few critical linchpin features can drastically reduce the amount of sampling required for accurate high-resolution structure prediction. These linchpin features are almost never sampled in normal Rosetta trajectories. This suggests two approaches to attacking the sampling problem. First, the sampling rate of rare feature values could be systematically increased in unbiased runs. We have experimented with such a “feature diversification” approach, thus far without strongly encouraging results; the problem is that feature diversification inevitably reduces the frequency of sampling the native values of most features, which are reasonably high in standard Rosetta trajectories. Second, rather than increasing the sampling rate of all rare features, it may be possible to specifically increase the sampling rate of linchpin features provided they can in some way be identified without knowledge of the native structure. We have had some success with such an approach using the energies of structures with specific feature values to identify under-sampled native features—these tend to be associated with lower energies than non-native features (Blum, submitted). Beyond the de novo structure prediction context, experimental data may be available which can help identify critical features. Most notably, NMR chemical shift information can largely specify the native values for torsion and secondary structure features, and with this information accurate structures can consistently be generated with Rosetta for proteins up to 120 residues¹⁷.

As summarized in the results section, there is considerable anecdotal evidence that the linchpin features also present bottlenecks to the folding of real proteins. It is likely that these regions are bottlenecks to folding in both cases because they lie in regions under considerable local strain, or which are locally suboptimal. Local strain can contribute barriers to both folding and unfolding as partially (un)folded states will be relatively high in free energy. Linchpin features may contribute to native state rigidity and the cooperativity of folding, in a manner analogous to the contortions necessary for the final step in assembling 3-D interlocking puzzles. Rosetta may have difficulty sampling these by stochastic Monte Carlo moves unlikely to hit upon exactly the right motion.

Natural selection can also favor locally suboptimal regions to reduce misfolding and improve function. We frequently observe linchpin features in highly irregular edge beta-strands which may reflect selective pressure against association of monomers into aggregates^{16; 18}. Consistent with numerous observations of unfavorable local interactions and strain at enzyme active sites, we frequently observe linchpin regions in functional regions in proteins.

There are many clear differences between a Rosetta folding simulation and the folding of real proteins. Nevertheless, the correspondence between bottlenecks to folding in silico and in actuality suggests that Rosetta folding trajectories may recapitulate some aspects of actual protein folding.

Materials and Methods

Test Set and Model Generation

Our test set consists of 32 small protein domains with all-alpha and alpha-beta topologies ranging in size from 49 to 128 residues; the PDB codes of these proteins are listed in Table 1. The proteins were chosen from a larger in-house benchmark set using the criteria that models within 4 Å RMSD to the native structure were attainable using Rosetta's fragment replacement search method. Since all-beta and larger protein domains with complex topologies are sampled rarely without broken chain fold-trees (described below)¹⁹, they were not considered in this study.

All models were generated using the distributed computing network, Rosetta@home, and each model was produced from an independent trajectory using a unique random seed and starting from an extended chain conformation. For each trajectory, the standard Rosetta fragment insertion method was used followed by full-atom refinement^{20; 21; 22; 23; 24}. Fragments from homologs (PSI-BLAST e-value < 0.05 or same SCOP superfamily) were excluded from the fragment libraries. Refined natives were generated using the full-atom refinement protocol starting from an idealized native conformation.

Discrete structural features

Three structural features were used in this study: torsion angle, secondary structure, and beta-contact features. These features consist of discrete values that can be enforced through the course of fragment replacement trials. Native feature values were determined from the structures of refined natives. Torsion angle and beta-contact features are described below; see also ref 25.

Torsion angle and secondary structure features

Torsion angle features (A, B, E, G, and O; Figure 1) are defined by distinct regions of the Ramachandran plot that are frequently populated in protien structures (O represents cis-peptide torsion angles). Secondary structure features are designated as either helix (H), strand (E), or loop (L) as assigned by DSSP²⁶. Both feature types were enforced through the course of a simulation by limiting fragments to only those that contained the feature in the position being constrained. These per-residue features are local in structure but may be influenced by non-local interactions.

Beta-contact features

Beta-contact features represent residue pairs that have two backbone hydrogen bonds with each other and are designated using the DSSP definition of beta pairing ²⁶. A beta-contact pair has two additional properties that specify the pleating orientation and whether the strand orientation is parallel or antiparallel. Thus, a beta-contact feature is defined for every triple (i, j, o) where i and j are the residue pair numbers and o is the parallel or antiparallel orientation, and its possible values are X, P1, or P2, indicating no pairing and the two possible pleating orientations, respectively. The pleating orientation specifies whether the NH or CO groups of the first residue point toward or way from the second residue. For simplicity, parallel or antiparallel and pleating orientation values are omitted throughout the text. Beta-contact features are enforced in Rosetta by representing the protein chain using a non-linear fold-tree, a connected acyclic graph composed of peptide segments and pseudo-backbone bonds between residue pairs that can be constrained to represent specific beta-contact features¹⁹. For every new pseudo-bond edge added to the graph, a peptide bond edge has to be removed, creating a chain-break. This is required to maintain an acyclic graph necessary for generating three-dimensional coordinates from the backbone torsion angles. Following a conformational search through fragment replacement using this graph representation of the protein backbone, chain-breaks may exist and are subsequently closed using the standard Rosetta loop modeling protocol that involves loop closure by cyclic coordinate descent^{2; 27}.

Linchpin feature identification

Native features that were enriched in low-RMSD models were identified from the control runs as probable linchpin features by comparing their frequency in the 200 lowest-RMSD models with their frequency in 200 random models. If the native feature was enriched in the lowest-RMSD models by at least 1.5 fold or was present in less than half of the lowest-RMSD and random models, the feature was considered as a potential linchpin feature and was enforced in a successive round of conformational sampling. For torsion bin features, if the PSIPRED²⁸ secondary structure prediction was incorrect at the position being enforced, the native secondary structure feature was also enforced. If low-energy low-RMSD models were not sampled in the enforced round, additional features were identified from the enforced sample set and were each enforced with the previously enforced features in another round of sampling. This process of identifying potential linchpin features after each round of sampling and then enforcing them individually with the previously enforced features in subsequent rounds continued until a minimal set of features that were associated with low-energy low-RMSD models were identified. The cutoffs used to define low-energy low-RMSD models are listed in the second and third columns of Table 2. The energy value of the 0.5 percentile lowest-energy model from the control run was used as the low-energy cutoff. The low-RMSD cutoff was determined by the RMSD of the 50^th lowest-RMSD model from the control run whose energy was below the low-energy cutoff. In cases where near native conformations were generated very rarely, the low-RMSD cutoff was manually chosen. These include 1bm8 (3.50), 1ctf (2.0), 1n0u (2.0), 1tif (2.50), and 2ci2 (2.50).

Estimating sampling requirements

Using Bayes' theorem, the probability of generating a low-energy low-RMSD structure, P(native structure), can be expressed as the frequency of models with linchpin features, P(linchpin features), multiplied by the frequency of close to native models when the linchpin features are enforced, P(native structure|linchpin features), divided by P(linchpin features|native structure), the frequency of native linchpin feature values in native structures:

$$\mathrm{P}\left(\text{native structure}\right)=\frac{\mathrm{P}\left(\text{linchpin features}\right)\mathrm{P}(\text{native structure}\mid \text{linchpin features})}{\mathrm{P}(\text{linchpin features}\mid \text{native structure})}$$

The term in the denominator is very close to 1.0, and thus we approximate P(native structure) in this paper as the product of the two terms in the numerator (for simplicity, the term in the denominator is not included in the expressions for P(native structure) in the main text). The reciprocal of P(native structure) provides an estimate of the amount of sampling necessary for a successful prediction.

For each protein, columns 7 and 8 in Table 2 list the probability of generating a low-energy low-RMSD model given that the linchpin features are present in the control and enforced runs, respectively. For many proteins, P(native structure|linchpin features) from the control run corresponds reasonably well with the probability calculated from the enforced run. However, there was a general trend of lower probabilities from the enforced runs compared to the values obtained from the control runs; control run models with linchpin features were more likely to be successful compared to models from the enforced runs for the majority of proteins. This was particularly true for proteins whose linchpin feature included a beta-contact feature and may be attributed to an unfavorable bias in the protocol used for forcing beta-contact features. The proteins with the largest discrepancies, 1bq9 and 1opd, provide good examples. Both proteins had a long-range beta-contact feature involving N and C-terminal strands, and in the original population generated using a continuous chain representation the subset of models with the beta-contact feature present, had a significantly higher fraction of close to native models compared to the population generated by forcing the beta-contact feature using a broken fold-tree. As described above, enforcing a beta-contact feature requires a break in the intervening chain in order to maintain an acyclic graph representation of the backbone required for fragment replacement trials. The chain break may disrupt local interactions important for guiding folding and reduce the frequency of generating close to native structures. Despite this problem, the majority of estimated probabilities were in reasonable agreement with the observed probabilities.