Effects of Refocusing Flip Angle Modulation and View Ordering in 3D Fast Spin Echo

Abstract

Recent advances have reduced scan time in three-dimensional fast spin echo (3D-FSE) imaging, including very long echo trains through refocusing flip angle (FA) modulation and 2D-accelerated parallel imaging. This work describes a method to modulate refocusing FAs that produces sharp point spread functions (PSFs) from very long echo trains while exercising direct control over minimum, center-k-space, and maximum FAs in order to accommodate the presence of flow and motion, SNR requirements, and RF power limits. Additionally, a new method for ordering views to map signal modulation from the echo train into k_y-k_z space that enables nonrectangular k-space grids and autocalibrating 2D-accelerated parallel imaging is presented. With long echo trains and fewer echoes required to encode large matrices, large volumes with high in- and through-plane resolution matrices may be acquired with scan times of 3–6 min, as demonstrated for volumetric brain, knee, and kidney imaging.

Fast spin echo (FSE, also known as rapid acquisition with relaxation enhancement [RARE] (1) and turbo spin echo [TSE]) plays a central role in clinical MRI. Acquisition of multiple echoes per excitation improves efficiency, reducing scan time or allowing increased resolution in a fixed scan time. A limitation of the technique, however, is that T₂ decay produces signal modulation in k-space that typically manifests as blurring or ringing artifacts, depending on view ordering, and in particular, on when the center of k-space is sampled with respect to other spatial frequencies (2,3).

Several techniques have been presented that affect signal modulation by varying the flip angles (FAs) of the refocusing RF pulses through the train. By modulating the FAs of the initial refocusing RF pulses, a static pseudo-steady state (PSS) may be established that exhibits relatively high signal even for low refocusing FAs (4,5). After establishing PSS conditions, the FAs may be continuously varied, for instance to reduce RF power (6–8).

In another approach, signal levels in a material with specific relaxation properties are considered, and the refocusing FAs that yield a given set of targeted signal levels at each echo in the train are calculated (9–11). These “relaxation-specific” algorithms have been demonstrated for three-dimensional (3D)-FSE imaging, producing relatively steady signal levels over very long echo trains in the given material with a train of refocusing FAs that initially decreases rapidly, as PSS conditions are established, and then gradually increases thereafter (10,11). This can be understood to work well for two complementary reasons: First, low refocusing FAs at the beginning of the train serve to slow the effective rate of T₂ relaxation (5). In a low-angle PSS, magnetization contains longitudinal and transverse components. These components can be modeled as “partitions” that are repeatedly “mixed” with each successive RF pulse (12). For most biological tissues, T₁ > T₂; thus when magnetization spends some considerable fraction of time in longitudinal partitions, the effective (observed) T₂ rate is lower (6). Second, as the FA is gradually increased, the “reserve” of longitudinal magnetization is transformed back into transverse magnetization, where it contributes to signal generation. Although they were developed independently, the relaxation-specific algorithms produce the same effect that is explicitly intended in the transitions between pseudo steady states (TRAPS) (6) method: echoes that become more fully refocused as the pulse train evolves. (In the case of TRAPS, maximum coherence is designed to coincide with the sampling of the center of k-space, whereas for the relaxation-specific approaches, maximum coherence typically occurs at the end of the echo train.)

For the relaxation-specific approaches, “target” signal levels are defined for each echo in the readout, then FAs are calculated that produce these signals in a material with some given T₁ and T₂ values. If the targets cannot be met, they are iteratively adjusted (either offline or by an automatic algorithm) until they are realizable with a sequence of refocusing FAs (10,11). Prescription parameters, such as the echo train length (ETL), echo spacing, and assumed T₁ and T₂ values, strongly affect the sequence of FAs. A limitation of this approach is that, since the refocusing FAs are not explicitly defined, other effects that may be dependent on these angles are uncontrolled. For instance, the FA in the center of k-space affects image SNR (6), FAs prior to sampling the center of k-space affect the effective TE (11,13), and the minimum FA affects flow and motion sensitivity (14,15).

While the signal for one particular material may be tailored, the signal of other materials deviates from this ideal curve. Nevertheless, clinical experience (16,17) and theoretical analysis (11) have demonstrated that sharp point spread functions (PSFs) may be produced in a variety of materials, not just the modeled one.

This observation led to our first hypothesis that a more flexible and direct method for generating the sequence of refocusing FAs could be devised that, like the TRAPS method, would provide explicit control of the minimum, maximum, and center of k-space FAs, while, like relaxation-specific methods, producing sharp PSFs for very long echo train readouts. Such a technique would facilitate the application of modulated refocusing FA FSE to a wider range of clinical imaging tasks and sequence parameters.

Even with a highly optimized sequence of refocusing FAs, some signal modulation will persist, given the range of relaxation rates that exist within the volume to be clinically imaged. When signal modulation is present, view ordering can strongly influence image quality. For 3D-FSE acquisitions, views are conventionally ordered such that a k_x-k_y or k_x-k_z plane is acquired in an integer number of echo trains (18). This produces smooth signal modulation over 3D k-space. For very long echo trains, an entire plane or even multiple planes may be encoded per shot, and methods have been developed to increase the flexibility of defining an ETL by designating separate “turbo factors” for k_y and k_z (19). Previous methods, however, were designed to sample a k-space grid that is regular and rectangular; there are several cases in which a more flexible sampling pattern would be useful to gain efficiency. For steady-state sequences (e.g., spoiled gradient-recalled echo sequence [SPGR] and steady-state free precession [SSFP]), it has been demonstrated that the corners of k_y-k_z space need not be sampled, cutting scan time by 22% without affecting resolution (20). Additionally, for autocalibrating 2D-accelerated parallel imaging (21,22), a nonseparable autocalibration region is ideally acquired such that only the center of k_y-k_z space is more densely sampled, with full acceleration in the outer portions of k-space. It is not possible to take advantage of the efficiency gains of these techniques with 3D-FSE view-ordering methods that have thus far been described in the literature.

This limitation led to our second hypothesis that a more flexible view-ordering method could be designed that would 1) allow the increased sampling efficiency afforded by elliptical k-space coverage and a nonseparable 2D autocalibration region, 2) enable ETLs to be controlled independently of matrix size, and 3) map signal modulation into k-space in such a way as to limit image artifacts.

In this work, we present an FA modulation technique for very long echo trains with explicit control over the minimum, center-k-space, and maximum FAs. Numerical simulations are performed to demonstrate the effect of motion on modulated FA sequences, and the utility of controlling the minimum FA. We also present a new view-ordering strategy for 3D-FSE to improve flexibility and efficiency. A PSF analysis is performed to demonstrate how signal modulation due to the combined effects of FA variation and relaxation is mapped into k-space and affects resolution in a variety of materials. Finally, these techniques are demonstrated for human imaging of the brain, knee, and kidney at 3T with scan times of 3–6 min.

MATERIALS AND METHODS

Refocusing FA Modulation Technique

Two alternative methods are considered that enable explicit control of the refocusing FAs while taking advantage of the extended echo trains afforded by relaxation-specific approaches. For both methods, a common set of input parameters is specified: refocusing FAs α_min, α_cent, and α_max; the echo number for the center of k-space n_cent; and the ETL.

The first alternative is an adaptation of Hennig’s prescribed echo envelope technique in which FAs are calculated based on the desired static PSS signal level (transverse coherence) at each echo (7). Rather than reaching peak coherence at the center of k-space (the TRAPS principle), here the PSS coherence is designed to increase throughout the train, reaching its peak at the end when the FA arrives at α_max. At the control points, the signal targets are set according to the input refocusing FAs α_min, α_cent, and α_max:

$$\begin{array}{c}{\mathrm{s}}_{\text{first}}={\text{sin}}^2({\mathrm{\alpha }}_{\text{max}}/2)\\ {\mathrm{s}}_{\text{min}}={\mathrm{s}}_{\text{spss}}({\mathrm{\alpha }}_{\text{min}})\\ {\mathrm{s}}_{\text{cent}}={\mathrm{s}}_{\text{spss}}({\mathrm{\alpha }}_{\text{cent}})\\ {\mathrm{s}}_{\text{max}}={\mathrm{s}}_{\text{spss}}({\mathrm{\alpha }}_{\text{max}})\end{array}$$ [1]

where s_spss is the static PSS signal level (5):

$${\mathrm{s}}_{\text{spss}}(\mathrm{\alpha })={\left(\text{sin}\frac{\mathrm{\alpha }}{2}\right)}^{1/2}{\mathrm{P}}_{-1/2}\left[\text{sin}\frac{\mathrm{\alpha }}{2}\left(1+\frac{{\text{sin}}^2\mathrm{\alpha }}{8{\text{sin}}^4\frac{\mathrm{\alpha }}{2}}\right)\right]$$ [2]

and P is a Legendre polynomial. Between these control points, a smooth function interpolates between these defined signals, according to

$$\mathrm{s}={\mathrm{s}}_0+\mathrm{\Delta }\mathrm{s}{\left(\frac{\mathrm{n}}{\mathrm{N}}\right)}^{\mathrm{p}}.$$ [3]

where p = 1.5 for the segment prior to the center of k-space, and p = 1 thereafter.

To transition into the static PSS for α_min, an asymptotic approach from s_first to s_min (11) is applied. Once the PSS-signal targets are defined, the extended phase graph (EPG) algorithm is used to determine the refocusing FAs.

The second alternative is a modification to Mugler’s relaxation-specific technique (10). Rather than iteratively determining a signal level that can be maintained (after an initial short exponential ramp down) at a constant level for the first half of the train and thereafter decreasing exponentially, here three exponential constants are iteratively determined to create a target signal profile that results in the specified FAs at four fixed points in the train: α_max at echo = 1, α_min at echo = 6, α_cent at echo = n_cent, and α_max again at echo = ETL.

Figure 1 compares these two alternatives. While both calculate FAs based on a sequence of target signals (a), the relaxation-specific method targets net signal—a combination of transverse coherence and relaxation—while the prescribed echo envelope method targets PSS signal—transverse coherence only, with relaxation ignored. The two alternatives, however, produce FA trains that are very similar (b), and consequently signal modulation that is nearly identical for a variety of relaxation values (c). Because the PSS-signal-envelope alternative is simpler and more direct, this approach was chosen for the simulations and experiments described hereafter.

FIG. 1.

Two methods for producing refocusing FA trains with explicit control of α_min, α_cent, and α_max. a: For the PSS-signal-envelope method (solid) targets are defined for the PSS signal level (transverse coherence), which increases throughout the train, while for the relaxation-specific method (dashed) targets are for the net signal, which includes relaxation as well as transverse coherence. b: Refocusing FAs that produce these targets are calculated, either ignoring relaxation with the PSS-signal-envelope method (solid), or given a set of T₁ and T₂ relaxation values with the relaxation-specific method (dashed). The two methods produce similar results given the same α_min, α_cent, and α_max values. c: The actual signals in materials with various T₁ and T₂ values are nearly identical for the two methods. Model parameters: α_min = 25°, α_cent = 70°, α_max = 120°, ETL = 100 +6 unacquired echoes at the start, echo spacing = 5 ms; relaxation-specific method: T₁ = 1000 ms, T₂ = 100 ms.

View-Ordering Technique

View ordering serves to map signal modulation that occurs through the echo train into k_y-k_z-space. First, consider which views are to be sampled. Figure 2 illustrates two possible grids for 2D acceleration with autocalibration. Figure 2a shows a grid that is separable in the k_y- and k_z-directions. Such a sampling pattern would be possible to sample with previously reported 3D-FSE view-ordering methods (2D acceleration with 3D-FSE was demonstrated in Ref. 23). Figure 2b is a nonseparable grid that contains one-third fewer views, and thus can potentially reduce scan time by the same amount. Compared to a full-Fourier rectangular matrix with no acceleration, the number of views is decreased by four-fifths (80%), and with half-Fourier by eight-ninths (~89%).

FIG. 2.

a: A separable sampling grid for 2D acceleration with autocalibration is compatible with previously described 3D-FSE view ordering techniques. b: A more efficient approach, however, is to acquire views on a nonseparable grid, which requires approximately one-third less scan time but requires a more advanced view-ordering method, such as that proposed.

The technique begins with a list of the k-space positions for all of the views to be acquired, the total number of views, N_views, and the user-input ETL. From this, the number of trains is calculated:

$${\mathrm{N}}_{\text{trains}}=\text{ceiling}({\mathrm{N}}_{\text{views}}/\text{ETL})$$ [4]

where the ceiling function rounds up to the nearest integer.

Since the number of trains (which is multiplied by TR to calculate scan time) is determined by the total number of views, rather than the number of views in a row or column of the matrix, the rounding inefficiency (which manifests as un-encoded echoes at the end of some trains) is less than TR/T_scan which is typically on the order of 1% to 2%.

Next, consider how signal modulation—the combined effect of relaxation and refocusing FA modulation—is mapped into this k-space grid via the view-ordering technique. Two variations of the view-ordering method are considered: linear and radial modulation. Both techniques involve sorting the views into trains and echoes based on their position in k-space in order to assure that signal modulation is smooth and that successive echoes sample k-space locations that are in close proximity to each other.

For the linear-modulation view ordering, a direction of modulation is chosen (e.g., k_y) and views are sorted first by their position along this direction. An echo number is assigned to each view (the first N_trains views in the k_y-sorted list are assigned to echo 1, the next N_trains views to echo 2, etc.). Figure 3a shows the views with echo number designated by the color incremented through the spectrum. Because similar colors may not be distinguishable in the figure, echoes 1, 15, and 45 are emphasized with black circles. Next, for the group of views assigned to a given echo number, views are sorted by the orthogonal phase-encode direction (e.g., k_z) and a train number is assigned to each view within the group. Figure 3b shows the views with the train number designated by color incremented through the spectrum. Trains 1, 6, 16, and 26 are emphasized with black circles, and connecting lines indicate the order of acquisition within each of these trains.

FIG. 3.

The proposed view-ordering algorithm can direct signal modulation along a given direction in k_y-k_z-space. a: For signal modulation directed along the k_y direction, views are sorted first by k_y location and assigned echo numbers based on this value —echo numbers are depicted by colors incremented through the spectrum with echoes 1, 15, and 45 circled. b: Next, all views of a given echo number are sorted by k_z location and assigned train numbers based on this value—train numbers are depicted by colors incremented through the spectrum with trains 1, 6, 16, and 26 circled, and connecting lines showing view order within these trains. c: Likewise, for signal modulation directed along the k_r direction, views are sorted first by k_r and assigned echo numbers, then by k_θ and assigned train numbers (d).

For radial signal modulation the process is similar, but views are sorted by radius and then angle. Figure 3c and d show radial signal modulation for a 60%-k_y partial Fourier acquisition. Note that for purposes of illustration, the size of the grid (100 × 80), ETL (60 for linear and 40 for radial), and number of trains (31 for linear, 32 for radial) depicted in Fig. 3 are smaller than would typically be used in practice.

This basic algorithm required two augmentations to make it robust for a wide variety of parameters. First, a small amount of quasi-random positional “jitter” was added to each view’s k-space position for the purposes of sorting. (No jitter was present when actually executing the sequence). These sub-grid-spacing shifts served to disrupt the regularity of the grid and produced better interleaving between trains, and ultimately smoother signal modulation. Second, a consolidation step was added to reduce the step size in k-space from echo to echo. Views within a small range of k_y (or k_r—the first sort direction) were resorted by k_z (or k_θ—the second sort direction) and a final sort by k_y (or k_r) was performed within each train.

The choice of linear (k_y or k_z) or radial (k_r) modulation depends on the desired contrast. Linear modulation lends itself well to providing T₂-weighted contrast, since the center of k-space is sampled halfway through the echo train (assuming a symmetric-Fourier “full-NEX (number of excitations)” or a partial k_y “half-NEX” with k_z signal modulation.) Radial modulation lends itself well to minimizing T₂-weighted contrast (e.g., T₁- or proton density (PD)-weighted), since the center of k-space is sampled at the beginning of the train. Other variations may be readily envisioned, but here two will be considered: 1) a full-NEX acquisition with k_y signal modulation, and 2) a half-NEX acquisition with k_r signal modulation.

Numerical Modeling Experiments

Numerical modeling experiments were conducted to study the effects of FA modulation and view ordering on scan time, motion sensitivity, and resolution.

To determine the impact of varying the minimum refocusing FA, FA trains were generated for α_min ranging from 15–65°, while α_cent and α_max were held fixed at 70° and 120°, respectively. ETL was adjusted to maintain a consistent TE_eff (defined according to Ref. 11) of 90 ms, assuming an echo spacing of 5 ms. For each train, signal was modeled in materials with {T₁, T₂} values of {1800 ms, 150 ms}, {1000 ms, 100 ms}, and {700 ms, 60 ms}. PSFs were calculated by performing an FFT on the signal modulation profile. (This assumes linear view ordering in a single k-space direction; the more sophisticated view ordering is addressed below.) The effect of motion on signal was also analyzed, with velocity ranging from 0 to 12 mm/s, based on a model described in the Appendix.

The effects of signal modulation in conjunction with view ordering were modeled and analyzed in terms of the 2D modulation transfer functions (MTFs) and 2D PSFs of materials with various {T₁, T₂} values. The model considered a 300 × 200 elliptically circumscribed k_y-k_z matrix with a 32-point diameter autocalibration region and 2 × 2 acceleration outside of this region. Two cases were considered: a full-Fourier matrix with linear-modulation view ordering (N_views = 12392, ETL = 100, N_trains = 124) and a half-Fourier matrix with radial-modulation view ordering (N_views = 7031, ETL = 50, N_trains = 141). Refocusing FAs were calculated given α_min = 25°, α_cent = 70° and α_max = 120° for linear modulation, and α_min = α_cent = 50° and α_max = 120° for radial modulation. Signal was calculated for materials with {T₁, T₂} values of {1800, 150}, {1000, 100}, and {700, 60} (in ms) and echo spacing of 5 ms. These signals were mapped into k-space and missing points due to parallel imaging acceleration and partial-Fourier acquisition were synthesized. The synthesis assumed that the parallel imaging technique effectively produced a smooth interpolation of the slowly varying signal modulation to unsampled points, and that the half-Fourier reconstruction reflected signal modulation across the origin into the unsampled portion of k-space. Zero-padding and elliptical apodization were performed prior to 2D-FFT to calculate the 2D-PSF.

Human Imaging Studies

The FA modulation and view-ordering techniques were implemented for a 3D-FSE pulse sequence. The sequence allowed direct control of the ETL, α_min, α_cent, and α_max while the host computer immediately displayed the resulting TE_eff (corrected for changes to the effective T₂ relaxation rate due to low refocusing FAs (11)), relative SNR (which includes the PSS signal level at the center of k-space) and scan time.

Human imaging experiments were performed on a GE Signa Excite HDx 3.0T scanner using eight-channel brain, knee, and cardiac array coils. Informed consent was obtained for all volunteers. Four protocols were designed: T₂-weighted whole-brain imaging, T₂ fluid-attenuated inversion recovery (T₂-FLAIR) whole-brain imaging, PD-weighted whole-knee imaging, and T₂-weighted volumetric kidney imaging. Acquisition and reconstruction parameters are listed in Table 1.

Table 1.

Acquisition Parameters for Human Imaging Studies

	T2w brain	T2-FLAIR brain	PD-knee	T2-kidney
TR (ms)	2000a	6200	2000	3500b
TEeff (ms)	90	130	18	120
Echo spacing (ms)	5.5	5.5	5.5	4.7
ETL	96	180	45	96
FOV (cm3)	25 × 21.3 × 15.4	25 × 21.3 × 15.4	15 × 15 × 14	32 × 32 × 17.9
NEX	1	1	0.53	1
Receive bandwidth (kHz)	±83.3	±50	±50	±83.3
Acquisition matrix	320 × 272 × 192	256 × 218 × 128	256 × 256 × 200	320 × 320 × 128
Reconstruction matrix	512 × 436 × 192	512 × 436 × 256	512 × 512 × 200	512 × 512 × 256
Acquisition voxel (mm3)	0.8 × 0.8 × 0.8	1.0 × 1.0 × 1.2	0.6 × 0.6 × 0.7	1.0 × 1.0 × 1.4
Reconstruction voxel (mm3)	0.5 × 0.5 × 0.8	0.5 × 0.5 × 0.6	0.3 × 0.3 × 0.7	0.6 × 0.6 × 0.7
Reformat slice thickness (mm)	1.5	3.0	1.0	2.5
αmin (°)	25	20	50	45
αcent (°)	70	70	50	70
αmax (°)	120	120	120	120
Acceleration	3.7	2.9	3.7	3.7
Fat suppression	Yes	Yes	Yes	Yes
View order	ky-Modulation	ky-Modulation	kr-Modulation	ky-Modulation
Flow compensation	Frequency (S/I)	None	None	None
Gating	Cardiaca	None	None	Respiratoryb
Scan time	3 min 49 s	4 min 30 s	4 min 25 s	5 min 19 s

^aTR = 2 × cardiac period.

^bTR = 1 × respiratory period.

Parallel imaging reconstruction was performed with autocalibrating reconstruction for Cartesian sampling (ARC), a data-driven autocalibrating 2D parallel imaging technique that uses a 3D calibration kernel (22) combined with hybrid-space synthesis (24) to efficiently fill in missing data in a 2D-accelerated volumetric acquisition. ARC reconstruction was executed automatically on the standard commercial reconstruction hardware to produce all images in less than 30 s per scan.

After reconstruction, three sets of reformats in the principal orthogonal planes (axial, sagittal, and coronal) were created from each volume using the scanner’s standard reformat tool.

RESULTS

Figure 4 shows several effects of varying the minimum refocusing FA when ETL is adjusted to maintain a consistent TE_eff for a T₂-weighted acquisition. Refocusing FA trains for α_min of 20°, 30°, and 40° (a) resulted in different signal modulation (b), but because the center of k-space was sampled halfway through the train, they produced very similar normalized PSFs (c). Increasing α_min required ETL to be decreased to maintain a given TE_eff resulting in longer scan times (d), but signal loss due to motion was also significantly reduced (e). The PSF full width at half maximum (FWHM) was found to be insensitive to α_min (f) when ETL was adjusted to maintain TE_eff. In studies with other parameters (not presented), the specific curves did vary with the model parameters, but the same trends were observed.

FIG. 4.

Several effects of changing the minimum refocusing FA, α_min, are demonstrated: (a) FA trains for α_min of 20°, 30°, and 40° (with ETL adjusted to maintain a given desired TE_eff = 90 ms) produce (b) different signal modulation curves in a material with T₁ = 1000 and T₂ = 100 ms; however, the (c) normalized PSFs are very similar. As a function of α_min, (d) ETL is decreased as α_min is increased in order to maintain the same TE_eff, making scans longer, but (e) signal loss due to motion also decreases as α_min is increased. Resolution (FWHM of the PSF) is relatively insensitive to α_min given a TE_eff-adjusted ETL. Model parameters: α_cent = 70°, α_max = 120°, echo spacing = 5 ms.

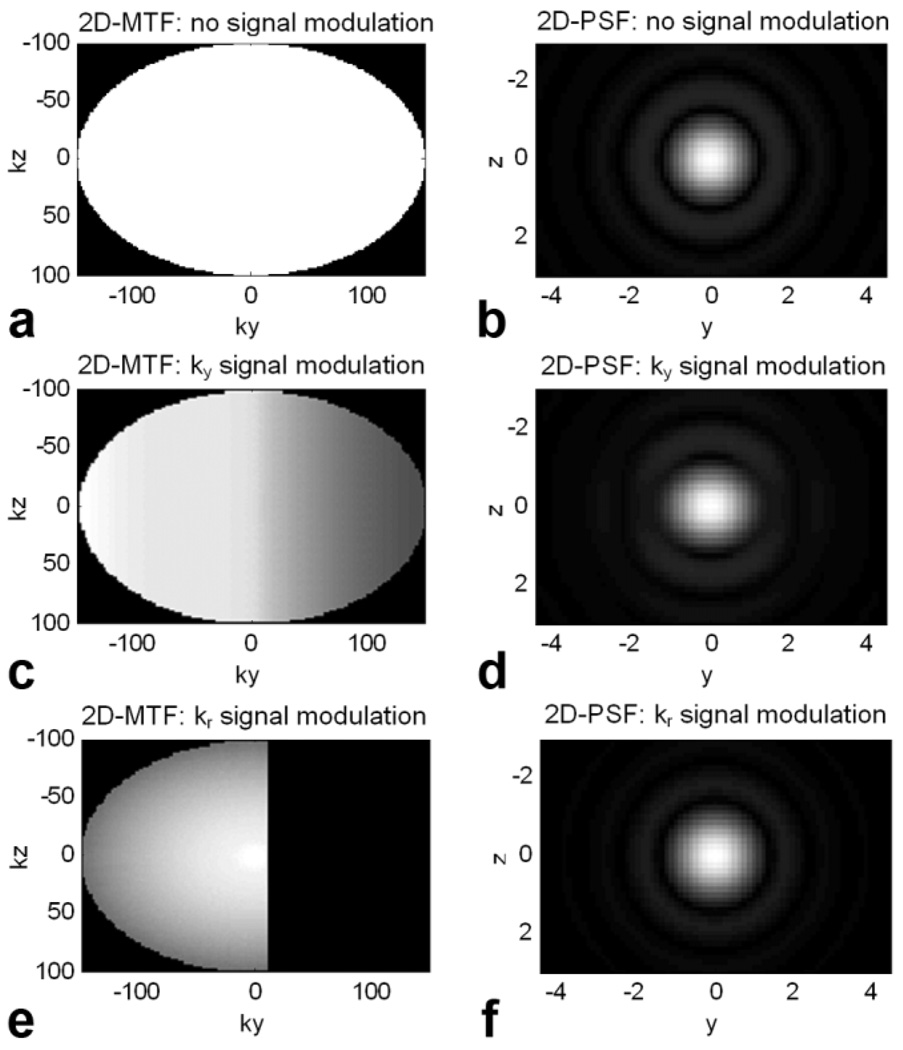
Figure 5 shows the view-order mapping of signal modulation into k_y-k_z-space and its effect on the 2D-PSF. For an ideal (baseline) case with no signal modulation (a), the PSF is flat (b). For a material with T₁ = 1000 ms and T₂ = 100 ms, view ordering that mapped signal modulation linearly into k-space (c) produced a PSF that was slightly increased in the y direction (d). View ordering that mapped signal modulation radially into k-space (e) produced a PSF that was slightly broadened equally in the y and z directions (f).

FIG. 5.

Signal modulation that results from the combined effect of relaxation and FA modulation is mapped into k-space via the specific view order employed. In an ideal situation, (a) no signal modulation would occur, resulting in (b) an optimal PSF. If view order is such that (c) signal modulation occurs in the k_y-direction, then (d) the PSF is broadened slightly in the y direction. If view ordering produces (e) radial signal modulation, then (f) the PSF is broadened slightly in both directions. Model parameters: α_min = 25°, α_cent = 70°, α_max = 120°, ETL = 100 +4 unacquired echoes at the start, echo spacing = 5 ms, T₁ = 1000 ms, T₂ = 100 ms.

Figure 6 presents cross sections through the 2D-PSFs in the y and z directions for materials with various T₁ and T₂ values. For view ordering that produced k_y signal modulation, a modest amount of point spread increase occurred with decreasing {T₁,T₂} values in the y direction (a), but no increase in the z direction (b). For view ordering that produced k_r signal modulation, the PSF increase was evenly distributed to the y (c) and z (d) directions. For k_y modulation, no FWHM increase occurred in the z direction, and an increase of 7%, 12%, and 23% occurred for {T₁, T₂} values of {1800 ms, 150 ms}, {1000 ms, 100 ms}, and {700 ms, 60 ms} respectively. For k_r modulation, FWHM increase occurred equally in y and z with 4%, 8%, and 15% for the same materials.

FIG. 6.

Profiles of the 2D PSF along the y- and z-axes for {T₁, T₂} values of {1800, 150} (solid black line), {1000, 100} (dashed black line), and {700, 60} ms (dotted black line) and an optimal PSF corresponding to no signal modulation (gray line). For view ordering that produces k_y signal modulation, (a) a small amount of point spread increase occurs with decreasing {T₁, T₂} values in the y direction, but (b) no increase in the z direction. For view ordering that produces k_r signal modulation, a small amount of PSF increase is evenly distributed to (c) y and (d) z directions.

Figure 7 shows T₂-weighted and FLAIR-T₂-weighted whole-brain images of a volunteer. The near-isotropic resolution allowed coronal and axial reformats to have comparable sharpness to the native sagittal acquisition. Since the slice thickness of the reformats was independent of the acquisition voxel size, the small voxels provided high in-plane resolution in all orientations, while averaging in the slice direction provided increased SNR.

FIG. 7.

Whole-brain imaging. a: A T₂-weighted image volume is acquired with a 320 × 272 × 192 matrix (0.8 mm superior/inferior [S/I] (frequency) × 0.8 mm anterior/posterior [A/P] (phase) × 0.8 mm right/left [R/L] (slice) acquired voxel size) in 3:49. b: A T₂w-FLAIR image volume with a matrix of 256 × 218 × 128 matrix (1.0 mm × 1.0 mm × 1.2 mm acquired voxel size) is acquired in 4:30. Very thin slice acquisitions enable high-resolution coronal and axial reformats, very similar in quality to the native sagittal acquisitions.

Figure 8 shows PD-weighted whole-knee images of a volunteer. The centric view ordering allowed short TEs, while FA modulation constrained blurring.

FIG. 8.

PD-weighted whole-knee imaging. Radial modulation view ordering produces PD-weighted contrast. A 256 × 256 × 200 (0.6 mm superior/inferior [S/I] (frequency) × 0.6 mm anterior/posterior [A/P] (phase) × 0.7 mm right/left [R/L] (slice) acquired voxel size) matrix is acquired in 4:25 with 2D-accelerated parallel imaging and half-Fourier encoding.

Figure 9 shows T₂-weighted abdominal images of a volunteer. Because the images were acquired during free breathing, the higher minimum FA (45°) made the sequence less sensitive to respiratory motion, while still allowing enough FA modulation to constrain blurring.

FIG. 9.

Volumetric kidney imaging. A T₂-weighted image volume with a 320 × 320 × 128 matrix (1.0 mm superior/inferior [S/I] (frequency) × 1.0 mm right/left [R/L] (phase) × 1.4 mm anterior/posterior [A/P] (slice) acquired voxel size) is acquired in 5:19 with respiratory gating.

DISCUSSION

For clinical imaging, the combination of FSE with 3D Fourier encoding is desirable in order to produce very thin slices with high SNR and soft-tissue T₂ weighting. Because long TRs are needed for contrast, and large acquisition matrices are needed to cover a volume with high in- and through-plane resolution, conventional 3D-FSE has required more scan time than is practical in a clinical setting. Several recent advancements have contributed to dramatic reductions in scan time, including very long echo trains through refocusing FA modulation and 2D-accelerated parallel imaging. Here we have described a method to modulate refocusing FAs that combines the advantages of the relaxation-specific approaches (9–11) with the PSS-signal-envelope technique (7). We have also presented a new view-ordering method for 3D-FSE acquisitions that enables 2D autocalibrated parallel imaging and elliptical k-space coverage to be fully utilized to reduce scan time.

Refocusing FA modulation can extend the useful length of an echo train by initially storing much of the magnetization in slowly-decaying longitudinal pathways, then drawing on this reserve, gradually converting it back to transverse magnetization to contribute to signal in later echoes, countering the effect of relaxation. Previous techniques that utilized this principle determined the refocusing FAs by modeling the decay of a tissue with a specific T₁ and T₂, and then calculating the refocusing FAs necessary to produce a specified signal curve for this tissue. While the maximum FA was constrained, the minimum FA and the FA at the center of k-space were dependent on ETL, matrix size, bandwidth, and assumed tissue relaxation properties. An unconstrained minimum FA can be a significant limitation considering that flow and motion sensitivity is strongly affected by this parameter, as demonstrated here theoretically and in previous in vivo studies (14). Perhaps because of this limitation, constant-FA PSS methods have been preferred to modulated FA methods outside the head, for spine and body imaging (25).

The proposed FA modulation technique produces sharp PSFs from very long echo trains while exercising direct control over minimum, center-k-space, and maximum FAs in order to accommodate the presence of flow and motion, SNR requirements, and RF power limits, respectively. It was demonstrated that this control could be accomplished with a modification to previous relaxation-specific methods, or more directly by utilizing the prescribed PSS-signal-envelope technique. Varying the minimum refocusing FA was shown to impact sensitivity to motion—higher minimum FAs result in less motion-induced signal loss. When the ETL was adjusted to maintain a consistent TE_eff for a T₂-weighted acquisition, higher minimum FAs necessitated shorter ETLs and thus longer scan times, but resolution was not impacted by the choice of minimum FA. While not presented here, the same trend was observed for centrically encoded PD-weighted acquisitions, where ETL was adjusted to limit the effective TE of the last acquired echo. Also not presented were data showing the effect of adjusting the center-k-space and maximum FAs. Reducing the center k-space FA caused SNR to decrease, but allowed longer ETLs and thus shorter scan time. Reducing the maximum FA caused modestly reduced resolution, but chiefly affected the RF pulse width (thus echo spacing) and RF power (which in these studies was not a limiting factor, even at 3T).

The method relies on the user having knowledge of the “contrast-equivalent” TE_eff, which is adjusted to account for the reduced effective T₂ decay rate that occurs when using a low-angle echo train (11,13). This was provided on the scanner’s user interface, where the displayed TE_eff value was automatically updated whenever any parameters, such as α_min or ETL, were changed. Likewise, an “SNR meter” on the scanner’s interface indicated the effect of adjusting α_cent (as well as voxel size, FOV, etc). While the adjusted TE_eff does not perfectly match the contrast of a conventional spin-echo sequence (26), we have found that qualitatively and for practical purposes, it works well for the range of α_min used in our practice (≥20°).

In addition to increasing the length of the echo train via FA modulation, 3D-FSE scan time can be decreased by reducing the number of views required to produce the image set. While techniques such as elliptical k-space coverage and 2D acceleration with nonseparable autocalibration have been demonstrated for steady-state gradient-echo sequences, the difficulty of ordering views to benignly handle signal modulation has previously precluded their use with 3D-FSE.

The proposed view-ordering technique overcomes this limitation, mapping signal modulation from the echo train into k-space such that the 2D-MTF is smooth, producing images with only very slight blurring and no other artifacts. The view-ordering technique could be applied not just to FSE, where signal variation is due to relaxation and refocusing FA modulation, but to any 3D sequence with periodic signal variation, for instance due to preparation pulses (intermittent fat suppression [e.g., LAVA, VIBE] or inversion recovery gradient echo [e.g., IR-SPGR, MP-RAGE]) or to cardiac or respiratory motion.

CONCLUSIONS

By significantly increasing the ETL compared to a conventional FSE readout and reducing the total number of views needed to encode a 3D image dataset, a 3D-FSE sequence can attain large volume coverage with high in- and through-plane resolution within clinically practical scan times of 3–6 min. The flexibility to independently control the minimum refocusing FA, ETL, and matrix size enable the sequence to be applied to a wide range of clinical applications for neurological, musculoskeletal, and abdomino-pelvic imaging.

APPENDIX

Modeling the Motion Sensitivity of PSS CPMG Sequences

PSS requires coherent superposition of numerous signal pathways. Motion, however, causes differing amounts of phase to accrue in different pathways. Signal loss results when signal pathways do not add constructively. The effect of motion on FSE with modulated FA refocusing was modeled to determine the extent to which the minimum refocusing FA affects signal.

Consider an isochromat’s position to be fixed during the interval τ (defined, by convention, as half the echo spacing). For constant velocity motion, the position during interval n (starting with n = 0, the interval immediately after excitation) will be

$${\stackrel{\rightharpoonup }{\mathrm{x}}}_{\mathrm{n}}={\stackrel{\rightharpoonup }{\mathrm{x}}}_0+\stackrel{\rightharpoonup }{\mathrm{v}}(\mathrm{n}·\mathrm{\tau })$$ [A1]

and the phase accrued during that interval will be

$$\begin{array}{cc}{\mathrm{\varphi }}_{\mathrm{n}}=\mathrm{\gamma }{\displaystyle {\int }_{\mathrm{t}=\mathrm{n}\mathrm{\tau }}^{(\mathrm{n}+1)\mathrm{\tau }}{\stackrel{\rightharpoonup }{\mathrm{x}}}_{\mathrm{n}}·\stackrel{\rightharpoonup }{\mathrm{G}}(\mathrm{t})\text{dt}}\hfill & =\mathrm{\gamma }\left({\stackrel{\rightharpoonup }{\mathrm{x}}}_0·{\displaystyle {\int }_{\mathrm{t}=\mathrm{n}\mathrm{\tau }}^{(\mathrm{n}+1)\mathrm{\tau }}\stackrel{\rightharpoonup }{\mathrm{G}}(\mathrm{t})\text{dt}}\right)\hfill \\ \hfill & +\mathrm{\gamma }\left(\stackrel{\rightharpoonup }{\mathrm{v}}·{\displaystyle {\int }_{\mathrm{t}=\mathrm{n}\mathrm{\tau }}^{(\mathrm{n}+1)\mathrm{\tau }}\stackrel{\rightharpoonup }{\mathrm{G}}(\mathrm{t})\text{dt}}\right)(\mathrm{n}·\mathrm{\tau })\hfill \end{array}$$ [A2]

The phase due to the initial position at excitation (x₀) is readily refocused and may be ignored, but the additional phase term that increases with each successive echo is proportional to the gradient area, velocity, and echo spacing. Net gradient area is consistent in every interval τ and controllable, and is usually set to produce at least a full cycle of phase dispersion across a voxel of size δx:

$$\frac{1}{\mathrm{\delta }x}=\frac{\mathrm{\gamma }}{2\mathrm{\pi }}{\displaystyle \int \stackrel{\rightharpoonup }{\mathrm{G}}(\mathrm{t})\text{dt}}$$ [A3]

therefore

$${\displaystyle \int \stackrel{\rightharpoonup }{\mathrm{G}}(\mathrm{t})\text{dt}=\frac{2\mathrm{\pi }/\mathrm{\gamma }}{\mathrm{\delta }\mathrm{x}}}$$ [A4]

Ideally, gradient crushers would be placed perpendicular to the direction of motion or flow, but for a worst-case scenario (since flow and motion can occur in multiple directions within the imaging volume) we will assume they are aligned, in which case we find

$${\mathrm{\varphi }}_{\mathrm{n}}=2\mathrm{\pi }\frac{\mathrm{v}}{\mathrm{\delta }\mathrm{x}}(\mathrm{n}·\mathrm{\tau })$$ [A5]

This additional phase term was incorporated into the EPG algorithm. The algorithm applies a matrix multiplication operation to enact the nutation at each RF pulse, which mixes partitions of equal order. During each interval of duration τ, exponential relaxation at the T₁ rate is applied to all longitudinal partitions and at the T₂ rate to all transverse partitions, and the order of each transverse partition is incremented to model the effect of the constant gradient area during this interval. The EPG algorithm implemented here also applied the increasing phase term (Eq.[A5]) to each transverse partition as well. For velocities greater than zero, this had the effect of causing signal to be reduced and somewhat erratic from echo to echo.

Figure 4e shows the “relative total signal.” This was defined as the sum of the signals at each echo for the given velocity, normalized by the sum of the signals at each echo given zero velocity:

$$\mathrm{S}(\mathrm{v})=\frac{{\displaystyle {\sum }_{\text{echo}=1}^{\text{ETL}}|{\mathrm{S}}_{\text{echo}}(\mathrm{v})|}}{{\displaystyle {\sum }_{\text{echo}=1}^{\text{ETL}}|S_{\text{echo}}(0)|}}$$ [A6]

The model assumed δx = 1 mm.