Abstract
We use various nonlinear partial differential equations to efficiently solve several surface modelling problems, including surface blending, N-sided hole filling and free-form surface fitting. The nonlinear equations used include two second order flows, two fourth order flows and two sixth order flows. These nonlinear equations are discretized based on discrete differential geometry operators. The proposed approach is simple, efficient and gives very desirable results, for a range of surface models, possibly having sharp creases and corners.
Keywords: Geometric PDE, Discrete Surface, Surface Blending, N-sided Hole Filling, Free-form Surface Fitting
1 Introduction
We use various partial differential equations (PDE) to solve several surface modelling problems. The PDEs we use include the mean curvature flow, the averaged mean curvature flow, two fourth order (surface diffusion flow and quasi surface diffusion flow) and even higher order flows. All these equations are nonlinear and the geometry is intrinsic, i.e., the PDEs do not depend upon any particular parameterization. The problems we solve include surface blending, N-sided hole filling and free-form surface fitting with high order boundary continuity.
For the problems of surface blending and N-sided hole filling, we are given triangular surface meshes of the surrounding area. Triangular surface patches need to be constructed to fill the openings enclosed by the surrounding surface mesh and interpolate the hole boundary with some specified order of continuity. For the free-form surface fitting problem, we are possibly given a set of points, or a wire frame of curves that defines an outline of the desired shape, or even some surface patches. We construct a surface which interpolates the points or curves or the boundaries of the patches with specified order of continuity. The free-form surface fitting problem is the most general, including the surface blending and N-sided hole filling problems, as its special cases.
Our twofold strategy for solving these problems is as follows: First we construct an initial triangular surface mesh (“filler”) using any of a number of automatic or semi-automatic free-form modelling techniques (see [1, 2, 23, 35, 52]). One may also interactively edit this “filler” to meet the weak assumptions for an initial solution shape. This “filler” may be bumpy or noisy, and in general this “filler” does not satisfy the smoothness boundary conditions, though it may roughly characterize the shape of the surface to be constructed. Second we deform the initial mesh by solving a suitable flow PDE. Unlike most of the previous free-form modelling techniques, our approach solves high-order boundary continuity constraints without any prior estimation of normals or derivative jets along the boundary. The solution of the PDE is time dependent. We consider two possibilities for the time span of the evolution. One is a short time evolution, where we require the solution to respect to the initial shape or geometry (see Fig. 4.4). The other is a long time evolution, where the initial filler provides a topological structure, and what we look for is a stable solution state of the flow (see Fig. 1.1 and Fig. 4.1). In this paper, we focus our attention on these twofold solutions of PDEs with boundary continuity constraints, rather than the construction of initial filler mesh. In section 3.4, we present automatic approaches for constructing the initial filler mesh, and our preferred choice.
Fig 4.4.
Interpolating curves and patches: (a) shows some input curves with G0 continuity requirement and some bands of mesh with G1 continuity requirement. (b) shows an initial construction of the surface mesh. (c) is the faired surfaces, after 12 iterations, generated using the the flow (2.9) with k = 2. The time step size is chosen to be 0.001. (d), (e) and (f) are the zoom in results of (a), (b) and (c), respectively.
Fig 1.1.
(a) shows a head mesh with a hole around the nose. (b) shows an initial filler construction of the nose with a piece of minimal surface. (c) the filler surface, after 30 iteration, generated using fourth order flow (k = 2 in (2.9)) with time step size 0.0002. (d) the filler surface, after 20 iteration, generated using sixth order flow (k = 3 in (2.9)) with time step size 0.00002.
Fig 4.1.
The first and second row show the results of (2.9) and (2.8), respectively. (a) (same as (g)) The input semi-sphere (left part) with an initial planar triangulation of the disk opening. The mean curvature flow does not change the disk (initial mesh). (b) The result of fourth order flow after 10 iteration with τ(n) = 0.1. (c) The result of the sixth order flow after 10 iteration with τ(n) = 0.01. (d), (e) and (f) show three intermediate results of the sixth order flow with τ(n) = 0.001, and 1, 6 and 10 iterations, respectively. (h) The result of the surface diffusion flow after 10 iteration with τ(n) = 0.2. (i) The result of the sixth order flow (2.8) after 10 iteration with τ(n) = 0.02. (j), (k) and (l) show three intermediate results of the sixth order flow (2.8) with τ(n) = 0.002, and 1, 6 and 10 iterations, respectively.
Previous Work
Earlier research on using PDEs to handle surface modelling problems trace back to Bloor et al’s papers at the end of the 1980s ([8, 9]). The basic idea of these papers is the use of biharmonic equations on a rectangular domain to solve the blending and hole filling problems. One of the advantages of using the biharmonic equation is that it is linear, and therefore easier to solve. However, the equation is not geometry intrinsic and the solution of the equation (the geometry of the surface) depends on the concrete parameterization used. Furthermore, these methods are inappropriate to model surfaces with arbitrary shaped boundaries.
The evolution technique, based on the heat equation ∂tp − Δp = 0, has been extensively used in the area of image processing (see [36, 44]. In [44], there are 453 relevant references listed), where Δ is a 2D Laplace operator. This was extended lately to smoothing or fairing noisy surfaces (see [14, 17, 30]). For a surface ℳ, the counterpart of the Laplacian Δ is the Laplace-Beltrami operator Δℳ (see [18]). One then obtains the geometric diffusion equation ∂tp − Δℳ p = 0 for a surface point p(t) on the surface ℳ (t). Taubin [42] discussed the discretized operator of the Laplacian and related approaches in the context of generalized frequencies on meshes. Kobbelt [26] considered discrete approximations of the Laplacian in the construction of fair interpolatory subdivision schemes. This work was extended in [28] to arbitrary connectivity for purposes of multi-resolution interactive editing. Desbrun et al. [17] used an implicit discretization of geometric diffusion to obtain a strongly stable numerical smoothing scheme. The same strategy of discretization is also adopted and analyzed by Deckelnick and Dziuk [16] with the conclusion that this scheme is unconditionally stable. Clarenz et al. [14] introduced anisotropic geometric diffusion to enhance features while smoothing. Ohtake et al. [32] combined an inner fairness mechanism in their fairing process to increase the mesh regularity. Bajaj and Xu [5] smooth both surfaces and functions on surfaces, in a C2 smooth function space defined by the limit of triangular subdivision surfaces (quartic Box splines). Similar to the surface diffusion using the Laplacian, a more general class of PDE based methods called flow surface techniques have been developed which simulate different kinds of flows on surfaces (see [45] for references) using the equation ∂tp − V (p, t) = 0, where V (p, t) represents the instantaneous stationary velocity field.
Level set methods were also used in surface fairing and surface reconstruction (see [3], [7], [12], [31], [34], [46], [54]). In these methods, surfaces are formulated as iso-surfaces (level surfaces) of 3D functions, which are usually defined from the signed distance over Cartesian grids of a volume. An evolution PDE on the volume governs the behavior of the level surface. These level-set methods have several attractive features including, ease of implementation, arbitrary topology (see [10]) and a growing body of theoretical results. Often, fine surface structures are not captured by level sets, although it is possible to use adaptive (see [36]) and triangulated grids as well as Hermite data (see [27]). To reduce the computationally complexity, Bertalmio et al [7] solve the PDE in a narrow band for deforming vectorial functions on surfaces (with a fixed surface represented by the level surface).
Recently, surface diffusion flow has been used to solve the surface blending problem and free-form surface fitting problem ([39, 40]). In [39], fair meshes with G1 conditions are created in the special case where the meshes are assumed to have subdivision connectivity. In this paper, local surface parameterization is still used to estimate the surface curvatures. The later paper [40] uses the same equation for smoothing meshes while satisfying G1 boundary conditions. Outer fairness (the smoothness in the classical sense) and inner fairness (the regularity of the vertex distribution) criteria are used in their fairing process. The finite element method is used by Clarenz et al [13] to solve the Willmore flow equation, based on a new variational formulation of the flow, for the aim of surface restoration. Willmore flow is also used to smooth triangular mesh in [53].
Main Results
We use second order flows (mean curvature flow and averaged mean curvature flow) for G0 continuity, fourth order flows for G1 continuity and sixth order flows for G2 continuity in each of several surface modelling problems. The proposed approach is simple and easy to implement. It is general, solves several surface modelling problems in the same manner, and gives very desirable results for a range of complicated free-form surface models, possibly having sharp features and corners. Furthermore, it avoids the estimation of normals or tangents or curvatures on the boundaries.
The rest of the paper is organized as follows: Section 2 describes several nonlinear PDEs used in this paper. In section 3, we give details of the discretization and the numerical computation for the solutions of the PDEs. Examples to illustrate the different effects achievable from the solution of the PDEs are given in section 4.
2 Partial Differential Equation Models
Let ℳ be a smooth surface and p ∈ ℳ be the surface point. The general form of the geometric flows we consider is in the following form (see [45])
where V (p, t) ∈ IR3 represents a velocity field. We shall focus our attention on using two classes velocity fields, one is curvature driven velocity field in the normal direction, the other is the higher order Laplace-Beltrami operators acting on surface point p.
2.1 Geometric Partial Differential Equations
We now describe several geometric PDE models we use in this paper. More details on the existence and uniqueness of the solutions, the numerical computations of the solutions and evolution behaviors can be found in a series of papers by Mayer, Simonett, Escher [21, 22, 41] and Huiskens’ paper [25]. Let ℳ0 be a compact closed immersed orientable surface in IR3. A curvature driven geometric evolution consists of finding a family {ℳ(t): t ≥ 0} of smooth closed immersed orientable surfaces in IR3 which evolve according to the flow equation
| (2.1) |
Here p(t) is a surface point on ℳ(t), Vn(k1, k2, p) denotes the normal velocity of ℳ(t), which depends on the principal curvatures k1, k2 of ℳ(t), N (p) stands for the unit normal of the surface at p(t). In this paper we identify the surface point p and surface normal N(p) as 3 × 1 matrices (column vectors). Hence, the arithmetic operations of these quantities are regarded matrix operations. The product of a scalar a ∈ IR and a matrix M is written as either aM or Ma.
Let A(t) denote the area of ℳ(t), V (t) denote the volume of the region enclosed by ℳ(t). Then it has been shown that (see [48], Theorem 4)
| (2.2) |
where is the mean curvature of ℳ(t).
1. Mean Curvature Flow (see [19, 47])
Taking in (2.1), we obtain the mean curvature flow PDE:
| (2.3) |
It follows from (2.2) that
| (2.4) |
(2.4) implies that the mean curvature flow is area reducing.
2. Averaged Mean Curvature Flow (see [22, 25, 38])
In (2.1), if we take Vn = h(t) − H(t), where h(t) = ∫ℳ(t) Hdσ/∫ℳ(t) dσ, then we have the averaged mean curvature flow PDE:
| (2.5) |
The existence proof of the global solutions to this flow can be found in Huiskens’ paper [25]. It follows from (2.2) that
| (2.6) |
since obviously ∫M(t) h(h−H) = h(h∫M(t) dσ − ∫M(t) Hdσ) = 0. On the other hand, the second equation of (2.2) implies that
Hence the averaged mean curvature flow is volume preserving and area shrinking. The area shrinking stops if H ≡ h.
3. Surface Diffusion Flow (see [40])
If we take Vn = ΔH, we get the so-called surface diffusion flow PDE:
| (2.7) |
where Δ:= Δℳ is Laplace-Beltrami operator which acts on functions defined on surface ℳ(t). The existence and uniqueness of solutions for this flow is given in [21]. From (2.2) and Green’s formula we have
where ∇ stands for the (tangential) gradient operator (see [11], pages 101–102) acting on differential functions defined on the surface ℳ. Hence, the surface diffusion flow is area shrinking, but volume preserving. The area stops shrinking when the gradient of H is zero. That is, ℳ is a surface with constant mean curvature.
4. Higher order Geometric Flows
| (2.8) |
Using Green formula, we have
Hence, the flow (2.8) is volume preserving if k ≥ 1 from the second equation of (2.2).
Remark 2.1
We should note that the area/volume preserving/shrinking properties for the flows mentioned above are valid for closed surfaces. In our application of these flows, these properties may not be true since the surfaces always have fixed boundaries. For a open surface with fix boundary, the volume V (t) could be defined as the directional volume between ℳ(0) and ℳ(t). It is easy to see that the volume preserving property for the averaged mean curvature flow is still valid. But for the higher order flow (2.8) (k ≥ 1), this property is no longer valid, because a term related to the boundary does not vanish when Green’s formula is used. For our modelling problems, volume preservation is not a desirable property (see Fig. 1.1 and 4.1).
Remark 2.2
In [40], Schneider and Kobbelt use elliptic equation N(p)ΔH(p) = 0, while we use several time dependent parabolic type equations. In our approach, we have a progressive process starting from an initial value, so that a family of solutions is obtained. Such an approach is very desirable if the initial value is an approximation of the required solution.
2.2 Quasi Geometric Partial Differential Equations
Now we generalize the heat equation on a surface to the following higher order flows:
| (2.9) |
Since Δp = −2H(x)N(p), it is easy to see that (2.9) is the mean curvature flow when k = 1 (up to a factor 2). But since (ΔkH)N ≠ Δk(HN) in general, (2.9) is different from the flow (2.8). To distinguish the difference between (2.8) and (2.9), we call (2.9) as a quasi geometric PDE.
The experiments conducted in this paper show that flows (2.9) sometimes behave better than the geometric flows mentioned above for our geometry modelling problems. However, the theoretical analysis on the existence and stability of their solutions is currently unavailable.
3 Solution of the PDEs
There are basically two classes of approaches for solving a PDE on any domain. One approach is based on finite divided differences, the other is based on finite elements (see [5, 13, 16]). The approach we adopt in this paper is based on finite divided differences. Since we are dealing with differential equations over 2-manifolds in IR3, the classical finite divided differences will be replaced by discretized differential geometric operators over surfaces. Section 3.1 deals with discretized geometric differential operators. Next in Section 3.2 we detail how the boundary conditions are respected. Discretizations of the PDEs in the spatial direction are described in section 3.3 and 3.4. Semi-implicit discretization in the time domain is considered in section 3.4. Other issues, such as mesh regularization and initial mesh construction, are addressed in section 3.5.
3.1 Discretized Laplace-Beltrami Operator
One of the fundamental problems in solving our PDEs is the discretization of the Laplace-Beltrami operator. On a triangular surface mesh, several discretized approximations of the operator have been proposed (see [17, 24, 43, 51]). In this paper we adopt the discretization developed by Meyer et al in [30]. A comparative research about the various discretized Laplace-Beltrami operators is conducted in [50]. It has been shown that the scheme of Meyer et al’s is better for discretizing our PDEs. Let f be a smooth function on a surface, then Δf is approximated over a triangular mesh M by
| (3.1) |
where N1(i) is the index set of 1-ring of neighbor vertices of vertex pi, αij and βij are the triangle angles shown in Fig 3.1 (Left). AM (pi) is the area for vertex pi as shown in Fig 3.1 (Right), where qj is the circumcenter point for the triangle [pj−1pjpi] if the triangle is non-obtuse. If the triangle is obtuse, qj is chosen to be the midpoint of the edge opposite to the obtuse angle. Since Δp = −2H(p)N(p) (see [48], page 151), we have
Fig 3.1.
Left: The definition of the angles αij and βij. Right: The definition of the area AM (pi).
| (3.2) |
This gives an approximation of the mean curvature normal (see [30]). The higher order Laplace-Beltrami operators are discretized recursively as
| (3.3) |
with Δ0f(pi) = f (pi). Note that Δkf (pi) involves function values on a k-ring of neighboring vertices of pi.
3.2 Handling of Boundary Conditions
1). Natural Boundary Conditions for Blending and Hole Filling
By the natural boundary conditions, we mean that no continuity conditions are specified at the boundary points, but the continuity is implied by the “outer” mesh incident to the boundary of the hole (see Fig 3.2). Such a treatment for boundary condition is suitable for both the blending problem and the N-sided hole filling problem, since the “outer” mesh always exists in such problems.
Fig 3.2.
Left: The involved vertices of the “outer” mesh for a G0 boundary condition. The “outer” mesh is just the boundary of the hole. Middle: The involved vertices of the “outer” mesh for a G1 boundary condition. Right: The involved vertices of the “outer” mesh for a G2 boundary condition.
Let gi be the order of continuity at a boundary point pi, g = max gi. Then we can use the order 2g flow for constructing the triangular surface patch with Ggi continuity at the boundary vertex pi. ΔgH is discretized recursively: ΔgH = Δ(Δg−1H). At a boundary vertex pi, ΔkH(pi) is evaluated according to the following rule:
Evaluation Rule at Boundary
ΔkH(pi) is evaluated recursively by formulas 3.6 and 3.7 if k ≤ gi, otherwise ΔkH(pi) is set to zero and the recursion stops.
Note that even for an inner vertex pj, the recursive definition may make ΔkH(pj) involve the evaluation of a lower order Laplace-Beltrami operator on the boundary. In general, the recursive evaluation of ΔkH(pi) at pi (for either pi being an inner or an outer vertex) involves k + 1-ring neighbor vertices of pi. Some of them may be inner vertices, and the remaining are outer vertices. The inner vertices are treated as unknowns in the discretized equations and the outers are incorporated into the right-hand side.
2). Natural Boundary Conditions for Free-Form Surface Filling
In the free-form surface filling problem, we are given a wireframe of curves (edges) and we wish to flesh the wireframe with surface patches that contain the curves as boundary with pre-specified order of continuity. At each of the intersection points of the patches, an order of continuity is pre-specified and the evaluation rule mentioned above is applied. For each inner point, a discretized linear equation is generated using the operator discretization (3.7). These linear equations for different patches are collected together and solved simultaneously. Note that one linear equation may involve inner vertices of several patches. However, if the continuity order at each boundary point is zero, any equation corresponding to an inner vertex does not involve inner vertices of other patches.
Remark 3.1
Schneider and Kobbelt in [40] use Moreton and Sequin’s least square fitting of the second fundamental form relative to a local parameterization to estimate the required data on the boundary. These estimations of the boundary derivative data are based on incomplete information. Hence, the estimated data maybe not reliable. Our approach is based on the identity Δℳp = −2H(p)N (p). Hence, we do not need to estimate boundary derivative data, such as normals, tangents or curvatures. Furthermore, the boundary conditions are treated in the same way for equations with different orders.
3.3 Spatial Discretization of Quasi Geometric Flows
Let us consider first the discretization of (2.9) in the spatial direction for k = 1, 2, 3. Let P = [p1, ···, pm]T ∈ IRm×3, ΔP = [Δp1; ···, Δpm]T ∈ IRm×3, where p1; ···, pm are all the unknown vertices to be determined in each of our modelling problems. Then (3.2) could be written in matrix form:
| (3.4) |
where is a diagonal matrix, with
Furthermore,  is a sparse, symmetric and positive definite matrix (see [40]). The constant term B(1) ∈ IRm×3 is obtained from the boundary conditions. It follows from (3.4) that
is a sparse, symmetric and positive definite matrix (see [40]). The constant term B(1) ∈ IRm×3 is obtained from the boundary conditions. It follows from (3.4) that
| (3.5) |
where B(2) ∈ IRm×3 is obtained from the boundary conditions. Again, 

 is a sparse, symmetric and positive definite matrix. In general,
is a sparse, symmetric and positive definite matrix. In general,
and the matrix for 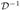 (
(
 )k is also sparse, symmetric and positive definite.
)k is also sparse, symmetric and positive definite.
3.4 Spatial Direction Discretization of Geometric Flows
Let
and N(i) = N1(i) ∪ {i}. Then we have
| (3.6) |
The higher order Laplace-Beltrami operators acting on H are discretized recursively as
| (3.7) |
with
| (3.8) |
Note that ΔkH(pi) involves values of the mean curvature on a k-ring of neighboring vertices of pi.
Using (3.6)–(3.8) and the evaluation rule at the boundary, we can write N(pi)ΔkH(pi) as the following form:
where J0 is the index set of the (unknown) vertices to be determined, comes from boundary condition. To be more specific, let J denote the index set of the mesh M, Jk be the union of J0 and the index set of the boundary vertices where Ck condition is specified. Then
| (3.9) |
where for j ∈ N(i) ∩ J0, otherwise, . Similarly,
| (3.10) |
| (3.11) |
(3.9)–(3.11) are used to discretize the right-handed side of (2.8) for k = 0, 1, 2. The discretization of N(pi)ΔkH(pi) for k > 2 is recursively calculated using (3.7) and boundary conditions.
3.5 Time Discretization
Given an approximate solution of the order 2k PDE at tn for all the inner vertices, we construct an approximate solution for the next time step tn+1 = tn + τ(n) by using a semi-implicit Euler scheme. That is, we replace the derivative with [p(tn+1) − p(tn)]/τ(n), and the quantities wij in (3.4), ωij and N (pi) in (3.6)–(3.8), h(t) in (2.5) are computed using the previous result at tn. Normals N (pi) are computed from Loop’s subdivision surface (see [5] for detail). Such a treatment yields a linear system of equations with the inner vertices as unknowns. Let . The linear system for the geometric flows can be written as the matrix form
| (3.12) |
The matrix  ∈ IR3m×3m is highly sparse, hence an iterative method for solving such a linear system is desirable. We use Saad’s iterative method [37], named GMRES, to solve the system. The experiment shows that this iterative method works very well.
∈ IR3m×3m is highly sparse, hence an iterative method for solving such a linear system is desirable. We use Saad’s iterative method [37], named GMRES, to solve the system. The experiment shows that this iterative method works very well.
Let . The linear system for the flows (2.9) can be written as the matrix form
| (3.13) |
where B(k) ∈ IRm×3, W(k) = 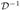 + τ(n)
+ τ(n) (
(
 )k ∈ IRm×m is a highly sparse, symmetric and positive definite matrix, and hence we use a conjugate gradient iterative method with diagonal preconditioning to solve the system.
)k ∈ IRm×m is a highly sparse, symmetric and positive definite matrix, and hence we use a conjugate gradient iterative method with diagonal preconditioning to solve the system.
Note that for the same size problem, the size of coefficient matrix in (3.12) is three times larger than that of coefficient matrix in (3.13). Furthermore, the matrix W(k) in (3.13) is symmetric and positive definite. The matrix in (3.12) is not. We also note that the discretization of (2.9) does not involve the computation of the surface normals.
Remark 3.2
It is well known that the condition of the linear system arising from the proposed semi-implicit discretization behaves like O(1 + τ(n)h−2k), where h is the minimal edge length of the mesh. Hence, if the mesh to be evolved is very irregular, the resulting system will be ill-conditioned. In such a case, a small time step size is required to make an iterative solver converge. Such a problem is relieved by the mesh regularization treatment (see section 3.6). On the other hand, more advanced iterative method, such as multi-grid techniques based on a hierarchical mesh representation (see [29]) or algebraic multi-grid techniques, could be used to accelerate the iteration process. In the current implementation, these techniques are not incorporated.
Upper-bound of time step
It is known that several surface evolutions (e.g. the mean curvature flow (see [19, 47]) and the surface diffusion flow (see [6])) may develop singularities. For our geometric modelling problems, suppose we have a topologically correct initial surface mesh construction and we look for solutions that have the same topology as the initial mesh. Hence, we require that our solution is within the time period in that no singularity occurs. Therefore, we shall determine the time step τ(n) so that tn should not go beyond the time moment when the singularity occurs. Let be the spatial discretization of V (p, t) at vertex over the mesh M(tn). Then from the approximate equality
and the requirement
| (3.14) |
we determine an upper-bound for τ(n) as follows
Requirement (3.14) guarantees that no vertex-collision happens. When the singularity is nearly to occur, the upper-bound Bn will approach to zero. Hence the evolution cannot move beyond the singular point for time.
Remark 3.3
When the singularity is nearly to occur, the upper-bound Bn will approach to zero. This will be a very low efficiency process. So a threshold value ε0 should be put on the minimal Bn. If the determined Bn is smaller than the threshold value, we terminate the evolution process (see (3.17)–(3.18)).
3.6 Other Important Issues
1. Mesh Regularization
The surface motion by the geometric PDEs described in section 2 may cause a very irregular (nonuniform) distribution of the mesh vertices. Hence, introducing a regularization mechanism in the evolution process is necessary. Since the tangential displacement does not influence the geometry of the deformation, just its parameterization (see [20]), we also add a tangential displacement to the motion. Hence, the general form of our geometric evolution problem could be written as
| (3.15) |
where T(p) is a tangent direction at the surface point p, Vt(p) is the tangential velocity. In the process of numerical solution of equation (3.15), Vt(p)T (p) is chosen as
| (3.16) |
where , N is the surface normal computed from the limit surface of Loop’s subdivision. This discretization of Vt(p)T (p) is very similar to the one given by Ohtake et al. [32], which is . The difference is that our displacement is in the tangent plane. In (3.16), could be replaced by to use as many of the new values as possible, and still yield a linear system. However, such a treatment destroys the symmetric property of the coefficient matrix. The tangential motion (3.16) is also used by Wood et al [49] and Ohtake et al [33].
2). Stopping Criteria
We need to determine the minimal iteration number n, so that the evolution procedure stops at t = tn. The following two criteria are used
| (3.17) |
| (3.18) |
where εi are given control constants, Bn is the determined upper-bound for τ(n). Criterion (3.17) is for short time evolution, where we require M(nτ(n)) near M(0). Criterion (3.18) is for long time evolution, where we are looking for a stable status of the solution. Condition Bn < ε0 is imposed for avoiding dead-loop around the singular point of time.
3). Construction of Initial Surface Mesh
To provide an initial solution to the geometric evolution problem, we need to construct an initial triangular surface mesh (“filler”) for each opening using any of a number of automatic or semi-automatic free-form surface construction techniques [1, 2, 15, 23, 35, 52]. One can also interactively edit this “filler” to meet the weak assumptions for an initial solution shape.
Since the opening to be filled could be topologically complicated, we solve the problem in two steps. In the first step we fit each opening by an implicit algebraic surface or spline which interpolates or approximates the boundary data [2, 4, 35]. The approach we used is the one developed by Bajaj et al [1, 2, 4]. In this approach, the data to be interpolated or approximated could be points or curves (even with normals). For ours, the boundary data are always points. Of course, this approach may not guarantee to produce topologically correct surfaces. If this happens, we break the opening into several parts by inserting a few curves (polygons) and then repeat the surface fitting for each part until we achieve a reasonable shape for the “filler”.
After the algebraic surface is obtained, a triangulation step is employed. Since this triangulation should be consistent with the boundary polygon of the opening, we adopted the expansion technique developed in [4]. Using this approach, we triangulate the surfaces starting from the boundary of the opening.
Remark 3.4
Comparing with finite element approach, the finite difference approach described above is easy to implement and it treats the equations with different orders in a uniform fashion. In the finite element approach, one has to make efforts to derive a variational form for each of the PDEs. For higher order flows, hybrid method is used in general, such an approach will introduce much more unknowns, and therefore the resulted linear system is much larger. For example, in order to use finite element method (linear element) for the surface diffusion flow, Bänsch et al [6] split the PDE into a system of four equations.
4 Comparative Examples
In this section, we give several examples to show how the PDEs are used to solve different problems in a uniform fashion. We also compare the effects of flows (2.8) and (2.9). All the figures produced by the fourth and sixth flows are generated using (2.9), except for the figures of the second row of Fig. 4.1 and third row of Fig. 4.3. These figures are produced using the flow (2.8). When we compare the effects of (2.8) and (2.9), we use the same number of iterations but double time step size for (2.8) because the factor 2 in the relation Δp = −2HN.
Fig 4.3.
(a) shows three cylinders to be blended. (b) shows the initial construction. (c), (e) and (g) are the faired blending meshes generated using the flow (2.9) with k = 1, 2, 3, respectively. These figures show the results after 32, 32 and 60 iterations with time step sizes 0.01, 0.001, and 0.0001, respectively. (d), (f) and (h) show the mean curvature plots correspondingly. (i) and (k) are the blending meshes generated using the flow (2.8) with k = 1, 2, respectively. These figures show the results after 32 and 60 iterations with time step sizes 0.002 and 0.0002, respectively. Figure (j) and (l) show the mean curvature plots of (i) and (k), respectively
1). Comparison of the Flows
The first three figures of the first row of Fig. 4.1 show the long time evolution solutions of the mean curvature flow, the fourth order flow, and the sixth order flow (2.9) for the input semi-sphere with an initial construction of the opening, a triangulated disk. The mean curvature flow does not change the disk. Figures (b) and (c) are the results after 10 iterations with τ(n) = 0.1 and τ(n) = 0.001, respectively. Further iterations do not have a significant change on the shape of the solution surface. The fourth and sixth order flows yield convex surfaces and the smoothness is clearly observed. Also notice that the sixth order flow recovers the sphere accurately. The last three figures show three intermediate results of the sixth order flow. The second and third figures of the second row of Fig. 4.1 show the evolution solutions of the surface diffusion flow and sixth order flows (2.8) for the input semi-sphere with an initial construction of the opening. Figure (h) and (i) are produced using the same number of iterations as (b) and (c), respectively, and double time step sizes. Again, the last three figures show three intermediate results of the sixth order flow. Comparing with the figures of the first row, the geometric flows change the surface shape in a much slower rate.
Remark 4.1
We have pointed that the geometric flows (2.8) have volume preserving properties for a closed surface. However, for an open surface with fixed boundary, the volume preserving properties are not guaranteed. Figures (h) and (i) show that the volume preserving property is not valid.
Fig. 4.2 shows the combined use of different flows. The aim of this toy example is to illustrate the difference of these flows, especially the continuity on the patch boundaries. Figure (a) shows four circles to be interpolated. Two of the circles are in the xz-plane, the other two are in the yz-plane. (b) shows an initial G0 surface mesh constructed using [1] with some additional noise added. (c), (e) and (g) are the faired interpolating surfaces after 6 iterations using different combinations of the flows. The time step sizes for the second, fourth and sixth order flows are chosen to be 0.1, 0.0025, and 0.0000625, respectively. Since the higher order flows evolve faster than the lower order flows, we use smaller time step sizes for higher order flows to obtain nearly the same surface evolution speed. Each of the meshes consists of four surface patches. The left two patches are in the regions R−+:= {(x, y, z): x ≤ 0, y ≥ 0} and R−−:= {(x, y, z): x ≤ 0, y ≤ 0}, respectively, and generated by one type of flow. The right two patches are in the regions R++:= {(x, y, z): x ≥ 0, y ≥ 0} and R+−:= {(x, y, z): x ≥ 0, y ≤ 0}, respectively, and generated by a different flow. Figures (d), (f) and (h) are the mean curvature plots of figures (c), (e) and (g), respectively. The mean curvature at each vertex is computed by (3.2).
Fig 4.2.
Comparison of different flows. Δk represents 2k order flow (2.9) is used. AM denote the averaged mean curvature flow. The time step sizes for the second, fourth and sixth order flows are chosen to be 0.1, 0.0025, and 0.0000625, respectively. Figures (c), (e), (g) are the faired interpolating surface meshes after 6 iterations, where the continuities at the boundary curves are set to 0, 2 and 0, respectively. Figures (d), (f), (h) are the mean curvature (MC) plots of figures (c), (e), (g), respectively.
The aim of figure (c) is to show the difference between the mean curvature flow and the averaged mean curvature flow, where the left part is generated by the averaged mean curvature flow and the right part is produced by the mean curvature flow. The mean curvature flow shrinks the surface very fast while the averaged mean curvature flow does not. Further evolution using the mean curvature flow will yield a pinch-off of the surface. Therefore, if we model a surface patch using second order flows with G0 boundary condition, the averaged mean curvature flow is more desirable than the mean curvature flow.
The patches in R−+ and R−− of figure (e) are produced by the sixth order flow (2.9) (with k = 3), while the patches in R++ and R+− are produced by the fourth order flow (2.9). As a whole, the surface looks smooth, our curvature plot reveals the smoothness difference at the intersection curves, the sixth order flow gives a smoother result than the fourth order flow.
Figure (g) is produced as (e), but the continuity order at the four circles are set to zero. Hence G0 continuity is achieved there.
2. Surface Blending
Given a collection surface mesh with boundaries, we construct a fair surface to blend the meshes at the boundaries with specified geometric continuity. Fig 4.3 shows the case, where three cylinders to be blended are given (figure (a)) with an initial G0 construction (figure (b)) using [1] with some additional noise added. The blending surfaces (c), (e) and (g) are the faired blending meshes generated using the flow (2.9) with k = 1, 2, 3, respectively. These figures show the results after 32, 32 and 60 iterations with time step sizes 0.01, 0.001, and 0.0001, respectively. Figure (d), (f) and (h) show the mean curvature plots correspondingly. These figures clearly show the difference of smoothness achieved at blending boundaries. The mean curvature flow gives G0 continuity results. The fourth order flow produces smooth surfaces at boundaries. The sixth order flow produces even smoother surfaces as expected.
Fig (i) and (k) are the faired blending meshes generated using the flow (2.8) with k = 1, 2, respectively. These figures show the results after 32 and 60 iterations with time step sizes 0.002 and 0.0002, respectively. Figure (j) and (l) show the mean curvature plots of (i) and (k), respectively. It should be noted that the flows (2.9) generate little fatter surface than the flows (2.8).
3. N-sided Hole Filling
Given a surface mesh with a hole, we construct a fair surface to fill the hole with specified geometric continuity on the boundary. Fig 1.1 shows such an example, where a head mesh with a hole in the nose subregion is given as input (figure (a)). An initial G0 reconstruction of the nose is shown in (b) using [1] and then evolved with the mean curvature flow. The blending surfaces (figures (c) and (d)) are generated using the flow (2.9) with k = 2 and 3, respectively. It should be observed that the sixth order flow yields a better restoration surface. The head mesh with the hole in the nose subregion is available from http://lsec.cc.ac.cn/~xuguo/xuguo2.htm.
4. Free-Form Surface Construction
For the free-form surface fiffing problem, we are given some curves, or partial patches, or points as input, and we wish to construct a fair surface mesh to interpolate this multi-dimensional data. Fig. 4.4 shows the approach of free-form surface construction, where some input curves with G0 continuity requirement are given to preserve the sharp edges, and also given are some surface bands with a G1 continuity requirement (see (a)). Figure (b) shows an initial construction of the G0 surface mesh using the patch filling scheme [52] with added noise. (c) is the faired surfaces, after 12 iterations, generated using the the flow (2.9) with k = 2. The time step size is chosen to be 0.001. Figures (d), (e) and (f) are zoomed in views of (a), (b) and (c), respectively.
Fig. 4.5 shows the free-form fitting approach from an input triangular mesh, where (a) shows the input surface triangular mesh with a G1 continuity requirement at the vertices (see (a)). Figure (b) shows an initial construction of the surface mesh, where each input triangle is approximated with 16 sub-triangles. The newly introduced vertices are treated as unknowns and the input vertices are fixed in the fairing process. Figures (c) and (d) are the faired meshes, after 2 iterations with τ(n) = 0.01, generated using the mean curvature flow and the averaged mean curvature flow, respectively. (e) is the faired mesh by fourth order flow, after 2 iterations with τ(n) = 0.001. (f) is the mean curvature plot of (e). The area shrinking of the mean curvature flow makes the input vertices to be interpolated become thorns (see (c)), while the area shrinking and the volume preservation of the averaged mean curvature flow make some of input vertices become thorns and some others become pits (see (d)). However, the fourth order flow does not suffer from this problem (see (e)). The obtained surface interpolates the input points and exhibits G1 smoothness everywhere as well.
Fig 4.5.
Interpolating points: (a) shows some input points and their triangulation. (b) shows an initial construction of the surface mesh. (c) and (d) are the faired surfaces, after 2 iterations with τ(n) = 0.01, using the mean curvature flow and the averaged mean curvature flow, respectively. (e) is faired surfaces, after 2 iterations with τ(n) = 0.001, using the fourth order flow (2.9). (f) is the mean curvature plot of (e).
5 Conclusions
We have presented a general scheme for using PDEs to solve several surface modelling problems and with high order boundary continuity conditions. Our scheme has the following features: It produces very fair and desirable solution surfaces. It is simple and easy to implement. Specifically, it solves the free-form blending problem, the N-sided hole filling problem and free-form surface fitting problem in a uniform fashion, and solves the high order boundary continuity problem in an easy and natural way and avoids prior estimation of normals or derivative jets on the boundaries. The implementation results show that our solution works well for a wide range of surface models. Note that the C1 or higher order continuity interpolatory surface blending solution produced by e.g. [1, 35] for complicated corners, or holes with many boundary curve segments, are usually of very high algebraic degree and thereby prone to be with unsuitable for certain applications. The current solution of starting with G0 low degree blends, coupled with higher order flow evolution, yields in general a much better alternative for very smooth surface solutions.
Both the geometric flows and quasi geometric flows yield smooth surfaces at the boundaries. However, quasi geometric flows (2.9) have some attractive features, including ease of implementation, smaller and better behaved coefficient matrices and no requirement of derivatives (normal) estimation.
Acknowledgments
The authors are grateful to the referees for their carefully reading of the manuscript and for their helpful comments on improving the final version of this paper.
Contributor Information
Guoliang Xu, State Key Laboratory of Scientific and Engineering Computing, Institute of Computational Mathematics, Academy of Mathematics and System Sciences, Chinese Academy of Sciences, Beijing, 100080, China.
Qing Pan, State Key Laboratory of Scientific and Engineering Computing, Institute of Computational Mathematics, Academy of Mathematics and System Sciences, Chinese Academy of Sciences, Beijing, 100080, China.
Chandrajit L. Bajaj, Center for Computational Visualization and Institute for Computational Engineering & Sciences, Department of Computer Science, University of Texas, Austin, TX 78712.
References
- 1.Bajaj C, Ihm I. Algebraic surface design with hermite interpolation. ACM Transactions on Graphics. 1992;19(1):61–91. [Google Scholar]
- 2.Bajaj C, Ihm I, Warren J. Higher order interpolation and least squares approximation using implicit algebraic surfaces. ACM Transaction on Graphics. 1993;12(4):327–347. [Google Scholar]
- 3.Bajaj C, Wu Q, Xu G. ICES Technical Report 03–10. University of Texas; Austin: 2003. Level-set Based Volumetric Anisotropic Diffusion for 3D Image Denoising. [Google Scholar]
- 4.Bajaj C, Xu G. Rational spline approximations of real algebraic curves and surfaces. In: Dikshit HP, Michelli C, editors. Approximations and Decomposition Series, Advances in Computational Mathematics. World Scientific Publishing Co; 1994. pp. 73–85. [Google Scholar]
- 5.Bajaj C, Xu G. Anisotropic Diffusion of Surface and Functions on Surfaces. ACM Transaction on Graphics. 2003;22(1):4–32. [Google Scholar]
- 6.Bansch E, Morin P, Nochetto RH. Finite element methods for surface diffusion. Proc. of the International Conference on Free Boundary Problems, Theory and Applications; Trento, Italy. 2002. [Google Scholar]
- 7.Bertalmio M, Sapiro G, Cheng LT, Osher S. CAM Report 00–43. UCLA, Mathematics Department; 2000. A framework for solving surface partial differential equations for computer graphics applications. [Google Scholar]
- 8.Bloor MIG, Wilson MJ. Generating Blend Surfaces Using Partial Differential Equations. Computer Aided Design. 1989;21(3):165–171. [Google Scholar]
- 9.Bloor MIG, Wilson MJ. Using Partial Differential Equations to Generate Free-Form Surfaces. Computer Aided Design. 1990;22(4):221–234. [Google Scholar]
- 10.Breen D, Whitaker R. A Level-Set Approach for the Metamorphosis of Solid Models. IEEE Transactions of Visualization and Computer Graphics. 2001;7(2):173–192. [Google Scholar]
- 11.Do Carmo MP. Differential Geometry of Curves and Surfaces. Englewood Cliffs; New Jersey: 1976. [Google Scholar]
- 12.Chopp DL, Sethian JA. Motion by Intrinsic Laplacian of Curvature. Interfaces and Free Boundaries. 1999;1:1–18. [Google Scholar]
- 13.Clarenz U, Diewald U, Dziuk G, Rumpf M, Rusu R. A finite element method for surface restoration with boundary conditions. Computer Aided Geometric Design. 2004;21(5):427–445. [Google Scholar]
- 14.Clarenz U, Diewald U, Rumpf M. Anisotropic Geometric Diffusion in Surface Processing. Proceedings of Viz2000, IEEE Visualization; Salt Lake City, Utah. 2000. pp. 397–505. [Google Scholar]
- 15.Davis J, Marschner SR, Garr M, Levoy M. Filling Holes in Complex Surfaces using Volumetric Diffusion. Proc. First International Symposium on 3D Data Processing, Visualization, Transmission; 2002. [Google Scholar]
- 16.Deckelnick K, Dziuk G. A fully discrete numerical scheme for weighted mean curvature flow. Numerische Mathematik. 2002;91:423–452. [Google Scholar]
- 17.Desbrun M, Meyer M, Schröder P, Barr AH. SIGGRAPH99. Los Angeles, USA: 1999. Implicit Fairing of Irregular Meshes using Diffusion and Curvature Flow; pp. 317–324. [Google Scholar]
- 18.do Carmo M. Riemannian Geometry. Boston: 1992. [Google Scholar]
- 19.Dziuk G. An algorithm for evolutionary surfaces. Numerische Mathematik. 1991;58:603–611. [Google Scholar]
- 20.Epstein CL, Gage M. The curve shortening flow. In: Chorin A, Majda A, editors. Wave Motion: Theory, Modeling, and Computation. Springer-Verlag; New York: 1987. [Google Scholar]
- 21.Escher J, Mayer UF, Simonett G. The Surface Diffusion Flow for Immersed Hypersurfaces. SIAM Journal on Mathematical Analysis. 1998;29(6):1419–1433. [Google Scholar]
- 22.Escher J, Simonett G. The Volume Preserving Mean Curvature Flow Near Spheres. Proceedings of the American Mathematical Society. 1998;126(9):2789–2796. [Google Scholar]
- 23.Greiner G. Variational design and fairing of spline surface. Computer Graphics Forum. 1994;13:143–154. [Google Scholar]
- 24.Guskov I, Sweldens W, Schröder P. Mutiresolution signal processing for meshes. SIGGRAPH ‘99 Proceedings; 1999. pp. 325–334. [Google Scholar]
- 25.Huiskens G. The Volume Preserving Mean Curvature Flow. J Reine Angew Math. 1987;382:35–48. [Google Scholar]
- 26.Kobbelt L. Discrete Fairing. In: Tim Goodman, Ralph Martin., editors. The Mathematics of Surfaces VII. 1996. pp. 101–129. Information Geometers. [Google Scholar]
- 27.Kobbelt L, Botsch M, Schwanecke U, Seidel HP. Feature sensitive surface extraction from volume data. Siggraph2001. 2001:51–66. [Google Scholar]
- 28.Kobbelt L, Campagna S, Vorsatz J, Seidel H-P. Interactive Muti-Resolution Modeling on Arbitrary Meshes. SIGGRAPH98. 1998:105–114. [Google Scholar]
- 29.Lang J. Adaptive multilevel solution of nonlinear parabolic PDE systems: theory, algorithm, and applications. Berlin; New York: Springer; 2001. [Google Scholar]
- 30.Meyer M, Desbrun M, Schröder P, Barr A. Discrete Differential- Geometry Operator for Triangulated 2-manifolds. Proceedings of Visual Mathematics’02; Berlin, Germany. 2002. [Google Scholar]
- 31.Museth K, Breen D, Whitaker R, Barr A. Level set surface editing operators. Siggraph02. 2002:330–338. [Google Scholar]
- 32.Ohtake Y, Belyaev AG, Bogaevski IA. Polyhedral surafce smoothing with simultaneous mesh regularization. Geometric Modeling and Processing Proceedings; 2000. pp. 229–237. [Google Scholar]
- 33.Ohtake Y, Belyaev AG, Bogaevski IA. Mesh regularization and adaptive smoothing. Computer Aided Design. 2001;33:789–800. [Google Scholar]
- 34.Osher SJ, Fedkiw RP. CAM Report 00–07. UCLA, Mathematics Department; 2000. Level set methods. [Google Scholar]
- 35.Peters J, Wittman M. IMA 96, The Mathematics of Surfaces. Dundee, UK: 1996. Smooth blending of basic surfaces using trivariate box spline. [Google Scholar]
- 36.Preußer T, Rumpf M. An adaptive finite element method for large scale image processing. Scale-Space Theories in Computer Vision. 1999:232–234. [Google Scholar]
- 37.Saad Y. Iterative Methods for Sparse Linear Systems. 2. 2000. corrections. [Google Scholar]
- 38.Sapiro G. Geometric Partial Differential Equations and Image Analysis. Cambridge: University Press; 2001. [Google Scholar]
- 39.Schneider R, Kobbelt L. Geometric Modeling and Processing. Hong Kong, China: 2000. Generating Fair Meshes with G1 Boundary conditions; pp. 251–261. [Google Scholar]
- 40.Schneider R, Kobbelt L. Geometric Fairing of Irregular Meshes for Free-form Surface Design. Computer Aided Geometric Design. 2001;18(4):359–379. [Google Scholar]
- 41.Simonett G. The Willmore Flow for Near Spheres. Differential and Integral Equations. 2001;14(8):1005–1014. [Google Scholar]
- 42.Taubin G. A signal processing approach to fair surface design. SIGGRAPH ‘95 Proceedings; 1995. pp. 351–358. [Google Scholar]
- 43.Taubin G. Signal processing on polygonal meshes. EUROGRAPHICS. 2000 [Google Scholar]
- 44.Weickert J. Anisotropic Diffusion in Image Processing. B. G. Teubner; Stuttgart: 1998. [Google Scholar]
- 45.Westermann R, Johnson C, Ertl T. A Level-Set Method for Flow Visualization. Proceedings of Viz2000, IEEE Visualization; Salt Lake City, Utah. 2000. pp. 147–154. [Google Scholar]
- 46.Whitaker R, Breen D. Level set models for the deformation of solid objects. Proceedings of the 3rd International Workshop on Implicit Surfaces, Eurographics Association; June, 1998.pp. 19–35. [Google Scholar]
- 47.White B. Evolution of curves and surfaces by mean curvature. Proceedings of the Inernational Congress of Mathematicians; Beijing. 2002. pp. 525–538. [Google Scholar]
- 48.Willmore TJ. Riemannian Geometry. Clarendon Press; Oxford, England: 1993. [Google Scholar]
- 49.Wood ZJ, Breen D, Desbrun M. Semi-regular mesh extraction from volumes. IEEE Visualization Proceedings of the conference on Visualization ‘00; Salt Lake City, Utah, United States. 2000. pp. 275–282. [Google Scholar]
- 50.Xu G. Convergence of Discrete Laplace-Beltrami Operators over Surfaces. Computers & Mathematics with Applications. 2004;48:347–360. [Google Scholar]
- 51.Xu G. Discrete Laplace-Beltrami Operators and Their Convergence. Computer Aided Geometric Design. 2004;21:767–784. [Google Scholar]
- 52.Xu G, Bajaj C, Huang H. C1 Modeling with A-patches from Rational Trivariate Functions. Computer Aided Geometric Design. 2001;18(3):221–243. [Google Scholar]
- 53.Yoshizawa S, Belyaev AG. Geometric Modeling and Processing. Saitama, Japan: 2002. Fair triangle mesh generation with discrete elastica; pp. 119–123. [Google Scholar]
- 54.Zhao HK, Osher S, Merriman B, Kang M. Implicit and Non-parametric Shape Reconstruction from Unorgainzed Points Using Variational Level Set Method. Computer Vision and Image Understanding. 2000;80(3):295–319. [Google Scholar]










