From Helix–Coil Transitions to Protein Folding

Abstract

An evolution of procedures to simulate protein structure and folding pathways is described. From an initial focus on the helix–coil transition and on hydrogen-bonding and hydrophobic interactions, our original attempts to determine protein structure and folding pathways were based on an experimental approach. Experiments on the oxidative folding of reduced bovine pancreatic ribonuclease A (RNase A) led to a mechanism by which the molecule folded to the native structure by a minimum of four different pathways. The experiments with RNase A were followed by development of a molecular mechanics approach, first, making use of global optimization procedures and then with molecular dynamics (MD), evolving from an all-atom to a united-residue model. This hierarchical MD approach facilitated probing of the folding trajectory to longer time scales than with all-atom MD, and hence led to the determination of complete folding trajectories, thus far for a protein containing as many as 75 amino acid residues. With increasing refinement of the computational procedures, the computed results are coming closer to experimental observations, providing an understanding as to how physics directs the folding process.

INTRODUCTION

After Pauling discovered the α-helix and the β-sheet,¹ it was natural to assume that an understanding of the interactions that lead to these conformations could be gained by studying the changes in conformation between these regular structures and the unfolded, statistical-coil form. This led to a flurry of both experimental^2-4 and theoretical^5-8 activity to consider, primarily, the helix–coil transition, with a later similar theoretical treatment of the transition between an antiparallel β-sheet and the statistical coil.⁹

Elkan Blout played a very important role in the experimental studies of the helix–coil transition by developing methods to synthesize high-molecular-weight poly-α-amino acids,^2,10-16 to study their properties, including the helix–coil transition,^17-21 with optical rotation,^22-29 circular dichroism,^30,31 and infrared spectroscopy,^32-38 and by demonstrating the biological properties of some of these homopolymers, e.g., their antigenicity.³⁹ He also developed synthetic methods to study polyproline and models of the triple helix of collagen,^31,40-48 including the triple helix-to-coil transition,⁴⁹ and demonstrated the presence of cis peptide bonds preceding proline.⁵⁰ Elkan was thus a leader among several other eminent scientists in studies of the conformational properties of poly-α-amino acids.

The theoretical work on the helix–coil transition was based on the one-dimensional Ising model, for which a matrix treatment was used to formulate the partition function to calculate the thermodynamic properties of the transitions in homopolyamino acids. This theoretical approach was extended to treat copolymers, in addition to the original focus on homopolymers of amino acids, and thereby to acquire information about the tendencies of each of the 20 naturally occurring amino acids to take on the helix conformation at a given temperature.⁵¹ Aside from this application, however, it was soon realized that the helix–coil transition is not a good model for conformational changes in globular proteins, because the one-dimensional Ising model does not capture the cooperative features, embodied in the interplay between short- and long-range interactions, of the folding/unfolding transition of globular proteins.^52-57

The parallel development of molecular mechanics (MM) was designed to overcome the failure of the one-dimensional Ising model to treat the protein folding problem. During the development of MM, the helix–coil transition was treated as one example^58-62 of the valid application of the developing MM methodology. This article describes our early experimental approach, which then evolved into a theoretical approach to determine protein structure and protein-folding pathways. The experimental approach focused on bovine pancreatic ribonuclease A (RNase A), and the theoretical approach evolved from some early applications of MM to treat the properties of the α-helix, and the extension of MM methodology to treat conformational changes in globular proteins, i.e., the protein-folding problem.

EARLY STUDIES OF HELIX–COIL TRANSITIONS

The early statistical mechanical treatment of the helix–coil transition is summarized in a book that provided the various theoretical approaches and also reprinted the seminal papers in which these approaches were described.⁶³ The factors relating to the question of a phase transition in polyamino acids⁶⁴ and polynucleotides,⁶⁵ the kinetics of the helix–coil transition in polyamino acids,^66-68 and the role of hydrophobic interactions between nonpolar side chains in stabilizing α-helices^69,70 received extensive early consideration.

Early MM studies were carried out to assess the factors stabilizing α-helices,^71,72 and determining the relative preferences for left- and right-handedness⁷³ in the α-helical forms of polyamino acids. With verification by experiment,⁷⁴ the MM method was extended to treat both the helical and coil forms, and hence the helix–coil transition in polyamino acids.^58-62 These studies were the forerunner for the application of MM to nonregular linear⁷⁵ and cyclic⁷⁶ oligopeptides, and fibrous^77,78 and globular^79-82 proteins.

EARLY CONSIDERATION OF INTERRESIDUE INTERACTIONS, AND MOTIVATION FOR DEVELOPMENT AND APPLICATIONS OF MM

While proteins were known to be copolymers of amino acids linked by peptide bonds, it was the determination of the amino acid sequence of insulin by Sanger⁸³ that established that such copolymers are unbranched, and consist of unique amino acid sequences. At about the same time, Pauling proposed the α-helix and β-sheet conformations by relying heavily on the presence of hydrogen bonds between the NH and CO groups of the backbone of the polypeptide chain.¹

Recognizing that the unique properties of proteins also depend on the interactions among their side chains,⁸⁴ we investigated the effect of hydrogen bonds on the acid-base equilibria (pKs) of ionizable side-chain groups⁸⁵ and on limited proteolysis.⁸⁶ For example, if a tyrosyl-OH group is hydrogen-bonded to a glutamyl-COO^– group, then the pK of the tyrosyl group will be raised, and that of the COOH group will be lowered by the free energy of formation of the hydrogen bond.⁸⁵ Therefore, identification of such “abnormal” pK's provides a clue as to the existence of such a hydrogen bond. In addition, the free energy for disrupting such a hydrogen bond will have to be paid in hydrolyzing the peptide group of the backbone whose side-chain hydrogen bonds must be broken to liberate the peptide fragment.⁸⁶ Therefore, in contrast to the hydrolysis of, say, a simple dipeptide, which thermodynamically goes to completion, the hydrolysis of a peptide group when the side chain is hydrogen-bonded will not go to completion; i.e., as demonstrated in the thrombin-catalyzed hydrolysis of peptides from fibrinogen,^87,88 such a limited hydrolytic reaction catalyzed by a proteolytic enzyme can be involved in a reversible equilibrium. In other words, a proteolytic enzyme can catalyze the formation of a peptide bond, because the hydrogen bonds between the fragment and the rest of the protein provide favorable thermodynamics for peptide-bond synthesis.⁸⁶ Supporting experimental evidence for this view of limited protolysis⁸⁶ was also provided by Seifter et al.⁸⁹

This model of peptide-bond synthesis takes on added significance in considering the role of the ribosome in the synthesis of peptide bonds.⁹⁰ Gindulyte et al.⁹⁰ carried out quantum mechanical calculations on a group of 50 atoms chosen to represent the formation of the transition state (TS) during peptide-bond formation on the ribosome. They computed the activation energy for the process, and found that the hydrogen bonds that are formed between the 3′ end of the A-site tRNA and atoms of the ribosomal environment, while translocating into the P-site, lowered the activation energy for formation of the TS. We may regard such hydrogen bonds as also providing the free energy of equilibrium stabilization of the newly formed peptide bond.

Hydrophobic interactions^91,92 can provide further stabilization of hydrogen bonds. For example, hydrophobic interactions, in which, say, a leucine side chain interacts with the nonpolar neck of a hydrogen-bonded glutamyl residue (as illustrated in Fig. 1 of Ref. 93) can strengthen such a lysyl · · · glutamyl hydrogen bond. The consequence of the earlier considerations is that hydrogen bonds can be located by potentiometric titrations that identify ionizable groups with abnormal pKs. With associated physical–chemical and biochemical studies⁹⁴ to identify hydrogen-bonded pairs, such hydrogen bonds provide distance constraints on how the backbone may fold.

The foregoing provided the rationale to obtain distance constraints⁹⁴ to determine the folded structure of a protein before the advent of X-ray or NMR methods to determine protein structures. In particular, 3 out of 6 tyrosyl side chains, and 3 out of 11 side-chain carboxyl groups, of RNase A were found to have abnormal pKs, which suggested the possible existence of three hydrogen bonds. In a series of chemical modifications (before the advent of recombinant DNA techniques) and physical–chemical and biochemical studies, three tyrosyl–aspartyl interactions (out of 19,800 ways to specifically pair 3 out of 6 tyrosyl side chains with 3 out of 11 side-chain carboxyl groups) were identified,⁹⁴ namely Tyr25 · · · Asp14, Tyr 92 · · · Asp 38, and Tyr 97 · · · Asp83. These interactions were confirmed by the subsequent determination of the crystal structure of RNase A.⁹⁵

These three Tyr · · · Asp interactions, plus the location of four disulfide bonds in RNase A, and the suggestion^96,97 that His12, His119, and Lys41 are in the active site of this enzyme, constituted distance constraints that motivated the development of computational methodology⁹⁸ to calculate the three-dimensional structure of the protein, by making use of these distance constraints in the minimization of the empirical conformational energy of the protein. Without introducing the conformational energy and minimizing its energy, this limited number of distance constraints is not sufficient to determine the backbone structure. In fact, ~80 distance constraints, with half of them between residues i and j in the range of 5 ≤ |i – j| ≤ 20 and the other half with |i – j| ≥ 21, would be required⁹⁹ in order to obtain the structure of a 57-residue protein with an RMSD < 2 Å with respect to the native structure if these distances are known exactly. If the distances in these two ranges are known only within an error no greater than ~2 Å, then more than ~150 such distances are required. Additional information is available⁹⁹ about how the distributions of |i – j| distances and through-space distances d_ij affect the RMSD. Hence, the evolution of computational methodology in our laboratory proceeded in two different directions making use of (1) knowledge-based information (distance constraints, homology modeling, etc.) together with an empirical potential-energy function and (2) a physics-based potential-energy function without reliance on knowledge-based information.

EXPERIMENTAL DETERMINATION OF FOLDING PATHWAYS

When Anfinsen identified spontaneous protein folding and introduced the thermodynamic hypothesis for a theoretical approach,¹⁰⁰ we expanded our interest in determining protein structure to also determine folding pathways (first by experiment and later by theoretical methods).

Our initial experimental work was carried out with insulin, the only protein whose amino acid sequence was known⁸³ at the time. However, experimental difficulties arose in the attempt to locate hydrogen bonds by potentiometric titration to determine pKs, because insulin is largely insoluble at neutral pH. But, as soon as the amino sequence of lysozyme was determined, our efforts turned to this protein which is soluble over the pH range of interest. However, lysozyme also presented experimental problems because of its relatively high tryptophan content. To locate hydrogen bonds by observing abnormal pKs of ionizable side-chain groups, it was necessary to carry out chemical modification and determine the amino acid composition of proteolytically obtained fragments. But, analysis for tryptophan was very difficult before the later development of improved methods for determining amino acid composition. Finally, with the availability of the amino acid sequence of RNase A, which is water-soluble and contains no tryptophan, it was possible to determine the kinetics and thermodynamics in the oxidative folding of RNase A, using either glutathione¹⁰¹ or dithiothreitol^102–104 as the oxidizing agent.

With dithiothreitol as the redox reagent, the following mechanism was deduced for the oxidative folding of RNase A: where R is the reduced protein, and 1S–4S are ensembles of one-, two-, three- and four-disulfide species, respectively (with the subscript U indicating that they are essentially unfolded species). The 1S–4S species are involved in a pre-equilibrium (quasi-steady-state condition). In the rate-determining step, the 3S_U ensemble reshuffles by SH/SS interchange along two different pathways (in the approximate ratio 78:18) to form native-like des [40 – 95]_N and des [65 – 72]_N, respectively, both of which go rapidly to the native form. The remaining ~5% of the protein goes through two separate pathways, which could be detected only by mutating the Cys40, Cys95 and Cys65, Cys72 residues, respectively, to prevent formation of the corresponding disulfide bonds.^105,106 The rate-determining step in the oxidative folding of each of these two mutants involves oxidation from the 2S_U ensemble to the native form, rather than SH/SS interchange, as illustrated in the following scheme: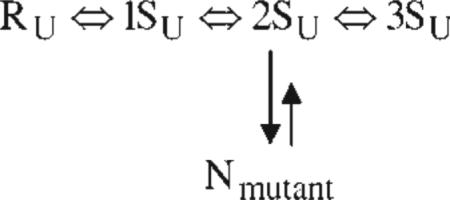

Thus, these experiments identified a minimum of four different pathways for the oxidative folding of wild-type RNase A.

In the initial folding stages, i.e., up to formation of the 1S ensemble of wild-type RNase A, 40% of the 28 theoretically possible 1S forms have the 65–72 disulfide bond,¹⁰⁷ which persists to an even greater extent in the formation of the 2S ensemble.¹⁰⁸ The following scheme illustrates some details of the folding pathways of wild-type RNase A: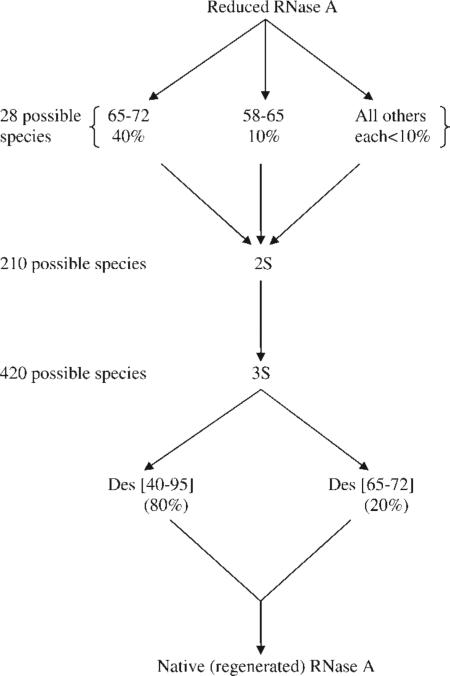

The preference of the 4:1 ratio for the native 65–72 disulfide bond relative to the non-native 58–65 disulfide bond is the same in the 1S folding stage of both the native protein and of an isolated 58–72 fragment.^109,110 Since both possible loops, 58–65 and 65–72, have the same number of residues and, hence, involve the same entropy of loop closure, this 4:1 ratio indicates that specific local interactions lead to the preference for formation of the 65–72 loop; such preferential interactions in this loop have been identified by NMR¹¹¹ and MM¹¹² computations.

COMPUTATIONS OF POLYPEPTIDE AND PROTEIN STRUCTURE WITH AN ALL-ATOM FORCE FIELD

The experimental work described earlier led to the development of MM^98,113 to compute protein structure. Using an all-atom representation of the polypeptide chain and an empirical potential-energy function, Empirical Conformational Energy Program for Peptides (ECEPP),¹¹⁴ together with a variety of procedures for global optimization of the potential energy,¹¹⁵ the low-energy (global-minimum) structures of various α-helices,^71-73 several linear⁷⁵ and cyclic⁷⁶ peptides, and fibrous proteins,^77,78 were computed. As an example, one of these global optimization procedures, Electrostatically Driven Monte Carlo (EDMC),¹¹⁶ together with an implicit hydration model, was used⁷⁹ in four simulations of the 46-residue three-helix bundle, protein A, providing structures within an RMSD of ~4 Å from the known native structure. This was the largest protein whose all-atom structure had been computed at the time, and the calculation was carried out in 11 days with 60 processors of a Beowulf-type cluster. By contrast, a single trajectory on a smaller, 36-residue protein, the villin headpiece, simulated by molecular dynamics (MD),¹¹⁷ required 4 months on a Cray computer. The villin headpiece was subsequently simulated⁸⁰ with the EDMC procedure.

COMPUTATION OF FOLDING PATHWAYS WITH AN ALL-ATOM FORCE FIELD

The folding pathway of protein A¹¹⁸ from an initial unfolded state i to a final folded state f was computed by use of a procedure, involving a stochastic difference equation (SDE), developed by Elber et al.¹¹⁹ Both states i and f must be known in order to compute the pathways from i to f with the SDE procedure. The folded state f, of course, is either an X-ray or NMR structure of the protein. But the initial state i is not a single structure, but rather an ensemble of unfolded structures. Therefore, 130 representative structures were generated by MD; each of them was treated as an initial state i, and then all 130 trajectories were averaged.

In the SDE procedure, the action, S, defined as ${\int }_i^f{\left[2(E-U)\right]}^{1∕2}\mathrm{d}l$, is required to remain stationary along the trajectory length l from i to f, where E is the total energy, and U is the potential energy. From the computed results, it appeared that the C-terminal helix folded first, followed by the N-terminal helix, and then the middle helix. Contrary to expectations, it was found¹¹⁸ that the radius of gyration did not decrease significantly until about halfway through the trajectory, i.e., an initial “hydrophobic collapse” was not observed. We have recently found¹²⁰ that the sequence of folding events is sensitive to the external conditions (temperature, friction, and random forces).

COMPUTATION OF STRUCTURE AND FOLDING PATHWAYS BY A HIERARCHIAL PROCEDURE

Although an all-atom representation of the polypeptide chain could be used to compute the structure⁷⁹ and folding pathway¹¹⁸ of the 46-residue protein A, it has not yet been possible to compute protein structures and folding pathways for proteins containing 100–200 residues with the all-atom representation. We have therefore developed a hierarchical approach in which the all-atom representation is initially replaced by a united-residue (UNRES) model,¹²¹ and the search of the UNRES potential energy is carried out with a conformational space annealing (CSA) method.¹²² The motivation of this search is to locate the region of the global minimum; then the results of the UNRES search are converted to an all-atom representation,^123,124 and the search is continued in this region with the EDMC procedure.

The UNRES model is obtained by averaging over all “unimportant” fast degrees of freedom, thereby reducing the number of force centers and the number of degrees of freedom, and rendering the search procedure feasible for large proteins. The CSA search procedure starts with a representative set of local minima in the multidimensional conformation energy space, and reduces their distribution (to the region of the global minimum) by selected moves in what is essentially a genetic algorithm. The results have been subjected to blind tests⁸² in successive (critical assessment of protein structure prediction procedures, CASP).

The predicted results have been sufficiently encouraging to motivate carrying out MD calculations with the UNRES model rather than with an all-atom one. Because all-atom MD trajectories require femtosecond moves to change conformation and, hence, do not reach the millisecond-to-second time-scale for folding all but the very fast-folding proteins, MD has not been successful in folding all-atom structures. However, because the fast degrees of freedom are averaged out in UNRES, it seemed possible that MD with UNRES might be able to simulate protein folding. Therefore, the mathematics for a Langevin-equation approach was formulated, and solved with a stochastic velocity Verlet algorithm.^125,126 This approach was successful in folding largely α-helical single-chain⁸¹ and two-chain¹²⁷ proteins, one containing as many as 75 residues, and in simulating folding kinetics.¹²⁸ To be able to treat α+β and β proteins, it was found to be necessary to introduce entropic effects.¹²⁹

CONCLUSIONS

Motivated originally by the experimental acquisition of distance constraints in RNase A by physical–chemical and biochemical procedures, a MM approach was developed to compute the three-dimensional structures of proteins. Later, in order to focus on the physics of inter-residue interactions in determining protein structures, reliance on knowledge-based information, such as experimental distance constraints, was abandoned in favor of the use of only the potential energy. Early investigations were carried out by global optimization of an all-atom representation of the potential energy but, in order to treat large protein structures, this approach evolved into a hierarchy procedure based on a UNRES representation of the potential energy. Subsequently, UNRES was used to compute not only protein structure but also folding pathways by means of the Langevin equation. Further, improvement¹²⁹ of the force field by including entropic effects and focusing on reproduction of thermodynamic properties, such as heat capacity, has led to improved predictions of protein structure.