Abstract
Cell-wall mechanical properties play an integral part in the growth and form of Saccharomyces cerevisiae. In contrast to the tremendous knowledge on the genetics of S. cerevisiae, almost nothing is known about its mechanical properties. We have developed a micromanipulation technique to measure the force required to burst single cells and have recently established a mathematical model to extract the mechanical properties of the cell wall from such data. Here we determine the average surface modulus of the S. cerevisiae cell wall to be 11.1 ± 0.6 N/m and 12.9 ± 0.7 N/m in exponential and stationary phases, respectively, giving corresponding Young's moduli of 112 ± 6 MPa and 107 ± 6 MPa. This result demonstrates that yeast cell populations strengthen as they enter stationary phase by increasing wall thickness and hence the surface modulus, without altering the average elastic properties of the cell-wall material. We also determined the average breaking strain of the cell wall to be 82% ± 3% in exponential phase and 80% ± 3% in stationary phase. This finding provides a failure criterion that can be used to predict when applied stresses (e.g., because of fluid flow) will lead to wall rupture. This work analyzes yeast compression experiments in different growth phases by using engineering methodology.
The response of a whole cell to applied forces is determined by the interplay of several factors, including the strength and elasticity of individual molecules composing the cell wall, the three-dimensional arrangement of those molecules, and genetic factors programming composition and assembly. Many genes that give rise to aberrant forms have been identified, although how the gene products affect form is not known (1). The cell-wall molecular structure is only partially understood (2, 3), and its mechanical properties are an area of “near-total darkness” (1). Recent advances in atomic force microscopy have enabled the elasticity of the glucopyranose ring (the main monomer in the Saccharomyces cerevisiae cell wall) to be measured (4), but it is not known what the mechanical properties of the assembly of molecules is (5), nor how environmental conditions affect these properties. Research is required in all these areas to understand growth and form at a fundamental level. It is clear that the determination of cell-wall mechanical properties is an essential part of this process and that, to date, they have been poorly studied. Understanding many bioprocess applications at the level of fluid-cell interactions is therefore not possible, because the response of whole cells to applied forces cannot be predicted (6).
Cell mechanical properties have been investigated by using experiments such as micropipette aspiration, osmotic swelling/shrinking, cell poking, and cell compression (7, 8). Atomic force microscopy techniques have also been applied (9). We have adopted the compression experiment because it allows the cell wall to be tested to the point of failure and data represent the whole-cell response. This approach is necessary if the equation describing the constitutive mechanical properties is to be used to describe the response of intact cells to applied forces.
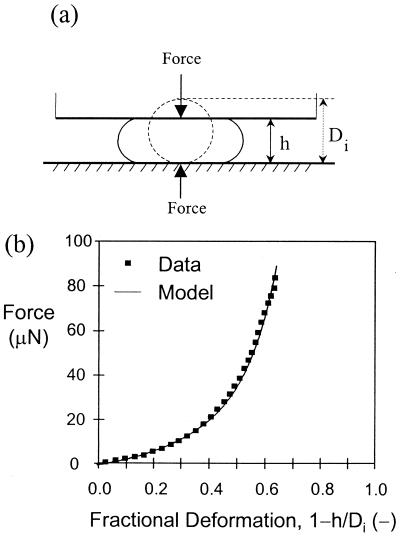
The compression experiment has been implemented by using a micromanipulation technique that enables the force required to compress a single yeast cell between two parallel surfaces to be measured as a function of cell deformation (10) (Fig. 1). A mathematical model for yeast-cell compression has been developed by using finite element analysis (11). The model idealizes the cell as an inflated, liquid-filled sphere with a cell wall that is permeable and described by a linear-elastic constitutive relationship. Although we accept that the wall is probably viscoelastic under certain stress environments, we have shown that an incompressible linear-elastic constitutive equation adequately describes the whole-cell response for yeast in the compression experiment (12). This assumption reflects the fact that yeast have a cell wall proper, unlike, for example, RBC, whose membranes exhibit considerable viscoelasticity (7). The use of this constitutive equation also prevents over-parameterization ensuring that the calculated parameters are meaningful and unique (11). The force-deformation response predicted by the model is then matched to that of the experiment by solving for the surface modulus (defined as the product of wall thickness and Young's modulus) and the wall hydraulic conductivity. The average Young's modulus for the wall is calculated as the surface modulus divided by the average corrected wall thickness (13). This parameter effectively defines the extent to which the material will deform in response to an applied load. Unique solution requires measurement of this wall thickness by transmission electron microscopy, and determination of the initial radial stretch because of turgor by using osmotic experiments (13). Information on the wall strain at cell breakage is also obtained from the analysis, allowing definition of a cell-wall failure criterion in terms of either maximum stress or strain (12).
Figure 1.
(a) An optic fibre probe is positioned above a single cell. The probe is then automatically moved by a motor controller at constant velocity to compress the cell to the point of bursting. The probe is connected to a force transducer that measures the force acting on the probe as a function of time. (b) Raw data are converted to force vs. deformation data, which are then analyzed by using our finite element model to provide the wall/surface modulus and permeability.
Using this approach, the wall surface modulus for a commercially available baker's yeast (Fermipan, Gist-Brocades, Delft, The Netherlands) was found to be 11.4 ± 0.4 N⋅m−1, which corresponded to a size-independent Young's modulus of 127 ± 4 MPa based on the average measured wall thickness of 90 nm (12). A breaking strain of 75% ± 8% was also determined (12). These properties were independent of large changes in both compression rate and suspending medium osmolality, demonstrating that the mathematical model adequately describes the mechanical behavior of yeast cells during the compression experiment. We also determined the hydraulic conductivity of the wall to be 0.1–1.0 μm⋅MPa−1⋅s−1, depending on the particular cell examined, which compares favorably with that of other cell types (e.g., RBC, 0.94 μm⋅MPa−1⋅s−1; erythroblastic leukemic cells, 0.89 μm⋅MPa−1⋅s−1; granulocytes, 0.19 μm⋅MPa−1⋅s−1; and Drosophila melanogaster embryos, 0.12 μm⋅MPa−1⋅s−1) (14). Here, we extend earlier work to quantitatively determine the cell-wall mechanical properties of a different S. cerevisiae strain in different phases of growth, and to determine the mechanism by which cells increase their resistance to mechanical stresses during the transition from exponential to stationary phase.
Materials and Methods
S. cerevisiae Y9 (NYCC strain 1006, kindly provided by T. W. Young, School of Biochemistry, University of Birmingham, U.K.) was grown on complex medium (Yeast Extract 8 g⋅liter−1, Bacteriological Peptone 4 g⋅liter−1, d-Glucose 80 g⋅liter−1, (NH4)2SO4 0.96 g⋅liter−1, NaCl 0.4 g⋅liter−1, CaCl2⋅2H2O 0.08 g⋅liter−1, MgCl2⋅6H2O 0.56 g⋅liter−1, KH2PO4 (anhydrous) 0.8 g⋅liter−1, and FeCl3⋅6H2O 0.0024 g⋅liter−1) in a 5-liter fermenter (Life Science Laboratories, Luton, U.K.). Air flow rate, stirrer speed, and temperature were controlled at 5 liter⋅min−1, 300 rpm, and 28°C, respectively. Initial model parameters were measured at 12 h and 36.5 h by using the methods outlined previously (13). Micromanipulation experiments were conducted at 13.4 h and 37.8 h. Compression velocity was 2.7 μm/s. The technique and custom-made apparatus are described elsewhere (10). Approximately 75 cells were tested in 90 min at 28°C. Medium supernatant was used as a diluent. The force-deformation data were analyzed with the mechanical model to extract the surface modulus and breaking strain by using the methods outlined previously (12).
Results and Discussion
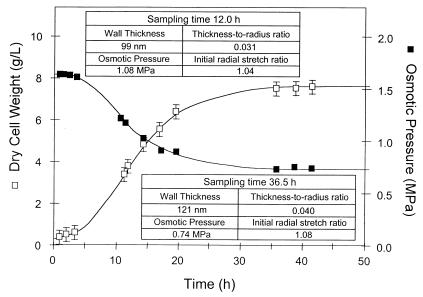
The fermentation time course for S. cerevisiae Y9 is given in Fig. 2. At the times indicated, force-deformation data and measurements of the initial radial stretch ratio and wall-thickness to cell-radius ratio were obtained. These data were analyzed with the mathematical model to extract the breaking strain and the surface modulus data given in Table 1. The Young's modulus was then calculated by using the thickness measurements in Fig. 2. Data were normally distributed at the 5% level. The Young's modulus and breaking strain are the same for each growth phase (P ≥ 0.05) despite significant differences in the surface modulus, suggesting that yeast cells strengthen as they enter stationary phase by increasing wall thickness without altering the elastic modulus of the wall material. Wall compositional changes thus appear to have only a secondary effect on yeast strength. This finding contrasts with that for Escherichia coli, where increased resistance to cellular disruption correlates with increased peptidoglycan crosslinkage as cells enter stationary phase (15).
Figure 2.
Fermentation time course for S. cerevisiae Y9. Raw data used to determine the initial radial stretch ratio and the initial thickness to radius ratio for the population were collected at 12.0 h and 36.5 h. Force-deformation experiments were conducted on 70–80 cells at 13.4 h and 37.8 h. Error bars represent twice the SE.
Table 1.
Mean and SD of the mean (given in parentheses) for cell-wall mechanical properties of exponential (70 cells) and stationary phase cells (79 cells) of S. cerevisiae Y9
| Growth phase | Initial parameters
|
Cell-wall mechanical properties
|
|||
|---|---|---|---|---|---|
| Radial stretch ratio | Thickness-to-radius ratio | Surface modulus, N⋅m−1 | Breaking strain, % | Young's modulus, MPa | |
| Exponential | 1.04 | 0.031 | 11.1 (0.29) | 82 (1.4) | 112 (2.9) |
| Stationary | 1.08 | 0.040 | 12.9 (0.34) | 80 (1.6) | 107 (2.8) |
| Statistical P value | 3 × 10−5 | 0.34 | 0.10 | ||
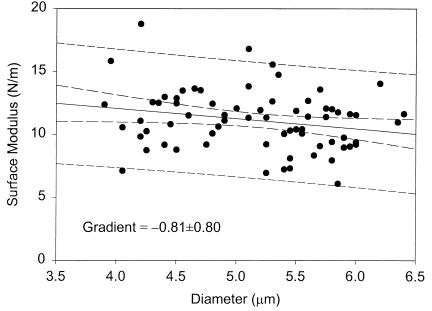
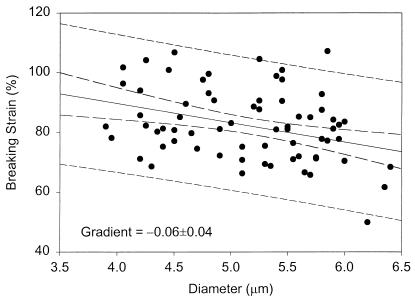
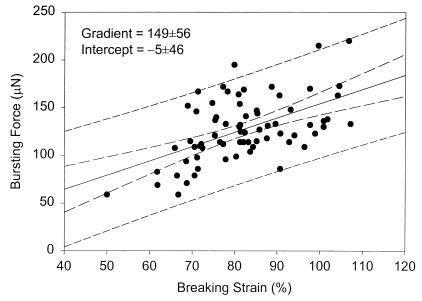
These results compare favorably with those for stationary-phase baker's yeast (127 ± 4 MPa and 75% ± 8%) (12), indicating only small variations in elastic modulus and breaking strain for significantly different S. cerevisiae strains and growth conditions. Surface modulus and breaking strain show only marginal dependence on cell size (Figs. 3 and 4) as observed previously for stationary-phase baker's yeast (12). Size-dependent variations in cell properties (e.g., bud-scar frequency) have only a secondary effect on the estimated surface modulus. Importantly, the force required to burst a single cell is directly correlated to the breaking strain and passes through the origin as required (Fig. 5).
Figure 3.
Size dependence of surface modulus (i.e., product of Young's modulus and wall thickness) for exponential-phase S. cerevisiae Y9 (13.4-h sample). A similar trend was found for stationary-phase cells (37.8-h sample). Dashed lines represent 95% confidence intervals on the mean and individual observations.
Figure 4.
Size dependence of breaking strain for exponential-phase S. cerevisiae Y9 (13.4-h sample). A similar trend was found for stationary-phase cells (37.8-h sample). Dashed lines represent 95% confidence intervals on the mean and individual observations.
Figure 5.
Correlation between the force required to burst a single cell and the cell-wall breaking strain for exponential-phase S. cerevisiae Y9 (13.4-h sample). A similar trend was found for stationary-phase cells (37.8-h sample). Dashed lines represent 95% confidence intervals on the mean and individual observations.
Similar mechanical properties have been measured at 100% relative humidity for the FJ7 mutant of the 168 strain of Bacillus subtilis, which forms threads suitable for measurement with standard fiber-measuring techniques (16), giving Young's modulus 30 MPa and breaking strain 60%–80%. The cell walls of S. cerevisiae are three to four times stiffer than those of B. subtilis, reflecting the differences in underlying molecular structure. Cell walls of B. subtilis consist of glycan chains with peptide substitutes that cross-link to form a molecular network (16). Cell walls of S. cerevisiae consist predominantly of glucan with (1,3)-β and (1,6)-β linkages, and mannan covalently linked to protein (mannoprotein) (2, 17). Mechanical properties are thought to be only a function of the β-glucans, whereas the role of mannoproteins is to control porosity (2). Differences in the mechanical properties of the polymer-types and the degree of cross-linking contribute to the 3- to 4-fold difference in stiffness. Interestingly, the breaking strain is similar in both cases.
Conclusions
Fundamental to life is the ability to assemble mechanical structures from molecular building blocks. Understanding the mechanical response of entire cells to applied forces is of importance to biology, but such understanding has not been rigorously obtained for even simple organisms such as yeast (1). Despite a lack of detailed published information on microscale architecture, we have shown that the average failure behavior of the S. cerevisiae cell is approximately constant across growth phases, and that the wall breaking strain is consistent with that for B. subtilis. The data suggest that the average surface modulus of yeast cell populations is altered in response to changes in growth conditions by variation in the wall thickness, without significant change in the average elastic modulus. Yeast populations therefore strengthen as they enter stationary phase simply by increasing their wall thickness. We have also demonstrated that the cell wall fails, on average, when a critical strain of 80% is exceeded at any point in the wall. This finding provides a useful failure criterion that can be used to predict whether imposed stresses will cause cell rupture, for example in response to applied fluid stresses (18).
Acknowledgments
This work was partially supported by the British Council in the form of a Postgraduate Bursary to A.E.S.
References
- 1.Harold F M. Microbiology. 1995;141:2765–2778. doi: 10.1099/13500872-141-11-2765. [DOI] [PubMed] [Google Scholar]
- 2.Klis F M. Yeast. 1994;10:851–869. doi: 10.1002/yea.320100702. [DOI] [PubMed] [Google Scholar]
- 3.Cid V J, Durán A, del Rey F, Snyder M P, Nombela C, Sánchez M. Microbiol Rev. 1995;59:345–386. doi: 10.1128/mr.59.3.345-386.1995. [DOI] [PMC free article] [PubMed] [Google Scholar]
- 4.Marszalek P E, Oberhauser A F, Pang Y-P, Fernandez J M. Nature (London) 1998;396:661–664. doi: 10.1038/25322. [DOI] [PubMed] [Google Scholar]
- 5.Ruiz-Herrera J. Fungal Cell Wall: Structure, Synthesis, and Assembly. Boca Raton, FL: CRC; 1992. [Google Scholar]
- 6.Thomas C R, Zhang Z. In: Advances in Bioprocess Engineering II. Galindo E, Ramírez O T, editors. London: Kluwer; 1998. pp. 137–170. [Google Scholar]
- 7.Fung Y C. Biomechanics: Mechanical Properties of Living Tissues. 2nd Ed. New York: Springer; 1993. [Google Scholar]
- 8.Zahalak G I, McConnaughey W B, Elson E L. J Biomech Eng. 1990;112:283–294. doi: 10.1115/1.2891186. [DOI] [PubMed] [Google Scholar]
- 9.Vinckier A, Semenza G. FEBS Lett. 1998;430:12–16. doi: 10.1016/s0014-5793(98)00592-4. [DOI] [PubMed] [Google Scholar]
- 10.Mashmoushy H, Zhang Z, Thomas C R. Biotechnol Lett. 1998;12:925–929. [Google Scholar]
- 11.Smith A E, Moxham K E, Middelberg A P J. Chem Eng Sci. 1998;53:3913–3922. [Google Scholar]
- 12.Smith A E, Moxham K E, Middelberg A P J. Chem Eng Sci. 2000;55:2031–2041. [Google Scholar]
- 13.Smith A E, Zhang Z, Thomas C R. Chem Eng Sci. 2000;55:2043–2053. [Google Scholar]
- 14.Martínez de Marañón I, Gervais P, Molin P. Biotechnol Bioeng. 1997;56:62–70. doi: 10.1002/(SICI)1097-0290(19971005)56:1<62::AID-BIT7>3.0.CO;2-T. [DOI] [PubMed] [Google Scholar]
- 15.Middelberg A P J, O'Neill B K, Bogle I D L, Gully N J, Rogers A H, Thomas C J. Trans Inst Chem Eng. 1992;70C:213–218. [Google Scholar]
- 16.Thwaites J J, Mendelson N H. Adv Microb Physiol. 1991;32:173–222. doi: 10.1016/s0065-2911(08)60008-9. [DOI] [PubMed] [Google Scholar]
- 17.Fleet G H. In: The Yeasts. 2nd Ed. Rose A H, Harrison J S, editors. Vol. 4. London: Academic; 1991. pp. 199–277. [Google Scholar]
- 18.Kleinig A R, Middelberg A P J. Chem Eng Sci. 1998;53:891–898. [Google Scholar]