On semiparametric efficient inference for two-stage outcome-dependent sampling with a continuous outcome

Summary

Outcome-dependent sampling designs have been shown to be a cost effective way to enhance study efficiency. We show that the outcome-dependent sampling design with a continuous outcome can be viewed as an extension of the two-stage case-control designs to the continuous-outcome case. We further show that the two-stage outcome-dependent sampling has a natural link with the missing-data and biased-sampling framework. Through the use of semiparametric inference and missing-data techniques, we show that a certain semiparametric maximum likelihood estimator is computationally convenient and achieves the semiparametric efficient information bound. We demonstrate this both theoretically and through simulation.

1. INTRODUCTION

The case-control design, in which one over-samples the diseased individuals, is the most well known outcome-dependent sampling scheme for binary outcomes (Cornfield, 1951; Prentice & Pyke, 1979). The principal idea of an outcome-dependent sampling design is to concentrate resources on where there is the greatest amount of information. The two-stage case-control design is an extension of the simple case-control design that has been shown to improve statistical efficiency and reduce study costs in epidemiology studies (White, 1982). In the first stage of a typical two-stage design, information about the outcome Y is available for a study population or its random sample. Information about an exposure variable X is only available on a subset of the first-stage population; which is termed the second-stage. The second-stage sampling usually depends on the outcome. There is a large literature on analyzing data from two-stage designs; see Breslow & Cain (1988), Zhao & Lipsitz (1992), Weinberg & Wacholder (1993), Wacholder & Weinberg (1994), Lawless et al. (1999), Breslow et al. (2003) and Wang & Zhou (2006).

For outcome-dependent sampling with a continuous response, Zhou et al. (2002; 2007) considered an empirical likelihood approach for studies with only second-stage data. For the two-stage design, Chatterjee et al. (2003) proposed a pseudoscore estimator and Weaver & Zhou (2005) proposed a maximum estimated likelihood estimator. Both methods are computationally easy at the expense of efficiency. Lawless et al. (1999) recommended discretization of the continuous response to achieve an easily calculable maximum profile likelihood estimator. As discussed in Chatterjee et al. (2003), such a simplification entails a loss of information and a decrease in the external validity of the analyses, because the results may be sensitive to the choice of cutpoints. In summary, these existing methods are based on some approximations to the likelihood function. As far as we know, no one has developed fully efficient estimation for two-stage outcome-dependent sampling designs with a continuous response, because of the challenge in terms of both theory and computation. In this note, we develop a semiparametric maximum likelihood estimator that achieves full efficiency for this setting, and we point out that the two-stage outcome-dependent sampling estimate has a natural connection with the missing data and biased sampling literature. The connection occurs because the covariates can be viewed as missing by design, with the sampling probability of the covariates depending on the outcome.

2. TWO-STAGE OUTCOME-DEPENDENT SAMPLING WITH A CONTINUOUS OUTCOME

We consider the outcome-dependent sampling setting of Weaver & Zhou (2005) and recast it into a two-stage outcome-dependent sampling design. This design with a continuous outcome can be considered as a direct extension of White (1982) and Breslow & Cain (1988). The two-stage outcome-dependent sampling design for a continuous outcome (Weaver & Zhou, 2005) allows researchers to sample in the second-stage a simple random sample and some supplementary outcome-dependent samples from the first-stage population. In this setting, the response Y is observed for all in the first-stage, but the exposure variable X is only observed for those in the second-stage, i.e., the simple random sample and the supplementary outcome-dependent samples, in which the selection probability of the supplementary outcome-dependent sampling samples depends on Y. We assume that the joint density of (Y,X) is f(Y|X;θ)g(X) with respect to a dominating measure ν × μ on 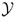× 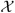, where f(·|·) is known up to a d-dimensional parameter θ of interest and g(·) is an unknown probability density function.

To fix notation, we further assume that the base population consists of n individuals (Y,X), and the domain of Y is a union of K mutually exclusive intervals, C_k = (c_k−1, c_k] for k = 1,…,K, with c_k, k = 0, 1,…,K, being prespecified constants satisfying c₀ = −∞ < c₁ < c₂ < … < c_K = ∞. Thus Y partitions the study population into K strata such that, for k = 1,…, K, the {Y ∈ C_k} stratum has N_k individuals, and we define $n={\displaystyle {\sum }_{k=1}^K{N}_k.}$ Conditional on n, (N₁, … ,N_K) follows a multinomial distribution with size n and probabilities (π₁, …, π_K), where π_k ≡ Pr(Y ∈ C_k) is the proportion of the population falling into the kth stratum, for k = 1, …, K. Among the n individuals, n₀ are obtained from the simple random sample, and n_k out of N_k individuals in stratum k, k = 1, …, K, are selected as the second-stage outcome-dependent supplemantary samples.

We consider two types of stage-two outcome-dependent sampling in this article: Bernoulli sampling and Negative Binomial sampling. With Bernoulli sampling, all subjects which are in the kth stratum, but not included in the simple random sample, are independently sampled with probability p_k such that, conditional on N_k and n_0k, En_k = (N_k − n_0k)p_k. In this sampling scheme, the sample size n is fixed and the second-stage outcome-dependent sample sizes {n₁, …, n_K} are random. With Negative Binomial sampling, all subjects which are in the kth stratum, but not included in the simple random sample, are sampled with the probability of success p_k, until a total of n_k subjects have been selected. In this sampling scheme, the sample size n is random and the values n_k, k = 1, …, K, are prespecified.

Although assuming the existence of a simple random sample is not necessary for the theoretical aspect, in practice it ensures the availability of the exposure variable X for every stratum of the response Y. Moreover, it is a prevailing choice for epidemiologists to include a simple random sample in their studies. This will afford them the flexibility to study other endpoints and to validate their models.

Let $n_V=n_0+{\displaystyle {\sum }_{k=1}^K{n}_k}$ be the total size of the second-stage sample for which we observe (Y,X), and let n_V̄ = n − n_V be the number of individuals in the first-stage population for whom only Y is observed. Define the sampling indicator for the ith individual, i = 1, …, n, as

$$R_i=\{\begin{array}{l}1\text{if}{X}_i\text{is observed}\\ 0\text{if}{X}_i\text{is not observed}.\end{array}$$

Then V ≡ {i : R_i = 1} represents the index set of all complete observations, and V̄ ≡ {i : R_i = 0} represents the index set of all incomplete observations, such that n_V = |V|, n_V̄ = |V̄| and n = |V ∪ V̄|. Furthermore, we define V_k ≡ {i : R_i = 1, Y_i ∈ C_k}, V̄_k ≡ {i : R_i = 0, Y_i ∈ C_k} and N_k ≡ |V_k ∪ V̄_k|, k = 1,…, K. Thus, the data structure of two-stage outcome-dependent sampling with a continuous Y can be summarized as follows: in the first stage, we sample Y_i, for i ∈ V_k + V̄_k; in the second stage, we sample X_i, given Y_i ∈ C_k, for i ∈ V_k.

In both sampling schemes, conditional on the sample size n and the first-stage sample, the individual (X_i, Y_i) falling into kth stratum is selected for full observation, giving R_i = 1, with prespecified probability p_k. Hence we have a ‘missing at random’ structure: Pr(R_i = 1|Y_i ∈ C_k) = p_k, k = 1, …, K. Thus we cast the two-stage outcome-dependent sampling design into a general missing-data framework.

With derivation based on integrating a multinomial law, as in Weaver & Zhou (2005), the likelihood function from the two-stage outcome-dependent sampling with Bernoulli sampling has the form

$$\begin{array}{ccc}\mathcal{L}(\theta ,G)\hfill & =\hfill & \left\{{\displaystyle \prod _{i\in V}{f}_{\theta }(Y_i|X_i;\theta )g(X_i)}\right\}\left\{{\displaystyle \prod _{j\in \overline{V}}{f}_Y(Y_j;\theta ,G)}\right\}\hfill \\ \hfill & =\hfill & \left\{{\displaystyle \prod _{i\in V}{f}_{\theta }(Y_i|X_i;\theta )g(X_i)}\right\}\left\{{\displaystyle \prod _{j\in \overline{V}}{\displaystyle {\int }_X{f}_{\theta }(Y_j|u;\theta )dG(u)}}\right\},\hfill \end{array}$$ (1)

where g(·) and G(·) are the probability function and the cumulative distribution function for X respectively, and f_Y (·; θ,G) is the probability density function of Y. Taking steps similar to those in the Appendix B of Scott & Wild (2001), we can show that the likelihood function from the two-stage outcome-dependent sampling with Negative Binomial sampling takes the same form even though the second-stage outcome-dependent sample sizes {n₁, …, n_K} are chosen without replacement.

To obtain the maximum likelihood estimators of (θ,G), we will maximize the log-likelihood by replacing the term g(X_i) in equation (1) by its point-mass equivalent, G{X_i}, and similarly for dG(u). The loglikelihood in (1) can also be written in terms of missing-data notation: ℙ_n{Rlog f_θ(Y|X; θ)+Rlog G{X}+(1 − R) log f_Y (Y; θ,G)}, where ℙ_n is the empirical measure of the observations; that is, for every measurable function f, ${\mathbb{P}}_{n}f(X_i,Y_i,R_i)=n^{-1}{\displaystyle {\sum }_{i=1}^{n}f(X_i,Y_i,R_i)}$.

When Y is discrete, van der Vaart & Wellner (2001) give some examples in which the maximum likelihood estimator of the full likelihood (θ̌_n, Ǧ_n) of (θ, G) does not exist; this is because the strata are defined by continuous covariates. However, this is not the case in outcome-dependent sampling since the sampling probability here depends only on the outcome, not on the covariates. The existence of the maximum likelihood estimator can be shown in the same way as in Murphy & van der Vaart (2001). In general, however, the maximum likelihood estimator (θ̌_n, Ǧ_n) is not unique (van der Vaart & Wellner, 1992), since Ǧ_n need not be concentrated on {X_i : R_i = 1}. Here we consider the restricted maximum likelihood estimator (θ̂_n, Ĝ_n) of the empirical likelihood, where G is concentrated on {X_i : R_i = 1}. The asymptotic equivalence of these two types of estimator can be established in the same way as in van der Vaart & Wellner (2001) and Zhang & Rockette (2005).

3. STATISTICAL INFERENCE

To maximize the loglikelihood over {g_i, i ∈ V}, the probability concentrated on i ∈ V, we consider the Lagrangian function

$$H(\theta ,g_i,\mathrm{\lambda })={\displaystyle \sum _{i\in V}\text{log}f(Y_i|X_i;\theta )+{\displaystyle \sum _{i\in V}\text{log}{g}_i+{\displaystyle \sum _{j\in \overline{V}}\text{log}\left\{{\displaystyle \sum _{i\in V}{g}_{i}f(Y_j|X_i;\theta )}\right\}-\lambda ({\displaystyle \sum _{i\in V}{g}_i-1),}}}}$$

where λ is the Lagrange multiplier corresponding to the normalizing restriction on the {g_i, i ∈ V}. We take the derivative of H with respect to g_i and set it equal to 0:

$$\frac{\partial H}{\partial g_i}=\frac{1}{g_i}+{\displaystyle \sum _{j\in \overline{V}}\frac{f(Y_j|X_i;\theta )}{{\displaystyle {\sum }_{k\in V}{g}_{k}f(Y_j|X_k;\theta )}}}-\lambda =0.$$ (2)

Multiplying both sides of (2) by g_i, summing over i, and taking the restrictions into account, we obtain

$${\displaystyle \sum _{i\in V}{g}_i\frac{\partial H}{\partial g_i}=n-\lambda =0,}$$

and thus λ = n. Substituting back into (2) and solving for g_i yields the restricted maximum likelihood estimator

$${\widehat{g}}_i={\left\{n-{\displaystyle \sum _{j\in \overline{V}}\frac{f(Y_j|X_i;\theta )}{{\displaystyle {\sum }_{k\in V}{\widehat{g}}_{k}f(Y_j|X_k;\theta )}}}\right\}}^{-1}.$$ (3)

In the outcome-dependent sampling literature, Zhou et al. (2002) implement the empirical likelihood method of Qin (1993) to simplify the computation. In our setting, it is unlikely that this approach can be adapted, because of the nature of the continuous outcome: the number of constraints increases as the sample size increases, and hence the number of parameters is the same as the sample size. This poses a challenge for the computation of the proposed estimator. We recommend maximizing the restricted loglikelihood using the following mixed Newton's method.

Step 1. Start with an initial estimate θ⁰ and $g_i^0,$ i ∈ V.

Step 2. Plug in θ⁰ and $g_i^0$ into the right-hand side of the score equations (3), solve the equations iteratively using the fixed-point algorithm until it converges, and call the solution $g_i^c.$

Step 3. Plug $g_i^c$ into the likelihood and maximize the parametric likelihood using Newton's method to update θ^c.

Step 4. Repeat steps 2 and 3 until convergence.

We found that the algorithm works well. The fixed-point algorithm is easy to solve and is particularly useful for cases with large sample sizes where the method avoids computing the inverse of a huge matrix, as required in the usual Newton method.

To obtain the variance estimator of θ̂_n, we will use the profile likelihood approach proposed by Murphy & van der Vaart (2000) for a general semiparametric model. The smoothness conditions of Theorem 1 in Murphy & van der Vaart (2000) can be verified and the profile likelihood function pL_n(θ) ≡ max_G∈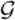 L_n(θ, G) can be shown to approximate a nondegenerate parabolic function around θ̂_n. Moreover the inverse of the curvature of the profile loglikelihood function at θ̂_n can be used to estimate consistently the asymptotic variance of θ̂_n.

Using empirical process techniques and semiparametric inference, we establish the model identifiability, consistency and the weak convergence results. The identifiability of (θ,G) is summarized in the Appendix. Using a Wald-type argument, together with the identifiability result, we establish the following consistency result.

Theorem 1

Suppose that assumptions A2–A4 hold as given in the Appendix. Then |θ̂_n − θ₀| + sup_h∈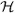 |(Ĝ_n − G₀)h| → 0, almost surely, for every Glivenko-Cantelli class 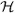that is bounded in L₁(G₀), where L₁(G₀) refers to the class of integrable functions under G₀.

To derive the weak convergence result, let ψ ≡ (θ,G), and l̇(y; ψ) ≡ ḟ(y; ψ)/f(y; ψ). The score operator for ψ takes the form U_n(ψ)(h) = ℙ_nU(ψ)(h), where U(ψ)(h) ≡ U₁(ψ)(h₁) + U₂(ψ)(h₂), and U₁(ψ)(h₁) ≡ l̇_θ(r, z)h₁ = {rl̇_θ(y|x; θ) + (1 − r)l̇(y; ψ)}h₁, U₂(ψ)(h₂) = rh₂(x) + (1 − r)E{h₂(X)|Y = y}, where h₁ ∈ ℝ^d, h₂ belongs to a class of square integrable functions, and ∫ h₂dG₀ = 0.

The adjoint operator of U₂(ψ)(h) can be computed as

$$U_2^{*}b(x)={\displaystyle \sum _{k=1}^K{p}_k{\displaystyle {\int }_{C_k}b\{1,(y,x)\}f(y|x;\theta )d\nu (y)+{\displaystyle \sum _{k=1}^K{q}_k{\displaystyle {\int }_{C_k}b(0,y)f(y|x;\theta )d\nu (y),}}}}$$

where q_k = 1 − p_k, and

$$U_2^{*}{U}_{2}h(x)={\displaystyle \sum _{k=1}^K{p}_k{\displaystyle {\int }_{C_k}h(x)f(y|x;\theta )d\nu (y)+{\displaystyle \sum _{k=1}^K{q}_k{\displaystyle {\int }_{C_k}E(h(x)|y)f(y|x;\theta )d\nu (y).}}}}$$

We note that the score operator shares the same form as the score in the general ‘missing at random’ framework, whereas its adjoint operator has a special feature of the outcome-dependent sampling design. To obtain the information operator, we can differentiate the expectation of the score operator using the map t ↦ ψ + tψ₁, where ψ, ψ₁ ∈ Θ × 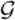. The information operator σ_ψ(h) = Pσ̂_ψ(h), where σ̂_ψ(h) takes a 2 × 2 ‘matrix’ form, with ${\widehat{\sigma }}_{\psi }^{11}(h_1)\equiv P{\dot{l}}_{\theta }^{\otimes 2},{\widehat{\sigma }}_{\psi }^{12}(h_2)\equiv U_2^{*}{\dot{l}}_{\theta }{h}_2,{\widehat{\sigma }}_{\psi }^{21}(h_1)\equiv P{U}_2{h}_1{\dot{l}}_{\theta }^{\prime }\text{and}{\widehat{\sigma }}_{\psi }^{22}(h_2)\equiv U_2^{*}{U}_2{h}_2$. It can be shown that σ_ψ0(h) is continuously invertible and onto.

The following theorem establishes the asymptotic distribution of ψ̂_n.

Theorem 2

Under assumptions A1–A8 as given in the Appendix, √n(ψ̂_n − ψ0) is asymptotically linear, with influence function $\t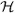ilde{l}(h)=U({\psi }_0)\{{\sigma }_{{\psi }_0}^{-1}(h)\},$ h ∈ ₁, converging weakly in the uniform norm to a tight, zero-mean Gaussian process ℤ with covariance E{l̃(g)l̃(h)}, for all g, h ∈ ℝ^d × 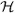₁, where ${\mathcal{H}}_1\equiv C_1^{\alpha }(\mathcal{X})$, α > max(d/2, 1), is the class of α-smooth functions; see § 2·7·1 of van der Vaart & Wellner (1996).

Remark 1

Since √n(ψ̂_n − ψ0) is asymptotically linear, with influence function contained in the closed linear span of the tangent space, ψ̂_n is regular and hence efficient, by Theorems 5.2.3 and 5.2.1 of Bickel et al. (1998). The information bounds thus share the same form as that in Nan et al. (2004) after some algebra.

4. NUMERICAL RESULTS

We carried out simulations to evaluate the behaviour of the proposed estimators with that of Weaver & Zhou (2005) and Chatterjee et al. (2003). The data were generated from a linear regression model of the form Y = β₀+β₁X+β₂Z+σϵ, where X ~ N(0, 1), Z ~ Ber(0·45) and ϵ ~ N0, 1); that is, given X and Z, Y ~ N(β₀ + β₁X + β₂Z, σ²). We fix β₀ = 1, β₂ = −0·5 and σ² = 1. We investigated the effect of strengthening the regression relationship between Y and X by allowing β₁ to take successively the values 0, 0·5 and 1. Parameter and standard error estimates were obtained for each of 2000 independently generated datasets. All simulations were conducted using programs written in Matlab. The results are summarized in Table 1.

Table 1.

Simulation results with (a) n₀ = 200, p₁ = p₃ = 0·185 and p₂ = 0, and (b) n₀ = 50, p₁ = p₃ = 1 and p₂ = 0.

	Mean		Mean	95% C.I.	Relative efficiencies
Model	θ̂n	SE(θ̂n)	ESE(θ̂n)	Coverage	MELE	PSE
(a) n0 = 200, p1 = p3 = 0·185 and p2 = 0
β0 = 1	1·000	0·048	0·048	0·948	0·973	0·998
β1 = 0	−0·002	0·049	0·048	0·944	0·976	0·987
β0 = 1	0·998	0·057	0·056	0·950	0·936	0·982
β1 = 0·5	0·504	0·045	0·047	0·957	0·964	0·973
β0 = 1	1·008	0·064	0·065	0·952	0·846	0·911
β1 = 1	0·991	0·047	0·046	0·948	0·934	0·883
(b) n0 = 50, p1 = p3 = 1 and p2 = 0
β0 = 1	0·999	0·033	0·033	0·949	0·821	0·974
β1 = 0	0·002	0·028	0·027	0·956	0·723	0·925
β0 = 1	1·003	0·036	0·034	0·944	0·413	0·539
β1 = 0·5	0·501	0·030	0·030	0·963	0·323	0·356
β0 = 1	0·996	0·052	0·049	0·944	0·367	0·802
β1 = 1	1·004	0·036	0·036	0·964	0·390	0·648

C.I., confidence interval; SE, standard error; ESE, estimated standard error; MELE, maximum estimated likelihood estimator; PSE, pseudoscore estimator.

The study population size was set to n = 2000. For Table 1(a), the outcome-dependent sampling design consisted of a simple random sample with n₀ = 200, supplemented with additional samples from individuals with Y values in the tails of the marginal distribution, with cutpoints μY ± σY, where μY and σY represent respectively the mean and standard deviation of Y. We took the Bernoulli sampling for the second-stage outcome-dependent sampling. All 1800 subjects which were not included in the simple random sample were independently sampled with probability (0·185, 0, 0·185) from the three strata respectively. This yields the average second-stage outcome-dependent sample sizes to be n₁ = n₃ = 50, n₂ = 0 and a validation sampling fraction ρV of about 0·15. In the second setting, presented in Table 1(b), we set the simple random sample n₀ to be 50 and increased the second-stage outcome-dependent sampling probability of X in the two tails to be one; that is, we tried to include all samples in the tails while keeping very few samples in the middle, where the proportion is small. This sampling scheme yields the average second-stage outcome-dependent sample sizes to be n₁ = n₃ = 290, n₂ = 0 and a validation sampling fraction ρV of about 0·32. Table 1 contains the results for β₀ and β₁ of three simulation settings corresponding to different values of β₁ and includes the finite-sample properties of the restricted maximum likelihood estimator, as well as the finite-sample relative efficiencies, i.e., ratios of empirical variances of the estimators, for the pseudoscore estimator and the maximum estimated likelihood estimator, all calculated relative to the restricted maximum likelihood estimator.

All estimators exhibits negligible bias for all four model parameters, the means of the standard error estimates agree very well with the sample standard errors of the 2000 simulations, and the confidence intervals attain coverage close to the nominal 95% level; the corresponding results for the pseudoscore estimator and maximum estimated likelihood estimator are not shown. In both settings, the restricted maximum likelihood estimator is the most efficient of the three estimators, as expected; as the regression effect of X gets stronger, the efficiency gains of the restricted maximum likelihood estimator over the competing estimators becomes larger. When β₁ = 0, the behaviour of these inefficient estimators is almost as good as that of the restricted maximum likelihood estimator. This is because the nonvalidation observations do not contain any information about X, although they still contain information about Z, and so we would not expect to see much gain in efficiency for the maximum likelihood estimator which can use more information contained in nonvalidation observations than can the other estimators.

The efficiency gains of the restricted maximum likelihood estimator are also associated with the validation sample proportion. For the same outcome-dependent sampling scheme, the efficiency gain of the restricted maximum likelihood estimator increases while the validation sample proportions of the two tails increase. In the extreme case of Table 1(b), the restricted maximum likelihood estimator has substantial efficiency gains when the regression effect of X is not zero. When the sampling proportion is not particularly ‘extreme’, such as with the sample validation proportion of the first setting (0·267, 0·1, 0·267), the restricted maximum likelihood estimator does not appear to lead to huge gains in efficiency over the maximum estimated likelihood estimator and the pseudoscore estimator. Nevertheless, the restricted maximum likelihood estimator never performs worse than either of the others.

APPENDIX

Technical details

First we present assumptions needed in section 3.

Assumption A1

The true parameters (θ₀;G₀) are identifiable in the model

$$\mathcal{F}=\{F_{\theta ,G}:d{F}_{\theta ,G}/d(\nu \times \mu )=f(y|x;\theta )g(x),\theta \in \mathrm{\Theta },G\in \mathcal{G}\},$$

where Θ is a compact metric space, and 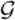≡ {G : G is a distribution on 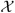with density g with respect to μ}.

Assumption A2

The space X ∈ 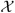is a semimetric space that has a completion that is compact and contains 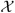as a Borel set.

Assumption A3

The maps (θ, x) ↦ f(y|x; θ) are uniformly continuous.

Assumption A4

We assume that P₀[sup_θ∈Θ log{f(y|x; θ)/f(y|x; θ₀)}] < ∞, and f(y|x; θ) > 0 for all y ∈ 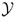and x ∈ .

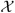Assumption A5

The set 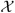is a bounded subset of ℝ^d with nonempty interior.

Assumption A6

We assume that ${\text{sup}}_{h\in \mathcal{H}}|(G-G_0)(U_2^{*}(\psi )U_2(\psi )-U_2^{*}({\psi }_0)U_2({\psi }_0))h|=o({\Vert G-G_0\Vert }_{\mathcal{H}})$, as θ → θ₀, G → G₀.

Assumption A7

The function x ↦ f(y|x; θ) is continuously differentiable for each y. For all x, x′ ∈ 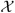and constants D and α > 0,

$${\displaystyle \int \left|\frac{\partial }{\partial x_i}f(y|x;{\theta }_0)-\frac{\partial }{\partial x_i}f(y|x\prime ;{\theta }_0)\right|}d\mu (x)\le D{\Vert x-x\prime \Vert }^{\alpha },$$

and

$${\displaystyle \int \left|\frac{\partial }{\partial x_i}f(y|x;{\theta }_0)\right|d\mu (x)\le D.}$$

Assumption A8

The map θ ↦ log f(y|x; θ) is three times differentiable with respect to θ, and the third-order derivatives are bounded by integrable functions of (Y;X) for θ ∈ Θ₀, where Θ₀ is a subset of Θ, and θ₀ ∈ Θ₀.

Identifiability result

Suppose that Assumption A1 holds. Then (θ;G) is identifiable in the model 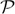= {P_θ,G : dP_θ,G/d(ν × μ) = p(·; θ,G), θ ∈ Θ, G ∈ 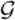}, where p(·; θ,G) is given by (1). This result can be proved by verifying the definition. Details can be found in a technical report available from the authors.

Proof of Theorem 1

If Ĝ_θ denotes the maximizer of G ↦ L_n(θ,G), the score function takes the form ℙ_n Rh = Ĝ_θ {s_n (x; θ, Ĝ_θ)h}, where

$$s_n(x;\theta ,G)=1-{\mathbb{P}}_n\left\{(1-R)\frac{f(y|x;\theta )}{f(y;\theta ,G)}\right\}.$$

With the asymptotic tightness of Ĝ_n not hard to verify, and with the Glivenko-Cantelli properties of the involved functions, shown in our technical report, we can establish the consistency by the Helly selection theorem.

Proof of Theorem 2

The proof mainly involves checking the conditions of Theorem 3.3.1 of van der Vaart & Wellner (1996). A critical step is to show that σ _ψ0 is continuously invertible and onto, which can be established by using Lemma 25.93 of van der Vaart (1998).