Abstract
This paper describes an approach to smooth the surface and improve the quality of quadrilateral/hexahedral meshes with feature preserved using geometric flow. For quadrilateral surface meshes, the surface diffusion flow is selected to remove noise by relocating vertices in the normal direction, and the aspect ratio is improved with feature preserved by adjusting vertex positions in the tangent direction. For hexahedral meshes, besides the surface vertex movement in the normal and tangent directions, interior vertices are relocated to improve the aspect ratio. Our method has the properties of noise removal, feature preservation and quality improvement of quadrilateral/hexahedral meshes, and it is especially suitable for biomolecular meshes because the surface diffusion flow preserves sphere accurately if the initial surface is close to a sphere. Several demonstration examples are provided from a wide variety of application domains. Some extracted meshes have been extensively used in finite element simulations.
Keywords: quadrilateral/hexahedral mesh, surface smoothing, feature preservation, quality improvement, geometric flow
1 Introduction
The quality of unstructured quadrilateral/hexahedral meshes plays an important role in finite element simulations. Although a lot of efforts have been made, it still remains a challenging problem to generate quality quad/hex meshes for complicated structures such as the biomolecule Ribosome 30S shown in Figure 1. We have described an isosurface extraction method to generate quad/hex meshes for arbitrary complicated structures from volumetric data and utilized an optimization-based method to improve the mesh quality [1] [2] [3], but the surface needs to be smoothed and the mesh quality needs to be further improved.
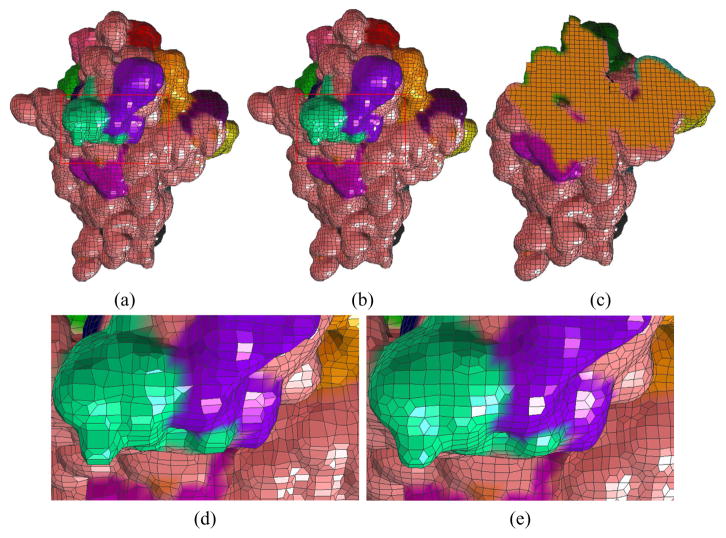
Fig. 1.
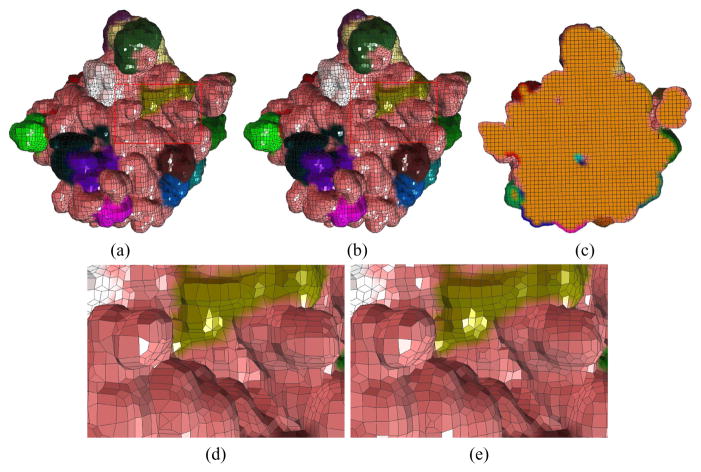
The comparison of mesh quality of Thermus Thermophilus small Ribosome 30S (1J5E) crystal subunit. The pink color shows 16S rRNA and the remaining colors are proteins. (a) the original quadrilateral mesh (13705 vertices, 13762 quads); (b) the improved quadrilateral mesh; (c) the improved hexahedral mesh (40294 vertices, 33313 hexes); (d) the zoom-in picture of the red box in (a); (e) the zoom-in picture of the red box in (b). The mesh quality is measured by three quality metrics as shown in Figure 10.
Geometric partial differential equations (GPDEs) such as Laplacian smoothing have been extensively used in surface smoothing and mesh quality improvement. There are two main methods in solving GPDEs, the finite element method (FEM) and the finite difference method (FDM). Although FDM is not robust sometimes, people still prefer to choosing FDM instead of FEM because FDM is simpler and easier to implement. Recently, a discretized format of the Laplacian-Beltrami (LB) operator over triangular meshes was derived and used in solving GPDEs [4] [5] [6]. In this paper, we will discretize the LB operator over quadrilateral meshes, and discuss an approach to apply the discretizated format on surface smoothing and quality improvement for quadrilateral or hexahedral meshes.
The main steps to smooth the surface and improve the quality of quadrilateral and hexahedral meshes are as follows:
Discretizing the LB operator and denoising the surface mesh - vertex adjustment in the normal direction with volume preservation.
Improving the aspect ratio of the surface mesh - vertex adjustment in the tangent direction with feature preservation.
Improving the aspect ratio of the volumetric mesh - vertex adjustment inside the volume.
For quadrilateral meshes, generally only Step 1 and Step 2 are required, but all the three steps are necessary for surface smoothing and quality improvement of hexahedral meshes.
Unavoidly the quadrilateral or hexahedral meshes may have some noise over the surface, therefore the surface mesh needs to be smoothed. In this paper, we derive a discretized format of the LB operator, and choose the surface diffusion flow (Equation (1)) to smooth the surface mesh by relocating vertices along their normal directions. The surface diffusion flow is volume preserving and also preserves a sphere accurately if the initial surface mesh is embedded and close to a sphere, therefore it is especially suitable for surface smoothing of biomolecular meshes since biomolecules are usually modelled as a union of hard spheres.
The aspect ratio of the surface mesh can be improved by adjusting vertices in the tangent plane, and surface features is preserved since the movement in the tangent plane doesn’t change the surface shape ([7], page 72). For each vertex, the mass center is calculated to find its new position on the tangent plane. Since the vertex tangent movement is an area-weighted relaxation method, it is also suitable for adaptive quadrilateral meshes.
Besides the movement of surface vertices, interior vertices also need to be relocated in order to improve the aspect ratio of hexahedral meshes. The mass center is calculated as the new position for each interior vertex.
Although our relaxation-based method can not guarantee that no inverted element is introduced for arbitrary input meshes, it works well in most cases with the properties of noise removal, feature preservation, mesh quality improvement. Furthermore, it is especially suitable for surface smoothing and quality improvement of biomolecular meshes. As the ‘smart’ Laplacian smoothing [8] [9], this method is applied only when the mesh quality is improved in order to avoid inverted elements. This method can also be combined with the optimization-based method to obtain a high quality mesh with relatively less computational cost.
The remainder of this paper is organized as follows: Section 2 reviews the previous related work; Sections 3 discusses the detailed algorithm of the LB operator discretization, surface smoothing and quality improvement of quadrilateral meshes; Sections 4 explains the quality improvement of hexahedral meshes; Section 5 shows some results and applications; The final section presents our conclusion.
2 Previous Work
It is well-known that poor quality meshes result in poorly conditioned stiffness matrices in finite element analysis, and affect the stability, convergence, and accuracy of finite element solvers. Therefore, quality improvement is an important step in mesh generation.
Some quality improvement techniques of triangular and tetrahedral meshes, such as the edge-contraction method, can not be used for quadrilateral and hexahedral meshes because we do not want to introduce any degenerated elements. Therefore, the mesh smoothing methods are selected to improve the quality of quad/hex meshes by adjusting the vertex positions in the mesh while preserving its connectivity. As reviewed in [10] [11], Laplacian smoothing and optimization are the two main quality improvement techniques.
As the simplest and most straight forward method for node-based mesh smoothing, Laplacian smoothing relocates the vertex position at the average of the nodes connecting to it [12]. There are a variety of smoothing techniques based on a weighted average of the surrounding nodes and elements [13] [14] [15]. The averaging method may invert or degrade the local quality, but it is computationally inexpensive and very easy to implement, so it is in wide use. Winslow smoothing is more resistant to mesh folding because it requires the logical variables are harmonic functions [16].
Instead of relocating vertices based on a heuristic algorithm, people utilized an optimization technique to improve mesh quality. The optimization algorithm measures the quality of the surrounding elements to a node and attempts to optimize it [17]. The algorithm is similar to a minimax technique used to solve circuit design problems [18]. Optimization-based smoothing yields better results but it is more expensive than Laplacian smoothing, and it is difficult to decide the optimized iteration step length. Therefore, a combined Laplacian/optimization-based approach [8] [9] [19] was recommended. Physically-based simulations are used to reposition nodes [20]. Anisotropic meshes are obtained from bubble equilibrium [21] [22].
When we use the smoothing method to improve the mesh quality, it is also important to preserve surface features. Baker [23] presented a feature extraction scheme which is based on estimates of the local normals and principal curvatures at each mesh node. Local parametrization was utilized to improve the surface mesh quality while preserving surface characteristics [24], and two techniques called trapezium drawing and curvature-based mesh improvement were discussed in [25].
Staten et al. [26] [27] proposed algorithms to improve node valence for quadrilateral meshes. One special case of cleanup in hexahedral meshes for the whisker weaving algorithm is presented in [28]. Schneiders [29] proposed algorithms and a series of templates for quad/hex element decomposition. A recursive subdivision algorithm was proposed for the refinement of hex meshes [30].
3 Quadrilateral Mesh
Noise may exist in quadrilateral meshes, therefore we need to smooth the surface mesh. The quality of some quadrilateral meshes may not be good enough for finite element calculations, and the aspect ratio also needs to be improved.
There are two steps for the surface smoothing and the quality improvement of quadrilateral meshes: (1) the discretization of Laplace-Beltrami opertor and the vertex movement along its normal direction to remove noise, (2) the vertex movement on its tangent plane to improve the aspect ratio while preserving surface features.
3.1 Geometric Flow
Various geometric partial differential equations (GPDEs), such as the mean curvature flow, the surface diffusion flow and Willmore flow, have been extensively used in surface and imaging processing [5]. Here we choose the surface diffusion flow to smooth the surface mesh,
| (1) |
where Δ is the Laplace-Beltrami (LB) operator, H is the mean curvature and n(x) is the normal vector at the node x. In [31], the existence and uniqueness of solutions for this flow was discussed, and the solution converges exponentially fast to a sphere if the initial surface is embedded and close to a sphere. It was also proved that this flow is area shrinking and volume preserving [5].
In applying geometric flows on surface smoothing and quality improvement over quadrilateral meshes, it is important to derive a discretized format of the LB operator. Discretized schemes of the LB operator over triangular meshes have been derived and utilized in solving GPDEs [4] [5] [6].
A quad can be subdivided into triangles, hence the discretization schemes of the LB operator over triangular meshes could be easily used for quadrilateral meshes. However, since the subdivision of each quad into triangles is not unique (there are two ways), the resulting discretization scheme is therefore not unique. Additionally in the discretization scheme, the element area needs to be calculated. If we choose to split each quad into two triangles and calculate the area of a quad as the summation of the area of two triangles, then the area calculated from the two different subdivisions could be very different because four vertices of a quad may not be coplanar. Therefore, a unique discretized format of the LB operator directly over quad meshes is required.
3.2 Discretized Laplace-Beltrami Operator
Here we will derive a discretized format for the LB operator over quadrilateral meshes. The basic idea of our scheme is to use the bilinear interpolation to derive the discretized format and to calculate the area of a quad. The discretization scheme is thus uniquely defined.
Area Calculation
Let [p1 p2 p4 p3] be a quad in ℝ3, then we can define a bilinear parametric surface S that interpolates four vertices of the quad as shown in Figure 2:
| (2) |
Fig. 2.
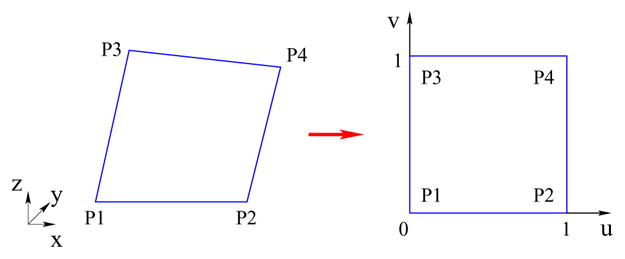
A quad [p1 p2 p4 p3] is mapped into a bilinear parametric surface.
The tangents of the surface are
| (3) |
| (4) |
Let ∇ denote the gradient operator about the (x, y, z) coordinates of the vertex P1, then we have
| (5) |
| (6) |
Let A denote the area of the surface S(u, v) for (u, v) ∈ [0, 1]2, then we have
| (7) |
It may not be easy to obtain the explicit form for integrals in calculating the area, numerical integration quadrature could be used. Here we use the following four-point Gaussian quadrature rule to compute the integral
| (8) |
where
The integration rule in Equation (8) is of O(h4), where h is the radius of the circumscribing circle.
Discretized LB Operator
The derivation of the discretized format of the LB operator is based on a formula in differential geometry [4]:
| (9) |
where A is the area of a region R over the surface around the surface point p, diam(R) denotes the diameter of the region R, and H(p) is the mean curvature normal.
From Equation (7), we have
| (10) |
where
∇A could be written as
| (11) |
with
| (12) |
Here we still use the four-point Gaussian quadrature rule in Equation (8) to compute the integrals in the αi j. It follows from Equation (12) that , we have
| (13) |
Now let pi be a vertex with valence n, and p2 j (1 ≤ j ≤ n) be one of its neighbors on the quadrilateral mesh, then we can define three coefficients α2, α3, α4 as in (13). Now we denote these coefficients as and for the quad [pi p2 j−1 p2 j p2 j+ 1] as shown in Figure 3. By using Equation (13), the discrete mean curvature normal can be defined as
Fig. 3.
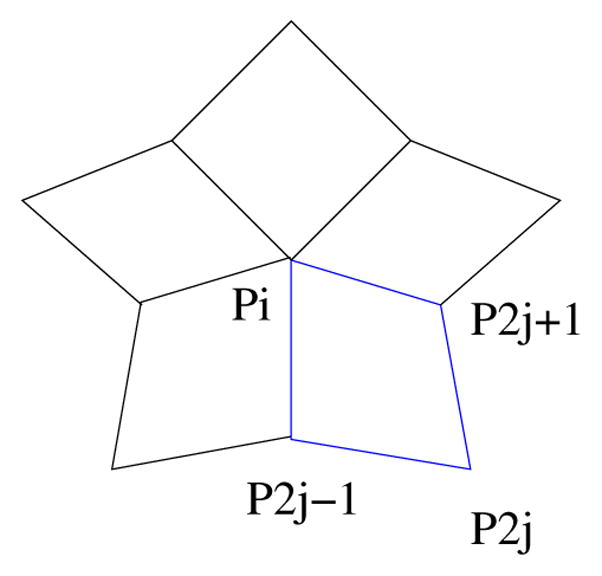
A neighboring quad [pi p2 j− 1 p2 j p2 j+1] around the vertex pi.
| (14) |
where H(pi) denotes the mean curvature normal, A(pi) is the total area of the quads around pi, and
Using the relation Δx = 2H(pi) ([32], page 151), we obtain
| (15) |
Therefore,
| (16) |
where H(pk) and H(pi) are further discretized by (14). Note that n(pi)n(pk)T is a 3 × 3 matrix.
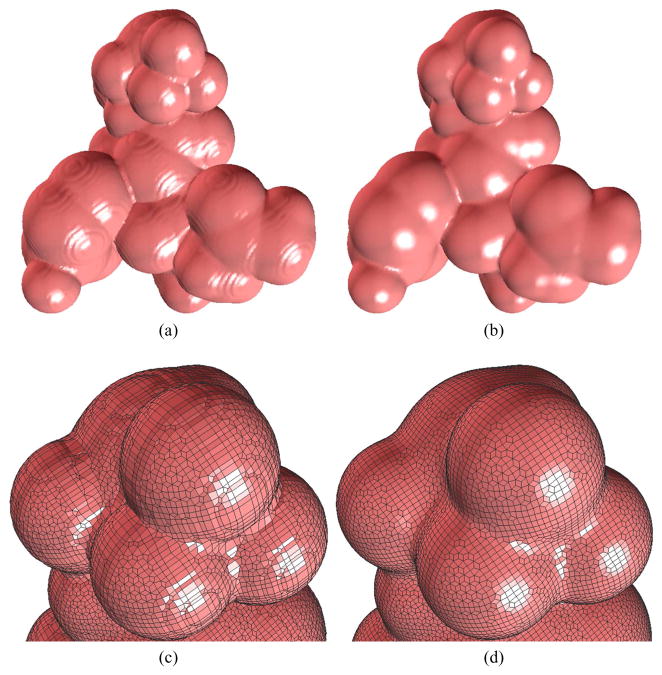
Figure 4 shows one example of the molecule consisting of three amino acids (ASN, THR and TYR) with 49 atoms. The molecular surface was bumpy as shown in Figure 4(a) since there are some noise existing in the input volumetric data, the surface becomes smooth after the vertex normal movement as shown in Figure 4(b).
Fig. 4.
Surface smoothing and quality improvement of the molecule consisting of three amino acids (ASN, THR and TYR) with 49 atoms (45534 vertices, 45538 quads). (a) and (c) - the original mesh; (b) and (d) - after surface smoothing and quality improvement.
3.3 Tangent Movement
In order to improve the aspect ratio of the surface mesh, we need to add a tangent movement in Equation (1), hence the flow becomes
| (17) |
where v(x) is the velocity in the tangent direction T(x). First we calculate the mass center m(x) for each vertex on the surface, then project the vector m(x) − x onto the tangent plane. v(x)T(x) can be approximated by [m(x) − x] − n(x)T [m(x) − x]n(x) as shown in Figure 5.
Fig. 5.
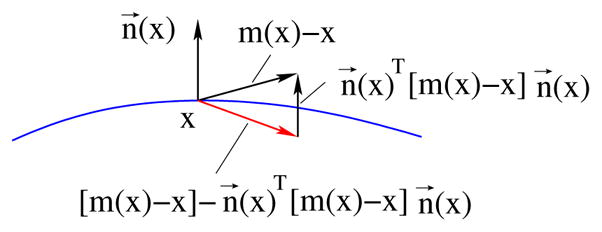
The tangent movement at the vertex x over a surface. The blue curve represents a surface, and the red arrow is the resulting tangent movement vector.
Mass Center
A mass center p of a region S is defined by finding p ∈ S, such that
| (18) |
S is a piece of surface in ℝ3, and S consists of quads around vertex x. Then we have
| (19) |
A j is the area of the quad [pi p2 j− p2 j p2 j+ 1] calculated from Equation (7) using the integration rule in Equation (8). Then we can obtain
| (20) |
where is the total of quad areas around pi. The area of a quad can be calculated using Equation (7).
In Figure 4, the vertex tangent movement is used to improve the aspect ratio of the quadrilateral mesh of the molecule consisting of three amino acids. Compared with Figure 4(c), it is obvious that the quadrilateral mesh becomes more regular and the aspect ratio is better as shown in Figure 4(d).
3.4 Temporal Discretization
In the temporal space, is approximated by a semi-implicit Euler scheme , where τ is the time step length. is the approximating solution at t = nτ, is the approximating solution at t = (n + 1)τ, and serves as the initial value at xi.
The spatial and temporal discretization leads to a linear system, and an approximating solution is obtained by solving it using a conjugate gradient iterative method with diagonal preconditioning.
3.5 Discussion
Vertex Normal Movement
The surface diffusion flow can preserve volume. Furthermore, it also preserves a sphere accurately if the initial mesh in embedded and close to a sphere. Suppose a molecular surface could be modelled by a union of hard spheres, so it is desirable to use the surface diffusion flow to evolve the molecular surface. Figure 4 shows one example, the molecular surface becomes more smooth and features are preserved after surface denoising.
Vertex Tangent Movement
If the surface mesh has no noise, we can only apply the tangent movement to improve the aspect ratio of the mesh while ignoring the vertex normal movement. Our tangent movement has two properties:
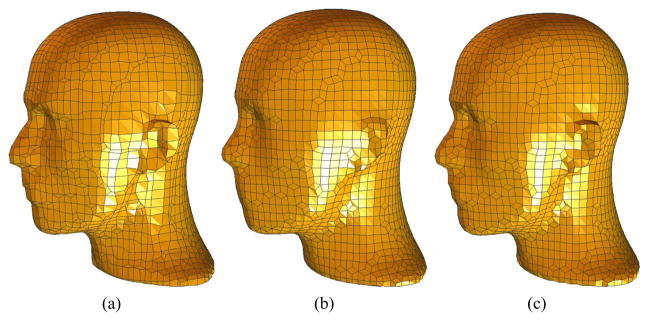
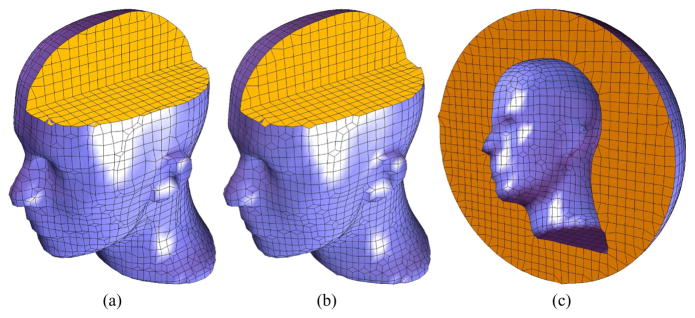
The tangent movement doesn’t change the surface shape ([7], page 72). Figure 6 shows the comparison of the human head model before and after the quality improvement. In Figure 6, each vertex is relocated to its mass center, so both normal movement and tangent movement are applied. After some iterations, the facial features, such as the nose, eyes, mouth and ears, are removed. In Figure 6(c), the vertex movement is restricted on the tangent plane, therefore facial features are preserved.
The tangent movement is an area-weighted averaging method, which is also suitable for adaptive quad meshes as shown in Figure 7 and 8. In Figure 7, there is a cavity in the structure of biomolecule mouse acetylcholinesterase (mAChE), and denser meshes are generated around the cavity while coarser meshes are kept in all other regions. In Figure 8, finer meshes are generated in the region of facial features of the human head.
Fig. 6.
The quality of a quadrilateral mesh of a human head model is improved (2912 vertices, 2912 quads) after 100 iterations with the time step length 0.01. (a) The original mesh; (b) Each vertex is relocated to its mass center, some facial features are removed; (c) Only tangent movement is applied.
Fig. 7.
The quality of an adaptive quadrilateral mesh of a biomolecule mAChE is improved (26720 vertices, 26752 quads). (a) the original mesh; (b) after quality improvement.
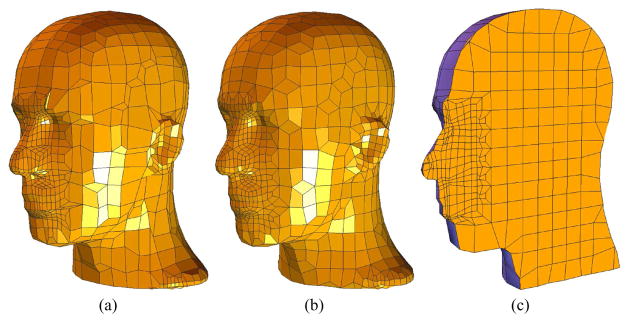
Fig. 8.
Adaptive quadrilateral/hexadedral meshes of the human head. (a) the original quad mesh (1828 vertices, 1826 quads); (b) the improved quad mesh; (c) the improved hex mesh (4129 vertices, 3201 hexes), the right part of elements are removed to shown one cross section.
From Figure 6, 7 and 8, we can observe that after tangent movement, the quadrilateral meshes become more regular and the aspect ratio of the meshes is improved, as well as surface features are preserved.
4 Hexahedral Mesh
There are three steps for surface smoothing and quality improvement of hexahedral meshes, (1) surface vertex normal movement, (2) surface vertex tangent movement and (3) interior vertex relocation.
4.1 Boundary Vertex Movement
The dual contouring hexahedral meshing method [1] [2] [3] provides a boundary sign for each vertex and each face of a hexahedron, indicating if it lies on the boundary surface or not. For example, a vertex or a face is on the surface if its boundary sign is 1, while lies inside the volume if its boundary sign is 0.
The boundary sign for each vertex/face can also be decided by checking the connectivity information of the input hexahedral mesh. If a face is shared by two elements, then this face is not on the boundary; if a face belongs to only one hex, then this face lies on the boundary surface, whose four vertices are also on the boundary surface.
We can use the boundary sign to find the neighboring vertices/faces for a given vertex. For each boundary vertex, we first find all its neighboring vertices and faces lying on the boundary surface by using the boundary sign, then relocate it to its new position calculated from Equation (17). There is a special situation that we need to be careful, a face/edge, whose four/two vertices are on the boundary, may not be a boundary face.
4.2 Interior Vertex Movement
For each interior vertex, we intend to relocate it to the mass center of all its surrounding hexahedra. There are different methods to calculate the volume for a hexahedron. Some people divide a hex into five or six tetrahedra, then the volume of the hex is the summation of the volume of these five or six tetrahedra. This method is not unique since there are various dividing formats. Here we use an trilinear parametric function to calculate the volume of a hex.
Volume Calculation
Let [p1 p2 ··· p8] be a hex in ℝ3, then we define the trilinear parametric volume V (u, v, w) that interpolates eight vertices of the hex as shown in Figure 9:
| (21) |
Fig. 9.
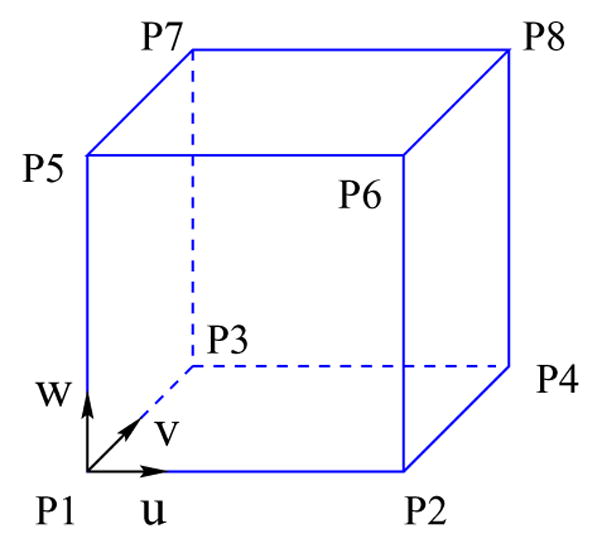
The trilinear parametric volume V of a hexahedron [p1 p2 ··· p8].
The tangents of the volume are
Let V denote the volume of V (u, v, w) for (u, v, w) ∈ [0, 1]3, then we have
| (22) |
where
| (23) |
Numerical integration quadrature could be used. Here we choose the following eight-point Gaussian quadrature rule to compute the integral
| (24) |
where
The integration rule in Equation (24) is of O(h4), where h is the radius of the circumscribing sphere.
Mass Center
A mass center p of a region V is defined by finding p ∈ V, such that
| (25) |
V is a piece of volume in ℝ3, and V consists of hexahedra around vertex x. Then we have
| (26) |
Vj is the volume of the hex [p1 p2 ··· p8] calculated from the trilinear function, then we can obtain
| (27) |
where N(i) is the index set of the one ring neighbors of pi, and is the total of hex volume around pi.
The same Euler scheme is used here for temporal discretization, and the linear system is solved using the conjugate gradient iterative method.
5 Results and Applications
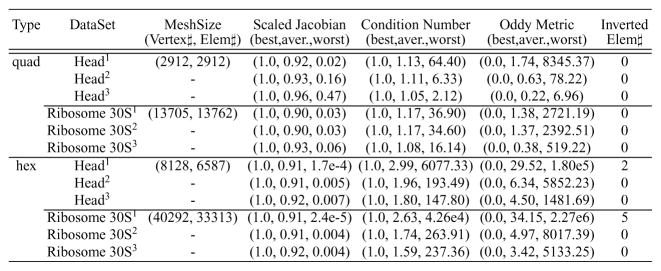
There are many different ways to define the aspect ratio for a quad or a hex to measure the mesh quality. Here we choose the scaled Jacobian, the condition number of the Jacobian matrix and Oddy metric [33] as our metrics [34][35][36].
Assume x ∈ ℝ3 is the position vector of a vertex in a quad or a hex, and xi ∈ ℝ3 for i = 1, …, m are its neighboring vertices, where m = 2 for a quad and m = 3 for a hex. Edge vectors are defined as ei = xi − x with i = 1, …, m, and the Jacobian matrix is J = [e1, …, em]. The determinant of the Jacobian matrix is called Jacobian, or scaled Jacobian if edge vectors are normalized. An element is said to be inverted if one of its Jacobians ≤ 0. We use the Frobenius norm as a matrix norm, |J| = (tr(JT J)1/2). The condition number of the Jacobian matrix is defined as κ(J) = |J||J−1|, where . Therefore, the three quality metrics for a vertex x in a quad or a hex are defined as follows:
| (28) |
| (29) |
| (30) |
where m = 2 for quadrilateral meshes and m = 3 for hexahedral meshes.
In [2] [3], an optimization approach was used to improve the quality of quad/hex meshes. The goal is to remove all the inverted elements and improve the worst condition number of the Jacobian matrix. Here we combine our surface smoothing and quality improvement schemes with the optimization-based approach. We use the geometric flow to improve the quality of quad/hex meshes overall and only use the optimization-based smoothing when necessary. Figure 10 shows the comparison of the three quality criteria before and after quality improvement. We can observe that the aspect ratio is improved by using the combined approach.
Fig. 10.
The comparison of the three quality criteria (the scaled Jacobian, the condition number and Oddy metric) before/after the quality improvement for quad/hex meshes of the human head (Figure 12) and Ribosome 30S (Figure 1). DATA1 – before quality improvement; DATA2 – after quality improvement using the optimization scheme in [2] [3]; DATA3 – after quality improvement using the combined geometric flow/optimization-based approach.
We have applied our surface smoothing and quality improvement technique on some biomolecular meshes. In Figure 4, the surface of a molecule consisting of three amino acids is denoised, the surface quadrilateral mesh becomes more regular and the aspect ratio is improved. The comparison of the quality of quad/hex meshes of Ribosome 30S/50S are shown in Figure 1, Figure 11 and Figure 10. The surface diffusion flow preserves a sphere accurately when the initial mesh is embedded and close to a sphere and the tangent movement of boundary vertices doesn’t change the shape, therefore features on the molecular surface are preserved. Our quality improvement scheme also works for adaptive meshes as shown in Figure 7.
Fig. 11.
The comparison of mesh quality of Haloarcula Marismortui large Ribosome 50S (1JJ2) crystal subunit. The light yellow and the pink color show 5S and 23S rRNA respectively, the remaining colors are proteins. (a) the original quad mesh (17278 vertices, 17328 quads); (b) the improved quad mesh; (c) the improved hex mesh (57144 vertices, 48405 hexes); (d) the zoom-in picture of the red box in (a); (e) the zoom-in picture of the red box in (b).
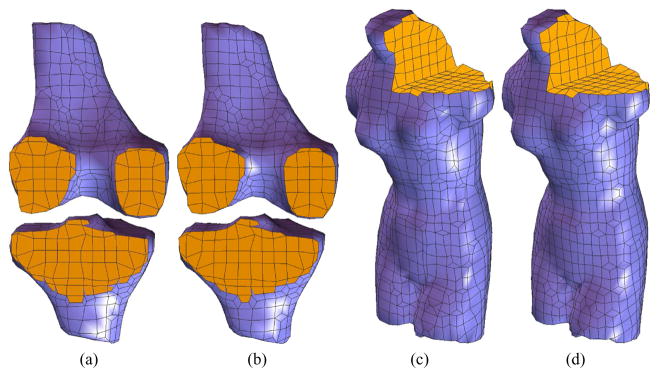
From Figure 6 and 8, we can observe that the mesh, especially the surface mesh, becomes more regular and facial features of the human head are preserved as well as the aspect ratio is improved (Figure 10). The interior and exterior hexahedral meshes of the human head as shown in Figure 12 have been used in the electromagnetic scattering simulations. Figure 13 shows the quality improvement of hexahedral meshes, as well as the surface quadrilateral meshes, of the human knee and the Venus model.
Fig. 12.
The comparison of mesh quality of the interior and exterior hexahedral meshes. (a) the original interior hex mesh (8128 vertices, 6587 hexes); (b) the improved interior hex mesh; (c) the improved exterior hex mesh (16521 vertices, 13552 hexes). The mesh quality is measured by three quality metrics as shown in Figure 10.
Fig. 13.
The comparison of mesh quality of the human knee and the Venus model. (a) the original hex mesh of the knee (2103 vertices, 1341 hexes); (b) the improved hex mesh of the knee; (c) the original hex mesh of Venus (2983 vertices, 2135 hexes); (d) the improved hex mesh of Venus.
Figure 14 shows the quadrilateral meshes for a bubble, which was used in the process of bubble elongation simulation using the boundary element method. First a uniform quad mesh (Figure 14(a)) is extracted from volumetric data for the original state of the bubble, then we use the templates defined in [2] [3] to construct an adaptive mesh as shown in Figure 14(b), the boundary element solutions such as the deformation error are taken as the refinement criteria. Finally we apply our quality improvement techniques to improve the mesh quality. The improved quad mesh is shown in Figure 14(c).
Fig. 14.
The comparison of mesh quality of the bubble. (a) a uniform quad mesh (828 vertices, 826 quads); (b) an adaptive quad mesh (5140 vertices, 5138 quads); (c) the improved adaptive quad mesh.
6 Conclusions
We have presented an approach to smooth the surface and improve the quality of quadrilateral and hexahedral meshes. The surface diffusion flow is selected to denoise surface meshes by adjusting each boundary vertex along its normal direction. The surface diffusion flow is volume preserving, and also preserves a sphere accurately when the input mesh is embedded and close to a sphere, therefore it is especially suitable for surface smoothing of biomolecular meshes because biomolecules are usually modelled as a union of hard spheres. The vertex tangent movement doesn’t change the surface shape, therefore surface features can be preserved. The interior vertices of hex meshes are relocated to their mass centers in order to improve the aspect ratio. In a summary, our approach has the properties of noise removal, feature preservation and mesh quality improvement. The resulting meshes are extensively used for efficient and accurate finite element calculations.
Acknowledgments
We thank Zeyun Yu for several useful discussions, Jianguang Sun for our system management, Prof. Gregory Rodin for finite element solutions of drop deformation, Prof. Nathan Baker for providing access to the accessibility volume of biomolecule mAChE.
The work at University of Texas was supported in part by NSF grants INT-9987409, ACI-0220037, EIA-0325550 and a grant from the NIH 0P20 RR020647. The work on this paper was done when Prof. Guoliang Xu was visiting Prof. Chandrajit Bajaj at UT-CVC and UT-ICES. Prof. Xu’s work was partially supported by the aforementioned grants, the J.T. Oden ICES fellowship and in part by NSFC grant 10371130, National Key Basic Research Project of China (2004CB318000).
Footnotes
References
- 1.Zhang Y, Bajaj C, Sohn BS. 3D Finite Element Meshing from Imaging Data the special issue of Computer Methods in Applied Mechanics and Engineering (CMAME) on Unstructured Mesh Generation. 2004 doi: 10.1016/j.cma.2004.11.026. in press www.ices.utexas.edu/~jessica/meshing. [DOI] [PMC free article] [PubMed]
- 2.Zhang Y, Bajaj C. Adaptive and Quality Quadrilateral/Hexahedral Meshing from Volumetric Data. 13th International Meshing Roundtable; 2004. pp. 365–376. [Google Scholar]
- 3.Zhang Y, Bajaj C. Adaptive and Quality Quadrilateral/Hexahedral Meshing from Volumetric Data. Computer Methods in Applied Mechanics and Engineering (CMAME) 2005 doi: 10.1016/j.cma.2005.02.016. in press www.ices.utexas.edu/~jessica/paper/quadhex. [DOI] [PMC free article] [PubMed]
- 4.Meyer M, Desbrun M, Schröder P, Burr A. VisMath’02. Berlin: 2002. Discrete Differential-Geometry Operators for Triangulated 2-Manifolds. [Google Scholar]
- 5.Xu G, Pan Q, Bajaj C. ICES Technical Report 03-38. the University of Texas; Austin: 2003. Discrete Surface Modeling using Geometric Flows. [Google Scholar]
- 6.Xu G. Discrete Laplace-Beltrami Operators and Their Convergence. Computer Aided Geometric Design. 2004;21:767–784. [Google Scholar]
- 7.Sapiro G. Geometric Partial Differential Equations and Image Analysis. Cambridge: University Press; 2001. [Google Scholar]
- 8.Canann S, Tristano J, Staten M. An Approach to Combined Laplacian and Optimization-based Smoothing for Triangular, Quadrilateral and Quad-dominant Meshes. 7th International Meshing Roundtable; 1998. pp. 479–494. [Google Scholar]
- 9.Freitag L. On Combining Laplacian and Optimization-based Mesh Smoothing Techniqes. AMD-Vol. 220 Trends in Unstructured Mesh Generation. 1997:37–43. [Google Scholar]
- 10.Owen S. A survey of Unstructured Mesh Generation Technology. 7th International Meshing Roundtable; 1998. pp. 26–28. [Google Scholar]
- 11.Teng SH, Wong CW. Unstructured Mesh Generation: Theory, Practice, and Perspectives. International Journal of Computational Geometry and Applications; 2000. pp. 227–266. [Google Scholar]
- 12.Field D. Laplacian Smoothing and Delaunay Triangulations. Communications in Applied Numerical Methods. 1988;4:709–712. [Google Scholar]
- 13.George PL, Borouchaki H. Delaunay Triangulation and Meshing, Application to Finite Elements. 1998 [Google Scholar]
- 14.Zhou T, Shimada K. An Angle-Based Approach to Two-Dimensional Mesh Smoothing. 9th International Meshing Roundtable; 2000. pp. 373–384. [Google Scholar]
- 15.Shontz SM, Vavasis SA. A Mesh Warping Algorithm Based on Weighted Laplacian Smoothing. 12th International Meshing Roundtable; 2003. pp. 147–158. [Google Scholar]
- 16.Knupp P. Winslow Smoothing on Two Dimensinoal Unstructured Meshes. Engineering with Computers. 1999;15:263–268. [Google Scholar]
- 17.Freitag L, Plassmann P. Local Optimization-based Simplicial Mesh Untangling and Improvement. International Journal for Numerical Method in Engineering. 2000;49:109–125. [Google Scholar]
- 18.Charalambous C, Conn A. An Efficient Method to Solve the Minimax Problem Directly. SIAM Journal of Numerical Analysis. 1978;15(1):162–187. [Google Scholar]
- 19.Freitag L, Ollivier-Gooch C. Tetrahedral Mesh Improvement using Swapping and Smoothing. International Journal Numerical Methathemical Engineeringg. 1997;40:3979–4002. [Google Scholar]
- 20.Lohner R, Morgan K, Zienkiewicz OC. Adaptive Grid Refinement for Compressible Euler Equations. In: Babuska I, et al., editors. Accuracy Estimates and Adaptive Refinements in Finite Element Computations. Wiley; 1986. pp. 281–297. [Google Scholar]
- 21.Shimada K, Yamada A, Itoh T. Anisotropic triangular meshing of parametric surfces via close packing of ellipsoidal bubbles. 6th International Meshing Roundtable; 1997. pp. 375–390. [Google Scholar]
- 22.Bossen FJ, Heckbert PS. A pliant method for anisotropic mesh generation. 5th International Meshing Roundtable; 1996. pp. 63–76. [Google Scholar]
- 23.Baker T. Identification and Preservation of Surface Features. 13th International Meshing Roundtable; 2004. pp. 299–310. [Google Scholar]
- 24.Garimella RV, Shashkov MJ, Knupp PM. Optimization of Surface Mesh Quality Using Local Parametrization. 11th International Meshing Roundtable; 2002. pp. 41–52. [Google Scholar]
- 25.Semenova IB, Savchenko VV, Hagiwara I. Two Techniques to Improve Mesh Quality and Preserve Surface Characteristics. 13th International Meshing Roundtable; 2004. pp. 277–288. [Google Scholar]
- 26.Staten M, Canann S. Post Refinement Element Shape Improvement for Quadrilateral Meshes. AMD-Trends in Unstructured Mesh Generation. 1997;220:9–16. [Google Scholar]
- 27.Kinney P. CleanUp: Improving Quadrilateral Finite Element Meshes. 6th International Meshing Roundtable; 1997. pp. 437–447. [Google Scholar]
- 28.Mitchell S, Tautges T. Pillowing Doublets: Refining a Mesh to Ensure That Faces Share at Most One Edge. 4th International Meshing Roundtable; 1995. pp. 231–240. [Google Scholar]
- 29.Schneiders R. Refining Quadrilateral and Hexahedral Element Meshes. 5th International Conference on Grid Generation in Computational Field Simulations; 1996. pp. 679–688. [Google Scholar]
- 30.Bajaj C, Warren J, Xu G. A Subdivision Scheme for Hexahedral Meshes. The Visual Computer. 2002;18(56):343–356. [Google Scholar]
- 31.Escher J, Mayer UF, Simonett G. The Surface Diffusion Flow for Immersed Hyper-surfaces. SIAM Journal of Mathematical Analysis. 1998;29(6):1419–1433. [Google Scholar]
- 32.Willmore TJ. Riemannian Geometry. Clareden Press; Oxford: 1993. [Google Scholar]
- 33.Oddy A, Goldak J, McDill M, Bibby M. A Distortion Metric for Isoparametric Finite Elements. 1988 Transactions of CSME, No. 38-CSME-32, Accession No. 2161. [Google Scholar]
- 34.Knupp P. Achieving Finite Element Mesh Quality via Optimization of the Jacobian Matrix Norm and Associated Quantities. Part I - A Framework for Surface Mesh Optimization. International Journal Numerical Methathemical Engineeringg. 2000;48:401–420. [Google Scholar]
- 35.Knupp P. Achieving Finite Element Mesh Quality via Optimization of the Jacobian Matrix Norm and Associated Quantities. Part II - A Framework for Volume Mesh Optimization and the Condition Number of the Jacobian Matrix. International Journal Numerical Methathemical Engineeringg. 2000;48:1165–1185. [Google Scholar]
- 36.Kober C, Matthias M. Hexahedral Mesh Generation for the Simulation of the Human Mandible. 9th International Meshing Roundtable; 2000. pp. 423–434. [Google Scholar]