Maximum Likelihood Ratio Tests for Comparing the Discriminatory Ability of Biomarkers Subject to Limit of Detection

Summary

In this article, we consider comparing the areas under correlated receiver operating characteristic (ROC) curves of diagnostic biomarkers whose measurements are subject to a limit of detection (LOD), a source of measurement error from instruments’ sensitivity in epidemiological studies. We propose and examine the likelihood ratio tests with operating characteristics that are easily obtained by classical maximum likelihood methodology.

1. Introduction

Receiver operating characteristic (ROC) curve is a well-accepted statistical tool for evaluating the discriminatory ability of biomarkers (e.g., Shapiro, 1999). An ROC curve plots the true positive rates of a biomarker versus its false-positive rates for various thresholds of the test result. It is a convenient way to compare diagnostic biomarkers because the ROC curve places tests on the same scale where they can be compared for accuracy.

The area under the ROC curve (AUC) is a common index of the diagnostic performance of a biomarker. Bamber (1975) showed that AUC = Pr(X > Y), where X and Y represent values of the biomarker from diseased and healthy populations, respectively. Obviously, the closer the AUC is to 1, the better the diagnostic accuracy of the biomarker. In a parametric setting the AUCs can generally be expressed as a function of unknown parameters and thus can be evaluated via estimation of these parameters. Nonparametric estimation of the AUC has also been well addressed in the biostatistical and epidemiological literature. However, the test-scores of biomarkers are frequently associated with measurement error, and in this article we focus on measurement errors due to the limit of detection (LOD).

The LOD is a source of bias in many experiments and is usually caused by the limitation of instruments in measuring very high or low concentrations (e.g., Lyles, Williams, and Chuachoowong, 2001; Lubin et al., 2004; Mumford et al., 2006; Schisterman et al., 2006; Vexler, Liu, and Schisterman, 2006). This inability to accurately determine values of biomarkers introduces bias in the analysis of data from such experiments. For example, biomarkers for polychlorinated biphenyl (PCB), which are associated with endometriosis (Louis et al., 2005), are limited by instrument sensitivity (e.g., Lubin et al., 2004). The LOD issue can be considered as a problem of censored data analysis (e.g., Vexler et al., 2006). Perkins, Schisterman, and Vexler (2007) as well as Mumford et al. (2006) have proposed methods for estimation of ROC curves based on samples with LOD.

Often it is necessary to determine whether a biomarker has satisfactory accuracy in correctly discriminating between cases and controls, for example, testing for AUC = 0.5 (i.e., a biomarker has no discriminatory ability), or whether one biomarker has better diagnostic accuracy than another (e.g., Molodianovitch, Faraggi, and Reiser, 2006). This can be achieved by comparing the AUCs of these biomarkers. The present article addresses these issues when the measurements of the biomarkers are subject to an LOD. We investigate the maximum likelihood ratio test (MLRT), utilizing the likelihood function proposed by Lyles et al. (2001). Operating characteristics of the proposed tests (e.g., significance level and power) can be obtained from classical results of the maximum likelihood method.

The article is organized as follows. Section 2 introduces the MLRT for comparing AUCs. Section 3 presents Monte Carlo simulation results. In Section 4, we apply the proposed tests to data from two studies to evaluate the AUCs of several biomarkers, with some concluding remarks in Section 5. One example is from a study conducted in Birmingham, Alabama, to investigate whether intrauterine inflammation is associated with neuron developmental abnormalities in early childhood, so that certain educational methods for improvement will be utilized. In this example the levels of intrauterine inflammation biomarkers are observed only if they are above the detection limits. Another example uses data from a study of atherosclerotic coronary heart disease to test for discriminatory ability of several biomarkers. This study sampled residents of Niagara and Erie counties in New York who were between the ages of 35 and 79. Adults between the ages of 35 and 65 were randomly selected using the New York State Department of Motor Vehicles drivers’ licenses rolls. Individuals between 65 and 79 years of age were sampled randomly from the Health Care Financing Administration database. A cohort of 942 individuals consisted of 143 people with myocardial infarction (cases) and 799 controls. The purpose of the study was to determine whether biomarkers that measure individuals’ oxidative stress and antioxidant status are good at determining an individual's disease status.

2. Maximum Likelihood Ratio Tests

2.1 Test Based on Complete Data

Let X_k and Y_k represent the values of biomarker k(=1, 2) associated with a diseased (X) and healthy (Y) population, respectively, and {x_k1, . . . , x_kn} and {y_k1, . . . , y_km} be the corresponding test-scores. Suppose the independent vectors (x_1i, x_2i)^T follow a normal distribution

$$\begin{array}{cc}\hfill {(x_{1i},x_{2i})}^T\sim N\left({({\mu }_{x_1},{\mu }_{x_2})}^T,\left[\begin{array}{cc}\hfill {\sigma }_{x_1}^2\hfill & \hfill {\rho }_x{\sigma }_{x_1}{\sigma }_{x_2}\hfill \\ \hfill {\rho }_x{\sigma }_{x_1}{\sigma }_{x_2}\hfill & \hfill {\sigma }_{x_2}^2\hfill \end{array}\right]\right),& \hfill \\ \hfill i=1,\dots ,n,& \hfill \end{array}$$

and similarly,

$$\begin{array}{cc}\hfill {(y_{1j},y_{2j})}^T\sim N\left({({\mu }_{y_1},{\mu }_{y_2})}^T,\left[\begin{array}{cc}\hfill {\sigma }_{y_1}^2\hfill & \hfill {\rho }_y{\sigma }_{y_1}{\sigma }_{y_2}\hfill \\ \hfill {\rho }_y{\sigma }_{y_1}{\sigma }_{y_2}\hfill & \hfill {\sigma }_{y_2}^2\hfill \end{array}\right]\right),& \hfill \\ \hfill j=1,\dots ,m.& \hfill \end{array}$$

Following Bamber (1975), the AUCs of the biomarkers are AUC₁ = P(X₁ > Y₁) and AUC₂ = P(X₂ > Y₂), respectively.

In this section, we formally consider testing hypothesis:

$${\mathrm{H}}_0:AU{C}_1=AU{C}_2\text{versus}{\mathrm{H}}_1:AU{C}_1\ne AU{C}_2.$$ (1)

It is clear that $AU{C}_k=\Phi \{({\mu }_{x_k}-{\mu }_{y_k})∕\sqrt{{\sigma }_{x_k}^2+{\sigma }_{y_k}^2}\}$, k = 1, 2, and therefore

$$AU{C}_1=AU{C}_2\mathrm{iff}{\mu }_{x_1}=\frac{\left({\mu }_{x_2}-{\mu }_{y_2}\right){\left({\sigma }_{x_1}^2+{\sigma }_{y_1}^2\right)}^{1∕2}}{{\left({\sigma }_{x_2}^2+{\sigma }_{y_2}^2\right)}^{1∕2}}+{\mu }_{y_1}.$$

In a simple case, where all the parameters are known and there is no measurement error, that is, (X₁, X₂) and (Y₁, Y₂) are observed completely, we can utilize the classical MLRT for testing H₀. To this end, note that under H₁ and H₀ the likelihood function has the form

$$\begin{array}{cc}\hfill & \prod _{\begin{array}{c}\hfill i=1,\dots ,n\hfill \\ \hfill j=1,\dots ,m\hfill \end{array}}f\left(x_{1i},x_{2i},y_{1j},y_{2j};{ϴ}_X^{{\mathrm{H}}_1},{ϴ}_Y^{{\mathrm{H}}_1}\right),\hfill \\ \hfill & \prod _{\begin{array}{c}\hfill i=1,\dots ,n\hfill \\ \hfill j=1,\dots ,m\hfill \end{array}}f\left(x_{1i},x_{2i},y_{1j},y_{2j};{ϴ}_X^{{\mathrm{H}}_0},{ϴ}_Y^{{\mathrm{H}}_0}\right),\hfill \end{array}$$

respectively, where the vectors of parameters ${ϴ}_X^{H_1},{ϴ}_Y^{H_1},{ϴ}_X^{H_0},{ϴ}_Y^{H_0}$ are

$$\begin{array}{cc}\hfill {ϴ}_X^{{\mathrm{H}}_1}& =\left({\mu }_{x_1},{\mu }_{x_2},{\sigma }_{x_1}^2,{\sigma }_{x_2}^2,{\rho }_x\right),\hfill \\ \hfill {ϴ}_Y^{{\mathrm{H}}_1}& =\left({\mu }_{y_1},{\mu }_{y_2},{\sigma }_{y_1}^2,{\sigma }_{y_2}^2,{\rho }_y\right),\hfill \\ \hfill {ϴ}_X^{{\mathrm{H}}_0}& =\left(\frac{\left({\mu }_{x_2}-{\mu }_{y_2}\right){\left({\sigma }_{x_1}^2+{\sigma }_{y_1}^2\right)}^{1∕2}}{{\left({\sigma }_{x_2}^2+{\sigma }_{y_2}^2\right)}^{1∕2}}+{\mu }_{y_1},{\mu }_{x_2},{\sigma }_{x_1}^2,{\sigma }_{x_2}^2,{\rho }_x\right),\hfill \\ \hfill {ϴ}_Y^{{\mathrm{H}}_0}& ={ϴ}_Y^{{\mathrm{H}}_1},\hfill \end{array}$$

and the density function f is f(x₁, x₂, y₁, y₂; Θ_X, Θ_Y) = ϕ(x₁, x₂; Θ_X) ϕ(y₁, y₂; Θ_Y), where, with Θ = (θ₁, θ₂, θ₃, θ₄, θ₅),

$$\begin{array}{cc}\hfill \varphi (u,v;ϴ)=& \frac{1}{2\pi {\theta }_3{\theta }_4\sqrt{1-{\theta }_5^2}}\hfill \\ \hfill & \times \exp [-\frac{1}{2}\left(\frac{1}{1-{\theta }_5^2}\right)\{\frac{{(u-{\theta }_1)}^2}{{\theta }_3^2}-2{\theta }_5\frac{(u-{\theta }_1)}{{\theta }_3}\phantom{\}}\phantom{]}\hfill \\ \hfill & \phantom{[}\phantom{\{}\times \frac{(v-{\theta }_2)}{{\theta }_4}+\frac{{(v-{\theta }_2)}^2}{{\theta }_4^2}\}].\hfill \end{array}$$

Therefore the classical likelihood ratio test-statistic is

$$z=\prod _{\begin{array}{c}\hfill i=1,\dots ,n\hfill \\ \hfill j=1,\dots ,m\hfill \end{array}}\frac{f\left(x_{1i},x_{2i},y_{1j},y_{2j};{ϴ}_X^{{\mathrm{H}}_1},{ϴ}_Y^{{\mathrm{H}}_1}\right)}{f\left(x_{1i},x_{2i},y_{1j},y_{2j};{ϴ}_X^{{\mathrm{H}}_0},{ϴ}_Y^{{\mathrm{H}}_0}\right)}.$$

Thus, we reject the null hypothesis iff z > z_α, where the threshold z_α corresponds to type I error α. It is clear that this test is the most powerfulunbiased test; see, for example, Lehmann (1997).

When the parameters ${ϴ}_X^{{\mathrm{H}}_1},{ϴ}_Y^{{\mathrm{H}}_1},{ϴ}_X^{{\mathrm{H}}_0},{ϴ}_Y^{{\mathrm{H}}_0}$ are unknown, Molodianovitch et al. (2006) propose the transformed normal approach by normalizing data through transformation and then applying the parametric test proposed by Wieand et al. (1989) in order to test for hypothesis (1). (This test is based on confidence intervals (CIs) of AUCs [e.g., Reiser and Faraggi, 1997]. We will investigate this method in detail in Section 4.2.) Alternatively, we can apply the maximum likelihood estimation and obtain the test-statistic:

$$z=\frac{\underset{{\stackrel{‒}{\mu }}_{x_1},{\stackrel{‒}{\mu }}_{x_2},{\stackrel{‒}{\mu }}_{y_1},{\stackrel{‒}{\mu }}_{y_2},{\stackrel{‒}{\sigma }}_{x_1}^2,{\stackrel{‒}{\sigma }}_{x_2}^2,{\stackrel{‒}{\sigma }}_{y_1}^2,{\stackrel{‒}{\sigma }}_{y_2}^2,{\stackrel{‒}{\rho }}_x,{\stackrel{‒}{\rho }}_y}{\sup }\prod _{\begin{array}{c}\hfill i=1,\dots ,n\hfill \\ \hfill j=1,\dots ,m\hfill \end{array}}f\left(x_{1i},x_{2i},y_{1j},y_{2j};{\stackrel{‒}{ϴ}}_X^{{\mathrm{H}}_1},{\stackrel{‒}{ϴ}}_Y^{{\mathrm{H}}_1}\right)}{\underset{{\stackrel{‒}{\mu }}_{x_2},{\stackrel{‒}{\mu }}_{y_1},{\stackrel{‒}{\mu }}_{y_2},{\stackrel{‒}{\sigma }}_{x_1}^2,{\stackrel{‒}{\sigma }}_{x_2}^2,{\stackrel{‒}{\sigma }}_{y_1}^2,{\stackrel{‒}{\sigma }}_{y_2}^2,{\stackrel{‒}{\rho }}_x,{\stackrel{‒}{\rho }}_y}{\sup }\prod _{\begin{array}{c}\hfill i=1,\dots ,n\hfill \\ \hfill j=1,\dots ,m\hfill \end{array}}f\left(x_{1i},x_{2i},y_{1j},y_{2j};{\stackrel{‒}{ϴ}}_X^{{\mathrm{H}}_0},{\stackrel{‒}{ϴ}}_Y^{{\mathrm{H}}_0}\right)},$$

where

$$\begin{array}{cc}\hfill {\stackrel{‒}{ϴ}}_X^{{\mathrm{H}}_1}& =\left({\stackrel{‒}{\mu }}_{x_1},{\stackrel{‒}{\mu }}_{x_2},{\stackrel{‒}{\sigma }}_{x_1}^2,{\stackrel{‒}{\sigma }}_{x_2}^2,{\stackrel{‒}{\rho }}_x\right),\hfill \\ \hfill {\stackrel{‒}{ϴ}}_Y^{{\mathrm{H}}_1}& =\left({\stackrel{‒}{\mu }}_{y_1},{\stackrel{‒}{\mu }}_{y_2},{\stackrel{‒}{\sigma }}_{y_1}^2,{\stackrel{‒}{\sigma }}_{y_2}^2,{\stackrel{‒}{\rho }}_y\right),\hfill \\ \hfill {\stackrel{‒}{ϴ}}_X^{{\mathrm{H}}_0}& =\left(\frac{\left({\stackrel{‒}{\mu }}_{x_2}-{\stackrel{‒}{\mu }}_{y_2}\right){\left({\stackrel{‒}{\sigma }}_{x_1}^2+{\stackrel{‒}{\sigma }}_{y_1}^2\right)}^{1∕2}}{{\left({\stackrel{‒}{\sigma }}_{x_2}^2+{\stackrel{‒}{\sigma }}_{y_2}^2\right)}^{1∕2}}+{\stackrel{‒}{\mu }}_{y_1},{\stackrel{‒}{\mu }}_{x_2},{\stackrel{‒}{\sigma }}_{x_1}^2,{\stackrel{‒}{\sigma }}_{x_2}^2,{\stackrel{‒}{\rho }}_x\right),\hfill \\ \hfill {\stackrel{‒}{ϴ}}_Y^{{\mathrm{H}}_0}& ={\stackrel{‒}{ϴ}}_Y^{{\mathrm{H}}_1}.\hfill \end{array}$$

It is well known (e.g., Lehmann, 1997) that under H₀, the statistic 2 log z asymptotically has a ${\chi }_1^2$ distribution and therefore the threshold z_α can be easily obtained from Pr(z > z_α) = α, as n, m → ∞. Moreover, this test is asymptotically most powerful (e.g., Choi, Hall, and Schick, 1996).

2.2 Test Based on Data Subject to Limit of Detection

If measurements of the biomarkers are subject to a LOD, then instead of observing x_1i, x_2i, y_1j, y_2j we have

$$\begin{array}{cc}\hfill x_{ki}^{\prime }& =\{\begin{array}{cc}{x}_{ki},\hfill & \mathrm{if}{x}_{ki}\ge d_x;\hfill \\ \mathrm{NA}\left(\text{not available}\right),\hfill & x_{ki}<d_x,\hfill \end{array}\phantom{\}}\hfill \\ \hfill y_{kj}^{\prime }& =\{\begin{array}{cc}{y}_{kj},\hfill & \mathrm{if}{y}_{kj}\ge d_y;\hfill \\ \mathrm{NA},\hfill & y_{kj}<d_y,\hfill \end{array}\phantom{\}}\hfill \end{array}$$

where k = 1, 2, i = 1, . . . , n, j = 1, . . . , m and d_x, d_y are the values of the LOD (e.g., Lynn, 2001; Lubin et al., 2004; Mumford et al., 2006; Schisterman et al., 2006; Vexler et al., 2006). In the present article we assume, without loss of generality, that d_x = d_y = d and d is known (if d is unknown, it can be easily estimated, for example, by min_i,j,k{x_ki, y_kj}). We can still obtain the MLRT statistic based on the left-censored data. Following Lyles et al. (2001), write the likelihood functions based on $X^{\prime }={\{x_{1i}^{\prime },x_{2i}^{\prime }\}}_{i=1}^n$ and $Y^{\prime }={\{y_{1j}^{\prime },y_{2j}^{\prime }\}}_{j=1}^m$ as $L(X^{\prime };{ϴ}_X^{{\mathrm{H}}_1})$ and $L(Y^{\prime };{ϴ}_Y^{{\mathrm{H}}_1})$, respectively, that are formally defined in Appendix A.

Thus the MLRT statistic is given by

$$\begin{array}{cc}\hfill & z^{\left(LOD\right)}\hfill \\ \hfill & =\frac{\underset{{\stackrel{‒}{\mu }}_{x_1},{\stackrel{‒}{\mu }}_{x_2},{\stackrel{‒}{\mu }}_{y_1},{\stackrel{‒}{\mu }}_{y_2},{\stackrel{‒}{\sigma }}_{x_1}^2,{\stackrel{‒}{\sigma }}_{x_2}^2,{\stackrel{‒}{\sigma }}_{y_1}^2,{\stackrel{‒}{\sigma }}_{y_2}^2,{\stackrel{‒}{\rho }}_x,{\stackrel{‒}{\rho }}_y}{\sup }L\left(X^{\prime };{\stackrel{‒}{ϴ}}_X^{{\mathrm{H}}_1}\right)L\left((Y^{\prime };{\stackrel{‒}{ϴ}}_Y^{{\mathrm{H}}_1}\right)}{\underset{{\stackrel{‒}{\mu }}_{x_2},{\stackrel{‒}{\mu }}_{y_1},{\stackrel{‒}{\mu }}_{y_2},{\stackrel{‒}{\sigma }}_{x_1}^2,{\stackrel{‒}{\sigma }}_{x_2}^2,{\stackrel{‒}{\sigma }}_{y_1}^2,{\stackrel{‒}{\sigma }}_{y_2}^2,{\stackrel{‒}{\rho }}_x,{\stackrel{‒}{\rho }}_y}{\sup }L\left(X^{\prime };{\stackrel{‒}{ϴ}}_X^{{\mathrm{H}}_0}\right)L\left((Y^{\prime };{\stackrel{‒}{ϴ}}_Y^{{\mathrm{H}}_0}\right)}.\hfill \end{array}$$

Subsequently, the test threshold z_α can be obtained by the MLRT's asymptotic result: $2\text{log}{z}^{\left(LOD\right)}~{\chi }_1^2$ as n, m → ∞, and d is fixed.

Remark 1. Numerical calculations

Note that, applying statistical software such as R, SPlus, etc., allows us to calculate test-statistics z and z^(LOD) without using closed forms of the estimators of the unknown parameters. A schematic example of programming in R is available upon request from the first author.

Remark 2. Transformed normal approach

The proposed method is based on the MLRT technique and hence the parametric assumptions regarding the data points are required. In order to relax the normal distribution assumptions, following Molodianovitch et al. (2006) we can fit the data to a Box–Cox power transformation modelto better achieve normality and then test for (1). Note that, Molodianovitch et al. (2006) have concluded that the transformed normal approach is efficient and robust when AUCs are compared. We present a modification of the proposed test in Appendix B.

3. Simulation

We conducted Monte Carlo simulations to examine the performance of the proposed method. To this end, we generated values of {x_1i, i = 1, . . . , n} from the normal distribution with mean μ_x1 and variance 1, and {x_2i = ax_1i + ε_i, i = 1, . . . , n}, where the independent and identically distributed (i.i.d.) random variables ε_i ∼ N(0, 1). Similarly, y_1j ∼ N(1, 0.5²) and y_2j = by_1j + ε_j(j = 1, . . . , m) were generated. Hence, ${\rho }_x=a{\sigma }_{x_1}∕{(1+a^2{\sigma }_{x_1}^2)}^{1∕2},{\sigma }_{x_2}={(a^2{\sigma }_{x_1}^2+1)}^{1∕2},{\sigma }_{y_2}={(b^2{\sigma }_{y_1}^2+1)}^{1∕2}$, and ${\rho }_y=b{\sigma }_{y_1}∕{(1+b^2{\sigma }_{y_1}^2)}^{1∕2}$, where a and b are specified below.

Significance level of the test

Setting a = 0.7, b = 0.5, μ_x1 = 1.274, we have AUC₁ = AUC₂ = 0.597. For each value of d = −3, −1, −0.5, 0, 0.5, and 0.75 we generated 10,000 samples of {x_1i, x_2i, i = 1, . . . , n} and {y_1j, y_2j, j = 1, . . . , m}. Based on the generated samples, in each repetition we calculated the values of the test-statistic z^(LOD).

In Table 1 we present the Monte Carlo estimation of type I error, where the test thresholds 2 log z_α are 3.84 and 6.63. These thresholds correspond to Pr(ξ > 3.84) = 0.05 and Pr(ξ > 6.63) = 0.01, where $\xi ~{\chi }_1^2$. Table 1 also provides the theoretical proportion of the number of observations of X₁, X₂, Y₁, and Y₂ that are below the LOD value d. As can be seen, asymptotically, the type I error of the proposed test can be obtained from the ${\chi }_1^2$ distribution of the 2 log z^(LOD) statistic. However, if, for example, n = m = 150 and d = 0.75 (in which case about 60% of Y₂'s are not observed numerically), then this assumption is dubious. (Note that for Type I error α we can assume for this simulation CI = α ± 1.96{α(1 − α)/10,000}^1/2.)

Table 1.

Monte Carlo results for the significance levels of the proposed test. F(u) = Pr(2 log z^(LOD) > u) and F(3.84) ≃ 0.05, F(6.63) ≃ 0.01.

n = m	d	F(3.84)	F(6.63)	P(x1 < d)	P(y1 < d)	P(x2 < d)	P(y2 < d)
150	−3	0.0504	0.0098	9.5 × 10−6	6.22 × 10−16	0.0007	0.0003
	−1	0.0510	0.0100	0.0115	3.17 × 10−5	0.0606	0.0728
	−0.5	0.0535	0.0114	0.0380	0.0013	0.1271	0.1660
	0	0.0573	0.0146	0.1013	0.0228	0.2325	0.3138
	0.5	0.0601	0.0153	0.2194	0.1587	0.3740	0.5000
	0.75	0.0634	0.0241	0.3000	0.3085	0.4537	0.5958
30	−3	0.0510	0.0110
	−0.5	0.0507	0.0120
	0	0.0593	0.0150

Power of the test

Here we examine the power of the test for situations where {AUC₁ = 0.5, AUC₂ = 0.6} and {AUC₁ = 0.6, AUC₂ = 0.9}. For the first case, we set μ_x1 = 1.3, a = 0.5, b = −1.5, and for the second μ_x1 = 1, a = 0.7, b = 0.3. For both cases n = m = 150. Table 2 displays the Monte Carlo estimation of the test's power for different values of d. Obviously, the power of the test is dependent on the proportion of X₁'s, X₂'s, Y₁'s, and Y₂'s below d.

Table 2.

Monte Carlo results for the power of the test. F = Pr(2 log z^(LOD) > 3.84).

d	AUC1	AUC2	F	P(x1 < d)	P(y1 < d)	P(x2 < d)	P(y2 < d)
−3	0.5	0.6	0.8394	3.2 × 10−5	6.2 × 10−16	1.1 × 10−3	5.5 × 10−4
−1	0.5	0.6	0.8284	2.3 × 10−2	3.2 × 10−5	8.2 × 10−2	9.9 × 10−2
0	0.5	0.6	0.8374	0.16	2.3 × 10−2	0.28	0.38
0.75	0.5	0.6	0.7372	0.40	0.31	0.52	0.67
−3	0.6	0.9	0.9995	8.5 × 10−6	6.2 × 10−16	5.5 × 10−4	0.12
−1	0.6	0.9	0.9985	1.1 × 10−2	3.2 × 10−5	0.07	0.66
0	0.6	0.9	0.9973	0.08	0.02	0.28	0.89

Table 2 demonstrates the high values of the power even in the situation where AUC₁ is close to AUC₂ and the proportions of the biomarker values below d is high (d = 0, 0.75).

Robustness

The simulations thus far assume that the samples follow normal distributions. In order to illustrate the robustness of our method, we performed the following Monte Carlo simulations. Suppose that, instead of following normal distributions, the diagnostic markers satisfy $x_{2i}=0.7x_{1i}^{\left(\mathrm{df}\right)}+{\epsilon }_i^{\left(fd\right)},y_{2j}=0.3y_{1j}^{\left(\mathrm{df}\right)}+{\epsilon }_j^{\left(fd\right)}$, where $x_1^{\left(\mathrm{df}\right)},y_1^{\left(\mathrm{df}\right)}$, and ε^(df) are independent identically t-distributed random variables with df degrees of freedom, mean 0 and variance 1, 1 ≤ i, j ≤ 150. Thus, AUC₁ = AUC₂ = 0.5. Here we ran 10,000 repetitions of the sample (X′, Y′) at each df = 5, 10, 15 and d = −3, −1, 0 (d is the value of LOD). We examined the significance level of the proposed test given the uncorrected distributional assumption. Table 3 corresponds to the case when we expect the type I error to be 0.05 (the test threshold 2 log z_α is 3.84).

Table 3.

The Monte Carlo type I error of the proposed test given the uncorrected distributional assumption

df	d	P̂r(2 log z(LOD) > 3.84)
15	−3	0.0506
10	−3	0.0524
5	−3	0.0518
15	−1	0.0590
10	−1	0.0610
5	−1	0.0651
15	0	0.0958
10	0	0.1507
5	0	0.3288

From these results we conclude that the proposed method is reasonable even when the distributional assumptions do not exactly satisfy normality. However, the accuracy of the expected significance level is poor when d = 0 (about 50% of the data are below the detection limit). In contrast, Table 1 indicates that under the corrected distributional assumption this proportion of observations below LOD is not critical.

Imputation method

Conventional approaches to dealing with data below LOD include omission, resulting in a truncated data set, and imputation with a constant, such as d or a fraction thereof (e.g., d/2, $d∕\sqrt{2}$); or the observed values may be used directly or indirectly (e.g., Lubin et al., 2004; Schisterman et al., 2006). Perkins et al. (2007) showed that the imputation method can lead to biased parametric/nonparametric estimation of AUCs. Here we report results of the Monte Carlo simulation corresponding to Table 1, where the test based on CIs (e.g., Wieand et al., 1989; Reiser and Faraggi, 1997; for details, see Section 4.2) has been calculated for observations:

$$x_{ki}^{″}=\{\begin{array}{cc}{x}_{ki},\hfill & x_{ki}\ge d;\hfill \\ Imp,\hfill & x_{ki}<d,\hfill \end{array}\phantom{\}}{y}_{kj}^{″}=\{\begin{array}{cc}{y}_{ki},\hfill & y_{kj}\ge d_y;\hfill \\ Imp,\hfill & y_{kj}<d,\hfill \end{array}\phantom{\}}$$

k = 1, 2, i = 1, . . . , n = 150, j = 1, . . . , m = 150, and Imp = d/2, $d∕\sqrt{2}$.

In contrast with Table 1, Table 4 demonstrates that when d = 0, −3, 0.75 these conventional approaches should not be recommended. (Investigation of the test based on the samples ignoring the NA values and the nonparametric test [Wieand et al., 1989] based on $x_{ki}^{\prime \prime },y_{kj}^{\prime \prime }$, k = 1, 2, i = 1, . . . , 150, j = 1, . . . , 150 led to similar conclusion.)

Table 4.

The Monte Carlo type I error of the test based on confidence intervals when the imputation method is applied and the expected significance level is 0.05

d	Imp = d/2	$Imp=d∕\sqrt{2}$
−3	0.0549	0.0546
0	0.0689	0.0687
0.5	0.1098	0.1455
0.75	0.1539	0.2273

4. Examples

We exemplify the proposed method with data from the two studies briefly described in the introduction.

4.1 The IQ Study

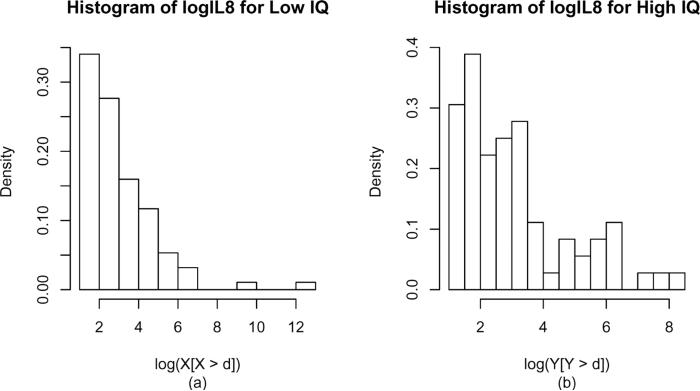
Here we examine whether biomarker IL8 has the ability to discriminate between low and high levels of IQ. The data include 369 subjects. The IQ indicator full-scale IQ (FSIQ) has values ranging from 46 to 118 with an average equal to 82.57. We split our data into two populations, where population A includes those with IQ less than 82.57 and population B includes those with IQ greater than 82.57. We associate biomarker IL8 with both populations separately. Denote X, Y as biomarker values related to population A and B, respectively. The total number of Xs is 189 and the total number of Ys is 180. According to the instrument manual, the LOD for IL8 is d = 3.2, yielding the numbers of NAs to be 95 and 108 for X and Y, respectively. The logarithmic values of the biomarkers are used in order to better achieve normality. The empirical histograms of the log-transformed biomarker corresponding to high and low levels of IQ are depicted in Figure 1.

Figure 1.

Histograms of the log-transformed biomarker of interest corresponding to low (a) and high (b) levels of IQ.

Under the assumption that log X and log Y have normal distributions, applying the maximum likelihood estimation proposed by Vexler et al. (2006) (or estimation based on censored data, see, e.g., Gupta [1952]) leads to estimated mean of log X and log Y as 1.02 and 0.38, respectively. The corresponding standard deviations are 2.60 and 2.88. In this case the estimated AUC is

$$\Phi \left[\frac{E\log X-E\log Y}{{\{\mathrm{var}\left(\log X\right)+\mathrm{var}\left(\log Y\right)\}}^{1∕2}}\right]=0.57.$$

Now, we test for AUC = 0.5 under the ROC curve of IL8 (i.e., no discriminatory ability of the biomarker). This is a particular case of the testing procedure considered in Section 2. Specifically, because the AUC = 0.5 iff E log X = E log Y, the test statistic has the form

$$\begin{array}{cc}\hfill 2\log z=& 2[\underset{{\mu }_x,{\mu }_y,{\sigma }_x,{\sigma }_y}{\sup }\{l(\log X,n_x,k_x;{\mu }_x,{\sigma }_x)\phantom{]}\hfill \\ \hfill & +l(\log Y,n_y,k_y;{\mu }_y,{\sigma }_y)\}\hfill \\ \hfill & -\underset{{\mu }_x,{\sigma }_x,{\sigma }_y}{\sup }\{l(\log X,n_x,k_x;{\mu }_x,{\sigma }_x)\hfill \\ \hfill & +\phantom{[}l(\log Y,n_y,k_y;{\mu }_x,{\sigma }_y)\}],\hfill \end{array}$$

where

$$\begin{array}{cc}\hfill & l(z,n,k;\mu ,\sigma )\hfill \\ \hfill & =-(n-k)\ln \left(\sigma \right)-{\Sigma }_{i;z_i>\log d}\frac{{(z_i-\mu )}^2}{2{\sigma }^2}+k\ln \Phi \left(\frac{\log d-\mu }{\sigma }\right),\hfill \\ \hfill & n_x=189,n_y=180,k_x=95,k_y=108,\hfill \end{array}$$

and the function exp(l) is proportional to the likelihood based on censored data. For details regarding this maximum likelihood function see Vexler et al. (2006). The value of the test-statistic is computed to be 2.97. Because the value of z_0.05 corresponding to Pr_H0(2 log z > z_0.05) ≃ 0.05 (from ${\chi }_1^2$ distribution) is 3.84, we do not reject H₀. Therefore we conclude that the discriminatory ability of biomarker IL8 is not significant.

4.2 Evaluating Biomarkers for Coronary Heart Disease

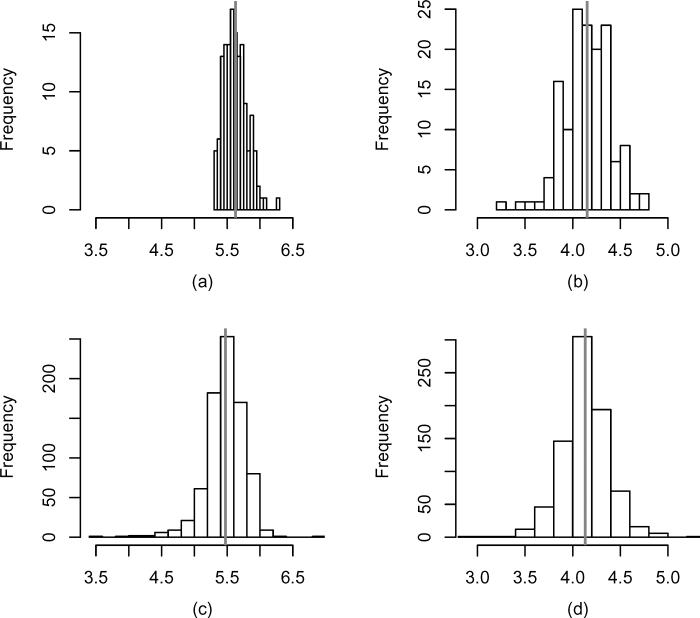
For this example, we compare the diagnostic accuracy of two biomarkers, cholesterol and hdl-cholesterol. To normalize the data, we log-transform the values of both biomarkers. It is obvious from a biological standpoint that the levels of cholesterol and hdl-cholesterol are correlated. Denote by X₁, Y₁ the log-transformed values of cholesterol for the cases and controls, respectively, and similarly, X₂, Y₂ the log-transformed hdl-cholesterol levels from cases and controls. The estimated means of X₁, X₂, Y₁, and Y₂ are 5.63, 4.15, 5.47, 4.13, and the estimated standard deviations are 0.18, 0.24, 0.30, 0.25, respectively. The estimators of the correlation between X₁ and X₂, as well as between Y₁ and Y₂ are ${\widehat{\rho }}_x=0.06$ and ${\widehat{\rho }}_y=0.04$, respectively. Figure 2 introduces empirical histograms of X₁, X₂, Y₁, and Y₂.

Figure 2.

Histograms of the log-transformed biomarkers of interest corresponding to cholesterol cases (a), hdl-cholesterol cases (b), cholesterol controls (c), and hdl-cholesterol controls (d). The vertical bold lines correspond to average values of the biomarkers.

Assume that the values of the log-transformed biomarkers are normally distributed. Simulation studies were conducted for each of the d = 0, 3, 3.25, 3.5, 3.75, 4, and 4.25. Table 5 presents estimators of the correlated AUCs and p-values obtained based on values of the test-statistic z for different d (theoretically 2 log z^(LOD) is approximately ${\chi }_1^2$ distributed). (Note that situation d = 0 corresponds to no LOD effect.)

Table 5.

Estimation of the AUCs and values of the test-statistic for different d. N_Xk, N_Yk are numbers of events {X_k < d} and {Y_k < d}, respectively (k = 1, 2).

d	NX1	NX2	NY1	NY2	AÛC1	AÛC2	2 1og z(LOD)	p-value
0.00	0	0	0	0	0.671	0.524	24.291	10.20 × 10−7
3.00	0	0	0	1	0.671	0.524	24.049	9.39 × 10−7
3.25	0	0	0	2	0.671	0.524	22.156	2.51 × 10−6
3.50	0	2	1	8	0.671	0.524	21.969	2.77 × 10−6
3.75	0	8	1	40	0.672	0.525	22.570	2.03 × 10−6
4.00	0	34	2	207	0.672	0.530	22.941	1.67 × 10−6
4.25	0	88	5	553	0.673	0.583	21.862	2.93 × 10−6

From Table 5, for any selected value of d, the null hypothesis H₀ is rejected with p-values increasing as d increases.

Although standard SPSS output gives the asymptotic 95% CI of AUC₁ as (0.628,0.708) and of AUC₂ as (0.481,0.585), in the simple case where d = 0, we cannot conclude that H₀ : AUC₁ = AUC₂ is rejected because the estimators of AUC₁ and AUC₂ are correlated. We utilize a method proposed by Wieand et al. (1989, p. 587). Following these authors, we have, if biomarkers’ values are normally distributed, the test-statistic

$$z_{CI}=\frac{{\widehat{\delta }}_1-{\widehat{\delta }}_2}{{\left\{(n+m)\mathrm{var}\left(T\right)\right\}}^{1∕2}}\sim N(0,1),n,m\to \infty ,$$

where

$$\begin{array}{cc}\hfill {\widehat{\delta }}_k& =\frac{{\widehat{\mu }}_{x_k}-{\widehat{\mu }}_{y_k}}{{\left({\widehat{\sigma }}_{x_k}^2+{\widehat{\sigma }}_{y_k}^2\right)}^{1∕2}},{\widehat{\mu }}_{x_k}=\frac{{\Sigma }_{i=1}^n{x}_{k_i}}{n},\hfill \\ \hfill {\widehat{\mu }}_{y_k}& =\frac{{\Sigma }_{j=1}^m{y}_{k_j}}{m},{\widehat{\sigma }}_{x_k}^2=\frac{{\Sigma }_{i=1}^n{(x_{k_i}-{\widehat{\mu }}_{x_k})}^2}{n-1},\hfill \\ \hfill {\widehat{\sigma }}_{y_k}^2& =\frac{{\Sigma }_{j=1}^m{(y_{k_j}-{\widehat{\mu }}_{y_k})}^2}{m-1},\hfill \\ \hfill \mathrm{var}\left({(n+m)}^{1∕2}T\right)& ={\sigma }_{11}-2{\sigma }_{12}+{\sigma }_{22},\hfill \\ \hfill {(n+m)}^{-1}{\sigma }_{ii}& ={\sigma }_i^{-2}\left(n^{-1}{\sigma }_{x_i}^2+m^{-1}{\sigma }_{y_i}^2\right)\hfill \\ \hfill & +\frac{1}{2}{\delta }_i^2{\sigma }_i^{-4}\left\{{(n-1)}^{-1}{\sigma }_{x_i}^4+{(m-1)}^{-1}{\sigma }_{y_i}^4\right\},\hfill \\ \hfill {(n+m)}^{-1}{\sigma }_{12}& ={\left({\sigma }_1{\sigma }_2\right)}^{-1}\left(n^{-1}{C}_x+m^{-1}{C}_y\right)+\frac{1}{2}{\delta }_1{\delta }_2{\left({\sigma }_1{\sigma }_2\right)}^{-2}\hfill \\ \hfill & \times \left\{{(n-1)}^{-1}{C}_x^2+{(m-1)}^{-1}{C}_y^2\right\},\hfill \\ \hfill {\sigma }_i^2& ={\sigma }_{x_i}^2+{\sigma }_{y_i}^2,C_x={\rho }_x{\sigma }_{x_1}{\sigma }_{x_2},\hfill \\ \hfill C_y& ={\rho }_y{\sigma }_{y_1}{\sigma }_{y_2},\hfill \\ \hfill \text{and}{\delta }_k& =\frac{{\mu }_{x_k}-{\mu }_{y_k}}{{\left({\sigma }_{x_k}^2+{\sigma }_{y_k}^2\right)}^{1∕2}},k=1,2.\hfill \end{array}$$

Thus, because the z_CI calculated from the data is 4.71, the p-value of the test |z_CI| > z_α is 0.0021, whereas our proposed method has p-value 10.20 × 10⁻⁷; see Table 5 (d = 0).

5. Discussion

In the present article, we have shown that the maximum likelihood ratio approach serves as a method of testing for the hypothesis regarding the comparison of AUCs. Such an approach yields a powerful test with characteristics that can be obtained by the well-established maximum likelihood theory. We used real data examples to illustrate how easily the MLRT method can be carried out in order to compare two biomarkers and to determine whether a biomarker has discriminatory ability.

The article assumes normal distributions for the values of the biomarkers when LOD is present. However, the proposed approach can be extended to other commonly used distributions, for example, gamma, lognormal, etc. Similarly, we can perform hypothesis testing for AUCs based on right, double-censored, or truncated data. We have focused on comparing paired correlated areas, but the proposed method can be adapted to multivariate cases as well.

Our article presented a method dealing with data subject to LOD with broad validity under a reasonable set of assumptions. Sensitivity analysis, though beyond the scope of the present article, is important to assess these distributional assumptions. This topic can be discussed in a generalcontext of missing data analysis; see Molenberghs and Kenward (2007). However, one must bear in mind that data below LOD are informative missing, in the sense that they are unobservable only if the actual values are below the detection limit.

We briefly investigated several imputation methods that are commonly applied among epidemiologists in dealing with LOD data. These methods, however, are not statistically justified and should not be confused with the popular method of multiple imputation (e.g., Rubin, 1987) in the missing data analysis literature. The use of multiple imputation in the analysis of LOD data deserves further investigation.

Note that nonparametric distribution function estimation based on censored data can be obtained and hence Kolmogorov–Smirnov-(or Shapiro–Wilk)-type tests for correctness of parametric assumptions can be evaluated (e.g., Verrill and Johnson, 1988). In the context of the ROC curves and Box–Cox power transformation models based on data subject to LOD, we will address nonparametric and semi-parametric methods in a subsequent article.

The proposed approach preserves the efficiency of the MLRT when applied to testing for biomarkers’ diagnostic accuracy subject to the LOD. When an additive measurement error is in effect, the appropriate maximum likelihood approach can also be utilized following a method similar to that of Section 2.

Appendix A

The Likelihood Functions Based on Data Subject to LOD

The likelihood function based on $X^{\prime }={\{x_{1i}^{\prime },x_{2i}^{\prime }\}}_{i=1}^n$ has the form of

$$\begin{array}{cc}\hfill L\left(X^{\prime };{ϴ}_X^{{\mathrm{H}}_1}\right)& =\left(\prod _{i=1}^{n_1}{t}_{i1}^{\left(x\right)}\right)\times \left(\prod _{i=n_1+1}^{n_2}{t}_{i2}^{\left(x\right)}\right)\hfill \\ \hfill & \times \left(\prod _{i=n_2+1}^{n_3}{t}_{i3}^{\left(x\right)}\right)\times {\left(t_4^{\left(x\right)}\right)}^{n_4},\hfill \end{array}$$

where

$$\begin{array}{cc}\hfill t_{i1}^{\left(x\right)}& ={\left(2\pi {\sigma }_{x_1}{\sigma }_{x_2\mid x_1}\right)}^{-1}\hfill \\ \hfill & \times \exp \left[-0.5\left\{\frac{{(x_{2i}^{\prime }-{\mu }_{x_2\mid x_{1i}})}^2}{{\sigma }_{x_2\mid x_1}^{}}+\frac{{(x_{1i}^{\prime }-{\mu }_{x_1})}^2}{{\sigma }_{x_1}^2}\right\}\right],\hfill \\ \hfill t_{i2}^{\left(x\right)}& ={\left(2\pi {\sigma }_{x_1}^2\right)}^{-1∕2}\exp \left\{-0.5\frac{{(x_{1i}^{\prime }-{\mu }_{x_1})}^2}{{\sigma }_{x_1}^2}\right\}\Phi \left(\frac{d-{\mu }_{x_2\mid x_{1i}}}{{\sigma }_{x_2\mid x_1}}\right),\hfill \\ \hfill t_{i3}^{\left(x\right)}& ={\left(2\pi {\sigma }_{x_2}^2\right)}^{-1∕2}\exp \left\{-0.5\frac{{(x_{2i}^{\prime }-{\mu }_{x_2})}^2}{{\sigma }_{x_2}^2}\right\}\Phi \left(\frac{d-{\mu }_{x_1\mid x_{2i}}}{{\sigma }_{x_1\mid x_2}}\right),\hfill \\ \hfill t_4^{\left(x\right)}& ={\int }_{-\infty }^d\Phi \left[\frac{d-\left\{{\mu }_{x_1}+\frac{{\rho }_x{\sigma }_{x_1}(x_2-{\mu }_{x_2})}{{\sigma }_{x_2}}\right\}}{{\sigma }_{x_1}\sqrt{1-{\rho }_x^2}}\right]{\left(2\pi {\sigma }_{x_2}^2\right)}^{-1∕2}\hfill \\ \hfill & \times \exp \left\{-0.5\frac{{(x_2-{\mu }_{x_2})}^2}{{\sigma }_{x_2}^2}\right\}d{x}_2,\hfill \\ \hfill {\mu }_{x_2\mid x_{1i}}& ={\mu }_{x_2}+({\rho }_x{\sigma }_{x_2}∕{\sigma }_{x_1})(x_{1i}^{\prime }-{\mu }_{x_1}),{\sigma }_{x_2\mid x_1}^2={\sigma }_{x_2}^2\left(1-{\rho }_x^2\right),\hfill \\ \hfill {\mu }_{x_1\mid x_{2i}}& ={\mu }_{x_1}+({\rho }_x{\sigma }_{x_1}∕{\sigma }_{x_2})(x_{2i}^{\prime }-{\mu }_{x_2}),{\sigma }_{x_1\mid x_2}^2={\sigma }_{x_1}^2\left(1-{\rho }_x^2\right),\hfill \end{array}$$

and n₁, n₂, n₃, n₄ (n₁ + n₂ + n₃ + n₄ = n) are the numbers of events ${\{x_{1i}^{\prime }\ne \mathrm{NA},x_{2i}^{\prime }\ne \mathrm{NA}\}}_{i=1}^n,{\{x_{1i}^{\prime }\ne \mathrm{NA},x_{2i}^{\prime }=\mathrm{NA}\}}_{i=1}^n,{\{x_{1i}^{\prime }=\mathrm{NA},x_{2i}^{\prime }\ne \mathrm{NA}\}}_{i=1}^n$, and ${\{x_{1i}^{\prime }=\mathrm{NA},x_{2i}^{\prime }=\mathrm{NA}\}}_{i=1}^n$, respectively. Here, the term $t_{i1}^{\left(x\right)}$ corresponds to situations where x_1i and x_2i are observed completely; $t_{i2}^{\left(x\right)}$ relates to situations where x_1i is observed, whereas x_2i is below the detection limit d and thus $x_{2i}^{\prime }$ is NA (the opposite case where x_1i is unobserved whereas x_2i is available, matches $t_{i3}^{\left(x\right)}$). Finally, when both x₁ and x₂ are not observed numerically, we have $t_4^{\left(x\right)}$ (i.e., $t_4^{\left(x\right)}$ represents the probability of both $x_1^{\prime }$ and $x_2^{\prime }$ to be NA).

The likelihood function based on $Y^{\prime }={\{y_{1j}^{\prime },y_{2j}^{\prime }\}}_{j=1}^m$ is defined in a similar manner:

$$\begin{array}{cc}\hfill L\left(Y^{\prime };{ϴ}_Y^{{\mathrm{H}}_1}\right)=& \left(\prod _{j=1}^{m_1}{t}_{j1}^{\left(y\right)}\right)\times \left(\prod _{j=m_1+1}^{m_2}{t}_{j2}^{\left(y\right)}\right)\times \left(\prod _{j=m_2+1}^{m_3}{t}_{j3}^{\left(y\right)}\right)\hfill \\ \hfill & \times {\left(t_4^{\left(y\right)}\right)}^{m_4},{\Sigma }_{r=1}^4{m}_r=m.\hfill \end{array}$$

Appendix B

Transformed Normal Approach

We denote the function

$$T(u,\lambda )=\{\begin{array}{cc}\frac{u^{\lambda }-1}{\lambda },\hfill & \lambda \ne 0,\hfill \\ \log \left(u\right),\hfill & \lambda =0\hfill \end{array}\phantom{\}}$$

and extend the likelihoods $L(X^{\prime };{ϴ}_X^{{\mathrm{H}}_1})$ and $L(Y^{\prime };{ϴ}_Y^{{\mathrm{H}}_1})$ by Appendix A to the forms of

$$\begin{array}{cc}\hfill L\left(X^{\prime };{ϴ}_X^{{\mathrm{H}}_1},{\lambda }_1,{\lambda }_2\right)=& \left(\prod _{i=1}^{n_1}{\tilde{t}}_{i1}^{\left(x\right)}\right)\times \left(\prod _{i=n_1+1}^{n_2}{\tilde{t}}_{i2}^{\left(x\right)}\right)\hfill \\ \hfill & \times \left(\prod _{i=n_2+1}^{n_3}{\tilde{t}}_{i3}^{\left(x\right)}\right)\times {\left({\tilde{t}}_4^{\left(x\right)}\right)}^{n_4},\hfill \\ \hfill L\left(Y^{\prime };{ϴ}_Y^{{\mathrm{H}}_1},{\lambda }_1,{\lambda }_2\right)=& \left(\prod _{i=1}^{m_1}{\tilde{t}}_{i1}^{\left(y\right)}\right)\times \left(\prod _{i=m_1+1}^{m_2}{\tilde{t}}_{i2}^{\left(y\right)}\right)\hfill \\ \hfill & \times \left(\prod _{i=m_2+1}^{m_3}{\tilde{t}}_{i3}^{\left(y\right)}\right)\times {\left({\tilde{t}}_4^{\left(y\right)}\right)}^{m_4},\hfill \end{array}$$

where for z = x, y

$$\begin{array}{cc}\hfill {\tilde{t}}_{i1}^{\left(z\right)}=& {\left(2\pi {\sigma }_{z_1}{\sigma }_{z_2\mid z_1}\right)}^{-1}\hfill \\ \hfill & \times \exp [-0.5\{\frac{{(T(z_{2i}^{\prime },{\lambda }_2)-{\mu }_{z_2\mid z_{1i}})}^2}{{\sigma }_{z_2\mid z_1}^2}\phantom{\}}\phantom{]}\hfill \\ \hfill & +\phantom{[}\phantom{\{}\frac{{(T(z_{1i}^{\prime },{\lambda }_1)-{\mu }_{z_1})}^2}{{\sigma }_{z_1}^2}\}],\hfill \\ \hfill {\tilde{t}}_{i2}^{\left(z\right)}& ={\left(2\pi {\sigma }_{z_1}^2\right)}^{-1∕2}\exp \left\{-0.5\frac{{(T(z_{1i}^{\prime },{\lambda }_1)-{\mu }_{z_1})}^2}{{\sigma }_{z_1}^2}\right\}\hfill \\ \hfill & \times \Phi \left(\frac{T(d,{\lambda }_2)-{\mu }_{z_2\mid z_{1i}}}{{\sigma }_{z_2\mid z_1}}\right),\hfill \\ \hfill {\tilde{t}}_{i3}^{\left(z\right)}& ={\left(2\pi {\sigma }_{z_2}^2\right)}^{-1∕2}\exp \left\{-0.5\frac{{(T(z_{2i}^{\prime },{\lambda }_2)-{\mu }_{z_2})}^2}{{\sigma }_{z_2}^2}\right\}\hfill \\ \hfill & \times \Phi \left(\frac{T(d,{\lambda }_1)-{\mu }_{z_1\mid z_{2i}}}{{\sigma }_{z_1\mid z_2}}\right),\hfill \\ \hfill {\tilde{t}}_4^{\left(z\right)}& ={\int }_{-\infty }^{T(d,{\lambda }_2)}\Phi \left[\frac{T(d,{\lambda }_1)-\left\{{\mu }_{z_1}+\frac{{\rho }_z{\sigma }_{z_1}(z_2-{\mu }_{z_2})}{{\sigma }_{z_2}}\right\}}{{\sigma }_{z_1}\sqrt{1-{\rho }_z^2}}\right]\hfill \\ \hfill & \times {\left(2\pi {\sigma }_{z_2}^2\right)}^{-1∕2}\exp \left\{-0.5\frac{{(z_2-{\mu }_{z_2})}^2}{{\sigma }_{z_2}^2}\right\}d{z}_2,\hfill \end{array}$$

and it is assumed that (T(z₁, λ₁), T(z₂, λ₂)) are jointly normally distributed. Thus, in this case, the MLR test-statistic is

$$\frac{\underset{{\stackrel{‒}{\mu }}_{x_1},{\stackrel{‒}{\mu }}_{x_2},{\stackrel{‒}{\mu }}_{y_1},{\stackrel{‒}{\mu }}_{y_2},{\stackrel{‒}{\sigma }}_{x_1}^2,{\stackrel{‒}{\sigma }}_{x_2}^2,{\stackrel{‒}{\sigma }}_{y_1}^2,{\stackrel{‒}{\sigma }}_{y_2}^2,{\stackrel{‒}{\rho }}_x,{\stackrel{‒}{\rho }}_y,{\lambda }_1,{\lambda }_2}{\sup }L\left(X^{\prime };{\stackrel{‒}{ϴ}}_X^{{\mathrm{H}}_1},{\lambda }_1,{\lambda }_2\right)L\left(Y^{\prime };{\stackrel{‒}{ϴ}}_Y^{{\mathrm{H}}_1},{\lambda }_1,{\lambda }_2\right)}{\underset{{\stackrel{‒}{\mu }}_{x_2},{\stackrel{‒}{\mu }}_{y_1},{\stackrel{‒}{\mu }}_{y_2},{\stackrel{‒}{\sigma }}_{x_1}^2,{\stackrel{‒}{\sigma }}_{x_2}^2,{\stackrel{‒}{\sigma }}_{y_1}^2,{\stackrel{‒}{\sigma }}_{y_2}^2,{\stackrel{‒}{\rho }}_x,{\stackrel{‒}{\rho }}_y,{\lambda }_1,{\lambda }_2}{\sup }L\left(X^{\prime };{\stackrel{‒}{ϴ}}_X^{{\mathrm{H}}_0},{\lambda }_1,{\lambda }_2\right)L\left(Y^{\prime };{\stackrel{‒}{ϴ}}_Y^{{\mathrm{H}}_0},{\lambda }_1,{\lambda }_2\right)}.$$