Characterization of arterial wall mechanical behavior and stresses from human clinical data

Abstract

This paper demonstrates the feasibility of material identification and wall stress computation for human common carotid arteries based on non-invasive in vivo clinical data: dynamical intraluminal pressure measured by applanation tonometry, and medial diameter and intimal-medial thickness measured by a high-resolution ultrasound echotracking. The mechanical behavior was quantified assuming an axially pre-stretched, thick-walled, cylindrical artery subjected to dynamical blood pressure and perivascular constraints. The wall was further assumed to be three-dimensional and to consist of a nonlinear, hyperelastic, anisotropic, incompressible material with smooth muscle activity and residual stresses. Mechanical contributions by individual constituents an elastin-dominated matrix, collagen fibers, and vascular smooth muscle were accounted for using a previously proposed microstructurally-motivated constitutive relation. The in vivo boundary value problem was solved semi-analytically to compute the inner pressure during a mean cardiac cycle. Using a nonlinear least-squares method, optimal model parameters were determined by minimizing differences between computed and measured inner pressures over a mean cardiac cycle. The fit-to-data from two healthy patients was very good and the predicted radial, circumferential, and axial stretch and stress fields were sensible. Hence, the proposed approach was able to identify complex geometric and material parameters directly from non-invasive in vivo human data.

1. Introduction

Numerous studies have formulated constitutive relations to describe the mechanical behavior of arteries and to compute the associated wall stresses that influence the mechanobiology (Holzapfel et al., 2000; Humphrey, 2002). In particular, in vitro inflation and extension tests allow characterization of the complex behavior of arteries and explanation of some results in terms of the microstructure. Such experiments are performed primarily on animal arteries due to the scarcity and difficulty of obtaining fresh human tissue. Fortunately, reports for different species suggest that general characteristic behaviors and thus basic functional forms of the constitutive relations hold for diverse arteries. Consequently, one can exploit relations identified in vitro and perform material identification using in vivo data, which is important because in vitro behavior differs from the natural in vivo behavior that is most important clinically(Boutouyrie et al., 1997).

Recent advances demonstrate that geometric and material parameters can be identified from in vivo human data (Schulze-Bauer and Holzapfel, 2003; Stalhand et al., 2004), which enables computations of in vivo wall stresses using methods of nonlinear mechanics. For example, Stalhand and colleagues modeled human aorta using a “two-fiber family” model (Holzapfel et al., 2000), which includes passive contributions to wall stiffness by an isotropic elastin matrix and two families of diagonally oriented collagen fibers. Residual stresses were included via an opening angle, which Chuong and Fung (1986) showed to be important in computing transmural stresses. Notwithstanding these important advances, the two-fiber family model is “not able to capture accurately the stress-strain response…” (Gasser et al., 2006) and vascular smooth muscle tone modulates wall stress (Humphrey and Na, 2002; Matsumoto et al., 1996; Rachev and Hayashi, 1999). For example, arteries tend to constrict when blood pressure increases above normal. Including the active contribution of vascular smooth muscle in a mechanical model yields a more homogeneous transmural stress distribution, which appears reasonable teleologically. Finally, perivascular tethering can be important in arterial mechanics in vivo; perivascular tissue can resist part of the distending action of the intraluminal pressure (Humphrey and Na, 2002) and thereby reduce circumferential wall stretch and stress (Liu et al., 2007).

In this paper, we demonstrate the feasibility of material identification for human common carotid arteries (CCAs) based on in vivo non-invasive measurements over a mean cardiac cycle. Echotracking and applanation tonometry measured geometric information and intraluminal pressure, respectively. A 3D mechanical model of the human CCA was constructed from these data by including residual stresses, perivascular tethering, the fiber-reinforced, hyperelastic character of the passive tissue, and smooth muscle tone. Values of the model parameters were obtained by solving the boundary problem semi-analytically and minimizing differences between experimental and computed luminal pressures using a Levenberg-Marquardt nonlinear regression. Data from two healthy subjects were used as illustrative examples. The optimized model parameters yielded more realistic wall stresses, which mayplay an important role in understanding better arterial diseases and their treatment.

2. Methods

2.1 Clinical data

All subjects signed an informed consent. Arterial dimensions and blood pressure were recorded successively following 15 minutes of recumbent rest in a room dedicated to echography. Data used herein are from two healthy subjects: a 62-year old woman (patient A) and a 33-year old man (patient B).

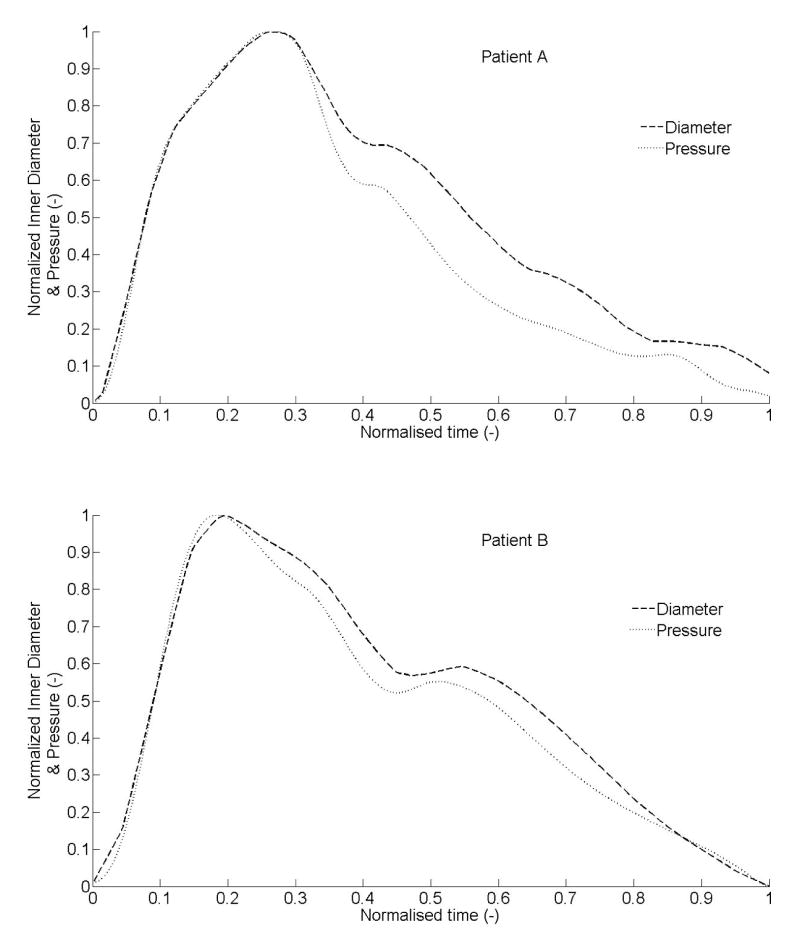
Right CCA medial diameter and intimal-media thickness (IMT) were recorded using a high-resolution echotracking device (ArtLab, Esaote), based on a 128 radio-frequency line multiarray over a 4-cm arterial segment, for 6 seconds at 30-Hz (Paini et al., 2007). Spatial resolution was 21 microns (Meinders et al., 2001). Right intraluminal CCA pressure waveforms were recorded non-invasively for 9 seconds at 128-Hz with a pressure tonometer (Sphygmocor, AtCor Medical) incorporating a high-fidelity Millar strain gauge transducer (Boutouyrie et al., 1999; Kelly et al., 1989). Previous very high-resolution recordings with simultaneous ECG signals showed that such diameter and pressure signals correlate perfectly during the systolic phase (data not shown). Hence, mean cycles of inner diameter and intraluminal pressure over a cardiac cycle were registered to align temporally during the systolic (inflation) phase despite the two recordings being successive (separated by 5 ± 2 minutes), not simultaneous. Moreover, time over the cardiac cycle was normalized to permit direct comparisons across patients (Figure 1).

Figure 1.

Measured intraluminal pressure and inner diameter, over a cardiac cycle, after temporal adjustment based on results from prior ECG augmented data sets. Data were normalized for comparison and represent inputs for material identification. Data were from two healthy subjects: patient A (62-year old woman) and patient B (33-year old man).

2.2 Kinematics

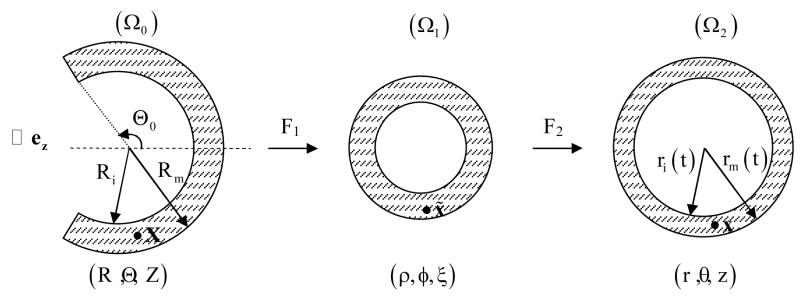
Considering CCAs as thick-walled circular cylinders, the kinematics is best described using a cylindrical coordinate system relative to the basis (e_r,e_θ,e_z). The deformation field over the cardiac cycle can be described via two successive motions, one mapping material particles from a nearly stress-free reference configuration to an unloaded configuration and another from the unloaded configuration to time-dependent in vivo configurations (Figure 2). Hence, consider (Humphrey, 2002)

Figure 2.

Kinematics of the arterial wall relative to a nearly stress-free reference configuration (Ω₀), the excised, unloaded configuration (Ω₁), and the in vivo loaded configurations (Ω₂) having coordinates (R,Θ, Z), (ρ,φ,ξ), (r,θ, z), respectively.

$$\begin{array}{l}\rho =\rho (\text{R}),\phi =\left(\frac{\pi }{{\mathrm{\Theta }}_0}\right)\mathrm{\Theta },\xi =\mathrm{\Lambda }\text{Z},\\ \text{r}=\text{r}(\rho ,\text{t}),\theta =\phi ,\text{z}=\lambda \xi ,\end{array}$$ (1)

where X(R,Θ, Z), x̃ = (ρ,φ,ξ), and x(r(t),θ,z) are, respectively, reference, unloaded, and currently loaded positions of a material particle. The parameter t denotes time over the cardiac cycle whereas an opening angle Θ₀ and an axial stretch Λ account for residual stresses (Chuong and Fung, 1986). The parameter λ accounts for the load-induced axial stretch in vivo, which is assumed to be constant over the cardiac cycle (van Loon et al., 1977). R_i and r_i(t) denote inner radii of the artery, in reference and in vivo configurations, respectively. R_m and r_m(t) similarly denote radii at the media-adventitial interface.

Let χ : X ↦ x =χ(X)be the mapping of a position vector from the reference to the current configuration. From (1), the deformation gradient tensor, defined as F=∂(χ X)/∂X,

$$\mathbf{F}=\text{diag}\left[\frac{\partial \text{r}}{\partial \text{R}},\frac{\pi \text{r}}{{\mathrm{\Theta }}_0\text{R}},\lambda \mathrm{\Lambda }\right]=\text{diag}[{\lambda }_{\text{r}},{\lambda }_{\theta },{\lambda }_{\text{z}}],$$ (2)

where λ_r,λ_θ,λ_z are principal stretches in radial, circumferential, and axial directions, respectively. The left and right Cauchy-Green tensors, denoted B and C, are

$$\mathbf{B}=\mathbf{F}\overline{\mathbf{F}},\mathbf{C}=\overline{\mathbf{F}}\mathbf{F},$$ (3)

where F̄ is the transpose of F. Arterial tissue is considered to be incompressible, thus the local volume ratio is

$$\text{J}=det\mathbf{F}={\lambda }_{\text{r}}{\lambda }_{\theta }{\lambda }_{\text{z}}=1.$$ (4)

From (2) and (4), we can express the reference radius as

$$\text{R}={\left({{\text{R}}_{\text{m}}}^2-\frac{\pi \lambda \mathrm{\Lambda }}{{\mathrm{\Theta }}_0}\left({{\text{r}}_{\text{m}}}^2-{\text{r}}^2\right)\right)}^{1/2}.$$ (5)

2.3 Constitutive relation

A four-fiber family model (Baek et al., 2007), which is a straightforward extension of the model by Holzapfel et al. (2000), accounts for passive behaviors by the isotropic elastin-dominated matrix and the anisotropic collagen. The associated strain energy function W is

$$\text{W}=\frac{\text{c}}{2}({\text{I}}_1-3)+\sum _{\text{k}=1}^4\frac{{\text{c}}_{1(\text{k})}}{4{\text{c}}_{2(\text{k})}}\left\{exp\left[{\text{c}}_{2(\text{k})}{\left({\text{I}}_{4(\text{k})}-1\right)}^2\right]-1\right\},$$ (6)

where c, c_1(k), c_2(k) are material parameters and the invariants I_j = (j = 1,4) are

$${\text{I}}_1=\text{tr}\mathbf{C},{\text{I}}_{4(\text{k})}={\mathbf{M}}_{{\alpha }_{\text{k}}}\left(\mathbf{C}{\mathbf{M}}_{{\alpha }_{\text{k}}}\right)(\text{k}=1,2,3,4),$$ (7)

where the fiber orientations are defined in the reference configuration by unit vectors M_αk, which depend on angles α_k defined between the direction of the k^th family of collagen fibers and the axial direction of the artery (Figure 3). These fiber directions M_αk relate to the direction a_αk in the in vivo deformed state by

Figure 3.

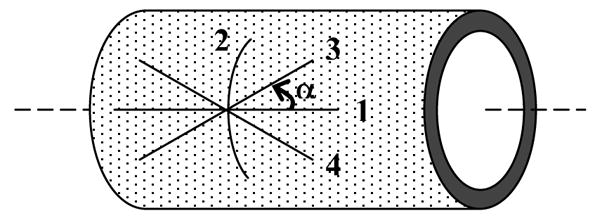
Representation of the four families of collagen fibers in an arterial segment: fiber-reinforcement is defined in the undeformed configuration by the unit vectors M_αk=[0,sinα_k,cosα_k] where α_k is the fiber angle defined between the direction of the k^th family of collagen fibers and the axial direction of the artery. For axial fibers: α₁ = 0°; for circumferential fibers: α₂ = 90°; and for diagonal fibers: α₃ =α and α₄ = −α.

$${\mathbf{a}}_{{\alpha }_{\text{k}}}=\mathbf{F}{\mathbf{M}}_{{\alpha }_{\text{k}}}.$$ (8)

The Cauchy stress tensor σ thus results from three contributions: a reaction stress that enforces incompressibility, an extra stress that models passive behaviors via strain energy functions, and an active stress due to smooth muscle tone:

$$\mathit{\sigma }=-\text{p}\mathbf{1}+{\mathit{\sigma }}^{\mathbf{p}}+{\mathit{\sigma }}^{\mathbf{a}},$$ (9)

where p is a Lagrange multiplier, 1 the identity tensor, σ^p and σ^a the passive and active stress contributions (Humphrey, 2002) computed as:

$$\begin{array}{l}{\mathit{\sigma }}^{\mathbf{p}}=2\mathbf{F}\frac{\partial \text{W}}{\partial \mathbf{C}}\overline{\mathbf{F}}=2{\text{W}}_1\mathbf{B}+2{\text{W}}_4\mathbf{F}{\mathbf{M}}_{{\alpha }_{\text{k}}}\otimes {\mathbf{M}}_{{\alpha }_{\text{k}}}\overline{\mathbf{F}},\\ {\mathit{\sigma }}^{\mathbf{a}}={\text{T}}_{\text{m}}{\lambda }_{\theta }\left[1-{\left(\frac{{\lambda }_{\text{m}}-{\lambda }_{\theta }}{{\lambda }_{\text{m}}-{\lambda }_0}\right)}^2\right]{\mathbf{e}}_{\theta }\otimes {\mathbf{e}}_{\theta },\end{array}$$ (10)

with W_j = ∂W/∂I_j (j = 1,4 ). This phenomenological form for the active stress (Rachev and Hayashi, 1999) assumes the smooth muscle is oriented primarily in the circumferential direction. The parameter T_m denotes the level of activation, λ_m is the stretch at which the contraction is a maximum, and λ₀ is the stretch at which active force generation ceases (i.e., minimum stretch possible). Using (9) and (10), with M_αk = [0,sinα_k,cosα_k], components of the Cauchy stress tensor are

$$\begin{array}{l}{\sigma }_{\text{rr}}=-\text{p}+\text{c}{{\lambda }_{\text{r}}}^2,\\ {\sigma }_{\theta \theta }=-\text{p}+\text{c}{{\lambda }_{\theta }}^2+{{\lambda }_{\theta }}^2\sum _{\text{k}=1}^4{\text{c}}_{1(\text{k})}\left({{\lambda }_{\text{k}}}^2-1\right)·exp\left[{\text{c}}_{2(\text{k})}{\left({{\lambda }_{\text{k}}}^2-1\right)}^2\right]{sin}^2{\alpha }_{\text{k}}+{\text{T}}_{\text{M}}{\lambda }_{\theta }\left[1-{\left(\frac{{\lambda }_{\text{m}}-{\lambda }_{\theta }}{{\lambda }_{\text{m}}-{\lambda }_0}\right)}^2\right],\\ {\sigma }_{\text{zz}}=-\text{p}+\text{c}{{\lambda }_{\text{z}}}^2+{{\lambda }_{\text{z}}}^2\sum _{\text{k}=1}^4{\text{c}}_{1(\text{k})}\left({{\lambda }_{\text{k}}}^2-1\right)·exp\left[{\text{c}}_{2(\text{k})}{\left({{\lambda }_{\text{k}}}^2-1\right)}^2\right]{cos}^2{\alpha }_{\text{k}},\end{array}$$ (11)

where I_4(k) = λ_k² = λ_θ² sin²α_k+λ_z² cos²α_k is the square of the stretch of the k^th fiber family.

2.4 Equilibrium

Assuming the Lagrange multiplier p depends only on radial direction and time, the equation of motion, in absence of body forces, reduces to (Humphrey, 2002)

$$\frac{\partial {\sigma }_{\text{rr}}}{\partial \text{r}}+\frac{{\sigma }_{\text{rr}}-{\sigma }_{\theta \theta }}{\text{r}}=\rho {\text{a}}_{\text{r}},$$ (12)

where ρ is the mass density of the wall and a_r is the radial acceleration. The contribution of the inertial term is only ~0.1% of the inner pressure (calculation not shown), thus the elastodynamics can be studied quasi-statically (Humphrey and Na, 2002). Because the arterial wall is layered (i.e., heterogeneous), (12) can be solved by integrating over radius from the inner wall to the medial-adventitial interface and then from the medial-adventitial interface to the outer surface (denoted by r_o):

$${\sigma }_{\text{rr}}({\text{r}}_{\text{o}})-{\sigma }_{\text{rr}}({\text{r}}_{\text{i}})={\int }_{{\text{r}}_{\text{i}}}^{{\text{r}}_{\text{m}}}\left(\frac{{\sigma }_{\theta \theta }-{\sigma }_{\text{rr}}}{\text{r}}\right)\text{dr}+{\int }_{{\text{r}}_{\text{m}}}^{{\text{r}}_{\text{o}}}\left(\frac{{\sigma }_{\theta \theta }-{\sigma }_{\text{rr}}}{\text{r}}\right)\text{dr},$$ (13)

where, by traction boundary conditions, the radial stress at the inner wall equals minus the luminal pressure and the radial stress at the outer wall can describe the radial traction due to perivascular tissue. Recall, however, that the in vivo clinical data on the CCA does not include the adventitia. Hence, we assume that the pressure-like contribution of the adventitial layer on the intima-media can be combined with that due to the perivascular tissue and described by a single term P_a (t). Consequently, integrating (12) between the measured inner r_i(t) and medial r_m(t) radii, the “transmural pressure” acting on the intimal-medial tissue is

$${\text{P}}_{\text{i}}(\text{t})={\text{P}}_{\text{a}}(\text{t})+{\int }_{{\text{r}}_{\text{i}}(\text{t})}^{{\text{r}}_{\text{m}}(\text{t})}\frac{{\sigma }_{\theta \theta }(\text{r},\text{t})-{\sigma }_{\text{rr}}(\text{r},\text{t})}{\text{r}}\text{dr},$$ (14)

where P_i(t) is the computed intraluminal pressure. The perivascular-like reactive radial stress is modeled using a lumped parameter exponential form (Humphrey and Na, 2002),

$${\text{P}}_{\text{a}}(\text{t})=\text{a}exp\left(\text{b}\frac{{\text{r}}_{\text{m}}(\text{t})}{{\text{r}}_{\text{m}}({\text{t}}_{\text{d}})}\right),$$ (15)

with a and b the material parameters and t_d the diastolic time over the cardiac cycle. In summary, (14) allows the intraluminal pressure to be computed given information on the kinematics, including residual stress effects, the individual structural constituents of the wall, and the perivascular-like reactive stress acting on the media.

2.5 Material identification

Following Stalhand et al. (2004), we estimated unknown geometric and material parameters using non-invasive in vivo data on luminal and medial diameters and intraluminal pressure. Noting that the residual stress related axial stretch Λ is typically near unity (Chuong and Fung, 1983; Humphrey, 2002), we let Λ=1. Moreover, although the constitutive model includes four collagen-fiber families characterized by fiber angles α_k, one family is assumed to be oriented axially (α₁ = 0°) and another circumferentially (α₂ = 90°). Hence, one fiber angle is unknown assuming symmetrically oriented diagonal fibers (i.e., α₃ = α and α₄ = −α). We also assumed diagonal and axial collagen fibers to have similar behaviors (c₁₍₁₎ = c_{1 (3)} = c_{1 (4)} =c₁ and c_{2 (1)} = c_{2 (3)} = c _{2 ( 4 )} = c₂), whereas the circumferential fibers may differ (c_{1 ( 2 )}= c_{1, circ} and c₂₍₂₎ = c_{2, circ}) because of possible interactions with circumferentially oriented smooth muscle. Consequently, from (5), (6), (10), (15) and the aforementioned assumptions, 14 parameters must be determined: residual stress related (R_m,Θ₀,λ), passive wall properties (c, c₁, c₂, c_1,circ, c_2,circ,α), muscle activation (T_M,λ₀,λ_m), and perivascular and adventitial effects on the media (a,b).

Best-fit values of these parameters were determined using a nonlinear least-squares (Levenberg-Marquardt) minimization of the difference between computed and measured intraluminal pressures over a cardiac cycle. That is, the following objective function was minimized

$$\text{e}=\sum _{\text{j}=1}^{\text{N}}\left[{{\left({{\text{P}}_{\text{i}}}^{\text{th}}(\mathbf{u})-{{\text{P}}_{\text{i}}}^{exp}\right)}_{\text{j}}}^2\right],$$ (15)

where N is the number of data points, u the vector of parameters to be optimized, P_i^th the computed intraluminal pressure from (14), and P_i^exp the measured inner pressure. As a metric of the goodness of fit, we computed the root mean square of the fitting error:

$$\text{RMSE}=\sqrt{\frac{\text{e}}{\text{N}}}.$$ (16)

3. Results

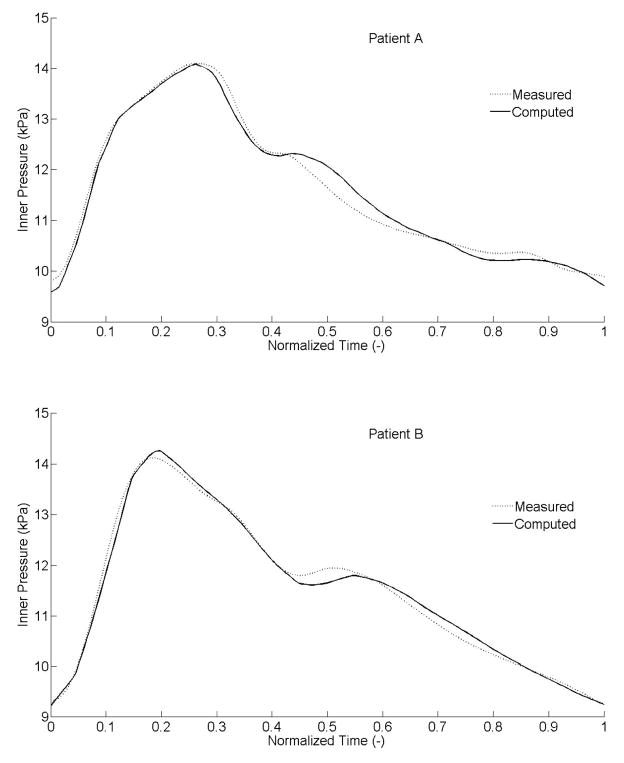
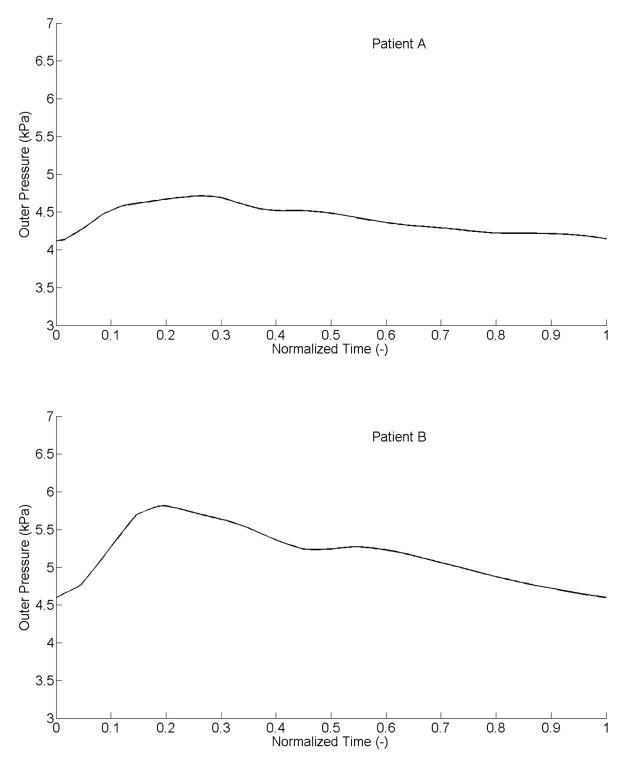
Separate sets of best-fit values of the parameters (Table 1) provided good fits to the measured intraluminal pressures (Figure 4) for both patients. Specifically, the systolic parts of the data, or increasing curves to the peak, fit very well. The fits for the diastolic parts, or decreasing curves, were less good but close nonetheless with a maximum difference between computed and experimental results ~0.4 kPa (i.e., ~3 mmHg). Corresponding “outer pressures”, which model both adventitial and perivascular tissue, ranged from 4.1 to 4.7 kPa (i.e., 31 to 35 mmHg) for patient A, and from 4.6 to 5.8 kPa (i.e., 34.5 to 43.5 mmHg) for patient B (Figure 5). Although not shown, the computed axial force remained nearly constant over the cardiac cycle (~0.1 N).

Table 1.

Best-fit geometrical and material parameters, and the goodness of fit for 2 healthy subjects.

Parameters	Patient A	Patient B
Rm (mm)	4.26	4.23
Θ0 (°)	128.7	131
λ (−)	1.11	1.09
c (kPa)	29.82	43.48
c1 (kPa)	9.45	22.84
c2 (−)	14.14	13.2
c1,circ (kPa)	16.13	11.76
c2,circ (−)	15.11	12.99
α (°)	65.7	51.18
Tm (kPa)	39.73	49.89
λ0 (−)	0.96	0.89
λm (−)	1.70	1.62
α (kPa)	0.12	0.13
b (−)	3.52	3.58
RMSE (kPa)	0.17	0.13

Figure 4.

Experimentally measured and theoretically computed intraluminal pressure over a cardiac cycle. The theoretical result is based on best-fit geometric and material parameters determined via nonlinear regression.

Figure 5.

Evolution of the predicted outer pressure, including both perivascular tethering and the effect of the adventitia on the intima-media.

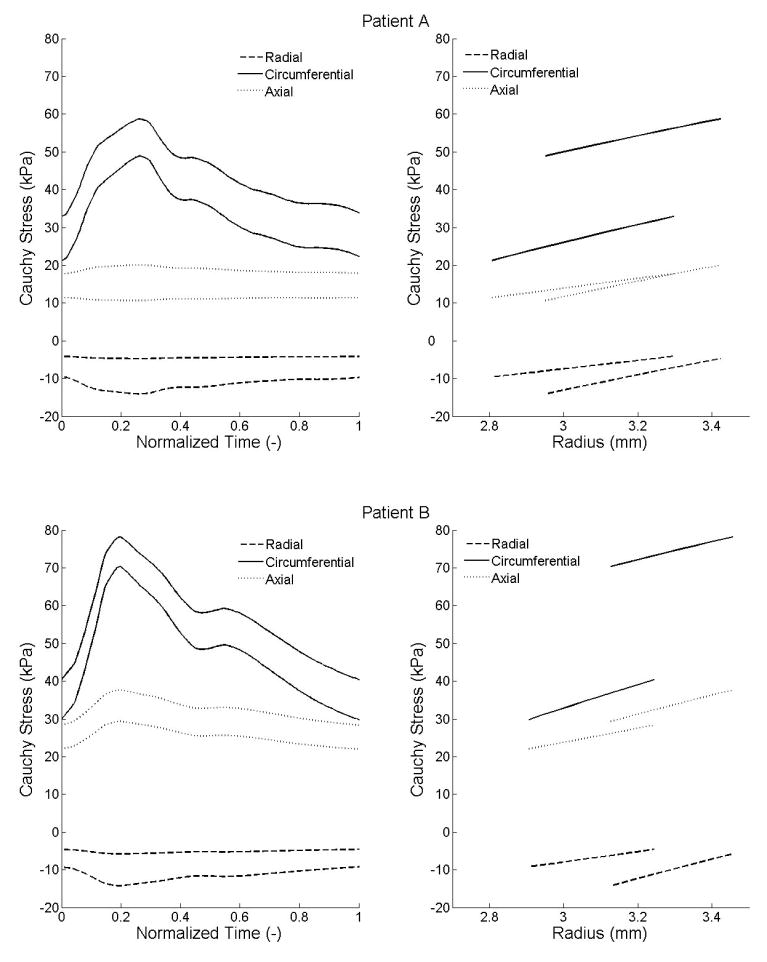
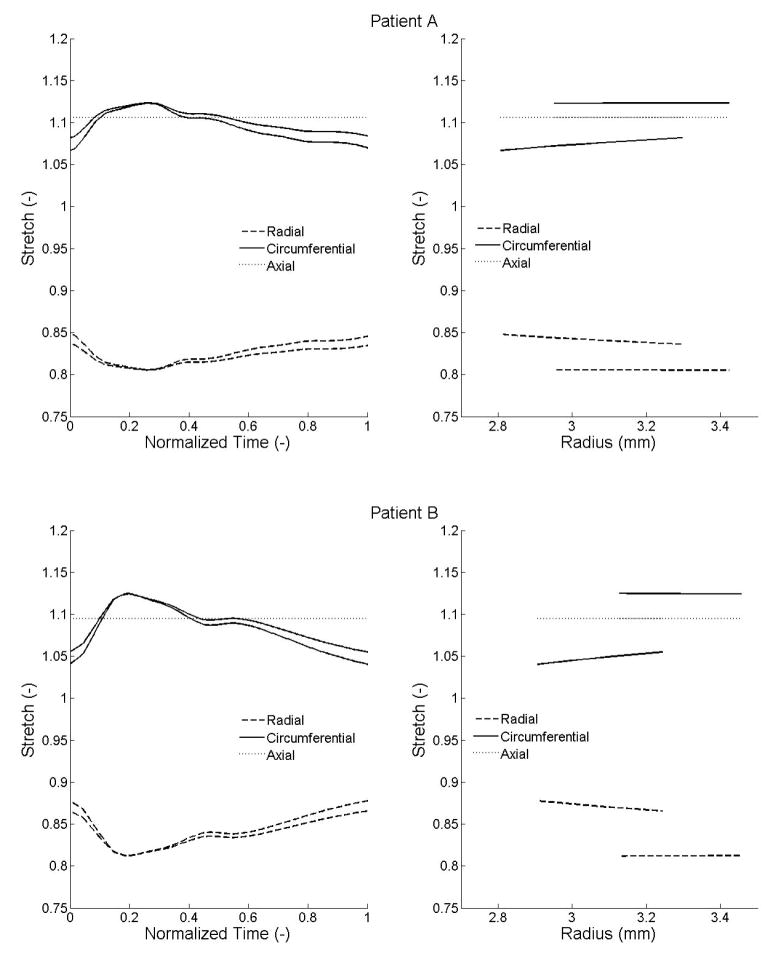
Using the best-fit parameters, we computed radial, circumferential, and axial stresses within the wall during the cardiac cycle. Illustrative results are shown over the cardiac cycle at the intimal and medial-advential interfaces (Figure 6a) as well as transmurally at diastole and systole (Figure 6b). Radial stresses ranged from −14.1 to −4.1 kPa and −14.3 to −4.6 kPa; circumferential stresses ranged from 21.2 to 58.7 kPa and 29.8 to 78.2 kPa; and axial stresses ranged from 10.6 to 20 kPa and 22 to 37.6 kPa, respectively, for patients A and B. Similarly, radial stretches ranged from 0.81 to 0.85 and 0.81 to 0.88; circumferential stretches ranged from 1.07 to 1.12 and 1.04 to 1.13; and axial stretches, assumed to be constant over the cardiac cycle, were 1.11 and 1.09. (Figure 7).

Figure 6.

Radial, circumferential, and axial Cauchy stresses computed from the identified parameters. (a) Left: stresses over the cardiac cycle at the inner and outer radii. For each component of stress, the lower curve corresponds to the inner radius and the upper one to the outer radius. (b) Right: stresses within the arterial wall at the diastolic and systolic pressures. For each component of stress, the curve which starts from the smaller radius corresponds to the diastolic pressure and the one that starts from the larger radius to the systolic pressure.

Figure 7.

Radial, circumferential, and axial Cauchy stretches computed from the identified parameters. (a) Left: stretches over the cardiac cycle at the inner and outer radii; the curve with the lowest circumferential stretches and the one with highest radial stretches correspond to the inner radius with the opposite description corresponding to the outer radius. (b) Right: stretches within the arterial wall at the diastolic and systolic pressures. For each component of stretch, the curve which starts from the smaller radius corresponds to the diastolic pressure and the one starting from the larger radius to the systolic pressure.

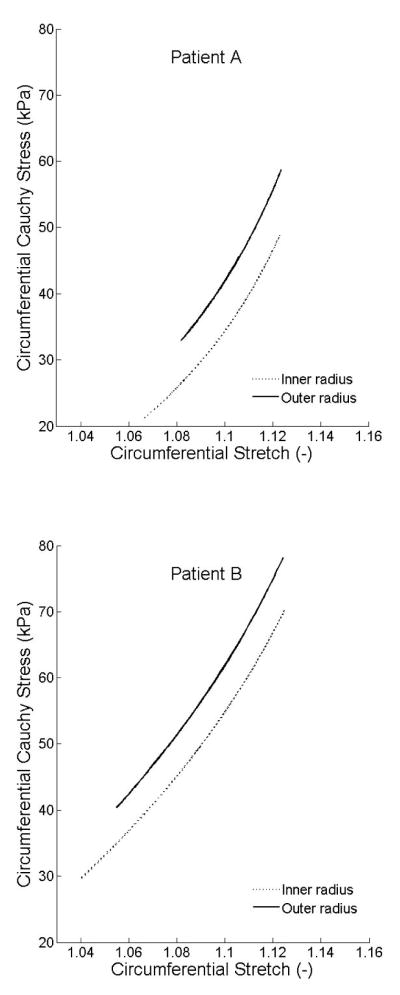
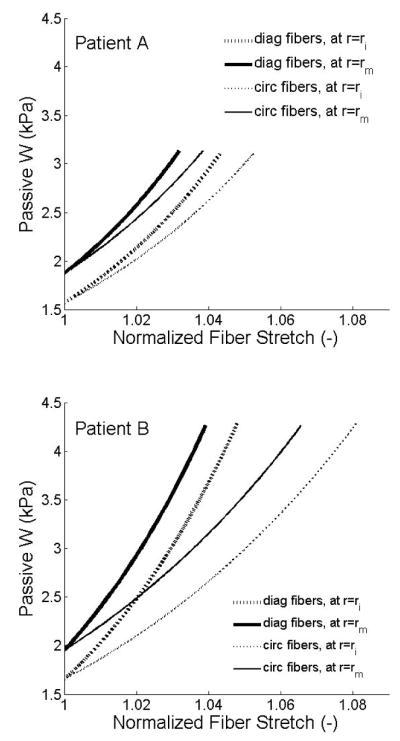
Figure 8 shows circumferential Cauchy stresses as a function of circumferential stretches, which reveal the intimal-medial behavior. Although overall slopes were similar, in vivo distensibility was less in patient A (older female) than patient B (younger male). Finally, Figure 9 shows strain energy stored passively in axial/diagonal versus circumferential fiber families, with stretches normalized to facilitate comparison. The axial/diagonal fibers were slightly stiffer, which may reflect thinner fibers or increased undulation.

Figure 8.

Circumferential Cauchy stresses as a function of circumferential stretches at the inner and outer radii.

Figure 9.

Passive strain-energy stored in the individual fiber families, axial/diagonal and circumferential. These fiber stretches were normalized by their respective minimum stretch for better comparison.

4. Discussion

Our main result is that one can characterize the complex mechanical behavior of human CCAs from non-invasive in vivo measurements of diameter and intraluminal pressure using a three-dimensional, nonlinear, fiber-reinforced, hyperelastic, incompressible model of the wall that includes residual stresses, smooth muscle tone, and perivascular tethering. This approach promises better estimations of wall stresses in vivo over a cardiac cycle, which in turn will enable increasing information on vascular mechanobiology to be incorporated within clinical interpretations of disease progression and treatment.

The lack of similar studies on human CCAs limits possible comparisons of our results to findings in the literature. Schulze-Bauer and Holzapfel (2003) employed a 2D Fung-type stored-energy function to study in vivo the human thoracic aorta. They considered a 2D model, thus computed wall stresses were mean values and residual stresses were not included. Stalhand et al. (2004) studied the human abdominal aorta, which they assumed to be a thick-walled, residually stressed, cylindrical tube described by a 3-D nonlinear, pseudoelastic, two-fiber family model of the wall subjected to luminal pressure alone. Albeit a significant advance, they neglected smooth muscle activity and perivascular tethering. Active stress plays an important role in wall mechanics by accounting for wall shear stress regulation of smooth muscle tone and hence luminal diameter. We employed a phenomenological model of active stress generation introduced by Rachev and Hayashi (1999) and used by Humphrey and Na (2002); best-fit values of the activation function (T_m) for our illustrative subjects were close to the previously reported value of 50 kPa, thus supporting the utility of this model. Nevertheless, structurally-motivated models, such as proposed by Stalhand et al. (2008), should be considered in future studies. Humphrey and Na (2002) showed that transmural stresses tend to be lower, for a given luminal pressure, when accounting for perivascular tethering. Indeed, we found that residual stresses, smooth muscle activation, and adventitial-perivascular tethering worked together to yield transmural intimal-medial stresses that were nearly homogeneous and ~50 kPa. To our knowledge, no similar study of in vivo human CCA mechanics is available for comparison. Nevertheless, recalling that the two patients were supine and resting, these values are reasonable compared to prior general findings (e.g., with stresses ≤ 100 kPa; Humphrey, 2002) that did not include all complexities that exist in vivo. Moreover, we obtained stresses qualitatively similar to those reported by Stalhand et al. (2004), which were for human in vivo abdominal aorta, and our results agreed with mean stress estimations by Laplace’s law.

In vitro mechanical data on human CCAs are also scant. Yet, Delfino et al. (1997) measured the residual stress related opening angle (130 ± 15°) and the axial prestretch (λ = 1.1) in 8 human CCAs. We included residual stresses theoretically using the method of Chuong and Fung (1986). Computed opening angles for both subjects were close to those reported by Delfino et al. (1997), and so too for axial prestretch (cf. van Loon et al. (1977), who reported λ = 1.2). Finally, there are few in vitro stress-strain data on human CCAs. Whereas Delfino and colleagues assumed an isotropic strain energy function, most arteries exhibit a strong anisotropy due mostly to the underlying collagen fiber orientations. Our strain energy function included four generic collagen-fiber families, which because of exponential response functions are progressively recruited as pressure increases. The specific exponential forms were proposed by Holzapfel et al. (2000), who considered two diagonal families. We employed the four-fiber family model of Baek et al. (2007) that extended the Holzapfel model by adding axial and circumferential fiber directions. Noting the finding by Gasser et al. (2006) that the two-fiber family model did not yield accurate stresses in particular experimental situations, the four-fiber family model describes biaxial data for rabbit basilar arteries and mouse carotid arteries better than the two-fiber family model (Gleason et al., 2008; Wicker et al., 2008). Indeed, data herein were also described well.

One of the primary challenges in estimating many (e.g., 14) model parameters from time-dependent in vivo pressure diameter data using nonlinear regression is identifying unique values. We submit that the success achieved herein resulted primarily from our ability to prescribe both structurally-motivated functional forms of the constitutive relations and reasonable values of the initial guesses for each parameter. Indeed, despite the lack of precise microstructural, biomechanical, and functional data from human CCAs and surrounding tissue, the extensive literature on CCAs from diverse species enabled us to prescribe appropriate constitutive relations; moreover, many of the parameters are physically meaningful and thereby have limited ranges of allowable values (e.g., R_m relates to in vivo dimensions, Θ₀ typically ranges from 0 to 180°, λ from 10 to 50%, T_M from 0 to 100 kPa, and λ₀,λ_m must fall within the range of maximum measured circumferential stretch whereas α must range from 0 to 90°). Actually, results from related studies provide further guidance for selecting initial guesses for the material parameters for elastin and collagen dominated behaviors: c, c₁, c₂, c_1,circ, c_2,circ. This reminds us, therefore, that in vitro data provide essential guidance for in vivo applications.

Notwithstanding the advances achieved herein, some issues require further attention. The in vivo pressure and diameter recordings were successive, not simultaneous, which necessitated a temporal adjustment for data analysis based on prior ECG augmented data sets. Even with patients at rest while supine, respiratory variability could introduce discrepancies between waveforms. It does not appear, however, that this caused the small differences between the computed and measured intraluminal pressures during diastole, especially around the dicrotic wave. Rather, such differences likely resulted from modeling assumptions. The CCA was modeled as a cylindrical tube and we considered purely radial motions using the standard equilibrium equation; this is reasonable locally but does not account for possible tapering or non-axisymmetric perivascular support or wall thicknesses. Moreover, the wall was assumed to be incompressible. Even though variations of wall cross-sectional area, at an assumed constant length (van Loon et al., 1977), were small in these two healthy patients (less than 5% over the cardiac cycle), they could be higher in diseased arteries like those with accumulated proteoglycans, which play a major role in sustaining the compression generated by pulsatile pressures (Boutouyrie et al., 2001). Further study of wall volume throughout the cardiac cycle is needed to quantify possible compressible effects (Zidi, 2001; Zidi and Cheref, 2002). Moreover, because we measured both wall diameter and thickness, the equilibrium equation was integrated between experimentally determined inner and outer radii in contrast to other studies (e.g., Humphrey and Na, 2002; Stalhand et al., 2004) that only used diameter data plus the incompressibility assumption to express one radius in terms of the other.

Viscoelastic effects are typically small for large arteries (Holzapfel et al., 2002) and smaller yet in vivo due to cyclic loading (Boutouyrie et al., 1997). Hence, the wall was assumed to exhibit a hyperelastic behavior. Indeed, our findings showed that both the systolic and the diastolic parts of the cardiac cycle were fit well with the same set of material parameters; this contrasted to the study of Stalhand et al. (2004) that considered loading and unloading separately using the concept of pseudoelasticity. We also assumed that the axial stretch remained constant during the cardiac cycle (Patel and Fry, 1966), but we did not enforce a constraint in the parameter identification to keep the axial force constant (van Loon et al., 1977). Although such constraints can improve parameter estimation (Stalhand and Klarbring, 2005), our results yielded a nearly constant computed axial force during the cardiac cycle, again suggesting overall utility of the model. Finally, we assumed four independent collagen-fiber families. Cross-links can increase within the collagen network with aging via advanced glycation end-products (Silacci, 2002; Yim et al., 2001), but this was not considered. Including interactions between, and exact distributions of, collagen-fiber families should be pursued in future in vivo modeling (Zulliger and Stergiopulos, 2007), particularly as the approach presented herein is extended to account for aging and hypertension. In addition, because of the lack of information on the adventitial-perivascular interface, analysis of wall properties and stress was restricted to the intima-media. Given the potentially important mechanical role of the collagenous adventitia and the increasingly recognized importance of mechanobiological responses by adventitial fibroblasts, there is a need to increase the spatial resolution of in vivo imaging and to advance biomechanical modeling accordingly.

In conclusion, we identified experimentally unknown geometric and material parameters directly from non-invasive in vivo human data. The modeling included finite deformations, nonlinear material behavior, collagen fiber-reinforcement, residual stresses, muscle tone, and perivascular tethering. This approach could be applied in vivo to different regions of the vasculature, given pressure and diameter measurements, to compute wall stress and strain fields that can play important roles in understanding better both diseases and their evolution or treatment. This approach reinforces the link between continuum biomechanics and vascular medicine to improve understanding and prediction of arterial biology.