Anomalous properties of the acoustic excitations in glasses on the mesoscopic length scale

Abstract

The low-temperature thermal properties of dielectric crystals are governed by acoustic excitations with large wavelengths that are well described by plane waves. This is the Debye model, which rests on the assumption that the medium is an elastic continuum, holds true for acoustic wavelengths large on the microscopic scale fixed by the interatomic spacing, and gradually breaks down on approaching it. Glasses are characterized as well by universal low-temperature thermal properties that are, however, anomalous with respect to those of the corresponding crystalline phases. Related universal anomalies also appear in the low-frequency vibrational density of states and, despite a longstanding debate, remain poorly understood. By using molecular dynamics simulations of a model monatomic glass of extremely large size, we show that in glasses the structural disorder undermines the Debye model in a subtle way: The elastic continuum approximation for the acoustic excitations breaks down abruptly on the mesoscopic, medium-range-order length scale of ≈10 interatomic spacings, where it still works well for the corresponding crystalline systems. On this scale, the sound velocity shows a marked reduction with respect to the macroscopic value. This reduction turns out to be closely related to the universal excess over the Debye model prediction found in glasses at frequencies of ≈1 THz in the vibrational density of states or at temperatures of ≈10 K in the specific heat.

Glasses are structurally disordered systems. As common experience shows, in the macroscopic limit they support sound waves as corresponding crystalline materials do. In fact, averaging on a large enough length scale, the details of the microscopic arrangement become essentially irrelevant. This holds true for sound waves with long wavelengths of at least several hundreds of nanometers, corresponding to wavenumbers q in the 10⁻²-nm⁻¹ range, as those probed with light scattering techniques (1). On further increasing q, the effect of the structural disorder must appear at one point. The much larger q scale of few nm⁻¹ is also well known because it can be accessed experimentally with inelastic X-ray (2) and neutron (3) scattering techniques, and numerically with molecular dynamics simulations (4–11). These studies typically probe the dynamic structure factor S(q,ω), that is, the space and time Fourier transform of the density–density correlation function. These studies clearly indicate the existence in glasses of excitations that appear in those spectra as very broad peaks whose position as a function of q is characterized by a sinusoidal-like dispersion curve. Thus, these excitations strongly recall the acoustic modes in (poly-)crystalline systems up to roughly one half of the pseudo-Brillouin zone (12), i.e., down to distances corresponding to the interatomic spacing. For this reason, they are often dubbed as acoustic-like. However, as their broadening clearly indicates, they are far from being crystal-like modes and correspond in fact to a complex pattern of atomic motions (6–11).

Unfortunately, experimental and numerical studies leave a gap between the few-nanometers scale and the hundreds-of-nanometers scale, which is extremely difficult to access. This keeps open a number of fundamental questions on the physics of glasses and, more generally, on the nature of the vibrational excitations in disordered systems. (i) How does the transition for the acoustic-like excitations look like between the small-q Debye-like behavior and the large-q regime? In other words, how does it happen that reasonably well-defined plane waves transform, on increasing q, into a complex pattern of atomic motions that mirror the structural disorder? (ii) Similar to crystalline systems, glasses are characterized by a universal behavior in some fundamental, low-temperature observables like specific heat and thermal conductivity (13). In particular, in the ≈10-K range the specific heat shows an excess with respect to the T³ Debye-model prediction, and the thermal conductivity shows a plateau. Despite a longstanding debate (14–27), their origin is still poorly understood. It is, however, generally accepted that they are related to the ubiquitous existence at frequencies of ≈1 THz of an excess of modes in the vibrational density of states, g(ω), over the Debye-model prediction g_D(ω) = 3ω²/ω_D³, with ω_D the Debye frequency. This excess of modes is best visible in the reduced density of states, g(ω)/ω², where it appears as a broad feature known as a boson peak (28, 29). Is, then, this universal behavior in the low-temperature thermal properties or in the vibrational density of states related to the peculiar nature of the acoustic-like excitations in the low-frequency range? Or, alternatively, do we have to imagine that glasses are characterized by additional low-frequency modes? (iii) What is the information content that we can extract from the high-q acoustic-like excitations measured in inelastic scattering experiments or numerical calculations? In which physical properties are these excitations' crystal-like features (e.g., existence of dispersion curves) reflected?

The experiments that have attempted to answer these questions by accessing the difficult 10⁻²−1-nm⁻¹ q range lead to contrasting interpretations. An experiment (30) based on a tunnel-junction technique reported linear dispersion for the transverse acoustic excitations in a silica glass up to frequencies 50% smaller than the boson-peak position in that glass (≈1 THz). This result indicated that the acoustic excitations are unaffected in the frequency range relevant for the thermal properties in the ≈10-K range and seemed to exclude any acoustic contribution to the low-temperature anomalies in the specific heat of glasses (30). Early inelastic X-ray scattering results (2) seemed to confirm that scenario and showed crystal-like dispersing, high-frequency, longitudinal acoustic-like excitations with a broadening that increases quadratically with the frequency. Again, a simple linear dispersion of the longitudinal acoustic-like modes was observed at frequencies corresponding to the boson-peak position, thus suggesting a smooth transition between the macroscopic and microscopic regime. Recent and more accurate inelastic X-ray scattering studies have, however, revealed that the boson peak marks the energy where a qualitative change takes place: The longitudinal acoustic-like excitations show, below the boson-peak position, a marked decrease of the phase velocity (31) and a broadening characterized by a remarkable fourth-power-law frequency dependence (31–33). A similar behavior for the broadening of the transverse acoustic modes had been found in a silica glass at low temperature and at frequencies below the boson-peak position by using a tunnel-junction technique (34). Conversely, a recent experiment using inelastic UV light scattering to measure the longitudinal acoustic modes in a silica glass at room temperature reported the onset of this peculiar ω⁴ regime at frequencies one order of magnitude smaller than the boson-peak position (35): The boson peak would then not be directly related to this regime. A complex and sometimes contradictory picture seems, therefore, to come out of the experiments performed so far.

Classical molecular dynamics simulations have provided a complementary tool with which to study the vibrational properties of glasses, starting with the pioneering investigations of Rahman and coworkers (4). The body of results available until now supports a scenario where the longitudinal acoustic-like excitations seem to be largely decoupled from the boson peak: They show a linear dispersion and a broadening that grows quadratically with frequency with no special feature in the frequency region where the boson peak appears (6–11). However, these studies could not provide a final answer on this issue because of the fact that the largest wavelengths that could be studied so far—fixed by the simulation box size and then ultimately by computer power—were still in the range of a few tens of interatomic spacings. As a consequence, the corresponding lowest-frequency acoustic-like excitations that were accessible lay too close to the boson-peak position to allow for definite conclusions in this supposedly crucial frequency range.

We report here on a study of the vibrational dynamics of the classical Lennard–Jones (LJ) monatomic glass model (4). The reason of our choice is simple: Despite the fact that this system easily crystallizes below the melting temperature and thus requires extremely fast and experimentally out-of-reach quenching rates to prepare a glass starting from the melt, it is the simplest realization of a structural glass at our disposal. This model thus provides the very basic ingredients of the vibrational dynamics of a structural glass that in other systems might be superimposed to additional, more-complex effects. Specifically, we present here results for an exceptionally large simulation box containing up to N = 10⁷ particles and clarify how the acoustic modes look in the frequency region where the boson peak appears. In particular, we managed to probe acoustic excitations down to frequencies one order of magnitude lower than the boson-peak position. Thanks to this achievement, the study of the q-dependence of the acoustic excitations allows us to establish that the boson peak originates from a deformation of the dispersion curves with respect to the crystal case. This result boils down to a direct connection between the boson peak and the breakdown of the Debye-continuum approximation for the acoustic excitations that takes place on a length scale matching that of the medium-range order of the glass (20, 24, 31).

Results and Discussion

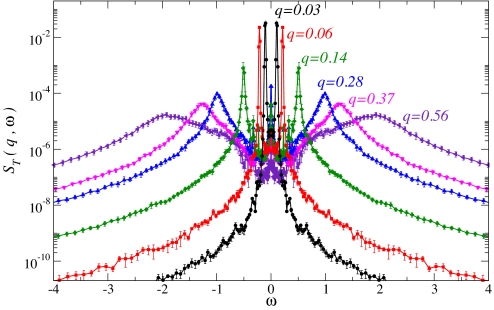
We have calculated both the transverse, S_T(q,ω), and the longitudinal, S_L(q,ω), dynamic structure factors, which yield information on the transverse and longitudinal acoustic-like excitations, respectively (see Materials and Methods for details). It is important to emphasize that although the latter can be obtained experimentally by using scattering techniques, the former can only be studied in the frequency range relevant here by using computer simulations. In what follows, we will use LJ units. To connect our findings to experiments, we recall that, if we model argon by using the LJ potential, then the temperature scale is in units of ϵ = 125.2 K, the length scale in units of σ = 3.405 Å, and the time scale is in units of τ = 2.11 ps. In Fig. 1, some representative S_T(q,ω) spectra are reported, including those that correspond to the lowest q value we could reach in our simulation.

Fig. 1.

Transverse dynamical structure factors, S_T(q,ω), for a LJ glass at number density ρ̂ = 1.015, temperature T = 10⁻³ and at the indicated q values, including the smallest one accessible, by using a simulation box containing ∼10⁷ atoms. The Brillouin peaks shift toward higher frequencies and show a clear broadening on increasing q.

For reference, we recall that at the studied number density ρ̂ = N/V = 1.015 (V being the simulation box volume), the melting temperature of the LJ system is T_m ≃ 1, and the glass-transition temperature T_g ≃ 0.4 (36). For what concerns the glass that we study, the Debye frequency and wavenumber are ω_D = 16.2 and q_D = 3.92, respectively; the first sharp diffraction peak is at q_m ≃ 7, which corresponds to an average nearest-neighbors distance of ≃2-π/q_m = 0.9. The spectra reported in Fig. 1 refer, then, to q values down to ∼10² times smaller than the border of the pseudo-Brillouin zone located at ≃q_m /2.

The S_T(q,ω) spectra are characterized by two symmetric peaks (Brillouin peaks) in addition to a sharp elastic peak at ω = 0. The Brillouin peaks can be characterized by the position of the maximum and the broadening. This information has been obtained by fitting a damped harmonic oscillator model to the spectral region, I_B(q,ω), around the Brillouin peaks:

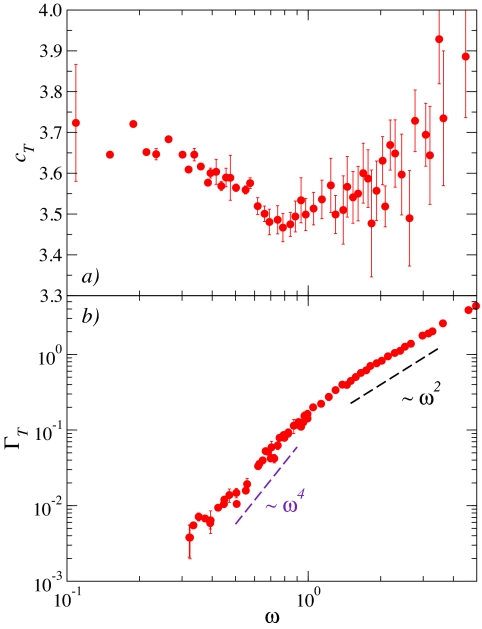
The parameters Ω_T(q) and Γ_T(q) represent the characteristic frequency and broadening [full width at half maximum (FWHM)] of the Brillouin peaks, respectively. The parameter Ω_T is used to obtain the transverse sound phase velocity, c_T(q) = Ω_T(q)/q, and is reported in Fig. 2A as a function of frequency. These data show an increase with frequency (positive dispersion) of the sound velocity for ω>0.8 as already reported for the longitudinal excitations in the same glass (9). It is interesting to observe that below this frequency, the macroscopic ω = 0 sound velocity limit is not directly recovered; instead, a previously unnoticed region where the phase velocity decreases with increasing frequency (softening) appears. This is exactly the region where the boson peak is found in this LJ glass, being the boson peak position at Ω ≃ 2. The boson peak, then, appears not in a frequency range where the acoustic-like excitations disperse linearly (constant phase velocity)—a finding at odds with what was previously thought (2, 30)—but where they experience a more-complex dispersion behavior. This finding is important because it clarifies that the Debye-continuum approximation for the acoustic excitations breaks down at frequencies comparable with the boson-peak position, i.e., at frequencies much lower than previously expected.

Fig. 2.

Phase velocity and broadening of the transverse acoustic-like excitations in a LJ glass. Frequency dependence of phase velocity (red circles in A) and FWHM (red circles in B) of the transverse acoustic-like excitations of the studied LJ glass. The dashed lines in B emphasize different regimes: ∼ω² at high frequencies and ∼ω⁴ at low frequencies. The transition between the two regimes appears at the frequency where the phase velocity in A shows a minimum.

Complementary information on this issue can be found in Fig. 2B, where the frequency-dependence of the broadening, Γ_T, of the transverse acoustic-like excitations is presented. These data clearly show two different regimes: a ω² regime at high frequencies, as already known from previous studies and associated with the structural disorder of the glass (7, 9, 10), and a previously unnoticed ω⁴ regime at low frequencies. The frequency that marks the change of regime is very close to, although slightly lower than, the boson-peak position. Moreover, the low-frequency regime appears in the same range where the softening of the sound velocity shows up in Fig. 2A, thus indicating that these two features must be connected. This finding, however, is not surprising if one recalls that the Brillouin position and broadening can be related to the real and imaginary parts, respectively, of a complex self-energy (25).

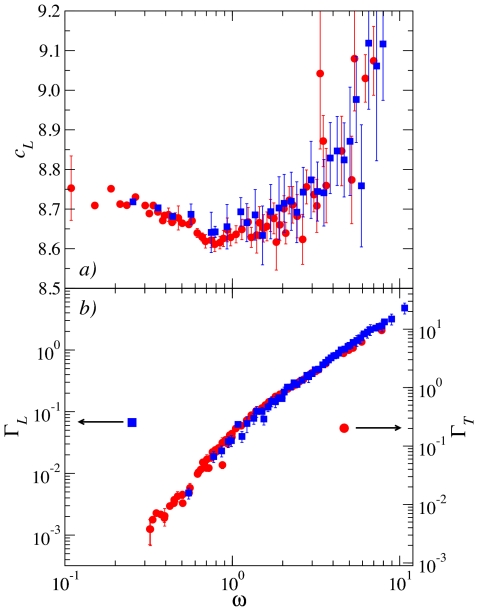
A similar scenario holds for the longitudinal acoustic-like modes. The longitudinal sound-velocity data (blue squares) are reported in Fig. 3A and show again a decrease at low frequency, followed by a positive dispersion for ω>0.8. The similarity with the behavior of the transverse data suggests a common origin for both. Indeed, the longitudinal and transverse sound velocities in an isotropic elastic medium are simply related by the expression

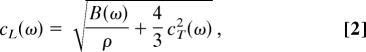where ρ is the mass density and B is the bulk modulus. This equation simply tells us that in a glass, the shear modulus, G = ρc_T², the longitudinal modulus, M = ρc_L², and the bulk modulus, B, are related and that only two of them give independent information. The low-frequency, macroscopic value for the bulk modulus B(ω → 0) = 59 can be obtained from the low-frequency data for c_L(ω) and c_T(ω) and is in good agreement with a literature value obtained for a slightly different system (24). Assuming a frequency-independent value for B, we can then estimate the longitudinal sound velocity by using the transverse data reported in Fig. 2A. The results of this calculation are shown in Fig. 3A (red circles). The good correspondence between the two sets of longitudinal velocity data derived directly from S_L(q,ω) or from S_T(q,ω) via Eq. 2 strongly supports a scenario where (i) the bulk modulus is frequency independent, and (ii) the frequency dependence of the longitudinal sound velocity simply derives from that of the transverse one. This picture is further reinforced by the comparison (shown in Fig. 3B) between the broadening of the longitudinal acoustic-like excitations (blue squares, left axis) and that of the transverse ones (red circles, right axis). It is clear here that these two quantities, within error bars, can be scaled one on top of the other. This finding confirms that, within the accuracy of our calculation, the frequency dependence that characterizes the longitudinal acoustic-like excitations comes into play through the shear component of the longitudinal response, whereas the bulk component is a mere spectator. The observation of the ω⁴ regime at low frequency in the acoustic attenuation for both polarizations is an interesting result and is predicted by several models (15, 21, 25, 37). The simplest model can be formulated in terms of Rayleigh scattering of the acoustic excitations from some kind of structural disorder (37). To make this argument quantitative, one needs to identify the scattering units that produce it, a difficult task that has led to different conclusions (38). Other approaches include a description of the disorder in terms of a continuum model with randomly fluctuating transverse elastic constants (25, 26) or of lattice models with disorder in the elastic constants (17). On this basis, it is quite puzzling that this strong scattering regime has not been observed in previous molecular dynamics studies (6–11). It has, for example, been argued that in contrast to lattice-based models, this feature would be absent in realistic glasses because of their intrinsically high level of frustration (large internal stress) (8). The present results solve the issue, clarifying that a strong scattering regime is also, in fact, present in realistic structural glasses in agreement with a number of theoretical (15, 17, 21, 25, 37) and experimental (31–34) results. We believe that the reason this regime has previously gone unnoticed is related to the fact that, aside from the obvious cases of too-small simulation boxes, attention was usually focused on the longitudinal excitations (the only ones experimentally accessible) where this regime is difficult to study in detail, even with a box as large as the one used here (see Fig. 3B). The present results in fact clarify that the signature of strong scattering appears for both polarizations at the same frequency, which implies that, as the longitudinal speed of sound is larger than the transverse one (by a factor 2.3 in the present case), the strong scattering regime appears for the longitudinal polarization at lower q's than for the transverse one; its observation is then definitively less favorable for the longitudinal polarization. More generally, the present results clearly show that the macroscopic and microscopic regimes for the acoustic-like excitations are connected by a cross-over region where the acoustic-like dispersion curves show a considerable deformation with respect to a simple linear dependence: The sound velocities decrease with increasing frequency, thus directly testifying to the existence of an abrupt breakdown of the Debye approximation in glasses (31). This finding comes together with the signature of strong scattering for the acoustic-like excitations, across which reasonably well-defined plane waves transform into a complex pattern of atomic vibrations. The connection to the boson peak is also clear: A softening of the transverse and longitudinal sound velocities implies an excess in the reduced vibrational density of states above the Debye level. Because this softening directly appears in the range where the boson peak is observed or at corresponding temperatures where the excess in the specific heat universally appears in glasses (13), we can conclude that these anomalies must have an acoustic contribution. In the following, we make this connection quantitative.

Fig. 3.

Comparison between transverse and longitudinal acoustic-like excitations in a LJ glass. Frequency dependence of phase velocity (blue squares in A) and broadening (blue squares in B, left axis) of the longitudinal acoustic-like excitations of the studied LJ glass. These data, similarly to those in Fig. 2, have been derived by fitting a damped harmonic oscillator model to the longitudinal dynamic structure factor spectra obtained from molecular dynamics. In A, the longitudinal phase velocity data are compared with data calculated from the corresponding transverse phase velocity (red circles), assuming a frequency-independent bulk modulus B = 59. Within error bars, we can conclude that the frequency dependence of the longitudinal phase velocity directly reflects that of the transverse one. In B, the longitudinal excitations broadening data are compared with data for the corresponding transverse excitations (red circles, right axis): The two sets of data can be convincingly scaled one on top of the other. Within error bars, we can again conclude that the frequency dependence of the longitudinal data directly reflects that of the transverse data.

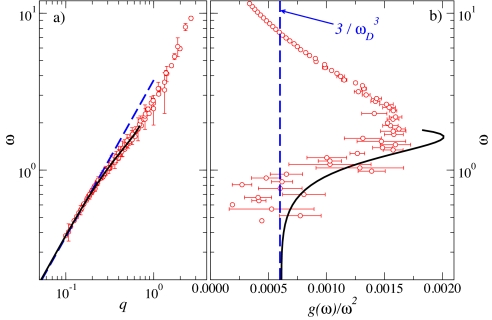
To gain further insight into these molecular dynamics results, we performed a standard normal-modes analysis of the glass in its inherent structures, i.e., we have diagonalized the dynamical matrix calculated in local minima of the potential energy landscape and derived eigenvalues and eigenstates. The lowest-frequency eigenstates of transverse polarization are close to being plane waves: It is possible to associate them with a leading q value (24) (see Materials and Methods for details). In Fig. 4A, we report the corresponding eigenvalues as a function of q (circles); the reduced vibrational density of states derived from the complete normal modes analysis is shown in Fig. 4B (circles).

Fig. 4.

Results of a normal-modes analysis of a LJ glass in its inherent structures. (A) q-dependence of the lowest frequency transverse eigenvalues of the studied LJ glass (circles) together with the function used to empirically describe it (full line). The initial slope of the curve corresponds to the q → 0 limit of the transverse phase velocity of Fig. 2A (dashed line). Note that here q is only an approximate quantum number and that it is increasingly difficult to associate higher-frequency eigenvalues to specific q values. (B) Reduced density of states of the studied LJ glass (circles) showing the boson peak at ω ≃ 2. The macroscopic Debye limit (dashed line) is indicated as well. The reduced density of states directly obtained from the data in A via Eq. 3 is reported (full line) up to the maximum frequency where this analysis is appropriate. The agreement between the two calculations is good—note that there is no adjustable parameter in this comparison. This implies that the density of states, up to the boson peak, is well described by the low-q inflection observed in A.

Fig. 4A corresponds to a pseudodispersion curve: It is not formally a dispersion curve but only an approximate one, because in a disordered system q is not a good quantum number, although one can still imagine that it is a reasonable mean to count the modes of low-enough frequency. This pseudodispersion curve must have a slope for q → 0 that corresponds to the transverse velocity. In fact, as shown in Fig. 4A, this slope corresponds well to the q → 0 limit of the transverse velocity (dashed line) derived from Fig. 2. On increasing q, the data in Fig. 4A show an early departure from linearity and a clear inflection at ω ≃ 2, which is the frequency where the boson peak appears (Fig. 4B). This inflection has been interpreted in terms of the failure of the classical Born approximation for the description of the continuum elasticity in disordered systems (24) and appears at the same frequency where the molecular dynamics results for the phase velocities in Fig. 2 and Fig. 3 show a softening. This finding is not surprising, as the acoustic-like frequencies can indeed be regarded as average values over a distribution of eigenvalues related to the broadening of the Brillouin peaks. In other words, the velocity decrease observed at frequencies around the boson-peak position in the acoustic-like excitations of transverse polarization (Fig. 2A) and—through the shear component of the longitudinal modulus—in those of longitudinal polarization (Fig. 3A) directly reflects an inflection that appears in the q dependence of the low-q transverse eigenvalues.

As far as we can consider q a reasonable quantum number, it is easy to directly estimate the vibrational density of states starting with the knowledge of the dispersion curves. In a simple plane–wave approach,

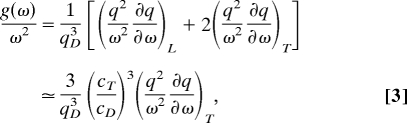where L and T stand for the longitudinal and transverse polarization, and c_D is the Debye velocity. The approximation in Eq. 3 is justified by the fact that the longitudinal contribution to the total vibrational density of states is small because it scales with c_T³/(2 c_L³) = 4%. Clearly, to follow this approach we shall use the pseudodispersion curve obtained from the normal-modes analysis because in that case the low-frequency eigenvalues are reasonably close to being plane waves. To compute Eq. 3, rather than directly differentiating the dispersion curve, we chose to use an empirical model to fit the simulation data (full line through the points in Fig. 4A) and then to differentiate the model function. The result of this calculation is shown in Fig. 4B (full line) and, as it can be appreciated, it well describes the boson peak. It is worth emphasizing that no additional input but the knowledge of the dispersion curve is required to perform this calculation. It is then clear that the reduced density of states of the studied glass, up to the boson peak, originates from a deformation of the pseudodispersion curve of eigenstates that can still be approximately described by using plane waves.

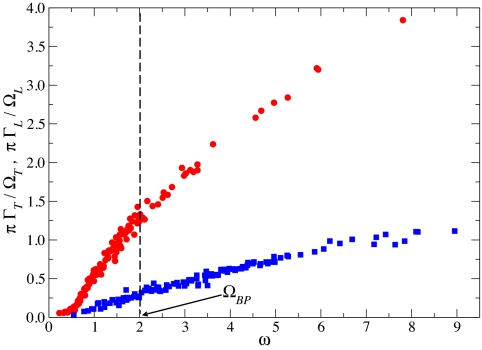
The molecular dynamics results presented above also allow us to calculate the Ioffe–Regel limit for the acoustic-like excitations, defined as the frequency where Ω = πΓ for both polarizations (33). This limit corresponds to the frequency where the decay time of the acoustic-like excitations first matches half of the corresponding oscillation period and therefore somehow marks an extreme upper bound in frequency for the validity of a plane–waves approach as a starting point from which to describe the acoustic-like excitations. As shown in Fig. 5, the present data confirm that the Ioffe–Regel limit for the transverse excitations is located close to the boson-peak position (11, 27). Fig. 5 also shows that the Ioffe–Regel limit is reached at different frequencies for the longitudinal and transverse excitations and that the longitudinal one shows up at a frequency higher than the boson-peak position (27). However, it is important to emphasize that this last result seems not to be general: In a simulation study of a silica glass, the Ioffe–Regel cross-over was found to appear at the same frequency for both polarizations (7). The connection between the Ioffe–Regel limit for the transverse excitations and the boson peak (27, 33) is clarified by the discussion above, which shows that this limit is, in fact, reached in the frequency range where the continuum approximation for the acoustic excitations breaks down.

Fig. 5.

The ratio πΓ/Ω is reported as a function of frequency for both the transverse (circles) and longitudinal (squares) polarization. The frequency where this ratio equals one defines the Ioffe–Regel limit. For the transverse case, this limit falls very close to the boson-peak position, indicated by the vertical dashed line. The case is different for the longitudinal polarization, where the Ioffe–Regel limit appears at a frequency ≈3 times higher than the boson-peak position.

To sum up, the present simulation results shed new light on the well-known universal anomaly observed in the specific heat of glasses in the T ≈ 10-K temperature range and related to the boson peak in the vibrational density of states at frequencies of ≈1 THz. We have shown that in glasses, the elastic continuum approximation for the acoustic-like excitations breaks down abruptly on the mesoscopic, medium-range-order length scale of ≈10 interatomic spacings, where it still works well for the corresponding crystalline systems. This breakdown is signaled by a deformation of the pseudodispersion curve and corresponds to a marked reduction of the sound velocity on the mesoscopic scale. This breakdown turns out to be closely related to the aforementioned anomalies in the specific heat and vibrational density of states, which can be finally traced back onto elastic properties specific to glasses.

Finally, to put the present results in some perspective and to connect them to experiments, it is important to emphasize once more that they refer to a simple, monatomic LJ glass quenched with a cooling rate out of reach experimentally. Still, we are convinced that such a simple model system has the great advantage of clearly grasping fundamental features that, although observed in bits and pieces in many experiments, are often hidden by a number of additional effects in real glasses. This, we believe, is the reason why the vibrational properties of glasses are still a debated issue after several decades of studies and discussions. For example, the high-frequency vibrational dynamics of the LJ monatomic glass has been proven to be well described within the harmonic approximation (6, 9). However, clearly real glasses are anharmonic systems—in what cases will anharmonicity start to play a role? Moreover, in contrast to the investigated model, real glasses are often characterized by the presence of intramolecular, or optic-like, modes; this issue is, of course, deliberately and completely disregarded here. All of these questions will require further studies on more complex models to be fully addressed.

Materials and Methods

The present numerical investigation has been performed by using simulation boxes of different sizes containing up to N ∼10⁷ atoms, interacting via a LJ potential with a cutoff r_c = 2.5 and periodic boundary conditions. This has been realized by using the large-scale, massively parallel molecular dynamics computer simulation code LAMMPS (39). A standard microcanonical, classical molecular dynamics simulation, carried out at the constant number density ρ̂ = 1.015 and at temperature T = 2 in the normal liquid phase is followed by a fast quench (dT/dt∼4 × 10²) down to T = 10⁻³. The quenched glass sample is relaxed for a time (dependent on the sample size) sufficient to have a constant total energy. The atomic positions r_i(t) and velocities v_i(t), have then been stored for a time (again dependent on the sample size) sufficient to get the desired resolution function. The time correlation functions required to obtain the dynamic structure factor S_L(q,ω) and its analogous function for the transverse excitations S_T(q,ω) have been computed as

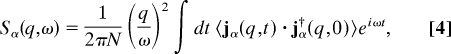where α is L or T and

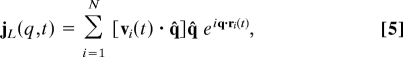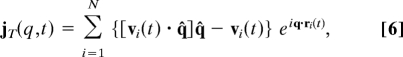with q̂ = q/|q|.

Addressing the issue of the dependence of the obtained results on the quenching rate is a difficult task for the studied system because of the fact that it easily crystallizes. The smallest quenching rate compatible with both the long simulation times needed to reach the desired resolution and with the large sizes of the simulation boxes is about five decades smaller (dT/dt ∼ 4 × 10⁻³) than the one used for this study. We have checked that the molecular dynamics results reported here are independent of the quenching rate in this range.

For the glass studied here, a standard normal-modes analysis has been carried out to derive the vibrational density of states g(ω) from the eigenvalues of the dynamical matrix calculated in the inherent structures of the glass. Moreover, the pseudodispersion curve for the transverse eigenvalues of the system reported in Fig. 4A has been constructed following ref. 24. More in detail, for each of the considered simulation boxes, we collected the four lowest-frequency degenerate eigenvalues obtained from the diagonalization of the dynamical matrix. These modes correspond to the largest wavelength standing waves for the simulation box. Because the transverse sound velocity is ≃2.3 times smaller than the longitudinal one, these four degenerate eigenvalues are all of transverse polarization. For example, the first eigenvalue has a degeneracy of 12 and can be associated to wavevectors of the (±1,0,0) family; the second eigenvalue has a degeneracy of 24 and can be associated to the wavevectors of the (±1,±1,0) family, and so on. These eigenvalues are size dependent; performing this analysis on simulation boxes of larger and larger size (up to n = 256,000 particles), we then selected transverse eigenvalues with smaller and smaller q's. A quite broad range of frequencies and q's could thus be explored. This procedure can be expected to lead to reasonable results only as far as the degeneracy of the eigenvalues shows up clearly enough to suggest a one-to-one relation to the corresponding values for q, and becomes less and less reliable on decreasing the box size or on increasing q. In the present case, we find that the highest q values up to which this analysis is still reasonable are q ≈ 0.2–0.3, corresponding to ω ≈ 2—i.e., basically up to the boson-peak position—and becomes less and less reliable on further increasing q.