Confidence Estimation via the Parametric Bootstrap in Logistic Joinpoint Regression

Abstract

We consider asymptotic properties of the maximum likelihood and related estimators in a clustered logistic joinpoint model with an unknown joinpoint. Sufficient conditions are given for the consistency of confidence bounds produced by the parametric bootstrap; one of the conditions required is that the true location of the joinpoint is not at one of the observation times. A simulation study is presented to illustrate the lack of consistency of the bootstrap confidence bounds when the joinpoint is an observation time. A removal algorithm is presented which corrects this problem, but at the price of an increased mean square error. Finally, the methods are applied to data on yearly cancer mortality in the United States for individuals age 65 and over.

1 Introduction

There are a wide variety of statistical methods for analyzing nonlinear models. If one is interested only in summarizing the trends in the data and in obtaining a good flexible non-linear fit, then one may take advantage of many types of spline models existing in the literature (see [10, 11, 13, 14, 20, 21, 23, 36, 42] and the references therein). On the other hand, if one’s interest lies mainly in estimating and making inferences on the location of structural changes in the underlying model, the model frequently considered is that of a segmented regression in which the knots (also referred to as joinpoints) are unknown (see, for instance, [15, 16, 25, 26, 27, 29, 31, 37]).

Segmented regression models are popular, for instance, as tools in modeling general disease trends and originally have been introduced in the context of epidemiological studies of occupational exposures for modeling threshold limit values in logistic regression models with a single joinpoint (see [18, 41]). Subsequently, various multiple joinpoint algorithms have also been applied to disease trend models. For instance, Kim et al. [28] suggested a sequential backward selection algorithm for testing the number of joinpoints in a model that uses the least-squares criteria under squared-error loss and a goodness-of-fit measure based on the F-statistic, and applied the algorithm to model U.S. yearly cancer rates. The algorithm has been implemented in the free software Joinpoint, version 3.3, (see http://srab.cancer.gov/joinpoint/) which facilitates fitting and testing the model for Gaussian and Poisson regressions. Czajkowski et al. [7] compared the above algorithm with a forward selection algorithm in the logistic joinpoint regression setting with multiple joinpoints where model parameters were estimated by maximum likelihood and applied the methods to model longitudinal data on cancer mortality in a cohort of chemical workers. An R package ljr [6] available at http://www.R-project.org [34] has been developed implementing both the backward and forward algorithms for the logistic joinpoint model. Many alternative approaches for selecting the number of change points based on information theory have been also considered in a variety of contexts (see [8, 30, 32, 40, 43] and the references therein).

When working with statistics having complicated distributions such as those encountered in segmented regression models, the bootstrap and parametric bootstrap are common tools used for confidence estimation (see, for instance, [4, 9, 12, 22]). In many cases, the bootstrap is effective, but there are also cases where the bootstrap is not consistent when parameters are on the boundary of the parameter space. Several examples are discussed in [1]. In this paper, we are interested in consistency of parametric bootstrap confidence bounds in the context of the logistic joinpoint regression. In particular, we describe herein a situation in which the consistency of the bootstrap confidence bounds fails, in the sense that they are not asymptotically correct. We refer to Section 7.4 of [39] for a general discussion of the bootstrap confidence bounds. The material in this paper discusses the behavior of the bootstrap for a segmented regression model; however, see [24] for a detailed discussion of the asymptotic behavior of the bootstrap for detecting changes in a multiphase linear regression model which differs from ours in that it does not impose continuity constraints.

The paper is organized as follows. In Section 2, we introduce a clustered logistic joinpoint model and discuss maximum likelihood estimation of its parameters. The consistency and asymptotic normality of the maximum likelihood and related estimators are discussed in Section 3. Section 4 gives sufficient conditions for the consistency of the parametric bootstrap, illustrates via simulation a situation when the parametric bootstrap is not consistent, and suggests a removal algorithm to restore consistency for the simulated example. Finally, in Section 5, the methods proposed are applied to data on yearly cancer mortality in the United States for individuals age 65 and over.

2 Clustered Logistic Joinpoint Model

Suppose that Y₁,…, Y_N are independent Binomial random variables such that Y_i is the sum of m_i independent Bernoulli random variables each with probability of success p_0i. Denote the realizations of these random variables as y₁,…, y_N, respectively, let y = [y₁,…, y_N]^Τ, and let $n={\displaystyle {\sum }_{i=1}^N{m}_i}$. Furthermore, let p_0i have the functional form

$$p_{0i}=\frac{e^{{\eta }_{0i}}}{1+e^{{\eta }_{0i}}}$$ (1)

where

$${\eta }_{0i}={\alpha }_0+{\beta }_0{t}_i+{\delta }_0{(t_i-{\tau }_0)}_{+}+{\gamma }_0^{\mathrm{{\rm T}}}{\mathit{x}}_i$$ (2)

and t₊ = max{t, 0}. Here x₁,…, x_N are fixed q-dimensional covariates, and the ‘times’ t₁ ≤ … ≤ t_N are ordered covariates. Also, α₀ is the unknown intercept, τ₀ is the unknown joinpoint, β₀ is the unknown slope coefficient for t_i before τ₀, δ₀ ≠ 0 is the change in the slope coefficient after τ₀, and γ₀ is the unknown q-dimensional vector of coefficients for the fixed covariates.

2.1 Maximum Likelihood Estimation

In this section, the maximum likelihood estimate of ${\mathit{\theta }}_0={[{\alpha }_0,{\beta }_0,{\tau }_0,{\delta }_0,{\gamma }_0^{\mathrm{{\rm T}}}]}^{\mathrm{{\rm T}}}$is derived. The log-likelihood function for the sample y₁,…, y_N is given by

$$l(\mathit{\theta })={\displaystyle \sum _{i=1}^N\{{\eta }_i(\mathit{\theta })y_i-m_i{\text{ln}(1+e}^{{\eta }_i(\mathit{\theta })})\}}$$

where θ = [α, β, τ, δ, γ^Τ]^Τ and

$${\eta }_i(\mathit{\theta })=\{\begin{array}{cc}\alpha +\beta t_i+{\gamma }^{\mathrm{{\rm T}}}{\mathit{x}}_i& \text{if}{t}_i\le \tau \\ \alpha +\beta t_i+\delta (t_i-\tau )+{\gamma }^{\mathrm{{\rm T}}}{\mathit{x}}_i& \text{if}{t}_i>\tau \end{array}.$$

It is useful to consider the jth super log-likelihood function

$$\begin{array}{ll}{l}_j(\mathit{\theta })\hfill & ={\displaystyle \sum _{i=1}^j\left\{(\alpha +\beta t_i+{\gamma }^{\mathrm{{\rm T}}}{\mathit{x}}_i)y_i-m_i\text{ln}(1+e^{\alpha +\beta t_i+{\mathit{\gamma }}^{\mathrm{{\rm T}}}{\mathit{x}}_i})\right\}}\hfill \\ \hfill & +{\displaystyle \sum _{i=j+1}^N\left\{(\alpha +\beta t_i+\delta (t_i-\tau )+{\gamma }^{\mathrm{{\rm T}}}{\mathit{x}}_i)y_i-m_i\text{ln}(1+e^{\alpha +\beta t_i+\delta (t_i-\tau )+{\mathit{\gamma }}^{\mathrm{{\rm T}}}{\mathit{x}}_i})\right\}}\hfill \end{array}$$ (3)

for j = 1,…,N − 1. Note that

$$l_j(\mathit{\theta })=l(\mathit{\theta })\text{if}\tau \in [t_j,t_{j+1}]$$

and l_j is infinitely differentiable with respect to θ, but l is not differentiable at τ = t_i for i = 1,…,N if δ ≠ 0. Letting ϕ(θ) = [α, β, α − δτ, β + δ, γ^Τ]^Τ, we can express (3) as

$$l_j(\mathit{\theta })={\displaystyle \sum _{i=1}^N\left\{{\varphi }^{\mathrm{{\rm T}}}(\mathit{\theta })z_i^{(j)}{y}_i-m_i\text{ln}\left(1+e^{{\varphi }^{\mathrm{{\rm T}}}(\mathit{\theta }){\mathit{z}}_i^{(j)}}\right)\right\}}$$

where ${\mathbf{z}}_i^{(j)}={[1-{\upsilon }_i^{(j)},(1-{\upsilon }_i^{(j)})t_i,{\upsilon }_i^{(j)},{\upsilon }_i^{(j)}{t}_i,{\mathit{x}}_i^{\mathrm{{\rm T}}}]}^{\mathrm{{\rm T}}}$and

$${\upsilon }_i^{(j)}=\{\begin{array}{ll}0\hfill & \text{if}i\le j\hfill \\ 1\hfill & \text{if}i>j\hfill \end{array}.$$

This is a logistic regression model with the design matrix ${\mathit{Z}}^{(j)}={[{\mathit{z}}_1^{(j)},\dots ,{\mathit{z}}_N^{(j)}]}^{\mathrm{{\rm T}}}$and the canonical parameter vector ϕ(θ).

The function l_j is an infinitely differentiable function with respect to ϕ. Differentiating l_j with respect to ϕ, we have

$$\frac{\partial l_j}{\partial \varphi }={\displaystyle \sum _{i=1}^N{\mathit{z}}_i^{(j)}\{y_i-m_i{\rho }_i^{(j)}(\mathit{\theta })\}}$$ (4)

where ${\rho }_i^{(j)}(\mathit{\theta })=e^{{\eta }_i^{(j)}(\mathit{\theta })}/(1+e^{{\eta }_i^{(j)}(\mathit{\theta })})$with ${\eta }_j^{(j)}(\mathit{\theta })={\varphi }^{\mathrm{{\rm T}}}(\mathit{\theta }){\mathit{z}}_i^{(j)}$. Setting (4) to zero, dividing by n, and simplifying, we obtain

$${\displaystyle \sum _{i=1}^N{u}_i{\mathit{z}}_i^{(j)}}\left(\frac{y_i}{m_i}-{\rho }_i^{(j)}(\mathit{\theta })\right)=\mathbf{0}$$ (5)

where u_i = m_i/n. If the matrix ${\mathit{Z}}^{(j)}={[{\mathit{z}}_1^{(j)},\dots ,{\mathit{z}}_N^{(j)}]}^{\mathrm{{\rm T}}}$ is of full rank, then the solution to (5) is the unique maximizer of l_j since

$$-\frac{{\partial }^2{l}_j}{\partial \varphi \partial {\varphi }^{\mathrm{{\rm T}}}}=n{({\mathit{Z}}^{(j)})}^{\mathrm{{\rm T}}}\mathit{U}{\mathit{W}}^{(j)}(\mathit{\theta }){\mathit{Z}}^{(j)}$$

is positive definite, where W^(j)(θ) is a diagonal matrix with diagonal elements ${\rho }_i^{(j)}(\mathit{\theta })(1-{\rho }_i^{(j)}(\mathit{\theta }))$i = 1,…,N and

$$U\text{is}\mathrm{a}\text{diagonal}\text{matrix}\text{with}\text{diagonal}\text{elements}{u}_1,\dots ,u_N.$$ (6)

For each j = 1,…,N − 1, denote the maximizer of l_j as

$${\widehat{\mathit{\theta }}}_n^{(j)}={\left[{\widehat{\alpha }}_n^{(j)},{\widehat{\beta }}_n^{(j)},{\widehat{\tau }}_n^{(j)},{\widehat{\delta }}_n^{(j)},{({\widehat{\mathit{\gamma }}}_n^{(j)})}^{\mathrm{{\rm T}}}\right]}^{\mathrm{{\rm T}}}.$$ (7)

Using the invariance property of the method of maximum likelihood (for example, see [33]) ${\widehat{\mathit{\theta }}}_n^{(j)}={\varphi }^{-1}(\widehat{\varphi ({\mathit{\theta }}_n^{(j)})})$where $\widehat{\varphi ({\mathit{\theta }}_n^{(j)})}$is the solution to (5).

The following algorithm can be used to compute the maximum likelihood estimate (MLE) θ̂_n of θ̂₀.

1. For j = 1,…,N −1, compute ${\widehat{\mathit{\theta }}}_n^{(j)}$. If ${\widehat{\tau }}_n^{(j)}\in (t_j,t_j+1)$, then compute $l({\widehat{\mathit{\theta }}}_n^{(j)})$; otherwise, the MLE of τ₀ is not in (t_j, t_j+1) and there is no need to evaluate l at any θ such that τ ∈ (t_j, t_j+1).

2. For j = 2,…,N − 1, fix τ = t_j so that the model is equivalent to logistic regression with covariates 1, t_i, (t_i − t_j)+, and x_i, i = 1,…,N. Then fit a logistic regression model to obtain respective possible estimates ${\tilde{\alpha }}_n^{(j)},{\tilde{\beta }}_n^{(j)},{\tilde{\delta }}_0^{(j)},\text{and}{\tilde{\gamma }}_0^{(j)}$of α₀, β₀, δ₀, and γ₀. Denote the possible estimate of θ₀ as

   $${\tilde{\mathit{\theta }}}_n^{(j)}={[{\tilde{\alpha }}_n^{(j)},{\tilde{\beta }}_n^{(j)},t_j,{\tilde{\delta }}_n^{(j)},{({\tilde{\gamma }}_n^{(j)})}^{\mathrm{{\rm T}}}]}^{\mathrm{{\rm T}}},$$

   and compute$l({\widehat{\mathit{\theta }}}_n^{(j)})$.

3. The MLE of θ₀ is the value of θ which maximizes l(θ) among the values at which we evaluate l in steps 1 and 2.

See [7] for a detailed description of an algorithm for computing the MLE in the logistic joinpoint regression model with multiple joinpoints.

3 Asymptotic properties

In this section, the consistency and the asymptotic distribution of the maximum likelihood estimator are established. Consider the function F^(j) : ℝ^N × ℝ^4+q → ℝ^4+q such that

$${\mathit{F}}^{(j)}(\mathit{p},\mathit{\theta })={\displaystyle \sum _{i=1}^N{u}_i{\mathit{z}}_i^{(j)}}\left(p_i-{\rho }_i^{(j)}(\mathit{\theta })\right),j=1,\dots ,N-1$$

where p = [p1,…, p_N]^Τ and p_i ∈ (0, 1) for i = 1,…,N. In particular, we will be interested in values of k such that

$${\tau }_0\in \left[t_k,t_{k+1}\right].$$ (8)

Throughout this paper, k shall be reserved for values such that (8) holds. If τ₀ ∈ (t_k, t_k+1), then k is unique. If τ₀ = t_ℓ for some ℓ, then (8) holds for both k = ℓ − 1 and k = ℓ.

Letting p₀ = [p₀₁,…, p_0N]^Τ, the following lemma uses the Implicit Function Theorem (see, for example, [35]) to express ϕ(θ) as a function of p. Proofs of lemmas and theorems are deferred to Appendix A.

Lemma 3.1

Suppose that F^(k)(p, θ) = 0 and (8) holds. If Z^(k) is full rank, then in an open neighborhood of (p₀, θ₀), say B_p0, there exists a function g^(k) such that g^(k)(p) = ϕ(θ) for (p, θ) ∈ B_p0 and the second partial derivatives of g^(k) exist and are continuous.

Implicit differentiation can be used to obtain the explicit form for the partial derivatives of g^(k). Differentiating both sides of F^(k)(p, θ) = 0 with respect to p^Τ, we obtain

$${({\mathit{Z}}^{(k)})}^{\mathrm{{\rm T}}}\mathit{U}={({\mathit{Z}}^{(k)})}^{\mathrm{{\rm T}}}\mathit{U}{\mathit{W}}^{(k)}(\mathit{\theta }){\mathit{Z}}^{(k)}{\mathit{G}}^{(k)}(\mathit{p})$$

Where${\mathit{G}}^{(k)}(\mathit{p})=\frac{\partial {\mathit{g}}^{(k)}(\mathit{p})}{\partial {\mathit{p}}^{\mathrm{{\rm T}}}}$is the matrix of partial derivatives of each component of g with respect to p^Τ. If Z^(k) is full rank, then we have

$${\mathit{G}}^{(k)}(\mathit{p})=({{({\mathit{Z}}^{(k)})}^{\mathrm{{\rm T}}}\mathit{U}{\mathit{W}}^{(k)}(\mathit{\theta }){\mathit{Z}}^{(k)})}^{-1}{({\mathit{Z}}^{(k)})}^{\mathrm{{\rm T}}}\mathit{U}.$$

Let p̂_n = [y₁/m₁,…, y_N/m_N]^Τ. Lemma 3.1 can be used to show that the maximizer of l_k is a strongly consistent estimator of θ₀ for any k such that the model is correctly specified. The following lemma states this result for the case when each of the m_i’s increases linearly, although the linearity can be relaxed to deal with differing rates of divergence. Let ${\widehat{\mathit{\theta }}}_n^{(k)}$be as defined by (7).

Lemma 3.2

For sufficiently large n₀, suppose there exist constants 0 < c₁ < c₂ such that nc₁ ≤ m_i ≤ nc₂ for i = 1,…,N when n ≥ n₀. If Z^(k) is full rank and (8) holds, then${\widehat{\mathit{\theta }}}_n^{(k)}\to {\mathit{\theta }}_{0}a.s.\mathit{\text{as}}n\to \mathrm{\infty }$.

In this lemma and the following theorems, N is taken to be fixed. This setting is reasonable for analyzing data retrospectively when there is a large amount of data at each observation time or in each time-specific cluster of observations (see, for example, [7]). Since N is fixed, few assumptions are required to achieve consistent estimators. In practice, the assumption that Z^(k) is full rank for values of k such that (8) holds is needed so that the parameters are identifiable. In other settings in which N is allowed to increase to infinity, additional assumptions are required on the spacing of the covariates and/or the location of the change-point parameter to ensure that there is enough data in each part of the input space to estimate all of the parameters consistently. However, the specific assumptions required depends on the particular way that N increases. For discussion about typical assumptions for some other change-point problems, see [2] and [32].

Under the conditions of Lemma 3.2, it is seen that the estimator of θ₀ based on k such that the model is correctly specified is consistent. Next, it must be shown that, for each j such that τ₀ ∉ [t_j, t_j+1], the maximum value of l_j is less than the maximum value of l_k. To prove this, we introduce the saturated likelihood function s : ℝ^N → ℝ defined by

$$s(\mathit{p})={\displaystyle \sum _{i=1}^N\left\{\text{ln}\left(\frac{p_i}{1-p_i}\right)y_i+m_i\text{ln}(1-p_i)\right\}}$$ (9)

which provides a parameter for each distinct set of observed covariates. Using this concept, it can be shown that the maximum likelihood estimator (maximizer of l) is strongly consistent. As before, let θ̂_n denote the maximum likelihood estimator of θ₀.

Theorem 3.1

Under the conditions of Lemma 3.2 for each k such that (8) holds, it follows that θ̂_n → θ₀ a.s. as n→∞.

Next, we examine the asymptotic distribution of θ̂_n. Since consistency has been established, it suffices to consider the distribution(s) of ${\widehat{\mathit{\theta }}}_n^{(k)}$with k given by (8).

There are two cases which must be examined. First consider the more complicated one when τ₀ = t_ℓ for some ℓ. In this case, we must consider the joint behavior of ${\widehat{\mathit{\theta }}}_n^{(\ell -1)}\text{and} {\widehat{\mathit{\theta }}}_n^{(\ell )}$. Denote by $\mathbf{\Phi }(\omega )=\frac{\partial {\varphi }^{-1}(\omega )}{\partial {\omega }^{\mathrm{{\rm T}}}}$ the (q+4)×(q+4) matrix of partial derivatives of the components of ϕ⁻¹. Let 𝒜(0,S) denote the (multivariate) normal distribution with zero mean vector and covariance matrix S. Also, let ⇒ denote convergence in distribution. The following theorem proves the asymptotic normality of the joint distribution of these quantities. The proof is given in Appendix A.

Theorem 3.2

For sufficient large n, suppose there exist constants 0 < c₁ < c₂ such that nc₁ ≤ m_i ≤ nc2. If τ₀ = t_ℓ for some ℓ and Z^(k) is full rank for k = ℓ − 1 and k = ℓ, then

$$\sqrt{n}\left(\left[\begin{array}{c}{\widehat{\mathit{\theta }}}_n^{(\ell -1)}\\ {\widehat{\mathit{\theta }}}_n^{(\ell )}\end{array}\right]-\left[\begin{array}{c}{\mathit{\theta }}_0\\ {\mathit{\theta }}_0\end{array}\right]\right)\Rightarrow \mathcal{N}(\mathbf{0},\psi \mathbf{G}{\mathbf{U}}^{-1}{\mathbf{W}}^{(\ell )}{\mathbf{G}}^{\mathrm{{\rm T}}}{\psi }^{\mathrm{{\rm T}}})$$ (10)

as n→∞ where $\mathit{G}=\mathit{G}({\mathit{p}}_0)=\left[\begin{array}{c}{\mathit{G}}^{(\ell -1)}({\mathit{p}}_0)\\ {\mathit{G}}^{(\ell )}({\mathit{p}}_0)\end{array}\right],\psi =\left[\begin{array}{cc}{\mathbf{\Phi }}^{(\ell -1)}& \mathit{O}\\ \mathit{O}& {\mathbf{\Phi }}^{(\ell )}\end{array}\right],{\mathbf{\Phi }}^{(k)}=\mathbf{\Phi }({\mathit{g}}^{(k)}({\mathit{p}}_0))$and W^(k) = W^(k)(θ₀) for k = ℓ − 1 and k = ℓ, and U is defined by (6).

The result for the second case where τ₀ ∈ (t_k, t_k+1) for some k is given in Theorem 3.3. The proof is omitted since it can be proven in a manner similar to Theorem 3.2. Note that ${\widehat{\mathit{\theta }}}_n={\widehat{\mathit{\theta }}}_n^{(k)}a.s.$when n is sufficiently large, as shown in the proof of Theorem 3.1.

Theorem 3.3

For sufficient large n, suppose there exist constants 0 < c₁ < c₂ such that nc₁ ≤ m_i ≤ nc₂. If τ₀ ∈ (t_k, t_k+1) for some k and Z^(k) is full rank, then

$$\sqrt{n}({\widehat{\mathit{\theta }}}_n-{\mathit{\theta }}_0)\Rightarrow \mathcal{N}(\mathbf{0},{\mathbf{\Phi }}^{(k)}{\mathit{G}}^{(k)}{\mathit{U}}^{-1}{\mathit{W}}^{(k)}{({\mathit{G}}^{(k)})}^{\mathrm{{\rm T}}}{({\mathbf{\Phi }}^{(k)})}^{\mathrm{{\rm T}}})$$

as n → ∞ where ${\mathit{G}}^{(k)}={\mathit{G}}^{(k)}(\mathit{p}0),{\mathbf{\Phi }}^{(k)}=\mathbf{\Phi }({\mathit{g}}^{(k)}({\mathit{p}}_0)),{\mathit{W}}^{(k)}={\mathit{W}}^{(k)}({\mathit{\theta }}_0)$, and U is defined by (6).

4 Consistency of Bootstrap Confidence Bounds

Suppose we use the parametric bootstrap to generate Binomial random variables $Y_{\mathit{\text{ib}}}^{*}$with sizes m_i and probabilities of success p̂_0i for i = 1,…,N and b = 1,…, B where B is the number of bootstrap samples. Set ${\mathit{Y}}_b^{*}={[Y_{1b}^{*},\dots ,Y_{\mathit{\text{Nb}}}^{*}]}^{\mathrm{{\rm T}}}$and let ${\widehat{\mathit{\theta }}}_{\mathit{\text{nb}}}^{*}$ denote the bth bootstrap replication of θ̂_n, with P and P* being the probability measures under θ₀ and${\widehat{\mathit{\theta }}}_n^{*}$, respectively.

4.1 Consistency when τ₀ ≠ t_ℓ for any ℓ

We shall consider the consistency of the bootstrap percentile method. For simplicity, we describe the one-sided interval for a parameter ζ₀, but the results extend to two-sided intervals with proper modifications. Set$K_B(x)=P^{*}({\widehat{\mathrm{\zeta }}}_n^{*}\le x)$. Then the bootstrap estimator of the upper bound of the α-level one-sided percentile confidence interval for ζ₀ is ${\mathrm{\zeta }}_{\mathit{\text{BP}}}=K_B^{-1}(\alpha )$. The following lemma gives sufficient conditions for the consistency of bootstrap confidence intervals of this form. For a proof, see Theorem 7.9 of [39].

Lemma 4.1

Let $H_n(x)=P(\sqrt{n}({\widehat{\mathrm{\zeta }}}_n-{\mathrm{\zeta }}_0)\le x)$and${\widehat{H}}_B(x)=P^{*}(\sqrt{n}({\widehat{\mathrm{\zeta }}}_n^{*}-{\widehat{\mathrm{\zeta }}}_n)\le x)$. Suppose that

1. sup_x|H_n (x) − H^B(x)| = op(1)

2. sup_x|H_n(x) − Ψ(x)| = o(1) for some continuous, strictly increasing and symmetric about zero distribution Ψ(x)

Then P(ζ_BP ≤ ζ₀) → 1 − α as n → ∞.

Thus, in order to prove consistency of bootstrap confidence intervals for a^Τθ₀ where a is a fixed non-zero (q + 4)-dimensional vector, we need to check conditions (1) and (2). If τ₀ ∈ (t_k, t_k+1), Theorem 3.3 verifies condition (2) of Lemma 4.1. So, for the case when τ₀ ∈ (t_k, t_k+1), we next verify condition (1) in the following result.

Theorem 4.1

Under the conditions of Theorem 3.3, it follows that

$$\underset{x}{\text{sup}}\left|P(\sqrt{n}({\mathit{a}}^{\mathrm{{\rm T}}}{\hat{\mathit{\theta }}}_n-{\mathit{a}}^{\mathrm{{\rm T}}}{\mathit{\theta }}_0)\le x)-P^{*}(\sqrt{n}({\mathit{a}}^{\mathrm{{\rm T}}}{\hat{\mathit{\theta }}}_n^{*}-{\mathit{a}}^{\mathrm{{\rm T}}}{\hat{\mathit{\theta }}}_n)\le x)\right|\to 0a.s.$$ (11)

as n → ∞.

Hence, from the last theorem, we see that the conditions for bootstrap confidence interval consistency given in Lemma 4.1 hold when τ₀ ∈ (t_k, t_k+1) since (11) implies convergence in probability. Continuity of Ψ will not hold if τ₀ = t_ℓ for some ℓ as shown by Theorem 3.2.

4.2 Simulation when τ₀ = t_ℓ for some ℓ

To illustrate the behavior of the bootstrap estimates and confidence bounds when τ₀ = t_ℓ for some ℓ, we perform the following simulation study. Suppose that we have equally-spaced observation times t_i = i for i = 1,…,N = 7, no additional covariates (q = 0), true coefficient values α₀ = β₀ = 0 and δ₀ = 0.2, and a joinpoint at τ₀ = 4 for the model specified by (1) and (2). For various choices of m₁ =…= m₇, we simulate R = 1, 000, 000 data sets and compute the estimate of τ₀ and the bootstrap estimate of τ₀ for each data set.

One simple way to see that Theorem 4.1 does not hold for this case is to use our simulation to estimate the proportion of times that τ̂_n equals τ₀ = 4 and compare this with the proportion of times that the bootstrap estimate ${\widehat{\tau }}_n^{*}$equals τ₀. These quantities, denoted by P̂ (τ̂_n = 4) and ${\widehat{P}}^{*}({\widehat{\tau }}_n^{*}=4)$, as well as empirical estimates of the mean square error $\widehat{\mathit{\text{MSE}}}({\widehat{\tau }}_n)=E[{({\widehat{\tau }}_n-{\tau }_0)}^2]$and the bootstrap estimate${\widehat{\mathit{\text{MSE}}}}^{*}({\widehat{\tau }}_n^{*})=E^{*}[{({\widehat{\tau }}_n^{*}-{\widehat{\tau }}_n)}^2]$of this quantity are reported in Table 1 for m_i = 100, 10⁵, 10⁷, and 10⁹ using the contributed R package ljr [6]. Clearly, the bootstrap underestimates the true probability that τ̂_n = 4 as seen in columns 2 and 4 of Table 1 and overestimates the true MSE of τ̂_n as seen in columns 3 and 5.

Table 1.

Simulation results for the bootstrap method applied to the MLE.

mi, i = 1,…, 7	P^(τ^n = τ0)	$\widehat{\mathit{\text{MSE}}}({\widehat{\tau }}_n)$	$\widehat{P}*({\widehat{\tau }}_n^{*}={\tau }_0)$	${\widehat{\mathit{\text{MSE}}}}^{*}({\widehat{\tau }}_n^{*})$
103	.2007	3.967 × 10−1	.1097	4.779 × 10−1
105	.2023	2.792 × 10−3	.1157	3.545 × 10−3
107	.2020	2.899 × 10−5	.1155	3.698 × 10−5
109	.2020	3.122 × 10−7	.1160	3.972 × 10−7

The estimate P̂(τ̂_n = 4) = .2020 when m_i = 10⁹ agrees with the theoretical value suggested by Theorem 3.2. As n → ∞, note that

$$\sqrt{n}\left(\left[\begin{array}{l}{\widehat{\tau }}_n^{(3)}\hfill \\ {\widehat{\tau }}_n^{(4)}\hfill \end{array}\right]-\left[\begin{array}{l}4\hfill \\ 4\hfill \end{array}\right]\right)\Rightarrow \mathcal{N}(\mathbf{0},\mathit{S})$$

where

$$\mathit{A}=\left[\begin{array}{llllllll}0\hfill & 0\hfill & 1\hfill & 0\hfill & 0\hfill & 0\hfill & 0\hfill & 0\hfill \\ 0\hfill & 0\hfill & 0\hfill & 0\hfill & 0\hfill & 0\hfill & 1\hfill & 0\hfill \end{array}\right]$$

and

$$\mathit{S}=\mathit{A}\psi \mathit{G}{\mathit{U}}^{-1}{\mathit{W}}^{(4)}{\mathit{G}}^{\mathrm{{\rm T}}}{\psi }^{\mathrm{{\rm T}}}{\mathit{A}}^{\mathrm{{\rm T}}}=\left[\begin{array}{cc}\hfill 2127.2073\hfill & \hfill 638.1622\hfill \\ \hfill 638.1622\hfill & \hfill 2167.1859\hfill \end{array}\right].$$

Thus, for large n, we have

$$P({\widehat{\tau }}_n=4)=P({\widehat{\tau }}_n^{(3)}>4\text{and}{\widehat{\tau }}_n^{(4)}<4)\to .2019703;$$

this bivariate normal probability can be computed using the contributed R package mvtnorm [17].

4.3 Removal Algorithm

Herein we discuss a modified estimator of τ₀ for which bootstrap consistency holds as a remedy for the lack of consistency of the parametric bootstrap when τ₀ = t_i for some i. First, compute θ̂_n. Then remove the observation(s) at the observation time t_ℓ which is closest to τ̂_n and re-fit the MLE without the observation(s), denoting the result as

$${\widehat{\mathit{\theta }}}_n^{-}={[{\widehat{\alpha }}_n^{-},{\widehat{\beta }}_n^{-},{\widehat{\tau }}_n^{-},{\widehat{\delta }}_n^{-},{({\widehat{\gamma }}_n^{-})}^{\mathrm{{\rm T}}}]}^{\mathrm{{\rm T}}}.$$

If the matrix Z^(k), with k defined by (8), is still full rank without the observation(s) and m_i satisifies the condition in Lemma 3.2, then bootstrap consistency holds for this algorithm even if τ₀ = t_ℓ for some ℓ (since these observations will be removed with probability 1 as n → ∞).

As an illustration of the effect of using this algorithm, we use the same simulated data sets considered in Section 4.2 and compare the results for the bootstrap based on the method of maximum likelihood with the bootstrap based on the removal algorithm. Letting τ̂ (.95) and ${\widehat{\tau }}_{(.95)}^{-}$represent the 95th percentiles of the empirical distributions of τ̂_n and ${\widehat{\tau }}_n^{-}$, Table 2 computes the estimated tail probabilities ${\widehat{P}}^{*}({\widehat{\tau }}_n^{*}-{\widehat{\tau }}_n\ge {\widehat{\tau }}_{(.95)})$and${\widehat{P}}^{*}({\left({\widehat{\tau }}_n^{-}\right)}^{*}-{\widehat{\tau }}_n^{-}\ge {\widehat{\tau }}_{(.95)}^{-})$for the bootstrap method. Clearly, the bootstrap overestimates the 95th percentile of the distribution of τ̂_n − τ₀, but provides a good estimate of ${\widehat{\tau }}_n^{-}-{\tau }_0$even for relatively small sample sizes. However, the tradeoff for obtaining accurate confidence bounds is the loss of information caused by discarding part of the data. This also can be seen in Table 2 by observing that the estimates of the mean square errors for ${\widehat{\tau }}_n^{-}$ are higher than those for τ̂_n.

Table 2.

Comparison of results for the MLE and the estimates based on the removal algorithm.

mi, i = 1,…, 7	$\widehat{P}*({\widehat{\tau }}_n^{*}-{\widehat{\tau }}_n\ge {\widehat{\tau }}_{(.95)})$	$\widehat{\mathit{\text{MSE}}}({\widehat{\tau }}_n)$	$\widehat{P}*({\left({\widehat{\tau }}_n^{-}\right)}^{*}-{\widehat{\tau }}_n^{-}\ge {\widehat{\tau }}_{(.95)}^{-})$	${\widehat{\mathit{\text{MSE}}}}^{-}({\widehat{\tau }}_n^{-})$
103	.0625	3.967 × 10−1	.0496	7.910 × 10−1
105	.0670	2.792 × 10−3	.0500	4.738 × 10−3
107	.0676	2.899 × 10−5	.0499	4.730 × 10−5
109	.0676	3.122 × 10−7	.0499	5.061 × 10−7

5 Example

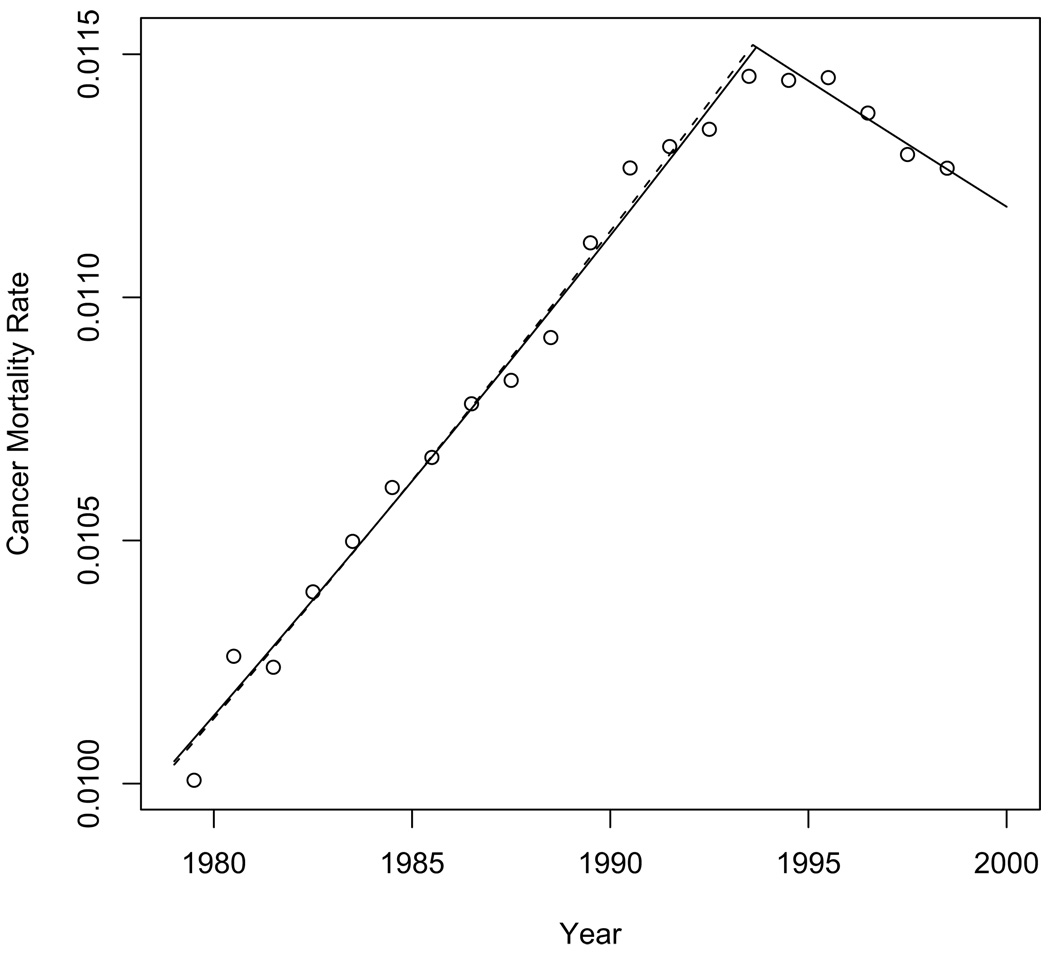
We now apply the method of clustered logistic joinpoint regression to model yearly cancer mortality in the United States for individuals age 65 and over during the period 1979–1998. The data set was obtained from the CDC wonder database [5], and it includes y_i – the number of deaths in the ith observed year due to neoplasms (ICD-9 codes 140–239), m_i –the population during the ith observed year, and t_i = 1978.5 + i – the midpoint of the ith observed year. So, we use the model given by (1) and (2) with q = 0. The observed cancer mortality rates y_i/m_i are plotted versus time in Figure 1.

Figure 1.

Observed US yearly cancer mortality rates for individuals age 65 and over. The solid line gives the fitted model based on all of the data. The dashed line gives the fitted model with the 15th observation (where t₁₅ = 1993.5) removed.

Table 3 gives the parameter estimates for each of the unknown parameters and the fitted probabilities based on maximum likelihood are illustrated by the solid curve in Figure 1. The estimated joinpoint τ̂_n = 1993.686 supports previous findings which attribute the decrease in cancer mortality to improvements in prevention, detection, and treatments [19].

Table 3.

Parameter estimates in the logistic joinpoint regression model for the US yearly 65+ cancer mortality data.

Parameter	Estimate	Value	Estimate	Value
α0	α^n	−23.17397	${\widehat{\alpha }}_n^{-}$	−23.44145
β0	β^n	.0093903	${\widehat{\beta }}_n^{-}$	.0095251
δ0	δ^n	−.0140205	${\widehat{\delta }}_n^{-}$	−.0141553
τ0	τ^n	1993.686	${\widehat{\tau }}_n^{-}$	1993.595

Next, we obtain estimated 95% confidence bounds for τ based on the parametric bootstrap. Using the estimates listed in Table 3 as our model parameters, we generate R = 100000 bootstrap samples and compute the estimate of τ for each sample. Then our estimated confidence bounds are the 2.5 and 97.5 percentiles of the bootstrap distribution of τ. In this manner, we obtain the confidence bounds (1993.371, 1993.930).

Note that the 15th observed year t₁₅ = 1993.5 falls within this interval. Thus, there might be a problem with consistency of the bootstrap as discussed in Section 4. We can attempt to remedy this possible bias by repeating our analysis with i = 15 removed from the data set. When the model is fit without the 15th observation, the estimate of the joinpoint changes slightly to ${\widehat{\tau }}_n^{-}=1993.595$. The estimated coefficients change very little (see Table 3) and the fitted probabilities based on the removal algorithm are illustrated by the dashed curve in Figure 1.

The 95% estimated confidence bounds with observation 15 omitted are (1993.318,1993.851). While it is true that the interval still contains 1993.5, this value is no longer in our data set since it has been removed, and it seems reasonable to claim that it is unlikely that we are dealing with a situation where τ₀ = t_ℓ for some ℓ and, thus, the consistency of the bootstrap confidence bounds is more plausible.

6 Summary and Conclusion

After presenting details necessary for the computation of the maximizer of the super log-likelihood functions and the MLE of the parameters in the clustered logistic joinpoint model, we considered the asymptotic properties of these estimators. Sufficient conditions for the consistency of the MLE were given. Asymptotic normality of the MLE was also shown under the same conditions as long as the true location of the joinpoint had not been at one of the observation times. Under this latter proviso we also showed the consistency of the bootstrap confidence bounds.

However, if the true location of the joinpoint was one of the observation times, then it was shown that the joint distribution of the maximizers of indices corresponding to the neighboring intervals was asymptotically normal. A simulation study was performed to illustrate the lack of consistency of the bootstrap method in generating confidence bounds in this case due to asymptotic bias. It was also shown that we could remove this bias and obtain consistent estimates via a removal algorithm at the cost of a higher MSE.

Finally, the model and the methods were used to analyze yearly cancer mortality in the United States for individuals age 65 and over. The bootstrap confidence interval included one observation time, so the model was refit without that observation. There is only a slight change in the resulting fitted model, but the consistency of the bootstrap is more plausible with the second fit. An R package ljr [6] capable of fitting these models is available in the contributed packages at http://www.R-project.org [34].

A Proofs

Proof of Lemma 3.1

Since F^(k) is infinitely differentiable and F^(k)(p₀, θ₀) = 0, it remains to verify that the determinant of${\frac{\partial {\mathit{F}}^{(k)}}{\partial {\varphi }^{\mathrm{{\rm T}}}}|}_{(\mathit{p}0,{\mathit{\theta }}_0)}=-{({\mathit{Z}}^{(k)})}^{\mathrm{{\rm T}}}{\mathit{\text{DZ}}}^{(k)}$is not zero in order to apply the Implicit Function Theorem. Here D = UW^(k)(θ₀) is a N × N diagonal matrix with diagonal elements d_i = m_ip_0i(1 − p_0i)/n for i = 1,…,N. Since d_i ∈ (0, 1),${\frac{\partial {\mathit{F}}^{(k)}}{\partial {\varphi }^{\mathrm{{\rm T}}}}|}_{(\mathit{p}0,{\mathit{\theta }}_0)}$has a nonzero determinant if and only if Z^(k) is full rank.

Proof of Lemma 3.2

The strong law of large numbers implies that p̂_n → p₀ a.s. as n → ∞. For all θ, the left side of (5) converges to F^(k)(p₀, θ) a.s. The continuity of F^(k) implies that.

$$\mathbf{0}=\underset{n\to \infty }{\text{lim}}{\mathit{F}}^{(k)}({\widehat{\mathit{p}}}_0,{\widehat{\mathit{\theta }}}_n^{(k)})={\mathit{F}}^{(k)}({\widehat{\mathit{p}}}_0,\underset{n\to \infty }{\text{lim}}{\widehat{\mathit{\theta }}}_n^{(k)}).$$

It is clear that θ₀ is the unique value of θ such that F^(k)(p₀, θ) = 0 by the same argument as the one used to show that the solution to (5) is a unique maximizer of l_j when y_i/n_i is replaced by p_i. Thus, it follows that ${\widehat{\mathit{\theta }}}_n^{(k)}\to {\mathit{\theta }}_{0}a.s.$as n→∞.

Proof of Theorem 3.1

In view of Lemma 3.2, it suffices to show that, with probability 1,$l({\widehat{\mathit{\theta }}}_n^{(k)})>l({\widehat{\mathit{\theta }}}_n^{(j)})$if τ₀ ∈ [t_k, t_k+1] but τ₀ ∉ [t_j, t_j+1] From Lemma 3.2, we have.${\widehat{\mathit{\theta }}}_n^{(k)}\to {\mathit{\theta }}_{0}a.s.$ Using the continuity of ${\rho }_i^{(k)}$, it follows that $p_i^{(k)}({\widehat{\mathit{\theta }}}_n^{(k)})\to p_i^{(k)}({\mathit{\theta }}_0)=p{0}_{i}a.s.$. for i = 1,…,N. Hence, we have $l({\widehat{\mathit{\theta }}}_n^{(k)})\to s({\mathit{p}}_0)a.s.$as n→∞.

Let $\mathcal{S}=\{(p_1,\dots ,p_N)|p_i\in [0,1],i=1,\dots ,N\}$be the set of points considered by the saturated model and let

$${\mathcal{A}}_{\ell }=\left\{(p_1,\dots ,p_N)\in \mathcal{S}|\tau \in [t_{\ell },t_{\ell +1}],p_i=p_i^{(\ell )}(\mathit{\theta }),i=1,\dots ,N\right\}$$

be the set of fitted probabilities corresponding to restricting τ ∈ [t_k, tk+1]. Clearly 𝒜_k ⊂ 𝒮 for all k. Furthermore, p₀ ∈ 𝒜_k if τ₀ ∈ [t_k, t_k+1] and p₀ ∉ 𝒜_j if τ₀ ∉ [t_j, t_j+1]. Thus, max_θ∈𝒜j l(θ) < s(p₀) and $l({\widehat{\mathit{\theta }}}_n^{(k)})\to s({\mathit{p}}_0)a.s.$ so that max_θ∈𝒜j l(θ) < maxθ∈𝒜_k l(θ) with probability 1.

Consequently, if k is unique, then τ̂_n ∈ (t_k, t_k+1) a.s. as n → ∞. If k is not unique, then τ̂_n ∈ (t_ℓ−1, t_ℓ+1) a.s. as n →∞, and we have ${\widehat{\mathit{\theta }}}_n^{(\ell -1)}\to {\mathit{\theta }}_0\text{and}{\widehat{\mathit{\theta }}}_n^{\ell }\to {\mathit{\theta }}_{0}a.s.$as n → ∞ by Lemma 3.2. In either case, it follows that θ̂_n → θ₀ a.s. as n → ∞.

Proof of Theorem 3.2

Take any a ∈ ℝ^2(q+4) and let$\mathit{g}(\mathit{p})=\left[\begin{array}{c}{\mathit{g}}^{(\ell -1)}(\mathit{p})\\ {\mathit{g}}^{(\ell )}(\mathit{p})\end{array}\right]$. Using a multivariate Taylor series expansion, we obtain

$$\begin{array}{l}{\mathit{a}}^{\mathrm{{\rm T}}}\left(\left[\begin{array}{c}\varphi ({\widehat{\mathit{\theta }}}_n^{(\ell -1)})\\ \varphi ({\widehat{\mathit{\theta }}}_n^{(\ell )})\end{array}\right]-\left[\begin{array}{c}\varphi ({\mathit{\theta }}_0)\\ \varphi ({\mathit{\theta }}_0)\end{array}\right]\right)={\mathbf{a}}^{\mathrm{{\rm T}}}(\mathit{g}({\widehat{\mathit{p}}}_n)-\mathit{g}({\mathit{p}}_0))\hfill \\ ={\mathit{a}}^{\mathrm{{\rm T}}}\mathit{G}({\mathit{p}}_0)({\widehat{\mathit{p}}}_n-{\mathit{p}}_0)+\frac{1}{2}{({\widehat{\mathit{p}}}_n-{\mathit{p}}_0)}^{\mathrm{{\rm T}}}\mathit{H}({\tilde{\mathit{p}}}_n)({\widehat{\mathit{p}}}_n-{\mathit{p}}_0)\hfill \end{array}$$ (12)

where $\mathit{H}({\tilde{\mathit{p}}}_n)=\frac{\partial {\mathit{a}}^{\mathrm{{\rm T}}}\mathit{G}({\tilde{\mathit{p}}}_n)}{\partial \mathit{p}}$is the Hessian matrix of a^Τg evaluated at a point p̂_n on the segment connecting p̂_n and p₀. Note that

$$\sqrt{n}({\widehat{\mathit{p}}}_n-{\mathit{p}}_0)\Rightarrow \mathcal{N}(\mathbf{0},{\mathit{U}}^{-1}{\mathit{W}}^{(\ell )}({\mathit{p}}_0))$$ (13)

as n → ∞. Since H(p̂_n) is symmetric, we can apply the singular value decomposition to obtain H(p̂_n) = C(p̂_n)Λ(p̂_n)C(p̂_n)^Τ where C(·) is orthogonal and Λ(·) is diagonal with entries λ₁ ≥ … ≥ λ_2(q+4). Note that λ₁ is bounded as n → ∞. Thus, (13) implies that

$$\frac{\sqrt{n}}{2}{({\widehat{\mathit{p}}}_n-{\mathit{p}}_0)}^{\mathrm{{\rm T}}}\mathit{H}({\tilde{\mathit{p}}}_n)({\widehat{\mathit{p}}}_n-{\mathit{p}}_0)\le \frac{{\lambda }_1}{\sqrt{n}}{\Vert \sqrt{n}({\widehat{\mathit{p}}}_n-{\mathit{p}}_0)\Vert }^2=o_P(1).$$ (14)

Hence, (12), (14), and Slutsky’s Theorem (see [3]) imply that

$$\sqrt{n}{\mathit{a}}^{\mathrm{{\rm T}}}\left(\left[\begin{array}{c}\varphi ({\widehat{\mathit{\theta }}}_n^{(\ell -1)})\\ \varphi ({\widehat{\mathit{\theta }}}_n^{(\ell )})\end{array}\right]-\left[\begin{array}{c}\varphi ({\mathit{\theta }}_0)\\ \varphi ({\mathit{\theta }}_0)\end{array}\right]\right)\Rightarrow \mathcal{N}(\mathbf{0},{\mathit{a}}^{\mathrm{{\rm T}}}\mathit{G}{\mathit{U}}^{-1}{\mathit{W}}^{(\ell )}{\mathit{G}}^{\mathrm{{\rm T}}}\mathit{a})$$

as n → ∞. So, the Cramér-Wold Criterion (see, for example, [38]) implies that

$$\sqrt{n}\left(\left[\begin{array}{c}\varphi ({\widehat{\mathit{\theta }}}_n^{(\ell -1)})\\ \varphi ({\widehat{\mathit{\theta }}}_n^{(\ell )})\end{array}\right]-\left[\begin{array}{c}\varphi ({\mathit{\theta }}_0)\\ \varphi ({\mathit{\theta }}_0)\end{array}\right]\right)\Rightarrow \mathcal{N}(0,{\mathit{\text{GU}}}^{-1}{\mathit{W}}^{(\ell )}{\mathit{G}}^{\mathrm{{\rm T}}})$$ (15)

as n → ∞. Since${\widehat{\mathit{\theta }}}_n^{(k)}={\varphi }^{-1}(\varphi ({\widehat{\mathit{\theta }}}_n^{(k)}))$for k =ℓ−1, ℓ and$\mathbf{\Phi }(\omega )=\frac{\partial {\varphi }^{-1}(\omega )}{\partial {\omega }^{\mathrm{{\rm T}}}},$, a similar argument can be used to show that (15) implies (10).

Proof of Theorem 4.1

Simple modifications can be made to the arguments given in Theorem 3.2 to show that

$$\sqrt{n}{\mathit{S}}_n^{-1/2}({\widehat{\mathit{\theta }}}_n^{*}-{\widehat{\mathit{\theta }}}_n)\Rightarrow \mathcal{N}(\mathbf{0},\mathit{I})a.s.$$

as n → ∞, where

$${\mathit{S}}_n={\mathbf{\Phi }}^{(k)}({\mathit{g}}^{(k)}({\widehat{p}}_n)){\mathit{G}}^{(k)}({\widehat{\mathit{p}}}_n){\mathit{U}}^{-1}{\mathit{W}}^{(k)}({\widehat{\mathit{\theta }}}_n){({\mathit{G}}^{(k)}({\widehat{\mathit{p}}}_n))}^{\mathrm{{\rm T}}}{({\mathbf{\Phi }}^{(k)}({\mathit{g}}^{(k)}({\widehat{\mathit{p}}}_n)))}^{\mathrm{{\rm T}}}.$$

As n → ∞, we have p̂_n → p₀ a.s. and θ̂_n → θ₀ a.s. so that S_n → S₀ a.s. where

$${\mathit{S}}_0={\mathbf{\Phi }}^{(k)}{\mathit{G}}^{(k)}{\mathit{U}}^{-1}{\mathit{W}}^{(k)}{({\mathit{G}}^{(k)})}^{\mathrm{{\rm T}}}{({\mathbf{\Phi }}^{(k)})}^{\mathrm{{\rm T}}}.$$

Thus, by Slutsky’s Theorem, we have

$$\sqrt{n}({\widehat{\mathit{\theta }}}_n^{*}-{\widehat{\mathit{\theta }}}_n)={\mathit{S}}_n^{1/2}\left(\sqrt{n}{\mathit{S}}_n^{-1/2}({\widehat{\mathit{\theta }}}_n^{*}-{\widehat{\mathit{\theta }}}_n)\right)\Rightarrow {\mathit{S}}_n^{1/2}\mathcal{N}(\mathbf{0},\mathit{I}) a.s.$$

as n → ∞. Thus for any non zero vector a ∈ R^q+4 with probability one ${\sqrt{\mathit{\text{na}}}}^{\mathrm{{\rm T}}}({\widehat{\mathit{\theta }}}_n-{\mathit{\theta }}_0)$and${\sqrt{\mathit{\text{na}}}}^{\mathrm{{\rm T}}}({\widehat{\mathit{\theta }}}_n^{*}-{\widehat{\mathit{\theta }}}_n)$have the same weak limit. The triangle inequality and the fact that in this case the weak convergence is uniform, yield (11).