Estimation of ROC curves based on stably distributed biomarkers subject to measurement error and pooling mixtures

SUMMARY

Additive measurement errors and pooling design are objectively two different issues, which have been separately and extensively dealt with in the biostatistics literature. However, these topics usually correspond to problems of reconstructing a summand’s distribution of the biomarker by the distribution of the convoluted observations. Thus, we associate the two issues into one stated problem. The integrated approach creates an opportunity to investigate new fields, e.g. a subject of pooling errors, issues regarding pooled data affected by measurement errors. To be specific, we consider the stated problem in the context of the receiver operating characteristic (ROC) curves analysis, which is the well-accepted tool for evaluating the ability of a biomarker to discriminate between two populations. The present paper considers a wide family of biospecimen distributions. In addition, applied assumptions, which are related to distribution functions of biomarkers, are mainly conditioned by the reconstructing problem. We propose and examine maximum likelihood techniques based on the following data: a biomarker with measurement error; pooled samples; and pooled samples with measurement error. The obtained methods are illustrated by applications to real data studies.

1. INTRODUCTION

One of the main issues of epidemiological research for the past several decades has been the relationship between biological markers (biomarkers) and disease risk. Commonly, a measurement process yields the operating characteristics of biomarkers. However, the high cost associated with evaluating these biomarkers as well as measurement errors corresponding to a measurement process can prohibit further epidemiological applications. When, for example, analysis is restricted by the high cost of assays, following Faraggi et al. [1], we suggest applying an efficient pooling design for collection of data. In order to allow for the instrument sensitivity problem corresponding to measurement errors, we formulate models with additive measurement errors. Obviously, these issues request assumptions on a biomarker distribution, under which operating characteristics of a biomarker can be evaluated. In this paper, we show that the distribution assumptions are related to reconstructing problems and can be formulated in terms of characteristic functions. To this end, we assume a wide family of biospecimen distributions. The considered cases associate the measurement errors issue and evaluation based on pooled data into one stated problem.

The existence of measurement error in exposure data potentially affects any inferences regarding variability and uncertainty because the distribution representing the observed data set deviates from the distribution that represents an error-free data set. Methodologies for improving the characterization of variability and uncertainty with measurement errors in data are proposed by many biostatistical manuscripts. Thus, the model, which corresponds to observing a biomarker of interest plus a measurement error, is not in need of extensive description. However, note that, since values of a biomarker are functionally convolute with noisy measurement errors, usually distribution functions of measurement errors are assumed to be known. Moreover, on account of the complexity of extracting biomarker distribution from observed convoluted data (say deconvolution), practically, normality assumptions related to biomarker distribution are assumed. Besides, parameters of an error distribution can be evaluated by applying an auxiliary reliability study of biospecimens (e.g. a cycle of remeasuring of biospecimens: Schisterman et al. [2]).

Another stated problem dealing with the deconvolution is the exploration based on pooled data. Without focusing on situations where pooled data is an organic output of a study, we touch on pooling in the context of the design issue. The concept of pooling design is extensively dealt with in the statistical literature starting with publications related to cost-efficient testing of World War II recruits for syphilis. In order to reduce the cost or labor intensiveness of a study, a pooling strategy may be employed whereby 2 or more (say p) individual specimens are physically combined into a single ‘pooled’ unit for analysis. Thus, applying pooling design provides a p-fold decrease in the number of measured assays. Each pooled sample test result is assumed to be the average of the individual unpooled samples; this is most often the case because many tests are expressed per unit of volume (e.g. [1, 3, 4]). Weinberg and Umbach [5] introduced pooling as a means to estimate odds ratios for case-control studies. Although pooling design has been widely used in biological and other practice, methods for analysis of pooled data from such experiments have not been fully and well developed in the literature, except for certain special cases (e.g. Faraggi et al. [1] considered normal and gamma cases). This is, perhaps, partly because, for a general distribution of a biomarker, the likelihood methods based on pooled data may not be feasible since the distribution of the averages involves convolution of p random variables of a biomarker distribution.

The purpose of the present paper is to develop a general methodology for reasonably efficient estimation of a biomarker distribution based on data with measurement errors and/or pooled biospecimens. By utilizing the maximum likelihood technique, which is founded on characteristic functions, we consider an approach that associates the measurement error and the pooled data issues into one stated deconvolution problem. Thus, the proposed approach provides possibilities to investigate new fields related to biospecimen evaluations (e.g. a methodology for analysis of pooled data with measurement errors). For example, by applying real data, we can address issues such as whether pooling increases measurement errors, whether a physical executing of pooled data leads to errors, etc.

We believe that the demonstrated focusing on estimation of the receiver operating characteristic (ROC) curves will assist in practical applications of the methods developed in the present paper. An important step in a biomarker’s development is the evaluation of its discriminating ability. The ROC curves are commonly estimated for this purpose (e.g. [6-10]). The most commonly used global index of diagnostic accuracy is the area under the ROC curve (e.g. [11]). Values of the area under the ROC curve close to 1 indicate that the marker has high diagnostic accuracy, while a value of 0.5 indicates a noninformative marker that does no better than a random (fair) coin toss. In the case of normal-distributed data, Schisterman et al. [2] proposed a method to obtain the adjusted area under the ROC curve with correction for measurement error. Several authors have proposed pooling as a way to cut costs in the evaluation of biomarkers and have evaluated ROC curve analysis when dealing with such data (e.g. [1, 3, 4]). In the context of estimation of ROC based on data with measurement error and pooling mixtures, we analyze biomarkers from a distribution family (which includes normal distributions) that satisfy conditions related to the ability of deconvoluting (reconstructing) the target distribution.

The paper is organized as follows. Section 2 details the formal statement of the problem and a general methodology of estimation of a biomarker distribution based on convoluted data. We consider the area under the ROC curve in Section 3. To display several special aspects of the considered issue (e.g. robustness of the proposed method), Section 4 presents the results of Monte Carlo simulations. By applying the proposed technique to real pooled data, Section 5 illustrates, ROC curve evaluations. The issue of the measurement error in an actual epidemiological study is deliberated in Section 6. We exemplify the combined case regarding real pooled data with measurement errors in Section 7. Section 8 concludes the paper with several remarks.

2. FORMALIZATION AND METHOD

Let X and Y be measurements of a biomarker of interest, where X and Y are independent random samples of the disease and healthy populations, respectively. In accordance with the presented issue, practical constraints force us to weigh up the case with the observed samples in the form of (Z ^X, Z^Y):

$$Z_j^X=\frac{1}{p}\sum _{i=p(j-1)+1}^{jp}{X}_i+J_{{\epsilon }_{Xj}},Z_k^Y=\frac{1}{q}\sum _{i=q(k-1)+1}^{kq}{Y}_i+J_{{\epsilon }_{Yk}}$$ (1)

j = 1,..., n, k = 1,..., m, where X_i are independent identically distributed (i.i.d.) random variables with density function f_X, Y_i are i.i.d. random variables with density function f_Y, p and q are the pool sizes in cases and controls, respectively, ε_Xj, ε_Yk are measurement errors (i.i.d. random variables, which have density functions f_εX and f_εY, respectively), and J = 0, 1 is a known indicator function that corresponds to the presence or absence of measurement error in the model. Mode (1) represents the mixture of notations related to the pooling design and the effect of measuring sensitivity (e.g. [2-4]). Thus, for example, the situations with {p = 1, q = 1, J = 1}, {p>1, q>1, J = 0}, and {p>1, q>1, J = 1} coincide with the classical additive measurement error-stated problem, the pooling model definition, and the combination of pooling and additive measurement error statements, respectively (the case of { p>1, q>1, J = 1} can also be interpreted in terms of the presence of pooling errors). And therefore, model (1) generalizes different sample situations of biomarkers, where data can be collected in pooled sets, which are subject to additive measurement error.

The discriminating ability of biomarkers is commonly evaluated using the ROC curve, which is usually obtained by

$$\mathrm{ROC}\left(t\right)=1-F_X\left(F_Y^{-1}\left(t\right)\right),t\in (0,1)$$ (2)

where F_X and F_Y are the distribution functions of X₁ and Y₁, and F^-1 is the inverse function of F (e.g. [9]). To this end, estimation of the distribution functions of X and Y is necessary. However, estimation based on the sample (Z^X, Z^Y) instead of (X, Y) leads to the problem of reconstructing a summand’s distribution by the distribution of their sums plus the measurement error. Formally, the main focus is then to estimate f_X and f_Y based on estimators of density functions f_Z^X and f_Z^Y of random variables $Z_1^X$ and $Z_1^Y$, where f_Z^X and f_Z^Y are the p+J- and q+J-folded distributions, respectively, i.e.

$$\begin{array}{c}{f}_{Z^X}\left(u\right)=\int \cdots \int f_X(pu-t_1-\cdots -t_{p-1}-p{t}_p)f_X\left(t_1\right)\dots f_X\left(t_{p-1}\right)f_{\epsilon X}{\left(t_p\right)}^J\mathrm{d}{t}_1\dots \mathrm{d}{t}_p\hfill \\ f_{Z^Y}\left(u\right)=\int \cdots \int f_Y(pu-t_1-\cdots -t_{p-1}-p{t}_p)f_Y\left(t_1\right)\dots f_Y\left(t_{p-1}\right)f_{\epsilon Y}{\left(t_p\right)}^J\mathrm{d}{t}_1\dots \mathrm{d}{t}_p\hfill \end{array}$$ (3)

This estimation problem is known as a deconvolution problem (e.g. van Es et al. [12]). Note that not all distribution functions can be reconstructed.

By centering in the analysis of characteristic function and deconvolution theory, Prokhorov and Ushakov [13] proposed necessary and sufficient conditions in the probability context on the distributions of X and Y such that their original distribution function can be reconstructed. Note that, even if density functions f_X and f_Y can be theoretically reconstructed, the problem of estimation of f_X and f_Y based on (Z ^X, Z^Y) is very complicated. For example, if we define estimators of f_X and f_Y based on the empirical characteristic functions, then a complex definition of a p-root should be introduced.

A general class of the suitable distribution functions is a set of infinitely divisible distribution functions. At this rate, characteristic functions of biomarkers X and Y are uniquely determined by the characteristic functions of Z^X, Z^Y (e.g. Lukacs [14]). The infinitely divisible distributions encompass many commonly used distributions such as Normal, Cauchy, Exponential, Gamma, etc. (e.g. [14]). In the context of the parametric statement of the considered problem, given the infinitely divisible assumption, characteristic functions can be represented in the Lévy-Khinchine canonical form as

$$\varphi \left(t\right)=\exp \left(\mathrm{i}t\mu +{\int }_{-\infty }^{\infty }\left({\mathrm{e}}^{\mathrm{i}tu}-1-\frac{\mathrm{i}tu}{1+u^2}\right)\frac{1+u^2}{u^2}\mathrm{d}K\left(u\right)\right),\mathrm{i}={(-1)}^{1∕2}$$

where μ is a real unknown constant, while K (u) is a nondecreasing, bounded and known (up to an unknown vector of parameters) function such that at the argument u = -∞ this function is equal to zero and the integrand in ϕ(t) is defined for u = 0 by continuity to be equal to -t²/2. Therefore, without loss of generality and for the sake of clarity of exposition, we assume that random variables X and Y have stable distributions with characteristic functions

$$\begin{array}{cc}\hfill {\varphi }_X\left(t\right)=& \varphi (t;{\alpha }_X,{\beta }_X,{\gamma }_X,a_X),{\varphi }_Y\left(t\right)=\varphi (t;{\alpha }_Y,{\beta }_Y,{\gamma }_Y,a_Y)\hfill \\ \hfill \varphi (t;\alpha ,\beta ,\gamma ,a)=& {\mathrm{e}}^{\mathrm{i}at-\gamma {\mid t\mid }^{\alpha }(1+\mathrm{i}\beta t\omega (t,\alpha )∕\mid t\mid )},t\in (-\infty ,\infty )\hfill \\ \hfill \omega (t,\alpha )=& \{\begin{array}{cc}\tan (\pi \alpha ∕2),\hfill & \alpha \ne 1\hfill \\ 2\ln \mid t\mid ∕\pi \hfill & \alpha =1\hfill \end{array}\phantom{\}}\hfill \\ \hfill \alpha \in & (0,2],\mid \beta \mid \le 1,\gamma \ge 0,a\in (-\infty ,\infty )\hfill \end{array}$$ (4)

where the unknown parameters α, β, γ, and a are the characteristic exponent, a measure of skewness, the scale parameter, and the location parameter, respectively.

Definition (4) is quite general and covers many practical distributions (e.g. [15-17]), for example, the normal, α = 2; the Cauchy, α = 1, and the stable law of characteristic exponent, $\alpha =\frac{1}{2}$ (i.e. changing of values of the parameters can provide a modification of the classical type of a density function corresponding to (4)). Although we consider the parametric approach to describe the characteristic functions, estimation of the unknown parameters by using directly density functions corresponding to the characteristic functions (4) is difficult; it is complicated by the fact that their densities are not generally available in closed forms (e.g. [14, p. 106]), making it difficult to apply conventional estimation methods (e.g. [17, p. 188]). Moreover, the stated issue leads to the necessity of finding the estimators based on the pooled data, and therefore, under the deconvolution problem, applying classical parametric methods is a strongly complex problem.

Since the Fourier inverse approach is a widely accepted method for the analysis of convolution and deconvolution of probability functions (e.g. [18-23]), we utilize the following well-known proposition (e.g. [17]).

Proposition 2.1

Let ϕ_ζ(t) = E exp(itζ) be the characteristic function of a random variable ζ, absolutely integrable. Then the corresponding distribution function F_ζ is absolutely continuous, its density function f_ζ is bounded and continuous, and

$$f_{\zeta }\left(u\right)=\frac{1}{2\pi }{\int }_{-\infty }^{\infty }{\mathrm{e}}^{-\mathrm{i}tu}{\varphi }_{\zeta }\left(t\right)\mathrm{d}t$$

And hence by applying Proposition 2.1, we have the log-likelihood function based on the observed data

$$L_Z(\alpha ,\beta ,\gamma ,a)=\sum _{j=1}^{n_Z}\ln \left(\frac{1}{2\pi }{\int }_{-\infty }^{\infty }\exp \left(\mathrm{i}t(a-Z_j)-{\left(s_Z\right)}^{1-\alpha }\gamma {\mid t\mid }^{\alpha }\left(1+\mathrm{i}\beta t\omega \left(\frac{t}{s_Z},\alpha \right)∕\mid t\mid \right)\right){\varphi }_{{\epsilon }_Z}{\left(t\right)}^J\mathrm{d}t\right)$$ (5)

where Z = Z^X, Z^Y; n_Z^X = n, n_Z^Y = m; s_Z^X = p, s_Z^Y = q; and ϕ_εZ^X = ϕ_εX, ϕ_εZ^Y = ϕ_εZ^Y are the characteristic functions of ε_X, ε_Y , respectively. Assuming that the distributions of ε_X, ε_Y are known (perhaps, estimated by applying additional samples [2]), the maximum likelihood estimators are

$$\begin{array}{c}\{{\widehat{\alpha }}_X,{\widehat{\beta }}_X,{\widehat{\gamma }}_X,{\widehat{a}}_X\}=\arg \underset{\{{\alpha }_X>\epsilon ,{\beta }_X,{\gamma }_X,a_X\}}{\sup }{L}_{Z^X}({\alpha }_X,{\beta }_X,{\gamma }_X,a_X)\hfill \\ \{{\widehat{\alpha }}_Y,{\widehat{\beta }}_Y,{\widehat{\gamma }}_Y,{\widehat{a}}_Y\}=\arg \underset{\{{\alpha }_Y>\epsilon ,{\beta }_Y,{\gamma }_Y,a_Y\}}{\sup }{L}_{Z^Y}({\alpha }_Y,{\beta }_Y,{\gamma }_Y,a_Y)\hfill \end{array}$$ (6)

where ε is arbitrary small and positive. Then, as is usual for maximum likelihood estimators (e.g. [24]), estimators (6) are consistent and asymptotically normal as n → ∞ and m → ∞ (see for details, DuMouchel [15, p. 952]). The asymptotic variances of {α̂, β̂, γ̂, â}, which are the inverses of the Fisher information matrices, are presented in the next section.

By applying (6) to Proposition 2.1, we obtain the estimators of the density functions of the biomarkers in the form

$$\begin{array}{c}\hfill {\widehat{f}}_X\left(r\right)=\frac{1}{2\pi }{\int }_{-\infty }^{\infty }{\mathrm{e}}^{\mathrm{i}t({\widehat{a}}_X-r)-{\widehat{\gamma }}_X{\mid t\mid }^{{\widehat{\alpha }}_X}(1+\mathrm{i}{\widehat{\beta }}_{X}t\omega (t,{\widehat{\alpha }}_X)∕\mid t\mid )}\mathrm{d}t\hfill \\ \hfill {\widehat{f}}_Y\left(r\right)=\frac{1}{2\pi }{\int }_{-\infty }^{\infty }{\mathrm{e}}^{\mathrm{i}t({\widehat{a}}_Y-r)-{\widehat{\gamma }}_Y{\mid t\mid }^{{\widehat{\alpha }}_Y}(1+\mathrm{i}{\widehat{\beta }}_{Y}t\omega (t,{\widehat{\alpha }}_Y)∕\mid t\mid )}\mathrm{d}t\hfill \end{array}$$ (7)

Moreover, if additional conditions E ln(1+|X₁|)<∞, E ln(1+|Y₁|)<∞ hold, via Theorem 1.2.4 of Ushakov [17, p. 5], we have the estimated distribution functions

$$\begin{array}{c}\hfill {\widehat{F}}_X\left(u\right)=\frac{1}{2}-\frac{1}{\pi }{\int }_{-\infty }^{\infty }\frac{\mathrm{Im}\left({\mathrm{e}}^{-\mathrm{i}tu}\varphi (t;{\widehat{\alpha }}_X,{\widehat{\beta }}_X,{\widehat{\gamma }}_X,{\widehat{a}}_X)\right)}{t}\mathrm{d}t\hfill \\ \hfill {\widehat{F}}_Y\left(u\right)=\frac{1}{2}-\frac{1}{\pi }{\int }_{-\infty }^{\infty }\frac{\mathrm{Im}\left({\mathrm{e}}^{-\mathrm{i}tu}\varphi (t;{\widehat{\alpha }}_Y,{\widehat{\beta }}_Y,{\widehat{\gamma }}_Y,{\widehat{a}}_Y)\right)}{t}\mathrm{d}t\hfill \end{array}$$ (8)

where Im denotes the imaginary part of a function. Estimators (7) or (8) directly provide an estimator

$$\mathrm{R}\widehat{\mathrm{O}}\mathrm{C}\left(t\right)=1-{\widehat{F}}_X\left({\widehat{F}}_Y^{-1}\left(t\right)\right),t\in (0,1)$$ (9)

of the ROC curve (2).

Remark

Paulson et al. [16], Heathcote [25], Koutrouvelis [26], and Ushakov [17] proposed estimations of functions parameters of the stable state laws characteristic founded on the method of moments and projection methods (the integrated squares error estimator). This idea was applied to testing problems, for example, by Koutrouvelis and Kellermeier [27]. These methods of estimation are also applicable at our rate. Since pooling sizes p and q are finite, properties of these estimators (see Ushakov [17, pp. 188-197]) are preserved in the considered statement of the problem.

Estimation procedures similar to the ones proposed in this paper have been investigated by Feuerverger and McDunnough [28] in a different context.

3. ESTIMATION OF THE AREA UNDER THE ROC CURVE

The area under the ROC curve is the most commonly used summary measure of diagnostic effectiveness ([6-9, 11, 29], etc.). In fact Bamber [11] showed that the area under the ROC curve is equal to P{X>Y}, with values close to 1, indicating high diagnostic effectiveness. In the case of normal and gamma-distributed data, parametric approaches to estimation of the area based on the observed partial sums have been discussed by several authors (e.g. [1] as well as [3]). Since we observe samples not from target densities f_X and f_Y but from their multiple convolutions, obtaining an estimator of the area based on classical parametric methods is a complex problem. For this reason, most parametric approaches have focused on normal or gamma densities. Note that a solution of this problem also requires that the densities f_X, f_Y and f_Z^X, f_Z^Y have one-to-one mapping.

We consider two ways of representing the area. Define A ≡ P{X>Y} and then directly we have

$$\begin{array}{cc}\hfill A=& {\int }_{-\infty }^{\infty }P\{Y<u\}{f}_X\left(u\right)\mathrm{d}u\hfill \\ \hfill =& {\int }_{-\infty }^{\infty }{\int }_{-\infty }^u{f}_Y\left(r\right)dr{f}_X\left(u\right)\mathrm{d}u\hfill \end{array}$$ (10)

However, if the expectation E ln(1 + |X₁ - Y₁|)<∞, by Theorem 1.2.4 of Ushakov [17, p. 5], we obtain a simpler expression

$$A=\frac{1}{2}+\frac{1}{2\pi }{\int }_{-\infty }^{\infty }\frac{{\varphi }_X\left(t\right){\varphi }_Y(-t)-{\varphi }_X(-t){\varphi }_Y\left(t\right)}{t}\mathrm{d}t$$ (11)

Thus, combining (10) with (7) or (11) with (4), (6) yields the estimator Â. Since the maximum likelihood estimators of the unknown parameters are utilized, we can evaluate the asymptotic distribution of  by applying the usual Taylor expansion. Following Kotz et al. [30, p. 122], we conclude that if the sample sizes n, m satisfy 0< lim_{n+m → ∞} m/(n + m) = ρ<1, then

$${(n+m)}^{1∕2}(\widehat{A}-A)~\mathrm{N}(0,{\sigma }_A^2)\mathrm{as}n,m\to \infty$$ (12)

where the asymptotic variance ${\sigma }_A^2$ is

$$\begin{array}{c}{\sigma }_A^2=\frac{1}{1-\rho }\sum _{i=1}^4\sum _{j=1}^4{W}_{ij}^{\left(X\right)}\frac{\partial A}{\partial {\theta }_i^{\left(X\right)}}\frac{\partial A}{\partial {\theta }_j^{\left(X\right)}}+\frac{1}{\rho }\sum _{i=1}^4\sum _{j=1}^4{W}_{ij}^{\left(Y\right)}\frac{\partial A}{\partial {\theta }_i^{\left(Y\right)}}\frac{\partial A}{\partial {\theta }_j^{\left(Y\right)}}\hfill \\ {\theta }^{\left(X\right)}=[{\alpha }_X,{\beta }_X,{\gamma }_X,a_X],{\theta }^{\left(Y\right)}=[{\alpha }_Y,{\beta }_Y,{\gamma }_Y,a_Y]\hfill \end{array}$$

where ${\left\{W_{ij}^{\left(X\right)}\right\}}^{-1}$ and ${\left\{W_{ij}^{\left(Y\right)}\right\}}^{-1}$ are the Fisher information matrices of the estimators {α̂_X, β̂_X, γ̂_X, a ^_X} and {α̂_Y, β̂_Y, γ̂_Y, a ^_Y}, respectively, i.e.

$${\left\{W_{ij}^{\left(X\right)}\right\}}^{-1}=\left\{-E\frac{{\partial }^2\ln \frac{1}{2\pi }{\int }_{-\infty }^{\infty }\mathrm{e}{-}^{\mathrm{i}t{Z}^X}{\varphi }_X{(t∕p;{\theta }^{\left(X\right)})}^p{\varphi }_{{\epsilon }_X}{\left(t\right)}^J\mathrm{d}t}{\partial {\theta }_i^{\left(X\right)}\partial {\theta }_j^{\left(X\right)}}\right\}$$

$${\left\{W_{ij}^{\left(Y\right)}\right\}}^{-1}=\left\{-E\frac{{\partial }^2\ln \frac{1}{2\pi }{\int }_{-\infty }^{\infty }\mathrm{e}{-}^{\mathrm{i}t{Z}^Y}{\varphi }_Y{(t∕p;{\theta }^{\left(Y\right)})}^p{\varphi }_{{\epsilon }_Y}{\left(t\right)}^J\mathrm{d}t}{\partial {\theta }_i^{\left(Y\right)}\partial {\theta }_j^{\left(Y\right)}}\right\}$$

(In the case of J = 0, Fisher information matrices ${\left\{W_{ij}^{\left(X\right)}\right\}}^{-1}$ and ${\left\{W_{ij}^{\left(Y\right)}\right\}}^{-1}$ are fully investigated by DuMouchel [31].)

4. MONTE CARLO SIMULATION STUDY

4.1. Normally distributed data

To apply the proposed method, the assumption of normal distribution is not necessary. Obviously, in the case where J = 0 in (1) and measurements of a biomarker are known to be normally distributed, the technique presented by Faraggi et al. [1] provides a more efficient estimation of an ROC than the approach based on stable distribution. Here, we perform the following Monte Carlo simulations. Let us assume that one believes the observations are normally distributed and chooses the method of [1]. Alternatively, we apply ROC curve estimation as proposed in Section 2. However, the true diagnostic markers satisfy (1), where J = 0, $X_i~\mathcal{N}(0.8,1)$, $Y_i~\mathcal{N}(0,1)$, and i = 1,..., N. We ran 2000 repetitions of the sample {$Z_j^X$, $Z_k^Y$, 1≤j, k≤n} at each argument u = -3, -2.55,..., 2.44, 2.89, 3.356 of the distribution functions F_X, F_Y, and pooling group size p = q = 2, 4, 5 (where n = N/p). Denote the ratios

$${\Delta }_Y\left(u\right)=\frac{\overline{{({\widehat{F}}_Y\left(u\right)-\Phi \left(u\right))}^2}}{\overline{{({\tilde{F}}_Y\left(u\right)-\Phi \left(u\right))}^2}}\text{and}{\Delta }_X\left(u\right)=\frac{\overline{{({\widehat{F}}_X\left(u\right)-\Phi (u-0.8))}^2}}{\overline{{({\tilde{F}}_X\left(u\right)-\Phi (u-0.8))}^2}}$$

where ā is the Monte Carlo expectation of a; estimators F̂_X, F̂_Y and ${\tilde{F}}_X$, ${\tilde{F}}_Y$ are defined by (8) and [1], respectively; and Π is the standard normal distribution function. In this case, Table I presents the relative efficiency of the proposed estimation in terms of Δ_X and Δ_Y.

Table I.

The ratios of the Monte Carlo variances related to the estimators of F_X(u) and F_Y (u)

	N = 100, p = 2		N = 100, p = 4		N = 300, p = 2
u	ΔY(u)	ΔX(u)	ΔY(u)	ΔX(u)	ΔY(u)	ΔX(u)
-3	1.999	2.551	1.976	2.955	1.775	1.903
-2.547	1.638	1.733	1.065	1.153	1.591	1.394
-2.093	1.034	1.121	0.891	0.999	1.087	1.107
-1.640	0.990	1.109	0.995	0.998	0.990	1.004
-1.187	1.075	1.044	1.215	1.198	1.039	1.021
-0.733	1.166	1.206	1.407	1.511	1.162	1.251
-0.280	1.255	1.247	1.607	1.612	1.299	1.311
0.173	1.255	1.278	1.614	1.711	1.253	1.321
0.627	1.166	1.209	1.416	1.541	1.099	1.008
1.080	1.090	1.107	1.128	1.119	1.028	1.011
1.533	1.022	1.111	0.923	1.005	1.001	1.102
1.987	1.023	1.035	0.922	1.012	1.007	1.014
2.440	1.385	1.393	1.351	1.255	1.255	1.199
2.893	2.119	2.422	2.571	2.482	1.784	1.898
3.347	2.689	3.039	3.036	2.953	2.053	2.147

Thus, when the information regarding the biomarker distribution is ignored (or called into doubt), the proposed method provides less efficient estimation of the tails belonging to the distributions than that based on Faraggi et al.’s [1] approach. In accordance with Table I, this loss in efficiency asymptotically decreases as N → ∞.

In this simulation study, the AUC is equal to A = P{X>Y}≃0.714. Following (12), the variance of the estimator  can be approximated by ${\sigma }_A^2∕(2N∕p)\simeq 0.1384∕(2N∕p)$. In the cases of (N = 300, p = 2), (N = 200, p = 2), and (N = 100, p = 2), ${\sigma }_A^2$’s were estimated by substituting of θ^(X) and θ(Y) by [α̂_X, β̂_X, γ̂_X, a ^_X] and [α̂_Y, β̂_Y, γ̂_Y, a ^_Y], and the Monte Carlo means $\stackrel{‒}{{\sigma }_A^2}$ (and variances $2N∕p\overline{{(\widehat{A}-A)}^2})$ were 0.1383 (0.1387), 0.1431 (0.1472), and 0.1474 (0.1685), respectively. (By Table 1 of [1], we can approximate $2N∕p\overline{{(\widehat{A}-A)}^2}\simeq (2\times 200∕2){\left(0.026\right)}^2=0.1352$ and $2N∕p\overline{{(\widehat{A}-A)}^2}\simeq (2\times 100)∕2{\left(0.037\right)}^2=0.1369$ when the unknown parameters are estimated under executed normal distributional assumptions.) Thus, when pooled data have less than 50 observations (Z^X, Z^Y), application of the asymptotic result (12) can lead to biased estimations of Ã’s variance.

Note that, when the information regarding normal distributions of X and Y in (1) is accepted, the special form of the characteristic function (4) leads to the estimation scheme that coincides with the method of Faraggi et al. [1].

4.2. Robustness

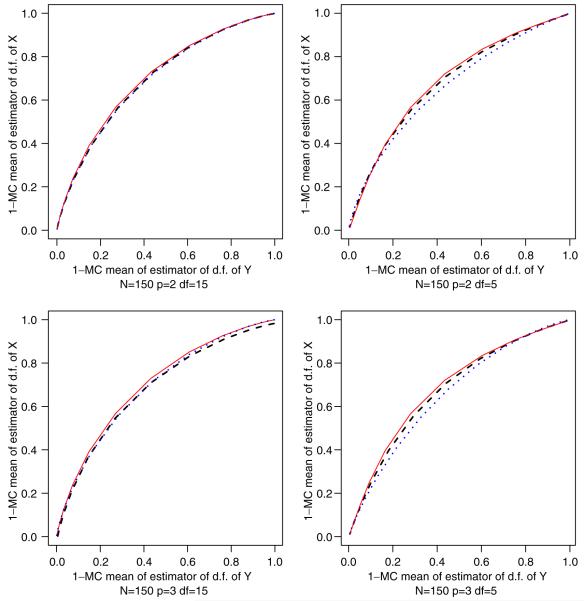
The simulations thus far assumed that the samples followed normal distributions. In order to illustrate the robustness of our methodology, in a similar manner to the previous paragraph, we perform the Monte Carlo simulations based on X’s and Y ’s from t-distributions with degrees of freedom (df) and means 0 and 0.8, respectively. Figure 1 depicts graphs $\overline{(1-{\widehat{F}}_Y\left(u\right)},\overline{1-{\widehat{F}}_X\left(u\right))}$ and $\overline{(1-{\tilde{F}}_Y\left(u\right)},\overline{1-{\tilde{F}}_X\left(u\right))}$ that are the Monte Carlo expectations of the estimators of the ROC curve (1 - F_Y (u), 1 - F_X (u)), which u = -3, -2.55 ,..., 2.44, 2.89, 3.356.

Figure 1.

Comparison between the ROC curve based on the t-distribution functions of X and Y (curve —) and the ROC estimators by (9) (- - -) and Faraggi et al. [1] (···).

In comparing with Table I, for example, when p = 2 and df = 5, Δ_X (u) and Δ_Y (u) are close to 0.989 for u≤-2 and u≥2.4, whereas 0.351≤Δ_X (u), Δ_Y (u)≤0.900 for u ∈ (-2, 2.4). Thus, we can conclude that the proposed method is more robust than the approach based on normal distributional assumptions.

5. POOLING STUDY

We exemplify the proposed methodology for the pooling design (i.e. J = 0 in (1)) from a case-control study of a biomarker of coronary heart disease. The interleukin-6 biomarker of inflammation has been suggested as having potential discriminatory ability for myocardial infarction (MI). However, since the cost of a single assay is 74 dollars, examination of its usefulness has been hindered. Hence, it is reasonable to investigate the effectiveness of pooling. In this study, the inflammation marker interleukin-6 (measured in mg/dl) was obtained from n = 40 cases who recently survived an MI and from m = 40 controls who had a normal rest electro cardiogram (ECG), were free of symptoms and had no previous cardiovascular procedures or MIs. In order to evaluate the success of the cost-efficient pooling design, blood specimens were randomly pooled in groups of p = q = 2 for the cases and the controls separately, and interleukin-6 was re-measured and treated as the average of the corresponding individual interleukin-6. The objective of the study is to evaluate, in the context of ROC curve analysis, the discriminating abilities of the biomarker in identifying patients at high risk of coronary heart disease. Throughout the section, X and Y represent, respectively, individual interleukin-6 measurements from a diseased and a healthy subject.

5.1. The unpooled (full) data

Preliminarily note that, empirically, the mean and standard deviation of X and Y are (X̄ = 4.288, σ‾_X = 2.176) and (Ȳ = 1.846, σ‾_Y = 1.366), respectively. Consider the problem of finding an ROC estimator based on the full data in the context of Section 2, where p = q = 1, J = 0, and the characteristic functions are represented in terms of (4). “R: A Programming Environment for Data Analysis and Graphics” is utilized, in order to solve the optimization problem (6), where we define the initial parameters for (α̂_X, β̂_X, γ̂_X, â_X) and (α̂_Y, β̂_Y, γ̂_Y, a ^_Y) as (2, 0, ${\stackrel{‒}{\sigma }}_X^2∕2$, X̄) and (2, 0, ${\stackrel{‒}{\sigma }}_Y^2∕2$, Ȳ). (Schematic R codes are mentioned in the Appendix A.) As a result, we have (α̂_X, β̂_X, γ̂_X, a ^_X) = (1.990, -0.414, 2.309, 4.288) and (α̂_Y, β̂_Y, γ̂_Y, a ^_Y) = (1.405, -0.901, 0.629, 2.201). Hence, the estimated density of X is very close to normal and the nonparametric test results presented in Table II coincide with this fact.

Table II.

Tests for normality of X and Z^Y ((a) and (b), respectively)

	(a)		(b)
Test statistic	Value	p-value	Value	p-value
Shapiro-Wilk	0.961368	0.1865	0.951419	0.3891
Kolmogorov-Smirnov	0.105298	>0.1500	0.130382	>0.1500
Cramer-von Mises	0.071906	>0.2500	0.057138	>0.2500
Anderson-Darling	0.461674	0.2489	0.373652	>0.2500

The estimation procedure (6), (8) leads to the estimators of the distribution functions of X and Y, which are plotted in graphs (a) and (b) of Figure 2.

Figure 2.

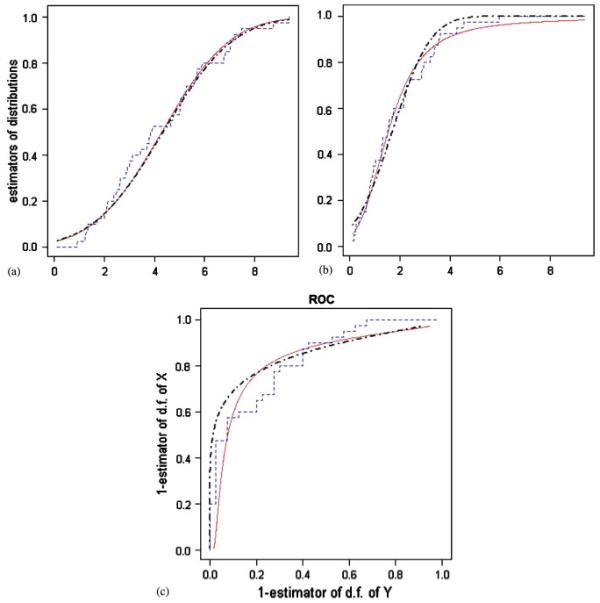
Comparison between the empirical distribution functions of X, Y, the empirical ROC curve (curves - - - - of the graphs (a)-(c), respectively) and the corresponding model-based estimators (curves— and - · -), which are based on unpooled and pooled data, respectively.

On the basis of (9), Figure 2(c) depicts the estimated ROC curve based on the empirical distribution functions and the proposed estimators based on unpooled data.

According to the literature in Section 3, we calculate the area under the ROC curve using the Wilcoxon U statistic as about 0.831 ± 0.046. By applying the proposed methodology, the area is estimated to be 0.818. Therefore, biomarker interleukin-6 has strong discriminating ability in identifying patients at high risk of coronary heart disease. At the same time, at this rate, the proposed methodology is reasonable but not so necessary because, for example, nonparametric techniques can be utilized. The results presented here will be compared with the following outputs.

5.2. The pooled data

Empirical characteristics based on the pooled data are $\stackrel{‒}{X}=\stackrel{‒}{Z^X}=4.342,{\widehat{\sigma }}_X=p^{1∕2}\stackrel{‒}{\mathrm{SD}}\left(Z^X\right)=2.266$ and $\stackrel{‒}{Y}=\stackrel{‒}{Z^Y}=1.701,{\widehat{\sigma }}_Y=q^{1∕2}\stackrel{‒}{\mathrm{SD}}\left(Z^Y\right)=1.234$. In a similar manner, with p = q = 2, J = 0 in (1), we estimate (based on the pooled sample) the parameters as (α̂_X, β̂_X, γ̂_X, a ^_X) = (1.997,-0.038, 2.439, 4.342) and (α̂_Y, β̂_Y, γ̂_Y, a ^_Y) = (1.963,-0.410, 0.723, 1.701). Now, the estimated densities of X and Y are both approximately normal density functions. For example, Table II presents nonparametric tests for normality of Z^Y . The estimation procedure (8) yields the estimators of the distribution functions of X and Y, which are plotted in Figure 2. Accordingly, Figure 2 also depicts the estimated ROC curve based on the empirical distribution functions and the proposed estimation based on the pooled data. By (11), we obtain  = 0.841. In this way, we demonstrate that use of the proposed methodology and the cost-efficient pooling design provides statistical conclusions similar to the results based on full data.

6. STUDY OF MEASUREMENT ERROR

In the context of a practical study, Schisterman et al. [2] proposed model (1) with normally distributed X and Y, assuming p = q = 1, J = 1. We briefly describe the study as follows. A thiobarbituric acid reaction substance (TBARS) is a biomarker that measures sub-products of lipid peroxidation and has been proposed as a discriminating measurement between cardiovascular disease cases (X) and healthy controls (Y). Blood samples, physical measurements, and a detailed questionnaire on different behavioral and physiological patterns were obtained from study participants. The cases are defined as individuals with MI. Due to skewness of the original data, the transformation (TBARS)^-2 was implemented in order to bring the data distribution closer to normality. Empirical evaluations based on the transformed data are n = 47, X̄ = 0.411, SD(X) = 0.260, and m = 891, Ȳ = 0.608, SD(Y) = 0.302. In order to analyze the influence of measurement errors (ε_X, ε_Y ), additional data were obtained by an extra sampling. A reliability study was conducted on a convenience sample of 10 participants. Twelve-hour fasting blood samples were obtained in seven women and three men over a period of six months. The blood samples were obtained every month on the same day of each female’s menstrual cycle and every month on the same calendar day for each male. Under the natural assumption that the distribution functions of ε_X, ε_Y are equal and normal, from the reliability study we obtain that ε_X has zero mean and 0.0567 variance. Without correction for measurement error, an estimator of A (the area under the ROC curve) based on Z^X and Z^Y is 0.699, with the estimated 95 per cent confidence interval being (0.616, 0.782). After correcting for the measurement error, Schisterman et al. [2] obtained the adjusted area estimate to be 0.735, with the 95 per cent confidence interval being (0.582, 0.888). Noting that the situation in which X and Y have normal distributions is the special case of the proposed methodology, in a similar manner to Section 5, we utilize the technique from Sections 2, and 3. We have (α̂_X, β̂_X, γ̂_X, â_X) = (1.349, -1.002, 0.013, 0.430) and (α̂_Y, β̂_Y, γ̂_Y, â_Y) = (1.888, -0.103, 0.010, 0.597). By (9), Figure 3 graphically displays these results, which lead to  = 0.831, with the estimated asymptotical 95 per cent confidence interval being (0.664, 0.998).

Figure 3.

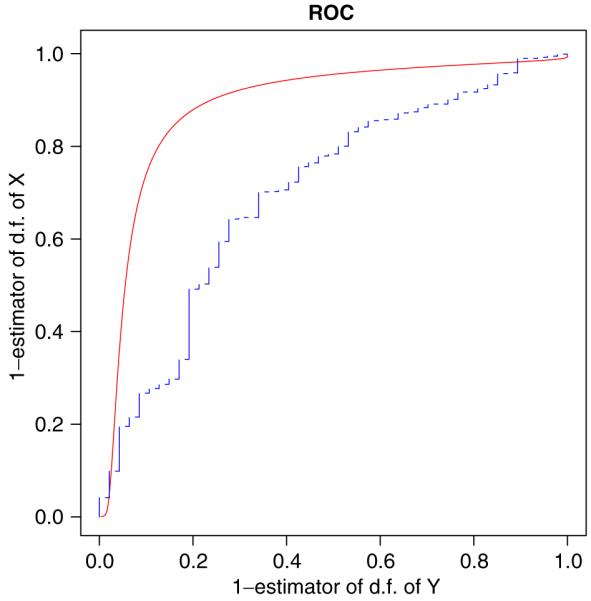
Comparison between the ROC curve based on the empirical distribution functions of Z ^X and Z^Y (- - -) and the adjusted ROC curve estimator (—).

Therefore, the correction for measurement error and the use of the proposed method increased the estimator of the area under the ROC curve and shifted the confidence interval to include much higher values. Use of the uncorrected results underestimates the effectiveness of TBARS as a biomarker capable of discriminating between subjects with and without cardiovascular disease.

7. MIXED STUDY

Let us consider the study that is described in Section 5 with J = 1 in model (1). Assume that measurement errors ε_X, ε_Y have identical distribution functions. Therefore, the fulfillment of the sampling strategy of the study yields observations

$$\begin{array}{cc}\hfill & Z_j^X=\frac{X_{2(j-1)+1}+X_{2j}}{2}+{\epsilon }_j,Z_k^Y=\frac{Y_{2(k-1)+1}+Y_{2k}}{2}+{\epsilon }_k^{\prime },j=1,...,20,k=1,...,20\hfill \\ \hfill & {Z^{\prime }}_j^X=X_j+{\epsilon }_j^{\prime \prime },{Z^{\prime }}_k^Y=Y_k+{\epsilon }_k^{\prime \prime \prime },j=1,...,40,k=1,...,40\hfill \end{array}$$

where ε, ε’, ε”, and ε”’ are i.i.d. random variables. It is natural to assume that ε, ε’, ε”, and ε”’ have characteristic function ϕ(t; α, β, γ, a), which is defined by (4) with a = 0 (e.g. a distribution function of ε is a normal with zero mean). Hence, the characteristic function of the observed i.i.d. random variables

$$T_j=\{\begin{array}{cc}{Z}_j^X-\frac{{Z^{\prime }}_{2(j-1)+1}^X+{Z^{\prime }}_{2j}^X}{2}\hfill & \left(={\epsilon }_j-\frac{{\epsilon }_{2(j-1)+1}^{\prime \prime }+{\epsilon }_{2j}^{\prime \prime }}{2}\right),j\le 20\hfill \\ Z_{j-20}^Y-\frac{{Z^{\prime }}_{2(j-21)+1}^Y+{Z^{\prime }}_{2(j-20)}^X}{2}\hfill & \left(={\epsilon }_j-\frac{{\epsilon }_{2(j-1)+1}^{\prime \prime \prime }+{\epsilon }_{2j}^{\prime \prime \prime }}{2}\right),20<j\le 40\hfill \end{array}\phantom{\}}$$

is ϕ_T (t; α, β, γ) = exp(-γ|t|^α(1 + iβtω(t, α)/|t|)-2γ|t/2|^α(1-iβtω(-t/2, α)/|t|)). By virtue of the proposed method (here,

$$L_T(\alpha ,\beta ,\gamma )=\sum _{j=1}^{40}\ln \left(\frac{1}{2\pi }{\int }_{-\infty }^{\infty }\exp (-\mathrm{i}t{T}_j){\varphi }_T(t;\alpha ,\beta ,\gamma )\mathrm{d}t\right)$$

is shown to be the log likelihood), we estimate the unknown parameters to be α̂=1.925, β̂=-0.981, γ̂ = 0.162 and represent the estimated distribution function of the measurement errors in Figure 4.

Figure 4.

Curves — and - - - present the estimated distribution function of measurement errors ε_j and the empirical distribution function of observed random variables T_j, respectively.

Since T and ε are not identically distributed, in this study, the issue of reconstructing the target distribution, which is considered in Section 2, is also in effect. In this practical example, we have considered the pooled data in the context of resampling to evaluate the problem related to instrument sensitivity. Note that applying the obtained result as in Section 6 to the correction of the ROC estimation does not provide palpable outcomes (Â = 0.831 is corrected up to 0.842). However, the example of alternative use of pooling design makes sense in the aspect of detection of the measurement error.

8. DISCUSSION

The paper demonstrates that the deconvolution issue is a very important field of practical and theoretical biostatistics. Certainly, considerations of non-normal distributions by way of reconstructed solutions of the deconvolution problem are reasonable topics. However, it is necessary to allow for the fact that the class of appropriated distribution functions is bounded by theoretical conditions related to the ability of reconstructing a target distribution. Due to this reason, practically, we can consider the family of infinitely divisible distribution functions.

In the present manuscript, we apply the stable distribution functions, which are a valuable subclass of infinitely divisible distributions. Even in the case of stable distributions, the proposed maximum likelihood method extends the classical parametric approach, because, in a sense, the classical type of the target distribution function is also estimated, i.e. for example, if the α estimated by (6) is close to 2 or 1, we can conclude that the estimated density is approximately normal or Cauchy, respectively. Besides, the considered density functions are not generally available in closed analytical forms.

Modern statistical software (e.g. R, S-PLUS) provides simplicity in applying the proposed methodology to the real data studies.

APPENDIX A: SCHEMATIC R CODES

Without loss of generality and for the sake of clarity of exposition, we assume J = 0 and that p is the pool size in (1). The characteristic function (4) of observations Z ^X (or Z^Y) can be coded in the form

fi<-function(t,alpha,beta,gamma,a){

 if (alpha==1) w<-2*log(abs(t)/p)/pi else w<-tan(pi*alpha/2)

 return(exp(1i*a*t-(p^(1-alpha)*gamma*abs(t)˄(alpha))*(1+1i*beta*sign(t)*w))) }

where (alpha,beta,gamma,a) are parameters of the characteristic function of X (or Y)and p is a known fixed parameter corresponding to the pool size. Following Proposition 2.1, we have the density function

fs<-function(u,alpha,beta,gamma,a){

 integ1<-function(t) exp(-1i*u*t)*fi(t,alpha,beta,gamma,a)

 integ1R<-function(t) Re(integ1(t))

 integrate(integ1R,-Inf,Inf)[[1]]/(2*pi) }

Assume that L(alpha, beta, gamma, a) is the log likelihood function (5) based on fs at sample Z. Denote LV<-function(r) -L(r[1],r[2],r[3],r[4])and estimate (alpha, beta,gamma,a) at Estim$par, where

Estim<-optim(par=c(alpha0,beta0,gamma0,a0) ,LV,lower =c(alphal,betal,gammal,al), upper = c(alphau,betau,gammau,au))

par, lower and upper are initial, lower and upper bound values for the parameters, respectively.