Keeping the Noise Down: Common Random Numbers for Disease Simulation Modeling

Abstract

Disease simulation models are used to conduct decision analyses of the comparative benefits and risks associated with preventive and treatment strategies. To address increasing model complexity and computational intensity, modelers use variance reduction techniques to reduce stochastic noise and improve computational efficiency. One technique, common random numbers, further allows modelers to conduct counterfactual-like analyses with direct computation of statistics at the individual level. This technique uses synchronized random numbers across model runs to induce correlation in model output thereby making differences easier to distinguish as well as simulating identical individuals across model runs. We provide a tutorial introduction and demonstrate the application of common random numbers in an individual-level simulation model of the epidemiology of breast cancer.

Introduction

Disease simulation models are increasingly used to conduct decision analyses of the comparative benefits and risks associated with a range of preventive and treatment strategies [1–5]. A microsimulation or Monte Carlo approach, in which individuals are simulated one at a time, allows for more complex design and application than cohort simulations [6]. With greater detail, these models can be used to explore hypotheses about the underlying natural history of disease and can reflect more heterogeneity across simulated individuals. However greater model complexity comes at an expense as these models are typically computationally intensive. For activities such as model calibration involving millions of model runs, computation time can become a rate limiting step. In addition, as is often the case for policy analysis in resource-rich countries, differences in outcomes across interventions may be very small and can be easily affected by stochastic noise induced from the simulation. A standard way to minimize noise for model comparisons is to simulate larger and larger cohorts of individuals to compensate but this too can also have the adverse effect of increasing computation time. An alternative method, a variance reduction technique known as common random numbers (CRN), is gaining in popularity among disease simulation modelers [7, 8].

Applied to disease simulation modeling, CRN reduces stochastic noise between model runs and has the additional benefit of enabling modelers to conduct direct “counterfactual-like” analyses at an individual level. Statistics such as the change in life expectancy from a treatment or the lead-time due to screening can be estimated by comparing individual level data between simulation runs. Without CRN, these types of statistics can only be inferred or approximated by comparing aggregate population level data. While general implementation of CRN has been previously discussed in the literature [7, 8], the capability the technique enables to conduct individual-level analysis has received less emphasis. To demonstrate, we first present a tutorial introduction for implementing CRN using a microsimulation model of the epidemiology of breast cancer as an example. Next we provide two applications to illustrate the benefits in both reduction in stochastic noise and analysis capability.

Basics about Common Random Numbers

Dating back to the 1950s from the larger discipline of computer simulation in engineering, CRN is the coordinated or synchronized use of random numbers such that the same random numbers are “common” to the same stochastic events across all model runs [9–11]. This synchronization yields model output correlated in stochastic variation across runs thereby reducing the overall variance in differences between model runs. The remaining variation is primarily about the effect of interest arising from a change in model parameters or assumptions across model scenarios. Unfortunately CRN does not reduce stochastic variation within a single model run as simulating larger cohorts of individuals might. Nonetheless, used in disease simulation models in which the unit of analysis is at the individual level, typically fewer individuals need to be simulated to produce stable estimates of the differences in the outcomes of interest across model runs reducing the total computational time; thus the efficiency of simulation analyses may yet be improved.

To implement, separate random number sequences are assigned to different stochastic events. For disease simulation, CRN is most useful if the synchronization in random numbers is taken a step further: the same random number sequences are also used within simulated individuals across model runs. This process generates “identical” simulated individuals across model runs while still generating unique, independent individuals within a model run. Because “identical” individuals are simulated across model runs, each individual can serve as his/her own control for counterfactual-like analyses.

Implementation of Common Random Numbers

Implementation is a straightforward process. For simplicity we divide the process into two phases. The first phase is the design of the use of random numbers. Stochastic events within an individual to be held common across model runs are identified and combined into groups based on their function in the simulated disease process. The second phase is the designation of unique sequences of random numbers to each group within each individual in simulation model code.

Phase One: Design

We illustrate phase one using a microsimulation model of the natural history of breast cancer that was developed in the C programming language. In this model, women are simulated individually, each facing stochastic events relevant to breast cancer including breast cancer onset, growth and progression, detection, treatment and death [5, 12]. The stochastic events are identified and combined into independent, mutually exclusive groups based on their function in the simulated disease process, ordering, and conditionality of the event within an individual’s lifetime (Table 1). Our groups include: 1) woman- and tumor-level characteristics including tumor onset and growth; 2) symptom detection; and 3) determination of screening schedules and screen detection. Each group of events within an individual is assigned an independent sequence of random numbers as described below in Phase 2.

Table 1.

Partitions of Stochastic Events in Breast Cancer Model

Partition 1 – Woman and Tumor Characteristics
Stochastic Event	Order and Frequency	Controlling Input parameters
Date of non-breast cancer death	Once at beginning of lifetime	Life tables by birth cohort
Tumor onset	Once per time cycle	Age- and birth cohort specific onset rate
Tumor growth rate	Once at onset	Growth rate distribution
Tumor progression	Once per cycle post onset	Growth rate, Poisson process
Time to breast cancer death	Once at distant stage	Survival curve
Treatment type	Once at detection	Dissemination of adjuvant treatment
Treatment effectiveness	Once at detection	Likelihood of treatment effectiveness as function of tumor characteristics
Partition 2 – Clinical/Symptom Detection
Stochastic Event	Order	Controlling Input parameters
Detection	Once per time cycle post onset	Likelihood as a function of tumor size
Partition 3 – Screen Detection
Stochastic Event	Order	Controlling Input parameters
Assignment of screening schedule	Once at beginning of lifetime	Screening dissemination sub-model
Result of Mammogram	Once per screen if tumor	Sensitivity of mammography by tumor size

Separating events in this manner allows a simulated woman to have a tumor identical in the timing of onset and growth, regardless of her screening schedule or the sensitivity of mammography and vice versa. A change in screening schedule may affect the timing of detection but not the timing of tumor onset and growth up to that point. For example, in an analysis that estimates incremental effects between frequent and infrequent mammography screening, if detection occurs earlier in the “frequent” screening scenario for a particular woman, subsequent events in her lifetime from different random number groups may no longer be in sync. The random number used to select treatment effectiveness, a stochastic event in the first grouping, may be different as the event may occur later in a woman’s lifetime. If desired, we can synchronize the random number for this event to ensure a woman has the same treatment “tendency” regardless of when the event occurs (Figure 1). If treatment is not effective for a woman’s breast cancer when it was diagnosed at an early stage, synchronizing this event ensures that treatment is not effective if it is diagnosed later. Thus, the “tendency” for treatment to be ineffective in this particular simulated woman is preserved. To implement, we can assign the event a separate grouping with a different sequence of random numbers or re-order when the random number is drawn. For example, pre-drawing and saving a random number at the beginning of a woman’s life ensures synchronization.

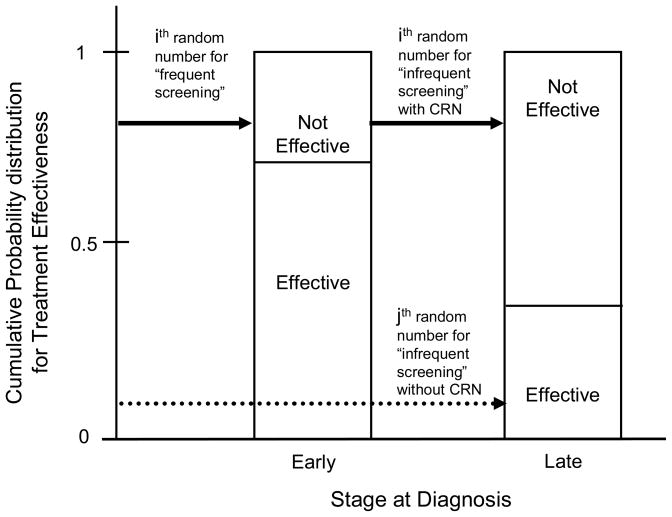
Figure 1. Stylized example of the synchronization of a random event under a frequent screening scenario compared with infrequent screening.

For frequent screening, the “ith” random number determines the treatment effectiveness event with a result of “not effective” for a breast cancer diagnosed in an ‘early’ stage (solid arrow, first column). With common random numbers, the ‘ith’ random number is also used determine the treatment effectiveness event in the infrequent screening scenario regardless of the stage at detection. If it was detected in Stage III, treatment tendency is preserved as her treatment is again determined to not be effective (solid arrow, second column). Without common random numbers, the event may be determined by a different random number, the “jth” number, regardless of the stage at detection. If it was detected in Stage III, treatment tendency is not preserved as the result is “effective” (dashed arrow, second column).

We note that the level of detail for synchronization should be determined in part by the strength of clinical evidence and level of detail necessary for the model analysis. For example, in breast cancer, the “tendency” for treatment response within an individual may be important to model as it may represent genetic factors or tumor markers (e.g., estrogen receptor status and tumor response to adjuvant treatments such as tamoxifen). There may be other situations where little clinical evidence supports such a relationship in which case synchronizing random numbers is not desired and could lead to incorrect conclusions.

Phase 2: Using random numbers

Once the events are grouped, random numbers that are “common” across model runs are assigned in the model code. We first discuss considerations for choosing a random number generator then provide several practical methods for implementation within model code.

Choosing a Random Number Generator for CRN

While a full discussion of random number generators is beyond the scope of this paper, we note a few properties important to consider when selecting a random number generator for CRN and highlight two random number generators in particular.

In general, random number generators produce sequences of numbers that appear to form a random sample from a particular distribution, typically a uniform distribution. From the uniform distribution, random numbers from all other distributions needed for modeling events can be simulated [11, 13]. As there are many random number generators available to modelers, we include several references that provide more information on random number generator properties and tests for their quality [11, 14–16].

For CRN, key features of the random number generator used are the length, reproducibility, and independence of random number sequences. As the sequences of random numbers from a random number generator are finite, the length or “period” of the sequence needs to be long enough such that the sequence is not repeated within any model run. If repeated, simulated individuals, for example, are not guaranteed to be independent which may bias model outcomes in unintended ways. Most generators allow for multiple, reproducible sequences of random numbers through the specification of a “seed” or initial value for the sequence. Initializing the generator with the same seed produces the same sequence of random numbers, functionality needed to coordinate the random numbers across model runs. Unique seeds produce unique sequences, functionality needed to simulate unique individuals within a model run. However, in many generators the independence of sequences with unique seeds is not always guaranteed. For example, the use of seeds that are linearly related can produce correlated sequences of random numbers in some generators [15, 17]. Unintended bias in model outcomes may result as simulated individuals are also not guaranteed to be independent. Caution should be used in choosing seed values [17]. Random number generators that have methods to guarantee the independence of sequences from different seeds are preferred for CRN as this will further ensure that unintended bias between individuals will not be introduced.

Two random number generators that we have experience with are the “Mersenne Twister” [18] and one developed by L’Ecuyer and colleagues which we will refer to as “RngStream” [19]. The first, the Mersenne Twister, is computationally very fast, is freely available in many languages including C, and has a sufficiently long period (2¹⁹⁹³⁷-1) for disease simulation models. (Available at: http://www.math.sci.hiroshima-u.ac.jp/~m-mat/MT/emt.html)

The second, the RngStream, was designed for CRN and is freely available in C (Available at: http://www.iro.umontreal.ca/~lecuyer/myftp/streams00/). It allows for the “instantiation” or creation of multiple independent sequences (called “streams”), each of which has a sufficiently long period (2 ¹⁹¹) for most disease simulation models. Within each stream, it allows for independent “substreams” which also have sufficiently long periods (2 ⁵¹). Although this generator is perhaps computationally slower than the Mersenne Twister, the independence properties and its ease of use in general make it desirable for CRN.

Methods for Implementation within Model Code

The first method, and least prone to unintended correlations, is to use a random number generator designed for common random numbers such as the RngStream generator developed by L’Ecuyer and colleagues described above [19]. We use that generator in the breast cancer model. To implement in the model code, we assigned a stream for each group and used a substream sequence for each individual for each group of stochastic events. Using the same initial seeds for the random number streams across runs ensures commonality. Because the generator has methods to ensure the independence of random number sequences across streams and substreams individuals should not be correlated in an unforeseen way.

If reprogramming to use the RngStream generator is not desired, a similar technique for the assignment can be implemented with most any random number generator. Like the “streams”, multiple instantiations (or copies) of the random number generator are declared in the code, one for each group of stochastic events. To ensure the same sequences are used for individuals across model runs (like the “substreams”), the random number generators are initialized for each individual using the same seeds per individual. A practical method for generating individual-level seeds is to use a separate instantiation of the random number generator where the sequence of random numbers serves as the seeds. However as noted above care should be taken in choosing seeds as this method has the potential to introduce unintended bias. Particular types of generators can produce sequences that are correlated across seeds and simulated individuals would not necessarily be guaranteed to be independent within a model run [15, 17].

As another alternative method, a fixed number of random numbers from a single instantiation of any random number generator can be designated for each group of events and each individual [8]. To ensure commonality across runs, the same set of numbers is used for individuals across model runs. This set of numbers can be pre-drawn. One consideration is that the length of the sequence per group per individual needs to be sufficiently large to accommodate all possible events in that group in any simulated individual’s lifetime. Since most individuals will not “use” all of their allotted random numbers, the generation of extra random numbers may be inefficient and potentially cumbersome depending on the random number generator used and how it is managed within the simulation model code. The benefit of this method is that independence across individuals is preserved and any potential bias induced during the seeding of the generator is avoided altogether [17].

We note that stochastic events need not be grouped at all for CRN. An alternative is to assign each event its own unique sequence of random numbers that is held constant across runs [7]. If separate instantiations of the random number generator are used for each event, this may require re-initializing all the generators with different seeds for each individual potentially increasing computational time. This downside is by far outweighed by the other gains in efficiencies that can be realized from the use of CRN. We also note that all events need not and perhaps should not be synchronized although benefit in terms of stochastic noise reduction across runs may be diminished [8]. While the capability for counterfactual analyses at an individual level is dependent on more complete synchronization, as noted above the degree of synchronization should follow the strength of clinical evidence.

Of practical concern is the management of model output for individual level analyses using CRN. This may require individual level data for a particular model run to either be stored in memory or outputted to a file to be compared post-hoc with individual level data from alternative model runs. As another option, the model may be programmed to rerun the same individual sequentially under alternative modeling scenarios and compute differences in outcomes in individuals as they are simulated.

Applications

CRN has many benefits for disease simulation analysis. We present two applications using the microsimulation model of breast cancer to illustrate.

Comparisons at the Population Level: Model Calibration

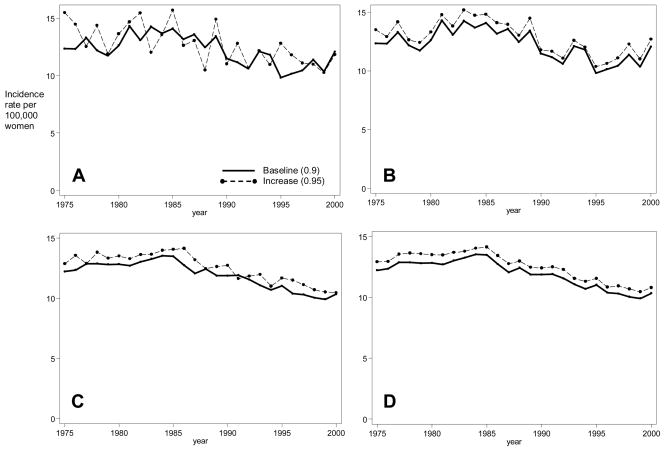
The process of calibrating models to estimate unknown model parameters often entails generating many model runs, each from a unique set of parameter values. Two competing issues that can affect this process are the computation time and the ability to detect differences in model output. As an illustration of the benefits of CRN, we compared model output using CRN to reduce the variance and increasing the cohort size to reduce the variance. Figure 2 shows model output across two runs that differ by one input parameter under these two methods. In the absence of CRN (Panel A), a small sample size led to sufficient stochastic variability in model output making it difficult to distinguish between small input parameter changes in the model output. With CRN for this same sample size (Panel B), differences are distinct as the output is correlated. Increasing the sample size ten-fold reduces the variance in the outcome within a run and the variance of the differences in outcomes across runs (Panels C and D, respectively). With CRN, the variance of the differences is reduced by 82% while increasing the sample size reduced the variance by 71% (i.e., comparing the variance in Panel A with Panel B and comparing the variance in Panel A with Panel C, respectively). While addition of CRN did increase our model computation time, it was still considerably more efficient than without because we can simulate fewer individuals for each parameter set.

Figure 2. Effects of Common Random Numbers and Sample Size on Model Outputs.

Each panel shows breast cancer incidence rates over time under two model scenarios, a baseline run (solid line) and an alternative run (dashed lines). Panels differ by the use of common random numbers and input sample size. For a standard model sample size, without common random numbers (Panel A) the two scenarios overlap while with common random number (Panel B) they are distinguishable. Increased sample size (Panels C and D) distinguishes the two scenarios regardless of common random numbers.

Comparisons at the Individual Level: Counterfactual analysis

CRN for disease simulation also enables direct counterfactual-like analyses. Each simulated individual can serve as his/her own control in a model experiment because stochastic events are synchronized at an individual level. In other words, simulated individual “i” under one scenario will have a corresponding alternate version of “his/herself” under the comparison scenario. We can take advantage of this property to compute outcomes of interest at an individual level by comparing the same individual under alternative scenarios. This provides a distribution of the differences in the outcome of interest across model runs for a population. These types of distributions may prove useful in examining the effect of a policy change on disparities within a population, for example. By comparing individuals, we can also can obtain direct estimates of certain disease statistics that otherwise could only be inferred from proxy statistics aggregated to the population level from each model run. In fact, individual-level comparisons of this sort are not possible without CRN. Even with CRN implemented, this benefit is not always capitalized on by the modeler, and has received less emphasis in the literature. We illustrate with an analysis of changes in life expectancy attributable to the timing of mammograms in the 1990s [20].

Our experiment compared each woman with mammographically diagnosed breast cancer with “herself” under the assumption that she instead missed that one mammogram of diagnosis (Figure 3). Each woman is identical up until the missed mammogram with CRN and may diverge afterwards as the missed mammogram alters her time of diagnosis which in turn may alter her time of death. By tracking the time to death from the selected mammogram under both scenarios, we are able to estimate the change in life expectancy from individual level comparisons. Without CRN we take the difference between two estimates of life expectancy, one from each model run to estimate the change in life expectancy. With CRN, we instead are able compare times to death for each individual from each run and the average of these individual changes in time to death is the change in life expectancy attributable to the mammogram of diagnosis.

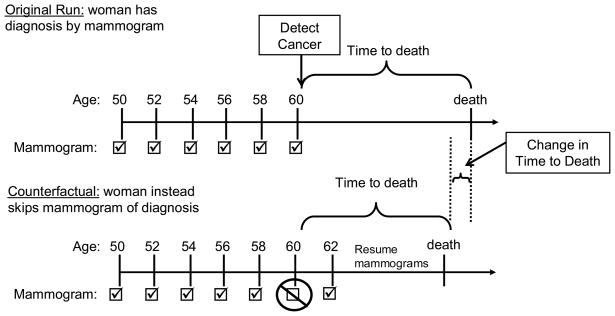
Figure 3. Change in Time to Death Attributable to the Mammogram of Diagnosis.

In the original model run, a woman’s time to death is recorded starting from the time of breast cancer is detected by a particular mammogram. In the counterfactual model run, a woman’s time to death is recorded starting from the same time that her breast cancer would have been detected by a particular mammogram in the original model run. However in this run, it is assumed that she instead did not attend the particular mammogram that led to breast cancer detection. The difference in times to death for this simulated woman under the original and counterfactual scenario is her change in time to death attributable to the mammogram of diagnosis.

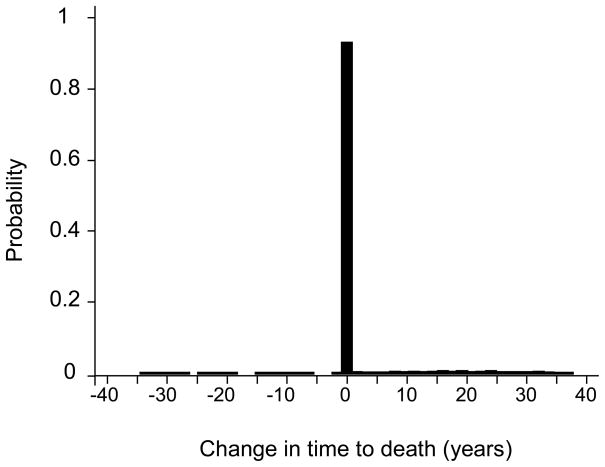
One benefit of the individual level CRN is that we have additional information not available without. We can compute the distribution of changes in time to death within the population. For example, according to our model, the change in life expectancy attributable to the mammogram of diagnosis for a 60 year old woman is approximately 1 year, a statistic we can estimate either at the population or individual level with CRN. However, from an individual level analysis, we also know that 92% of these women diagnosed with breast cancer may not experience any change in time to death by skipping the mammogram of diagnosis (Figure 4). Of the 8% who benefit, the gains in time to death were up to 40 years. Our model also shows a very small subset of individuals who had negative changes in time to death implying delaying the mammogram of diagnosis led to a better length of life. CRN combined with the individual level comparisons exposed that the negative change arose from treatment innovation during the delay time in diagnosis.

Figure 4. Distribution of Change in Time to Death Attributable to the Mammogram of Diagnosis.

The histogram of the distribution of change in time to death across all simulated women shows that 92% of 60 year old women would not experience a change in time to death if they instead skipped the mammogram that would have detected breast cancer at age 60. The average across this distribution is the change in life expectancy.

The distribution of changes in time to death may provide information useful for individual level decision making. The difference in population life expectancy that can be calculated without CRN masks the variation in changes in time to death within a population. From the above example, the majority of women have no adverse effect on their length of life from skipping a mammogram that diagnosed their breast cancer, an indication of the “value” of a single mammogram.

Statistical Considerations with CRN

To understand the variation from stochastic events in model outcomes, multiple executions or replications of the model using different sequences of random numbers are needed. For common random numbers, sequences used for each replication are synchronized across model runs. The difference in outcomes across runs is computed for each replication. The induced correlation in stochastic variability in differences in output between model runs poses additional considerations for modelers wishing to test the statistical significance of hypotheses based on these differences. Statistical tests like the paired t test which account for this correlation should be used while two-sample t tests which assume independence between the model runs should not [21]. The benefit of CRN is that fewer replications are needed to test for “true” differences induced by a change in parameter value or assumptions between the model runs.

With or without CRN, modelers may wish to use a technique like the Bonferroni adjustment for making statistical comparisons among multiple model runs such as might be done during the process of calibration [21]. With CRN, the Bonferroni approach which adjusts the level of statistical significance to account for comparisons being statistically significant spuriously by chance alone leads to more conservative assessments of statistical significance because of the correlation in model output between runs.

The simulation literature also offers alternative methods to make comparisons across model runs with CRN [22–25].

Summary

By reducing variance across runs, CRN increases both analysis capability and efficiency of disease simulation models. The technique is straightforward to implement and debug and can be done at any point in model development. While the use of CRN in general may increase computation time because the random number generator may need to be reinitialized for each simulated individual, this downside is by far outweighed by the other gains in efficiencies such as the simulation of smaller cohorts.

For disease simulation, CRN adds the ability to perform direct counterfactual-like analyses. Analyses examining the effects of alternative disease prevention or intervention strategies can be evaluated directly at the individual level. The result is a distribution about the effect of interest rather than only the difference in population means and variance. Multiple outcomes of interest can be compared to understand the trade-offs between them further aiding decision making, a method that might be particularly useful for identifying disparities within a population.