Canonical Correlation Analysis for Feature-Based Fusion of Biomedical Imaging Modalities and Its Application to Detection of Associative Networks in Schizophrenia

Abstract

Typically data acquired through imaging techniques such as functional magnetic resonance imaging (fMRI), structural MRI (sMRI), and electroencephalography (EEG) are analyzed separately. However, fusing information from such complementary modalities promises to provide additional insight into connectivity across brain networks and changes due to disease. We propose a data fusion scheme at the feature level using canonical correlation analysis (CCA) to determine inter-subject covariations across modalities. As we show both with simulation results and application to real data, multimodal CCA (mCCA) proves to be a flexible and powerful method for discovering associations among various data types. We demonstrate the versatility of the method with application to two datasets, an fMRI and EEG, and an fMRI and sMRI dataset, both collected from patients diagnosed with schizophrenia and healthy controls. CCA results for fMRI and EEG data collected for an auditory oddball task reveal associations of the temporal and motor areas with the N2 and P3 peaks. For the application to fMRI and sMRI data collected for an auditory sensorimotor task, CCA results show an interesting joint relationship between fMRI and gray matter, with patients with schizophrenia showing more functional activity in motor areas and less activity in temporal areas associated with less gray matter as compared to healthy controls. Additionally, we compare our scheme with an independent component analysis based fusion method, joint-ICA that has proven useful for such a study and note that the two methods provide complementary perspectives on data fusion.

I. Introduction

Biomedical imaging studies collect multiple measurements, e.g., functional magnetic resonance imaging (fMRI),¹ structural MRI (sMRI),² electroencephalography (EEG),³ and other covariates from the same participant. Each modality records specific facets of structure or function and provides information that may either be unique or common to other modalities. Typically, these modalities are studied separately, however, collectively analyzing modalities promises to piece together different aspects of the brain providing new insights to help detect and treat diseases; particularly appropriate for a disease like schizophrenia which impacts many aspects of the brain (structure, networks, function, etc. as shown in [1]–[4]). Techniques for combined analysis perform either data integration (based on simple co-registration or using one modality to constrain the other) or data fusion (incorporating interactions among imaging types) [5], [6]. Unlike data integration methods, which tend to use information from one modality to improve the other, data fusion techniques incorporate both modalities in a combined analysis, thus allowing for true interaction between the different data types. Brain imaging data types, however, are intrinsically dissimilar in nature, making it difficult to analyze them together without making a number of assumptions, most often unrealistic about the nature of the data. Instead of entering the entire datasets into a combined analysis, an alternate approach, which is used in data fusion techniques such as the independent component analysis (ICA) based joint-ICA (jICA) method [7], is to reduce each modality to a feature corresponding to a particular activity or structure and then to explore associations across these feature datasets through variations across individuals [8].

In this paper, we introduce a feature-based fusion scheme based on canonical correlation analysis (CCA) to identify linear relationships between two modalities. The multimodal CCA (mCCA) method, we introduce is based on a linear mixing model in which each feature dataset is decomposed into a set of components (such as spatial areas for fMRI/sMRI or temporal segments for EEG), which have varying levels of activations for different subjects. A pair of components, one from each modality, are linked if they modulate similarly across subjects. Thus, CCA is used to find the transformed coordinate system that maximizes these intersubject covariations across the two datasets, and based on these covariations, we determine the associations between the components across modalities. The scheme is flexible as the connections are based only on the linear mixing model and inter-subject covariances across modalities and the modulation profiles of components are not constrained to be exactly the same as in other approaches. The method is also invariant to differences in the range of the data types and can be used to jointly analyze very diverse data types. Previously, CCA has been used to identify spatial correlations to decompose fMRI data as in [9] and to analyze fMRI data from multiple subjects as in [10]; however, using inter-subject covariances for multimodal data fusion is a novel application of CCA.

In what follows, we first explain the fusion model and the procedure to perform mCCA. We present simulation results to demonstrate the capabilities of the approach and then present results for its application to real data. The first study demonstrates the application of the method to fuse fMRI and EEG data from participants performing an auditory motor task. We also demonstrate the fusion method on sMRI data and fMRI data from patients with schizophrenia and healthy controls carrying out a sensorimotor task. The results demonstrate the promising performance of the application of mCCA to multimodal fusion. Additionally, we compare the fusion model and the performance of mCCA with that of jICA, which has been successfully used to jointly analyze information from a number of data types [11]. We note that the mCCA method relaxes a number of constraints imposed by the jICA method, thus promising to discover associations across a larger network of areas, as demonstrated in our experiments. We discuss the advantages and limitations of both methods and observe that they provide complementary perspectives into the multimodal integration problem.

II. CCA for Data Fusion

In this section, we explain the proposed generative data fusion model and the modeling assumptions in mCCA.

A. Generative Model for Data Fusion

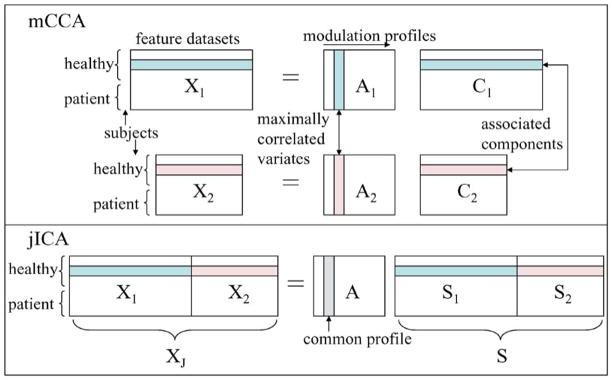
We develop the following generative model for data fusion. Given two feature datasets X₁ and X2, we seek to decompose them into two sets of components, C₁ and C₂, and corresponding modulation profiles (inter-subject variations), A₁ and A₂. The connection across the two modalities can be evaluated based on correlations of modulation profiles of one modality with those of the other. If the modulation profiles are uncorrelated within each modality, each component can be associated with only one component across modalities. This one-to-one correspondence aids in the examination of associations across modalities. The generative model is thus given by

$${\mathbf{X}}_k={\mathbf{A}}_k{\mathbf{C}}_k,\text{for}k=1,2$$

where X_k ∈ ℝ^{N × V_k}, A_k ∈ ℝ^{N × D}, C_k ∈ ℝ^{D × V_k}, V_k is the number of variables in X_k, N is the number of observations in X_k and D is the min(rank(X₁,X₂)). The modeling assumptions imply that the modulation profiles, A_1d and A_2d (d = 1, …, D) satisfy the following:

$$E\left[{\mathbf{A}}_{1i},{{\mathbf{A}}_2}_i^T\right]\ge 0$$ (1)

$$E\left[{\mathbf{A}}_{1i},{{\mathbf{A}}_2}_j^T\right]=0,\text{for}i\ne j$$ (2)

$$E\left[{\mathbf{A}}_{ki},{{\mathbf{A}}_k}_j^T\right]=0,\text{for}i\ne j,k=1,2.$$ (3)

B. Canonical Correlation Analysis for Data Fusion

We propose to use CCA, which is a statistical tool for identifying linear relationships between two sets of variables [12], to determine the inter-subject co-variances. CCA seeks two sets of transformed variates such that the transformed variates assume maximum correlation across the two datasets, while the transformed variates within each data set are uncorrelated. Thus, CCA solves the following maximization problem:

$$\begin{array}{l}\underset{\mathbf{P},\mathbf{Q}}{max}\text{corr}\left(\mathbf{P}{\mathbf{X}}_1^T,\mathbf{Q}{\mathbf{X}}_2^T\right)=\frac{\mathbf{P}{\mathbf{R}}_{X_1,X_2}{\mathbf{Q}}^T}{\sqrt{(\mathbf{P}{\mathbf{R}}_{X_1}{\mathbf{P}}^T)(\mathbf{Q}{\mathbf{R}}_{X_2}{\mathbf{Q}}^T)}}\\ \text{where}\mathbf{P}\in {\mathbb{R}}^{D\times V_1}\text{and}\mathbf{Q}\in {\mathbb{R}}^{D\times V_2}\end{array}$$

to obtain canonical variates given by

$${\mathbf{A}}_1^T=\mathbf{P}{\mathbf{X}}_1^T\text{and}{\mathbf{A}}_2^T=\mathbf{Q}{\mathbf{X}}_2^T$$

which satisfy the constraints given in (1)–(3). The solution involves constraining the two terms in the denominator: PR_X1P^T and QR_X2, Q^T to be identity and the constrained optimization problem using Lagrange multipliers turns out to be a generalized eigenvalue solution, where P and Q are the eigenvectors of the two matrices

$$\begin{array}{l}({\mathbf{R}}_{X_2}^{-1}{\mathbf{R}}_{X_2,X_1}{\mathbf{R}}_{X_1}^{-1}{\mathbf{R}}_{X_1,X_2}-\mathbf{rI})\mathbf{P}=\mathbf{0}\text{and}\\ ({\mathbf{R}}_{X_1}^{-1}{\mathbf{R}}_{X_1,X_2}{\mathbf{R}}_{X_2}^{-1}{\mathbf{R}}_{X_2,X_1}-\mathbf{rI})\mathbf{Q}=\mathbf{0}\end{array}$$

where r is vector of eigenvalues or squared canonical correlations, R_X1,X2 is the cross-correlation matrix of X₁ and X₂ ( ${\mathbf{R}}_{X_2,X_1}={\mathbf{R}}_{X_1,X_2}^T$), and R_X1 and R_X2, are the autocorrelation matrices of X₁ and X₂, respectively. Thus, mCCA models the inter-subject covariations as the canonical covariates obtained by CCA, and based on these covariations, the associated components can be calculated using least-squares approximations given by

$${\widehat{\mathbf{C}}}_k={({\mathbf{A}}_k^T{\mathbf{A}}_k)}^{-1}{\mathbf{A}}_k^T{\mathbf{X}}_k,\text{for}k=1,2.$$

C. Related Work

Recently, there has been increased interest in the use of CCA for feature fusion in various pattern recognition applications [13]–[17]. In [13], CCA is used to fuse features for handwritten character recognition. Different kinds of features are extracted from the same handwriting data samples and CCA is performed on them to obtain two sets of canonical features which are combined to form a new feature set. This method not only finds a discriminative set of features but also somewhat eliminates redundant information within the features. In [14], the same idea is used in a block-based approach where the sample images are divided into two blocks and canonical features are extracted which are then combined linearly to obtain better discriminating vectors for recognition. The first two methods discussed above use CCA to combine features obtained from a single modality whereas the next three methods involve data from two modalities. A kernel based CCA approach for feature fusion is proposed in [15] for ear and profile face based multimodal recognition. The kernel CCA approach allows for a nonlinearly associated ear and face feature. In [16], CCA is used to fuse feature vectors extracted from face and body cues to form a joint feature and then utilize the multimodal information to discriminate between affective emotional states. In [17], CCA is used to fuse features from speech and lip texture/movement to form audiovisual feature synchronization which aids in speaker identification. Thus, CCA has been used to fuse two sets of features to obtain a more a discriminative set of features for recognition problems. Our approach differs from these methods in that it uses CCA to fuse information from two sets of features to discover the associations across two modalities and to ultimately estimate the sources responsible for these associations.

III. Comparison With Joint-ICA

Joint-ICA has been successfully used for the fusion analyses of fMRI, EEG, and sMRI data [7], [18]. Similar to mCCA, jICA examines intersubject covariances of sources to discover associations between feature datasets from different modalities, however, as we shall see in this section, jICA poses a more constrained approach to the data fusion problem. Next, we briefly describe the jICA model and discuss the similarities and differences between the two fusion methodologies.

The jICA fusion scheme discovers relationships between modalities by utilizing ICA to identify sources from each modality that modulate in the same way across subjects. ICA is a popular data-driven blind source separation technique and has been applied to a number of biomedical applications such as for fMRI data in [19]. It is based on the generative model, X = AS, where X is the mixture which is factorized into a mixing matrix A and independent components S. A number of approaches have been proposed to solve the ICA problem, one of them being the maximum likelihood estimation technique that finds an approximation of the underlying sources by using the maximum likelihood estimator of the unmixing matrix W such that S● = WX. Joint-ICA is an extension of ICA, however, ICA is typically used as a first-level analysis and is applied directly to the data while jICA is a feature-level analysis. Given two feature datasets X₁ and X₂, the first step in the jICA method is to concatenate the datasets along side each other (Fig. 1) to form X_J and the likelihood is written as

Fig. 1.

Data model for mCCA and jICA.

$$\begin{array}{l}\mathcal{L}(\mathbf{W})=\prod _{n=1}^N\prod _{v=1}^V{p}_{J,n}(u_{J,v})\\ \text{where}{\mathbf{u}}_J=\mathbf{W}{\mathbf{x}}_J.\end{array}$$

In this formulation, each entry in the vectors u_J and x_J correspond to a random variable, which is replaced by the observation for each sample n = 1, …, K, …, N as rows of matrices U_J and X_J. When posed as a maximum likelihood problem, jICA estimates a joint demixing matrix W such that the likelihood ℒ(W) is maximized. Let the two datasets X₁ and X₂ have dimensionality N × V₁ and N × V₂, then we have

$$\mathcal{L}(\mathbf{W})=\prod _{n=1}^N\left(\prod _{v_1=1}^{V_1}{p}_{1,n}(u_{1,v_1})\prod _{v_2=1}^{V_2}{p}_{2,n}(u_{2,v_2})\right).$$ (4)

In Fig. 1, we present the models of mCCA and jICA. There are a number of differences in the assumptions posed by the two models. Joint-ICA assumes that the sources have a common modulation profile across subjects whereas mCCA models the modulation profiles as separate. Inter-subject covariations of multimodal sources provide a dimension of coherence to identify associations across the modalities, however, assuming these variations to be exactly the same for different modalities is a very strong constraint. Additionally, the associations across modalities in mCCA are solely based on inter-subject covariations whereas the associations in jICA are based on the assumptions of common profiles as well as statistical independence among the joint sources. While statistical independence may be a reasonable assumption to detect a network of areas linked by a particular function, the ICA algorithms may not be able to satisfy both of these constraints at the same time and may end up achieving a tradeoff solution between the two constraints as we demonstrate in the simulation results. Hence, jICA examines the common connection between independent networks in both modalities while mCCA allows for common as well as distinct components and describes the level of connection between the two modalities. Moreover, the jICA model requires contributions from both modalities to be similar (V₁ ≈ V₂), so that one modality does not falsely dominate the other in the estimation of the joint source. Also, if the two feature datasets to be fused have values with very different ranges, then the jICA model requires the two datasets to be normalized before being entered into a joint analysis, as done for sMRI data in [18]. These normalization issues, to ensure equal contribution from both modalities, are not encountered in the mCCA model. Furthermore, the underlying assumption of p_J = p₁ = p₂ made in jICA as seen in (4), is more reasonable when fusing information from two datasets that originate from the same modality. Thus, in general mCCA provides a relatively less constrained solution to the fusion problem; however, ICA might offer certain advantages as well, as we discuss in the results section.

A question that arises here is whether the two methods are equivalent if the independence assumption in jICA is relaxed to decorrelation. There would be a direct relationship between the CCA scheme and the relaxed jICA scheme if the decorrelation assumption in jICA is imposed on the profiles. However, in the jICA method employed in this work, the independence assumption (correspondingly, the decorrelation) is along the feature dimension and hence it is the joint features that would be maximally independent/uncorrelated whereas in CCA it is the variation profiles across the subjects that are maximally uncorrelated. Hence, the two methods used here reveal different characteristics of the datasets based on the assumptions made on the statistical properties of features and profiles respectively.

IV. Experiments

In this section, we describe the procedure to perform mCCA on two modalities and demonstrate the use of mCCA with simulated data and actual fMRI, EEG, and sMRI data. We first show an example of combining fMRI and EEG data, to take advantage of their complementary spatio-temporal scales: high temporal resolution in EEG and localized spatial information of fMRI. Next, we present an example in which we combine fMRI and sMRI data to examine associations between brain structure and function. This is important since brain structure underlies (and hence impacts) brain function. It is also relevant for studying disease, since disorders such as schizophrenia and Alzheimer’s disease are well known to exhibit wide spread functional and structural changes. Finally, we discuss an example using regression to identify relationships of fMRI and sMRI to subject age. In summary, we show that the mCCA method provides a powerful and flexible tool to identify interesting associations between modalities as well as changes in these associations due to disease.

A. Experimental Set Up

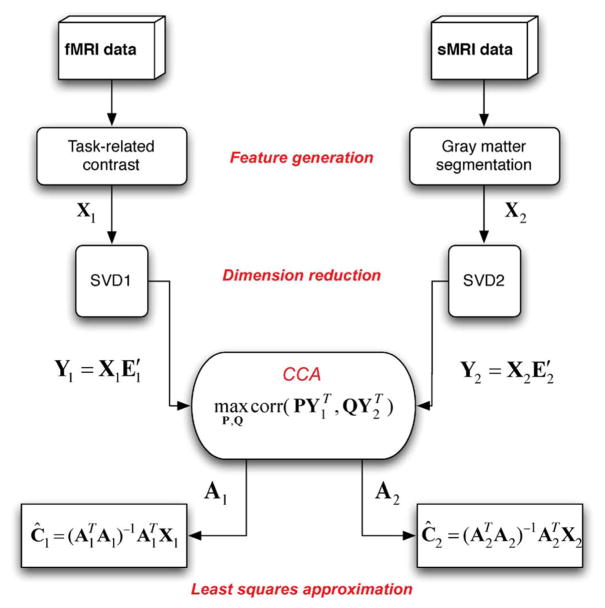
The mCCA method involves a number of steps: feature generation, dimension reduction, CCA, and least-squares estimation of the sources (shown schematically in Fig. 2).

Fig. 2.

Steps to perform mCCA to identify associations between fMRI and sMRI data.

1) Feature Generation

Lower-dimensional features of interest related to specific brain activity or structure are first extracted from the data [8]. For each subject, a feature vector is extracted from each modality and entered into the fusion analysis at the group level to detect associations across modalities. Here, we explain the feature generation process for the three modalities that we focus on in this paper.

For the fMRI data, we use the software package (SPM2) [20] to preprocess the data (slice timing correction, motion correction, spatial normalization, smoothing with a 10 × 10 × 10 mm³ Gaussian kernel) and to obtain contrast images related to task as in [18]. ICA is used to remove ocular artifacts from the EEG data [21] and the data is low pass filtered at 20 Hz. EEG features, event-related potentials (ERPs) are calculated by averaging epochs of EEG, time-locked to the event of correct target detection—details are given in [7], from the midline central position (Cz) because it appeared to be the best single channel to detect both anterior and posterior sources. We label the ERPs based on their ordinal position following the stimulus onset (e.g. P3 for the third positive peak or N2 for the second negative peak). Probabilistic segmentation of gray matter images calculated from the sMRI data using SPM2 are smoothed with a 10 × 10 × 10 mm³ Gaussian kernel and used as features as in [18].

2) Dimension Reduction

Typically, the number of variables in the feature datasets is much larger than the number of observations. Due to the high dimensionality and high noise levels in the brain imaging data, order selection is critical to avoid over-fitting the data. Transforming each set of features to a subspace with smaller number of variables helps reduce any redundancy in the analysis. Dimension reduction is performed on the feature dataset using singular value decomposition (SVD). SVD of X₁ and X₂ is given by

$${\mathbf{X}}_k^T={\mathbf{E}}_k{\mathbf{D}}_k{\mathbf{F}}_k=[{\mathbf{E}}_k^{\prime }{\mathbf{E}}_k^{″}]{\mathbf{D}}_k{\mathbf{F}}_k,\text{for}k=1,2$$

where ${\mathbf{E}}_1^{\prime }$ and ${\mathbf{E}}_2^{\prime }$ contain the eigenvectors corresponding to the significant eigenvalues in D₁ and D₂, respectively, ${\mathbf{E}}_k^{″}$ contain the eigenvectors which are treated as noise and hence omitted from the next steps of the analysis. We perform CCA on the dimension-reduced datasets which are given by

$${\mathbf{Y}}_k={\mathbf{X}}_k{\mathbf{E}}_k^{\prime },\text{for}k=1,2.$$

We assume a noiseless generative model since we perform dimension reduction, i.e., the assumption in the SVD-based dimension reduction scheme is that small singular values of the matrix that are discarded correspond to additive noise.

B. Simulated Data

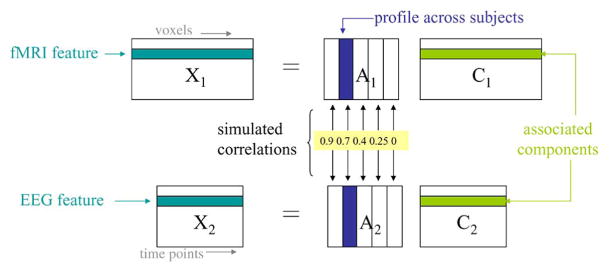
For brain imaging data, there is no a priori knowledge about the ground truth, i.e., the underlying components and their modulation profiles across subjects are not known. Hence, in order to test the performance of mCCA, we generate a simulated fMRI-like set of components and an ERP-like set of components and mix each set with a different set of modulation profiles to obtain two sets of mixtures. The modulation profiles are chosen from a random normal distribution. The profiles are kept orthogonal within each set. Connections between the two modalities are simulated by generating correlation between profile pairs formed across modalities as shown in Fig. 3. We simulate five fMRI and five ERP components. Each simulated fMRI component is a 60 × 60 pixel image, similar to the simulated fMRI sources in [22]. The image is then reshaped to form a vector by concatenating columns of the image. The reshaped fMRI images form the rows of C₁. The corresponding 200-subject modulation profiles for the fMRI components are the columns of A₁. For the ERP data set, we use the peaks of the actual ERP time course from the data described in the Section IV-C. Each ERP component is a 451 time-point segment and the ERP components form the rows of C₂ and the corresponding 200-subject modulation profiles form the columns of A₂. The two simulated data sets X₁ and X₂ are generated by multiplying the simulated profiles with the simulated components and the performance of mCCA and jICA are tested on these simulated datasets.

Fig. 3.

Correlations across the two datasets for the simulated data in Example 1.

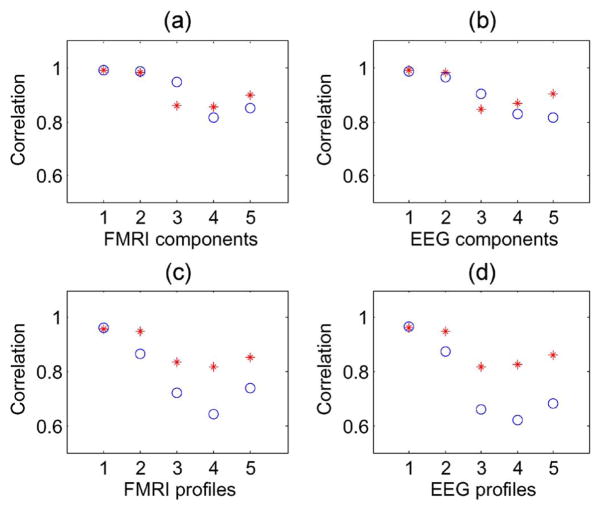
We evaluated the performance of mCCA for a number of different correlations, and here, present two representative examples to demonstrate its performance. In the first example, the correlations between the profiles of the five fMRI components and the five ERP components are chosen as 0.9, 0.7, 0.4, 0.25, and 0, respectively, as shown in Fig. 3. The results are an average of 20 runs, each with independent realizations of the modulation profiles, which are chosen randomly from a normal distribution. After the correlations across different modalities were built into the profiles, each one is normalized to have zero mean and unit variance. The criteria we use for performance evaluation are the correlations between the true and estimated components and profiles as well as the differences between the actual and estimated correlations.

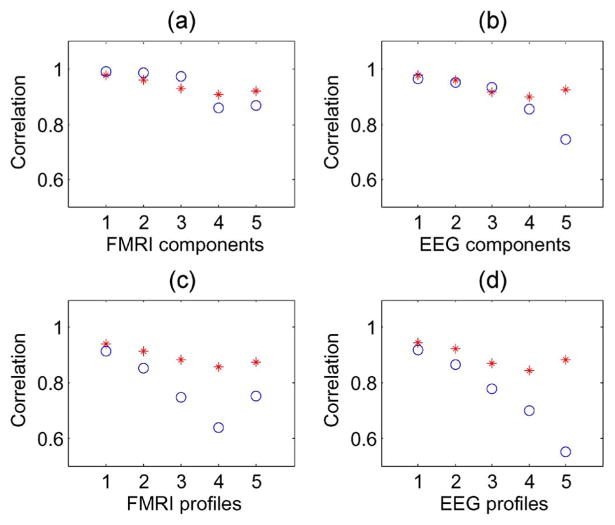
Figs. 4(c) and (d) show that the profile correlation values are higher for mCCA than for jICA. Unlike jICA, mCCA estimates a separate set of modulation profiles for both modalities, thus allowing better estimation of the modulation profiles. In Fig. 4(a) and (b), the component correlation values of both mCCA and jICA are quite similar for the first three components. These three components have a considerable amount of correlation between profiles of the two modalities (0.9, 0.7, and 0.4) and thus, a common profile estimated by jICA, that forms a tradeoff between the actual separate profiles, suffices to efficiently estimate these components. However, when the correlation between the two modalities is weak, the common profile departs further from the ground truth as seen in Fig. 4(c) and (d), in the case of components 4 and 5, which have correlations of 0.25 and 0, respectively. Consequently, in Fig. 4(a) and (b), we see that components 4 and 5 as estimated by mCCA are closer to the ground truth than the ones estimated by jICA. The five correlations estimated by mCCA are found to be exact up to one decimal place.

Fig. 4.

Example 1: Correlations across modalities simulated to be 0.9, 0.7, 0.4, 0.25, and 0, for component pairs 1, 2, 3, 4, and 5, respectively. Correlation with ground truth of components and profiles as estimated by mCCA (*) and jICA (○).

In the second simulation case, the correlations are selected to be 0.9, 0.7, 0.27, 0.25, and 0, for the same set of sources, as in the previous example. In this example, two sources have correlations that are close to each other (0.27 and .25) and the performance of mCCA degraded for one of these sources [Fig. 5(a) and (b)], however, the estimation of the modulations profiles was better than that of jICA [Fig. 5(c) and (d)]. In our experiments on simulated data, we noticed that when the correlations are close together, the performance of mCCA for estimating these sources degrades and is similar to that of jICA when these correlations were low; however, jICA performed better when these sources have higher correlations.

Fig. 5.

Example 2: Correlations strengths across modalities simulated to be 0.9, 0.7, 0.27, 0.25, and 0, for component pairs 1, 2, 3, 4, and 5, respectively. Correlation with ground truth of components and profiles as estimated by mCCA (*) and jICA (○).

C. fMRI and EEG Dataset

FMRI and EEG data are acquired from 39 subjects (16 patients with schizophrenia and 23 healthy controls) performing an auditory oddball (AOD) task that requires the subjects to press a button when they detect a particular infrequent sound among three kinds of auditory stimuli. Two runs of auditory stimuli were presented to each participant by a computer stimuli presentation system (VAPP: http://www.nilab.psychiatry.ubc.ca/vapp/) via insert earphones embedded within 30 dB sound attenuating MR compatible headphones. The standard stimulus was a 500 Hz tone, the target stimulus was a 1000 Hz tone, and the novel stimuli consisted of non-repeating random digital noises (e.g., tone sweeps, whistles). The target and novel stimuli each occurred with a probability of 0.10; the non-target stimuli occurred with a probability of 0.80. The stimulus duration was 200 ms with a 1000, 1500, or 2000 ms inter-stimulus interval. The participants were instructed to respond as quickly and accurately as possible with their right index finger every time they heard the target stimulus and not to respond to the nontarget stimuli or the novel stimuli. Further details of the task design and the participants are given in [23]. Both the fMRI and EEG data are processed into lower dimensional features using feature generation techniques described in Section IV-A.1 and dimension reduction described in Section IV-A.2. The fMRI feature selected in this case, is the contrast image associated with the target stimulus (infrequent sound). For this dataset, the reduced dimension for both features is chosen empirically as 12.

A number of interesting associations are identified by mCCA, three of which have modulation profiles that are significantly different (α ≤ 0.05) between healthy and schizophrenic treatment groups. We report the results for these three pairs of components in Fig. 6. The results are thresholded based on Z-score, that is, the normalized activation levels within each map, to mark out the activated voxels. Different Z-score thresholds lead to differences in regions identified as activated areas. In the figure, the slices are axial with the front of the brain at the top of each slice and the back of the brain at the bottom of each slice. The slices in the figure are arranged from left to right, top to bottom: the upper left corner image is the top slice and the bottom right corner image is the bottom slice.

Fig. 6.

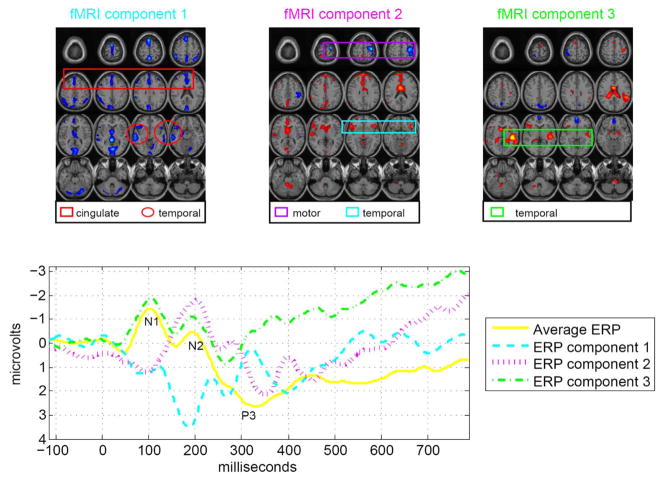
Three pairs of fMRI and ERP components that are significantly different (α = 0.05) between patients and controls show associations of the temporal and motor areas with the N2 and P3 peaks. The fMRI maps are scaled to Z values and thresholded at Z = 3.

The first pair of components, having a correlation given by 0.85, has the fMRI map (Fig. 6: fMRI component 1) showing activations in the temporal lobe (activations enclosed in red circles) and the middle anterior cingulate region (activations enclosed in red box) and the ERP (Fig. 6: ERP component 1) showing a maximum peak at around 300 ms (N2) after the stimulus onset. This is similar to the result obtained in [11] using jICA on a similar dataset. Another pair of components, having a correlation of 0.66, shows activation in the motor areas (activations enclosed in purple box) and the bilateral temporal lobe (activations enclosed in blue box) (Fig. 6: fMRI component 2) which are associated with the N2 peak (Fig. 6: ERP component 2). The final pair of components of interest shows significant differences between patients and controls for only the ERP component and not the fMRI component. This finding is not possible with jICA since it assumes the same profile for both modalities and it is quite plausible that for this particular component pair, fMRI is not sensitive to the differences in controls and patients. The association for this pair is obtained as 0.58. The fMRI activation map (Fig. 6: fMRI component 3) shows temporal lobe areas (activations enclosed in green box) and the ERP (Fig. 6: ERP component 3) shows the P3A peak (early part of P300) as well as portions of the N1 and N2 peaks.

D. fMRI and sMRI Dataset

SMRI and fMRI data are acquired from 73 subjects (36 healthy and 37 schizophrenic subjects). The functional data are acquired while the subjects performed an auditory sensorimotor task in which they are presented with a pattern of 8 consecutive tones, beginning with the tone of lowest pitch and the gradually ascending until the tone with the highest pitch is reached. Then the tone presentation pattern is reversed following a scaled tone presentation, each tone of subsequently lower pitch. Each tone is of 200 ms duration and the pattern of ascending and descending tones followed for the duration of 16 sec. The subjects are instructed to press a button with their right thumb for each presented tone. Details of the experimental set up are given in [24]. The fMRI data and sMRI data are converted into lower dimensional features using the preprocessing techniques described in Sections IV-A-1 and IV-A-2. The reduced dimension for both features was empirically chosen to be 18.

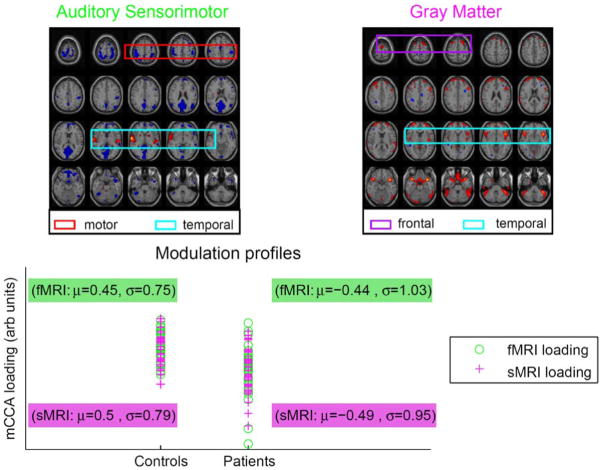
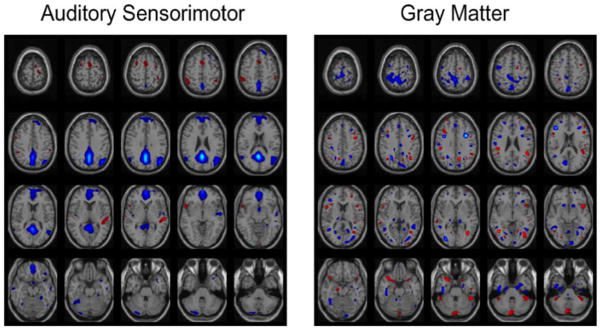
The pair of components corresponding to profiles showing the strongest correlation (r = 0.87) across the two datasets also demonstrate significant group differences (α ≤ 0.05: t_fmri = −4.9167 and t_smri = −4.8048) between patients with schizophrenia and healthy controls (fMRI map, sMRI map, and scatter plots of the profiles shown in Fig. 7). The fMRI component map shows that healthy controls have more functional activity in the temporal areas (activations enclosed in blue box) and less motor activity (activations enclosed in red box) compared to patients with schizophrenia. The gray matter map shows that healthy controls have more gray matter compared to the patients in frontal (activations enclosed in purple box) and temporal areas (activations enclosed in blue box). These results reveal associations between the modalities in adjacent or close sets of voxels as well as remotely located voxels. This is consistent with many previous studies showing changes in both brain structure and brain function in frontal and temporal lobe regions in schizophrenia and is also in agreement with previous studies on fusion of fMRI and gray matter [2], [18], [25]. We also perform jICA on this dataset using the fusion ICA toolbox [26]. The joint component showing maximum difference between patients and controls obtained using jICA is displayed in Fig. 8. The result obtained using jICA is similar to the one obtained using mCCA (Fig. 7). However, mCCA shows additional motor and temporal areas. Also the structural regions are more localized and well defined in the mCCA result. This may be due to the fact that mCCA relaxes the strong constraint of common profiles for the pair of components enabling the method to identify associations across a larger network of areas.

Fig. 7.

FMRI component, sMRI component, and scatter plots of profiles for pair of components identified by mCCA as maximally correlated. Patients with schizophrenia show more functional activity in motor areas and less activity in temporal areas associated with less gray matter as compared to healthy controls. The activation maps are scaled to Z values and thresholded at Z = 3.5.

Fig. 8.

Joint components estimated by jICA corresponding to common profile demonstrating significant difference between patients and controls. The activation maps are scaled to Z values and thresholded at Z = 3.5.

Additionally, we performed a regression analysis using the age of the participants in order to identify associations of fMRI and sMRI data with age. The mean age in our dataset is 31.96 and the standard deviation is 12.41. The beta maps normalized with the standard deviations of the error show that with increase in age, activation in motor and visual regions increase for the sensorimotor task while there is a decrease in gray matter in temporal areas, anterior cingulate, and smaller regions in frontal and parietal areas. The second most correlated pair of components as estimated by mCCA have profiles that are correlated with the age information of the subjects and the component maps show similar areas as those obtained in the regression analyses with age. This is consistent with previous studies which show increased fMRI activity in older participants [27] as well as decreased gray matter volume in healthy aging [28]. Our example demonstrated that mCCA can identify interesting relationships between imaging modalities and other variables such as age, neuropyschological tests, or symptom scores.

V. Discussion

We introduce a feature-level data fusion technique based on CCA to identify linear associations across brain imaging modalities. The mCCA method uses a linear mixing model to decompose the two feature datasets into component pairs and takes advantage of intersubject covariations to measure the association across the two modalities. Through the examples on simulated and actual brain imaging data and a comparison with the jICA scheme, we illustrate the potential of this new fusion tool for discovering hidden factors in the data.

We highlight the key findings from the fusion examples demonstrated in our experiments. Multimodal CCA is used for the fusion of fMRI and EEG data to take advantage of their high spatial and temporal resolutions, respectively. The results obtained mainly show temporal and motor activations linked to the N2 and P3 peaks of the ERP. Activation in the auditory cortex in the temporal lobe is an effect of the auditory stimuli from the task and the motor activity is seen due to the button pressing response. Task-related auditory stimuli is known to elicit activations in the N2 peak, which is linked with matching stimuli to an internally generated contextual template [29]. Also, the P3 peak is known to be associated with attention, decision making, and memory, and is shown to be abnormal in schizophrenia [4]. Thus, the results of the fusion analyses are consistent with what we would expect for an auditory oddball task.

We also illustrate the use of mCCA to find relationships between brain function and structure associated with schizophrenia. Our mCCA results on sensorimotor fMRI and sMRI data show that patients with schizophrenia have more motor activity and less temporal activity as well as less gray matter concentrations. An interesting point to observe here is that the mCCA method allows for associations in local voxels as well as remotely located voxels, thus enabling discoveries of structural changes causing compensatory functional activation. The functional areas picked up in the results are once again consistent with our expectation for a sensorimotor task. Generally, studies have shown that schizophrenia is associated with less functional activity [3], [30] as seen in the temporal areas of the fMRI result; however, patients suffering from catatonic schizophrenia have been known to demonstrate more motor activity. The amount of gray matter concentrations in patients with schizophrenia has contradictory reports in different studies; some are consistent with our results reporting less gray matter concentrations as in [31]–[33] while some show more gray matter concentration as in [18].

The mCCA data fusion scheme offers a number of advantages. It jointly analyzes the two modalities to fuse information without giving preference to either modality. It circumvents the inherent problem of the need to deal with data from diverse imaging modalities by performing the fusion analyses on lower-dimensional features and identifying relationships based on the natural intersubject covariances between the modalities. Unlike jICA, mCCA does not assume a common mixing matrix and does not require the data to be preprocessed to ensure equal contribution from both modalities. This provides flexibility to the model allowing joint analysis of very different modalities. An important point to note is that while mCCA provides a relatively less constrained solution to the fusion problem, jICA utilizes higher order statistical information by employing ICA. When correlations are strong between the two modalities, the assumption of a common mixing matrix may be justified and the jICA technique could potentially improve approximation of the joint sources by employing higher-order statistics in the estimation. However, by allowing for separate mixing matrices, mCCA promises to identify common as well as distinct components and reliably estimates the amount of association between the two modalities.

The mCCA data fusion method has some limitations. The generative linear model used by mCCA assumes that the components are linearly mixed across subjects (components have varying activation levels across subjects), an assumption that may not always hold given the diverse nature of the modalities but highly simplifies the fusion scheme. In future studies, this limitation can be addressed by using different modality specific models. The mCCA method is a feature-level analysis method and does not utilize the information in the entire dataset, however, this helps identify associations based on covariations of the components across subjects without making unreasonable assumptions about the data. In the future, we would like to look at ways to incorporate more information from the data, possibly by entering several features from each modality into a multiple CCA analysis [34]. Similarly, we can use multiple CCA to study the fusion of more than two modalities. Since brain imaging data is high dimensional and noisy, we have used dimension reduction to preprocess the data. The appropriate choice of this reduced dimension is important to correctly identify and quantify the relationships between the modalities. There are a number of information-theoretic criteria that can be used for order selection and an appropriate order selection scheme can be adopted for this case as well. For eigen-analysis based solutions such as mCCA, identical eigenvalues are known to pose problems in the source separation as seen in the simulation example for similar correlation values. This problem can be mitigated by performing the CCA analysis on more than two datasets as shown in [35]. In addition, our discoveries have been limited to linear relationships across modalities and an interesting direction would be to investigate nonlinear associations by using nonlinear CCA techniques [36] for data fusion.

Thus, we have introduced a new feature-based data fusion technique. Our results show that mCCA is a powerful tool for exploring brain imaging data and identifies interesting relationships between modalities. We have also noted the complementary aspects of the mCCA and jICA fusion schemes. Using these two methods in conjunction with each other promises to provide a better perspective on multimodal data fusion.

Biographies

Nicolle M. Correa (S’05) received the Bachelor’s degree in electronics and telecommunications engineering from St. Francis Institute of Technology, Mumbai University, Mumbai, India, in 2003 and the Master’s degree in electrical engineering from the University of Maryland Baltimore County (UMBC), Baltimore, in 2005, where she is currently pursuing the Ph.D. degree in the Machine Learning for Signal Processing Laboratory.

Her research interests include statistical signal processing, machine learning, and their applications to medical image analysis and proteomics.

Yi-Ou Li (S’03) was born in Beijing, China, in 1975. He received the B.S. degree in electrical engineering in 1998 from Beijing University of Posts and Telecommunications, Beijing, China. He is currently pursuing the Ph.D. degree in the Machine Learning for Signal Processing Laboratory, University of Maryland Baltimore County, Baltimore.

He was a Field Application Engineering at Conexant Systems Inc. from 2000 to 2002. His research interests include statistical signal processing and multivariate analysis, with applications to functional magnetic resonance imaging data.

Tülay Adalı (SM’89–M’93–SM’98–F’09) received the Ph.D. degree in electrical engineering from North Carolina State University, Raleigh, in 1992.

She joined the faculty at the University of Maryland Baltimore County (UMBC), Baltimore, the same year. She is currently a Professor in the Department of Computer Science and Electrical Engineering. She has held visiting positions at the Technical University of Denmark, Lyngby, Katholieke Universiteit, Leuven, Belgium, University of Campinas, Brazil, and Ecole Suprieure de Physique et de Chimie Industrielles, Paris, France. Her research interests are in the areas of statistical signal processing, machine learning for signal processing, biomedical data analysis (functional MRI, MRI, PET, CR, ECG, and EEG), bioinformatics, and signal processing for optical communications.

Dr. Adalıhas assisted in the organization of a number of international conferences and workshops, including the IEEE International Conference on Acoustics, Speech, and Signal Processing (ICASSP), the IEEE International Workshop on Neural Networks for Signal Processing (NNSP), and the IEEE International Workshop on Machine Learning for Signal Processing (MLSP). She was the General Co-Chair, NNSP (2001–2003); Technical Chair of MLSP (2004–2006); Publicity Chair of ICASSP (2000 and 2005); and Publications Co-Chair of ICASSP 2008. She is currently the Technical Chair for the 2008 MLSP and Program Co-Chair for the 2008 Workshop on Cognitive Information Processing and 2009 ICA Conference. She Chaired the SPS Machine Learning for Signal Processing Technical Committee (2003–2005); was a Member of the SPS Conference Board (1998–2006); Member of the Bio Imaging and Signal Processing Technical Committee (2004–2007); and an Associate Editor of the IEEE Transactions on Signal Processing (2003–2006). She is currently a Member of the Machine Learning for Signal Processing Technical Committee and an Associate Editor of the IEEE Transactions on Biomedical Engineering, Signal Processing Journal, Research Letters in Signal Processing, and Journal of Signal Processing Systems for Signal, Image, and Video Technology. She is a Fellow of the AIMBE. She is the recipient of a 1997 National Science Foundation (NSF) CAREER Award with more recent support from the National Institutes of Health, NSF, NASA, the US Army, and industry.

Vince D. Calhoun (M’88–SM’05) received the Bachelor’s degree in electrical engineering from the University of Kansas, Lawrence, in 1991, the Master’s degrees in biomedical engineering and information systems from Johns Hopkins University, Baltimore, MD, in 1993 and 1996, respectively, and the Ph.D. degree in electrical engineering from the University of Maryland Baltimore County, Baltimore, in 2002.

He was a Senior Research Engineer at the Psychiatric Neuro-Imaging Laboratory, Johns Hopkins, from 1993 until 2002. Then he took a position as the Director of Medical Image Analysis at the Olin Neuropsychiatry Research Center and as an Associate Professor at Yale University. He is currently Director of Image Analysis and MR Research at the Mind Research Network and is an Associate Professor in the Department of Electrical and Computer Engineering, Neurosciences, and Computer Science at the University of New Mexico, Albuquerque. He is the author of more than 80 full journal articles, over 200 technical reports, abstracts and conference proceedings. Much of his career has been spent on the development of data driven approaches for the analysis of functional magnetic resonance imaging (fMRI) data. He has multiple NSF and NIH grants on the incorporation of prior information into independent component analysis (ICA) for fMRI, data fusion of multimodal imaging and genetics data, and the identication of biomarkers for disease.

Dr. Calhoun is a Senior Member of the Organization for Human Brain Mapping and the International Society for Magnetic Resonance in Medicine. He has participated in multiple NIH study sections. He has worked in the organization of workshops at conferences including the society of biological psychiatry (SOBP) and the international conference of independent component analysis and blind source separation (ICA). He currently serves on the IEEE Machine Learning for Signal Processing (MLSP) Technical Committee and has previously served as the General Chair of the 2005 meeting. He is a reviewer for a number of international journals and is on the Editorial Board of the Human Brain Mapping journal and an Associate Editor for the IEEE Signal Processing Letters and the International Journal of Computational Intelligence and Neuroscience.