A Parallel Independent Component Analysis Approach to Investigate Genomic Influence on Brain Function

Abstract

Relationships between genomic data and functional brain images are of great interest but require new analysis approaches to integrate the high-dimensional data types. This letter presents an extension of a technique called parallel independent component analysis (paraICA), which enables the joint analysis of multiple modalities including interconnections between them. We extend our earlier work by allowing for multiple interconnections and by providing important overfitting controls. Performance was assessed by simulations under different conditions, and indicated reliable results can be extracted by properly balancing overfitting and underfitting. An application to functional magnetic resonance images and single nucleotide polymorphism array produced interesting findings.

I. Introduction

With the rapid developments of genotyping and medical imaging, high-dimensional data from different modalities are commonly collected and require advanced analysis approaches. With genomic data, one can use the information obtained to study inherited disorders or to design personalized pharmacologic interventions [1]. Currently, there is much interest in studying the relationships between genomic data and endophenotypes (intermediate phenotypes). For instance, schizophrenia susceptibility genes, such as Disrupted-In-Schizophrenia 1, Catechol-O-methyl transferase, and brain-derived neurotrophic factor, have been closely investigated using imaging techniques during different tasks [2].

Independent component analysis (ICA) is generally used to reveal factors embedded in large datasets without knowing specific prior knowledge of the properties of these factors. A modified ICA approach to accommodate two modalities simultaneously, parallel ICA (paraICA), was initially introduced by our group [3], [4] to reveal independent components from each modality and also to estimate the relationship among them. In this letter, we present an extension of the algorithm to incorporate multiple interconnections between components and also to address the important problem of overfitting. With such an extension, we are able to reliably evaluate the interconnections between modalities. The paraICA methodology is first introduced, including the addition of dynamic constraints. Next, the method is evaluated via simulation under various conditions. We then demonstrate a practical application to functional magnetic resonance imaging (fMRI) data and single-nucleotide polymorphism (SNP) array data from patients with schizophrenia and healthy controls. Finally, we briefly discuss our approach.

II. Parallel ICA

A. Mathematical Model

The parallel ICA approach is formulated as a generative linear model with constraints as in (1). Two observation matrices, X₁ and X₂, can be measurements from different modalities such as MRI images or SNP genotypes. Two component matrices, S₁ and S₂, contain independent sources such as brain activation networks or genetic associations for various phenotypes. The two mixing matrices are A₁ and A₂. The constraint term, g(.), can be a user-defined relationship among two A matrices or two 5 matrices, and it is best identified to be a physiologically meaningful relationship. For simplicity, we choose the squared correlation between A matrices as the constraint term, where a_1i is the ith column of A₁, a_2j is the jth column of A₂, Cov is the covariance function, and Var is the variance function, as follows:

$$\begin{array}{l}{X}_1=A_1·S_1;X_2=A_2·S_2\\ \mathit{subject}to:\mathit{Arg}max\{g(A_1,A_2,S_1,S_2,\dots )\}\\ g(A_1,A_2)=\sum _{i,j}\mathit{Corr}{(a_{1i},a_{2j})}^2=\sum _{i,j}\frac{\mathit{Cov}{(a_{1i},a_{2j})}^2}{\mathit{Var}(a_{1i})·\mathit{Var}(a_{2j})}\\ \forall (i,j):\mid \mathit{Corr}(a_{1i},a_{2j})\mid >\mathrm{0.3.}\end{array}$$ (1)

Based upon the infomax algorithm [5], maximization of the entropy H (Y) is used to maximize the independence between components. The relationship between modalities is determined by maximizing the squared correlation. Thus, the final cost function for maximization is derived in (2), where U is the estimated independent source and W is the unmixing matrix [5]. The update of the W matrix for Infomax ICA has been achieved by natural gradient maximization. We utilize this approach in the parallel ICA algorithm and arrive at the update rules shown in (3), where λ₁, λ₂, and λ_c are the learning rates for modalities 1,2 and the correlation terms and η is the step size calculated at each step according to the Wolfe conditions [6]. The algorithm thus identifies 1) the optimal W matrices, 2) the components from both modalities, and 3) a specific relationship between the two modalities, as follows:

$$\begin{array}{l}max\left\{H(Y_1)+H(Y_2)+\sum _{i,j}\mathit{Corr}{(a_{1i},a_{2j})}^2\right\}\\ =max\{-E[ln{f}_y(Y_1)]-E[ln{f}_y(Y_2)]\\ +\sum _{i,j}\frac{\mathit{Cov}{(a_{1i},a_{2j})}^2}{\mathit{Var}(a_{1i})\mathit{Var}(a_{2j})}\}\\ \forall (i,j):\mid \mathit{Corr}(a_{1i},a_{2j})\mid >0.3\\ Y_1=\frac{1}{1+e^{-U_1}},U_1=W_1·X_1+W_{10};A_1=W_1^{-1}\\ Y_2=\frac{1}{1+e^{-U_2}},U_2=W_2·X_2+W_{20};A_2=W_2^{-1}.\end{array}$$ (2)

B. Dynamic Constraints

The constraint term is the bridge between two modalities, which is the essence of parallel ICA and different from two totally separate ICA optimizations. The proper optimization of the constraint plays a key role in convergence and avoiding overfitting and underfitting. There are many potential reasons for overfitting or underfitting including data dimensionality and noise, but critical parameters to adjust include the learning rates in (3) for the two entropy terms from the two modalities and for one correlation term representing the interconnections between the modalities. We employ the following two strategies to conduct constraint optimization: dynamically forced interconnections and adaptive learning rates:

For the first term:

$$\mathrm{\Delta }{W}_1=\frac{\partial H(Y_1)}{\partial W_1}={\lambda }_1·[I+(1-2Y_1)U_1^T]$$

For the second term:

$$\mathrm{\Delta }{W}_2=\frac{\partial H(Y_2)}{\partial W_2}={\lambda }_2·[I+(1-2Y_2)U_2^T]$$

For the third term:

$$\begin{array}{l}\mathrm{\Delta }{a}_{1i}=\frac{\partial \mathit{Corr}{(a_{1i},a_{2j})}^2}{\partial a_{1i}}\\ ={\lambda }_{c1}·{\eta }_1\frac{2\mathit{Corr}(a_{1i},a_{2j})}{\mathit{Std}(a_{2j})\mathit{Std}(a_{1i})}\\ \times \left\{(a_{2j}-\overline{a_{2j}})+\frac{\mathit{Cov}(a_{1i},a_{2j})(\overline{a_{1i}}-a_{1i})}{\mathit{Var}(a_{1i})}\right\}\\ \mathrm{\Delta }{a}_{2j}=\frac{\partial \mathit{Corr}{(a_{1i},a_{2j})}^2}{\partial a_{2i}}\\ ={\lambda }_{c2}·{\eta }_2\frac{2\mathit{Corr}(a_{2j},a_{1i})}{\mathit{Std}(a_{2j})\mathit{Std}(a_{1i})}\\ \times \left\{(a_{1i}-\overline{a_{1i}})+\frac{\mathit{Cov}(a_{1i},a_{2j})(\overline{a_{2j}}-a_{2j})}{\mathit{Var}(a_{2j})}\right\}.\end{array}$$ (3)

For the dynamically forced interconnections, we allow the paraICA constraints to vary during the optimization process. Under a subjective/empirical assumption of a correlation higher than 0.3 most likely being true, any pair of components with such a correlation at each iteration are selected and the correlations are emphasized by constraints; one component can only be selected once for each iteration. Thus, constrained interconnections can vary from iteration to iteration based on their concurrent properties, in terms of which correlation and how many correlations being stressed. This flexibility allows the constraints to be updated dynamically while the algorithm is converging.

For the second strategy, we employ adaptive learning rates, which refer to continuously changing learning rates of the three terms in the cost function. The reason to adaptively change the learning rates is twofold. Firstly, the three terms have different characteristics, so they will converge at different rates. However, they also interact with one another, so if one of the terms dominates, then the learning will be suboptimal. To compensate for this, we assign learning rates for each term and update them in parallel. Secondly, we adaptively adjust the learning rate of the correlation term (λ_c in (3)) to mitigate against overfitting. By monitoring the entropy term H(.) online, we can, to some degree, assess the overall effect of the connection term on the overall cost function. The tolerance level for the H(.) is empirically selected in our study based upon our simulation results. We adjust the λ_c based upon tolerance level to balance independence and interconnection terms in the cost function. Therefore, we attempt to emphasize the interconnections without jeopardizing the independence of the components in each modality using the adaptive learning rates.

III. Experimental Evaluation

We evaluate the performance of paraICA by examining both the component accuracy and the connection accuracy, which are the correlation between the true source and the estimated component, and the comparison of the extracted connection with the known connection.

A. Simulation

We generated two datasets with similar dimensionalites as the fMRI and SNP data investigated. Data 1, resembling the fMRI data, had a dimension of 43-by-8000. Data 2, resembling the SNP data, had a dimension of 43-by-367. Eight source signals with different distributions were included for each dataset separately, as well as two random mixing matrices. One (for simplicity) source from each dataset was correlated by making one column of the fMRI mixing matrix similar to one column of the SNP mixing matrix to a certain degree. Random Gaussian noise was superimposed into the mixed source data. To present a more comprehensive understanding of potential overfitting and underfitting issues, we generated simulation data with different connection strengths, estimated different numbers of components, and simulated with different tolerance levels for the entropy term H (.). The connection strength is the simulated relationship between the two modalities. The number of components embedded within the data is usually unknown and hence must be estimated. The tolerance level defines the proper weight associated with the constraint term.

B. fMRI and SNP Application

Sixty-three participants, all Caucasians, including 20 Schizophrenia patients and 43 healthy controls, were recruited. FMRI data provide information about brain function whereas SNP data can reveal genetic influences. FMRI data were collected during performance of an auditory oddball task, which consists of detecting an infrequent sound within a series of frequent sounds. Three types of sounds were presented: standard sound, target sound, and novel random digital noises [7]. Images were preprocessed, including realignment, spatial normalization, and spatially smoothed with a 10 mm³ Gaussian kernel, using the software package SPM2 (http://www.fil.ion.ucl.ac.uk/spm/). Data for each participant were analyzed by a multiple regression incorporating regressors for the novel, target and standard stimuli, and their temporal derivatives plus an intercept term. The resulting target-related contrast images were utilized in this study, after using a mask to select only activated voxels. The resultant images with a size of 7060 voxels were the input from fMRI modality to parallel ICA. A blood sample was obtained for each subject and DNA extracted. Genotyping was performed using the Illumina BeadArray platform and the GoldenGate assay. The PG Array of Genomas, Inc. was used, which contains 384 SNPs from 222 genes from six physiological systems. Genotyping analysis software, GenCall, was used to cluster the resultant intensities from the genotyping microarray into three clusters: AA, AB, and BB, represented as 1, 0, and −1. Reliable genotype results from 367 SNPs were selected as a modality for the paraICA.

IV. Results

We first present the simulation results followed by the results from the actual fMRI and SNP data. Table I(a) lists the simulation results under different tolerance level, with eight estimated components and a true inter-modal correlation of 0.6. Table I(b) lists the results for different connection strengths, and a tolerance level of −1.0e – 3 and eight components. Table I(c) lists the accuracies with different numbers of estimated components, when the tolerance level is −1.0e – 3 and connection is 0.6. All the results are derived from ten runs.

Table I.

Simulation Results

	Extracted correlation	Accuracy of SNP	Accuracy of fMRI
(a) Tolerance level
−1e-1	0.64±0.06	0.96±0.10	0.98±0.01
−1e-2	0.62±0.04	0.99±0.01	0.97±0.01
−1e-3	0.59±0.03	0.99±0.00	0.98±0.01
−1e-4	0.56±0.02	1.00±0.00	0.98±0.01
−1e-5	0.55±0.03	1.00±0.00	0.98±0.01
(b) True correlation strength
1.00	0.96±0.03	1.00±0.00	0.99±0.00
0.80	0.77±0.04	1.00±0.00	0.99±0.00
0.60	0.59±0.03	0.99±0.00	0.98±0.01
0.40	0.41±0.05	0.99±0.01	0.98±0.01
0.20	0.17±0.02	1.00±0.00	0.97±0.01
(c) Estimated component number
4/4	0.48±0.03	0.98±0.04	0.80±0.00
6/6	0.52±0.15	0.98±0.01	0.86±0.22
8/8	0.59±0.03	0.99±0.00	0.98±0.01
10/10	0.64±0.04	0.84±0.34	0.98±0.01
12/12	0.74±0.08	0.65±0.35	0.97±0.01

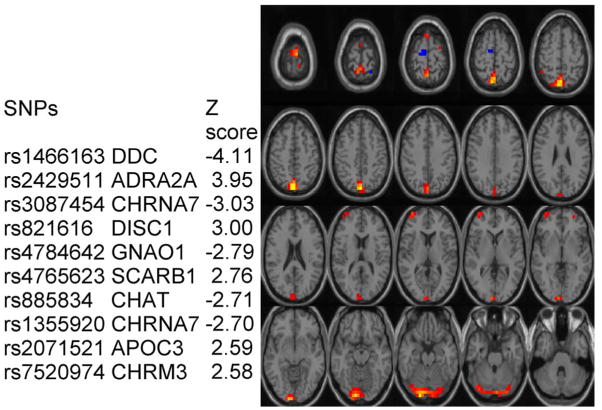
For investigating the fMRI and SNP array, the dimensionality (number of components) is estimated using a modified Akaike information criterion (AIC) [8] for the fMRI data and five fMRI components are selected. For the SNP array, we first use regular AIC method to estimate components’ number and then reduce the component number to seven cautiously and empirically to reach a consistence level among different runs, since the regular AIC tends to overestimate for smoothed data. The paraICA results revealed a correlation of 0.38 between one fMRI component and one genetic component, shown in Fig. 1. For display, only important SNPs (weight |Z| score >2.5, representing the genetic component) and high activation regions of brain (|Z| > 2.5) are presented.

Fig. 1.

Linked fMRI component and genetic component.

V. Discussion and Conclusion

In our previous study [4], we demonstrated an earlier version of our paraICA algorithm and showed improved performance compared to regular ICA, especially in terms of the connection accuracy. In this letter, we update our algorithm and focus on how the parameters affect the paraICA performance. We also apply our algorithm to new data to evaluate associations between brain function and genomic factors. Under different tolerance levels, we show the paraICA can provide different results for the same dataset, hence emphasizing the importance of controlling for both overfitting and underfitting. Based on the simulation, we empirically selected a tolerance level of −1.0e – 3. The simulation also demonstrates that paraICA is robust to different connection strengths (see Table I(b)). However, the number of components estimated, typically unknown in real data, has a large effect on the paraICA performance. An over-estimated component increases overfitting and lowers the accuracy of the component, and it produces a higher but false correlation. An underestimated component number also decreases performance and underestimates the connection strength, illustrated in Table I(c).

For the real data, the related fMRI and SNP components found by paraICA present an interesting relationship between brain function and its possible genetic traits. The largest portion of brain function is located in precuneus, cuneus, and lingual gyrus areas, mainly involved in memory retrieval [9]. Some of these regions were previously implicated in schizophrenia and other psychiatric disorders [10], [11]. The linked genetic association consists of ten contributing SNPs (in nine genes). Three of them, CHRNA7, DISC1, and CHAT, have been previously reported to be closely associated with schizophrenia [12]–[14]. Gene DDC, an enzyme implicated in two metabolic pathways, synthesizes important neurotransmitters, dopamine, norepinephrine, epinephrine, and serotonin. Gene ADRA2A has a critical role in regulating neurotransmitter in the cental nervous system. Both gene SCARB1 and gene GNAO1 are expressed in the brain. These results are encouraging and show the utility of our algorithm combining fMRI and SNP.

In summary, using an approach called parallel ICA, we built up a framework to combine two high-dimensional data types, aiming to find hidden factors and connections between them. With properly controlled constraints, avoiding overfitting and underfitting caused by multiple reasons, reliable results can be obtained using this extended paraICA algorithm. Our algorithm provides a promising way to assess multivariate genetic influence on endophenotypes, such as brain function related to mental disorders. Given that current technology can investigate over 500000 SNPs, the analysis of such data will provide a more comprehensive means to identify possible SNP/fMRI associations, and the proposed approach is well-suited to perform such an analysis.