Magnetic Resonance Imaging with Composite (Dual) Gradients

Abstract

The tradeoff between gradient performance factors, size of the imaging region, and physiological factors such as nerve stimulation typically leads to compromises in gradient design and ultimately suboptimal imaging performance. Local gradient systems can add some performance flexibility, but are cumbersome to set up and remove. In nearly all conventional MRI systems, the use of local gradients precludes the use of the more homogeneous whole body gradients. This paper presents the concept of dynamically selectable composite gradient systems where local gradients and whole body gradients can be selected independently and simultaneously. The relative performance of whole body, insert, and composite gradients is predicted for echoplanar (EPI), turbo spin echo (TSE), and steady state free precession (SSFP). A realization of the concept is presented.

INTRODUCTION

Many useful and important MRI techniques perform better with very high gradient amplitudes and switching (slew) rates. Improvements in gradient amplitude and slew rate (SR) have led to substantial image quality improvements for many speed-limited acquisition techniques. However, even with recent improvements in conventional gradient systems, gradient amplitude and speed are still limitations in a number of important applications. Although further increases in gradient amplitudes and slew rates are technically feasible, we have reached the point that further increases in gradient performance will also increase the likelihood of peripheral nerve stimulation, which results in patient pain or discomfort (1–3).

Examples of MRI techniques where image quality is limited by gradient amplitudes and rise time limits include echoplanar (EPI), turbo spin echo (TSE), steady state free precession (SSFP), and dynamic contrast enhanced 3D gradient echo (DCE MRI) techniques. For EPI, which alternates polarity of the readout gradient to acquire all measurements for an image after a single excitation pulse, the minimum readout time is determined by the maximum gradient slew rate and amplitude. During readout, the magnetization decreases due to T2* decay, resulting in substantial image blurring and distortion. When operating at the gradient limits, increasing resolution requires a longer readout causing increased blurring and image distortion. Thus, gradient performance factors dictate a resolution limit for EPI sequences. Similar blurring problems occur for long echotrain TSE sequences where gradient performance can limit maximum spatial resolution or require shorter echotrains and longer scan times. Acquiring at higher resolutions requires longer echo times (TE) in nearly all conventional sequences, which can cause, at a minimum, a loss in SNR.

Gradient performance is a major limitation in achieving high spatial and temporal resolution in dynamic MRI techniques such as in DCE MRI of the breast. Both contrast-enhanced lesion morphology and temporal pattern of contrast enhancement are useful in the detection and characterization of breast cancer (4–6). DCE MRI is typically performed with a 3D gradient-recalled echo (GRE) sequence, with the shortest repetition time (TR) allowed by the gradient capabilities. Faster and stronger gradients allow shorter TR's, leading to reduced susceptibility artifacts and faster imaging. Faster imaging allows higher spatial resolution for better lesion morphology assessment and higher temporal resolution for better characterization of lesion enhancement.

Gradient induced physiological effects

With improvements in gradient coils and amplifiers allowing increased voltages and currents, gradient amplitudes and slew-rates have reached a point where physiological effects such as nerve stimulation can be induced by the rapidly varying magnetic field. Extensive studies on nerve stimulation due to gradient transitions have demonstrated that stimulation is primarily related to the maximum excursion of the gradient magnetic field (7–14). In general these studies demonstrate that stimulation thresholds decrease as the homogeneous gradient volume (HGV) decreases (3). Although the largest excursion of the magnetic field occurs outside of the HGV, the magnitude of this excursion is still related to the gradient and the size of the HGV. To avoid stimulation, the imaging volume on advanced, high-performance, MRI systems has decreased.

Performance and Field Limitations

Nearly all clinical MRI scanners are equipped with a permanent set of gradients with a fixed size “Homogeneous Gradient Volume” (HGV) in which the gradients are sufficiently linear for imaging. The trade-off between performance, nerve stimulation, and HGV is made at the time of design and cannot be modified after production. Usually, the largest HGV consistent with the magnet homogeneous region, which can be as large as 50cm in diameter, is selected. Although a smaller image FOV can be used, the limitations on nerve stimulation are set by the hardware limited HGV. Reduced volume Insert gradients, switchable system gradients, and multiple region gradients have been proposed to provide improved gradient performance in specific situations,

Reduced volume gradients

Within the limits of nerve stimulation, gradient performance can be improved by reducing the coil HGV. Application specific insert gradient coils with small diameters have been built (15). Gradients formed on one or two flat surfaces can reduce the gradient volume and be positioned in close proximity to the body (16–19). Biplanar flat gradients have good homogeneity, at the expense of reduced openness. Although not uniform, the gradients from single plane flat gradients are very strong near the surface and of high potential interest for breast and abdomen MRI.

Switchable gradient systems

Recently (in the late 1990's), switchable systems were developed with two sets of whole-body gradient coils, one providing the standard full HGV to match the homogeneous region of the main magnetic field, and the second providing a reduced HGV for higher performance imaging (20). These dual gradient systems provide the ability to select between one or a combination of the two systems and permit the adjustment of the linear volume in discrete steps (21) or continuous HGV variation (22). In addition to the extra expense of the system, the fact that the reduced HGV gradients still have the diameter of whole-body gradients means that the improvement in gradient performance is minimal. In general, these systems do not provide the substantial increase in image quality that would justify the increased expense.

Multiple region gradients

To overcome nerve stimulation limits and still increase gradient performance, we and others have proposed using magnetic fields which oscillate throughout the imaging volume, such that sub-images can be obtained from multiple subvolumes. A complete image is formed by “stitching together” these subvolumes. Our technique consisted of dividing the image volume into smaller rectilinear subregions (23). Hennig et al. has proposed a local gradient with radial and angular components. The angular gradient oscillates in angle thereby providing multiple volumes as a function of angle (24).

In this paper, we return to the concept of reduced volume insert gradients, and demonstrate the relative advantages to be obtained by using the insert gradients alone or simultaneously in conjunction with the body gradients. The potential problems of such a system are discussed and a physical realization of dual gradients is presented and evaluated.

THEORY

Composite gradient systems

Insertable, reduced-volume gradient coils can provide substantial improvement in gradient speed and amplitude. Because conventional MRI systems have only one set of gradient amplifiers, connecting an insert gradient set requires disconnection of the body gradient coil. Thus, to use a gradient insert for one pulse sequence on a patient usually requires that the gradient insert be used for all pulse sequences of the exam. Further, when the body gradient are disconnected, the linear first order gradient shimming that is normally performed with static currents applied to the three axes of the body gradients must be performed using the insert gradients which are typically less homogeneous than the body gradients. It is, in fact, possible that only part of a single pulse sequence may require high gradient performance and that part may allow reduced homogeneity or reduced volume or both. As a simple example, slice selection that is performed using the insert gradients will be less uniform than that performed with the more uniform whole-body gradients. The shape of the excited slice can be distorted more like a potato chip than the flat plane that might be desired, and correction for that shape is difficult at best.

Given the experience and issues with reduced volume and switchable gradient systems, it is logical to consider the evaluation of insertable gradients that can operate simultaneously with the system body gradients. Local and whole-body gradients could be combined in such a manner as to exhibit the best advantages of both gradient systems. Small gradients can be used to achieve high amplitudes and fast slew rates within the limits of nerve stimulation. The local gradient set might be used to provide diffusion encoding, flow encoding, and gradient spoiling pulses while imaging is performed with the more homogeneous body gradients.

Because local gradients generally show a decrease in gradient uniformity over the imaging volume, the inclusion of some fraction of the body gradient with the local gradient can add an improved homogeneous component to the net gradient. Combining the body gradients with the small local gradients will also increase gradient strength over that of the local gradients alone.

Performance improvement with simultaneous operation

The simplest implementation of a dual or composite gradient system is simultaneous operation in such a manner that the gradient waveform shapes and timing are identical for both gradient systems. We investigate potential improvements to be obtained from simultaneous dual gradients for EPI, SSFP, and TSE sequences.

EPI

where the entire signal for an image is acquired after a single excitation, is very sensitive to the total readout duration, T_total. Any distortion, ΔB_o, in the main magnetic field (E.g. susceptibility variations) will result in a shift of image voxels: Δy = ΔB_o /BW. The BW for the phase encoding direction is 1/T_total and T_total can be quite long (around 100ms or more) for EPI. T_total is a function of many factors, including the desired resolution and gradient performance factors:

$$T_{total}=N_y[2T_{rise}+T_{DAQ}]=N_y\left[2\frac{G}{R_s}+\frac{1}{{\gamma }_{f}G\Delta x}\right]$$ [1]

where T_rise is the rise time for each ramp, T_DAQ is the time to acquire the data from a single echo in the echotrain, G is the amplitude of the readout gradient, R_s is the maximum allowed slew rate, γ_f is the gyromagnetic ratio in Hz/T and Δx is the resolution. To minimize distortion, G is selected to minimize T_total:

$$\frac{\partial T_{total}}{\partial G}=N_y\left[\frac{2}{R_s}-\frac{1}{{\gamma }_f{G}^2\Delta x}\right]=0\mathrm{or}{G}^2=\frac{R_s}{2{\gamma }_f\Delta x}.$$ [2]

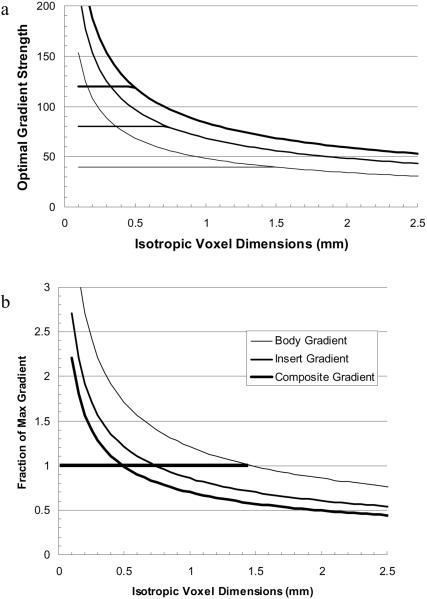
Thus for any given gradient slew rate, the best (desired) gradient is only a function of resolution (until G reaches and remains at the maximum gradient for the system, G_max,). In Figure 1a, the optimal gradient is plotted for a typical high performance body gradient (G_max = 40mT/m and R_s= 200T/m/s), an insert gradient (G_max = 80mT/m and R_s= 400T/m/s), and the composite gradient (G_max = 120mT/m and R_s= 600T/m/s). The fraction of the given maximum value is plotted in Figure 1b. The horizontal lines in (1a) and the thick horizontal line in (1b) indicate where the optimal gradient strength is at the maximum available for the given gradient system. At higher resolution (smaller voxels) the optimal gradient strength cannot be attained. These insert performance values are those of a commercially available head insert. The limits are conservative and are actually set by concerns over audible gradient sound levels rather than heat dissipation limits. Sound levels can be reduced by improved design. The total acquisition time, T_total, obtained using the optimal gradient strength (limited by the maximum allowed gradient for each system) is plotted in Figure 1c. For comparison, we define the fractional improvement (fractional reduction in total readout time) for the insert gradient as f_insert =1.0-T_total(insert)/T_total(body) and similarly for the composite gradient. As seen in Figure 1b, for nearly all resolutions, the insert and composite gradients yield fractional reductions in T_total of 30% and 44% respectively. The thin line is the fraction of total time reduction (T_total(body)- T_total(composite)) that comes from combining the body gradients with the insert gradients (see caption). The flat segment for Δx < 0.5 is due to the fact that the maximum gradient strength is attained for each system.

Figure 1.

a) Optimal gradient strength as a function of resolution as defined by the slew rates for the body, insert and composite gradients. The horizontal lines represent the limiting gradient amplitude for each gradient system. b) The ratio of the optimal gradient to the maximum gradient for each system. c) T_total (echotrain readout time) for an EPI sequence using the body, insert, and composite gradients. d) T_total is reduced by 30% and 44% (for voxels > 1mm) using the insert and composite gradients respectively. Reduction is greater for smaller voxels. The thin line is the fraction of total time reduction (T_total(body)- T _total(composite)) that comes from adding the body gradients to the insert gradients: (T_total(insert)- T_total(composite))/ (T_total(body)- T_total(composite)).

SSFP

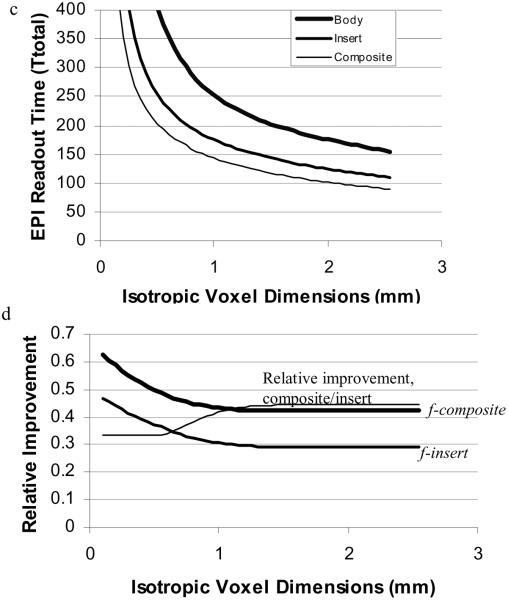
Improved gradient performance can allow shorter TR's for SSFP sequences such as “True FISP” or “FIESTA” where the frequency bandwidth that can be imaged without artifact is 1/TR. If magnetic field inhomogeneity causes a larger frequency variation in the imaging volume than 1/TR, dark banding is observed. To calculate the TR as a function of increased gradient strength, we consider the TR reduction that would occur if we simply used larger voxels. If the insert gradient amplitude and slew rate are a factor of 2 greater than the body gradient, then the composite gradients could achieve a factor of 3 increase in resolution with no change in the timing of the imaging gradient pulses. This is illustrated in Figure 2a, which plots TR for balanced SSFP as a function of readout bandwidth for several isotropic voxel resolutions on a Siemens TIM Trio 3T MRI scanner. For any line plotted, it is assumed that the insert gradient can achieve double the resolution while the composite gradients can achieve triple the resolution. Thus, the insert gradients with the TR for 0.5mm resolution would achieve 0.25 mm isotropic resolution. Similarly, the composite gradients with the TR for 0.75mm resolution would achieve the 0.25 mm resolution. In Figure 2b we plot the fractional reduction in TR for the insert and composite gradients, respectively: f_insert = 1.0-TR_insert/TR_body. Note that because the interdependence of the various gradient pulses makes it difficult to predict minimum TR, we prescribed the sequence on the Siemens TIM Trio and have used the solver on the MRI scanner to determine the minimum TR. This method results in the “bumpiness” of the lines plotted.

Figure 2.

a) TR for balanced SSFP (eg. True FISP or FIESTA) as a function of readout bandwidth for several isotropic voxel resolutions (0.25, 0.5, 0.75, 1.0, 1.5, 2.0, 3.9mm) on a Siemens TIM Trio 3T MRI scanner. Where the body gradients could achieve 0.25mm isotropic resolution, the insert (or composite) gradients could achieve the same resolution with the TR of 0.5mm (or 0.75 mm) resolution. b) The relative improvements for insert (thin line) and composite gradients (thick line) for 0.25mm (solid) and 0.5mm (dashed) isotropic resolution respectively.

TSE

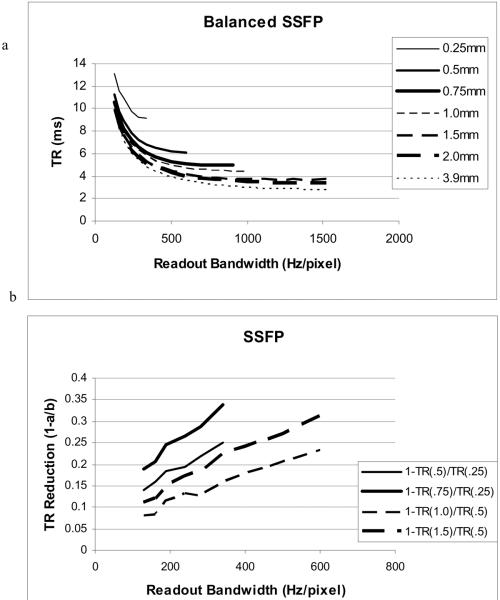
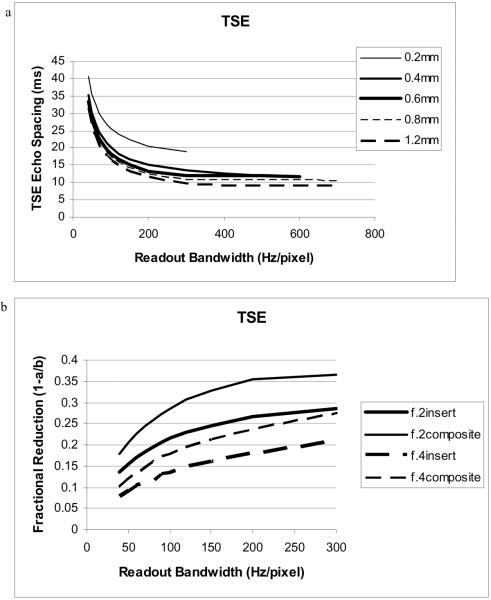
Calculating the echo-spacing (ESP) in a TSE sequence is more involved because the ESP also includes non-imaging (crusher and spoiler) gradient pulses that may not change with resolution as well as the slice selective refocusing pulses that depend upon the desired slab thickness and RF bandwidth. To estimate the reduction in ESP that might be obtained, we prescribe a 3D TSE sequence with isotropic voxels of 0.2, 0.4, 0.6, 0.8, and 1.2 mm³, using a range of readout bandwidths from 40 to 300 Hz/pixel (Figure 3). Again, in this case, the body gradient ESP for 0.4mm isotropic resolution would be the same ESP as for the insert gradients (with twice the performance as the body gradients) at 0.2mm isotropic resolution. The composite gradients with triple the performance would achieve 0.2mm isotropic resolution with an ESP equivalent to the body gradients at 0.6mm isotropic resolution. Similarly, insert and composite gradients with ESPs corresponding to the body gradients at 0.8 and 1.2 mm isotropic resolution, respectively, would attain 0.4mm isotropic resolution. The fractional reduction is plotted in Figure 3b. The expected reduction is most evident for high resolution where the imaging gradients have a greater amplitude (area) relative to the spoiler and crusher gradients. Using composite gradients (ESP of body gradients at 0.6mm isotropic voxels) yields a 35% reduction in ESP over that of the body gradients for 0.2mm isotropic voxels. TSE images (especially T1 and PD images) can be highly blurred for long echo trains. Thus a 35% reduction in the ESP should result in a substantial decrease in blurring as well as allow the interleaving of more slices. The shorter ESP could also be used to shorten the total acquisition time (by putting more echoes into the echotrain in order to keep the total time for each echotrain constant). The reduction for lower resolution is less in this plot because the system is not reducing the crusher and spoiler gradients. For composite gradients, the duration of these non-imaging gradients would likely be reduced, so the ESP reductions would be comparable (greater than 35%) at all resolutions.

Figure 3.

a) Echospacing (ESP) for TSE vs. bandwidth and resolution. At BW = 200 Hz/pixel, ESP for 0.2mm isotropic voxels is reduced from 20.6 to 15.1 and 13.3ms for the insert and composite gradients respectively. b) The fractional reduction in ESP (f=1.0-ESP_insert/ESP_body) for insert (thick line) and composite (thin line) gradients for 0.2mm (solid) and 0.4mm (dashed) resolution.

METHODS

Composite Gradient System

Experiments were performed on a Siemens TIM Trio 3 Tesla MRI scanner (Siemens Healthcare AG, Erlangen, Germany) that has been modified, using hardware and software provided by Siemens, to simultaneously control the body gradient system and an insert gradient system. The body gradient system is controlled using the standard Siemens host computer (master-host), gradient control lines, and gradient amplifiers. The insert gradient is controlled by a separate slave-host computer, control lines and an additional set of gradient amplifiers. To allow complete generality, independent pulse sequences are executed on the master and slave, computer systems. Pulse sequences can then be designed that independently control each individual gradient waveform on each gradient system. During scanning, the master and slave computers are synchronized to provide synchronized gradient operation.

For simplicity in these first experiments, we have designed the pulse sequences for each gradient set to have identical gradient waveform shapes and timing, with the insert waveform amplitude controlled by the modifications to the gradient sensitivity tables. For these experiments, transmit RF, receive RF, and data acquisition are controlled by the master-host computer, and reconstruction is performed using the standard reconstruction system. The master-host system also maintains the first and second order gradient shims on the standard body gradients.

In our experiments, a head gradient insert was positioned within the bore of the 3T MRI scanner and attached to the slave gradient system while the whole-body gradients remained attached to the host system. The gradient insert was designed and developed by Blaine Chronik, at the University of Western Ontario, in London, Ontario (15). This coil was designed with an efficiency goal of 0.4 mT/m/A and an inductance goal of less than 1000 uH. The inner coil diameter is 32cm, and the outer diameter is 42cm. The coil is unshielded because of the relatively small diameter. The measured X, Y, and Z gradient parameters were: efficiency = 0.4, 0.35, 0.35 mT/m/A, inductance = 770, 810, 860 uH, and resistance = 220, 235, and 153 mOhms, respectively (at 10 kHz) (15). With a current of 200A, these efficiencies result in gradients of 84, 70, and 70 mT/m, which are substantially stronger than the technical limits of 40 mT/m on most high performance whole-body gradient systems. This coil has been successfully used at field strengths between 0.5 and 4.0T.

Imaging

This insert gradient coil was designed with the homogeneous region at the end of the gradient insert and extending a few centimeters outside of the insert gradient bore to allow high resolution imaging of the head and neck. A Siemens circularly polarized transmit/receive (Tx/Rx) wrist coil (model # 1P8622701) was used for the images displayed in this paper and identical waveforms were used on both gradient systems, yielding a doubling of gradient strength over that obtained with the whole-body gradients alone when the gradients were used simultaneously.

A lemon was used as the imaged phantom, since it was small enough to fit in the wrist Tx/Rx coil and provided fine internal detail necessary for qualitative assessment. All images displayed were acquired with a basic FLASH sequence. EPI, TSE, and SSFP sequences are being developed for the composite gradient system and results will be reported later. Acquisition parameters were: repetition time (TR) 300 ms, echo time (TE) 6 ms, bandwidth (BW) 200 Hz/pixel, slice thickness 5 mm, image matrix 256×256 pixels, and a field of view (FOV) 200 mm except when the gradients were operated together resulting in a FOV of 100mm.

RESULTS

Images of the lemon were obtained using each gradient system separately and then in combination. The head insert was positioned on the table within the bore of the Siemens Trio 3T MRI scanner. The lemon was scanned with a 200 cm FOV using the basic FLASH sequence with parameters given above. Example images are shown in Figure 4 displaying the acquisition of axial lemon images using different combinations of the gradient insert and standard imaging gradients.

Figure 4.

Images of three non-adjacent axial slice locations of a lemon (a, b) using the body gradients without (a) and with (b) the gradient insert in place, c) using the head insert gradients, and d) using composite head and body gradients. There is a slight repositioning error between (a) and (b) because the lemon had to be repositioned after the gradient insert was placed on the table. For simplicity, the same FOV was used for the body and head insert such that the combined gradient image had the FOV cut by 50% in both x and y directions. Only the body gradients were used for slice selection. e) To compare the different resolutions obtained between the insert and the composite gradient, the images of (c) are scaled by a factor of 2 in x and y.

In this experiment, and in upwards of 15 experiments performed after, we have found no difference between images obtained using the body gradients with and without the gradient insert in place. We have not yet had time to make the pulse sequence completely general – but we were able to image with the body gradients alone (with and without the head insert in place), with the head insert gradients alone, and with both together using the same parameters. The images shown (Figure 4) have not been resized, but demonstrate that the images from the combined gradient appear twice as large as those from the individual gradients, implying that the FOV has been reduced from 200mm to 100mm. It is evident that simultaneous operation of the two gradient systems works quite well. This experiment gives strong evidence that the composite gradient concept will work.

DISCUSSION

This short note has demonstrated that MR imaging performance can be improved by operating insert gradients in concert with the system whole body gradients. It is generally true that different MRI studies place different demands on the performance characteristics of the imaging gradients. Thus, judicious use of composite gradients can better satisfy these varying demands than either whole body gradients or insert gradients alone. To our knowledge, this is the first work to consider the feasibility and added value of composite gradients. Two specific advantages of composite gradients have been demonstrated.

First, the concept of composite gradients eliminates the need to disconnect the body gradients when the insert gradients are used. These experiments demonstrate that standard imaging can be performed using the body gradients with the insert gradients in place. Thus, insert gradients can be used for special sequences on patients where standard clinical protocols are also required. In conventional MRI systems, where the insert gradient would replace the body gradients, it would be necessary to perform all imaging sequences as well as apply all required first order shims with the insert gradients. Thus, any advantages brought by the insert gradients are offset by disadvantages of not being able to use the body gradients.

Second, in this composite gradient system, the insert gradients and body gradients may be used simultaneously. Not only does this simultaneous use increase the total gradient strength that can be obtained with the insert gradients (without increased PNS), but it also improves the homogeneity that can be obtained. Calculations have shown that echotrain length can be substantially shortened in EPI and TSE sequences, and that repetition time can be reduced in steady state sequences.

We have performed a large number of experiments using larger phantoms and all axes of the aHGV insert gradient. These experiments have demonstrated minimal effects due to coupling of the z-gradient with the housing or eddy current-related distortions. For example, the ability to do oblique images has been tested and works well. We are beginning to develop 2D and 3D TSE, EPI, and SSPF sequences for the dual gradient system and have evaluated the image quality obtained using Flash, 3DTOF (3D FLASH), and 2D and 3D TSE with and without the insert gradient coil in place. Again, no noticeable coupling or image degradation has been observed.

Imaging with the body gradients with and without the gradient insert in place gave images with no noticeable differences in distortion or SNR. Because removing and inserting the local gradient coils is tedious, we have established that the image geometry is essentially the same when the local gradients are present but not used. It is therefore possible to use images obtained using the body gradients with the insert in place as baseline images relative to which image distortion and SNR can be measured.

The experiments presented here demonstrate that the gradient systems can be operated independently. There is no evidence of reduced SNR when operating the body gradients with the insert gradients in place. To the extent that this remains true for all pulse sequences, it will, for example, be possible to perform a brain scan with conventional gradients and high performance fMRI or DTI scan using composite gradients in the same study. And the high performance fMRI and DTI studies will have reduced distortion and increased coverage in the same imaging time.

Composite gradients will be especially useful in studies involving fMRI, high resolution DTI, intracranial MRA and flow, short TE imaging and many other related applications. The 33 to 44% reduction in EPI echotrain length will have a huge effect on inherently signal starved fMRI where it will allow nearly double the amount of information to be acquired in the same amount of study time. All of these improvements to imaging capabilities will come with no increase, and perhaps even a reduction in PNS.

We are actively working to develop more general pulse sequences to study general composite gradient systems. These pulse sequences will be designed to selectively operate each gradient axis of each system, choosing the desired functionality of each gradient for each gradient pulse. This functionality will allow us to study the possibility of operating a small gradient system in conjunction with the body gradients in such a manner that the small gradients are used only for the pulses where the advantages of the local gradients outweigh the disadvantages.

In the design and development of composite gradient systems, it will be necessary to eliminate as much as possible, any cross-talk between gradient systems. Such cross-talk could cause distortions in the resulting images. It appears from all of our experiments that such cross-talk is very small and may be negligible. For maximum SNR, RF coils must be developed that are consistent with each set of local gradients. The smaller space available for the RF coil and electronics increase the number of challenges in achieving high RF performance in the local gradient system comparable to that obtained with just the whole-body gradients.

CONCLUSION

The results presented here demonstrate that imaging can be performed using an insert gradient coil in concert with standard whole body gradients. The images acquired with the insert gradient were not appreciably degraded compared to the images acquired with standard gradients alone. This work demonstrates that composite gradients can improve EPI, TSE, and SSFP sequences and may have a strong beneficial impact on fMRI and DTI studies.