A Unified Hydrophobicity Scale for Multi-Span Membrane Proteins

Abstract

The concept of hydrophobicity is critical to our understanding of the principles of membrane protein folding, structure, and function. In the last decades several groups have derived hydrophobicity scales using both experimental and statistical methods that are optimized to mimic certain natural phenomena as closely as possible. The present work adds to this toolset the first knowledge-based scale that unifies the characteristics of both, α-helical and β-barrel multi-span membrane proteins. This Unified Hydrophobicity Scale (UHS) distinguishes between amino acid preference for solution, transition, and trans-membrane states. The scale represents average hydrophobicity values of amino acids in folded proteins, irrespective of their secondary structure type. We furthermore present the first knowledge-based hydrophobicity scale for mammalian α-helical MPs (Mammalian Hydrophobicity Scale - MHS). Both scales are particularly useful for computational protein structure elucidation, for example as input for machine learning techniques, such as secondary structure or trans-membrane span prediction, or as reference energies for protein structure prediction or protein design. The knowledge-based UHS shows a striking similarity to a recent experimental hydrophobicity scale introduced by Hessa and co-workers. Convergence of two very different approaches onto similar hydrophobicity values consolidates the major differences between experimental and knowledge-based scales observed in earlier studies. Moreover, the UHS scale represents an accurate absolute free energy measure for folded, multi-span membrane proteins - a feature that is absent from many existing scales. The utility of the UHS was demonstrated by analyzing a series of diverse MPs. It is further shown that the UHS outperforms nine established hydrophobicity scales in predicting trans-membrane spans along the protein sequence. The accuracy of the present hydrophobicity scale profits from the doubling of the number of integral membrane proteins in the PDB over the past years. The UHS paves the way for an increased accuracy in the prediction of trans-membrane spans.

Introduction

The hydrophobicity of an amino acid is related to its transfer free energy from a polar medium (such as the cytoplasm) to an apolar medium (like a membrane). While the transfer free energy depends on the chemical nature of the two solvents, it also depends on the structural context of the amino acid residue. An obvious influence is the degree of exposure to the solvent - which functional groups of an amino acid are exposed and hence available for interaction with the solvent. In turn the transfer free energy for a single amino acid will be much different from the transfer free energy in a model peptide, which again will differ from the transfer free energy of an amino acid in the structural context of a folded protein, given the various levels of exposure to the solvent.

This picture of direct interactions between amino acid and solvent is further complicated because the transfer from one medium into another may trigger structural changes in model peptides or proteins that will affect the free energy change of an amino acid.

Given the diverse biophysical properties of membranes and their hydration in various compartments of the cell, the challenge to model these complex systems accurately in experiments, and the different structural contexts in which amino acids are transferred from one medium into another make it impossible to design a single transfer free energy scale that is optimal under all circumstances. The existence of many transfer free energy scales is a logical consequence.

An older experimental scale is that of Hopp & Woods (HW) ¹, who described a hydrophilicity scale to predict antigenic sites on proteins. Goldman, Engelman and Steitz (GES) derived a hydrophobicity scale based on energetic considerations of residues in α-helices ². Wimley & White (WW) achieved a significant step forward ^3-6 by introducing a three-state scale based on experimental hydrophobicities between water-interface and water-bilayer in model systems.

Although most hydrophobicity scales have been derived experimentally, there are also examples of knowledge-based approaches. A database of known protein structures is utilized to derive free energies from statistics using an inverse Boltzmann relation. Advantages of knowledge-based hydrophobicity scales include flexibility in the choice of the composition of the database (e.g. all folded, multi-span MPs). In turn, the reference point of the scale as well as the absolute size of the hydrophobicity values will match the chosen dataset and accurately describe the characteristics of amino acids in multi-span MPs. In contrast, an experimental scale (e.g. derived for α-helical peptides) will display a bias in absolute size of the hydrophobicity values as well as the reference point when used in the context of folded, multi-span MPs.

One of the oldest knowledge-based scales was published by Janin ⁷ who used the known X-ray structures of 22 soluble proteins and derived a scale based on burial versus solvent accessibility of residues. In 2003 Punta & Maritan (PM) ⁸ derived knowledge-based hydrophobicity scales from two databases containing 118 and 228 trans-membrane α-helices. Very recently, Senes et. al from the DeGrado laboratory derived a knowledge-based potential where the energy is dependent on the depth of the residue in the membrane bilayer ⁹.

It has been common in the past to derive consensus hydrophobicity scales that seek to combine the advantages of several approaches. The scale by Kyte & Doolittle (KD) ¹⁰ is based on a variety of experimental observations from the literature ^11-14 and uses the display method of Rose et al. ^15,16 to detect trans-membrane spans along the protein sequence. Eisenberg et al. (EW) ¹⁷ published a consensus hydrophobicity scale derived from five different scales (Nozaki & Tanford, von Heijne & Blomberg, Janin, Chothia, Wolfenden). In 1985 Guy ¹⁸ developed a scale based on statistical and experimental results of several studies ^{7,11,12,19-22}.

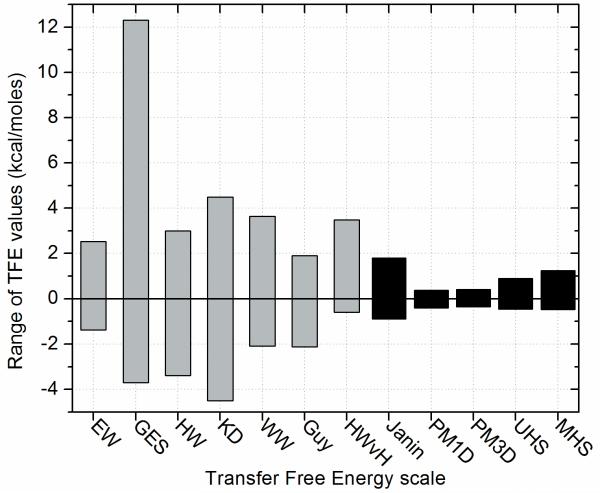
For most of the experimentally derived scales the range of hydrophobicity values is rather large in comparison to the knowledge-based ones (Figure (1)). This is expected since experimentally derived scales use mostly model peptides that form α-helices where the residue in question is exposed and other structural context is removed. These scales capture neatly the nature of the chemical interactions between apolar solvent and amino acid. In contrast, knowledge-based scales derive statistics from multi-span MPs to arrive at a hydrophobicity that might be biologically more relevant in the structural context of intact proteins. In multi-span MPs polar residues are somewhat more likely to occur in the membrane since these side chains can be buried from the interaction with the apolar membrane.

Figure (1).

The diagram shows the range of transfer free energy values in kcal/moles for the different scales (EW: Eisenberg & Weiss; GES: Goldman, Engelman, Steitz; HW: Hopp & Woods; KD: Kyte & Doolittle; WW: Wimley & White; HWvH: Hessa, White & von Heijne; PM: Punta & Maritan; UHS: Unified Hydrophobicity Scales derived here; MHS: Mammalian Hydrophobicity Scale derived here). Note, that the last five scales are knowledge-based scales and cover a much smaller range of values than any of the other scales.

To this end, a remarkable series of experiments has been carried out by Hessa et. al in the von Heijne laboratory ^23,24 leading to a ‘biological’ hydrophobicity scale for α-helical proteins. By measuring the ratio of singly vs. doubly glycosylated Lep molecules that insert into the membrane bilayer via the Sec61 translocon, a ‘biological’ hydrophobicity scale ²⁴ was derived. This study has been beautifully extended ²³ to a position-dependent free-energy scale across a 19-residue α-helix that inserts into the membrane. These experimentally derived ‘biological’ hydrophobicities match our knowledge-based ones very closely in size and distribution (see below).

Obviously, highly specialized hydrophobicity scales can be derived if assumptions regarding secondary structure (such as separation of α-helices from β-strands) or tertiary structure (such as level of exposure) are made. For instance, Beuming & Weinstein derived a knowledge-based prediction method to distinguish between the burial and exposure of certain amino acids ^25,26. Another example is the RosettaMembrane algorithm, which features a knowledge-based potential for folding of α-helical MPs ^27-29.

The objective of this work, however, is to derive a hydrophobicity scale for multi-span integral MPs with no a priori assumptions regarding secondary or tertiary structure (structural context). This scale measures the likelihood of an amino acid to reside in membrane, transition, or soluble region within a folded protein. The scale can be used as absolute reference energy for folded multi-span MPs, applied in protein structure elucidation, for example as input for machine learning techniques for the prediction of secondary structure, trans-membrane spans, or other structural features, or as reference energy for MP folding simulations or design. The scale is optimized to describe the characteristics of both α-helical proteins and β-barrels equally well. One application of the scale is the prediction of trans-membrane spans from amino acid sequence only, a method that could be applied to detect integral MPs in ORFs of newly sequenced genomes where no structural information is available, or in the early stages of a MP structure determination project. In addition, the identification of a MP or membrane spanning regions within a sequence is of particular interest in the initial phase of de novo computational tertiary structure prediction of proteins²⁷. Furthermore, we derived a specialized hydrophobicity scale from α-helical mammalian MPs only to be able to identify α-helical trans-membrane spans in the ORF of the human genome and the genome of other mammals.

To demonstrate the usefulness of these scales for such applications and to allow comparison with other hydrophobicity scales we implemented a simple version of such a prediction scheme for trans-membrane regions: The hydrophobicity values are averaged over a window of 15 residues. While we realize that this simple scheme is sub-optimal to achieve high-quality predictions in particular for β-barrel proteins, it proves efficient to benchmark these scales and compare it to other hydrophobicity scales.

Methods

Creation of the databases of non-redundant multi-span membrane proteins

Knowledge-based potentials are derived from a database of known properties and have shown to be especially suitable to describe features of proteins in structural biology (e.g., see 30 and 31). For the derivation of such potentials, the ProteinDataBank (PDB) is an invaluable resource. It contains ∼46,000 three-dimensional structures of soluble proteins and ∼850 structures of MPs (as of 02/2008), about 70% of which are multi-span MPs. Tusnady et al. compiled the PDBTM ³², a sub-database of the PDB which contains all MPs and includes additional information such as the bilayer thickness for each protein determined by the Tmdet algorithm ^33,34. In this database coordinates of symmetric domains were reconstructed from the crystallographic symmetry transformations (SYMTR) in the PDB entry and conversely coordinates of redundant atoms (from crystallization) are removed.

For the derivation of the UHS the complete list of multi-span MPs from the PDBTM was submitted to the PISCES server ^35,36 to identify proteins with low sequence similarity. The input parameters used for culling are the following: sequence percentage identity <= 25%, resolution = 0.0Å - 3.0Å, R-factor = 0.3, sequence length 40 - 10,000 amino acids. The resulting database of unique structures contained 60 MPs. Before proceeding with the analysis, all non-standard amino acids were converted into the closest standard amino acid type. Further details about the composition of this database are given in the results section. For a complete list of all proteins see Supplementary Table (I).

For deriving the MHS all MPs in the PDBTM were classified according to their host organism. The list of mammalian proteins (156 PDB entries in total) was culled with the PISCES server using the following culling parameters: sequence identity <= 25%, resolution <= 0.0Å - 3.0Å, R-factor 0.3, sequence length 40-10,000 amino acids. The resulting database consisted of 16 α-helical proteins (from cattle, human, mouse, pig, rat, rabbit, and sheep) with 12,389 residues in total. The PDB codes of these proteins are: 1afo, 1okc, 1p49, 1ppj, 1u19, 1v54, 1vry, 1wpg, 1zll, 1zoy, 2b6o, 2hac, 2hfe, 2jwa, 2uui, 2z9a. Since these proteins have large extra-membrane domains only 2,563 amino acids were located in the membrane bilayer and the remaining 9,826 belonged to the soluble phase. For the three-state scenario, 2563 residues were located in the TM, 3122 in the TR, and 6704 in the SOL. These biases were corrected by appropriate normalization procedures (see below).

Definition of membrane, transition, and soluble regions

We distinguish between two different scenarios: (a) the two-state scenario, where only the trans-membrane (TM) and soluble region (SOL) is defined and no transition region exists and (b) the three-state scenario, where trans-membrane, transition (TR) and soluble region exist. A UHS was derived for both scenarios. While the two state scenario allows for comparison with most of the published hydrophobicity scales, the three state scenario gives a more comprehensive and detailed picture of free energies and can be compared to the Wimley & White hydrophobicity scale⁵.

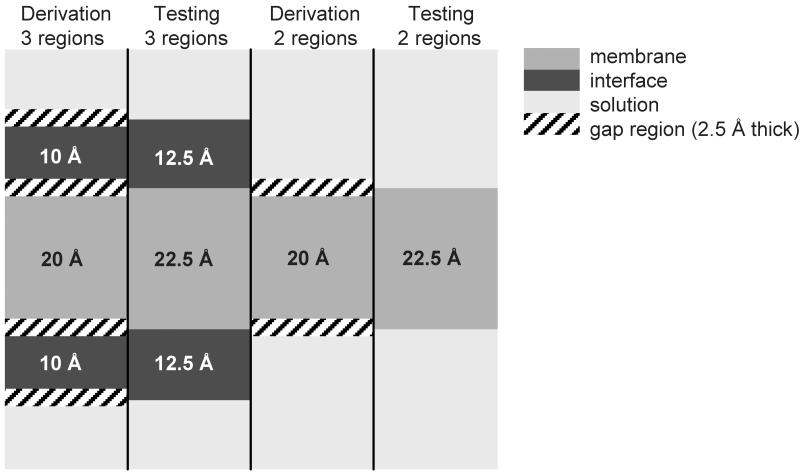
In the three-state scenario we assume a thickness of 20 Å for the TM core region ³⁷. On either side this region is flanked by a 2.5 Å buffer zone, before the TR regions begins. Its thickness is assumed with 10 Å on either side of the membrane and connects to another buffer zone of 2.5 Å. Adjacent to this second buffer zone the SOL regions starts (Figure (2)).

Figure (2).

Definition of the different regions for the derivation and the testing of the scale in the two- state- and three-state scenario. Thicknesses are indicated in black and white. The gap region of 2.5 Å thickness was introduced to more cleanly distinguish between the different regions. For the derivation the thicknesses were assumed as below. For the calculation of the agreements the derived scale was used for the prediction of TM spans from the sequence only and the prediction on a per-residue basis was compared to the ‘actual’ locations of the regions (see testing as in the figure). In the two-state scenario the interface region was added to the SOL because its characteristics are more similar to the soluble phase (due to the polar headgroups of the lipid molecules) than to the membrane interior.

In the two-state scenario the SOL and TR regions are combined and the buffer zone between them vanishes. This procedure was chosen since SOL and TR share a higher similarity when compared to their respective similarity to the TM region.

The buffer zones were added to distinguish more cleanly between the different regions and account for differences in the membrane thicknesses. We abstained from using the membrane layer thicknesses given in the PDBTM to avoid a somewhat recurrent influence of another prediction method on our results. We also found that usage of individual membrane thicknesses influenced the hydrophobicity values only marginally.

Derivation of amino acid propensities in the respective regions

To derive the free energies from the database the occurrence of each amino acid in each region was counted, which resulted in a total of 60 frequencies for the three-state scenario (20 amino acids × 3 regions) and 40 frequencies for the two-state scenario (20 amino acids × 2 regions). To eliminate a bias in the original data with respect to any region, the number of amino acids in each region was normalized to 20. Afterwards the propensity as defined by Shortle³⁸ was computed:

$$P=\frac{number(region,AA)∕number\left(region\right)}{number\left(AA\right)∕number\left(total\right)}.$$ (1)

The expected propensity for a randomly selected cell in the resulting matrix is 1, which is important for the proper definition of the reference energy (see below).

Translation of propensities into free energies

The resulting propensities P were used to derive the free energies, ΔG, for each amino acid kcal/mol using the equation

$$\Delta G=-RT\ln P$$ (2)

with R = k_BN_A (k_B being Boltzmann’s constant and N_A being Avogadro’s constant) at a temperature of T = 293 K. In the two-state scenario one can rewrite equation (2) to directly arrive at water to trans-membrane phase transfer free energies ΔΔG for each amino acid using the equation

$$\Delta \Delta G_{TM-SOL}=\Delta G_{TM}-\Delta G_{SOL}=-RT\ln \left(\frac{P_{TM}}{P_{SOL}}\right)$$ (3)

A corresponding equation applies for water to transition phase transfers.

Averaging of free energies over a sequence window of variable size for prediction

In order to obtain a prediction for a particular amino acid to be in one of the three regions (TM, TR, or SOL) the hydrophobicity values are averaged over a certain number of residues.

Two different approaches for averaging were tested: (a) all residues within the window have the same weight (rectangular weight function), and (b) the central residue has the highest weight with a linear decrease towards the edges of the window where the weight is set to zero (triangular weight function). The resulting averaged free energy was utilized to predict the state of the central residue. Predictions over a complete sequence were achieved by sliding the window over the whole sequence (Supplementary Figure (2)). Window sizes from 1 residue (no window) to 31 residues were tested. Only odd window sizes were considered to unambiguously assign a central residue.

Comparison of the hydrophobicity scales

In order to test the performance of the scale the average value of the free energies over a certain window size was calculated for SOL, TR, and TM free energies in the three-state scenario and TM, and SOL region in the two-state scenario. The amino acid in the center of the window was assigned the state that corresponds to the lowest of the average energies. Agreement for a specific region was computed as percentage of correctly predicted amino acids. The overall agreement was computed by averaging the agreements in all regions. For the assignment of the correct state the 2.5 Å buffer zones were split in half, i.e. the membrane was 22.5 Å and the TR was 12.5 Å thick with no buffer zones in between (Figure (2)).

Construction of datasets for cross-validation

To perform cross-validation and to obtain standard deviations for the free energies and transfer free energies the database was divided into subsets. For the UHS the dataset was divided into five subsets, where four sets were taken for the derivation and the performance was tested on the fifth independent set. All experiments were repeated five times with the independent test-set permuting through the five datasets. The subsets were chosen to contain approximately the same number of α-helix, β-strand, and coil residues (Supplementary Table (I)). Since the proteins vary considerably in size the numbers of proteins within the subsets fluctuate. A two-fold cross-validation was set up for the MHS as the dataset was significantly smaller with only 16 proteins.

Testing of the scale on four proteins

To test the algorithm four different example proteins from the PDBTM which were not present in the MP-database of 60 proteins, were investigated. The examples comprise the voltage-gated potassium channel KcsA (PDB code 1K4C), the chloride channel ClC (PDB code 1KPK), the Glycerol facilitator protein GlfP (PDB code 1LDI), and the outer membrane protein W OmpW (PDB code 2FIT). The examples were chosen so as to test both α-helical and β-barrel proteins. Furthermore, the α-helical proteins present difficult examples because of short or broken α-helices as in GlfP and in the selectivity filter of KcsA and the unusually large tilt angles of the α-helices in ClC.

Results and Discussion

Composition of the database of 60 non-redundant multi-span membrane proteins

The database of 60 non-redundant multi-span MPs encompasses a total of 43,523 amino acids. 31.4% of which reside in the TM region, 33.6% reside in the TR region, and 35.0% reside in the SOL region. Including the extra-membrane domains 21 proteins were purely α-helical, 5 were purely β-strand, and 34 were mixed α-helical/β-strand proteins. Around 50% of all secondary structure elements reside in extra-membrane domains. In total 977 α-helices (605 of which were TM) and 1056 β-strands (405 of which were TM) were present in the database. For a summary of these data see Supplementary Table (I). When deriving the free energy scales, amino acid counts were normalized by region to avoid a bias in the hydrophobicity values that resulted from an imbalanced database.

The two-state scale allows direct comparison with other hydrophobicity scales

Most of the hydrophobicity scales in the literature have been derived for two regions, i.e. no TR is defined (see equation (2)). Although we strongly encourage ultimate usage of a three-state scale, a two-state UHS was derived in order to facilitate comparison with other methods. All hydrophobicity values are summarized in Table (I) and the characteristics of the different scales are given in Table (II). Correlation with other hydrophobicity scales is plotted in Figure (3) and Supplementary Figure (1).

Table (I).

Values of the water-membrane transfer free energies in kcal/mol

		2-state scales														3-state scales
		experimental				consensus			knowledge-based
		HW*	GES*	WW	HWvH	EW*	KD*	Guy	Janin	PM1D	PM3D	UHS	SD	MHS	STD	WWint	UHSint	SDint
polar	C	-1.00	-2.00	-0.02	-0.13	-0.29	-2.50	-1.42	-0.90	-0.06	-0.15	0.01	0.15	0.01	0.02	-0.24	0.78	0.07
	N	0.20	4.80	0.85	2.05	0.78	3.50	0.48	0.50	0.18	0.22	0.50	0.03	0.55	0.03	0.42	-0.04	0.01
	Q	0.20	4.10	0.77	2.36	0.85	3.50	0.95	0.70	0.26	0.03	0.46	0.07	0.78	0.07	0.58	0.18	0.04
	S	0.30	-0.60	0.46	0.84	0.18	0.80	0.52	0.10	0.05	0.16	0.06	0.04	0.18	0.39	0.13	0.06	0.04
	T	-0.40	-1.20	0.25	0.52	0.05	0.70	0.07	0.20	0.02	-0.08	-0.01	0.01	-0.05	0.01	0.14	0.02	0.01
charged	D	3.00	9.20	3.64	3.49	0.90	3.50	0.78	0.60	0.37	0.41	0.73	0.05	1.10	0.26	1.23	0.13	0.04
	E	3.00	8.20	3.63	2.68	0.74	3.50	0.83	0.70	0.15	0.30	0.70	0.03	1.09	0.08	2.02	0.41	0.02
	K	3.00	8.80	2.80	2.71	1.50	3.90	1.40	1.80	0.32	0.24	0.90	0.04	1.24	0.15	0.99	0.09	0.04
	R	3.00	12.30	1.81	2.58	2.53	4.50	1.91	1.40	0.37	0.32	0.55	0.05	1.24	0.17	0.81	0.04	0.02
apolar	A	-0.50	-1.60	0.50	0.11	-0.62	-1.80	0.10	-0.30	-0.17	-0.15	-0.16	0.03	-0.24	0.01	0.17	0.02	0.02
	G	0.00	-1.00	1.15	0.74	-0.48	0.40	0.33	-0.30	0.01	0.08	-0.20	0.03	-0.10	0.06	0.01	-0.25	0.02
	I	-1.80	-3.10	-1.12	-0.60	-1.38	-4.50	-1.13	-0.70	-0.28	-0.29	-0.39	0.03	-0.43	0.01	-0.31	-0.06	0.03
	L	-1.80	-2.80	-1.25	-0.55	-1.06	-3.80	-1.18	-0.50	-0.28	-0.36	-0.30	0.03	-0.48	0.07	-0.56	-0.08	0.03
	M	-1.30	-3.40	-0.67	-0.10	-0.64	-1.90	-1.59	-0.40	-0.26	-0.19	-0.20	0.02	-0.17	0.09	-0.23	-0.12	0.06
	P	0.00	0.20	0.14	2.23	-0.12	1.60	0.73	0.30	0.13	0.15	0.50	0.04	0.50	0.11	0.45	0.07	0.03
	V	-1.50	-2.60	-0.46	-0.31	-1.08	-4.20	-1.27	-0.60	-0.17	-0.24	-0.25	0.02	-0.35	0.04	0.07	0.09	0.02
aromatic	F	-2.50	-3.70	-1.71	-0.32	-1.19	-2.80	-2.12	-0.50	-0.41	-0.22	-0.46	0.04	-0.43	0.10	-1.13	-0.36	0.02
	H	-0.50	3.00	2.33	2.06	0.40	3.20	-0.50	0.10	-0.02	0.06	0.38	0.05	0.64	0.47	0.96	-0.07	0.05
	W	-3.40	-1.90	-2.09	0.30	-0.81	0.90	-0.51	-0.30	-0.15	-0.28	-0.03	0.03	-0.06	0.01	-1.85	-0.38	0.04
	Y	-2.30	0.70	-0.71	0.68	-0.26	1.30	-0.21	0.40	-0.09	-0.03	-0.12	0.04	0.23	0.17	-0.94	0.01	0.02

HW: Hopp & Woods ¹, GES: Goldman, Engelman, Steitz ², WW: Wimley & White ⁵, HWvH: Hessa, White & von Heijne²⁴, EW: Eisenberg & Weiss ¹⁷, KD: Kyte & Doolittle ¹⁰, Guy: Guy ¹⁸, Janin: Janin ⁷, PM1D and PM3D: Punta & Maritan ⁸, UHS: the knowledge-based scale derived in this paper with its standard deviation (SD), MHS: the mammalian scale derived here with its standard deviation. The last three columns show the values for the transition between water-interface from the Wimley & White scale and the values from the UHS with its standard deviations (SD). Shaded regions are negative.

^*The values from the literature have been inverted to match the direction of transfer from water to bilayer.

Table (II).

Chart summarizing the different hydrophobicity scales and their applicability

scale	ref	year	derivation*	α/β	2-state/3-state	characteristics/applicability
Hopp & Woods	1	1981	exp	n/a	2	• hydrophilicity scale for antigenic sites on the protein surface; • derived from the values of Levitt44; • some values were adjusted to fit immunochemical data of 12 proteins; • for the proteins only the primary sequence was available!; • window used is 6 residues ≈ length of antigenic determinant
Goldman, Engelman, Steitz	2	1986	exp	α	2	• hydrophobicity scale for single trans-membrane helices; • semi-theoretical approach based on energetic considerations of residues undergoing hydrogen bonds in helices derived from experimental data in the literature; • hydrophobicity scale as a sum of hydrophilic and hydrophobic components
Wimley & White	3,4	1996	exp	α	2 + 3	• derived by measuring the partitioning energies of host-guest penta-peptides; • whole residue scale that considers the polar peptide bond; • interface: POPC vesicle interface; bilayer: n-octanol; • for unfolded peptides in all 3 phases (solution, interface, bilayer)
Hessa et al.	23,24	2005/2007	exp	α	2 / pot	• designed TM helix within the Lep protein that is inserted via the Sec61 translocon; • TM helix is 19-residue helix with amino acid in question incorporated in the center; • measured fraction of singly vs. doubly glycosylated Lep molecules to derive the scale; • therefore applicable to folded MPs; • scale has been extended to position-dependent free energy scale (2007)
Eisenberg & Weiss	45	1982	cons	n/a	2	• normalized consensus scale of five different scales
Kyte & Doolittle	10	1982	cons	n/a	2	• normalized consensus scale based on experimental observations of different scales; • refinement by studying hydropathy plots of proteins of known X-ray structure;
Guy	18	1985	cons	n/a	2	• based on experimental and statistical results from several studies; • considers solvent accessibility according to accessible layers of amino acids in globular proteins
Janin	7	1979	KB	n/a	2	• derived from X-ray structures of 22 soluble proteins; • looked at molar fraction of buried and accessible residues
Punta & Maritan	8	2003	KB	α	2	• derived two membrane propensity scales from two TM helix databases using a simple perceptron algorithm; • databases contained 118/228 TM helices; • sequence identity of the proteins was 30%
Beuming & Weinstein	25	2004	KB	α	n/a	• calculated surface propensities of amino acids (probability of finding a residue on the surface of a TM protein); • based on surface fractions of residues; • considered 28 α-helical MPs
Senes et al.	9	2007	KB	α	2 / pot	• calculated membrane depth-dependent potential for amino acid side-chains; • considered 24 α-helical MPs
UHS		2008	KB	α/β	2 + 3	• derived from 60 known structures of folded MPs; • considers folded structures both in solution and membrane bilayer; • both α, β, and α/β structures were taken into account with approximately equal distribution of helices and strands; • considers only depth in membrane bilayer and no accessibility or secondary structure
MHS		2008	KB	α	2 + 3	• derived from 16 known structures of folded MPs from mammalian organisms; • only α-helical structures could be taken into account; • considers folded structures both in solution and membrane bilayer; • considers only depth in membrane bilayer and no accessibility or secondary structure

^*exp: experimental; cons: consensus; KB: knowledge-based; pot: potential

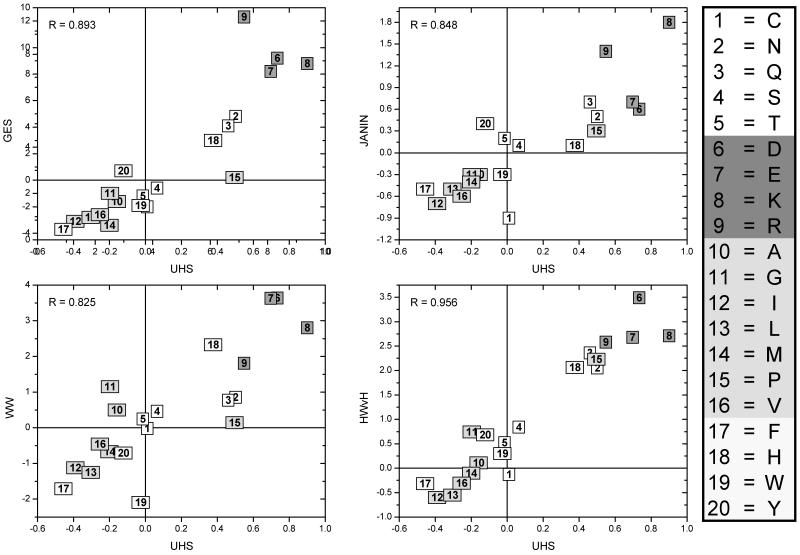
Figure (3).

Plots showing the correlation between the UHS and the scales from GES, Janin, WW, and HWvH. The correlation coefficients are shown in the upper left corner of the plots. The amino acids are numbered according to the numbering scheme on the right and colored according to their class: white = polar, red = charged, green = apolar, yellow = aromatic. The highest correlation coefficient is seen for the scale of HWvH (Hessa, White & von Heijne) with a correlation coefficient of 0.956.

Three-state scale demonstrates the preference of Trp for interface region

Table (III) shows the free energy values in kcal/mol for all 20 amino acids and for all three regions (TM, TR, SOL). As for the two-state scenario, Cys has a large standard deviation for TM (0.09) and SOL (0.06) and its large value within TR indicates that it does not prefer to be in the TR. Ser and Thr have almost no preference for any of the three regions (Ser: TM = 0.02, TR = 0.02, SOL = -0.04; Thr: TM = -0.01, TR = 0.02, SOL = 0.00), which agrees with the findings of Senes ⁹ and Hessa ²³. The fact that Trp is often found in the TR ^9,39-41 is confirmed by our results. It has been previously noted that Tyr also has a preference for the interface between TM and TR region. However, this preference of Tyr for the interface region is less distinct when compared to Trp ^9,23. In the UHS Tyr shows a slight preference for residing within the TM region which could be a result of a slightly larger membrane thickness in our definition when compared to other scales ²³. Further, we find strong preferences for Ile, Phe, Leu, Val, and Met to be in the TM region and for Glu, Lys, Cys, Asp, and Gln to be in the SOL region.

Table (III).

Free energy values of the UHS and MHS in kcal/mol

		UHS						MHS
		TM ± SD		TR ± SD		SOL ± SD		TM ± SD		TR ± SD		SOL ± SD
polar	C	-0.07	0.09	0.56	0.03	-0.22	0.06	-0.01	0.01	0.14	0.14	-0.09	0.10
	N	0.37	0.03	-0.14	0.01	-0.10	0.01	0.41	0.04	-0.15	0.03	-0.12	0.04
	Q	0.31	0.05	-0.01	0.03	-0.19	0.03	0.60	0.09	-0.13	0.07	-0.19	0.04
	S	0.02	0.03	0.02	0.03	-0.04	0.02	0.13	0.28	-0.01	0.07	-0.06	0.14
	T	-0.01	0.01	0.02	0.01	0.00	0.01	-0.02	0.01	-0.04	0.04	0.06	0.04
charged	D	0.52	0.04	-0.08	0.03	-0.21	0.02	0.82	0.28	0.05	0.18	-0.34	0.05
	E	0.47	0.02	0.10	0.02	-0.31	0.01	0.84	0.05	0.06	0.10	-0.36	0.04
	K	0.69	0.03	-0.13	0.03	-0.22	0.03	0.99	0.15	-0.08	0.03	-0.30	0.04
	R	0.40	0.04	-0.11	0.02	-0.15	0.01	1.06	0.13	-0.22	0.08	-0.18	0.10
apolar	A	-0.10	0.02	0.07	0.02	0.05	0.01	-0.15	0.01	0.12	0.02	0.07	0.01
	G	-0.09	0.02	-0.06	0.01	0.19	0.02	-0.07	0.03	0.05	0.03	0.03	0.06
	I	-0.22	0.02	0.12	0.02	0.18	0.02	-0.24	0.01	0.13	0.08	0.23	0.07
	L	-0.16	0.01	0.06	0.02	0.14	0.02	-0.26	0.03	0.15	0.07	0.24	0.00
	M	-0.12	0.03	0.01	0.05	0.13	0.04	-0.07	0.04	-0.06	0.02	0.16	0.02
	P	0.34	0.04	-0.08	0.02	-0.15	0.02	0.36	0.07	-0.09	0.07	-0.14	0.09
	V	-0.16	0.01	0.15	0.02	0.06	0.01	-0.22	0.03	0.22	0.05	0.09	0.01
aromatic	F	-0.19	0.02	-0.02	0.02	0.34	0.01	-0.22	0.05	0.00	0.01	0.35	0.11
	H	0.29	0.03	-0.14	0.03	-0.07	0.04	0.55	0.41	-0.28	0.03	0.03	0.12
	W	0.08	0.02	-0.19	0.02	0.19	0.03	0.07	0.11	-0.24	0.15	0.36	0.24
	Y	-0.07	0.02	0.04	0.01	0.03	0.02	0.20	0.09	-0.13	0.04	-0.02	0.12

The table shows the knowledge-based values for the free energies in kcal/mol and their corresponding standard deviations (SD) for the 20 amino acids in the three regions of the membrane bilayer (TM), the transition region (TR) and the soluble region (SOL) for both scales, the UHS and the MHS. The shaded cells indicate the preference of the amino acid for that region. Note that Serine and Threonine in the UHS show almost no preference for any of the three regions.

The absence of structural context leads to less distinct free energy values relevant for multi-span membrane proteins

It can be seen from Table (I) and Figure (1) that the values of knowledge-based hydrophobicity scales are in general not as pronounced as in scales that were derived experimentally. This observation holds for the newly derived hydrophobicities: for example, while the GES scale ranges from -3.70 (Phe) to 12.30 (Arg), the Wimley & White scale from -2.09 (Trp) to 3.64 (Asp), the Hessa, White & von Heijne ranges from -0.60 (Ile) to 3.49 (Asp), the values in the UHS derived here range only from -0.46 (Phe) to 0.90 (Lys). However, the correlation diagrams indicate that despite the deviation in absolute values the scales agree very well in general trends with correlation coefficients between R=0.804 and R = 0.956. The UHS has higher correlation coefficients to knowledge-based scales such as PM1D and PM3D, and surprisingly, the highest correlation coefficient (R = 0.956) is found for the Hessa, White & von Heijne scale, the most recent experimental scale considered (see below).

By disregarding structural context such as the level of exposure when deriving the scale the absolute size of the free energies derived is reduced. This originates in the MP database used for derivation containing only multi-span MPs. These proteins have both hydrophobic cores and active polar sites within the TM shielded from direct contact with the membrane lipids, as f.ex. in ion channel proteins. Similarly, the extra-membrane domains of these proteins also have both hydrophobic cores and polar active sites shielded from direct interaction with the solvent. This reduces the absolute size of the free energies obtained. This has to be compared to e.g. an experimental scale that was observed for model peptides forming single α-helices within the membrane exposing their amino acid side chains almost completely to the lipid and having no extra-membrane domains with hydrophobic interior.

When compared to all the other tested experimental scales, the ‘biological’ transfer free energies from Hessa et al.²⁴ match the knowledge-based ones very closely in size and distribution. The scale yields the highest correlation coefficient of R = 0.956 to the UHS (compare Figure (3) and Supplementary Figure (1)). The reason for the smaller range is the measurements on an intact protein (E. coli leader peptidase) consisting of three TM segments where the structural context for the residue in question is maintained.

Hessa’s study was extended to a position-dependent free energy scale derived from 324 (!) constructs²³. The authors compared their hydrophobicity scale to a statistical distribution derived from known structures of MPs which showed the same trends as their experimentally derived potentials. We do not directly compare this scale to the three-state UHS, because according to our definition of TM and TR thicknesses (see above), 19-residue α-helices would be too short to reach completely into solution and hence only TR and TM could have been compared to the UHS. Furthermore, to obtain single values for the regions, the free energies would have to be averaged over a whole range, which removes information from the scale.

Triangular window function of 15 residues used for predicting trans-membrane spans

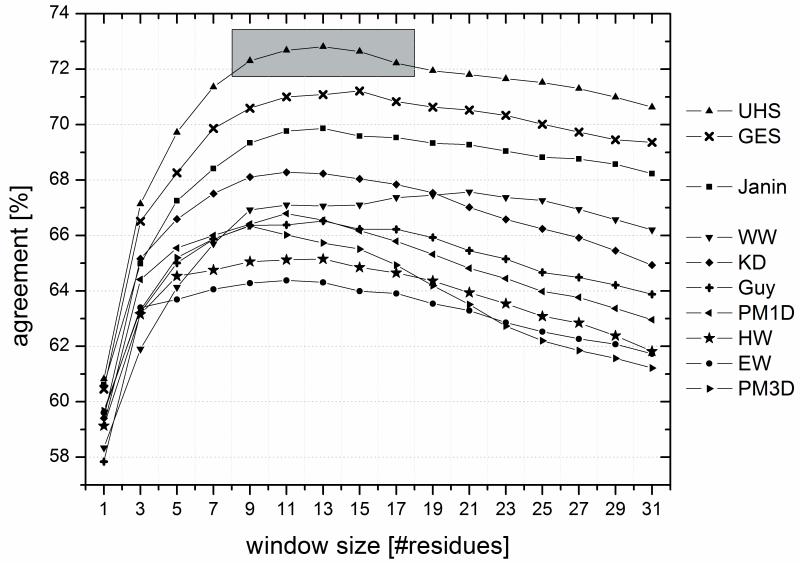
In order to test the usefulness of the derived UHS it was applied towards predicting the state of an amino acid (TM, TR, or SOL) from primary sequence only. To achieve increased prediction accuracies the hydrophobicities were averaged over a sequence window. This procedure allows for identification of spans of similar dielectric environments along the protein sequence.

Preliminary prediction trials have shown that the triangular window function performed better than the rectangular window. Since hydrophobicity is a local measure and therefore depends more on neighboring residues than on residues further away, this result is expected. In addition, these preliminary trials showed that the prediction accuracy in the two-state scenario (distinguishing TM from SOL region) is dependent on the window size as can be seen in Figure (4). Note, that there is a plateau range between 9 and 17 residues where all scales gave consistently good results. Therefore, for all further experiments we chose a window size of 15 residues. This number agrees with the average length of an α-helix spanning the core region of the membrane (15 residues × 1.5Å rise = 22.5Å membrane thickness).

Figure (4).

For predicting trans-membrane spans from the sequence, the hydrophobicity values have to be averaged over a certain number of residues (“window”). The percent per-amino acid agreements between prediction and known location of the residues were computed as a function of window size for the scales from the literature (EW: Eisenberg & Weiss ¹⁷, GES: Goldman, Engelman, Steitz ², HW: Hopp & Woods ¹, KD: Kyte & Doolittle ¹⁰, WW: Wimley & White ⁵, Guy: Guy ¹⁸, Janin: Janin ⁷, PM1D and PM3D: Punta & Maritan ⁸) and for the Unified Hydrophobicity Scale (UHS). The shaded region indicates a range of window lengths for the UHS, which all yield similarly good performance. The best performance is seen for the UHS scale and the scale from GES.

Two-state scenario: UHS achieves 72.6% correct classifications

Table (IV) displays the percentages of agreement for the TM and SOL with their average value. The scales of EW, HW, PM3D, PM1D, and Guy display a bias towards predicting an amino acid within the TM (>80% agreement) but poorly agree in the SOL (<50% agreement). Conversely, the scales of WW and HWvH bias towards the SOL (87% and 99%) with a lower performance in the TM (48% and 11%). These biases are indicative of offsets in the absolute TFE values when applied to intact multi-span MPs and may not exist in other applications. This is not unexpected given that the reference point for every experimental scale is imposed by the experimental setup. For example, the bias in the WW scale originates from the fact that the scale was derived for unfolded peptides in both solution and membrane bilayer.

Table (IV).

Per amino acid agreements for the two-state scenario

		PDB				PDB
			TM	SOL	avg		TM	SOL	avg
pred		UHS				Guy
	TM		70 ± 10	25 ± 7			81	49
	SOL		30 ± 10	75 ± 7			19	51
					73 ± 2				66
pred		GES				PM1D
	TM		66	23			86	53
	SOL		34	77			14	47
					71				66
pred		Janin				PM3D
	TM		72	32			83	52
	SOL		28	67			17	48
					70				66
pred		KD				HW
	TM		76	39			89	59
	SOL		24	61			11	41
					68				65
pred		WW				EW
	TM		48	13			88	60
	SOL		52	87			12	40
					67				64
pred		HWvH
	TM		11	1
	SOL		89	99
					55

The table shows the percentage per amino acid agreements for the two-state scenario between the prediction and the PDB for the hydrophobicity scales from the literature and the UHS. (TM) membrane bilayer; (SOL) soluble phase (SOL); (avg) average value of agreement between TM and SOL. The values are computed for a window size of 15 residues for averaging. The first four scales on the left show similar performances for the TM and the SOL, whereas the other scales exhibit an uneven distribution.

The other scales predict amino acids in an approximately balanced distribution (KD_TM = 76%, KD_SOL = 61%; Janin_TM = 72%, Janin_SOL = 67%; GES_TM = 66%, GES_SOL = 77%; KB_TM = 70%, KB_SOL = 75%). While the good performance of our UHS scale is remarkable considering the simple approach it was derived with, it should be acknowledged that particularly good performance is expected in this experiment since the scale was derived with particular focus on such applications.

Even though the improvement of UHS above the GES scale is small in the two-state scenario, this translates into a significant improvement when the accuracy of detecting full-length TM spans from the sequence is analyzed. Here the UHS identifies 81.1% of the TM spans, the GES scale identifies 76.6%, and the WW scale identifies 59.9%.

False positive rate on soluble proteins is comparable to GES scale

To assess the over-prediction of regions in soluble proteins as as being in the TM region the scale was tested on a non-redundant set of soluble proteins (<25% sequence identity). This set was created by culling the PDB with the PISCES server with the same culling parameters as for the MHS and UHS (see Methods section). The database comprised 2,569 proteins with 3,538 chains and 526,422 amino acids.

Detailed results can be found in Supplementary Table (II). The scales of Hessa et al. and of Wimley & White predict amino acids as being in the SOL more than 95% of the time and hence have a corresponding false positive rate for prediction TM spans of smaller than 5%. This originates in the tendency of these scales to over-predict amino acids as being in the SOL. In result both scales have a significantly reduced accuracy in the TM (compare Table (IV)). The scales of GES, Janin, KD, and the UHS have (according to Table (IV)) an approximately balanced distribution between SOL and TM and have a high agreement in SOL with a small number of false positives. Among these four scales, the UHS performs comparably well to the GES with an accuracy of ∼86% in solution and ∼14% over-prediction. Both scales are significantly better that the scales of Janin or KD in this experiment. The remaining scales (Punta & Maritan, Guy, Hopp & Woods, Eisenberg & Weiss) have a lower agreement in the SOL coupled with an increased rate of false positives caused by the tendency of these scales towards over-predicting amino acids as being in the TM.

The over-prediction of amino acids in soluble proteins as being in the TM region is reduced by about 10% when compared to the SOL of MPs (Supplementary Table (II, IV)). In MPs many residues close to the membrane surface are counted as soluble in the two-state scenario. These residues are difficult to be accurately predicted as they often interact with the membrane surface and not only with the solvent. Further, the window for averaging will include some membrane amino acids for these residues. The absence of such difficult residues improves the prediction accuracy when looking at soluble proteins.

Comparison of UHS and GES for individual amino acids

Supplementary Figures (3) and (4) summarize the results for individual amino acids for the two-state scenario in comparison to the Goldman, Engelman, Steitz (GES) scale, which gave, according to Figure (4), for this experiment the best results besides the UHS. Both scales over-predict the polar amino acids Arg, Asn, Asp, Glu, Gln, and Lys in the SOL region. For the UHS the average agreements are higher for the polar residues Arg, Asp, Glu, and Lys.

Comparing the GES scale with the UHS, the average agreements have increased most for Arg (51% to 58%), Cys (72% to 78%), and Glu (58% to 62%). Note that the average agreement in the UHS is lower than in the GES scale only for His (72% to 69%). This indicates a slightly better representation of polar residues in the present UHS.

Three-state scenario: UHS displays agreement of 57.1%

As discussed earlier, one strength of the UHS scale is that in contrast to many existing methods it distinguishes three regions. Only one of the nine scales used for comparison was derived with a TR region. Hence, comparison for the three-state scenario is limited to the Wimley & White (WW) scale. The data are summarized in Table (V). For classifying an amino acid correctly in one of the three regions TM, TR, SOL the UHS scale achieves 57.1% as compared to 49.8% obtained for the WW scale. For the UHS the agreements for the different regions are relatively balanced (TM = 63.2%, TR = 43.8%, SOL = 64.4%). As already observed for the two-state scenario, the WW scale is biased in its prediction towards the SOL with an agreement of 89.1%. However, the agreement drops to 24.4% for the TR and 35.9% in the TM. Again, we wish to emphasize that these biases result from a different experimental setup and occur when applied to intact multi-span MPs, and may not exist in other applications.

Table (V).

Per amino acid agreements for the three-state scenario

			TM	TR	SOL	avg
pred		UHS
	TM		63 ± 11	29 ± 10	9 ± 6
	TR		23 ± 7	44 ± 3	26 ± 4
	SOL		13 ± 6	27 ± 9	64 ± 8
						57 ± 3
pred		WW
	TM		36	14	2
	TR		29	24	9
	SOL		35	62	89
						50
pred		MHS
	TM		71 ± 1	17 ± 4	5 ± 2
	TR		19 ± 3	48 ± 1	30 ± 4
	SOL		10 ± 2	35 ± 2	65 ± 2
						61 ± 0

The table shows the percentage per amino acid agreements between the prediction and the PDB for the different regions for the UHS (with its standard deviation) in comparison to the Wimley & White scale. The performance of the MHS is also shown. The window size for averaging is 15 residues and (TM) represents the trans-membrane, (TR) the transition and (SOL) the soluble region. The percentages were calculated by dividing the correctly predicted number of amino acids by the total number of amino acids in that region. An average agreement (avg) was calculated by averaging the percentages of agreement for the diagonal elements of the matrix. While the average prediction agreement seems to be relatively low, note that there are three regions defined, so that the threshold between a good and a bad percentage of agreement would be 33% and not 50% as in the two-state system. For the Wimley & White scale both the octanol and the interface scale were used to establish a scale for three regions. The standard deviations for the UHS and MHS arise from cross-validation, whereas the scale of WW was tested on the whole dataset without cross-validation.

Supplementary Figures (3) and (4) illustrate the individual amino acid agreements for the three-state scenario in comparison to the Wimley & White scale. As in the two-state scenario, the polar residues Arg, Asn, Asp, Glu, Gln, His, Lys, and Ser are predicted in a more balanced manner in the UHS than in the WW scale. When comparing the overall prediction accuracies, all amino acids either display an improvement or at least a similar accuracy for the UHS. Highest changes are observed for Asp and Glu (from 36% to 47%), Asn (from 41% to 50%), and His (from 44% to 53%).

It should be noted that the Wimley & White scale was derived for unfolded peptides in all three phases (solution, interface, and membrane bilayer). In contrast to folded secondary structure elements or domains where most backbone amide and carbonyl groups are undergoing hydrogen bonds, unfolded peptides can only engage in hydrogen bonds with polar solvents such as water, not with hydrophobic solvents or the membrane core. This fact offsets the WW scale towards a preference of the SOL region which explains the over-prediction for that region. Obviously, the Wimley & White scale was not derived for the current application of predicting TM spans from the sequence only, ^3-5,42 and is an exceptional scale in its own right. We focus on its performance since it is the only available scale for three-state scenario we can use for comparison. The lack of suitable scales for the present application presents another justification for the development of the UHS.

The UHS enables prediction of TM spans from sequence only

We realize that different and more specialized hydrophobicity scales can be derived if assumptions on secondary structure (like separation of α-helices from β-strands) or tertiary structure (like level of exposure) were made. On purpose, such assumptions were forgone to make the hydrophobicity scale applicable in the absence of any structural information about the sequence of interest.

We also abstained from use of secondary structure prediction techniques since their accuracy is limited and most of these tools are highly specialized. However, we appreciate that the incorporation of secondary structure (e.g. the separate prediction for α-helices and β-strands) and/or the exposure of an amino acid is likely to be superior to the presented scale for certain applications.

The UHS is largely independent of the protein fold

To date, only a small fraction of the proteins stored in the PDB are MPs and only about 60 MP folds are known. When deriving a knowledge-based scale from such a limited database, the question arises whether this scale is applicable to the MP universe whose folds have not been elucidated yet. The scale could for example have a compositional bias of certain amino acid types due to the under-representation of distinct folds in the database.

While we believe that such a bias is unavoidable given the very limited number of MP structures known, we argue that it is small as the hydrophobicity of an amino acid is governed by more general rules of MP fold formations such as α-helix/α-helix packing or β-barrel formation. We tested this hypothesis by excluding folds one by one when deriving the UHS scale and analyzing the effects on the hydrophobicity values. Note that for some MP folds multiple representatives are found in the database of 60 proteins, as it was culled purely by sequence and not by fold identity. Further we tested the prediction accuracies of these “leave-one-fold-out” UHS scales on the excluded folds. The details of this experiment are included in the supplementary data section. Briefly, we find the hydrophobicity values robust with respect to exclusion of a single fold (changes in hydrophobicity values are on average well below one standard deviation) and the prediction accuracy for TM and SOL regions is within 2.4% to the one observed with the UHS scale.

Applications of the scale

The UHS is optimized for usage as reference hydrophobicity values in computational protein structure prediction of α-helical and β-strand multi-span MPs. The scale fills a gap since most existing scales were optimized for usage with α-helical MPs only and distinguish only two states (TM and SOL). Furthermore, it can be used for the prediction of trans-membrane spans from genomic data (see below), in the early stages of a MP structure determination project when no structural information is available, or to assess the overall and local stability of folded multi-span MPs. To exemplify the latter, the UHS values for Trp, Tyr, and Phe were compared to Lukas Tamm’s thermodynamic free energy changes (see Table 1 in ⁴³) by measuring the unfolding of wt OmpA and OmpA mutants as described in ⁴³. The correlation coefficients are 0.715 for the single mutants, and 0.759 for the double mutants, excluding one outlier Y168A. No extensive conclusions can be drawn from the moderate agreement with these 11 data points for three amino acids, however, we believe that this possible application of the UHS warrants further investigation.

A hydrophobicity scale for mammalian α-helical membrane proteins

Since the amino acid occurrences are variable among organisms and there is interest in applying hydrophobicity scales to ORFs of mammalian genomes (specifically the human genome), a hydrophobicity scale was derived only from mammalian proteins. A database of 16 mammalian MPs was created as described in the Methods section and a mammalian scale (Mammalian Hydrophobicity Scale - MHS) was derived using two-fold cross-validation. The MHS was established for the two- and three-state scenario. The scale will be most applicable to α-helical proteins since the database used for derivation contained exclusively multi-span α-helical MPs. The hydrophobicity values and their standard deviations are given in Tables (I) and (III). The standard deviations are somewhat larger for the MHS when compared to the UHS because of the smaller dataset and the only two-fold cross-validation.

Overall amino acid abundance is quite similar between bacterial and mammalian MPs (data not shown) with an average difference of 0.18 when the amino acid abundances for all amino acids are normalized to 20. Ala, Asn, and Gly are somewhat more abundant in the bacterial dataset with differences of 0.32, 0.25, and 0.60 respectively, whereas Leu and Pro are more abundant in the mammalian dataset (-0.32 and -0.26). Furthermore, comparing the distribution between TM and SOL, it was found that Arg, Gly, Phe, and Tyr tend to be more abundant in the TM in the bacterial dataset than in the mammalian dataset. The differences for these amino acids are 0.29, 0.29, 0.26, and 0.50 when the occurrence for each amino acid is normalized to 2.

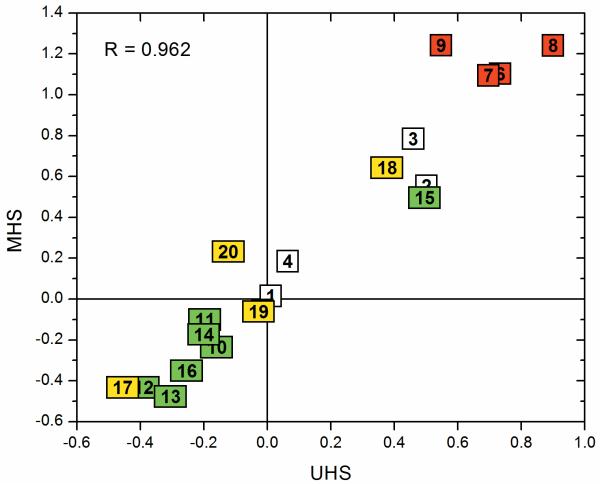
Overall UHS and MHS are similar with deviations of 1.3 standard deviations on average and 3.8 standard deviations at maximum for Glu. Even though these seem to be relatively large changes, the change in actual numbers remains small, because of the small standard deviations for the UHS. A correlation plot of the two scales is shown in Figure (5) with a correlation coefficient of 0.962.

Figure (5).

Correlation plot for the hydrophobicity values in kcal/mol between the Unified Hydrophobicity Scale and the Mammalian Hydrophobicity Scale with the amino acids being numbered and colored according to the scheme in Figure (3).

Comparison of the hydrophobicity values from the UHS with the MHS reveals that the largest deviations occur for Arg (UHS: 0.55 / MHS: 1.24), Asp (0.73 / 1.10), Glu (0.70 / 1.10), Leu (-0.30 / -0.48), Lys (0.90 / 1.24), and Tyr (-0.12 / 0.23). A test of the prediction accuracy of the MHS is available in Table (V) and in the supplement (Supplementary Table (V)). Briefly, the scale achieves an average prediction accuracy of 83.1% in the two-state scenario (see Supplementary Table (V)) and 61% in the three-state scenario (see Table (V)).

It is important to note, that although this is the first mammalian hydrophobicity scale ever derived, care has to be taken in its application. The dataset used for its derivation is with only 16 MPs very small and does not guarantee very accurate hydrophobicity values. A refinement of the scale is to be expected when more MPs structures are elucidated. Nevertheless, we hope the MHS will find widespread application in the scientific community.

Four examples show that the UHS accurately reflects the character of α-helical and β-barrel MPs

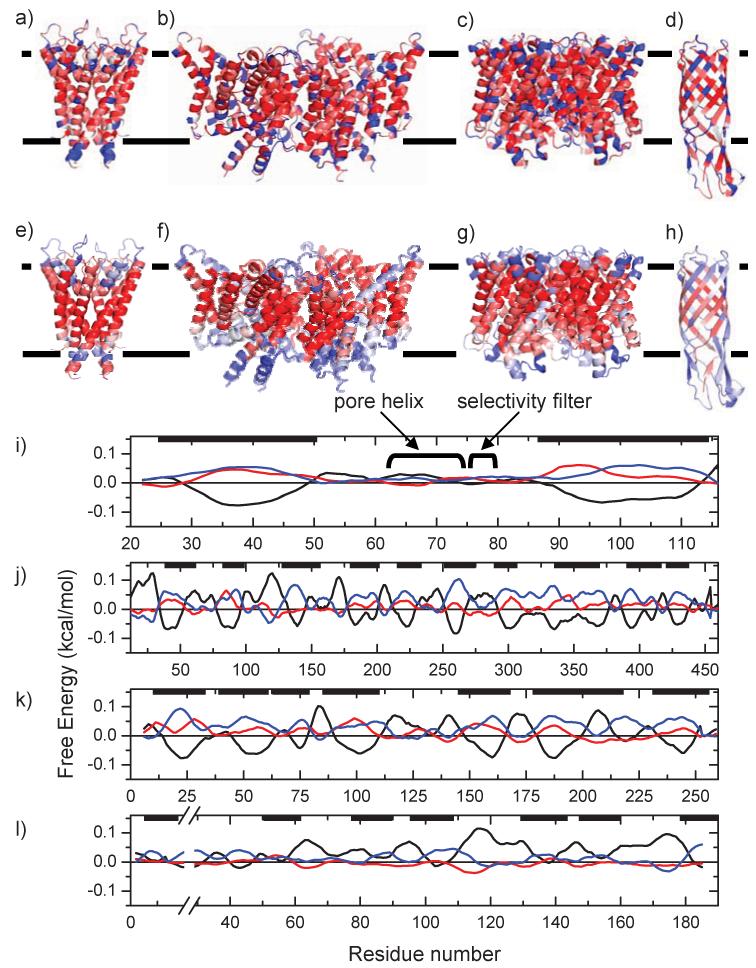
Four proteins not present in the MP database (used for derivation of the UHS) were used as examples to demonstrate the usefulness of the UHS and the prediction algorithm. The hydrophobicity values of the UHS for all residues in the sequence were mapped onto the known crystal structures in Figure 6a) to d). In Figure 6e) to h) the average free energy values were mapped onto the same crystal structures to illustrate the prediction of TM, TR, and SOL regions. Panels i) to l) in Figure 6 show the predicted free energies averaged over a window length of 15 residues (compare to panels e) to h)) vs. the residue number.

Figure (6).

The derived UHS has been used to calculate the free energies (with a window length of 15 residues) for four examples: a), e) and i) KcsA - potassium channel (PDB code 1K4C), b), f) and j) ClC - chloride channel (PDB code 1KPK), c), g) and k) GlfP - Glycerol facilitator protein (PDB code 1LDI), and d), h) and l) OmpW - outer membrane protein W (PDB code 2F1T). The upper panels a) to d) show the three-state predictions from the sequence without any averaging procedure mapped onto the known crystal structure. The central panels e) to h) display the predictions for a window length of 15 residues. Dark blue indicates a prediction for the aqueous phase, white indicates interface, and dark red indicates a prediction for the TM. Lighter colors refer to a lower confidence in the prediction (as seen by smaller differences between the lowest and second lowest free energy in the bottom panels of the figure). The location of the membrane is displayed by the black lines. The lower panels i) to l) show the predictions of the free energies vs. the residue number as in panels e) to h) (black is TM, red is TR, and blue is SOL). Membrane locations are indicated by the black bars at the top. Panel i) shows one of four identical chains, j) shows one of two chains (chain A), k) shows one of four identical chains, and l) shows the whole protein sequence.

UHS distinguishes core TM α-helices from functional sites in potassium channel KscA

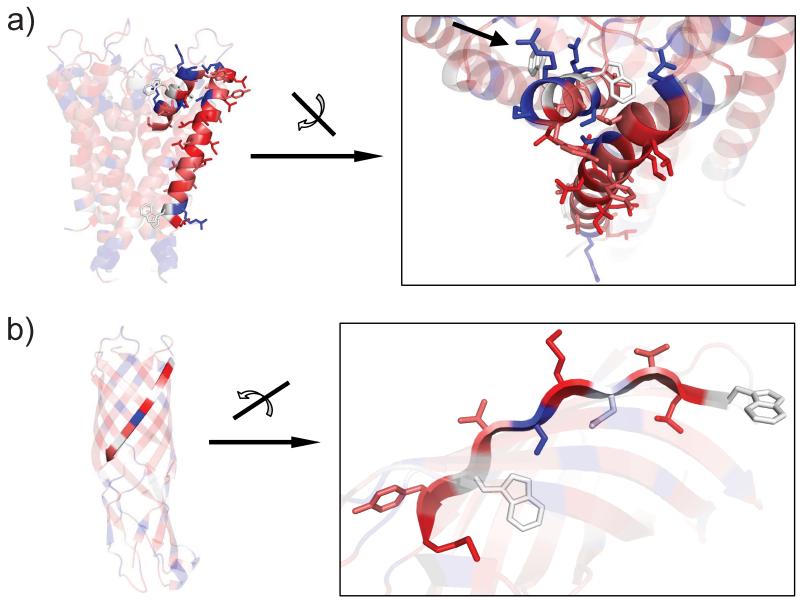
The first example (Figure 6a), e) and i)) is the crystal structure of the potassium channel KscA which was determined by Roderick McKinnon et al. at a resolution of 2.0 Å (PDB code 1K4C). This example demonstrates the ability of the UHS to distinguish a typical hydrophobic, membrane-spanning α-helix from a functional site such as the pore α-helix and the selectivity filter. The pore α-helix is too short to even reach the center of the bilayer and the attached loop region returns to the extra-cellular side. This region is rich in polar amino acids as it is exposed to the SOL and has no direct contact to the membrane. The UHS clearly identifies the pore α-helix as an amphiphilic helix (short helix on the top of Figure (7a)) where the polar side-chains point to the aqueous cavity (arrow) and the apolar side-chains are in contact with other hydrophobic α-helices. This compares to a fully hydrophobic α-helix (long helix at the bottom) where all non-polar side-chains interact with the hydrophobic environment. It illustrates that the UHS is well able to identify the structural context of the individual residues even though no structural information is used in its derivation.

Figure (7).

Close-ups of Figure (6) a) and d). The figure demonstates the ability of the UHS to correctly identify the structural context of the amino acids within a functional protein. Figure (7a) displays the prediction for the pore helix of the KcsA potassium channel (short helix on the top). Figure (7b) demonstrates that the UHS is clearly able to distinguish the different hydrophobicities of the side-chains in the β-barrel. More details are given in the Results and Discussion section.

The prediction algorithm is clearly able to distinguish the membrane region from the sequence only. Figure (6i) demonstrates that the TMs are perfectly identified with a very high confidence and with their approximate lengths. However, the pore helix and selectivity filter of the protein have a small preference for the SOL region, which is indicated by the light blue α-helices at the top of the molecule (6e). This is not surprising because - as detailed above - both structural features are not in contact with the membrane at all but form a polar pore filled with water and ions (see Figure (7a)).

Chloride channel ClC

The second example (Figure 6b), f) and j)) is the crystal structure of the chloride channel ClC determined by Roderick McKinnon and co-workers at a resolution of 3.5 Å (PDB code 1KPK). In this case all TM α-helices are reliably identified and the predicted membrane locations agree well with the actual ones. However, the lengths deviate from the predicted spans slightly more than in the first example.

Glycerol facilitator protein GlfP

The third example (Figure 6c), g) and k)) is the crystal structure of the glycerol facilitator protein GlfP determined by Robert Stroud et al. at a resolution of 2.7 Å (PDB code 1LDI). Generally, the UHS is able to identify polar residues within the trans-membrane domains of the protein which mostly face the interior of the protein and are therefore protected from the hydrophobic environment of the membrane bilayer. The α-helix at residues 204-217 is a short helix dipping into the membrane and the attached loop residues return to the same side of the membrane. The UHS clearly identifies this short α-helix as an amphiphilic helix where the polar side of this short helix faces inwards into one of the four channels of the homo-tetramer. Again, this shows the capability of the UHS to distinguish between regular, fully hydrophobic trans-membrane α-helices and functional sites in the protein.

Figure (6k) shows that the TM α-helices are correctly identified with a high reliability. The lengths of the α-helices agree well with the actual lengths except for the one α-helix at residue numbers 175-215 which is predicted to be too short. As discussed, under-prediction is unsurprising due to the amphiphilicity of this short α-helix that faces one of the pores of the channel. In Figure (6g) this α-helix is the light blue helix on the lower left side of the protein.

The UHS identifies alternative hydrophobicity pattern in the β-barrel of the outer membrane protein W

The fourth example (Figure 6d), h) and l)) is a β-barrel protein which is the crystal structure of the outer membrane protein W (OmpW) determined by van den Berg and Tamm et al. at a resolution of 3.0 Å (PDB code 2F1T). Figure (7b) shows that the UHS correctly identifies the polarity of the side-chains pointing to the aqueous interior of the β-barrel whereas apolar side-chains face the hydrophobic milieu of the membrane bilayer. It can be seen, that consecutive side-chains along the β-strand alternately face the polar interior and apolar membrane environment. These patterns are nicely detected by the UHS (Figure (6d)). This demonstrates the efficiency of the UHS to depict structural features of the amino acids although no structural information is required for the application of the UHS.

Figure (6) h) and l) show, that for β-barrels the prediction has lower confidence and only some of the TM spans are identified. However, this behavior is expected because this simple window function is insufficient to reliably identify trans-membrane spans if an alternating pattern of hydrophobicity values complicates the prediction, as is the case for β-barrel proteins. To optimize the prediction accuracies for β-barrels, we plan to utilize the UHS as an input for an artificial neural network or a hidden Markov model in the future.

In summary these four examples illustrate the ability of the UHS scale to accurately reflect the hydrophobicity of a certain residue within a folded protein. In particular the scale distinguishes nicely between the core of the protein and functional sites and highlights the alternating hydrophobicity pattern seen in β-barrel proteins. The scale is therefore suitable as input for MP secondary and tertiary structure prediction tools. This was demonstrated by usage of the UHS for prediction of TM spans from sequence only. Although the prediction accuracies are somewhat lower for β-barrel proteins when using such a simple averaging scheme, they are better than random (60% average prediction accuracy in the two-state scenario and 45% in the three-state scenario). For α-helical bundles the prediction accuracy increases up to 77% in the two-state scenario and even 66% in the three-state scenario (compared to 33% for a random prediction).

Conclusions

In this paper we derive a three-state Unified Hydrophobicity Scale (UHS) exclusively from multi-span membrane proteins of known structure. The database of membrane proteins contained both α-helical and β-barrel proteins. The absolute hydrophobicity values in the UHS range between -0.46 for Phe and 0.90 for Lys. This reduced amplitude when compared to most experimentally derived scales was previously observed for other knowledge-based scales and results from averaging over a wide variety of structural contexts, in particular different degrees of burial in the protein core or different types of secondary structure. This makes the UHS applicable for the prediction of trans-membrane spans from the proteins primary sequence only.

This scale is applicable as an unbiased average hydrophobicity value for an amino acid that is equally valid for both α-helical and β-strand multi-span membrane proteins, which is of high importance for computational protein structure prediction. Furthermore, it can be used in the early stages of a membrane protein structure determination project when no structural information is available. The overall and local stability of folded multi-span membrane proteins can be assessed as demonstrated for OmpA. It can also be used for the prediction of trans-membrane spans from genomic data. For this application we specifically derived a hydrophobicity scale only from mammalian proteins (Mammalian Hydrophobicity Scale - MHS) to be applicable to mammalian genomes or the human genome in particular. This scale is optimized for α-helical multi-span membrane proteins and reaches average accuracies of up to 83%.

In general, we observe a bias in many existing hydrophobicity scales when applied to folded, multi-span membrane proteins. This offset applies to both the reference point of the scale (which we chose to be multi-span membrane proteins) as well as the absolute size of the free energy values. These biases are imposed by the respective experimental setup and may not exist in other applications. It emphasizes the importance to carefully choose the hydrophobicity scale based on the given task.

The UHS scale was tested for predicting trans-membrane spans from primary sequence only. It was found that prediction improves when free energies are averaged over a window of 9-17 amino acids with a triangular weight giving the central amino acid the highest influence. For a two-state prediction scenario (classifying an amino acid as being either in the TM or SOL) it was found that in comparison to other hydrophobicity scales the UHS yields an average prediction accuracy of 73%. The scales of GES (71%) and Janin (70%) perform almost as well. For a three state scenario that includes a TR region the UHS performs at an accuracy of 57%. This is significantly better than the WW scale (50% correct classifications).

Application of the UHS scale to four proteins illustrates its ability to very accurately map the hydrophobicity of a certain residue within a folded protein. In particular, the scale distinguishes nicely between the core of the protein and functional sites and highlights the alternating hydrophobicity pattern seen in β-barrel proteins. The scale is therefore suitable as input for membrane protein secondary and tertiary structure prediction tools. This was demonstrated by the usage of the UHS for prediction of TM spans from the sequence only.

When predicting TM spans in these four proteins, the lengths and positions of the predicted α-helices agree well with the actual lengths and locations. For β-barrel proteins the prediction tool is less reliable because the alternating hydrophobicity pattern thwarts the effectiveness of the simple averaging procedure. This is a general observation for β-barrel proteins across the scales and does not imply that the UHS poorly describes the characteristics of β-barrel proteins. It rather emphasizes the fact that the type of window function is not optimal for the prediction of β-barrels.

Abbreviations

EW

Eisenberg & Weiss

GES

Goldman, Engelman & Steitz

HW

Hopp & Woods

KB

knowledge-based

KD

Kyte & Doolittle

MP

Membrane Protein

MHS

Mammalian Hydrophobicity Scale

NMR

Nuclear Magnetic Resonance

PDB

ProteinDataBank

PDBTM

ProteinDataBank for Trans-Membrane proteins

RMSD

Root Mean Square Deviation

SOL

soluble region

TM

trans-membrane region

TR

transition/interface region

UHS

Unified Hydrophobicity Scale