Traveling wave ion mobility spectrometry (TW IMS) is a new IMS method implemented in the Synapt IMS/mass spectrometry system (Waters). Despite its wide adoption, the foundations of TW IMS were only qualitatively understood and factors governing the ion transit time (the separation parameter) and resolution remained murky. Here we develop the theory of TW IMS using derivations and ion dynamics simulations. The key parameter is the ratio (c) of ion drift velocity at the steepest wave slope to wave speed. At low c, the ion transit velocity is proportional to the squares of mobility (K) and electric field intensity (E), as opposed to linear scaling in drift tube (DT) IMS and differential mobility analyzers. At higher c, the scaling deviates from quadratic in a way controlled by the waveform profile, becoming more gradual with the ideal triangular profile but first steeper and then more gradual for realistic profiles with variable E. At highest c, the transit velocity asymptotically approaches the wave speed. Unlike with DT IMS, the resolving power of TW IMS depends on mobility, scaling as K1/2 in the low-c limit and less at higher c. A nonlinear dependence of the transit time on mobility means that the true resolving power of TW IMS differs from that indicated by the spectrum. A near-optimum resolution is achievable over a ~300 - 400% range of mobilities. The major predicted trends are in agreement with TW IMS measurements for peptide ions as a function of mobility, wave amplitude, and gas pressure. The issues of proper TW IMS calibration and ion distortion by field heating are also discussed. The new quantitative understanding of TW IMS separations allows rational optimization of instrument design and operation, and improved spectral calibration.
Introduction
“Ion mobility spectrometry” (IMS)1 methods separate and characterize ions based on their gas-phase transport in electric fields. The combination of IMS with mass spectrometry (MS) dates back to 1960-s. It was used in physical and structural chemistry,1-4 and, more recently, in biological analyses to fractionate complex mixtures prior to the MS step.5-8 This transition was facilitated by introduction of several commercial IMS/MS systems since 2003. However, none employs the original drift tube (DT) IMS approach where axial field of constant intensity E pushes an ion through a gas-filled tube with velocity of
| (1) |
where coefficient K is mobility.1 Thus different species traverse the tube in different times.1-6 Early DT IMS systems had poor sensitivity because of low duty cycle (~1%): ions were injected into the tube in narrow pulses and, with no accumulation prior to IMS, most ions from continuous sources were lost. Though recent development of effective ion accumulation and multiplexing schemes has dramatically improved the duty cycle, it is still short of perfect.9,10
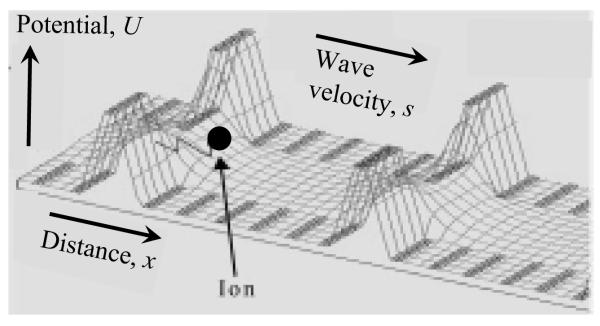
Instead, existing commercial IMS/MS systems exploit other IMS methods that permit high ion utilization: field asymmetric waveform IMS (FAIMS),7,8,11,12 differential mobility analysis (DMA),13 or traveling wave IMS (TW IMS).14,15 FAIMS sorts ions by the difference between values of K at high and low E, elicited using a periodic asymmetric field orthogonal to the ion path.11,12 In DMA, a fixed field pulls ions across a perpendicular gas flow and species angularly spread depending on the ratio of their v (and thus K) to flow velocity. In TW IMS, a sequence of symmetric potential waves continually propagating through a tube propels ions along with velocity dependent on K, and different species transit the tube in unequal times (Fig. 1). As filtering techniques, FAIMS and DMA process continuous ion beams and can provide good transmission for targeted species, but not in global analyses where the separation parameter must be scanned. In contrast, TW IMS disperses ion mixtures similarly to DT IMS, and multiple species can be measured simultaneously. As a dispersion method, TW IMS must also use pulsed ion injection and thus faces same duty cycle issues as DT IMS, requiring accumulation upfront for high ion utilization. Recently, TW IMS was coupled to orthogonal acceleration time-of-flight MS in Synapt HDMS15 (Waters, Manchester, UK). The ion dispersion capability and good sensitivity has made this platform attractive for practical analyses, and applications to structural biology16-19 and complex separations20,21 are expanding.
Fig. 1.
Traveling wave propelling ions in the Synapt system. Adapted from (K. Giles al., Applications of a travelling wave-based radio-frequency-only stacked ring ion guide, Rapid Commun. Mass Spectrom. 18, 2401), © 2004, with permission from John Wiley & Sons.
As DT IMS, DMA, and TW IMS are all based on K values,1,13,14 they are not orthogonal. However, since their mechanisms differ, the actual separation parameters and performance metrics (such as resolution and sensitivity) also differ and depend on K and instrument properties differently. One must know those dependences to deduce K values from observables and to perfect the instrument design and operation. The DT IMS and DMA separations have been studied via mathematical22,23 and numerical24,25 modeling of ion dynamics that accounts for diffusion and, to an extent, space-charge effects.23 That has enabled conversions of raw separation parameters (drift time in DT IMS and voltage in DMA) into mobility,1-6 validation and calibration of spectra using ions with established K, comparisons of data from different platforms, and comprehensive performance optimizations within hardware limitations.9,10 While the modeling of ion motion in DT IMS or DMA is simplified by their use of static electric fields, much more complex nonlinear dynamics of ions in a time-dependent field of FAIMS has been sufficiently grasped26 to guide the improvement of devices and operational schemes.27,28
Despite successful commercialization of TW IMS, its fundamentals have been understood only qualitatively. The dependence of transit time on ion mobility, though believed to not be linear as in DT IMS, was not elucidated. Hence K values could be extracted from TW IMS data only via empiric multipoint calibrations using ions of known mobility (determined by DT IMS or DMA),16,17 which limited the method utility and accuracy. The factors governing the resolving power have also remained obscure. Here we explore the TW IMS operation using first-principles derivations and numerical simulations, clarifying the relationship of separation performance to ion and instrument properties. This work enables outlining the limits of TW IMS technology and some avenues for its improvement.
Mathematical Description of TW IMS Operation
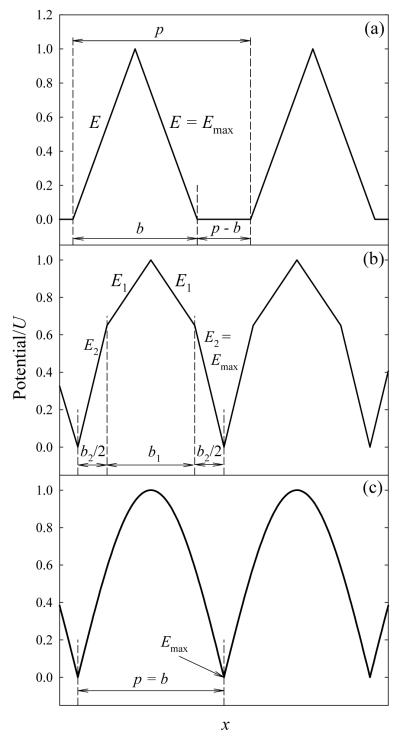
TW IMS has parallels to both FAIMS (use of a periodic waveform) and DT IMS (separation by absolute mobility). A wave comprising identical symmetric oscillations with peak potential U, maximum E of Emax, baseline width b, and wavelength p (Fig. 2a) is set up along a stacked ring ion guide (SRIG) by raising the voltages of selected electrodes spaced by fixed intervals, and is moved at speed s by switching those electrodes. In the Synapt, the voltage is raised on two adjacent rings spaced by five identical pairs,14,15 but other options are possible. The rings also carry alternating (rf) voltages that create a pseudopotential bottoming on the axis.14,29 The resulting ion focusing suppresses diffusion and Coulomb expansion, ensuring high transmission even for larger ion currents. This focusing is independent of the traveling wave and is same as in SRIGs without it (ion tunnels).29 Though some species are confined better than others, the focusing is radial and separation is not affected. As our concern here is with TW IMS as an ion separator, we ignore the focusing field and restrict the dynamics to axial coordinates.
Fig. 2.
Model traveling wave profiles: triangular (a), bitriangular (b), and half-sinusoidal (c). Characteristic parameters are labeled.
Propagating waves push all ions along, but the motion depends on c - the maximum v at the front relative to s. By eq (1):
| (2) |
This parameter is critical to TW IMS analyses: ions bob with only slight axial displacement as waves pass underneath if c << 1, but are “shoved” ahead of the lead wave if c > 1. In the intermediate case of c ≈ 1, ions “surf” the wave, traveling with mean velocity comparable to s but occasionally falling over the tops. For an analytical model in this section, we treat ion diffusion as independent from drift. Then the separation parameters depend only on the drift, while diffusion determines the ion packet width and thus the resolution. In the next section, the resulting formulas are compared to numerical simulations that combine drift and diffusion.
Triangular waveform
The simplest wave profile has a triangular potential with E = 2U/b at both edges (Fig. 2a). Species with c < 1 climb the front with relative velocity of (s − KE), reaching the crest in the time of
| (3) |
and slide down the rear with relative velocity of −(s + KE), falling to the baseline in
| (4) |
Then they rest awaiting the next wave for
| (5) |
The whole cycle lasts
| (6) |
and the net ion displacement over it equals
| (7) |
Hence the average ion velocity over the cycle is
| (8) |
and the transit time through TW IMS of length L equals
| (9) |
Thus, TW IMS exploits that ion residence times on the front and rear edges differ. As eq (9) contains K only as K2, the separation depends on K squared rather than linear K in DT IMS.
During field-free segments between the waves, ions are not separated but keep on diffusing. Hence the best separation calls for minimum field-free downtime. For immediately adjacent waves (p = b), eq (8) condenses to
| (10) |
Hence the net drift velocity in optimum TW IMS regime scales with mobility quadratically, rather than linearly in DT IMS by eq (1). Then eq (9) converts to
| (11) |
whereas the drift time in DT IMS is:1,30
| (12) |
Waveforms of varying field intensity
An electric field in space must be continuous, which precludes true triangular waveforms (with or without gaps). In reality, superposition of contributions from multiple electrodes produces smooth axial potential. The inevitable variation of field intensity E in a traveling wave fundamentally affects the separation properties.
For example, in a “bitriangular” profile with no gaps (Fig. 2b), each wave comprises two segments with unequal E values (E1 and E2, where E2 > E1) and arbitrary lengths (b1 and b2). Eqs (6) and (7) apply for any pair of rising and falling segments with constant E, including those in a waveform with varying E. The addition of resulting tC,1; tC,2 and d1; d2 quantities yields:
| (13) |
| (14) |
and the mean drift velocity is:
| (15) |
For E2 = E1 (i.e., a triangular profile), this expression reduces to eq (10). Otherwise, the and [or ] dependences are generally not quadratic. However, eq (15) condenses to:
| (16) |
in the limit of low-mobility ions (K << s/E2), and
| (17) |
for the most mobile species that can be analyzed (K = s/E2). The formulas for profiles featuring three or more E values are analogous.
While bitriangular waveforms help to clarify why variation of E results in non-quadratic dependences, realistic smooth waveforms are closer to a half-sinusoidal profile (Fig. 2c). For such gradually varying E(x) functions (where x is the axial coordinate), the summation is replaced by integration, leading to:
| (18) |
When K << s/Emax, eq (18) reduces to
| (19) |
This is a generalization of eq (8) with fixed E2 replaced by the average of E2 over the waveform.
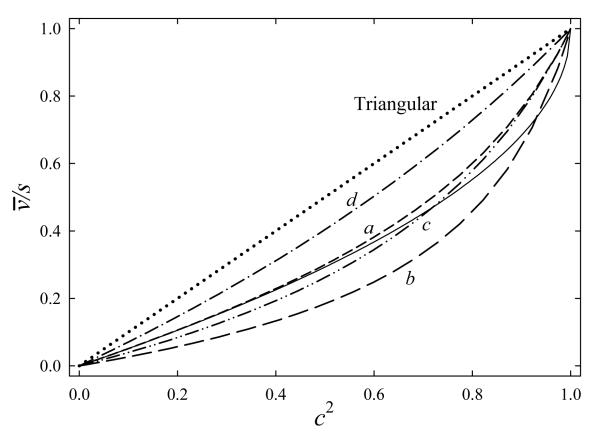
Hence, with any E(x), the drift velocity is proportional to the mean square of field intensity at lowest K, but to the square of maximum intensity at highest K. Thus v(K) graphs always curve up from a quadratic, increasingly so at higher K (Fig. 3). The deviation grows with increasing difference between the mean and maximum E2 values, i.e., with the expanding spread of field intensities in the wave.
Fig. 3.
Ion transit velocities in TW IMS calculated for the triangular profile (dotted line), bitriangular waveforms (dashed lines) with {b2/b1; E2/E1} ratios of {0.5; 2} (a); {0.25; 4} (b); {0.5; 4} (c), and {2; 4} (d), and half-sinusoidal profile (solid line). Note the horizontal scale in terms of c2.
Resolving power of TW IMS
Any analytical separation is characterized by resolving power (R): a method that can distinguish features with minimum relative difference of separation parameters equal to X has R ~1/X. We customarily define R as the separation parameter divided by the peak width at half maximum (w) that can be expressed in temporal or spatial variables. For the latter, w is the physical width of packets of identical ions at TW IMS exit and
| (20) |
Except at extreme ion currents where Coulomb repulsion dominates,31,32 the peaks in IMS methods primarily broaden due to ion diffusion1,22,26,28 and, with the diffusion coefficient30 D:
| (21) |
The diffusion separate from ion drift is thermal and, by the Einstein equation,30
| (22) |
where k is the Boltzmann constant, T is the gas temperature, z is the ion charge state, and e is the elementary charge. Combining eqs (18), (20), (21), and (22), one obtains:
| (23) |
For comparison, in DT IMS:1,30
| (24) |
Reflecting the universality of diffusional broadening, both eqs (23) and (24) are proportional to (z/T)1/2: gas cooling improves the resolution of DT IMS33,34 and ought to for TW IMS with any waveform. Unlike eq (24), eq (23) contains K: the resolving power becomes species-dependent.
For a triangular profile with gaps (Fig. 2a), eq (23) provides
| (25) |
As was expected, RTW for a given b maximizes at p = b. Then eq (25) simplifies to
| (26) |
Hence dropping the wave speed enhances resolution. However, we must have c < 1 for all ions involved and the optimum s slightly exceeds KhiE, where Khi is the highest K for species of interest. Substituting that into eq (26), we obtain:
| (27) |
Thus the separation power of TW IMS optimized for a set of species is sensitive to the spread rather than the absolute magnitude of their mobilities, with R reaching the maximum (Rmax) at K = Khi and decreasing for ions with lower K:
| (28) |
When c = 1, eq (27) is same as eq (24). However, U = Eb/2 and, setting n = L/b for the number of wave cycles in the guide at any moment, we may write eq (27) as
| (29) |
To compare, in DT IMS, where the drift voltage U equals EL:
| (30) |
Hence cumulative action of multiple waves in TW IMS improves the maximum resolution over that provided by DT IMS using same voltage, in proportion to n1/2. Therefore the resolving power of TW IMS at constant peak voltage scales as L1/2, unlike in DT IMS where the tube length is immaterial by eq (30). Similarly to RDT, the RTW value scales as U1/2 for any K. Thus separation can be improved by raising the wave amplitude at fixed wavelength. Equivalently, one can compress the wavelength for fixed amplitude, increasing the number of waves in the tube. Either way, the wave should be commensurately accelerated to maintain c < 1 for all ions. This process is limited by maximum E permitted by the electrical breakdown in gas35 or field heating that avoids isomerization or dissociation of ions of interest,36 as discussed below.
In the low-mobility limit where eq (19) applies, eq (26) is valid for any waveform if fixed E is replaced by the root-mean-square of E(x). This substitution does not work with eq (27) because, to separate ions, s must exceed KhiEmax. Instead:
| (31) |
Thus, at a given Emax, the triangular profile provides best resolution for all species. This reflects the resolving power rising at higher field intensity.
By eq (12), the drift times of species A and B in DT IMS relate as their inverse mobilities:
| (32) |
Thus ions with relative mobility difference of 1/R produce peaks with same td difference, and, by definition of R, can just be separated. In TW IMS with a triangular waveform, eq (11) leads to:
| (33) |
At a reasonable resolution, the magnitude of ΔK = K (B) − K (A) for just-separable species is much smaller than K(A) or K(B). Then we may expand eq (33) as:
| (34) |
Here the relative difference of transit times is twice that of mobilities, allowing separation of ions with mobility difference of 1/(2R): the effective resolving power REF is twice the apparent value by eq (20). In general, the difference equals the logarithmic derivative of :
| (35) |
Hence, with non-triangular waveforms out of the low-mobility limit where rises faster than K2 (Fig. 3), REF exceeds R by a factor of >2. The distinction between true and apparent resolving power [caused by nonlinearity of ] will prove crucial when considering the separation power of TW IMS and comparing it to that of DT IMS.
All above derivations for the resolving power of TW IMS assume the independence of diffusion and ion drift. For that, the diffusion must negligibly affect the residence times at wave edges given by eqs (3) and (4), i.e., the diffusional ion displacement during those times must be nil compared to that (with respect to the wave) due to electric field. As tF > tB, it suffices to meet this condition for the wave front. It is obviously feasible for c under some threshold cth when the wave rapidly passes the ions, but not for c just below 1 when ions substantially diffuse while slowly climbing the wave. Using eq (21) for the diffusional ion spread, we can quantify c < cth as
| (36) |
Substitution of eqs (3), (27), and (28) into eq (36) leads to
| (37) |
This derivation may undervalue the diffusion and thus the needed 1/c because (i) a large fraction of ions in a peak spreads by more than its width at half-maximum and (ii) diffusion skews the Gaussian profile of the peak in time domain, increasing mean tF and thus w. Still, eq (37) should suffice for an estimate given the flexibility of “>>” condition. With values of n ~20 (with L = 20 cm) and Rmax ~10 in Synapt, eq (37) requires (1/c − 1) >> 0.4. Then we can likely neglect diffusion when c < ~0.5, that is, the wave travels at least twice faster than ions drift at its slope. However, R maximizes at minimum s exceeding KhiEmax as we discussed, and engineering a slower wave is simpler. So it is important to quantify TW IMS performance at c > cth where the ion diffusion and drift are dynamically coupled. That is achieved using numerical simulations.
Simulations Incorporating Diffusion
The ion dynamics in TW IMS was modeled using a Fortran code resembling tested FAIMS simulations.26 Similar to SIMION,25 the trajectories for a representative ion ensemble are propagated through the device in finite real-time steps (Δt). Calculations start from defining the wave profile U(t, x), where t is time, and a set of ions with some K and x values. In each step (Δt), we find E at the location of each i-th ion (xi) as ∂U/∂x and translate the ion by
| (38) |
Then the ion is moved by diffusional displacement Δdi, picked randomly with the probability p given by the distribution for 1-D diffusion:26
| (39) |
The cycle is repeated until all ions exit (xi > L for all i), and their transit times are registered.
Simulations were performed for the triangular (Fig. 2a) and half-sinusoidal (Fig. 2c) profiles. Following the common conditions in TW IMS,14 we adopted L = 0.183 m, U = 2 V, s = 300 m/s, b = 5 mm, and the gas pressure of 0.5 Torr. For adequate waveform representation, Δt must be much smaller than the period of tC ≅ b/s, here ≅ 1.7 μs. Presently, we used Δt = 0.04 μs to provide >400 points over the cycle, and ensembles of 10,000 ions. Those values ensure good convergence under all conditions tried, but waveforms with shorter period may necessitate lower Δt. As the model includes no space charge, we employed a point-like initial ion distribution.
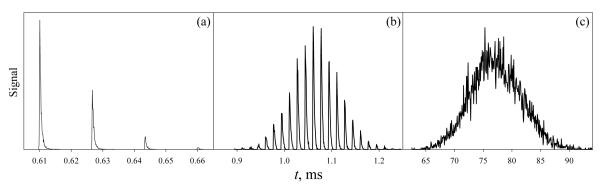
Typical results for species of low, intermediate, and high mobility are shown in Fig. 4. At high c values, most ions are shoved by the lead wave, with some falling over the crest and coming with the following wave(s), Fig. 4a. At somewhat lower c, the distribution of arriving ions remains discrete, but spread almost symmetrically over many successive waves (Fig. 4b). At yet lower c, the distribution assumes a continuous near-Gaussian shape, as in DT IMS (Fig. 4c).
Fig. 4.
Simulated arrival time distributions in TW IMS using a half-sinusoidal waveform for ions with c = 1.173 (a), 0.922 (b), and 0.126 (c). The spectra with triangular profile are similar.
To address the waveforms with variable E, we modify eq (2) to define average c for the average (rather than maximum) E:
| (40) |
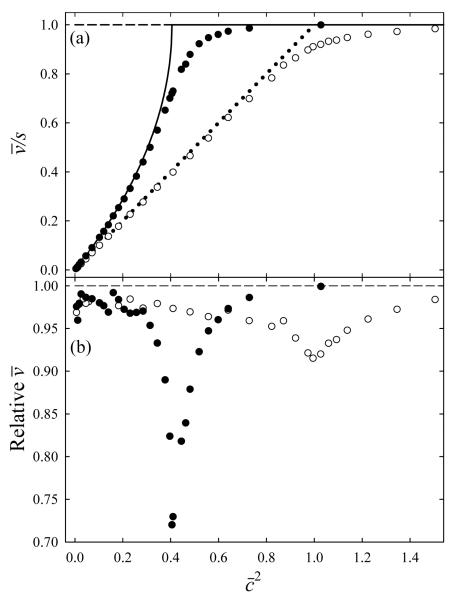
For a triangular waveform, . For the half-sinusoidal profile, c = 1 corresponds to c ≅ 0.64. This change for non-triangular U(x) does not affect the shapes of curves, but rescales them to lie above those for triangular U(x) once mobility exceeds the low-K limit of c << 1, Fig. 5a. In that limit, the mean ion transit velocity with any waveform equals that by eq (18), Fig. 5a. With increasing mobility, the velocity falls progressively short of the analytical value and asymptotically approaches the wave speed. In effect, the diffusion rounds the break of theoretical curves at c = 1. This provides some separation for species with c slightly above 1, when, in the analytical treatment, all ions are indiscriminately shoved by the wave. The greatest deviation of simulated velocities from eq (18) is at that point and can be large (up to ~30% for the half-sinusoidal profile), but rapidly decreases for lower or higher c values (Fig. 5b). This is the case because ion transit through TW IMS is materially affected by diffusion only when its velocity is close to that of ion drift with respect to the wave, i.e., at s ≈ KEmax. As estimated from eq (37), for c < ~0.5 the deviations are negligible and simple formulas for are accurate.
Fig. 5.
Ion transit velocities calculated with diffusion ignored (lines) and included (symbols) for the triangular waveform (dashed line and empty symbols) and half-sinusoidal profile (solid line and filled symbols). We show the velocity relative to the wave speed (a) and relative velocities with and without diffusion (b). The horizontal scale is in terms of .
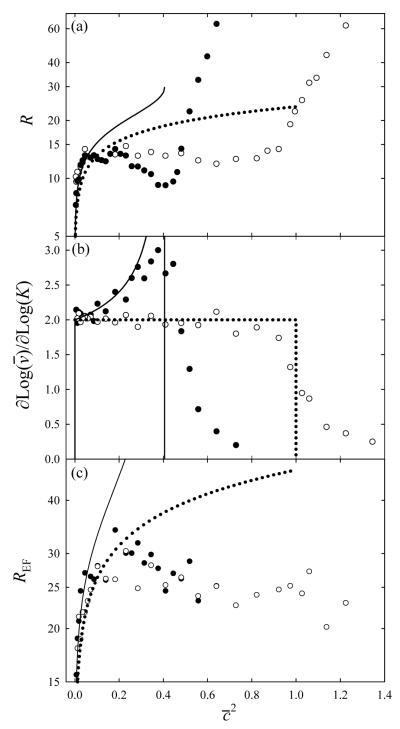
In the low-mobility limit (Fig. 4c), the resolving power (R) simulated for any waveform is close to eq (23), Fig. 6a. However, R drops below the a priori curve at higher K as the diffusion and wave impacts get coupled, spreading ions beyond simple diffusional broadening (Fig. 4b). For either triangular or half-sinusoidal U(x), the effect becomes notable at c ≈ 0.4, which is also close to the estimate from eq (37). Then the value of R somewhat decreases with c increasing up to ≈ 1, where the apparent R rapidly rises (Fig. 6a). The latter reflects the arrival time spectrum collapsing into a single peak coming with the lead wave (Fig. 4a), with R approaching infinity. Of course, the real resolution does not increase to infinity. As seen in Fig. 6b, the logarithmic derivative of simulated trends close to analytical formulas, with diffusion smoothing the discontinuity at c = 1. A sharp drop of this derivative near c = 1 offsets the rise of R, and the effective resolving power by eq (35) changes little (Fig. 6c). In the end, REF for either waveform profile reaches a maximum of ~30 at and gradually decreases to ~25 at highest c. The REF values for both profiles appear to maximize at equal , in contrast to other variables that depend primarily on c, as discussed above. Understanding this point is left to future work.
Fig. 6.
Calculated characteristics of TW IMS resolution: (a) apparent resolving power, (b) logarithmic derivative of , and (c) effective resolving power. The resolving power in (a, c) is on the logarithmic scale, other nomenclature follows Fig. 5.
A moderate variation of REF over the c ≈ 0.25 - 1 interval (Fig. 6c) provides >80% of the maximum resolution for species with mobilities ranging within a factor of ~4, and the whole range can be shifted arbitrarily by control of the wave velocity and/or amplitude according to eq (2). This range width suffices for many practical analyses: for example, the mobilities vary within factors of ~2.5 for tryptic peptide ions generated by electrospray ionization (ESI)37 or matrix-assisted laser desorption ionization (MALDI),38 ~3 for electrosprayed combinatorial peptide libraries,39 and ~5 for a more diverse set comprising peptide, nucleotide, and lipid ions extracted from tissues using MALDI.40,41 However, as the function substantially deviates from quadratic above c ≈ 0.5 (Fig. 5b), both near-optimum resolution and simple scaling can be assured only over a tighter range of c ≈ 0.25 − 0.5. This allows varying K within ~2 times, which is enough for some applications such as explosive detection42 but too little for many others. Hence achieving reasonable resolution while measuring absolute ion mobilities over a broad range requires deducing the form of beyond the low-mobility limit using simulations or calibrations such as performed in some TW IMS studies.16
These simulations have assumed continuous wave travel. In Synapt, the voltages on electrodes are switched abruptly and the wave moves in steps. The effects of such discretization will be explored in the future but expected to be limited, as the potential near the tube axis is smoothened by superposition of voltages from multiple electrodes.
Comparisons with Experiment
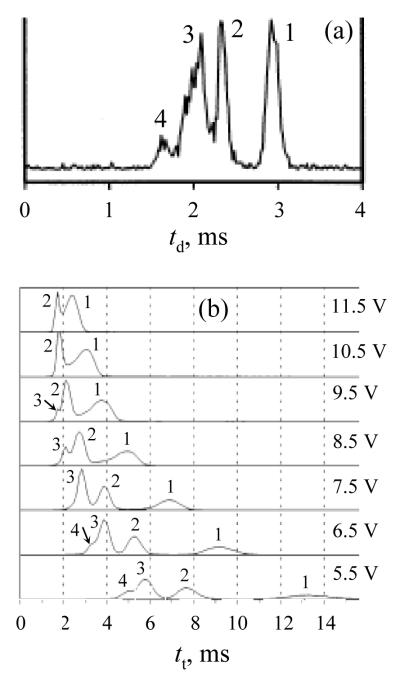
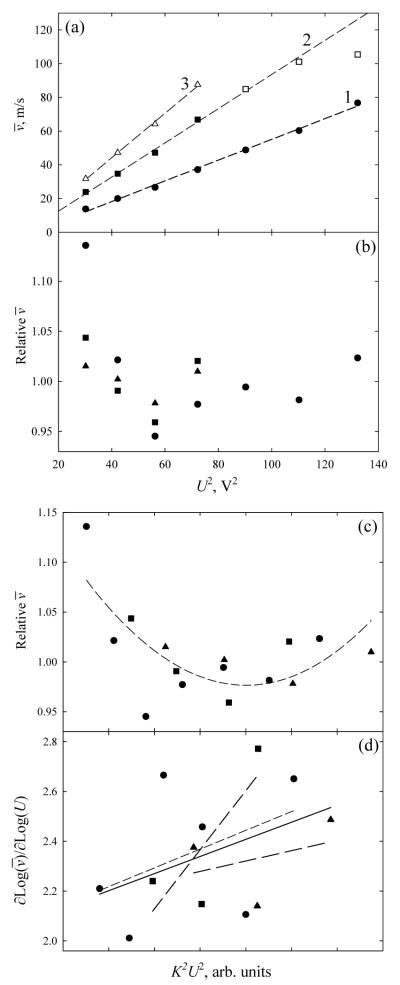
Present modeling may be compared with experiment using the data14 for multimers of nonapeptide bradykinin (Bk) - a common model peptide in biophysics and biological MS. ESI of concentrated peptide solutions usually produces monomers and non-covalently bound oligomers.43 For n = 1 - 4, (H+Bk)n ions with m/z = 1061 have been resolved, at least partly, by DT IMS in He buffer (Fig. 7a) and TW IMS in Ar (Fig. 7b). For all those species, the measured transit velocities in TW IMS scale closely to the wave amplitude squared (Fig. 8a), which, for any given waveform, means the quadratic dependence on E stated in eq (10). This allows extracting the relative mobilities of observed ions from the ratios of slopes of lines:
| (41) |
For n = 4, the peak was resolved at one U value only, and the slope cannot be determined. For n = 2 and 3, the resulting values (relative to K for n = 1) are 1.28 and 1.46, respectively. This is in excellent agreement with the values of 1.26 and 1.46 measured directly using DT IMS (for peak centroids in Fig. 7a), especially as (i) DT IMS and TW IMS data are in different gases and (ii) geometries and thus mobilities of Bk oligomers somewhat depend on the solution and ESI conditions.43 (In fact, the widths of features in DT IMS indicate that many unresolved structures are virtually always present.43) Therefore, the ion transit times in TW IMS are approximately proportional to the inverse square of both wave amplitude and ion mobility, in agreement with present theory in the low-mobility limit.
Fig. 7.
Ion mobility spectra for (H+Bradykinin)n ions obtained using DT IMS in He gas (a) and TW IMS in Ar gas as a function of wave amplitude U (b). The values of n for all peaks are labeled. Panel (a) is reprinted with adaptation from (A. E. Counterman et al., High-order structure and dissociation of gaseous peptide aggregates that are hidden in mass spectra, J. Am. Soc. Mass Spectrom. 9, 743), © 1998, with permission from Elsevier. Panel (b) is adapted from (K. Giles al., Applications of a travelling wave-based radio-frequency-only stacked ring ion guide, Rapid Commun. Mass Spectrom. 18, 2401), © 2004, with permission from John Wiley & Sons.
Fig. 8.
Analysis of TW IMS data in Fig. 7b: (a) mean transit velocities for n = 1 (triangles), 2 (squares), and 3 (circles) as a function of wave amplitude, with linear regressions for each curve; (b, c) deviations of functions in (a) from linear regressions; (d) logarithmic derivatives of the functions in (a), with linear regressions for each (dashed lines) and for all data (solid line). The horizontal scales are quadratic, in terms of U2 in (a, b) and (KU)2 in (c, d). In (a) for n = 2, solid squares and the regression are for the data at U ≤ 8.5 V, blank squares are for U ≥ 9.5 V.
We have discussed that the real waveform is never exactly triangular and the v(U 2) curves must be concave. This is confirmed by the deviations of measured points from linear regressions (Fig. 8b). As those deviations should be a function of the parameter c determined by KE via eq (2) and different species have unequal mobility, the values of ought to coincide when plotted versus (KU)2 rather than U2. Indeed, the relative deviations of curves for n = 1 - 3 from linearity seem to overlap on a concave trend (Fig. 8c). This proves that the dependence of on KU and thus KE is somewhat stronger than quadratic, as we predicted for ions of moderate mobility. The logarithmic derivative of shows that v scales as E to the power of ~2.0 - 2.8, with the exponent generally increasing at higher KE (Fig. 8d). This behavior is consistent with theory (Fig. 6b), though no quantitative agreement can be expected as the experimental U(x) differs from the half-sinusoidal profile in the model.
Another important parameter of TW IMS is the gas pressure, P. In the low-field regime, the ion mobility scales as1,30 1/P:
| (42) |
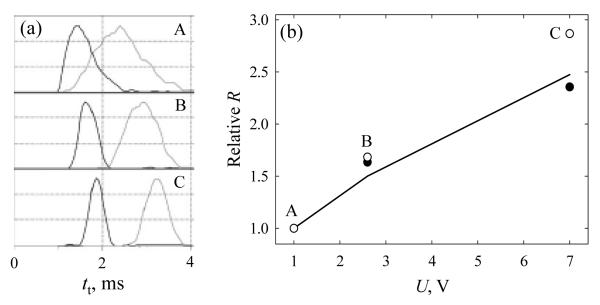
where N is the number density of gas molecules, N0 is the Loschmidt number - the value of N at standard temperature (T0 = 273 K) and pressure (P0 = 1 Atm), and K0 is the mobility under those conditions (the “reduced mobility”). Hence, adjusting P in proportion to U should keep constant the value of KE and, by eq (18), the mean ion velocity with any waveform. This is analogous to DT IMS, where varying the pressure and drift voltage in proportion does not affect the drift time.1 This conclusion can be verified by the measurements for peptides gramicidin S 2+ (m/z = 571) and leucine enkephalin (m/z = 556) over P = 0.025 - 0.2 mbar (Fig. 9a). When U was varied from 1 to 7 V roughly in proportion to P, the transit times for both species changed little, as expected. The shifts of both peaks to longer times between panels A and C are due to a mismatch between the variations of 7 times for U and 8 times for P. That should increase tt by a factor of (8/7)2 ≅ 1.31 or slightly more considering the super-quadratic scaling of for non-triangular waveforms, in agreement with the observed increase of ~30 - 40% (Fig. 9a).
Fig. 9.
Resolving power of TW IMS: (a) spectra for gramicidin S 2+ (left peak) and leucine enkephalin 1+ (right peak) obtained using the wave amplitudes and Ar gas pressures of 1 V and 0.025 mbar (panel A), 2.6 V and 0.075 mbar (B), and 7 V and 0.2 mbar (C); (b) resolving power in panels B and C relative to the values in panel A — measured (solid circles for gramicidin S, blank circles for leucine enkephalin) and calculated (line). Panels in (a) are adapted from (K. Giles al., Applications of a travelling wave-based radio-frequency-only stacked ring ion guide, Rapid Commun. Mass Spectrom. 18, 2401), © 2004, with permission from John Wiley & Sons.
These data also allow testing the calculations for TW IMS resolution. By eq (26), at fixed KE the resolving power of TW IMS using a triangular waveform scales as E1/2 (or P1/2). Then R would increase by 2.7 - 2.8 times between panels A and C in Fig. 9a. This is very close to the measurements for both species (Fig. 9b), even though the actual waveform is not triangular. Thus the present TW IMS model adequately describes both the transit time and the resolving power.
Proper TW IMS Calibration Using Mobility Values
In the absence of a physical model for TW IMS, the mobilities of resolved ions were extracted via empiric calibration using a set of species with mobilities measured by DT IMS or DMA.16 This approach is valid as long as one does not extrapolate the calibration significantly beyond the measured range, which is risky for an unknown nonlinear function.
In some studies,16 the calibration results are discussed in terms of the cross sections (Ω) rather than ion mobilities. The two quantities are related by the Mason-Schamp law:30
| (43) |
where m is the ion mass and M is the gas molecule mass. Hence the mobility scales as z/Ω: at a fixed z, the cross section uniquely defines the mobility and the two presentations are equivalent. That is not true when some ions involved (in the calibration and/or measured sets) have different z, such as protein ions produced by ESI.16
In particular, the mean z for compact protein ions generated by ESI under mild (“non-denaturing”) conditions scales roughly44 as m1/2. As the cross sections of near-spherical macro ions scale as ~(volume)2/3 or m2/3, their mobilities scale as m−1/6: the K0 values for ESI-derived protein ions depend on their mass only weakly45 and, in N2 at room temperature, cluster around 1 cm2/(V s) though the cross sections span a broad range.45-50 Further, the mobilities for ions of a particular protein depend on z much weaker than linearly as the geometries for higher z tend to be more unfolded (elongated) by the Coulomb repulsion between protonated sites, and thus have greater cross sections.46-50 For instance, the mobilities of lysozyme 6+, cytochrome c (z = 7 - 10), and myoglobin (z = 11 - 16) ions used for TW IMS calibration16 are within 30% of each other even though their cross sections differ by ~2.5 times, ranging from ~1300 to ~3300 A2 in He gas.46-50 In the result, a calibration based on even an extensive set of protein ions produced by ESI actually covers only a narrow range of K values and may be flawed for ions of much smaller or larger mobility. A positive correlation between Ω and z that compresses the mobility range for a set of ions with different z is not limited to proteins or ESI sources, highlighting the importance of presenting and testing TW IMS calibration in terms of mobilities and not cross sections.
Heating and Distortion of Ions by High Electric Field in TW IMS
The resolving power at fixed pressure should be proportional to E and thus U by eq (26), but the measured resolution for features in Fig. 7a decreases at higher U. This likely reflects the breakdown of Bk oligomers in TW IMS by collisional heating at high electric field, which partially fills the gaps between discrete peaks in IMS spectra by drift times corresponding to the weighted averages of values for interconverting species.51 Indeed, the (H+Bk)4 feature decreases and then disappears between U of 5.5 and 7.5 V, (H+Bk)3 follows it between 7.5 and 10.5 V, and finally (H+Bk)2 drops relative to H+Bk between 10.5 and 11.5 V. Such stepwise dissociation with increasing ion temperature (TI) is standard, as the energy needed to remove a neutral from a homomolecular ion-molecule cluster normally falls for larger assemblies. Also, larger (H+Bk)n species get hotter at equal U because of their greater mobility, as quantified below.
While the voltages of ~5 - 10 V seem small, the heating depends on the field intensity relative to the gas pressure:30
| (44) |
Low pressure in Synapt results in strong heating even at moderate E. To gauge it for Bk oligomers, we need to estimate their mobility in Ar gas. The mobilities of peptide ions such as hexaglycine (360 Da), kemptide (773 Da), or neurotensin (1674 Da) in argon are ~0.28 - 0.29 times those in helium,52,53 reflecting the mass factor of [M(He)/M(Ar)]1/2 ~0.32 arising from eq (43) for m >> M and that Ar atoms are larger than He atoms. Hence, as H+Bk at room temperature has K ≅ 2.2 cm2/(V s) in helium,43 the value in argon should be ≅ 0.6 cm2/(V s) and, based on the relative mobilities for (H+Bk)n (Fig. 7a), we would have K ≅ 0.8, 0.9, and 1.1 cm2/(V s) for n = 2, 3, and 4, respectively. With K0 = 0.9 cm2/(V s), the values of ΔT for b = 5 mm and P = 0.2 mbar (used in experiments of Fig. 7a) would be ~1600 K for the lowest U = 5.5 V and as high as ~7000 K for U = 11.5 V. However, the wave amplitude at TW IMS axis is smaller than the quoted U values at the electrodes, and ΔT is much lower.14 For realistic14 U = 2 V, eq (44) produces ΔT ~210 K, not inconsistent with the extent of declustering in Fig. 7a. While accurate quantification of ΔT in TW IMS requires modeling of axial U(t) in specific electrode geometries that is beyond the scope of this work, the field heating of common ion species in TW IMS is clearly substantial and may suffice for their destruction.
As the value of E in TW IMS varies from zero to some maximum, it matters whether ion transformations are governed by maximum or average ΔT. This issue is consequential because ΔT is proportional to E2 by eq (44), and the maximum ΔT may exceed the average by 4 times or more, depending on the waveform profile.45 While there are no relevant data for TW IMS, the issue has been explored for FAIMS where E also periodically varies from zero to a maximum. Measurements for protein ions using FAIMS/IMS36 and temperature-controlled FAIMS45 systems show that structural transitions in FAIMS are largely determined by the maximum E value. Same should apply to TW IMS, especially as the typical duration of near-maximum E is normally much greater in TW IMS (with a waveform period of tF + tB ~ b/s ~10 s) than in FAIMS where that period is ~1 s. As in FAIMS,36,45 such field heating may materially distort the geometries of macro ions and destroy their non-covalent complexes. One should bear that in mind when using TW IMS to characterize the tertiary or quaternary protein structure.
Conclusions
We have explored the fundamentals of traveling wave ion mobility spectrometry (TW IMS) using a priori theory and numerical simulations of ion dynamics. As in conventional drift tube (DT) IMS, in TW IMS electric field moves distinct ion species through gas with unequal mean velocity (), dispersing them in space by mobility, K. However, the dependence of on K and the field intensity E is linear in DT IMS but nonlinear in TW IMS. If thermal ion diffusion is ignored, the function can be derived analytically for TW IMS employing any waveform profile. The dependence of on K and E is quadratic for the ideal triangular waveform with fixed field intensity E. For realistic profiles with variable E, the dependence is quadratic in the limit of low KE (where KE is much smaller than the wave velocity, s) but becomes progressively stronger with increasing KE. In any case, v cannot exceed s, limiting the maximum K for separable species to s/Emax, where Emax is E at the steepest wave slope. Simulations show that ion diffusion reduces at higher K such that approaches s asymptotically rather than abruptly. This allows some separation of species with mobility slightly exceeding s/Emax.
The characteristics of TW IMS resolution also differ from those in DT IMS. First, the apparent resolving power (R) obtained from arrival time distributions depends on mobility, whereas DT IMS provides constant R for ions of any given charge state.1 In TW IMS, R in the low-KE limit scales as the square root of mobility, regardless of waveform. With increasing K, the value of R falls below that trend, maximizes at ≈ 0.5 s/Emax, then somewhat decreases, and finally rises rapidly when K approaches s/Emax. Second, a nonlinear dependence of the drift time on mobility in TW IMS using any waveform means that the effective resolving power (REF) differs from formal R by a factor equal to the logarithmic derivative of function (that is unity in DT IMS). This raises REF above R, typically by ~2 - 3 times, except for highest K near s/Emax where that derivative falls below 1 and REF < R. In the result, the effective resolving power of TW IMS still scales as K1/2 in the low-KE limit, but plateaus at K ≈ 0.4 s/Emax and remains roughly level for higher K as the dependences of R and derivative on K largely cancel. This allows TW IMS to provide near-optimum resolution within a mobility range of ~300 - 400%. However, utilizing most of that range requires leaving the low-KE limit where the ion transit time is a quadratic function of K.
The calculated dependences of transit time and resolution in TW IMS on the ion mobility and instrument parameters agree with the measurements for peptides and their complexes. As predicted by simulations for practical waveform profiles, the scaling of transit times for bradykinin monomers, dimers, and trimers with wave amplitude (U) varies from 1/U2 at low KE to ~1/U3 at high KE. The model also well describes the dependence of TW IMS separations on mobility, as is evidenced by comparisons with (ii) separation properties for bradykinin oligomers and other peptide ions of known mobility and (ii) transit times depending on the gas pressure. The computed evolution of resolving power as a function of both pressure and wave amplitude is consistent with experiment, as well.
Low gas pressure in TW IMS means strong fields in E/N terms and thus substantial heating of ions. This may cause fragmentation or distortion of macromolecular structures, complicating their detection and characterization.
The quantitative understanding of TW IMS fundamentals developed in this work provides the basis for rational optimization of instrument design and operation, and for the more accurate and reliable data calibration that is needed for ion structure characterization using TW IMS.
Acknowledgments
Our understanding of TW IMS and its implementation in Synapt has benefited from discussions with Drs. Keqi Tang, Michael Belov, and Aleksey Tolmachev (PNNL), Kevin Giles (Waters), and Brandon Ruotolo (Cambridge), and Professors Juan de la Mora (Yale), John McLean (Vanderbilt), James Scrivens (Warwick), and Michael Bowers (UC Santa Barbara). We also thank Dr. Giles for providing his published TW IMS data. This work was supported by the Battelle Internal Research and Development program and the NIH National Center for Research Resources, and performed in the Environmental Molecular Sciences Laboratory located at PNNL.
References
- 1.Eiceman GA, Karpas Z. Ion Mobility Spectrometry. CRC Press; Boca Raton: 2004. [Google Scholar]
- 2.Hill HH, Siems WF, Louis RH, McMinn DG. Anal. Chem. 1990;62:A1201. doi: 10.1021/ac00222a001. [DOI] [PubMed] [Google Scholar]
- 3.Hoaglund-Hyzer CS, Counterman AE, Clemmer DE. Chem. Rev. 1999;99:3037. doi: 10.1021/cr980139g. [DOI] [PubMed] [Google Scholar]
- 4.Shvartsburg AA, Hudgins RR, Dugourd P, Jarrold MF. Chem. Soc. Rev. 2001;30:26. [Google Scholar]
- 5.Taraszka JA, Gao X, Valentine SJ, Sowell RA, Koeniger SL, Miller DF, Kaufman TC, Clemmer DE. J. Proteome Res. 2005;4:1238. doi: 10.1021/pr050037o. [DOI] [PubMed] [Google Scholar]
- 6.Valentine SJ, Plasencia MD, Liu X, Krishnan M, Naylor S, Udseth HR, Smith RD, Clemmer DE. J. Proteome Res. 2006;5:2977. doi: 10.1021/pr060232i. [DOI] [PubMed] [Google Scholar]
- 7.Kapron J, Wu J, Mauriala T, Clark P, Purves RW, Bateman KP. Rapid Commun. Mass Spectrom. 2006;20:1504. doi: 10.1002/rcm.2505. [DOI] [PubMed] [Google Scholar]
- 8.Wu ST, Xia YQ, Jemal M. Rapid Commun. Mass Spectrom. 2007;21:3667. doi: 10.1002/rcm.3264. [DOI] [PubMed] [Google Scholar]
- 9.Tang K, Shvartsburg AA, Lee H-N, Prior DC, Buschbach MA, Li F, Tolmachev AV, Anderson GA, Smith RD. Anal. Chem. 2005;77:3330. doi: 10.1021/ac048315a. [DOI] [PMC free article] [PubMed] [Google Scholar]
- 10.Belov ME, Buschbach MA, Prior DC, Tang K, Smith RD. Anal. Chem. 2007;79:2451. doi: 10.1021/ac0617316. [DOI] [PMC free article] [PubMed] [Google Scholar]
- 11.Guevremont R. J. Chromatogr. A. 2004;1058:3. [PubMed] [Google Scholar]
- 12.Barnett DA, Belford M, Dunyach JJ, Purves RW. J. Am. Soc. Mass Spectrom. 2007;18:1653. doi: 10.1016/j.jasms.2007.06.009. [DOI] [PubMed] [Google Scholar]
- 13.de la Mora JF, Ude S, Thomson BA. Biotechnol. J. 2006;1:988. doi: 10.1002/biot.200600070. [DOI] [PubMed] [Google Scholar]
- 14.Giles K, Pringle SD, Worthington KR, Little D, Wildgoose JL, Bateman RH. Rapid Commun. Mass Spectrom. 2004;18:2401. doi: 10.1002/rcm.1641. [DOI] [PubMed] [Google Scholar]
- 15.Pringle SD, Giles K, Wildgoose JL, Williams JP, Slade SE, Thalassinos K, Bateman RH, Bowers MT, Scrivens JH. Int. J. Mass Spectrom. 2007;261:1. [Google Scholar]
- 16.Ruotolo B, Giles K, Campuzano I, Sandercock AM, Bateman RH, Robinson CV. Science. 2005;310:1658. doi: 10.1126/science.1120177. [DOI] [PubMed] [Google Scholar]
- 17.Ruotolo BT, Hyung SJ, Robinson PM, Giles K, Bateman RH, Robinson CV. Angew. Chem. Int. Ed. 2007;46:8001. doi: 10.1002/anie.200702161. [DOI] [PubMed] [Google Scholar]
- 18.Smith DP, Giles K, Bateman RH, Radford SE, Ashcroft AE. J. Am. Soc. Mass Spectrom. 2007;18:2180. doi: 10.1016/j.jasms.2007.09.017. [DOI] [PMC free article] [PubMed] [Google Scholar]
- 19.Riba - Garcia I, Giles K, Bateman RH, Gaskell SJ. J. Am. Soc. Mass Spectrom. 2008;19:609. doi: 10.1016/j.jasms.2008.01.005. [DOI] [PubMed] [Google Scholar]
- 20.Vakhrushev SY, Langridge J, Campuzano I, Hughes C, Peter-Katalinic J. Anal. Chem. 2008;80:2506. doi: 10.1021/ac7023443. [DOI] [PubMed] [Google Scholar]
- 21.Bagal D, Zhang H, Schnier PD. Anal. Chem. 2008;80:2408. doi: 10.1021/ac7020163. [DOI] [PubMed] [Google Scholar]
- 22.Revercomb HE, Mason EA. Anal. Chem. 1975;47:970. [Google Scholar]
- 23.Spangler GE, Collins CI. Anal. Chem. 1975;47:403. [Google Scholar]
- 24.Gillig KJ, Ruotolo BT, Stone EG, Russell DH. Int. J. Mass Spectrom. 2004;239:43. [Google Scholar]
- 25.Dahl DA, McJunkin TR, Scott JR. Int. J. Mass Spectrom. 2007;266:156. [Google Scholar]
- 26.Shvartsburg AA, Tang K, Smith RD. J. Am. Soc. Mass Spectrom. 2004;15:1487. doi: 10.1016/j.jasms.2004.06.018. [DOI] [PubMed] [Google Scholar]
- 27.Shvartsburg AA, Tang K, Smith RD. Anal. Chem. 2006;78:3706. doi: 10.1021/ac052020v. [DOI] [PMC free article] [PubMed] [Google Scholar]
- 28.Shvartsburg AA, Smith RD. J. Am. Soc. Mass Spectrom. 2007;18:1672. doi: 10.1016/j.jasms.2007.06.013. [DOI] [PubMed] [Google Scholar]
- 29.Tolmachev AV, Kim T, Udseth HR, Smith RD, Bailey TH, Futrell JH. Int. J. Mass Spectrom. 2000;203:31. [Google Scholar]
- 30.McDaniel EW, Mason EA. Transport Properties of Ions in Gases. Wiley; NY: 1988. [Google Scholar]
- 31.Spangler GE. Anal. Chem. 1992;64:1312. [Google Scholar]
- 32.Xu J, Whitten WB, Ramsey JM. Anal. Chem. 2000;72:5787. doi: 10.1021/ac0005464. [DOI] [PubMed] [Google Scholar]
- 33.Wyttenbach T, von Helden G, Bowers MT. J. Am. Chem. Soc. 1996;118:8355. [Google Scholar]
- 34.Shvartsburg AA, Jarrold MF. Phys. Rev. A. 1999;60:1235. [Google Scholar]
- 35.Meek JM, Craggs JD. Electrical Breakdown of Gases. Wiley; NY: 1978. [Google Scholar]
- 36.Shvartsburg AA, Li F, Tang K, Smith RD. Anal. Chem. 2007;79:1523. doi: 10.1021/ac061306c. [DOI] [PubMed] [Google Scholar]
- 37.Taraszka JA, Kurulugama R, Sowell R, Valentine SJ, Koeniger SL, Arnold RJ, Miller DF, Kaufman TC, Clemmer DE. J. Proteome Res. 2005;4:1223. doi: 10.1021/pr050038g. [DOI] [PubMed] [Google Scholar]
- 38.Ruotolo BT, Gillig KJ, Woods AS, Egan TF, Ugarov MV, Schultz JA, Russell DH. Anal. Chem. 2004;76:6727. doi: 10.1021/ac0498009. [DOI] [PubMed] [Google Scholar]
- 39.Hilderbrand AE, Myung S, Barnes C. A. Srebalus, Clemmer DE. J. Am. Soc. Mass Spectrom. 2003;14:1424. doi: 10.1016/j.jasms.2003.08.002. [DOI] [PubMed] [Google Scholar]
- 40.Jackson SN, Wang H-YJ, Woods AS, Ugarov M, Egan T, Schultz JA. J. Am. Soc. Mass Spectrom. 2005;16:133. doi: 10.1016/j.jasms.2004.10.002. [DOI] [PubMed] [Google Scholar]
- 41.Tempez A, Ugarov M, Egan T, Schultz JA, Novikov A, Della-Negra S, Lebeyec Y, Pautrat M, Caroff M, Smentkowski VS, Wang H-YJ, Jackson SN, Woods AS. J. Proteome Res. 2005;4:540. doi: 10.1021/pr0497879. [DOI] [PubMed] [Google Scholar]
- 42.Steiner WE, Clowers BH, Matz LM, Siems WF, Hill HH. Anal. Chem. 2002;74:4343. doi: 10.1021/ac025687f. [DOI] [PubMed] [Google Scholar]
- 43.Counterman AE, Valentine SJ, Srebalus CA, Henderson SC, Hoaglund CS, Clemmer DE. J. Am. Soc. Mass Spectrom. 1998;9:743. doi: 10.1016/S1044-0305(98)00052-X. [DOI] [PubMed] [Google Scholar]
- 44.De la Mora JF. Anal. Chim. Acta. 2000;406:93. [Google Scholar]
- 45.Robinson EW, Shvartsburg AA, Tang K, Smith RD. Anal. Chem. 2008;80:7508. doi: 10.1021/ac800655d. [DOI] [PMC free article] [PubMed] [Google Scholar]
- 46.Valentine SJ, Counterman AE, Clemmer DE. J. Am. Soc. Mass Spectrom. 1997;8:954. doi: 10.1016/S1044-0305(99)00079-3. [DOI] [PubMed] [Google Scholar]
- 47.Valentine SJ, Anderson SJ, Ellington AE, Clemmer DE. J. Phys. Chem. B. 1997;101:3891. [Google Scholar]
- 48.Shelimov KB, Clemmer DE, Hudgins RR, Jarrold MF. J. Am. Chem. Soc. 1997;119:2240. [Google Scholar]
- 49.Shelimov KB, Jarrold MF. J. Am. Chem. Soc. 1997;119:2987. [Google Scholar]
- 50.Shvartsburg AA, Li F, Tang K, Smith RD. Anal. Chem. 2006;78:3304. doi: 10.1021/ac060283z. [DOI] [PubMed] [Google Scholar]
- 51.Hudgins RR, Dugourd Ph., Tenenbaum JM, Jarrold MF. Phys. Rev. Lett. 1997;78:4213. [Google Scholar]
- 52.Beegle LW, Kanik I, Matz L, Hill HH. Int. J. Mass Spectrom. 2002;216:257. doi: 10.1016/S1044-0305(01)00366-X. [DOI] [PubMed] [Google Scholar]
- 53.Hill HH, Hill CH, Asbury GR, Wu C, Matz LM, Ichiye T. Int. J. Mass Spectrom. 2002;219:23. [Google Scholar]